剪切和扭转应力1
紧固螺栓等效应力计算公式
紧固螺栓等效应力计算公式在机械设计和工程中，紧固螺栓是一种常用的连接元件，用于连接机械零件和构件。
在实际工程中，螺栓连接的可靠性和安全性是非常重要的，因此需要对螺栓的等效应力进行计算和分析。
本文将介绍紧固螺栓等效应力的计算公式及其应用。
紧固螺栓的等效应力是指在螺栓连接中，由于外载荷和预紧力的作用，螺栓所受到的综合应力状态。
在计算螺栓的等效应力时，需要考虑螺栓的拉伸、剪切和扭转等多种应力形式，因此需要采用适当的计算公式进行综合计算。
首先，我们来看一下螺栓的拉伸应力计算公式。
螺栓在受到外载荷作用时，会产生拉伸应力，其计算公式为：σt = F/A。
其中，σt为螺栓的拉伸应力，F为外载荷，A为螺栓的截面积。
在实际工程中，螺栓的截面积可以通过螺栓的直径和材料的抗拉强度来计算。
接下来，我们来看一下螺栓的剪切应力计算公式。
螺栓在受到外载荷作用时，会产生剪切应力，其计算公式为：τ = F/A。
其中，τ为螺栓的剪切应力，F为外载荷，A为螺栓的截面积。
在实际工程中，螺栓的截面积可以通过螺栓的直径和材料的抗剪强度来计算。
此外，螺栓在受到外载荷作用时，还会产生扭转应力，其计算公式为：τ = T/J。
其中，τ为螺栓的扭转应力，T为扭矩，J为螺栓的极惯性矩。
在实际工程中，螺栓的极惯性矩可以通过螺栓的直径和材料的弹性模量来计算。
综合考虑螺栓的拉伸、剪切和扭转应力，可以得到螺栓的等效应力，其计算公式为：σe = √(σt² + 3τ²)。
其中，σe为螺栓的等效应力，σt为螺栓的拉伸应力，τ为螺栓的剪切应力。
通过这个公式，可以综合考虑螺栓在受到外载荷作用时所受到的综合应力状态，从而评估螺栓的安全性和可靠性。
在实际工程中，螺栓的等效应力计算是非常重要的，可以帮助工程师评估螺栓连接的可靠性和安全性，从而指导工程设计和实际应用。
通过合理计算螺栓的等效应力，可以有效避免螺栓的断裂和松动现象，确保机械设备和构件的安全运行。
材料力学第三章剪切和扭转
T
Ⅰ
T
d1
(a)
l
T (b)
D2
Ⅱ
T
l
36
3.3 等直圆杆扭转时的应力
解：
Wp1
πd13 16
Wp2
πD23 14
16
1,maxW Mpt11
T Wp1
16T πd13
2,ma xW M pt2 2W Tp2πD 2 311T 6 4
D 2 31 4 d 1 3
螺栓连接[图(a）]中，螺栓主要受剪切及挤压（局部压
缩）。
F
3
3.1 剪切
键连接[图(b）]中，键主要受剪切及挤压。
4
3.1 剪切
剪切变形的受力和变形特点： 作用在构件两侧面上的外力的合力大小相等、方向相 反，作用线相隔很近，并使各自推动的部分沿着与合 力作用线平行的受剪面发生错动。
受剪面上的内力称为剪力； 受剪面上的应力称为切应力；
3.3 等直圆杆扭转时的应力
传动轴的外力偶矩：
已知：
T2
T1
从动轮
n 主动轮
T3 从动轮
传动轴的转速 n ；某一轮上 所传递的功率
NK (kW)
作用在该轮上的外力偶矩T 。
一分钟内该轮所传递的功率等于其上外力偶矩所 作的功：
NK60 13 0(J)T2πn(Nm)
33
3.3 等直圆杆扭转时的应力
26
3.3 等直圆杆扭转时的应力
dj M t
d x GI pBiblioteka G djdx
GGMItp
Mt
Ip
等直圆杆扭转时横截面上切应力计算公式
Mt
O
土的剪切和扭矩之间的计算公式
土的剪切和扭矩之间的计算公式在土工工程中，土的剪切和扭矩的计算是十分重要的，因为它能够帮助工程师们了解土体的力学特性，从而更好地设计和施工工程结构。
本文将通过讲解土的剪切和扭矩之间的计算公式来帮助读者更好地了解这个领域。
一、剪切的定义和计算公式剪切是指两个相邻平面之间的相对滑动。
在土的剪切中，较高的应力沿着一个截面的边缘作用于较低的应力，土壤中的颗粒向着相反方向移动，从而产生剪切力。
因此，剪切力是产生剪切的主要力量。
计算土壤的剪切力需要用到剪切力公式：τ = c + σtanφ。
其中，τ代表土壤的剪切力，c代表土壤的凝聚力，φ代表土壤的内摩擦角，最后一个参数σ代表土壤的正应力。
二、扭矩的定义和计算公式扭矩是指施力于物体的扭转力矩，它是施力于物体以产生扭转的力。
在土工工程中，扭矩的大小决定了工程结构的稳定性，因为如果扭矩不足够强大，那么结构就会变形或崩溃。
计算扭矩需要用到扭矩公式：T = Fd。
其中，T代表扭矩，F代表施力物体的力，d代表力的作用点与物体的旋转中心之间的距离。
三、土的剪切与扭矩的关系土的剪切和扭矩之间存在着密切的关系，因为土壤中的颗粒在受到扭矩作用时，会发生剪切。
在土壤中的剪切力和扭矩之间，存在着以下关系：τ = kT/2πr³.其中，τ代表土壤的剪切力，T代表土的扭矩，r代表力的作用点与物体的旋转中心之间的距离，最后一个参数k是相关系数，它代表土壤的剪切模量和弯曲模量之比。
总结本文讲解了土的剪切和扭矩之间的计算公式，包括剪切公式、扭矩公式以及二者之间的关系公式。
只有深入理解这些公式，工程师才能更好地进行结构设计和相关施工工作，以确保工程质量。
剪切和扭转的强度计算
解： AC段：
A C 1 3kN.m 2 B 2kN.m T2 扭矩图 3kN.m ⊕ 2kN.m
○ -
m 0 m 0
T1 3 0; T1 3kN.m
BC段：
Hale Waihona Puke T1T2 2 0; T2 2kN.m
7
二、圆截面杆扭转时的应力
Mn Ip
实心圆截面的极惯性距： IP
学习情境五 剪切和扭转杆的强度计算
甘肃省有色冶金职业技术 学 院
子情境一 剪切强度计算
一、剪切的概念
2
二、剪切强度的实用计算
剪切面上的内力可用截面法求的。假想将铆钉沿剪切面截开 分为上下两部分，任取其中一部分为研究对象，由平衡条件知， 剪切面上的内力必然与外力方向相反，大小由平衡方程得V=F
这种平行于截面的内力V称为剪力。
5
2、圆截面杆扭转时横截面上的内力—扭矩
一、扭矩
圆杆扭转横截面的内力合成 结果为一合力偶，合力偶的力偶
Ⅰ
矩称为截面的扭矩，用T 表示之。 m
扭矩的正负号按右手螺旋法 则来确定，即右手握住杆的轴线，
Ⅰ
m
卷曲四指表示扭矩的转向，若拇
指沿截面外法线指向，扭矩为正， m 反之为负。
T
x
6
例1 画图示杆的扭矩图 3kN.m 1 5kN.m 2 2kN.m
3
（1）实际： 从有限元计算结果看剪切面上 应力的分布情况十分复杂，工 程中采用近似计算。
（2）假设：
切应力在剪切面上均匀分布；
V ＝ A
式中：A为剪切面的面积
V为剪切面上的剪力
（3）剪切时的强度条件 为保证构件不发生剪切破坏，要求剪切面上的平均剪应力 不超过材料的许用剪应力，即剪切时的强度条件为
材料力学扭转切应力计算公式
材料力学扭转切应力计算公式材料的力学性质是表征其对外力作用的响应能力的重要指标。
扭转切应力是材料在受到扭转力矩作用时所产生的应力。
在许多工程和科学研究中，通过计算和测量扭转切应力可以获得材料的力学性能参数，如剪切模量和剪切强度等。
在材料力学中，扭转切应力计算公式主要有两种形式：切应力公式和剪切应力公式。
1.切应力公式：切应力（Shear Stress）指材料内部产生的由于外力而对于材料内部其中一剖面的剪切应力。
一般情况下，切应力可以采用切应力图形表示。
τ=T/S其中，τ是切应力，T是扭转力矩，S是截面积。
切应力的单位一般是帕斯卡（Pa）或兆帕（MPa）。
在实际应用中，我们常常会遇到不同形状的材料，如圆形、方形、矩形等。
对于这些不同形状的截面，切应力的计算公式也有所不同。
对于圆截面，切应力的计算公式为：τ=T/(π*r^2)对于矩形截面，切应力的计算公式为：τ=T/(b*h)其中，b是矩形截面的宽度，h是矩形截面的高度。
2.剪切应力公式：剪切应力（Shear Strain）是材料在受到剪切力作用时所产生的应变。
在扭转切应力的计算中，剪切应力是切应力的一个重要参数。
剪切应力的计算公式如下：γ=θ*h/l其中，γ是剪切应力，θ是材料的扭转角度，h是扭转试样的高度，l是扭转试样的长度。
剪切应力可以用来计算材料的剪切模量（Shear Modulus），剪切模量可以通过下式计算得到：G=τ/γ其中，G是剪切模量。
综上所述，材料力学扭转切应力计算公式主要有切应力公式和剪切应力公式，通过这些公式可以计算得到材料的扭转切应力、剪切模量等力学性能参数。
这些参数可以用于工程设计和科学研究中，帮助人们了解材料的力学性能和应用范围。
材料力学(第五版)扭转切应力
(
)
d 2 = 0.8D2=43 mm π 2 d1 A1 452 4 = = =1.95 2 2 A2 π D2 1 α2 53.7 1 0.8 2 4
(
)
(
)
空心圆轴能比实心圆轴更充分的使用材料。 空心圆轴能比实心圆轴更充分的使用材料。
理由？ 理由？
空心圆轴能比实心圆轴更充分的使用材料的原因： 空心圆轴能比实心圆轴更充分的使用材料的原因：
(
)
五、圆轴扭转时的强度条件 圆轴扭转时的最大切应力不能超过 材料的许用切应力
τmax
T ax m = ≤ [τ] W p
例题 d2
A
B
C
d1 mA mB mC
已知： 已知：阶梯轴尺寸如图 mA = 22 kN m, mB = 36 kN m, mC =14 kN m
[τ]= 80 MPa
d1 =120 m , d2 =100m m m
对于钢材: 对于钢材:
200 G= = 80GPa 2(1+ 0.25)
§3-4 圆轴扭转时的应力
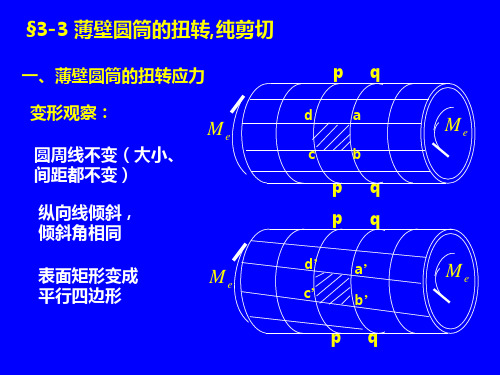
一、变形几何条件 1、变形观察： 变形观察：
圆周线不变（大小、 圆周线不变（大小、 间距都不变） 间距都不变） 纵向线倾斜， 纵向线倾斜， 倾斜角相同 表面矩形变成 平行四边形
薄壁圆筒由于壁很薄， 薄壁圆筒由于壁很薄，表 面变形即为内部变形。 面变形即为内部变形。
圆轴内部任意一点的切应力 圆轴内部任意一点的切应力 τ ρ 与该点到圆心的距离ρ 与该点到圆心的距离ρ成正比
d τ ρ = Gρ dx
(c)
ρ =0
τρ = 0
ρ=R
τ ρ =τ max
d = GR dx
三、静力关系
剪切和扭转应力
Fbs Abs
F/4 dt
100 103 4 1610
156MPa [ bs ]源自铆钉满足强度条件，安全。×
123
2—2截面
F/4
上板受力图
F/4
F/4
F
F/4
上板轴力图
1
2
3F/4
3
F
F⊕/4 ⊕
⊕
3—3截面
22
FN 2 A2
3P / 4 (b 2d)t
75 103 68 10
110MPa
A
极惯性矩。
T
GI p
×
于是得横截面上任一点的切应力为
T
Ip
式中：T—横截面上的扭矩，由截面法通过外力偶矩求得；
—求应力那点到圆心的距离；
Ip—截面对圆心的极惯性矩，纯几何量，无物理意 义。
×
⒋ 极惯性矩
d
I p A 2dA
D
2 2 2 d 0
D 4
32
环形截面：
IP
32
②各纵向线长度不变，但均倾斜了同一微小角度 。
③所有矩形网格均歪斜成同样大小的平行四边形。
×
剪切虎克定律： 单元体ab 的倾角 称为切应变，
´
a
b
切应变是单元体直角的改变量。实 验表明，在弹性范围内，切应力与 dy 切应变成正比，即
´
c
d
G
t
z
dx
这就是剪切虎克定律，比例常数G 称为剪切弹性模量。
×
t P
d
tP
多铆钉连接件，为计算方便，各铆钉受力可视作相同。
F/4
上板受力图
F/4
F/4
F
F/4
剪切力和扭矩
πd 4 π Ip (50)4 mm 4 61.36 104 mm 4 32 32
500 AD (2 2 106 1106 ) 80 103 61.36 104 0.051 rad
例题7.5
主传动钢轴，传递功率 P 60 kW ，转速
n 250 r min，传动轴的许用切应力 40 MPa
T2 M eB M eA 143.2 N m-318.3 N m -175 N m （图d） T3 M eD 63.7 N m （图e）
T2 ，T3 为负值说明实际方向与假设的相 175N m
7.3 等直圆轴扭转时横截面上的切应力
d 76 mm
对于精密机器的轴
0.15 ( )
m ~ 0.30 ( ) m
例题7.4
图示轴的直径 d 50 mm ，切变模量
G 80 GPa 试计算该轴两端面之间的扭转角。
解：两端面之间扭转为角：
AD
TABl TBC l TCDl l (2TAB TBC ) GI p GI p GI p GI p
n------轴的转速，单位为r/min。
7.2
圆轴扭转时横截面上的内力及扭矩图
7.2.1 扭矩 平衡条件
M x 0
T Me
内力偶矩T称为扭矩
扭矩的单位：
N m 或 kN m
扭矩的正负号规定为：自截面的外法线向截面看， 逆时针转向为正，顺时针转向为负
扭矩图
常用与轴线平行的x坐标表示横截面的位置，以与 之垂直的坐标表示相应横截面的扭矩，把计算结果 按比例绘在图上，正值扭矩画在x轴上方， 负值扭矩画在x轴下方。这种图形称为扭矩图。 例题7.1 图示传动轴，转速 n 300 r min ，A轮为 主动轮，输入功率 N A 10 kW，B、C、D为从动 轮，输出功率分别为
扭转切应力计算
新材料与新工艺的应用
高强度材料
随着新材料技术的不断发展，高强度材 料在扭转切应力计算中的应用越来越广 泛。这些材料具有更高的强度和刚度， 能够承受更大的扭矩，从而提高结构的 安全性和稳定性。
VS
复合材料
复合材料由多种材料组成，具有优异的力 学性能和化学稳定性。在扭转切应力计算 中，复合材料的应用有助于提高结构的抗 疲劳性能和耐久性，降低维护成本。
扭矩过大导致的结构破坏。
02
建筑结构分析
在建筑设计阶段，扭转切应力计算对于评估高层建筑、大跨度结构等复
杂建筑的稳定性至关重要。通过精确计算，可以优化结构设计，提高建
筑的抗风、抗震能力。
03
施工设备设计
在土木工程施工中，如打桩机、吊车等重型设备的转轴和传动系统需要
进行扭转切应力分析。这有助于确保设备在承受高扭矩时仍能保持稳定
连接件设计
在机械结构中，螺栓、键等连接件在传递扭矩时也会受到扭转切应力的作用。通过计算该 应力，可以确保连接件的强度和稳定性，防止因扭矩过大而导致的连接失效。
土木工程
01
桥梁设计
在土木工程中，桥梁的斜拉索和吊索等关键构件在承受外部扭矩时，需
要进行扭转切应力计算。这有助于确保桥梁的安全性和稳定性，防止因
有限元分析法
总结词
通过建立有限元模型，模拟物体的扭转行为并计算出切应力分布。
详细描述
有限元分析法是一种数值模拟方法，通过将物体离散化为有限个小的单元（即有限元），然后对每个单元进行受 力分析和平衡方程求解，最终得到整个物体的应力分布。这种方法可以处理复杂的结构和非线性材料，但需要建 立准确的有限元模型和进行大量的计算。
实验测量法
总结词
第10章 剪切和扭转讲解
等。）
解：受力分析如图
P
P
Fs F P 4
t
b
t
P
123
P
P
d
P/4
123
切应力和挤压应力的强度条件
t Fs P 110 107 136 .8MPa t
A d 2 3.14 1.62
s bs
F Abs
P 4td
110 107 411.6
171.9MPa sbs
23
外力特点：平衡力偶系作用在垂直于杆轴线的
平面内.
变形特点：各横截面绕杆轴线作相对转动。
24
任意两截面间相对转动的角度——扭转角, 如 ； 杆的纵线也转过一角度γ——剪切角。
以扭转变形为主要变形的受力杆件——轴.
圆形截面的扭转构件——圆轴.
工程实例:。 机器中的传动轴;。
地质勘探中的钻杆等。
Me
B
T图
31
例 10-3 一传动轴如图，转速n = 300r/min； 主动轮 输入的功率P1= 500kW，三个从动轮输出的功率分 别为： P2= 150kW， P3= 150kW， P4= 200kW。 试作轴的扭矩图。
32
解： 首先必须计算作用在各轮上的外力偶矩
M2 1
M3 2 M1
3
M4
§10-3 扭转的概念与工程实例
一、引例 F
F
二、概念
M
作用于杆件上的外力，为两个大小相等、方向相反、且作
用平面垂直于杆件轴线的力偶时，杆件中任意两个横截面即会
发生绕杆件轴线相对转动，这种形式的变形就称为扭转变形。
受力特征：杆受一对大小相等、方向相反的力偶，力偶作用
材料力学扭转应力
材料力学扭转应力
材料力学中，扭转应力是指作用于材料内部的扭转力产生的应力。
当材料受到扭转力作用时，其内部会产生一个对扭转力的阻抗，即扭转应力。
扭转应力主要在圆柱体或轴的表面上产生，其大小与扭转力的大小成正比，与材料的性质和几何形状有关。
扭转应力可以通过许多方式进行计算和描述。
其中最常用的描述方式是采用剪应力。
扭转应力可以通过剪应力（也称为切应力）的定义进行计算，即扭转力与扭转体的横截面面积的比值。
扭转应力可以在不同的横截面上具有不同的分布。
扭转应力的大小可以通过扭转弹簧常数（也称为剪切模量）衡量。
扭转弹簧常数是一个材料属性，描述了材料在扭转载荷下的应变与扭转应力之间的关系。
扭转弹簧常数越大，扭转应力产生的抵抗就越强。
扭转应力在很多工程应用中都是一个重要参数。
例如，在轴传动系统中，扭转应力是评估轴的耐久性和疲劳寿命的关键指标。
在材料加工中，扭转应力是评估材料变形和断裂的重要因素。
了解和控制材料的扭转应力可以帮助工程师设计更可靠和耐用的结构和零件。
《建筑力学》第六章-剪切与扭转
04
剪切与扭转的实验研究
实验设备与实验方法
实验设备
包括剪切试验机、扭转试验机、 应变计、扭矩计等。
实验方法
采用标准试件进行剪切和扭转实 验，记录相关数据，分析其力学 性能。
实验结果与分析
实验结果
通过实验，得到了试件在剪切和扭转 作用下的应力-应变曲线，以及相应 的力学性能参数。
结果分析
总结词
高层建筑的剪切与扭转分析是提高其抗震性能的重要手段。
详细描述
高层建筑由于其高度和结构特点，更容易受到地震等外部载荷的影响，发生剪切和扭转。为了提高高层建筑的抗 震性能，需要进行剪切与扭转分析，优化结构设计和加强构造措施。
大跨度结构的剪切与扭转分析
总结词
大跨度结构的剪切与扭转分析是实现其跨度和结构优化的关键步骤。
对实验结果进行统计分析，得出试件 在不同条件下的剪切和扭转强度、弹 性模量等力学性能指标，并对其变化 规律进行探讨。
实验结论与建议
结论
通过实验研究，验证了剪切和扭转理论的正确性，并得出了试件在不同条件下的 剪切和扭转力学性能指标。
建议
为进一步深入研究剪切和扭转理论，建议采用不同材料、不同尺寸、不同形状的 试件进行实验研究，以获得更全面的数据和结论。同时，加强实验设备的维护和 更新，提高实验精度和可靠性。
详细描述
大跨度结构如大型体育场馆、会展中心等，需要承受较大的载荷和变形。通过剪切与扭转分析，可以 优化结构设计，减小变形和应力集中现象，提高结构的承载能力和稳定性。
THANKS
感谢观看
剪切与扭转的基本概念
剪切应力
剪切面上的正应力称为剪切应力。 剪切应力的大小与剪切力成正比，
与剪切面面积成反比。
拉压、弯曲、扭转和剪切变形的特点以及应力分布
拉压、弯曲、扭转和剪切变形的特点以及应
力分布
当外力作用于物体时，会产生各种各样的变形，其中包括拉压、弯曲、扭转和剪切变形。
这些变形都有其独特的特点和应力分布。
拉压变形是物体受到同向作用力的影响，导致物体沿着作用力方向伸展或收缩的变形。
这种变形的特点是杆件的截面积保持不变，而两端的长度发生变化。
在拉压变形时，应力的分布是均匀的，且沿整个杆件都是一致的。
在拉伸中，物体的应力分布会呈现出正比例增加的趋势，而在压缩中则是反比例增加的趋势。
弯曲变形是物体受到偏向作用力的影响，导致物体的一端上升而另一端下降的变形。
这种变形的特点是杆件的截面形状会发生变化，截面面积也会影响变形特点。
弯曲变形的应力分布最大的一点位于中心面，并逐渐向两端递减。
扭转变形是物体受到两个对称作用力的影响，在轴线周围旋转的变形。
这种变形的特点是杆件的截面形状会发生变化，且扭曲会使得截面形状变得不规则。
扭转变形的应力分布最大的一点位于中心轴线上，逐渐向周围递减。
剪切变形是物体受到两个垂直于轴线方向的作用力的影响，导致物体在不同平面上发生剪切变形。
这种变形的特点是物体的形状变得
不规则，且在两个平面上的应力不同。
在剪切变形时，应力的分布均匀，沿着切面方向的应力最大，而切面下方没有应力。
以上几种变形及其应力分布特点，在实际工程及生产中都有着广泛的应用。
在设计和制造过程中，要考虑到不同变形及其应力分布的特点，选择合适的材料和结构，以保证物体的稳定性、可靠性和安全性。
第六章 材料力学剪切与扭转
第六章
• • • • 6.1 6.2 6.3 6.4
剪切与扭转
剪切和挤压的实用计算 扭矩的概念 圆轴扭转的应力及强度计算 圆轴扭转时的变形及刚度计算
6.1 剪切和挤压的实用计算
6.1.1
剪切和挤压的概念
1、连接件 在构件连接处起连接作用的部件，称为连接件。例如： 螺栓、铆钉等。连接件虽小，起着传递载荷的作用。 螺栓 P
F /2 F /2 2 d A 4
d
2F
11.97(mm)
选取d=1 2mm。 3)校核销钉的挤压强度为
jy
F 150( MPa) jy Ajy
故选取d= 1 2mm，可以同时满足挤压和剪切强度的要求。
Fs 4 F 2 A d Fbs F bs Abs dh
6.2.3 扭矩和扭矩图
1. 扭矩：构件受扭时，横截面上的内力偶矩，记作“T”。
2. 截面法求扭矩
M
x
0
Me Me
T Me 0 T Me
3. 扭矩的符号规定：
Me
T
x
“T”的转向与截面外法线方向满足右手螺旋规则为正，
反之为负。
右手螺旋法则
右手拇指指向外法线方向为 正(+),反之为 负(-)
P4 25 M 4 9550 9550 1194 ( N .m) n 200
2) 计算各截面上的扭矩(分段应用截面法) 各截面上的扭矩假设为正值。
• • • •
• • •
①沿截面I—I截开，取左侧为研究对象[图 6．11(b)]，则根据平衡条件∑m=0，有 T1+M2=0 T1=–M2=–9 5 5N· m ②沿截面Ⅱ一Ⅱ截开，取左侧为研究对象[图 6．11(c)]，则根据平衡条件∑m=0，有 T2+M2一M1=0 T2=M1一M2=3 8 2 0—9 5 5=2 8 6 5N· m ③沿截面Ⅲ一Ⅲ截开，取右侧为研究对象[图 6．11(d)]，则根据平衡条件∑m=0，有
拉伸、剪切、挤压、扭转许用应力
拉伸、剪切、挤压、扭转许用应力剪应力与抗拉强度关系我们在设计的时候常常取许用剪切应力,在不同的情况下安全系数不同,许用剪切应力就不一样...校核各种许用应力常常与许用拉应力有联系,而许用材料的屈服强度(刚度)与各种应力的关系一拉伸钢材的屈服强度与许用拉伸应力的关系[σ ]= σu/n n为安全系数a.ASME VIII-II, [σ ]=0.67σs二剪切许用剪应力与许用拉应力的关系1 对于塑性材料 [τ]=0.6—0.8[σ]2 对于脆性材料 [τ]=0.8--1.0[σ]三挤压许用挤压应力与许用拉应力的关系1 对于塑性材料 [σj]=1.5—2.5[σ]2 对于脆性材料 [σj]=0.9—1.5[σ]注：：[σj]=(1.7—2)[σ]（部分教科书常用）四扭转许用扭转应力与许用拉应力的关系:1 对于塑性材料 [σn]=0.5—0.6[σ]a.ASME VIII-II AD132-0.6Sm(Key,shear ring and pin),b.ASME VIII-II AD132-0.8Sm(Sm=0.67σs(circle round of stem )2 对于脆性材料 [σn]=0.8—1.0[σ]轴的扭转变形用每米长的扭转角来衡量。
对于一般传动可取[υ]=0.5°--/m;对于精密传动，可取[υ]=0.25°—0.5°/M；对于要求不严格的轴，[υ]可大于1°/M计算。
五弯曲许用弯曲应力与拉应力的关系:1 对于薄壁型钢一般采用轴向拉伸应力的许用值.2 对于实心型钢可以略高一点,具体数值可参见有关规范..拉应力与材料的屈服强度有关,。
材料力学第五章扭转应力
建筑工业中的应用
建筑结构中的梁、柱等构件在承受扭矩时会产生扭转应力。
在建筑设计过程中，工程师需要考虑材料的抗扭性能，合理 设计梁、柱等构件的截面尺寸和连接方式，以确保建筑结构 的稳定性和安全性。
学习有限元分析方法，掌 握如何利用计算机软件进 行结构分析，提高解决实 际问题的能力。
ABCD
结合实际工程问题，分析 不同材料的抗扭性能，以 及如何优化设计以提高结 构的稳定性。
关注相关领域的最新研究 进展，了解材料力学在工 程实践和科学研究中的应 用。
THANKS
感谢观看
扭转应力的计算公式
计算公式
扭转应力的大小可以通过以下公式计算：$tau = frac{T}{A}$，其中$tau$是扭转应 力，$T$是扭矩，$A$是物体的截面面积。
截面面积
截面面积是指物体横截面的面积，通常用于计算物体在扭矩作用下的扭转应力。
扭转应力的单位和符号
单位
扭转应力的单位是帕斯卡（Pa），在国际单位制中，1Pa=1N/m²。
弹性模量
弹性模量是材料在弹性变形范围内，抵抗外力作用的能力， 它反映了材料的刚度。对于同一材料，弹性模量越大，抵抗 扭转变形的能力越强，因此，弹性模量越大，扭转应力也越 大。
总结
在材料力学中，弹性模量是影响材料扭转应力的关键因素之 一。高弹性模量的材料具有较高的抵抗扭转变形的能力，因 此会产生较大的扭转应力。
剪切模量对扭转应力的影响
剪切模量
剪切模量是指在剪切应力作用下，材料抵抗剪切变形的刚度。剪切模量的大小与材料的剪切应力成正比，即剪切 模量越大，材料抵抗剪切变形的能力越强，因此，扭转应力也越大。
工字钢剪应力
工字钢剪应力工字钢剪应力包括以下几种：一、剪切应力剪切应力是指工字钢在受力过程中，由于受到剪切力的作用而产生的应力。
剪切应力通常是由于工字钢受到弯曲、扭转等变形而产生的。
在工字钢的截面上，剪切应力的大小和分布是不均匀的，最大剪切应力发生在工字钢截面的上下边缘处，而最小剪切应力则发生在截面的中心部位。
二、弯曲应力弯曲应力是指工字钢在受力过程中，由于受到弯曲力的作用而产生的应力。
弯曲应力通常是由于工字钢受到外力作用而产生的。
在工字钢的截面上，弯曲应力的大小和分布也是不均匀的，最大弯曲应力发生在工字钢截面的上边缘或下边缘处，而最小弯曲应力则发生在截面的中心部位。
三、扭转应力扭转应力是指工字钢在受力过程中，由于受到扭力的作用而产生的应力。
扭转应力通常是由于工字钢受到旋转外力的作用而产生的。
在工字钢的截面上，扭转应力的大小和分布也是不均匀的，最大扭转应力发生在工字钢截面的外边缘处，而最小扭转应力则发生在截面的中心部位。
四、残余应力残余应力是指工字钢在制造、加工或使用过程中，由于受到不均匀变形或加载等因素的影响而在工字钢内部产生的剩余应力。
残余应力的存在会影响工字钢的力学性能和使用寿命，因此需要进行有效的控制和消除。
五、温度应力温度应力是指工字钢在温度变化过程中，由于材料热胀冷缩的特点而产生的应力。
温度应力通常发生在工字钢的截面尺寸较大或温度变化较为剧烈的部位。
温度应力的存在也会影响工字钢的力学性能和使用寿命，需要进行有效的控制和消除。
综上所述，工字钢剪应力包括剪切应力、弯曲应力、扭转应力、残余应力和温度应力等方面。
这些应力的存在会影响工字钢的力学性能和使用寿命，因此在进行工字钢的制造、加工和使用过程中，需要对这些应力进行有效的控制和消除，以确保工字钢的安全性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F/4 F/4
Fs F / 4 100103 124MPa [ ] As d 2 / 4 162
铆钉挤压应力
bs
Fbs Abs
F/4 dt
100 103 4 1610
156MPa [ bs ]
铆钉满足强度条件，安全。
×
123
2—2截面
F/4
上板受力图
F/4
F/4
F
F/4
上板轴力图
×
五、扭转时的变形
d T
dx GI p
l
T
dx
0 GI p
当T 、GIP 为常量时，长为l 一段杆两端面相对扭转角为
Tl
GI P
其中GIP 表示杆件抵抗扭转变形的能力，称为抗扭刚度。
×
d D
例6 已知空心圆截面的扭矩T =1kN.m，D =40mm， d=20mm，求最大、最小切应力。
§8–6 圆轴扭转时强度和刚度条件
一.强度条件：
max
T Wt
[ ]
其中容许切应力[]是由扭转时材料的极限切应力除以安全系
数得到。
×
二、刚度条件
d
dx
T GIp
max
T GIp
(rad/m) (rad/m)
[ ]称为许用单位扭转角。若许用单位扭转角给的是 / m，
则上式改写为
max
T GI p
同一截面，扭矩T ，极惯性矩IP 为常量，因此各点切应
力 的大小与该点到圆心的距离 成正比，方向垂直于圆的
半径，且与扭矩的转向一致。
⒌ 最大切应力
max
T IP
max
令：Wt
IP ,
max
Wt 称为抗扭截面模量，单位：m3
max
T Wt
Wt
16
D3
16
D3 (1
d4 D4
)
实心圆截面
空心圆截面
180
(/m)
×
例8 图示圆轴，已知mA =1kN.m， mB =3kN.m， mC
=2kN.m；l1 =0.7m，l2 =0.3m；[]=60MPa，[ ]=0.3°/m，
G=80GPa；试选择该轴的直径。
1
2
3F/4
3
F
F⊕/4 ⊕
⊕
3—3截面
22
FN 2 A2
3P / 4 (b 2d)t
75 103 68 10
110MPa
t
33
FN 3 A3
P (b d)t
100103 84 10
119MPa
max 33
板也满足拉压强度条件，铆接件安全。
×
[例2]已知图示圆梯形杆D=32mm，d=20mm，h=12mm，材 料的[]=100MPa，[bs]=200MPa。受拉力F =50kN 作用，试 校核此杆的强度 。
t P
d
tP
P
P
铆钉（或螺栓）连接件要安全工作，铆钉即要满足剪切 强度条件，又要满足挤压强度条件，同时板还要满足拉压强 度条件。
×
t P
d
tP
多铆钉连接件，为计算方便，各铆钉受力可视作相同。
F/4
上板受力图
F/4
F/4
F
F/4
上板轴力图
3F/4
F
F⊕/4 ⊕
⊕
铆钉受力图
F/4 F/4
×
铆钉剪应力
剪切弹性模量G 、与弹性模量E 和泊松比 一样，都是 表征材料力学性质的材料常数。对于各向同性材料，这三 个材料常数并不是独立的，它们存在如下关系。
G E
2(1 )
×
四、等直圆杆扭转横截面上的切应力
o1
o2
o1 o2
AB
D C B’
C’
dx
a b
A dB
bc’ d c’
B’
DC
dx C’
⒈ 变形的几何条件
解： max
T Wt
16
T D3 (1
d4 D4
)
max
min
161000
43[1
(
1 2
)4
]
T
84.9MPa
min
max
d D
84.9
1 2
42.45MPa
×
例7 图示圆杆BC 段为空心，已知 D =50mm，d=25mm； a =250mm，b =150mm；G=80GPa；试求该杆的最大切应力 和自由端的扭转角。
§8–1 剪切概念与实例
工程上的剪切件
1）受力特点 杆件两侧作用大小相等，方向相反，作用线相距很近的外力。 2）变形特点 两外力作用线间截面发生错动，由矩形变为平行四边形。 构件在这两个平行面间的任一横截面只有剪力作用，产生剪切 变形。
F
F
×
§8–2 连接接头的强度计算
1、 剪切实用计算
铆接件
F
F
D
d
F
圆轴扭转时应力与变形
×
一、实验： 1.实验前：①绘纵向线，圆周线； ②两端施加一对外力偶 m。
2.实验后：
①圆周线不变； ②纵向线变成螺旋线。 3.结果：
①圆筒表面各圆周线的形状、大小和间距均未改 变，只是绕 轴线作了相对转动。圆周线实际代表一个横截面，此结果表明 横截面仍保持平面，且大小、形状不变，满足平面假设。
F
F
n
n
F
F
×
剪切面
F n
FS
n
n
n F
F
Fx称为剪力。
×
FS F
F
设剪切面的剪力沿截面是均匀分布的，则有
Fs
As
为剪切面的剪应力，As为剪切面的面积。剪切强度条件为
Fs
As
[]为容许切应力，由材料破坏时的极限剪应力除以安全系数。
×
于是得横截面上任一点的切应力为
T
Ip
式中：T—横截面上的扭矩，由截面法通过外力偶矩求得；
—求应力那点到圆心的距离；
Ip—截面对圆心的极惯性矩，纯几何量，无物理意 义。
×
I p A 2dA
D
2 2 2 d 0
D 4
32
环形截面：
IP
32
(D4
d
4)
d D
极惯性矩的单位：m4
×
2、 挤压实用计算
挤压应力
bs
Fbs Abs
计算挤压面
Fbs为挤压力，Abs为计算挤压 面的面积。
实际挤压面 F
挤压强度条件
bs
Fbs Abs
bs
[bs]为容许挤压应力，由 极限挤压应力除以安全系数。
×
3、 连接板强度计算
拉压应力
FN
Aj
F
FN为轴力，Aj为截面面积。
×
例1 图示铆接件，P=100kN，铆钉的直径d=16mm，容许剪 应力[]=140MPa，容许挤压应力[bs]=200MPa；板的厚度 t=10mm ，b=100mm，容许正应力[]=170MPa，试校核铆 接件的强度。
横截面上b 点的切应变： bb' d
dx dx 其中 d 为单位长度杆两端面相对扭转角，称单位扭转角
dx
×
⒉ 物理条件
横截面上b 点的切应力： G G
⒊ 静力条件
T A dA A G 2 dA G A 2dA G IP
dA b dA
O2
IP
2dA
A
T
GI p
②各纵向线长度不变，但均倾斜了同一微小角度 。
③所有矩形网格均歪斜成同样大小的平行四边形。
×
剪切虎克定律： 单元体ab 的倾角 称为切应变，
´
a
b
切应变是单元体直角的改变量。实 验表明，在弹性范围内，切应力与 dy 切应变成正比，即
´
c
d
G
t
z
dx
这就是剪切虎克定律，比例常数G 称为剪切弹性模量。