天津市北部四区高三年级12月联考
2022年高三12月大联考(全国乙卷)英语答案

2022年高三12月大联考(全国乙卷)英语·全解全析及评分标准第一部分 听力(共两节,满分30分)1—5 BBACB 6—10 BABCA 11—15 CBCAB 16—20 CBACA第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)A【语篇解读】这是一篇应用文,介绍了四个适合自行车骑行的美国国家公园。
21. A 【解析】细节理解题。
根据Glacier National Park, Montana 中的“Note that you’ll be meeting this popularroad with cars and RVs (野营车)”可知,在Glacier National Park,自行车道与其他交通车辆共用。
故A 选项符合题意。
22. C 【解析】细节理解题。
根据Theodore Roosevelt National Park, North Dakota中的 “Keep your binocularsclose and watch for bison and wild horses, sightings of which are almost guaranteed”可知,在这个国家公园骑行可以观测到bison 和wild horses等野生动物。
故选C。
23. B 【解析】细节理解题。
对比四个国家公园的时间安排,不难看出另外三个都是夏天最合适,唯独Cuyahoga Valley National Park最佳骑行时间是春秋季节。
余项均与原文有出入,予以排除。
故选B。
B【语篇解读】本文是一篇记叙文,讲述了一家面包圈店的员工不辞辛苦,驱车六小时送回顾客落下的车钥匙的感人故事。
24. B 【解析】细节理解题。
根据第二段中的“to drop off a set of car keys that customer Diana Chong left in hisshop”可知,Proscia不辞辛苦地连夜驱车近六个小时去宾夕法尼亚东北部,目的是送还顾客Diana Chong 落下的车钥匙。
天津市高三上学期12月四校联考英语试卷含答案

高三第一学期英语试卷本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟。
第I卷(共115分)听力部分第一节:听下面五段对话,每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. How much did the pink coat cost?A.$35B. $50C.$852. What will the woman do next?A.Make a telephone callB.Go to her officeC.Visit a library3. Why is Alex applying for financial aid?A.He is out of workB.He has lost lots of moneyC.He has to support his little brother4. When does the conversation take place?A.On MondayB.On WednesdayC. On Friday5.What are the speakers mainly talking about?A strike B. An employee C. A piece of news第二节:听下面几段材料,每段材料后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段材料前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段材料读两遍。
听下面一段对话,回答第6至8三个小题6.How will the speakers travel this time?A.By planeB. By shipC. By train7.what does the man say about the last trip?A.The schedule was tight.B.It took him too much time.C.It gave him a surprising experience.8.What will the speakers do tomorrow morning?A.Visit Joseph.B.Withdraw some money.C.Buy traveller's cheques. 听下面一段对话,回答第9至11三个小题9. What relation is the woman to Mr. Calington?A. His secretaryB. His managerC. His wife10 Where is Mr. Calington now?A. In his officeB.Out of townC. In Houston11. Why does the man make the telephone call?A. To call off a meetingB.To know about a trip planC.To change the time of an appointment听下面一段独白,回答第12至15四个小题12. What could the man probably be?A. A writer.B. A zoo keeper.C. A journalist.13. What will a defender cat do before a fight?A. Lie down its ears flat against its head.B. Turn its ears toward the side.C. Hold its tail straight up.14. What part of a cat’s body shows its feeling the best?A. The eyes.B. The tail.C. The legs.15. How does a cat try to understand humans?A. By listening to their tones.B. By watching their gestures.C. By watching their eyes.第一部分:英语知识运用(共两节,满分45分)第二节:单项填空(共15小题:每小题1分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
2024届天津市九十六中学高三上学期12月月考数学试题及答案

高三年级阶段性检测 数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷(共45分)一、选择题(每题只有一个选项符合题意,每题5分共45分)1 设全集{}34U x x =∈-<<Z ,集合{}2,0,1,2A =-,{}1,0,1B =-,则()U A B =ð( )A {}2,2- B. {}1,3- C. {}2,2,3- D. {}1-2. “01x <<”是“2log (1)1x +<”的A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 命题2:0,01xp x x ∀>>+的否定是( )A. 20,01xx x ∀>+… B. 20,01xx x ∀><+C. 20,01xx x ∃><+ D. 20,01xx x ∃>+…4. 设153a =,315b ⎛⎫= ⎪⎝⎭,31log 5c =,则a , b ,c 的大小关系为( ).A. b a c << B. a c b<< C. c<a<bD. c b a<<5. 函数()cos f x x =+在[],ππ-上的大致图象为( )A. B.C. D.6. 某区为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[)0,0.5,[)0.5,1,…[]4,4.5分成9组,制成了如图所示的频率分布直方图.若该区有40万居..民,估计居民中月均用水量在[)2.5,3的人数为()A. 4.8万B. 6万C. 6.8万D. 12万7. 已知双曲线22221(0,0)y xa ba b-=>>的一条渐近线过点)2,且双曲线的一个焦点在抛物线2x=的准线上,则双曲线的方程为()A.2212128y x-= B.2212821x y-=C22143x y-= D.22143y x-=8. 已知矩形ABCD的顶点都在球心为O的球面上,6AB=,BC=,且四棱锥O ABCD-的体积为O的表面积为()A. 64πB. 52πC. 48πD.44881π9.已知函数)22()2sin cos sin cosf x x x x x=-,判断下列给出的四个命题,其中正确的命题有()个.①()f x的最小正周期为2π;②将函数()y f x=的图象向左平移12π个单位,将得到一个偶函数;③函数()y f x=在区间7,1212ππ⎛⎫⎪⎝⎭上是减函数;④“函数()y f x=取得最大值”的一个充分条件是“12xπ=”A. 0B. 1C. 2D. 3.第Ⅱ卷(共105分)二、填空题10. i 是虚数单位,则复数312ii-=+___________.11.若2nx ⎛⎝展开式的二项式系数之和为64,则展开式中的常数项是___________.12. 一袋中有大小相同的4个红球和2个白球若从中任取3球,则恰有一个白球的概率是__________,若从中不放回的取球2次,每次任取1球,记“第一次取到红球”为事件A , “第二次取到红球”为事件B ,则()|P B A =__________.13. 已知正数a ,b 满足1a b +=,则1aa b+的最小值是___________.14. 已知圆C 圆心坐标是(0,)m ,若直线230x y -+=与圆C 相切于点(2,1)A --,则圆C 的标准方程为___________.15. 已知平行四边形ABCD 中,4AB =,2AD =,8AC AD ⋅= ,则AC = ________;若CE ED =,DF DB λ= ,则AF FE ⋅最大值为________.三、解答题16. 在ABC ∆中,角,,A B C 的对边分别为,,a b c ,4B π=,c =ABC ∆的面积为6.(1)求a 及sin A 的值;(2)求26sin A π⎛⎫- ⎪⎝⎭的值.17. 如图,在四棱锥P -ABCD 中,底面ABCD 是直角梯形,90ABC BAD ∠=∠=︒,AP ⊥平面ABCD ,222AB BC AP AD ====,点M 、N 分别为线段BC 和PD 的中点.(1)求证:AN ⊥平面PDM ;(2)求平面PDM 与平面PDC 夹角的正弦值;(3)在线段PC (不包括端点)上是否存在一点E ,使得直线BE 与平面PDC 所成角的正弦值为23,若存的的在,求出线身PE 的长:若不存在,请说明理由.18. 已知椭圆C :22221x y a b +=(0a b >>)的离心率e =,点(),0A a 、()0,B b之间的距离为(1)求椭圆C 的标准方程;(2)若经过点(且斜率为k 的直线l 与椭圆C 有两个不同的交点P 和Q ,则是否存在常数k ,使得OP OQ + 与AB共线?如果存在,求k 的值;如果不存在,请说明理由.19. 已知等比数列{}n a 的前n 项和为n S ,0n a >且1336a a =,()34129a a a a +=+.(1)求数列{}n a 的通项公式;(2)若13n bn S +=,求数列{}n b 及数列{}n n a b 的前n 项和n T .(3)设()()111nn n n a c a a +=++,求{}n c 的前2n项和2n P .20. 已知函数221()2ln (R)2f x a x x ax a =-++∈.(1)当1a =时,求曲线()y f x =在()()1,1f 处的切线方程;(2)求函数()f x 的单调区间;(3)当a<0时,求函数()f x 在区间[]1,e 的最小值.高三年级阶段性检测 数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷(共45分)一、选择题(每题只有一个选项符合题意,每题5分共45分)1. 设全集{}34U x x =∈-<<Z ,集合{}2,0,1,2A =-,{}1,0,1B =-,则()U A B =ð( )A. {}2,2-B. {}1,3-C. {}2,2,3- D. {}1-【答案】A 【解析】【分析】首先确定全集U ,根据交集和补集定义直接求解即可.【详解】{}{}342,1,0,1,2,3U x x =∈-<<=--Z ,{}2,2,3U B ∴=-ð,(){}2,2U A B ∴=- ð.故选:A.2. “01x <<”是“2log (1)1x +<”的A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A 【解析】【分析】根据2log (1)111x x +<⇔-<以及充分不必要条件的定义可得.【详解】因为2log (1)111x x +<⇔-<<,所以(0,1) (1,1)-,所以01x <<”是“2log (1)1x +<”的充分不必要条件.故选A .【点睛】本题考查了对数不等式以及充分必要条件,属基础题.3. 命题2:0,01xp x x ∀>>+的否定是( )A. 20,01xx x ∀>+… B. 20,01xx x ∀><+C. 20,01xx x ∃><+ D. 20,01xx x ∃>+…【答案】D 【解析】【分析】根据全称命题的否定方法:先改变量词,然后再否定结论,求解即可.【详解】由全称命题的否定可得:命题2:0,01x p x x ∀>>+的否定是20,01xx x ∃>+….故选:D4. 设153a =,315b ⎛⎫= ⎪⎝⎭,31log 5c =,则a , b ,c 的大小关系为( ).A. b a c <<B. a c b<< C. c<a<b D. c b a<<【答案】D 【解析】【分析】利用指数、对数函数性质并借助“媒介”数即可得解.【详解】指数函数13,(5xx y y ==分别是R 上的增函数和减函数,10,305>>,则1035133()05>>>,对数函数3log y x =在(0,)+∞上单调递增,1015<<,则331log log 105<=,所以有1353113(log 55>>,即c b a <<.故选:D5. 函数()cos f x x =+在[],ππ-上的大致图象为( )A. B.C. D.【答案】C 【解析】【分析】先求函数的定义域,根据函数的奇偶性,排除部分选项,再利用特殊点处的函数值排除不合适的选项,即可得解.【详解】由题知()f x 的定义域为R ,()()()cos cos f x x x f x -=-=+=,所以()f x 是偶函数,排除A ;()ln 1ln e 10f π=<-=,排除B ,D.故选:C.6. 某区为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[)0,0.5,[)0.5,1,…[]4,4.5分成9组,制成了如图所示的频率分布直方图.若该区有40万居民,估计居民中月均用水量在[)2.5,3的人数为( )A. 4.8万B. 6万C. 6.8万D. 12万【答案】B 【解析】【分析】由频率分布直方图求出a 可得答案.【详解】由()210.040.080.080.120.160.40.520.50.6=-++++++⨯=a 得0.3a =,估计居民中月均用水量在[)2.5,3的人数为0.30.5406⨯⨯=万,故选:B .7. 已知双曲线22221(0,0)y x a b a b-=>>的一条渐近线过点)2,且双曲线的一个焦点在抛物线2x =的准线上,则双曲线的方程为( )A. 2212128y x -= B. 2212821x y -=C. 22143x y -= D. 22143y x -=【答案】D 【解析】【分析】根据题意列出,,a b c 满足等量关系式,求解即可.【详解】因为)2在双曲线22221(0,0)y x a b a b-=>>的一条渐近线a y x b =上,2b =;因为抛物线2x =的准线为y =,故c -=又222a b c +=;解得224,3a b ==,故双曲线方程:22143y x -=.故选:D.8. 已知矩形ABCD 的顶点都在球心为O 的球面上,6AB =,BC =,且四棱锥O ABCD -的体积为O 的表面积为( )A. 64π B. 52πC. 48πD.44881π【答案】A 【解析】【分析】由题意求出矩形的对角线的长,即截面圆的直径,根据棱锥的体积计算出球心距,进而求出球的【详解】解:由题可知矩形ABCD 所在截面圆的半径即为ABCD 的对角线长度的一半,=6AB,BC =,r ∴==,由矩形ABCD的面积S AB BC == 则O 到平面ABCD 的距离为h满足:13⨯=解得2h =,故球的半径4R ==,故球的表面积为:2464R ππ=,故选:A .的为9. 已知函数)22()2sin cos sin cos f x x x x x =-,判断下列给出的四个命题,其中正确的命题有( ) 个.①()f x 的最小正周期为2π;②将函数()y f x =的图象向左平移12π个单位,将得到一个偶函数;③函数()y f x =在区间7,1212ππ⎛⎫⎪⎝⎭上是减函数;④“函数()y f x =取得最大值”的一个充分条件是“12x π=”A. 0B. 1C. 2D. 3【答案】D 【解析】【分析】利用二倍角公式进行化简得()2sin(2)3f x x π=+,求出最小正周期;利用左加右减得出()2cos 2g x x =为偶函数;32(,)322x πππ+∈,函数单调递减;令2232x k πππ+=+,求出函数取最大值时x 的集合.【详解】)22()2sin cos sin cos sin 22f x x x x x x x=--=+2sin(2)3x π=+(1)最小正周期为2=2ππ ;(2)()y f x =的图象向左平移12π个单位得到()2sin[2(]2sin(2)2cos 21232g x x x x πππ=++=+= ,()2cos(2)2cos 2()g x x x g x -=-==,所以()g x 为偶函数;(3)当7(,)1212x ππ∈ 时,32(,)322x πππ+∈,所以函数()2sin(2)3f x x π=+在7(,1212ππ上单调递减;(4)令2232x k πππ+=+ ,得到{|,}12x x k k z ππ=+∈,并且{|}{|,}1212x x x x k k z πππ==+∈Ø,函数()y f x =取得最大值”的一个充分条件是“12x π=”.所以正确的有3个.故选:D【点睛】二倍角公式的熟练运用,将函数化简为最简形式,求最小正周期,平移,单调区间,以及最值等都要熟练掌握.第Ⅱ卷(共105分)二、填空题10. i 是虚数单位,则复数312ii-=+___________.【答案】1755i -【解析】【分析】对复数进行分母实数化即可化简.【详解】()()()()3123171212125i i i i i i i ----==++-1755i =-11. 若2nx ⎛⎝展开式的二项式系数之和为64,则展开式中的常数项是___________.【答案】60【解析】【分析】先根据二项式系数之和求出n ,然楼根据展开式的通式,令x 的次数为零即可得常数项.【详解】由2nx ⎛ ⎝展开式的二项式系数之和为64得264n=,解得6n =,即62x ⎛- ⎝,其展开式的通式为()()36662166C 212C rrr r r r r r T x x ---+⎛==- ⎝令3602r-=得4r =,()42441612C 60T +∴=-=故答案为:60.12. 一袋中有大小相同的4个红球和2个白球若从中任取3球,则恰有一个白球的概率是__________,若从中不放回的取球2次,每次任取1球,记“第一次取到红球”为事件A , “第二次取到红球”为事件B ,则()|P B A =__________.【答案】 ①.35 ②. 35【解析】【分析】(1)直接使用公式;(2)条件概率公式的使用.【详解】恰有一个白球的概率12243635C C P C ==;由题可知A =“第一次取到红球”, B =“第二次取到红球”,则()23P A =,()432655P AB ⨯==⨯,所以()()()3|5P AB P B A P A ==.故答案为:35,35.13. 已知正数a ,b 满足1a b +=,则1aa b+的最小值是___________.【答案】3【解析】【分析】利用“1的代换”将1aa b +转化为1a b a b a a b a b++=++,最后利用基本不等式求得最小值即可.【详解】解:因为正数a ,b 满足1a b +=,则1113a a b a b a a b a b a b ++=+=++≥+=,当且仅当a b b a =且1a b +=即12a b ==时取等号,此时1aa b+的最小值3.故答案为:3.【点睛】在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.14. 已知圆C 圆心坐标是(0,)m ,若直线230x y -+=与圆C 相切于点(2,1)A --,则圆C 的标准方程为___________.【答案】22(2)5x y ++=【解析】【分析】根据圆心和切点的连线与直线230x y -+=垂直列方程,由此求得m 的值,利用两点间的距离的公式求得圆的半径,进而求得圆的标准方程.【详解】因圆心坐标为(0,)m ,直线230x y -+=与圆C 相切于点(2,1)A --根据圆心和切点的连线与直线230x y -+=垂直,所以(1)10(2)2m --=---,解得2m =-,根据两点间的距离公式,可得圆C的半径r ==故圆C 的标准方程为22(2)5x y ++=.故答案为:22(2)5x y ++=15. 已知平行四边形ABCD 中,4AB =,2AD =,8AC AD ⋅= ,则AC = ________;若CE ED =,DF DB λ= ,则AF FE ⋅的最大值为________.【答案】 ①.②.114【解析】【分析】由8AC AD ⋅= 求出AB AD ⋅,然后由AC AB AD =+ 平方后求得AC ,把,AF FE 用,AB AD表示后求数量积化为λ的函数可得最大值.【详解】由已知AC AB AD =+,所以2()8AC AD AB AD AD AB AD AD ⋅=+⋅=⋅+= ,所以4AB AD ⋅=,AC AB AD =+===;因为CE ED = ,DF DB λ=,所以()(1)AF AD DF AD DB AD AB AD AB AD λλλλ=+=+=+-=+- ,11(1)()22FE AD DE AF AD AB AB AD AB AD λλλλ=+-=+---=-+ ,AF FE ⋅= 222131()(2)(1)222AB AB AD ADλλλλλλ-+-+⋅+- 213116()4(24(1)222λλλλλλ=-+-++-22111112()212()244λλλ=--+=--+,所以14λ=时,AF FE ⋅ 取得最大值114.故答案为:;114.为三、解答题16. 在ABC ∆中,角,,A B C 的对边分别为,,a b c ,4B π=,c =ABC ∆的面积为6.(1)求a 及sin A 的值;(2)求26sin A π⎛⎫- ⎪⎝⎭的值.【答案】(1)4;(2.【解析】【详解】试题分析:(1)由4B π=,c =,ABC ∆的面积为6可求得a 的值,利用余弦定理可求得b =sin A 的值;(2)利用(1)的结论,由同角三角函数之间的关系可求得cos A ,再利用二倍角的正弦公式、二倍角的余弦公式以及两角差的正弦公式可得26sin A π⎛⎫-⎪⎝⎭的值.试题解析:(1)由已知,,,且,b ∴= ,在中,,.(2) , 又,,,sin 2sin2.cos cos2.sin 666A A A πππ⎛⎫∴-=- ⎪⎝⎭431552⎛⎫=--⨯=⎪⎝⎭ .17. 如图,在四棱锥P -ABCD 中,底面ABCD 是直角梯形,90ABC BAD ∠=∠=︒,AP ⊥平面ABCD ,222AB BC AP AD ====,点M 、N 分别为线段BC 和PD 的中点.(1)求证:AN ⊥平面PDM ;(2)求平面PDM 与平面PDC 夹角的正弦值;(3)在线段PC (不包括端点)上是否存在一点E ,使得直线BE 与平面PDC 所成角的正弦值为23,若存在,求出线身PE 的长:若不存在,请说明理由.【答案】(1)证明见解析; (2)13; (3)存在,PE =13.【解析】【分析】(1)证明AN ⊥PD ,再证MD ⊥平面APD 得MD ⊥AN 即可;(2)以A 为原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,求出各点坐标,求出平面PDM 和平面PDC 的法向量,利用向量方法即可求解;(3)利用(2)【小问1详解】方法一:∵AD BC ∥,且12AD BC =,∴BM ∥AD ,且BM =AD ,∴四边形ADMB 是平行四边形,∴AB DM ∥,∵90BAD ∠=︒,则AD ⊥DM ,∵AP ⊥平面ABCD ,DM⊂平面ABCD ,∴AP ⊥DM ,又AD AP A = ,∴DM ⊥平面PAD ,又AN ⊂平面PAD ,∴DM ⊥AN ,∵AP AD =,N 是PD 的中点,∴PD ⊥AN ,又DM PD D = ,PD 、DM⊂平面PDM ,∴AN ⊥平面PDM ;方法二:以A 为原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.则()0,0,0A ,()2,0,0B ,()2,2,0C ,()0,1,0D ,()0,0,1P ,()2,1,0M ,110,,22N ⎛⎫ ⎪⎝⎭.则()0,1,1PD =- ,()2,0,0DM =,110,,22AN ⎛⎫= ⎪⎝⎭.设平面PDM 的法向量为(),,m x y z =,则00m PD m DM ⎧⋅=⎪⎨⋅=⎪⎩,即020y z x -=⎧⎨=⎩,取1y =,则1z =,0x =,则()0,1,1m = ,∴12AN m = ,则AN m ∥,∴AN ⊥平面PDM ;【小问2详解】()0,1,1PD =- ,()2,1,0DC =,设平面PDC 的法向量为(),,n a b c = ,则00n PD n DC ⎧⋅=⎪⎨⋅=⎪⎩ ,则020b c a b -=⎧⎨+=⎩,取2b =,则1a =-,2c =,则()1,2,2n =- ,由(1)知平面PDM 的一个法向量为()0,1,1m =,设平面PDM 与平面PDC 的夹角为θ,则cos cos ,m n m n m nθ⋅=〈〉=== ,∴1sin 3θ==,∴平面PDM 与平面PDC 夹角的正弦值为13;【小问3详解】假设存在点E ,设()01PE PC λλ=<<,()2,0,1BP =- ,()2,2,1PC =-,()2,2,PE λλλ=- ,则()22,2,1BE BP PE λλλ=+=--,设直线BE 与平面PDC 所成角为ϕ,由(2)知平面PDC 的一个法向量为()1,2,2n =-,则2sin cos ,3BE n BE n BE n ϕ⋅=<>===,化简得291010λλ-+=,即()()9110λλ--=,∵01λ<<,∴19λ=,故19PE PC = ,∵()2,2,1PC =-,则3PC = ,∴1113993PE PC ==⨯= ,∴线段PE 的长为13.18. 已知椭圆C :22221x y a b +=(0a b >>)的离心率e =,点(),0A a 、()0,B b之间的距离为(1)求椭圆C 的标准方程;(2)若经过点(且斜率为k 的直线l 与椭圆C 有两个不同的交点P 和Q ,则是否存在常数k ,使得OP OQ + 与AB共线?如果存在,求k 的值;如果不存在,请说明理由.【答案】(1)2212x y +=;(2)不存在,理由见解析.【解析】【分析】(1)根据两点间距离公式,结合椭圆离心率公式进行求解即可;(2)设出直线l 的方程与椭圆的标准方程联立,根据一元二次方程根与系数关系、根的判别式,结合平面向量线性运算的坐标公式、平面共线向量的性质进行求解判断即可.【小问1详解】因为点(),0A a 、()0,B b=e =,所以有c a =,而222a b c =+,因此组成方程组为:2222221a c a b a b c =⎧⎪==⇒⇒⎨⎨=⎩⎪=+⎪⎩2212x y +=;【小问2详解】设l的方程为y kx =22221(12)202x y k x y kx ⎧+=⎪⇒+++=⎨⎪=+⎩,于是有2221)4(12)202k k -+⋅>⇒>,此时设1222(,),(,)P x y Q x y ,于是有12x x +=,假设存常数k ,使得OP OQ +与AB共线,因为1212(,)OP OQ x x y y +=++,(,)(ABa b =-= ,12121212)()()y y x x kx kx x x +=-+⇒+=-+,1212()4()x x x x ⇒++=-+,因为12x x +=,4k =⇒=,不满足212k >,因此不存在常数k ,使得OP OQ + 与AB共线.【点睛】关键点睛:利用一元二次方程的判别式和根与系数的关系是解题的关键.19. 已知等比数列{}n a 的前n 项和为n S ,0n a >且1336a a =,()34129a a a a +=+.(1)求数列{}n a 的通项公式;(2)若13n bn S +=,求数列{}n b 及数列{}n n a b 的前n 项和n T .在(3)设()()111nn n n a c a a +=++,求{}n c 的前2n 项和2n P .【答案】(1)1*23(N )n n a n -=⨯∈;(2)()2131,22n n n n b n T -⨯==+;(3)2116432n -⨯+.【解析】【分析】(1)由()()212129a a q a a +=+及0n a >可得q 的值,由1336a a =可得1a 的值,可得数列{}n a 的通项公式;(2)由13n bn S +=可得n b n =,可得n n a b =123n n -⨯,利用错位相减法即得;(3)可得()()11123111()2231231231231n n n n n nc ---⨯==-⨯+⨯+⨯+⨯+,利用裂项相消法即得.【小问1详解】由题意得:()34129a a a a +=+,可得()()212129a a q a a +=+,∴29q =,由0n a >,可得3q =,由1336a a =,可得22136a q =,∴12a =,可得1*23(N )n n a n -=⨯∈;【小问2详解】由123n n a -=⨯,可得1(1)2(31)31131n n n n a q S q --===---,由13n bn S +=,可得3113n b n -+=,∴n b n =,可得{}n n a b 的通项公式:n n a b =123n n -⨯,可得:01221232232332(1)323n n n T n n --=⨯+⨯⨯+⨯⨯++⨯-⨯+⨯⨯ ,12313232232332(1)323n n n T n n -=⨯+⨯⨯+⨯⨯++⨯-⨯+⨯⨯ ,∴112313(31)222323232323222331n n nnn T n n ----=+⨯+⨯+⨯++⨯-⨯⨯=+⨯-⨯⨯- 23323n n n =+--⨯(12)31nn =-⨯-,∴(21)3122n n n T -⨯=+;【小问3详解】由()()111nn n n a c a a +=++,可得()()11123111()2231231231231n n n nn n c ---⨯==-⨯+⨯+⨯+⨯+,可得:2n P =2121111111()237719231231n n --+-++-⨯+⨯+ 2111(23231n =-⨯+2116432n =-⨯+.20. 已知函数221()2ln (R)2f x a x x ax a =-++∈.(1)当1a =时,求曲线()y f x =在()()1,1f 处的切线方程;(2)求函数()f x 的单调区间;(3)当a<0时,求函数()f x 在区间[]1,e 的最小值.【答案】(1)32y =(2)答案见解析(3)()()2min2211,,022e 12ln 2,,221e 2e e,,22a a f x a a a a a a ∞⎧⎡⎫+∈-⎪⎪⎢⎣⎭⎪⎪⎛⎫=--∈--⎨ ⎪⎝⎭⎪⎪⎛⎤-++∈--⎪ ⎥⎝⎦⎩【解析】【分析】(1)根据切点和斜率求得切线方程.(2)求得()f x ',对a 进行分类讨论,由此求得()f x 的单调区间.(3)结合(2)中()f x 的单调区间,对a 进行分类讨论,从而求得函数()f x 在区间[]1,e 的最小值.【小问1详解】当1a =时,21()2ln 2f x x x x =-++,∴()312f =,2()1f x x x '=-++,∴()01f '=,故切线方程为:32y =.【小问2详解】221()2ln 2f x a x x ax =-++,∴22(2)()()a x a x a f x x a x x+-=-++=',0x >,∴①当0a =时,()0f x x '=>,∴()f x 仅有单调递增区间,其为(0,)+∞,②当0a >时,20x a +>,∴当(0,)x a ∈时,()0f x '<;当(,)x a ∈+∞时,()0f x '>,∴()f x 的单调递增区间为(,)a +∞ ,单调递减区间为(0,)a .③当a<0时,0x a ->,∴当(0,2)x a ∈-时,()0f x '<;当(2,)x a ∈-+∞时,()0f x ¢>.∴()f x 的单调递增区间为(2,)a -+∞,单调递减区间为(0,2)a -.综上所述:当0a =时,()f x 仅有单调递增区间,单调递增区间为(0,)+∞.当0a >时,()f x 的单调递增区间为(,)a +∞,单调递减区间为(0,)a .当a<0时,()f x 的单调递增区间为(2,)a -+∞,单调递减区间为(0,2)a -.【小问3详解】当a<0时,由(2)中③知,()f x 在(0,2)a -上单调单调递减,在(2,)a -+∞上单调递增,∴①当021a <-≤,即1,02a ⎡⎫∈-⎪⎢⎣⎭时,()f x 在[]1,e 上单调递增,min 1()(1)2f x f a ==+,②当12e a <-<,即e 1,22a ⎛⎫∈-- ⎪⎝⎭时,()f x 在(1,2)a -上单调递减,在(2,e)a -上单调递增,∴2min ()(2)2ln(2)f x f a a a =-=--,③当2e a -≥,即e ,2a ∞⎛⎤∈-- ⎥⎝⎦时,()f x 在[]1,e 上单调递减,∴22min 1()(e)2e e 2f x f a a ==-++.第17页/共17页∴()()2min 2211,,022e 12ln 2,,221e 2e e,,22a a f x a a a a a a ∞⎧⎡⎫+∈-⎪⎪⎢⎣⎭⎪⎪⎛⎫=--∈--⎨ ⎪⎝⎭⎪⎪⎛⎤-++∈--⎪ ⎥⎝⎦⎩.【点睛】利用导数研究函数的单调区间,首先要求函数的定义域,当导函数含有参数时,要对参数进行分类讨论,分类讨论要做到不重不漏.。
语文丨天津市四校联考2021届高三第一学期12月阶段性检测语文试卷及答案

静海区2020—2021学年度第一学期12月份四校阶段性检测高三语文本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,试卷满分150分。
考试时间150分钟。
第Ⅰ卷一、(9分,每小题3分)“薜荔”是古诗文中的意象。
古代文人仕途困惑,怀才不遇,身处逆境,常借薜荔抒情,以解心愁。
中唐诗人柳宗元被贬柳州时写道“惊风乱飐芙蓉水,密雨斜侵薜荔墙”,晚唐诗人沈彬亦有诗云“薜荔惹烟笼蟋蟀,芰荷翻雨泼鸳鸯”,诗中因薜荔而生出凄楚的意味。
有趣的是,薜荔也有另外一面,薜荔不,在寂寞中生长,延伸着碧绿的藤蔓,任密雨侵,依然绿意盎然,活出自己的精彩。
屈原《离骚》中就有“揽木根以结茝兮,贯薜荔之落蕊”的诗句,借薜荔这种芳草来表达清高芳洁之意,夏天来了,薜荔更显出一片生机,藤条,坚韧地攀缘吸附于墙壁,构成一扇天然的绿壁,任凭风雨雷电轰击,也不能撕扯分离它们。
()。
待到挂果时,薜荔藤叶丛里挂满了青果,煞是可爱,初唐宋之问“薜荔摇青气,桄榔翳碧苔”,描写了蔓生浓绿的薜荔、亭亭玉立的桄榔与碧苔相映成趣的景致,令人。
1. 依次填入文中横线上的成语,全都恰当的一项是()A. 司空见惯同流合污青云直上心驰神往B. 层出不穷随波逐流青云直上爽心悦目C. 司空见惯随波逐流扶摇直上心驰神住D. 层出不穷同流合污扶摇直上爽心悦目2. 文中画横线的句子有语病,下列修改最恰当的一项是()A. 古代一些文人仕途不顺,他们怀才不遇,身处逆境,常借薜荔抒情,以解心愁。
B. 古代文人仕途多困惑或怀才不遇,或身处逆境,常借薜荔抒情,以解心愁。
C. 古代文人仕途不顺或怀才不遇,他们常常为解心愁而借薛荔抒情。
D. 古代文人大多仕途困惑或怀才不遇,他们身处逆境之时常借薜荔抒情,以解心愁。
3. 下列在文中括号内补写的语句,最恰当的一项是()A. 若是晴朗的夏日,远远去仿佛一片彩霞,阳光为它涂上一层金色B. 若是天气晴朗,阳光为它涂上一层金色,远远望去仿佛一片彩霞C. 远远望去,阳光为它涂上一层金色,简直是一片彩霞D. 远远望去,简直是一片彩霞,阳光为它涂上一层金色二、阅读下面的文字,完成下面小题。
天津市北部四区高三年级12月联考(政治)

天津市和平区2007—2008学年度第二学期高三年级第二次质量调查数学(文)试卷本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分。
第I 卷(选择题,共50分)一. 选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知向量)2,1(),,218(+=+=x x x ,其中0>x ,若//,则x 的值为( ) A. 8 B. 4 C. 2 D. 02. 已知集合},1log |{},,11|{2R x x x B R x x x A ∈<=∈≤-=是“x ∈A ”是“x ∈B ”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 53)4sin(=-x π,则x 2sin 的值为( )A. 257B. 2514C. 2516D. 25194. 若βα,是两个不同的平面,m ,n 是两条不同的直线,则下列命题不正确...的是( ) A. αβα⊥m ,//,则m ⊥βB. m//n ,m ⊥α,则n ⊥αC. n//α,n ⊥β,则α⊥βD. α∩β=m ,n 与α,β所成角相等,则m ⊥n5. 函数)13(log )(-=x x f a (0>a 且1≠a )的反函数的图象过定点( ) A.(1,0) B.(0,1) C.(0,32) D.(32,0) 6. 函数)(x f y =在定义域(3,23-)内可导,其图象如下图所示,记)(x f y =的导函数为)(x f y '=,则不等式0)(≤'x f 的解集为( )A. )3,2[]1,31[⋃- B. ]38,34[]21,1[⋃-C. )2,1[]21,23(⋃-D. )3,38[]34,21[]1,23(⋃⋃--7. 在等差数列}{n a 中,有48)(2)(31310753=++++a a a a a ,则此数列前13项之和为( )A. 24B. 39C. 52D. 104那么第5组的频率为( ) A. 0.15 B. 0.1 C. 10 D. 159. 设F 1、F 2是双曲线-22a x 122=by (0,0>>b a )的两个焦点,P 在双曲线上,若021=⋅PF ac 2=(c 为半焦距)则双曲线的离心率为( )A.213- B. 213+ C. 2 D. 215+ 10. 设正数x ,y 满足y x y x 222log log )3(log +=++,则x+y 的取值范围是( ) A. ),71[+∞+ B.(0,71+) C. ),6[+∞ D. ]6,0(第II 卷(非选择题 共100分)二. 填空题:本大题共6小题,每小题4分,共24分。
天津市北部四区高三年级12月联考
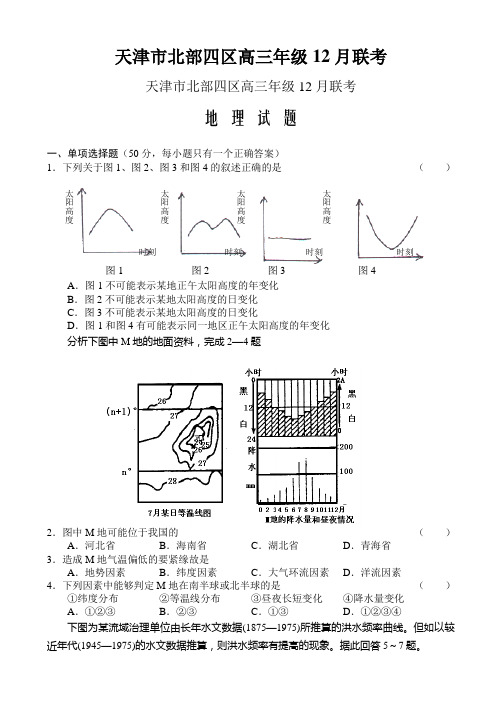
天津市北部四区高三年级12月联考天津市北部四区高三年级12月联考地 理 试 题一、单项选择题(50分,每小题只有一个正确答案) 1.下列关于图1、图2、图3和图4的叙述正确的是 ( )A .图1不可能表示某地正午太阳高度的年变化B .图2不可能表示某地太阳高度的日变化C .图3不可能表示某地太阳高度的日变化D .图1和图4有可能表示同一地区正午太阳高度的年变化 分析下图中M 地的地面资料,完成2—4题2.图中M 地可能位于我国的 ( )A .河北省B .海南省C .湖北省D .青海省 3.造成M 地气温偏低的要紧缘故是 A .地势因素 B .纬度因素 C .大气环流因素 D .洋流因素 4.下列因素中能够判定M 地在南半球或北半球的是 ( ) ①纬度分布 ②等温线分布 ③昼夜长短变化 ④降水量变化 A .①②③ B .②③ C .①③D .①②③④下图为某流域治理单位由长年水文数据(1875—1975)所推算的洪水频率曲线。
但如以较近年代(1945—1975)的水文数据推算,则洪水频率有提高的现象。
据此回答5~7题。
太阳高度太阳高度太阳高度太阳高度时刻 时刻 时刻 时刻图1 图2 图3 图45.原百年—次的洪水位,在1945年一1975年的洪水频率曲线上其再现周期约为()A.70年B.50年C.20年D.10年6.开始显现灾难的水位,在1945年一1975年的洪水频率曲线上,其再现周期较1875年至1975年的洪水频率曲线约缩短了()A.1年B.3年C.5年D.7年7.如该流域的降雨量及降雨特性没有变化,那么近年洪水频率提高的缘故最有可能的是()①河道疏浚②旱田还牧③水田转作④林地转牧⑤都市化⑥地下水禁用A.①②③B.①②⑥C.③④⑤D.①③⑤8.下面四幅等高线图所示各项内容正确的是()9.目前,青藏地区要紧的运输方式是()A.公路运输B.内河航运C.铁路运输D.航空运输10.下列现象之间呈正相关的是()A.海水的温度和盐度B.太阳黑子和降水量的变化周期C.土壤有机质和土壤肥力D.气温顺气压11.读我国“西气东输”路线示意图,下列正确的是()A.从西向东依次通过第一、二、三阶梯B.自西向东依次通过玉门油田、陕甘宁天然气田C.向西向东依次通过北疆线、兰新线、陇海线、京沪线D.自西向东依次通过南疆棉田、鲁北棉田、长江下游滨海、沿江棉田12.云贵高原、青藏高原、河套平原、新疆的农业,它们各自具有的特色依次是()A.河谷农业、绿洲农业、灌溉农业、坝子农业B.灌溉农业、河谷农业、绿洲农业、坝子农业C.坝子农业、灌溉农业、绿洲农业、河谷农业D.坝子农业、河谷农业、灌溉农业、绿洲农业13.埃及大金字塔高度从建成时期的146.5米降至现在的136.5米,其高度变化的缘故是()A.遭受尼罗河洪水的冲刷作用B.遭受风沙的腐蚀作用C.遭受人为的破坏作用D.遭受强烈的地震作用14.解决京津唐地区供水紧张问题,目前最有效的方法是()A.节约用水,实行跨流域调水B.人工降水C.大量抽取地下水D.回收净化被污染的废水15.下列描述,其序号与所指名胜相符且排序完全正确的一组是()①奇松、怪石、云海、温泉②山奇、水秀、石美、洞异③会当凌绝顶,一览众山小④横看成岭侧成峰,远近高低各不同A.①庐山②泰山③桂林④黄山B.①黄山②桂林③泰山④庐山C.①桂林②泰山③黄山④庐山D.①泰山②庐山③黄山④桂林16.对“一场秋雨一场寒”感受最明显的都市是()A.拉萨B.郑州C.海口D.乌鲁木齐17.2001年11月,中科院宣布我国已成为少数几个把握煤变石油技术的国家之一,我国把握这项技术的重要意义是A.能够提高煤炭的利用效率B.能够改变我国的能源消费结构C.能够降低对空气污染的程度D.能够缓解我国石油缺口18.我国已连续8年成为世界上外商直截了当投资最多的进展中国家,平均每年都有400亿美圆以上的国际资金流入中国。
(定稿)2024年天津市十二区重点学校高三毕业班联考(一)答案
2024年天津市十二区重点学校高三毕业班联考(一)数学参考答案一、选择题:每小题5分,满分45分10. }1{- 11. 189- 12. 72 13.51;32 14. b a 3431+ ;3134- 15. )(),322,22322(----- 三、解答题:本大题5小题,共75分.解答应写出文字说明,证明过程或演算步骤. (16)(本小题满分14分) 解析:(I )由正弦定理得:(2sin )cos cos A C B B C =,…………1分显然则, …………3分又,故; …………4分∴由余弦定理可得,整理可得2233a b a -+=, …………5分又2a b +=,解得1a b ==, …………6分 ∴; …………8分(III )由正弦定理得:,则1sin A , …………9分∵b =,即,则B A >,故A 为锐角,∴cos A,…………10分∴,…………11分,…………12分∴. …………14分(17)(本小题满分15分)解析(I)【方法1】在三棱柱111ABC A B C-中,连接11AB A B E=,连接DE,由1//AC C P,D是棱1CC的中点,得D是AP的中点,由11ABB A为平行四边形,得E为线段1AB中点,于是1//DE PB,而DE⊂平面1BDA,1PB⊄平面1BDA,所以1//PB平面1BDA.【方法2】在三棱柱111ABC A B C-中,1A A⊥平面ABC,90BAC∠=︒,则直线11111,,A B AC A A两两垂直,以点1A为原点,直线11111,,A B AC A A分别为,,x y z轴建立空间直角坐标系,…………1分由21===AAACAB,得),(0,01A,),(0,021B,),(2,02B,),(1,2D,),(2,0A,),(2,2C,),(2,11M,),(0,4P…………2分设平面1BDA的法向量(,,)n x y z=,则),2,02(1=BA,),1,20(1=DA则⎪⎩⎪⎨⎧=+=⋅=+=⋅22211zyDAmzxBAn,令1=y,得),(2,12-=n,…………4分),(0,421-=PB 因为004221=+-⨯=⋅n PB ,所以n PB ⊥1 又因为⊄1PB 平面1BDA ,所以1//PB 平面1BDA . …………5分 (II )由(I )平面1BDA 的法向量),(2,12-=n ,又),2,31(--=MP , 则52145314|432||||||cos |=⨯++-==><n MP n MP n MP ,…………9分所以直线MP 与平面1BDA 所成角的正弦值为52145 …………10分 (III )设平面1MPB 的一个法向量)(z y x m ,,=,),1,11(1-=M B ,),0,42(1-=P B , 则⎪⎩⎪⎨⎧=+-=⋅=++-=⋅0420211y x P B m z y x M B m 令1=z ,的),(1,24=m 设平面1MPB 与平面1BDA 夹角为θ,则63218321|228||||||cos |cos =⨯-+==><=n m n m n m ,θ, …………13分所以平面1MPB 与平面1BDA 夹角的余弦值63218. …………15分 (18)(本小题满分15分)解(I ):设椭圆的半焦距c ,由题意知⎪⎪⎪⎩⎪⎪⎪⎨⎧+===+222223221431c b a b c b a ,解得⎪⎩⎪⎨⎧==1422b a , 椭圆的方程1422=+y x …………5分(II )分析得B A ,两点关于x 轴对称,由题意直线PA 斜率k 存在且不为0,并且纵截距不为0设直线(),,:00≠≠+=m k m kx y PA …………6分⎪⎭⎫⎝⎛-0,k m M …………7分 ⎪⎩⎪⎨⎧+==+m kx y y x 1422,化简得()044841222=-+++m kmx x k , …………8分 设()()2211,,,y x P y x A ⎪⎪⎪⎩⎪⎪⎪⎨⎧>∆+-=⋅+-=+041444182221221k m x x k km x x , …………10分 直线(),212122x x x x y y y y BP --+=-: …………11分,0=y 令()()()()12122112212212221212.y y y x y x y y x y y y x x x y y y x x x N ++=+++--=+-+-=()()()()mx x k x x m x kx m kx m kx m kx x m kx x 22212121121221++++=++++++=m k m k km k k km m k m k 42418418414422222-=+⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛+-=…………14分所以44=-⋅-=⋅kmm k ON OM . …………15分(19)(本小题满分15分) 解析:(I )1213++=n n n a a ,1=n 令3213=a a 则92=∴a ,,2=n 令5323=a a 则273=∴a ; …………2分由1213++=n n n a a ①,∴当2n ≥时,1213--=n n n a a ②,由÷①②得,当2n ≥时,119n n a a +-=, …………3分 所以数列{}()*2N n a n ∈和数列{}()*21N n a n -∈是等比数列.因为,31=a 1213++=n n n a a ,所以,92=a所以12112393---=⋅=n n n a ,n n n a 212399=⋅=-,因此n n a 3=,从而()1322nn a n a -=>≥,所以数列{}n a 是“G 型数列”. …………6分 (II )(i )因为数列{}n a 的各项均为正整数,且{}n a 为“G 型数列”, 所以12n na a +>,所以12n n n a a a +>>,因此数列{}n a 递增.又1n nb a =+, 所以110n n n n b b a a ++-=->,因此{}n b 递增,所以公比1q >. 又{}n b 不是“G 型数列”,所以存在*0n ∈N ,使得0012n n b b +≤,所以2q ≤, …………8分又公比q 为正整数,所以2q =.又1112b a =+=,所以2nn b =,则12-=n n a . …………10分(ii )()()12121121212321232n n n n n nn n a a ++++=--=-⨯+>-⨯,因为()()21232422342n n n n n n n +-⨯=+->≥, 所以()142n n n a a n +>≥,所以)(24111≥<+n a a n n n , …………13分令∑=+=nk k k n a a S 111, 当1n =时,113S =, 当2n ≥时,231223341111111113444n n n n S a a a a a a a a +⎛⎫=+++⋅⋅⋅+<+++⋅⋅⋅+ ⎪⎝⎭21111111111154411331243121214n n --⎛⎫- ⎪⎛⎫⎝⎭=+=+-<+= ⎪⎝⎭- …………15分(其他答案酌情给分)(20)(本小题满分16分)解析:(I )2)(x x e e x ch -+=,则2)('x x e e x ch --= …………1分所以2)2(22'--=e e ch 所以)(x ch y =在2=x 处的切线斜率为222--ee …………2分(II )令x x a x e a x x G x sin 2cos )(2)1()(--+--=,则)sin 2)((cos 2sin )(2cos 2)1()('x e a x x x a x x e e a x x G x x x --=---++--= …………3分下面证明:对任意0>x ,0sin 2>-x e x 恒成立 先证明:对任意0>x ,ex e x >.证明如下:设()e e xn x x =-,则()e e xn x '=-,当(),1x ∈-∞时,()0n x '<,函数单调递减, 当()1,x ∈+∞时,()0n x '>,函数单调递增,故()()10n x n ≥=,故e e x x ≥, …………5分 继续证明:对任意0>x ,x x sin >.证明如下:令()sin g x x x =-,则()1cos 0g x x '=-≥,因此()g x 在),0(+∞上单调递增;所以()()sin 00g x x x g =-≥=,故x x sin > …………7分 当0a ≤时,对()0,x ∀∈+∞,都有0)('>x G ,函数)(x G 在()0,∞+上单调递增, 则013)0()(≥--=>a G x G ,解得31-≤a ; …………8分 当0a >时,对()0,x a ∀∈,都有0)('<x G ,对(),x a ∞∀∈+,都有0)('>x G , 函数()F x 在()0,a 上单调递减,在(),a +∞上单调递增,则对()0,x a ∀∈,都有013)0()(<--=<a G x G 成立,不符合题意,舍去. 综上所述,实数a 的取值范围是31-≤a . …………9分 (III )(ⅰ)2)(xx e e x sh --=,令x e e x x sh x F x x --=-=-2)()(,则012)('>-+=-x x e e x F 所以)(x F 在),0(+∞上单调递增,所以00)0()0()()(=-=>-=sh F x x sh x F 所以当0>x 时,x x sh >)(成立; …………10分 (ⅱ)下面证明:当0>x 时,21cos 12x x ≥-成立, 令2211cos )(x x x H +-=,则x x x H +-=sin )(' 由(II )解答过程,对任意0>x ,x x sin >成立,所以0sin )('>+-=x x x H 所以)(x H 在),0(+∞上单调递增,所以0211cos )(2>+-=x x x H 所以当0>x 时,21cos 12x x ≥-成立 …………11分 令1x n =,1n ≥且*N n ∈,可得211cos 12n n>-, 即222112211cos111124412121n n n n n n ⎛⎫>-=->-=-- ⎪--+⎝⎭, 由题意)()(2)2(x ch x sh x sh ⋅=, 令1x n =,1n ≥且*N n ∈,可得)1()1(2)2(nch n sh n sh ⋅=, 因为12)(>+=-xx e e x ch 所以)1(2)1()1(2)2(n sh n ch n sh n sh >⋅= …………12分由①当0>x 时,x x sh >)(,所以令1x n =,1n ≥且*N n ∈,可得nn sh 1)1(>所以nn sh n ch n sh n sh 2)1(2)1()1(2)2(>>⋅= …………13分 由(II )解答过程,对任意0>x ,x x sin >成立令1x n =,1n ≥且*N n ∈,可得)1sin(1n n > …………14分 所以)nn n n n sh n ch n sh n sh 1tan()1cos(2)1sin(22)1(2)1()1(2)2(⋅=>>>⋅=又1n ≥且*N n ∈,所以101n<≤,所以)121121(1[2)1cos(2)1tan()2(+--->>n n n nn sh …………15分所以可得)121`121(1)5131(1)311(1[21tan )2(31tan )32(21tan )22(1tan )2(+---++--+-->++++n n n n sh sh sh sh 124212222+-=++-=n nn n n即可得12421tan )2(31tan )32(21tan )22(1tan )2(+->++++n n n nn sh sh sh sh ,(*N n ∈). …………16分。
天津市五校2024届高三上学期12月联考物理含答案
2023-2024天津市五校联考高三年级物理学科本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,总分100分。
答题时,将答案填涂在答题卡上,答在试卷上的无效。
第I 卷(选择题)注意事项:i .每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
ii .本试卷共8小题,共40分。
在1-5题列出的四个选项中,只有一项是符合题目要求的,每小题5分;在6-8题列出的四个选项中,有多个选项是符合题目要求的,每小题5分(选错不得分,选不全得3分)。
一、单选题1.在物理学的发展中,有许多科学家做出了重大贡献,下列说法中正确的有A .库仑通过扭秤实验测量出万有引力常量B .牛顿通过观察发现了行星运动的规律C .伽利略利用斜面实验观察到了小球合力为零时做匀速直线运动D .胡克总结出弹簧弹力与形变量间的关系2.一定质量的理想气体温度不变时,体积减小,压强增大,下列说法中正确的是A .气体分子的平均动能增大B .气体的分子势能增大C .单位时间内撞击器壁上单位面积的分子数增加D .气体从外界吸收热量3.如图所示为玻尔理论的氢原子能级图,当一群处于激发态3n =能级的氢原子向低能级跃迁时,发出的光中有两种频率的光能使某种金属发生光电效应,以下说法中正确的是A .这群氢原子由3n =能级向低能级跃迁时能发出6种不同频率的光B .这种金属的逸出功一定小于10.2eVC .用发出的波长最短的光照射该金属时产生光电子的最大初动能一定大于3.4eVD .由3n =能级跃迁到2n =能级时产生的光一定能够使该金属发生光电效应4.在某次遥控车挑战赛中,若a b 、两个遥控车从同一地点向同一方向做直线运动,它们的v t -图像如图所示,则下列说法不正确的是A .b 车启动时,a 车在其前方2m 处B .运动过程中,b 车落后a 车的最大距离为1.5mC .b 车启动3s 后恰好追上a 车D .b 车超过a 车后,两车不会再相遇5.如图所示,倾角为30°的斜面体放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的柔性轻绳与小球B连接,O点为轻绳与定滑轮的接触点。
天津市北部四区高三年级12月联考.doc
天津市北部四区高三年级12月联考地 理 试 题一、单项选择题(50分,每小题只有一个正确答案) 1.下列关于图1、图2、图3和图4的叙述正确的是 ( )A .图1不可能表示某地正午太阳高度的年变化B .图2不可能表示某地太阳高度的日变化C .图3不可能表示某地太阳高度的日变化D .图1和图4有可能表示同一地区正午太阳高度的年变化 分析下图中M 地的地面资料,完成2—4题2.图中M 地可能位于我国的 ( )A .河北省B .海南省C .湖北省D .青海省 3.造成M 地气温偏低的主要原因是 A .地形因素 B .纬度因素 C .大气环流因素 D .洋流因素 4.下列因素中可以判断M 地在南半球或北半球的是 ( ) ①纬度分布 ②等温线分布 ③昼夜长短变化 ④降水量变化 A .①②③ B .②③ C .①③D .①②③④下图为某流域管理单位由长年水文数据(1875—1975)所推算的洪水频率曲线。
但如以较近年代(1945—1975)的水文数据推算,则洪水频率有提高的现象。
据此回答5~7题。
太阳高度太阳高度太阳高度太阳高度时间 时间 时间 时间图1 图2 图3 图45.原百年—次的洪水位,在1945年一1975年的洪水频率曲线上其再现周期约为()A.70年B.50年C.20年D.10年6.开始出现灾害的水位,在1945年一1975年的洪水频率曲线上,其再现周期较1875年至1975年的洪水频率曲线约缩短了()A.1年B.3年C.5年D.7年7.如该流域的降雨量及降雨特性没有变化,那么近年洪水频率提高的原因最有可能的是()①河道疏浚②旱田还牧③水田转作④林地转牧⑤都市化⑥地下水禁用A.①②③B.①②⑥C.③④⑤D.①③⑤8.下面四幅等高线图所示各项内容正确的是()Array 9.目前,青藏地区主要的运输方式是()A.公路运输B.内河航运C.铁路运输D.航空运输10.下列现象之间呈正相关的是()A.海水的温度和盐度B.太阳黑子和降水量的变化周期C.土壤有机质和土壤肥力D.气温和气压11.读我国“西气东输”路线示意图,下列正确的是()A.从西向东依次经过第一、二、三阶梯B.自西向东依次经过玉门油田、陕甘宁天然气田C.向西向东依次经过北疆线、兰新线、陇海线、京沪线D.自西向东依次经过南疆棉田、鲁北棉田、长江下游滨海、沿江棉田12.云贵高原、青藏高原、河套平原、新疆的农业,它们各自具有的特色依次是()A.河谷农业、绿洲农业、灌溉农业、坝子农业B.灌溉农业、河谷农业、绿洲农业、坝子农业C.坝子农业、灌溉农业、绿洲农业、河谷农业D.坝子农业、河谷农业、灌溉农业、绿洲农业13.埃及大金字塔高度从建成时期的146.5米降至现在的136.5米,其高度变化的原因是()A.遭受尼罗河洪水的冲刷作用B.遭受风沙的侵蚀作用C.遭受人为的破坏作用D.遭受强烈的地震作用14.解决京津唐地区供水紧张问题,目前最有效的办法是()A.节约用水,实行跨流域调水B.人工降水C.大量抽取地下水D.回收净化被污染的废水15.下列描述,其序号与所指名胜相符且排序完全正确的一组是()①奇松、怪石、云海、温泉②山奇、水秀、石美、洞异③会当凌绝顶,一览众山小④横看成岭侧成峰,远近高低各不同A.①庐山②泰山③桂林④黄山B.①黄山②桂林③泰山④庐山C.①桂林②泰山③黄山④庐山D.①泰山②庐山③黄山④桂林16.对“一场秋雨一场寒”感受最明显的城市是()A.拉萨B.郑州C.海口D.乌鲁木齐17.2001年11月,中科院宣布我国已成为少数几个掌握煤变石油技术的国家之一,我国掌握这项技术的重要意义是A.可以提高煤炭的利用效率B.可以改变我国的能源消费结构C.可以降低对空气污染的程度D.可以缓解我国石油缺口18.我国已连续8年成为世界上外商直接投资最多的发展中国家,平均每年都有400亿美圆以上的国际资金流入中国。
2021届天津市静海区四校高三上学期12月阶段性检测物理试卷(解析版)
2021届天津市静海区四校高三上学期12月阶段性检测物理试卷本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷第1页至第2页,第Ⅱ卷第3页至第4页.试卷满分100分。
考试时间60分钟。
一、单项选择题1. 如图,水平拉力F的作用下,小车在光滑的水平面上向右加速运动时,物块A与车厢壁相对静止,当的水平拉力F增大时,则()A. 物块A受的摩擦力变大B. 物块A受的摩擦力不变C. 物块A可能相对于车厢滑动D. 车厢壁对物块A的支持力不变【答案】B【解析】【详解】设物块的质量为M,以物块为研究对象,分析受力,作出力图如图。
当作用在小车上的水平拉力F增大时,小车和物块的加速度增加。
ABD.当加速度增大时,支持力物块受到的支持力增大,竖直方向根据平衡条件可得,摩擦力f=Mg,保持不变。
故B正确、AD错误。
C.小车的加速度增大时,弹力N=ma增大,物块受到的最大静摩擦力增大,则物块A不可能相对于车厢滑动,故C错误。
故选B。
2. 下列说法正确的是()A. 一定质量的理想气体,体积越大,压强越小B. 外界对气体做功,气体内能一定增大C. 分子间作用力随分子间距离的增大而减小D. 温度越高,布朗运动越显著【答案】D【解析】【详解】A.由理想气体的状态方程pVCT=可知,在温度T不确定的情况下,体积越大,压强不一定越小,A错误;B.由热力学第一定律可知,改变气体内能的方式有做功和热传递,只考虑外界对气体做功,气体内能不一定增大,B错误;C.当分子力表现为斥力时,分子间作用力随分子间距离的增大而减小,当分子力表现为引力时,分子间距离的增大,分子间作用力先增大后减小,C错误;D.布朗运动是小微粒受到的液体分子的撞击力不平衡产生的;液体的温度越高,液体分子热运动的平均动能越大,碰撞的不平衡性越明显,布朗运动越显著,D正确。
故选D。
3. 如图所示,小球用细绳系住放在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,绳上的拉力将()A. 逐渐增大B. 逐渐减小C. 先增大后减小D. 先减小后增大【答案】D【解析】【详解】根据力的三角形法则,如图所示在小球的重力G 不变,斜面对小球的支持力方向不变时,当细绳由水平方向逐渐向上偏移时,绳上的拉力将先减小后增大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津市北部四区高三年级12月联考生 物 试 题一、选择题(单选题。
每题2分,共50分)1.水是细胞的重要组成成分,在生物体内是一种良好的溶剂,是各种生化反应的介质.在下列说法中不正确的是 ( ) A .休眠或越冬的植物体,往往是自由水与结合水的比例下降 B .水是光合作用的反应物,是最终的电子供体 C .在丙酮酸彻底分解成CO 2的过程中必须加水D .在海洋生态系统中,水是决定生物分布最重要的非生物因素2生命现象: ①生长素的浓度对根和茎生长速度的影响;②恒温动物、变温动物体温变化与温度的关系; ③光照强度与光合作用速度的关系;变量:Ⅰ CO 2的吸收量(释放量); Ⅱ 温度; Ⅲ 生长速度下列关于甲、乙、丙所表示的生命现象及a 、b 、c 所表示的变量组合正确的一组为( ) A .甲为① a 为Ⅲ; 乙为③ b 为Ⅲ; 丙为② c 为Ⅰ B .甲为② a 为Ⅱ; 乙为③ b 为Ⅲ; 丙为① c 为Ⅰ C .甲为③ a 为Ⅰ; 乙为① b 为Ⅲ; 丙为② c 为ⅡD .甲为① a 为Ⅲ; 乙为③ b 为Ⅰ; 丙为② c 为Ⅱ3.某女性产生的卵细胞中性染色体为XX ,某男性产生的精子中性染色体为XY ,它们均是 由于减数分裂过程出现异常造成的,那么它们分别可能出现在减数分裂的什么时候( ) A .前者减数第一次或第二次分裂,后者减数第一次分裂B .前者减数第二次分裂,后者减数第一次或第二次分裂C .前者减数第二次分裂,后者减数第一次分裂D .前者减数第一次分裂,后者减数第二次分裂 4.下列关于原核生物的叙述中,正确的是( )A .原核生物的遗传物质是DNA 或RNAB .细菌没有线粒体,不能进行有氧呼吸C .圆褐固氮菌的固氮基因位于拟核中的DNA 分子上D .原核生物繁殖过程中不会出现基因重组5.孟德尔通过杂交实验发现了一些有规律的遗传现象,通过对这些现象的研究他揭示出了甲乙 c遗传的两个基本定律.在下列各项中,除哪项以外,都是出现这些有规律遗传现象不可 缺少的因素 ( ) A .F 1体细胞中各基因遗传信息表达的机会相等 B .F 1自交后代各种基因型发育成活的机会相等 C .各基因在F 2体细胞中出现的机会相等 D .每种类型雌配子与每种类型雄配子相遇的机会相等 6.右图是具有两种遗传病的某家族系谱图,设甲病显性基因为A ,隐性基因为a ,乙病显性 基因为B ,隐性基因为b 。
若Ⅰ-2无乙病基因。
下列说法不正确的是()A .甲病为常染色体显性遗传病 B .乙病为性染色体隐性遗传病C .该遗传系谱中,Ⅱ-6为Ⅱ-4的直系血亲D .假设Ⅱ-4与一正常男性结婚,生下正常男孩的概率为3/87( )A .硝化细菌B .乳酸菌C .根瘤菌D .衣藻8.豌豆的圆滑种皮对皱缩种皮为显性,黄色子叶对绿色子叶是显性。
现用纯种圆滑种皮、黄色子叶的豌豆花粉,授在纯种皱缩种皮、绿色子叶的豌豆柱头上进行杂交。
将杂交所得的种子播下,自交所结的果实中( )A .圆滑种皮:皱缩种皮=3:1,子叶全部为黄色B .圆滑种皮:皱缩种皮=3:1,子叶全部为绿色C .种皮全部为圆滑,黄色子叶:绿色子叶=3:1D .种皮全部为皱缩,黄色子叶:绿色子叶=3:19.当饮食中缺碘时,人的甲状腺会代偿性增生。
那么人体在轻度慢性缺氧环境下生活时, 一般不会出现的现象是( )A .血液中的红细胞数目会增加B .红细胞内运输氧气的血红蛋白会增加C .细胞中线粒体的数量会增加D .线粒体中酶的含量会减少10.右图为发育着的胚珠结构示意图,下列有关此图的叙述中不正确的是 ( )甲病男女甲、乙两病男 正常男女ⅠⅡ3456A .②和③的发育起点相同B .④处细胞中的染色体有2/3来自雌配子C .在正常情况下,若①的基因型为aa ,②的基因型为Aa ,则④的基因型为Aaa D .②将发育成种子,①将发育成果皮 11.右图表示在土壤溶液中施入阴离子肥料数量不等的两种条件下,谷物产量和施入的阳离子肥料数量之间的关系曲线图。
据图判断, 土壤在用20kg (hm 2)-1阳离子和20kg (hm 2)阴离子施入时,限制谷物产量的因素( )A .只有阳离子B .只有阴离子C .两种离子都不是D .两种离子都是12.下列有关基因的说法中,正确的是 ( )A .水稻(体细胞中含12对染色体)的单倍体基因组由13条双链DNA 分子组成B .已知某真核生物的一条多肽链的氨基酸序列,就能确定其基因编码区脱氧核苷酸序列C .酵母菌细胞基因的编码区中存在非编码序列D .基因的编码区下游的非编码区中含有终止密码子 13.下列过程中利用基因重组原理的是 ( )①大肠杆菌生产人的胰岛素 ②克隆羊“多莉”的产生 ③“试管婴儿”的培育 ④通过嫁接繁殖优质苹果 ⑤基因治疗 ⑥我国育种专家袁隆平利用杂交方法培育出的“超级水稻” A .①②③⑤ B .②④⑥ C .①③⑤⑥ D .②④⑤ 14.由于海水污染,某养殖场测试海带吸碘能力下降。
主要原因是 ( ) A .海带的呼吸强度减弱 B .海水中碘离子浓度下降 C .海带细胞膜上的载体种类减少 D .海带细胞膜上的载体数目减少 15.在缺硼的土地上,不适宜种植 ( ) A .白菜 B .甘蔗 C .萝卜 D .大豆16.1995年,我国培育出了抗棉铃虫效果明显的“抗虫棉”新品系。
抗虫棉细胞内的抗虫基因在表达过程中,在细胞核内形成信使RNA 。
则信使RNA 至少要穿越( )层磷脂分子,才能从细胞核中到达核糖体上指导蛋白质的合成。
( ) A .3 B .2 C .1 D .0 17.组织培养出来的植物一般很少有植物病毒危害,其主要原因在于 ( ) A .进行组织培养的过程都是在无菌条件下进行的 B .人工配制的培养基上,植物病毒根本无法生存 C .组织培养出来的植物体内水分太少,无机盐含量高 D .在组织培养过程中细胞进行的是快速分裂和分化 18.健康是人类社会永恒的主题,各种疾病在不同程度上影响着人们的健康,下列关于各种疾病的叙造正确的是( )20kg/hm 2 阳离子kg/hm 250kg/hm 2A .给低血糖晚期的患者吃一些含糖较多的食物或喝一杯浓糖水就可以恢复正常B .如果人在幼年时期甲状腺激素分泌不足就会引起侏儒症C .获得性免疫缺陷综合症和风湿性心脏病都属于免疫缺陷病D .利用DNA 探针检查出肝炎病毒,为肝炎诊断提供了一种快速简便的方法 19.关于水盐平衡调节的叙述中,正确的是( )A .大肠排出的水都是食物中未被吸收的水B .人体意外失血而使血量减少时,抗利尿激素分泌增加C .钠盐在细胞外液中而钾盐在细胞内液中D .水的排出一定伴随盐的排出20.下面对生物工程的应用成果说法正确的是( )① 用白血病患者细胞中分离出的癌基因制备DNA 探针可检测肝炎② 鸡蛋白基因可在大肠杆菌或酵母苗中表达出卵清蛋白 ③ 在单抗上连接抗癌药物可制成定向消灭癌细胞的“生物导弹” ④ 利用发酵工程可获得大量微生物的代谢产物即单细胞蛋白 A . ①② B . ③④C .②③D .①④ 21.在人体的内环境中可以发生的生理过程是( )A .丙酮酸的氧化分解B .记忆细胞增殖分化成效应B 细胞、产生特异性抗体与抗原结合C .RNA 聚合酶与特定的位点结合,转录形成信使RNA 的过程D .食物中的淀粉经过消化分解成葡萄糖22.细菌的生长与温度有着密切的联系,大肠杆菌在不同温度下每产生一代所需的时间(简称代时)见下表根据上表内容作出的以下结论中,错误的是( )A .温度对微生物的生长速率有明显的影响B .温度影响细胞周期长短,可能是影响了DNA 的复制和蛋白质的合成C .大肠杆菌的代谢与酶的活性有关D .大肠杆菌生长繁殖的最适温度是40℃23.下图是两类不同植物叶片部分结构的示意图,根据图回答下列叙述合理的是 ( ) A .甲植物可能是小麦, 乙植物可能是甘蔗B .甲、乙两种植物细胞中的叶绿体都是结构完整的叶绿体C .甲、乙两种植物细胞中的光反应都可以为暗反应提供NADPH 与ATPD .对于甲植物CO 2不是影响光合作用的因素,对于乙植物叶绿体只存 在叶肉细胞24.根据美国《农业研究》杂志报道,科学家发现半胱氨酸能增强艾滋病 感染者的免疫力,对控制艾滋病病毒有奇效,下列关于氨基酸的说法中正确的是( ) A .氨基酸是合成生长激素的原料 B .细胞内的氨基酸通过脱氨基作用可以形成新的氨基酸 C .氨基酸在人体内可以作为抗原 D .氨基酸是微生物的次级代谢产物25.下图是用集合的方法,表示各种概念之间的关系,其中与图示相符的是 ( )二、非选择题(共50分) 26.(7分)下图为某DNA 分子片段图,请据图回答:(1)请用“——”连接图中所缺的化学键。
(2)图示结构主要位于大肠杆菌 和 结构中。
(3)DNA 分子复制如发生差错, (会、不会、不一定)发生变异,原因是。
(4)若该DNA 分子中A 占20%,则由它转录成的mRNA 分子中C+G 占多少? (5)若该DNA 分子片段为根瘤菌细胞中的固氮基因(G)则其分布部位及表示方法为 A .核区、G B .质粒、GG C .质粒、G D .核糖体、GG 27.(13分)右图为某种反射弧示意图,结合下述实验回答问题:(1)电激(即用电刺激)E ,结果A 发生运动反应;电刺激B,结果A反应而E无反应。
这表明图中A是,E是。
(2)用有关字母和箭头写出神经冲动在整个反射弧中的传导方向。
(3)给你提供必要的实验用具,如电刺激设备、电位测量仪等,请设计实验方案,以验证兴奋在神经纤维上和在相邻两神经元之间的传递特点(是双向的还是单向的),并预期可能的实验结果及结论。
a 验证冲动在神经纤维上的传导方法步骤:结果及结论:b验证冲动在神经元之间的传递方法步骤:结果及结论:(4)在正常情况下,你认为神经冲动在一个完整反射弧中的传导是的。
决定这一传导特点的原是。
28.(6分)下图为某草原原始部落人食物结构示意图(1)相对于森林生态系统而言,草原生态系统的主要特点是。
草原生态系统恢复力稳定性于森林生态系统。
(2)该部落人的膳食结构为70%植物,20%草食动物,10%肉食动物,若能量传递率为10%~20%,那么人获取的能量至少占生产者所固定的总能量的。
(3)该原始部落的生活状况非常艰难,科学家们建议开发生态农业来提高人们的生活水平。
建立生态农业所依据的生态学基本原理是。
(4)目前影响我国西部草原物种数量的关键生态因素是。
我国西部大开发应注意的首要问题是。
29.(10分)(一)过去人们以为作物播种密度越大,产量越高。
在保证营养需要的情况下,有人对小麦的产量与播种的关系进行了研究,结果如图所示。
