北航高等数学课件9-习题课
理论力学课第一次习题课讲义-北航-9页word资料

第一次习题课讲义第一次习题课分为两部分内容,第一部分是两个作业题,意图通过它们讲述作业中所发现和需要解决的问题,第二部分是六个习题,意图通过它们介绍解题的思路、方法以及解题步骤。
而整个习题课围绕“关联”的概念,讲述已知运动信息与待求运动信息间的关联,并有次形成解题的契机,步步为营,直至得到最终结果。
下面便是本次习题课的主要内容。
不管是在理论力学还是数学,抑或是物理等其它学科中,碰到一个问题,第一步是分析问题,分析问题性质,找出待求量与已知信息间的关联,然后根据不同的问题性质,用相应的方法予以解决。
在而实际上任何问题的分析方法也都大同小异,重要的在于总结,对不同类的问题进行归纳整理,使相应问题的基础和方法系统化、条理化。
第一个题是第一次作业的1-15,从作业可以看出它的困难在于计算的繁复,利用解析法,在极坐标系下,最后速度大小的计算是两个两项和的平方和,而加速度却是两个四项和的平方和。
1-15 杆AB 长为L ,M 在AB 杆上,AM 长为b 。
A端以均速v A 沿直线导轨CD 运动,杆AB 始终穿过套筒O ,套筒与导轨相距为a 。
取O 为极点,试用极坐标ϕ,r 表示M 点的速度和加速度。
分析:此题要求解的是M 点的运动信息,而已知的是点A 的运动信息,那我们的目的就是要设法建立这两点之间的关联,并且利用这一关联求解出M 的速度及其加速度。
而且此题明确了解题方法,那就是极坐标法,因此问题就是一个在极坐标方法中怎么描述点的运动的问题。
解:如图所示,对A 点:()()()A A t t t ρρ=r e ……………A 点的极坐标表达式,定义式而已对M 点:()()()M M t t t ρρ=r e ………….M 点的极坐标表达式,定义式而已同时A 点和M 点在空间位置上的关系为:M A b ρρ=-……………………………点M 与点A 之间的关联从而有 ()()()M A t t b t ρ=-r r e 于是点M 的速度为()()sin (cos )M A A A t t b v v b ϕρϕϕϕϕϕ=-=+-v v e e e 这其实就是第二章所讲的基点法于是点M 的加速度为…….…大小只是两项的平方和再求ϕϕ, 由几何关系可知:再对ϕ求一次导:代入,M M v a 经运算可得:第二个题是第二次作业中的补充题2,重点在于分析定点运动中瞬时转动轴的确定及其角加速度的计算。
高数第9章习题课

x2 a2
by22
cz22
1
z c c abc
由实际意义可知
M a a b a c,
bb , a b c
a c b c c
为所求切点 .
例11 求旋转 zx抛 2y2与 物平 面 xy面 2z2 之间的最短距离. 解 设P(x,y,z)为抛物 z面 x2y2上任一 ,则点 P到平x面 y2z20的距离 d, 为
2) 显式情况. 空间光滑曲面 :zf(x,y)
法向量
n(fx,fy,1)
法线的方向余弦
co s fx ,co s fy ,
1 fx 2 fy 2
1 fx 2 fy 2
cos
1
1fx2fy2
切平面方程
z z 0 f x ( x 0 , y 0 ) ( x x 0 ) f y ( x 0 , y 0 ) ( y y 0 )
x y
(t) (t)
切向量
z (t)
T ( ( t 0 ) ,( t 0 ) ,( t 0 ))
切线方程 xx0 yy0 zz0
(t0) (t0) (t0)
法平面方程
(t0)x (x0)(t0 )(y y 0 )(t0 )z( z 0 ) 0
2) 一般式情况. 空间光滑曲线 : G F((xx,,yy,,zz)) 0 0
dx hz
dxgyhz gy
代 (1 )得 入 d d u x fxfy g y g xfy g y g zh zh x.
例7 设函 ux数 3y.而 x,y是由x5方 y程 t与 方x程 2y3t2所 确 定 d.u, 求 dt
答d d案 u t1x 3 5 x y : 2 2 [3 y (3 y 2 2 t) 2 x 2 (5 x 3 t 1 )].
北京航空航天大学 线性代数 课件 空间向量

刘敬伟 博士 jwliu_2005@
机动
目录
上页
下页
返回
结束
相 关 事 宜
学习辅导用书:
《高等代数方法指导》姚幕生编---复旦大学出版社 参考书: 1.《高等代数》第三版,北京大学数学系编—高教出版社 2.《线性代数》第三版,同济大学数学系编—高教出版社 作业规格:16开作业纸,注明姓名、学号 交作业时间:每周四上完《高代》课后 答疑时间:每周三、四、五 19:00---21:00
机动 目录 上页 下页 返回 结束
2. 向量的减法
规定: b a = b + ( a ) 特别地,当 b = a 时
b a = a a = a + ( a ) = 0
a
b b a b + ( a )
a
三角不等式:
ab a b
ab a b
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
推论2. 向量a, b, c 不共面的充分必要条件是: 由k1a + k2b + k3c = 0 可以推出 k1 = k2 = k3= 0 . 由于上述命题, 使得向量的线性运算可以用 来解决有关点的共线或共面问题以及线段的 定比分割问题. 例2. 设向量a, b, c , 证明 a + b, b + c, c a 共面. 证: 因为 1(a + b) + (1)(b + c) + 1(c a)=0, 且 1, 1, 1 不全为零, 由命题3可知, a + b, b + c, c a 共面.
c=a+b.
机动 目录 上页 下页 返回 结束
北航学生高等数学教材

北航学生高等数学教材北航学生高等数学教材,是北航学院为学生准备的一本专门针对高等数学课程的教材。
该教材广泛涵盖了高等数学的各个知识点,旨在帮助学生全面、系统地掌握高等数学的理论和应用。
第一章:函数与极限本章主要介绍了函数的概念和性质,以及极限的定义与运算法则。
通过对各种函数类型的分析,学生将学会如何求解函数的极限值,并了解到极限在数学中的重要性和应用。
第二章:导数与微分导数是高等数学中的一个基本概念,本章着重介绍了导数的定义、性质和运算法则。
通过学习导数的应用,学生将能够求解函数的最值和刻画函数的变化趋势。
第三章:数列与级数数列与级数是高等数学中的另一个重要概念,本章主要介绍了数列的定义、性质和收敛定理。
通过对各类数列和级数的分析,学生将能够判断数列和级数的收敛性,并应用相关技巧解决实际问题。
第四章:多元函数在现实生活和科学研究中,许多问题需要用多元函数来进行描述和求解。
本章通过引入多元函数的概念和性质,以及对偏导数和全微分的讨论,使学生能够理解多元函数的特点和应用。
第五章:多重积分多重积分是数学中的一个重要工具,本章着重介绍了二重积分和三重积分的定义、性质和计算方法。
通过学习多重积分的应用,学生将能够解决多元函数相关的面积、体积等问题。
第六章:曲线与曲面积分曲线与曲面积分是多元函数积分的扩展,本章主要介绍了曲线积分和曲面积分的定义、性质和计算方法。
通过学习曲线积分和曲面积分的应用,学生将能够解决与流体力学、电磁学等领域相关的实际问题。
第七章:无穷级数无穷级数在数学中具有重要地位,本章主要介绍了数项级数和函数项级数的性质、应用和判敛方法。
通过学习无穷级数的应用,学生将能够解决与泰勒级数、傅里叶级数等相关的实际问题。
第八章:常微分方程常微分方程是数学中重要的一部分,本章主要介绍了一阶和二阶常微分方程的基本概念、解法和应用。
通过学习常微分方程的应用,学生将能够解决与物理、工程等领域相关的实际问题。
通过对北航学生高等数学教材的系统学习,学生将能够全面、深入地理解高等数学的理论和应用,提高数学分析和问题解决能力。
高等数学 课后习题答案第九章
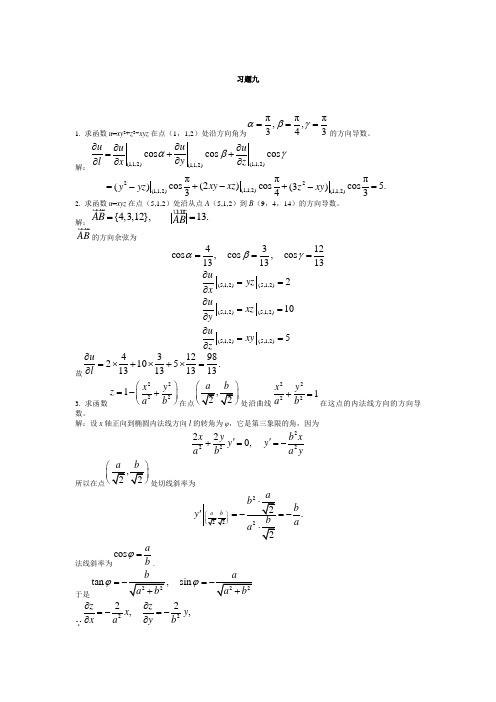
习题九1. 求函数u =xy 2+z 3-xyz 在点(1,1,2)处沿方向角为πππ,,343αβγ===的方向导数。
解:(1,1,2)(1,1,2)(1,1,2)cos cos cos u u u uy l x z αβγ∂∂∂∂=++∂∂∂∂22(1,1,2)(1,1,2)(1,1,2)πππcoscos cos 5.(2)()(3)343xy xz y yz z xy =++=---2. 求函数u =xyz 在点(5,1,2)处沿从点A (5,1,2)到B (9,4,14)的方向导数。
解:{4,3,12},13.AB AB ==AB的方向余弦为4312cos ,cos ,cos 131313αβγ=== (5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)2105uyz x uxz yuxy z ∂==∂∂==∂∂==∂故4312982105.13131313u l∂=⨯+⨯+⨯=∂ 3. 求函数22221x y z a b ⎛⎫=-+ ⎪⎝⎭在点处沿曲线22221x y a b +=在这点的内法线方向的方向导数。
解:设x 轴正向到椭圆内法线方向l 的转角为φ,它是第三象限的角,因为2222220,x y b x y y a b a y ''+==-所以在点处切线斜率为2.b y a a '==-法线斜率为cos ab ϕ=.于是tan sin ϕϕ== ∵2222,,z z x y x a y b ∂∂=-=-∂∂∴2222zl a b⎛∂=--=∂⎝4.研究下列函数的极值:(1)z=x3+y3-3(x2+y2); (2)z=e2x(x+y2+2y);(3)z=(6x-x2)(4y-y2); (4)z=(x2+y2)22()e x y-+;(5)z=xy(a-x-y),a≠0.解:(1)解方程组22360360xyz x xz y y⎧=-=⎪⎨=-=⎪⎩得驻点为(0,0),(0,2),(2,0),(2,2).z xx=6x-6, z xy=0, z yy=6y-6在点(0,0)处,A=-6,B=0,C=-6,B2-AC=-36<0,且A<0,所以函数有极大值z(0,0)=0.在点(0,2)处,A=-6,B=0,C=6,B2-AC=36>0,所以(0,2)点不是极值点.在点(2,0)处,A=6,B=0,C=-6,B2-AC=36>0,所以(2,0)点不是极值点.在点(2,2)处,A=6,B=0,C=6,B2-AC=-36<0,且A>0,所以函数有极小值z(2,2)=-8.(2)解方程组222e(2241)02e(1)0xxxyz x y yz y⎧=+++=⎪⎨=+=⎪⎩得驻点为1,12⎛⎫-⎪⎝⎭.22224e(21)4e(1)2exxxxxyxyyz x y yz yz=+++=+=在点1,12⎛⎫-⎪⎝⎭处,A=2e,B=0,C=2e,B2-AC=-4e2<0,又A>0,所以函数有极小值e1,122z⎛⎫=--⎪⎝⎭. (3) 解方程组22(62)(4)0(6)(42)0xyz x y yz x x y⎧=--=⎪⎨=--=⎪⎩得驻点为(3,2),(0,0),(0,4),(6,0),(6,4).Z xx=-2(4y-y2),Z xy=4(3-x)(2-y)Z yy=-2(6x-x2)在点(3,2)处,A=-8,B=0,C=-18,B2-AC=-8×18<0,且A<0,所以函数有极大值z(3,2)=36. 在点(0,0)处,A=0,B=24,C=0,B2-AC>0,所以(0,0)点不是极值点.在点(0,4)处,A=0,B=-24,C=0,B2-AC>0,所以(0,4)不是极值点.在点(6,0)处,A=0,B=-24,C=0,B2-AC>0,所以(6,0)不是极值点.在点(6,4)处,A=0,B=24,C=0,B2-AC>0,所以(6,4)不是极值点.(4)解方程组2222()22()222e(1)02e(1)0x yx yx x yy x y-+-+⎧--=⎪⎨--=⎪⎩得驻点P0(0,0),及P(x0,y0),其中x02+y02=1,在点P0处有z=0,而当(x,y)≠(0,0)时,恒有z>0,故函数z在点P0处取得极小值z=0.再讨论函数z=u e-u由de(1)duzuu-=-,令ddzu=得u=1,当u>1时,ddzu<;当u<1时,ddzu>,由此可知,在满足x 02+y 02=1的点(x 0,y 0)的邻域内,不论是x 2+y 2>1或x 2+y 2<1,均有2222()1()e e x y z x y -+-=+≤.故函数z 在点(x 0,y 0)取得极大值z =e -1(5)解方程组(2)0(2)0x y z y a x y z x a y x =--=⎧⎨=--=⎪⎩ 得驻点为12(0,0),,33a a P P ⎛⎫⎪⎝⎭z xx =-2y , z xy =a -2x -2y , z yy =-2x .故z 的黑塞矩阵为222222ya x y H a x y x ---⎡⎤=⎢⎥---⎣⎦ 于是122033(),().0233aa a H P H P a a a ⎡⎤--⎢⎥⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦ 易知H (P 1)不定,故P 1不是z 的极值点,H (P 2)当a <0时正定,故此时P 2是z 的极小值点,且3,2733a a a z ⎛⎫=⎪⎝⎭,H (P 2)当a >0时负定,故此时P 2是z 的极大值点,且3,2733a a a z ⎛⎫=⎪⎝⎭.5. 设2x 2+2y 2+z 2+8xz -z +8=0,确定函数z =z (x ,y ),研究其极值。
高等数学课件-习题课2

哈 尔
解 x 0 :f( x ) ( 3 x 2 ) 6 x ;
滨 工
x 0 :f( x ) ( x 2 ) 2 x ;
程 大 学
f(0)lim 2x2x|x|0;
x 0
x
高
f (0)x l i0m f(x)x f(0)
lim2x02; x0 x
等 数 学
f (0)x l i0m f(x)x f(0)
滨
工 解 首,先 f(x)在x0处必须 ,从 连 而 续
程
大
f(00)f(00).
学
f(0 0 ) lism a in x 0 , x 0
高
等
f ( 0 0 ) li [m 1 l n x ) b ( ] b ,
数
x 0
学
b0.
对任意 a ,当 x 给 0 ,f定 (x )都 的 存 ; 在
dy
y
t
dx x t
1
1 1 t2
1 1 t2
2t
t; 2
等
数 学
1
d2y
2 t dx2
(
dy dx
)t
xt
2
1 1 t2
1 t2
4t
例8
用微分法则求函数
y
arctan1 1
x2 x2
的微分和
哈 尔 滨 工 程 大
导数.
解
dy1(111xx22)2d(11xx22)
学
高 等
1(1 11 x x2 2)2(1x2) (2(x 1)d x x 2)(2 1x2)2xdx u vduudv
6x0 lim 6;
x0 x
因 f (0 为 ) f (0 ),所以 f(0)不存 . 在
北航理论力学部分课件
空间力系
FR y FR z
∑F =∑ F =∑ F
∑ ∑
ix iy
iz
= 0 = 0 = 0
有三个独立的平衡方程
FR = FRx i + FRy j + FRz k = 0
FR =
F
+F
2 Ry
+F
2 Rz
=0
平面力系
FRx = FRy =
F ix = 0 F iy = 0
2010-11-27 8
理论力学
§1 - 0
力学模型与力系
•共点力系 共点力系(concurrent force system):力作用线汇交于一点的力系。 力作用线汇交于一点的力系。 共点力系 力作用线汇交于一点的力系 F1 F1
Fn
Fn
A
F2
A
F2
若共点力系中,力的作用线在同一平面内,则称为平面 若共点力系中,力的作用线在同一平面内,则称为平面 共点力系(concurrent coplanar force system)。 共点力系 。 若共点力系中,力的作用线不在同一平面内,则称为空 若共点力系中,力的作用线不在同一平面内,则称为空 间共点力系(concurrent noncoplanar force system) 。 间共点力系
§1 - 0
力学模型与力系
•刚 (rigid body):具有质量,考虑其形状和尺寸大小,其上 刚 ) 具有质量,考虑其形状和尺寸大小, 任意两点间的距离保持不变(或距离变化可以不计)的物体。 任意两点间的距离保持不变(或距离变化可以不计)的物体。
• 特点:所研究的问题与 特点: 物体的质量和姿态有关, 物体的质量和姿态有关, 其变形可以忽略不计。 其变形可以忽略不计。
北京航空航天大学本科理论力学习题课动.ppt
dvr dvr dR dt dR dt
dR dt
vr
cos
mvr
cos
dvr dR
mR 2
cos
vrdvr R2dR
v2 r
2R2
C
22
aa 0, ae 2R, aC 2 vr
x': 0 ae arx' aC cos450 y': 0 0 ary' aC sin 450
ar
a2 rx '
a2 ry '
12
习题1-10:求滑块A的加速度绳索的拉力。
v0
s FvA
FN
mg
ma F FN mg
x : mx F cos mg
x
(
x2
2R4x R2)2
mx Fx
15
y’
方法三:求滑块的速度
动点:滑块A
vr
动系:ox’y’,x’轴平行于绳
速度分析
θ
运动分析
va v x’ e
绝对运动: 直线运动 相对运动: 直线运动 牵连运动: 定轴转动
va ve vr ve x vr ( )R
y : 0 ve vr sin x : x va vr cos
动点:圆盘中心O 动系:AB杆
A
AB
运动分析: 绝对运动: 直线运动
v r 300 n ae
相对运动: 直线运动 AB 牵连运动: 定轴转动
y'
aa
o ve Rar va
aB et
速度分析
vr 0,
va ve vr va ve
AB
ve OA
va 2R
加速度分析 aa aet aen ar aC
高考数学 第二篇 函数、导数及其应用 第9节 函数模型及其应用课件 文 北师大
2 16
2 16
解得 t≥ 19 ,即税率的最小值为 19 .
192
192
反思归纳
应用指数函数模型应注意的问题
(1)指数函数模型的应用类型.常与增长率相结合进行考查,在实际问题中
有人口增长、银行利率、细胞分裂等增长问题可以利用指数函数模型来
解决. (2)应用指数函数模型时的关键.关键是对模型的判断,先设定模型,再将已 知有关数据代入验证,确定参数,从而确定函数模型.
考点二 指数函数与对数函数模型
【例 2】 (2015 泰兴模拟)我国加入 WTO 后,根据达成的协议,若干年内某产品
的关税与市场供应量 P 的关系允许近似的满足:y=P(x)= 2(1kt)(xb)2 (其中 t 为
关税的税率,且 t∈[0, 1 ),x 为市场价格,b,k 为正常数),当 t= 1 时的市场供应
夯基自测
1.下列函数中随 x 的增大而增大速度最快的是( A )
(A)v= 1 ·ex 100
(C)v=x100
(B)v=100ln x (D)v=100×2x
解析:只有 v= 1 ·ex 和 v=100×2x 是指数函数,并且 e>2,所以 v= 1 ·ex
100
100
的增大速度最快.
2.物价上涨是当前的主要话题,特别是菜价,我国某部门为尽快实现稳 定菜价,提出四种绿色运输方案.据预测,这四种方案均能在规定的时间 T内完成预测的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如 图所示,在这四种方案中,运输效率(单位时间内的运输量)逐步提高的 是( B )
越来越_慢___
相对平稳
2.解答函数应用题的一般步骤 (1)审题 弄清题意,分清条件和结论,理顺数量关系,初步选择函数模型. (2)建模 将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知 识,建立相应的函数模型. (3)求模 求解函数模型,得出数学结论. (4)还原 将数学问题还原为实际问题的意义. 以上过程用框图表示如下:
高等数学第九章9-8ppt精选课件
4z100确定的函数z f(x,y)的极值
解 将 方 程 两 边 分 别 对 x , y 求 偏 导 2x2zzx24zx0 2y2zzy24zy0
由 函 数 取 极 值 的 必 要 条 件 知 ,驻 点 为 P (1 , 1 ),
将 上 方 程 组 再 分 别 对 x , y 求 偏 导 数 ,
与一元函数相类似,我们可以利用函数的 极值来求函数的最大值和最小值.
求最值的一般方法:
将函数在D内的所有驻点处的函数值及在D
的边界上的最大值和最小值相互比较,其中最 大者即为最大值,最小者即为最小值.
在(0,0) 处无极值.
(3)
湘潭大学数学与计算科学学院 王文强 上一页 下一页
5
2、多元函数取得极值的条件
定理 1(必要条件)
设函数z f ( x, y)在点( x0, y0 )具有偏导数,且 在点( x0, y0 )处有极值,则它在该点的偏导数必 然为零: fx ( x0 , y0 ) 0, f y ( x0, y0 ) 0.
fy(yx0,y0)C,
则f (x, y)在点(x0, y0)处是否取得极值的条件如下: (1)AC B2 0时具有极值,
当A 0时有极大值, 当A 0时有极小值;
(2)AC B2 0时没有极值;
(3)AC B2 0时可能有极值,也可能没有极值,
还需另作讨论.
湘潭大学数学与计算科学学院 王文强 上一页 下一页
6
故 当 y y 0 , x x 0 时 , 有 f ( x ,y 0 ) f ( x 0 ,y 0 ) ,
说 明 一 元 函 数 f ( x , y 0 ) 在 x x 0 处 有 极 大 值 , 必 有 f x ( x 0 ,y 0 ) 0 ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在点 M 处的方向导数为
u r0
M
u x
u M cos y
u M cos z
M
cos
2 2 2 x y z 2 0 2 x 0 x 0 2 y0 y0 2 z 0 z 0 0 ( 2 2 02 ) 2 2 2 r0 a b c a r0 b r0 c r0
一、主要内容
多元函数概念
极 限 运 算 多元连续函数 的性质
多元函数 的极限
多元函数 连续的概念
方向导数
复合函数 求导法则
全微分形式 的不变性全微分 Leabharlann 念梯 度高阶偏导数
偏导数 概念
隐函数 求导法则
微分法在 几何上的应用
多元函数的极值
多元函数连续、可导、可微的关系 函数连续 函数可导
函数可微 偏导数连续
x y 二、讨论函数z 3 的连续性,并指出间断点类型. 3 x y
三、求下列函数的一阶偏导数: 1、 z x ln y ; 2、 u f ( x, xy, xyz ), z ( x, y ); x2 y 2 2 x y 0 2 2 3、 f ( x , y ) x y . 2 2 0 x y 0 四、设 u f ( x , z ),而 z( x , y ) 是由方程 z x y ( z )所 确的函数,求 du .
x3 八 .设 函 数 f ( x , y ) y , y 0,证 明 在 原 点 处 0, y 0, 函数不可微 , 但 沿 任 何 方 向 的 方 向数 导均 存 在 .
测验题答案
一、1、A; 2、B; 3、B; 4、B; 5、D ; 6、C; 7、A; 8、A; 9、D; 10、B. 二、(1)当 x y 0 时,在点( x , y ) 函数连续; (2)当 x y 0 时,而( x , y ) 不是原点时, 则( x , y ) 为可去间断点,( 0,0 ) 为无穷间断点. ln x ln y ln y 1 x ; 三、1、 z x (ln y ) x ,z y y 2、 u x f 1 yf 2 ( yz xyz x ) f 3 , u y xf 2 ( xz xyz y ) f 3 . 2 xy 3 2 2 , x y 0 2 2 2 , 3、 f x ( x , y ) ( x y ) 0, x 2 y 2 0
1 6
;
(D)
1 8
.
( x , y ) 的某邻 10、设函数 u u( x , y ), v v ( x , y ) 在点 ( x , y ) 处有 域内可微分,则 在点 grad ( uv ) ( ). ( A) gradu gradv;
( B) (C ) ( D)
u gradv v gradu; u gradv; v gradu.
3 4
yf 22 . 4 x 3 f1 2 xf 2 x 4 yf11
设 u f ( x , y , z ), ( x 2 , e y , z ) 0, y sin x , du ( f , 具有一阶连续偏导数), 且 0, 求 . z dx
x2(x2 y2 ) 2 2 , x y 0 2 2 2 f y ( x, y) ( x y ) . o, x 2 y 2 0 f2 f 2 ( z ) 四、 ( f 1 )dx dy . y ( z ) 1 y ( z ) 1 e y f uy xe y f xu f xy e y f u . 五、 xe 2 y f uu
测 验 题
一、选择题:
4 1 arcsin 2 1 、 二元函数 z ln 2 的定义 2 2 x y x y 域是( ). (A)1 x 2 y 2 4 ; (B)1 x 2 y 2 4 ; 2 2 2 2 (C)1 x y 4 ; (D)1 x y 4 . x 2 f ( xy , ) ( x y ) 2、设 ,则 f ( x , y ) ( ). y 1 2 x 2 2 x ( y ) ( 1 y ) (A) ; (B) ; y y 1 2 y 2 (C) y ( x ) ; (D) (1 y ) 2 . x x
3
解
z 1 3 x ( f1x f 2 ) x 4 f1 x 2 f 2, y x
2z 1 1 4 2 x f12 ) x ( f 21 x f 22 ) x ( f11 2 y x x
2 x 3 f12 xf 22 , x 5 f11
例3 解
du f f dy f z f z dy , dx x y dx z x z y dx
z z dy 2 y , ,得 显然 cos x , 在 ( x , e , z ) 0 中 求 dx x y
z 2 x 1 , x 3
2z 2z 4 ( x f1 x 2 f 2) xy yx x
y 4 x f1 x [ f11 y f12 ( 2 )] 2 xf2 x y 2 y f 22 ( 2 )] x [ f 21 x
x 2 y2 z 2 例5 求 u 2 2 2 在点 M ( x 0 , y0 , z0 ) 处沿点 a b c 的向径 r0 的方向导数 .
解
r0 x0 , y0 , z0 ,
2 r0 x 0 y02 z02 ,
x0 y0 z0 cos , cos , cos . r0 r0 r0
1 2 2 2 2 ( x y ) sin , x y 0 2 2 x y 5、设 f ( x , y ) 0, x 2 y 2 0 则在原点( 0,0 ) 处 f ( x , y ) ( ). (A)偏导数不存在; (B)不可微; (C)偏导数存在且连续; (D)可微 . 6、设 z f ( x , v ), v v ( x , y ) 其中 f , v 具有二阶连续偏 2z 导数.则 2 ( ). y 2 f v f 2 v f 2 v 2 ; (B) 2 ; (A) vy y v y v y 2 f v 2 f 2 v 2 f v f 2 v 2 ; (D) 2 2. (C) 2 ( ) v y v y v y v y
xy 0, xy 0,
解
f ( x ,1) f (0,1) f x (0,1) lim . x 0 x
sin( x ) lim 1. 2 x 0 ( x )
2
f (0,1 y ) f (0,1) f y (0,1) lim . 0. x 0 y
4 3 35 六、 ( , , ). 5 5 12
例6 求旋转抛物面 z x 2 y 2 与平面 x y 2 z 2
之间的最短距离.
解 设 P ( x , y , z ) 为抛物面 z x 2 y 2 上任一点, 则
P 到平面 x y 2 z 2 0 的距离为 d , 1 d x y 2z 2 . 6 分析: 本题变为求一点P ( x , y , z ),使得 x , y , z 1 2 2 满足 x y z 0且使 d x y 2z 2 6 1 2 (即 d ( x y 2 z 2)2 ) 最小. 6
3、lim ( x y )
2 2 x0 y0
x2 y2
(
).
(A) 0 ; (B) 1 ; (C) 2 ; (D) e . 4、函数 f ( x , y ) 在点( x 0 , y 0 ) 处连续,且两个偏导数 f x ( x 0 , y 0 ), f y ( x 0 , y 0 ) 存在是 f ( x , y ) 在该点可微 的( ). (A)充分条件,但不是必要条件; (B)必要条件,但不是充分条件; (C)充分必要条件; (D)既不是充分条件,也不是必要条件.
y z 2e y 3
du f f 1 f sin x ) . 故 cos x ( 2 x 1 e cos x 2 dx x y 3 z
1 2 sin( x y ), 例4 设函数 f ( x , y ) xy 0, 试求 f x (0,1), f y (0,1).
7、曲面 xyz a 3 (a 0) 的切平面与三个坐标面所围 成的四面体的体积 V=( ). 3 3 3 a a (A) 3 ; (B) ; 2 3 3 6 a a (C) 9 ; (D) . 2 3 3 8 、 二 元 函 数 z 3( x y ) x y 的 极 大 值 点 是 ( ). (A) (1,1); (B) (1.-1 ); (C) (-1,1); (D) (-1,-1). 9、函数 u sin x sin y sin z 满足 x y z ( x 0, y 0, z 0) 的条件极值是( ). 2 (A) 1 ; (B) 0 ; (C)
二、典型例题
( y x) x 例1 求极限 lim . 2 2 x 0 x y y 0 解
0
x
x y
2
2
1
( y x) x 故 lim 0. 2 2 x 0 x y y 0
y 例2 设 z x f ( xy , ), ( f 具有二阶连续偏导数), x z 2 z 2 z 求 , 2, . y y xy
f 具有连续的二阶偏导 五、设 z ( u, x , y ), u xe y ,其中 2z 数,求 . xy
x y z 和柱面 x 2 y 2 1的交线上与 xoy平面距 六、 面 1 3 4 5 离最短的点
