崇文区2009-2010学年度第二学期统一练习(理)题
北京市崇文区2009届高三3月统练(理综)

崇文区2008—2009学年度第二学期高三统一练习(一)理科综合能力测试2009.3本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分300分,考试时间150分钟。
注意事项:1、答第1卷前,考生务必将自己的姓名、学校、准考证号涂写在答题卡上,考试结束,将答题卡交回。
2、答第I卷时.每小题选出答案后,用2B铅笔答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
3、答第Ⅱ卷时,请在各题目的答题区域内作答,超过黑色矩形边框限定区域的答案无效。
第I卷(选择题共120分)肯能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 S 32 Cl 35.5Fe 56 Cu 64本卷共20题,每题6分,共120分。
在每题列出的四个选项中,选出符合题目要求的一项。
1、下列过程中不涉及植物组织培养技术的是A、由马铃薯的茎尖培育出无病毒植株B、白菜和甘蓝经体细胞交杂过程培育出杂种植株C、转入抗卡那霉素基因的烟草细胞培育出转基因植株D、二倍体水稻的种子经秋水仙素处理后培育出四倍体植物2、近年来在疫苗家族中增加了第三代疫苗—DNA疫苗,它们是由病原微生物中的一段表达抗原的基因制成,这段基因编码的产物仅是引起抗体的免疫反应。
以下关于DNA疫苗的叙述正确的是A、能引起特异性免疫反应是因为DNA疫苗具有抗原决定族B、DNA疫苗引起免疫反应前必须经过转录和翻译的过程C、DNA疫苗导入人体后效应B细胞分化为记忆细胞D、接种后若感染此病原微生物则体内记忆细胞会产生大量抗体3、某学校生物兴趣小组用伊乐藻进行光合作用的实验,将一枝伊乐藻侵在加有适宜培养液的大试管中,以白炽灯作为光源,移动白炽灯调节其与大试管的距离,分别在10℃,20℃和30℃下进行实验,观察并记录不同距离下单位时间枝条产生的气泡数目,结果如图所示。
下列相关叙述不正确的是A 、该实验研究的是光照强度和温度对光合速率的影响B 、A 点和C 点的限制因素分别为温度和光照强度C 、B 点条件下伊乐藻能进行光合作用D 、若在缺镁的培养液中进行此实验则B 点向右移动4、下图为人体的生命活动调节示意图,以下叙述不正确的是A 、血糖的平衡可以通过A →C →D →F 和H →D →F 途径进行调节B 、处于炎热环境中可通过A →B 途径使散热大于产热C 、G 过程可表示甲状腺激素对神经系统的发育和功能的影响D 、E 过程具有使血液中的激素维持在正常相对稳定水平的作用5、某合作学习小组讨论辨析:①漂白粉和酸雨都是混合物 ②煤和石油都是可再生能源 ③蔗糖、硫酸钡和水分别属于非电解质、强电解质和弱电解质 ④不锈钢和目前流通的硬币都是合金 ⑤硫酸、纯碱、醋酸钠和生石灰分别属于酸、碱、盐和氧化物 ⑥豆浆和雾都是胶体。
北京市崇文区2009—2010学年度高三第二学期统一练习(二)
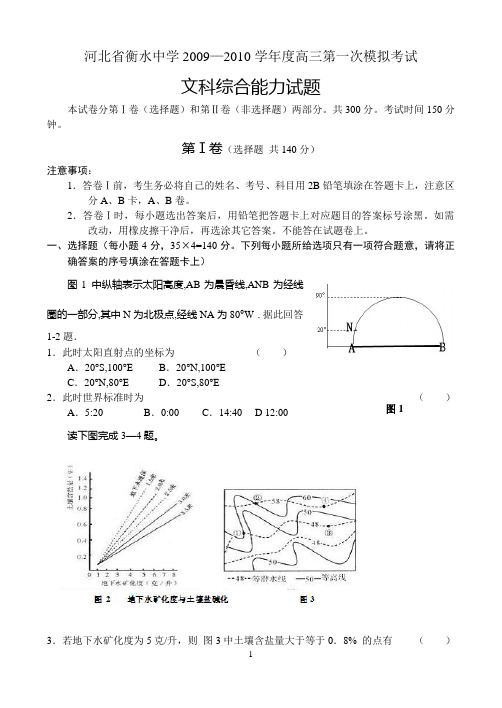
河北省衡水中学2009—2010学年度高三第一次模拟考试文科综合能力试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共300分。
考试时间150分钟。
第Ⅰ卷(选择题 共140分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、考号、科目用2B 铅笔填涂在答题卡上,注意区分A 、B 卡,A 、B 卷。
2.答卷Ⅰ时,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案。
不能答在试题卷上。
一、选择题(每小题4分,35×4=140分。
下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)图1 中纵轴表示太阳高度,AB 为晨昏线,ANB 为经线圈的一部分,其中N 为北极点,经线NA 为80°W .据此回答1-2题.1.此时太阳直射点的坐标为 ( )A .20°S,100°EB .20°N,100°EC .20°N,80°ED .20°S,80°E2.此时世界标准时为 ( )A .5:20B .0:00C .14:40D 12:00读下图完成3—4题。
3.若地下水矿化度为5克/升,则 图3中土壤含盐量大于等于0.8% 的点有 ( )A .①B .①②C .②③④D .①③4.读图,下列判断正确的是 ( )A .若地下水矿化度较低则无论地下水埋藏深浅土壤含盐较低图1图4 B .若地下水埋深相同则土壤含盐量与地下水矿化度成负相关C .地下水埋深越大则土壤含盐量越大,土壤盐碱化就越严重D .若地下水矿化度相同则土壤含盐量与地下水埋深成正相关图4 是某月份海平面平均气压沿两条纬线的变化图,回答5—6题。
5.该月份,①、②两地的平均风力相比较 ( )A .①地的较大B .两地相当C .②地的较大D .上半月①地的较大6.③地以南到赤道以北地区,此时的盛行风向为 ( )A .西北风B .西南风C .东北风D .东南风服务外包是指企业将其非核心的业务外包出去,利用外部最优秀的专业化团队来承接业务,从而使其专注核心业务,达到降低成本的一种管理模式。
作业15(崇文一模答案)

崇文区2009—2010学年度第二学期初三统一练习(一)数学试题参考答案 2010.5一、选择题三、解答题13.解:原式=2152⨯-- =6.14.解:去分母,得 3(31)213x --=. 解得 2x =.经检验,2x =是原方程的解. ∴原方程的解是2x =.15.证明:,ED BD ⊥ 90D A ∴∠=︒=∠.90E ECD ∴∠+∠=︒.又 AC CE ⊥,90ACB ECD ∴∠+∠=︒.ACB E ∴∠=∠. 在ABC 和DCE 中,,,,A D ACB E BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC ≅DCE . ∴AB CD =.16.解:由题意,可知点A 的横坐标是2,由点A 在正比例函数2y x =的图象上,∴点A 的坐标为()24,.又 点A 在反比例函数1m y x-=的图象上, 142m -∴=,即9m =.17.解:222(1)(1)(1)121x x x x x x x --÷+---+ =2121(1)(1)[]11(1)x x x x x x x ---+⋅--+-=11()11x x x x +--- =21x x -- 210x x +-=,∴21x x -=-∴原式=1.18.解:设火车从北京到武汉的平均时速为x 公里每小时,提速后武汉到广州的平均时速为y 公里每小时.依题意,有250,158(1584).y x x x y =+⎧⎨=+--⎩解方程组,得150,350.x y =⎧⎨=⎩ 答:火车从北京到武汉的平均时速为150公里每小时,提速后武汉到广州的平均时速为350公里每小时.19.答案:解:作AE BC ⊥于E DF BC ⊥,于F . DF ∥AE ∴, AD BC ∴ ∥,四边形AEFD 是矩形. 3EF AD AE DF ∴===,.BD CD DF BC =⊥ ,,DF ∴是BDC △的BC 边上的中线. 19042BDC DF BC BF ∠=∴=== °,. 4431AE BE BF EF ∴==-=-=,.在Rt ABE △中,222AB AE BE =+AB ∴== 20.解:(1)AC 与O 的相切.证明如下:OC AD ⊥∵290AOC ∴∠+∠=°.又2C BED ∠=∠=∠ , 90AOC C ∠+∠=∴°. AB AC ⊥∴CAOBED1 2即AC 与O 的相切.(2)解:连接BD .AB ∵是O 直径,90ADB ∴∠=︒在Rt AOC ∆中,90CAO ∠=︒, 8AC = ,90ADB ∠= °.4cos cos 5C BED ∠=∠=. 6AO ∴=,12AB ∴=在Rt ABD ∆中,4cos 2cos 5BED ∠=∠=, 4cos 2125AD AB ∴=⋅∠=⨯=485.21.解:(1)15000,10000;(2)3.75%,5.25% ; (3)3700,3700.22.(1)(2)21. 23.解:(1)因为点P 、Q 在抛物线上且纵坐标相同,所以P 、Q 关于抛物线对称轴对称并且到对称轴距离相等.所以,抛物线对称轴3142b x -+=-=,所以,4b =. (2)由(1)可知,关于x 的一元二次方程为2241x x ++=0.因为,24b ac =- =16-8=8>0. 所以,方程有两个不同的实数根,分别是1122b x a -+==-+,2122b x a -==--. (3)由(1)可知,抛物线2241y x x =++的图象向上平移k (k 是正整数)个单位后的解析式为2241y x x k =+++.若使抛物线2241y x x k =+++的图象与x 轴无交点,只需22410x x k +++= 无实数解即可.由24b ac =- =168(1)k -+=88k -<0,得1k >又k 是正整数,所以k 得最小值为2.24.(1)CF 与BD 位置关系是垂直; 证明如下: AB=AC ,∠ACB=45º,∴∠ABC=45º. 由正方形ADEF 得 AD=AF ,∵∠DAF=∠BAC =90º,∴∠DAB=∠FAC ,∴△DAB ≌△FAC , ∴∠ACF=∠ABD . ∴∠BCF=∠ACB+∠ACF= 90º.即 CF ⊥BD . (2)CF ⊥BD .(1)中结论成立.理由是:过点A 作AG ⊥AC 交BC 于点G ,∴AC=AG 可证:△GAD ≌△CAF ∴∠ACF=∠AGD=45º ∠BCF=∠ACB+∠ACF= 90º. 即CF ⊥BD(3)过点A 作AQ ⊥BC 交CB 的延长线于点Q , ①点D 在线段BC 上运动时, ∵∠BCA=45º,可求出AQ= CQ=4.∴ DQ=4-x ,易证△AQD ∽△DCP ,∴CP CD DQ AQ = , ∴44CP xx =-,24x CP x ∴=-+.②点D 在线段BC 延长线上运动时, ∵∠BCA=45º,可求出AQ= CQ=4,∴ DQ=4+x .过A 作AC AG ⊥交CB 延长线于点G ,则ACF AGD ∆≅∆.∴ CF ⊥BD ,∴△AQD ∽△DCP ,∴CP CD DQ AQ = , ∴44CP xx =+,24x CP x ∴=+.25.解:(1)依题意:31,142 1.a b a b =++⎧⎨=++⎩解得2,4.a b =-⎧⎨=⎩ ∴抛物线的解析式为2241y x x =-++.(2)点A (1,3)关于y 轴的对称点A '的坐标是(-1,3),点B (2,1)关于x 轴的对称点B '的坐标是(2,-1).由对称性可知AB BC CD DA +++=''AB B C CD DA +++≥AB A B ''+ 由勾股定理可求5A B ''=.GABCD EF所以,四边形ABCD 周长的最小值是5AB A B ''+= (3)确定F 点位置的方法:过点E 作直线EG 使对称轴到直线EG 成45︒角,则EG 与对称轴的交点为所求的F 点.设对称轴于x 轴交于点H ,在Rt HEF ∆中,由HE=1,90,45FHE EFH ∠=︒∠=︒,得HF=1.所以,点F 的坐标是(1,1).。
崇文区2009—2010学年度第二学期初三统一测试

崇文区2009—2010学年度第二学期初三统一练习(一)数 学 2010.5一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1.3-的倒数是A .31 B . 31- C . 3- D . 3 2.《国家中长期教育改革和发展规划纲要(2010-2020)》征求意见稿提出“财政性教育经费支出占国内生产总值比例不低于4%”,去年我国全年国内生产总值为335353亿元.335353亿元的4%,也就是约13400亿多元.将13400用科学记数法表示应为A .134210⨯ B . 13.4310⨯ C .1.34410⨯ D .0.134510⨯ 3.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差是1.8.下列说法中不一定正确的是 A .甲、乙射中的总环数相同 B .甲的成绩稳定 C .乙的成绩波动较大 D .甲、乙的众数相同4.若右图是某几何体的三视图,则这个几何体是 A .三棱柱 B .圆柱 C .正方体 D .三棱锥5.若一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是A .4B .5C .6D . 76.如图,在梯形ABCD 中,A D B C ∥,7040B C ∠=∠=°,°,DE AB ∥交BC 于点E .若3AD =,10BC =,则CD 的长是A .7B .10C .13D .147.在 6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆. 在看不见图形的情况下随机摸出1张,这张卡片上的图形是中心对称图形的概率是A .61B .31C .21D .328.函数y=x 2-2x-2的图象如右图所示,根据其中提供的信息,可求得使y ≥1成立的x 的取值范围是A .31≤≤-xB .31<<-xC .31>-<x x 或D .31≥-≤x x 或二、填空题(本题共16分,每小题4分)9.在函数y =x 的取值范围是 .10.分解因式:32232a b a b ab -+= .11.如图,AB 是O 的直径,CD 是O 的弦,DAB ∠=48︒,则ACD ∠= ︒.12.如图,在梯形ABCD 中,AB ∥CD ,AB =a ,CD =b ,E 为边AD 上的任意一点,EF ∥AB ,且EF 交BC 于点F .若E 为边AD 上的中点,则EF = (用含有a ,b 的式子表示);若E 为边AD 上距点A 最近的n 等分点(2n ≥,且n 为整数),则EF = (用含有n ,a ,b 的式子表示).三、解答题(本题共30分,每小题5分)132cos 45-︒-0(2010)-11()5--.14.解分式方程311323162x x -=--.15.如图,在ABC 中,90A ∠=︒,AC CE ⊥,且BC C E =,过E 作BC 的垂线,交BC 延长线于点D .求证:AB CD =.16.如图,点A 是直线2y x =与曲线1m y x-=(m 为常数)一支的交点.过点A 作x 轴的垂线,垂足为B ,且OB =2.求点A 的坐标及m 的值.17.已知210x x +-=,求222(1)(1)(1)121x x x x x x x --÷+---+的值.18. 一列火车从北京出发到达广州大约需要15小时.火车出发后先按原来的时速匀速行驶8小时后到达武汉,由于2009年12月世界时速最高铁路武广高铁正式投入运营,现在从武汉到广州火车的平均时速是原来的2倍还多50公里,所需时间也比原来缩短了4个小时.求火车从北京到武汉的平均时速和提速后武汉到广州的平均时速.四、解答题(本题共20分,第19题5分,第20题5分,第21题6分,第22题4分)19.如图,在梯形ABCD 中,AD BC ∥,9038BD CD BDC AD BC =∠===,°,,.求AB 的长. 20. 如图,AB 是半圆O 的直径,过点O 作弦AD 的垂线交半圆O 于点E ,交AC 于点C ,使BED C ∠=∠.(1)判断直线AC 与圆O 的位置关系,并证明你的结论;(2)若8AC =,4cos 5BED ∠=,求AD 的长.CAOBE D21.应对全球经济危机,中国政府投资40000亿元人民币以拉动内需, 5月21日国家发改委公布了40000亿元投资构成.具体内容如下:请你根据统计图表中所提供的信息,完成下列问题: (1)在统计表中,投向“铁路等重大基础设施建设和城市电网改造”的资金测算和投向“汶川地震灾后恢复重建”的资金测算分别是多少亿元; (2)在扇形统计图中,“卫生、教育等社会事业发展”部分和 “节能减排和生态建设工程”部分所占的百分数分别是多少;(3)统计表“资金测算”栏目下的七个数据中,中位数和众数分别是多少亿元.22.正方形ABCD 的边长为a ,等腰直角三角形FAE 的斜边AE b =(a b 2<),且边AD 和AE 在同一直线上 .小明发现:当b a =时,如图①,在BA 上选取中点G ,连结FG 和CG ,裁掉FAG ∆和CHD ∆的位置构成正方形FGCH .(1)类比小明的剪拼方法,请你就图②和图③两种情形分别画出剪拼成一个新正方形的示意图.(2)要使(1)中所剪拼的新图形是正方形,须满足=AEBG.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知P (3,m -)和Q (1,m )是抛物线221y x bx =++上的两点.(1)求b 的值;(2)判断关于x 的一元二次方程221x bx ++=0是否有实数根,若有,求出它的实数根;若没有,请说明理由;(3)将抛物线221y x bx =++的图象向上平移k (k 是正整数)个单位,使平移后的图象与x 轴无交点,求k 的最小值.24.在△ABC 中,∠ACB=45º.点D (与点B 、C 不重合)为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .(1)如果AB=AC .如图①,且点D 在线段BC 上运动.试判断线段CF 与BD 之间的位置关系,并证明你的结论.(2)如果AB ≠AC ,如图②,且点D 在线段BC 上运动.(1)中结论是否成立,为什么?(3)若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ,设AC =3=BC ,CD=x ,求线段CP 的长.(用含x 的式子表示)25.已知抛物线21y ax bx =++经过点A (1,3)和点B (2,1).(1)求此抛物线解析式;(2)点C 、D 分别是x 轴和y 轴上的动点,求四边形ABCD 周长的最小值;(3)过点B 作x 轴的垂线,垂足为E 点.点P 从抛物线的顶点出发,先沿抛物线的对称轴到达F 点,再沿FE 到达E 点,若P 点在对称轴上的运动速度是它在直线FE 倍,试确定点F 的位置,使得点P 按照上述要求到达E 点所用的时间最短.(要求:简述确定F 点位置的方法,但不要求证明)崇文区2009—2010学年度第二学期初三统一练习(一)数学试题参考答案 2010.5一、选择题三、解答题13.解:原式=2152⨯-- =6.14.解:去分母,得 3(31)213x --=. 解得 2x =.经检验,2x =是原方程的解. ∴原方程的解是2x =.15.证明:,ED BD ⊥ 90D A ∴∠=︒=∠.90E ECD ∴∠+∠=︒.又 AC CE ⊥,90ACB ECD ∴∠+∠=︒.ACB E ∴∠=∠. 在ABC 和DCE 中,,,,A D ACB E BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC ≅DCE . ∴AB CD =.16.解:由题意,可知点A 的横坐标是2,由点A 在正比例函数2y x =的图象上,∴点A 的坐标为()24,.又 点A 在反比例函数1m y x-=的图象上, 142m -∴=,即9m =.17.解:222(1)(1)(1)121x x x x x x x --÷+---+ =2121(1)(1)[]11(1)x x x x x x x ---+⋅--+-=11()11x x x x +--- =21x x -- 210x x +-=,∴21x x -=-∴原式=1.18.解:设火车从北京到武汉的平均时速为x 公里每小时,提速后武汉到广州的平均时速为y 公里每小时.依题意,有250,158(1584).y x x x y =+⎧⎨=+--⎩解方程组,得150,350.x y =⎧⎨=⎩ 答:火车从北京到武汉的平均时速为150公里每小时,提速后武汉到广州的平均时速为350公里每小时.19.答案:解:作AE BC ⊥于E DF BC ⊥,于F . DF ∥AE ∴, AD BC ∴ ∥,四边形AEFD 是矩形. 3EF AD AE DF ∴===,.BD CD DF BC =⊥ ,,DF ∴是BDC △的BC 边上的中线. 19042BDC DF BC BF ∠=∴=== °,. 4431AE BE BF EF ∴==-=-=,.在Rt ABE△中,222ABAE BE =+ AB ∴=20.解:(1)AC 与O 的相切.证明如下:OC AD ⊥∵290AOC ∴∠+∠=°.又2C BED ∠=∠=∠ , 90AOC C ∠+∠=∴°. AB AC ⊥∴CAOBED1 2即AC 与O 的相切.(2)解:连接BD .AB ∵是O 直径,90ADB ∴∠=︒在Rt AOC ∆中,90CAO ∠=︒, 8AC = ,90ADB ∠= °.4cos cos 5C BED ∠=∠=. 6AO ∴=,12AB ∴=在Rt ABD ∆中,4cos 2cos 5BED ∠=∠=, 4cos 2125AD AB ∴=⋅∠=⨯=485.21.解:(1)15000,10000;(2)3.75%,5.25% ;(3)3700,3700.22.(1)(2)21. 23.解:(1)因为点P 、Q 在抛物线上且纵坐标相同,所以P 、Q 关于抛物线对称轴对称并且到对称轴距离相等.所以,抛物线对称轴3142b x -+=-=,所以,4b =. (2)由(1)可知,关于x 的一元二次方程为2241x x ++=0.因为,24b ac =- =16-8=8>0. 所以,方程有两个不同的实数根,分别是1122b x a -==-+,2122b x a -==--. (3)由(1)可知,抛物线2241y x x =++的图象向上平移k (k 是正整数)个单位后的解析式为2241y x x k =+++.若使抛物线2241y x x k =+++的图象与x 轴无交点,只需22410x x k +++= 无实数解即可.由24b ac =- =168(1)k -+=88k -<0,得1k >又k 是正整数,所以k 得最小值为2.24.(1)CF 与BD 位置关系是垂直; 证明如下: AB=AC ,∠ACB=45º,∴∠ABC=45º. 由正方形ADEF 得 AD=AF ,∵∠DAF=∠BAC =90º,∴∠DAB=∠FAC ,∴△DAB ≌△FAC , ∴∠ACF=∠ABD . ∴∠BCF=∠ACB+∠ACF= 90º.即 CF ⊥BD . (2)CF ⊥BD .(1)中结论成立.理由是:过点A 作AG ⊥AC 交BC 于点G ,∴AC=AG可证:△GAD ≌△CAF ∴∠ACF=∠AGD=45º ∠BCF=∠ACB+∠ACF= 90º. 即CF ⊥BD (3)过点A 作AQ ⊥BC 交CB 的延长线于点Q , ①点D 在线段BC 上运动时, ∵∠BCA=45º,可求出AQ= CQ=4.∴ DQ=4-x ,易证△AQD ∽△DCP ,∴CP CD DQ AQ = , ∴44CP xx =-,24x CP x ∴=-+.②点D 在线段BC 延长线上运动时, ∵∠BCA=45º,可求出AQ= CQ=4,∴ DQ=4+x .过A 作AC AG ⊥交CB 延长线于点G ,则ACF AGD ∆≅∆.∴ CF ⊥BD ,∴△AQD ∽△DCP ,∴CP CD DQ AQ = , ∴44CP xx =+,24x CP x ∴=+.25.解:(1)依题意:31,142 1.a b a b =++⎧⎨=++⎩解得2,4.a b =-⎧⎨=⎩ ∴抛物线的解析式为2241y x x =-++.(2)点A (1,3)关于y 轴的对称点A '的坐标是(-1,3),点B (2,1)关于x 轴的对称点B '的坐标是(2,-1).由对称性可知AB BC CD DA +++=''AB B C CD DA +++≥AB A B ''+ 由勾股定理可求5A B ''=.GAB CD E F所以,四边形ABCD 周长的最小值是5AB A B ''+= (3)确定F 点位置的方法:过点E 作直线EG 使对称轴到直线EG 成45︒角,则EG 与对称轴的交点为所求的F 点.设对称轴于x 轴交于点H ,在Rt HEF ∆中,由HE=1,90,45FHE EFH ∠=︒∠=︒,得HF=1.所以,点F 的坐标是(1,1).。
2009-2010学年北京市崇文区八年级(下)期末物理试卷
2009-2010学年北京市崇文区八年级(下)期末物理试卷一、下列各小题均有四个选项,其中只有一个符合题意.(共24分,每小题2分)1.(2分)在国际单位制中,电压的单位是()A.J(焦)B.V(伏)C.A(安)D.W(瓦)2.(2分)下列家用电器中正常工作时的功率最接近1000W的是()A.数码相机B.电视机C.笔记本电脑D.家用微波炉3.(2分)第一个发现通电导线周围存在磁场,表明电与磁之间有联系的科学家是()A.牛顿B.欧姆C.奥斯特D.法拉第4.(2分)下面的装置中,利用电磁感应原理工作的是()A.电磁继电器B.发电机C.电动机D.电磁炉5.(2分)如图所示的四个电路图中,各开关都闭合后,仅有L1发光的是()A.B.C.D.6.(2分)下列如图所示现象中,符合用电安全的是()A.电器失火应切断电源B.湿衣服晾在电线上C.用湿布擦抹电器D.家用电器未加接地保护7.(2分)图中的四个电路中,电源电压U相同,R1<R2,电路消耗的总功率由小到大的顺序是()A.P丙<P乙<P甲<P丁B.P丁<P丙<P乙<P甲C.P丁<P甲<P乙<P丙D.P甲<P乙<P丙<P丁8.(2分)两只普通的照明灯泡上标有如图所示字样,为了比较两灯的亮度和耗电情况,将甲、乙两灯分别接入家庭电路中进行观察,若甲灯通电20min,乙灯通电5min,则()A.乙灯较亮,乙灯消耗电能多B.甲灯较亮,乙灯消耗电能快C.乙灯较亮,甲灯消耗电能多D.甲灯较亮,甲灯消耗电能快9.(2分)在如图所示的电路中,闭合开关S,电路正常工作。
一段时间后,灯L熄灭,电路中只有一个故障,且只发生在灯L或电阻R上。
现将一完好的电压表并联在灯L两端()A.若电压表有示数,则一定是电阻R断路B.若电压表有示数,则一定是灯L断路C.若电压表无示数,则一定是电阻R短路D.若电压表无示数,则一定是灯L断路10.(2分)电阻R1、R2串联,已知R1:R2=3:2,则电阻R1、R2的电功率之比为()A.9:4B.4:9C.3:2D.2:311.(2分)一台电动机正常工作时线圈两端的电压为380V,线圈电阻为2Ω,线圈中电流为10A.这台电动机正常工作1s消耗的电能为W,产生的热量为Q,则()A.W=72200J Q=3800J B.W=3800J Q=3800JC.W=72200J Q=200J D.W=3800J Q=200J12.(2分)如图所示电路,电源电压保持不变,开关闭合后,移动滑动变阻器滑片P到某一位置时,电压表示数是10V,滑动变阻器的功率是10W;移动滑动变阻器的滑片P到另一位置时,电压表示数是5V,此时滑动变阻器的功率是7.5W.则()A.电源电压为10VB.电阻R0的阻值为10ΩC.滑动变阻器的最大阻值为20ΩD.电路总功率的最大值为20W二、下列各小题均有四个选项,其中至少有两个符合题意.(共12分,每小题3分.错选、多选不得分,选不全的得2分)13.(3分)下列说法正确的是()A.地磁场的南极在地理的北极附近B.电动机将机械能转化成为电能C.电流周围一定存在着磁场D.导体的电阻与导体的长度无关14.(3分)如图所示电路中,开关S闭合后,电流表A1、A2的示数相等。
[高考]2010年北京崇文区高三理综一摸试卷与答案
![[高考]2010年北京崇文区高三理综一摸试卷与答案](https://img.taocdn.com/s3/m/bb79dd858e9951e79b8927fb.png)
崇文区2009-2010学年度笫二学期统一练习(一)高三理科综合能力测试20W.4本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第】卷1至6页.第II卷7至15 页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答BT卡一并交回。
以下效据可供解JS时参考:可能用到的相对原子质量:H 1 C 12 N 14 0 16第I卷(选择题共120分)本岩共20小瓦每小赃6分,共120分。
在每小1!列出的四个选项轧选出符舍题目要求的一项。
L下列生物细胞结构的说法下年理的是A.酵母09有染色体,而硝没有B.酵母BF有核精体,而硝化细菌没有C.黑藻细胞有线粒体,而蓝藻细胞没有D.黑藻细胞有叶绿体•而蓝藻细胞没有2.下图表示甲型H1N1流感病毒在人体细胞中的一些变化以及相关反应e有关叙述不正确•♦•的是&细胞1和B细胞都属于保留分裂能力的细随B.细胞2的作用是使靶细胞裂解暴5S病原体C.合成a所需原料及合成场所都是由人体细胞提供的D.注射的疫苗可宜接剌激细胞3产生大量物质b3.筛选是生物技术中的一个重要环节。
下列叙述不年段的是A基因工程中,利用目的基因对受体细胞进行浦M *B.杂交育种中,利用病原体够染法筛选出F,中抗病植株C.细胞工程中,利用特定的选择培养基筛选出杂交细胞D.微生物培养中,利用尿素作为唯一氤源的培养基第选出分解尿素的细菌4. 已知家鸡的无尾(A )对有尾(时是显性。
现用有尾鸡(甲群体)自交产生的受精卵来解小 鸡.在料化早期向卵内注射微量胰岛素,孵化出的小鸡就表现出无尾性状(乙群体)。
为研 究胰岛素在小鸡孵化过程中是否引起基因突变,可行性方案是A. 甲群体x 甲群体,孵化早期不向卵内注射胰岛素B. 乙群体x 乙群体,蜉化早期向卵内注射(岛素C 甲群体*乙群体■!?化早期向卵内注射胰岛素D. 甲群体x 乙群体,孵化早期不向卵内注射胰岛素5. 将某种植物量于CO 2浓度适宜、水分充足的环境中,温度分别保持在55C J5T 、25笆和 35幻下•改变光照强度,测定CO 2的吸收速率,得到图1所示的结果。
北京崇文区2010年二模理综化学
崇文区2009—2010学年度第二学期高三统一练习(二)理科综合能力测试2010.5本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至页,第II卷至页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
以下数据可供解题时参考:可能用到的相对原子质量:H 1 C 12 N 14 O 16 S 32 Zn 65第I卷(选择题共120分)本卷共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出符合题目要求的一项。
6.下列说法正确的是①世博会中国馆一一“东方之冠”使用的钢筋混凝土属于高分子化合物;②CH s COONa、BaSO4都是强电解质;③明矶和氯气可用于饮用水的净化和杀菌消毒,且两者的作用原理不同;④0.1 mol/L NaOH 溶液与0.1 mol/L Ba (OH)2溶液的pH相同;⑤一定温度下,适量CO2分别通入饱和碳酸钠溶液和澄清石灰水中,都会出现浑浊。
7.下列装置或操作能达到实验目的的是9. X、Y、Z、W均为短周期主族元素,右图为周期表的一部分。
下列说法正确的是A .通常情况下,X元素只存在两种氧化物B . Y元素气态氢化物的还原性最强C . X元素的非金属性比Y元素非金属性强A .①③④B.①②④C.②③⑤ D .③④⑤①A .①②③④&在加入铝粉能放出A . NH4+、Na+、②B .②④H2的无色溶液中,NO3「、S2「C. K +、NO3「、SO42「、Cl旳烧郝中,搗并帳Ei髀,配就1职朗了曲“薄洛C.②③④可能大量共存的离子组是B. Na+、K+、CH3COO-、HCO3D. K+、Al3+、MnO4「、NO3「D .①③X YZ W 分离确猫中D • Z和X可能以共价键结合形成一种无机非金属材料10. 下列说法不正确的是A .在一定条件下,催化分解80g SO3,混合气体中氧原子数为 3 >6.02 X023B .一定条件下,铁与水蒸气反应生成8.96L H2时(已折合成标况),转移的电子数为0.8 >02 >023C.各100mL 1mol/L AICI 3与3mol/L NaCI 溶液混合后,Cl-的个数为0.6 >.02 >023D .含有非极性键的数目为 6.02 >023的Na2O2与水充分反应产生标况下22.4L O2+ 2-放电11. ----------------------------------------------------------------------------- 用铅蓄电池(总反应:Pb+PbO2+4H +2SO42• -------------------------------------------------------------------- -2PbSO4+2H2O)电解苦卤水(含^充电C1—、Br—、Na + > Mg2+)的装置如图所示(a、b为石墨电极)。
北京市崇文区二模数学(理科)试题及答案
崇文区2009—2010学年度第二学期统一练习㈡高三数学(理科) 2010.5一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.⑴“关于x 的不等式220x ax a -+>的解集为R ”是“0≤a <1”的A.充分非必要条件B.必要非充分条件C.充分必要条件D.既非充分又非必要条件⑵一个几何体的三视图如图所示,则这个几何体的体积等于A.12B.4C.563D.⑶设函数f(x)=2log (1),(0),,(0).a x x x qxb x +>⎧⎨++≤⎩若f(3)=2,f(-2)=0,则a +b= A.-1 B.0 C.1 D.2⑷把函数y=sinx(x ∈R)的图象上所有的点向左平移6π个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为A.y=sin(23x π-,x ∈R B. y=1sin(26x π+,x ∈R C. y=sin(2)3x π+,x ∈R D. y=1sin()26x π-,x ∈R ⑸已知点P 是抛物线22y x =上的一个动点,则点P 到点M(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为俯视图侧(左)视图正(主)视图A.3B.92⑹若非零向量,a b 满足+=a b b,则( )A.2>2+a a b B.22<+a a bC.2>+2b a bD.22<+b a b⑺用5,6,7,8,9组成没有重复数字的五位数,其中恰好有一个奇数夹在两个偶数之间的五位数的个数为A.120B.72C.48D.36⑻已知圆的方程2225x y +=,过M(-4,3)作直线MA,MB 与圆交于点A,B ,且MA,MB 关于直线y=3对称,则直线AB 的斜率等于A.43-B.34-C.54-D.45-二、填空题:本大题共6小题,每小题5分,共30分.⑼函数的定义域为 .⑽如图,⊙O 中的弦AB 与直径相交于点P ,M 为DC 延长线一点,MN 为⊙O 的切线,N 为切点,若AP=8,PB=6,PD=4,MC=6,则MN= .⑾甲、乙、丙三名射击运动员在某次测试中各射击20次,三人的测试成绩如下表1x -,2x -,3x -分别表示甲、乙、丙三名运动员这次测试成绩的平均数,则1x -,2x -,3x -的大小关系是 ;123,,s s s 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则123,,s s s 的大小关系是 .⑿若直线l 的参数方程为31,545x t y t ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),则直线l 的斜率为 ;在极坐标系中,直线m 的方程为sin()42πρθ+=,则点A7(2,)4π到直线m 的距离为 .⒀给定下列四个命题:①若110a b <<,则22b a >;②已知直线l ,平面,αβ为不重合的两个平面.若l ⊥α,且αβ⊥,则l ∥β; ③若-1,a ,b ,c ,-16成等比数列,则b=-4;④若()52x -=5432543210a x a x a x a x a x a +++++,则12345a a a a a ++++=-1.其中为真命题的是 .(写出所有真命题的序号)⒁设不等式组*0,0,()4x y n y nx n >⎧⎪>∈⎨⎪≤-+⎩N 所表示的平面区域n D 内的整点(横坐标,纵坐标都是整数的点)个数为n a ,则x如图,在平面直角坐标系xOy 中,以x 轴为始边作两个锐角,αβ,它们的终边分别与单位圆交于A ,B 两点.已知A ,B的横坐标分别为,10.⑴求tan()αβ+的值; ⑵求2αβ+的值 ⒃正方体ABCD-1111A B C D 的棱长为2,O 是AC 与BD 的交点,E 是1B B 上一点,且1B E =12.⑴求证:1B D ⊥平面1D AC ;⑵求异面直线1D O 与1A D 所成角的余弦值; ⑶求直线1D O 与平面AEC 所成角的正弦值⒄(本小题13分)某学校高一年级开设了A,B ,C ,D ,E 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.⑴求甲、乙、丙三名学生参加五门选修课的所有选法种数; ⑵求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;⑶设随机变量X 为甲、乙、丙这三名学生参加A 课程的人数,求X 的分布列与数学期望.⒅(本小题共14分)设函数()(2)ln()f x a x =--+1x +2ax(a ∈R).EOCBADD 1C 1B 1A 1⑴当a=0时,求f(x)的极值; ⑵当a ≠0时,求f(x)的单调区间. ⒆(本小题共14分)已知椭圆22221x y a b +=(a >b >0)和圆O :222x y b +=,过椭圆上一点P 引圆O 的两条切线,切点分别为A,B.⑴①若圆O 过椭圆的两个焦点,求椭圆的离心率e ;②若椭圆上存在点P ,使得∠APB=90°,求椭圆离心率的取值范围; ⑵设直线AB 与x 轴、y 轴分别交于点M ,N ,求证:2222a b ONOM+为定值⒇(本小题共13分)已知集合M={1,2,3,4,5,6},对于i a ,i b ∈M ,记ii i a e b =且i a <i b ,由所有i e 组成的集合设为A={12,,e e …,k e }.⑴求k 的值;⑵设集合B={'i e |'i e =1i e ,i e ∈A},对任意i e ∈A ,'j e ∈B ,试求'i j i j e e ≠∑ ;⑶设i e ∈A ,'j e ∈B ,试求i e +'j e ∈Z 的概率.xy一切为了学生的发展一切为了家长的心愿。
北京崇文区2009—2010学年高三第二学期统一练习理综
北京市崇文区2009- 2010学年度第二学期统一练习(二)理科综合能力测试2010. 5 本试卷分第I卷(选择题)和第n卷(非选择题)两部分,第I卷1至6页,第n卷7至14页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
以下数据可供解题时参考:可能用到的相对原子质量:H 1 C 12 N 14 0 16 S 32 Zn 65第I卷(选择题共120 分)本卷共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1•右图表示某动物细胞合成的分泌蛋白运输到细胞外的过程示意图。
下列叙述不正确的是()A •②、③膜的组成成分和结构相似B •分泌蛋白的分泌借助膜的选择透过性来完成C •此围所示各种膜中糖蛋白含量最高的可能是①D .细胞内许多生化反应部是在生物膜内或膜表面进行的2.下列有关人体细胞分裂的叙述,正确的是()A •有丝分裂与减数分裂相比基因突变和基因重组的概率增加B •减数第二次分裂前期细胞中的DNA数目与有丝分裂中期的相同C .减数第二次分裂的细胞中无同源染色体,染色体数都为23个D •减数第一次分裂后期与减数第二次分裂后期细胞中都有两个染色体组3•植物激素中的赤霉素能诱导一淀粉酶的产生,促进种子萌发;6 一甲基嘌呤是mRNA合成的抑制剂。
分别用三组淡剂对种子进行处理:①赤霉素;②赤霉素和脱落酸;③赤霉素和 6 一甲基嘌呤(6 一甲基嘌呤在第11小时加入,见图中)。
结果如图所示,下列说法不正确的是()A . 6 一甲基嘌呤可抑制tt 一淀粉酶的产生B •对Q一淀粉酶的合战,脱落酸与赤霉素表现为拮抗作用C •脱落酸作用机理是促进mRNA的合成D •种子的萌发受多种激素共同调节4•为研究某种药物对人体细胞的毒害作用,研究人员以哺乳动物组织块下列实验分析正确的是培养瓶编号12345药物浓度(mg/L)1050100300900变异细胞比例01/1061/1062/1068/106A •安验应在氧气充足,25 C环境条件下进行B •可利用显微镜观察或稀释涂布平板法进行计数C .实验结果表明浓度低于50mg/L时该药物对细胞没有毒害作用D •实验还需设置一个不加药物的空白对照组5. 以下对生物进化的叙述,正确的是A •二倍体生物用秋水仙素处理形成四倍体,二者之间不存在生殖隔离B •物种之间的共同进化都是通过物种之间的生存斗争实现的C .不同物种之间、生物与环境之间共同进化导致生物多样性D .突变和基因重组都会引起种群基因频率的定向改变6.下列说法正确的是 () ① 世博会中国馆一一 “东方之冠”使用的钢筋混凝土属于高分子化合物;② CH s COONa 、BaSO 4 —都是强电解质;③ 明矶和氯气可用于饮用水的净化和杀菌消毒,且两者的作用原理不同:④ O.lmol / L NaOH 溶液与 0.1 mol /L Ba (OH ) 2溶液的 pH 相同;⑤ 一定温度下,适量 CO 2分别通入饱和碳酸钠溶液和澄清石灰水中,都会出现浑浊。
崇文区度第二学期统一练习(理)答案doc
崇文区2009-2010学年度第二学期统一练习(一)高三数学(理科)参考答案及评分标准 2010.4一、选择题(本大题共8小题,每小题5分,共40分)(9)1- (10)1- (11)()2214x y -+= (12)13,21(13)11(1)(2)n nn T n b T n T -=⎧⎪=⎨≥⎪⎩ ;()221(1)(2)1n n b n n n =⎧⎪=⎨≥⎪-⎩(14)132三、解答题(本大题共6小题,共80分) (15)(共12分) 解:(Ⅰ)∵,552sin=A π<<A 0 ∴cos25A =. ∴4sin 2sin cos 225A A A ==. ∵2sin 21==∆A bc S ABC , ∴5=bc . --------------------6分(Ⅱ)∵,552sin=A ∴532sin21cos 2=-=A A . ∵5=bc ,6=+c b ,∴A bc c b a cos 2222-+=)cos 1(2)(2A bc c b +-+=20=∴52=a . -----------12分 (16)(共13分)解:(Ⅰ)根据直方图可知产品件数在[)20,25内的人数为50.066m ⨯⨯=,则20m =(位). ---------------- 6分(Ⅱ)根据直方图可知产品件数在[)10,15,[)15,20,[)20,25,[)25,30,[30,35],组内的人数分别为2,4,6, 5,3. 设选取这5人不在同组为B 事件,则5202465315()323P B C ⨯⨯⨯⨯==. 答:选取这5人不在同组的概率为15323. ---------------- 13分 (17)(共14分)(Ⅰ)证明: 连结1BC ,1AC . 在1ABC 中,,M N 是AB ,C A 1的中点, ∴||MN 1BC .又 MN ⊄平面11B BCC ,∴||MN 平面11B BCC . --------------------4分(Ⅱ)如图,以1B 为原点建立空间直角坐标系xyz B -1.则)0,0,0(1B ,(0,2,2)C ,1(2,0,0)A -,(1,0,2)M -,(1,1,1)N -∴1BC =(0,2,2),)0,0,2(11=B A ,(0,1,1)NM =-. 设平面C B A 11的法向量为(,,)x y z =n .111000B C x y z A B ⎧⋅==⎧⎪⇒⎨⎨=-⋅=⎩⎪⎩n n 令1=z ,则0,1x y ==-,∴(0,1,1)=-n .NM ∴n =.∴⊥MN 平面C B A 11. --------------------9分(Ⅲ)设平面C MB 1的法向量为000(,,)x y z =m 1(1,0,2)B M =-. 001001200x z B C y z B M ⎧=⋅=⎧⎪⇒⎨⎨=-⋅=⎩⎪⎩m m 令01z =,则002,1x y ==-∴(2,1,1)=-m .∴cos ,||||⋅<>===⋅n m n m n m . 所求二面角11A C B M --的余弦值为33. --------------------14分解:(Ⅰ)22'()31293()(3)0f x x ax a x a x a =-+=--<(1)当3a a =,即0a =时,2'()30f x x =>,不成立.(2)当3a a >,即0a <时,单调减区间为(3,)a a .(3)当3a a <,即0a >时,单调减区间为(,3)a a .-------------------5分 (Ⅱ)22'()31293()(3)f x x ax a x a x a =-+=--,()f x 在(0,)a 上递增,在(,3)a a 上递减,在(3,)a +∞上递增.(1)当3a ≥时,函数()f x 在[0,3]上递增, 所以函数()f x 在[0,3]上的最大值是(3)f ,若对[]0,3x ∀∈有()4f x ≤恒成立,需要有(3)4,3,f a ≤⎧⎨≥⎩解得a ∈∅.(2)当13a ≤<时,有33a a <≤,此时函数()f x 在[0,]a 上递增,在[,3]a 上递减,所以函数()f x 在[0,3]上的最大值是()f a ,若对[]0,3x ∀∈有()4f x ≤恒成立,需要有()4,13,f a a ≤⎧⎨≤<⎩解得1a =.(3)当1a <时,有33a >,此时函数()f x 在[,3]a a 上递减,在[3,3]a 上递增, 所以函数()f x 在[0,3]上的最大值是()f a 或者是(3)f .由2()(3)(3)(43)f a f a a -=--, ①304a <≤时,()(3)f a f ≤, 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有(3)4,30,4f a ≤⎧⎪⎨<≤⎪⎩解得3[1,]94a ∈-. ②314a <<时,()(3)f a f >, 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有()4,31,4f a a ≤⎧⎪⎨<<⎪⎩ 解得3(,1)4a ∈.综上所述,[19a ∈-. -------------14分解:(Ⅰ)设直线l 的方程为()1(0)y k x k =-≠.由()21,4,y k x y x ⎧=-⎪⎨=⎪⎩ 可得 ()2222240k x k x k -++=.设()()1122,,,A x y B x y ,则21212224,1k x x x x k++==. 124y y ∴=-()1,0N -1212221212441144NA NB y y y yk k x x y y +=+=+++++ ()()()()()()2212212112222212124444(4444)04444y y y y y y y y y y y y ⎡⎤+++-+-+⎣⎦===++++. 又当l 垂直于x 轴时,点,A B 关于x 轴,显然0,NA NB NA NB k k k k +==-. 综上,0,NA NB NA NB k k k k +==-. ---------------- 5分 (Ⅱ)12NAB S y y ∆=-===4>. 当l 垂直于x 轴时,4NAB S ∆=.∴ANB ∆面积的最小值等于4. ----------------10分 (Ⅲ)推测:①NA NB k k =-;②ANB∆面积的最小值为4 ---------------- 14分(20)(共13分) 解:(Ⅰ)当2n ≥时,11+111111n n n n n n nS a a S S S S +-=-=---, 化简得211(2)n n n S S S n -+=≥,又由1210,0S S a =≠=≠,可推知对一切正整数n 均有0n S ≠, ∴数列{}n S 是等比数列. ---------------- 4分 (Ⅱ)由(Ⅰ)知等比数列{}n S 的首项为1,公比为a , ∴1n n S a -=.当2n ≥时,21(1)n n n n a S S a a --=-=-, 又111a S ==,∴21,(1),(1),(2).n n n a a a n -=⎧=⎨-≥⎩ ----------8分 (Ⅲ)当4,2a n =≥时,234n n a -=⨯,此时22119934(3)(3)(343)(343)n n n n n n n a b a a ---+⨯⨯==++⨯+⨯+ 221213411(41)(41)4141n n n n n -----⨯==-++++, 又111293(3)(3)8a b a a ==++,∴213,(1)811,(2)4141n n n n b n --⎧=⎪⎪=⎨⎪-≥⎪⎩++1138T b ==, 当2n ≥时,1222212131111()()841414141n n n n T b b b ----=+++=+-++-++++ 171841n -=-+. 若1n =,则等式13758n n T a λ++=为37858λ+=,52λ=不是整数,不符合题意.若2n ≥,则等式13758n n T a λ++=为11717841548n n λ---+=+⨯,15541n λ-=-+ λ是整数,∴141n -+是5的因数.∴当且仅当2n =时,1541n -+是整数, ∴4λ=综上所述,当且仅当4λ=时,存在正整数2n =,使等式13758n n T a λ++=成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
崇文区2009-2010学年度第二学期统一练习(一)
高三数学(理科) 2010.4
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
注意事项:
1.考生务必将答案答在答题卡上,在试卷上作答无效。
2.答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号,然后再用2B 铅笔将与准考证号对应的信息点涂黑。
3.答题卡上第Ⅰ卷必须用2B 铅笔作答,将选中项涂满涂黑,黑度以遮住框内字母为准,修改时用橡皮擦除干净。
第Ⅱ卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区域内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目
要求的一项.
(1)已知全集U =R ,集合{}|12A x x =->,{}2|680B x x x =-+<,则集合
()U
A B ⋂=ð
(A ){}|14x x -≤≤ (B ){}|14x x -<< (C ){}|23x x ≤< (D ) {}|23x x <≤
(2)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人. 为
了调查职工的健康状况,用分层抽样的方法从全体职工中抽出一个容量为25的样本,应抽取不超过45岁的职工人数为
(A) 5 (B) 10 (C )15 (D )50 (3)已知P A 是 O 的切线,切点为A ,2PA =,A C 是 的直径,P C 交 O 于点B ,30PAB ∠=
,则 O 半径为
(A )1 (B
)2 (C
(D )
(4)已知等比数列{}n a 为递增数列,且373a a +=,282a a ⋅=,则
117
a a =
(A )2 (B )
43
(C )
32
(D )
12
(5)已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的为
(A )若,,αγβγ⊥⊥则αβ (B )若,,m n αα⊥⊥则m n (C )若,m n αα ,则m n (D )若,,m m αβ 则αβ (6
)设33,,2
x
y
x y
M N P ++=
==0x y <<), 则,,M N P 大小关系为
(A )M N P << (B )N P M << (C )P M N << (D )P N M << (7)2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两
位女生相邻,则不同排法的种数为
(A )36 (B )42 (C ) 48 (D ) 60 (8)设定义在R 上的函数1,(1),
1
()1,(1)x x f x x ⎧≠⎪
-=⎨⎪=⎩
.
若关于x 的方程
2
()()0f x bf x c ++=有3个不同的实数解1x ,2x ,3x ,则123x x x ++等于
(A ) 3 (B )2 (C )1b -- (D )c
崇文区2009-2010学年度第二学期统一练习(一)
高三数学(理科) 2010.4
第Ⅱ卷(共110分)
二、填空题:本大题共6小题,每小题5分,共30分.
(9)如果复数()()2i 1i m m ++(其中i 是虚数单位)是实数,则实数m =___________. (10)若12
)a x
的展开式中的常数项为220-,则实数a =___________.
(11)将参数方程12cos ,
2sin ,x y θθ=+⎧⎨=⎩
(θ为参数)化成普通方程为 .
(12)某程序框图如图所示,该程序运行后输出,M N 的值分别为 .
(13)若数列{}n a 的前n 项和为n S ,则11,
(1),,(2)n n n S n a S S n -=⎧=⎨-≥⎩.
若数列{}n b 的前n 项积为n T ,类比上述结果,则n b =_________;
此时,若2()n T n n *
=∈N ,则n b =___________.
(14)定义在R 上的函数满足1(0)0,()(1)1,(()5
2
x f f x f x f f x =+-==
,
且当1201x x ≤<≤时,12()()f x f x ≤,则1(
)2010
f =_________________.
10 15 20 25 30 35
产品数量
0 0.02
0.03 0.04
0.05 0.06
1
1
C
A 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题共12分)
在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,
满足sin 2
5
A =
,且ABC ∆的面积
为2.
(Ⅰ)求bc 的值;
(Ⅱ)若6=+c b ,求a 的值.
(16)(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了m 位工人某天生产该产品的数量,产品数量的分组区间为[)10,15,[)15,20,[)20,25,[)25,30,[30,35],频率分布直方图如图所示.已知生产的产品数量在[)20,25之间的工人有6位. (Ⅰ)求m ;
(Ⅱ)工厂规定从各组中任选1人进行再培训,则选取5人的概率是多少?
(17)(本小题共14分)
三棱柱111C B A ABC -中,侧棱与底面垂直,
90=∠ABC ,12AB BC BB ===,
,M N 分别是AB ,1A C 的中点.
(Ⅰ)求证:MN 平面11B BCC ; (Ⅱ)求证:⊥MN 平面C B A 11; (Ⅲ)求二面角11A C B M --的余弦值.
(18)(本小题共14分)
已知322()69f x x ax a x =-+(a ∈R ). (Ⅰ)求函数()f x 的单调递减区间;
(Ⅱ)当0a >时,若对[]0,3x ∀∈有()4f x ≤恒成立,求实数a 的取值范围.
(19)(本小题共14分)
已知抛物线24y x =,点(1,0)M 关于y 轴的对称点为N ,直线l 过点M 交抛物线于
,A B 两点.
(Ⅰ)证明:直线,NA NB 的斜率互为相反数; (Ⅱ)求A N B ∆面积的最小值;
(Ⅲ)当点M 的坐标为(,0)(0m m >,且1)m ≠.根据(Ⅰ)(Ⅱ)推测并回答下列问题
(不必说明理由):
① 直线,NA NB 的斜率是否互为相反数? ② A N B ∆面积的最小值是多少?
(20)(本小题共13分)
已知数列{}n a 中,11a =,21(0a a a =-≠且1)a ≠,其前n 项和为n S ,且当2
n ≥时,
1
111n
n
n S a a +=-
.
(Ⅰ)求证:数列{}n S 是等比数列; (Ⅱ)求数列{}n a 的通项公式; (Ⅲ)若4a =,令19(3)(3)
n
n n n a b a a +=
++,记数列{}n b 的前n 项和为n T .设λ是整数,
问是否存在正整数n ,使等式1
3758
n n T a λ
++=成立?若存在,求出n 和相应的λ值;
若不存在,请说明理由.
(考生务必将答案答在答题卡上,在试卷上作答无效)。
