直角三角形性质应用(讲义)
直角三角形性质应用讲义及答案
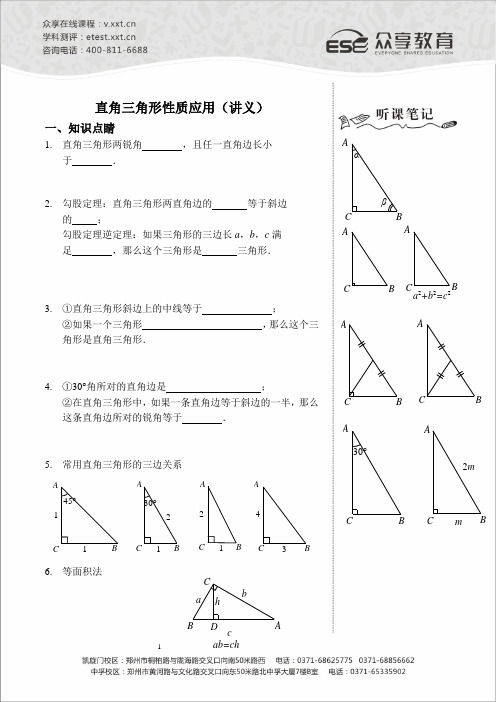
直角三角形性质应用(讲义)一、知识点睛1. 直角三角形两锐角 ,且任一直角边长小于 .2. 勾股定理:直角三角形两直角边的 等于斜边的 ;勾股定理逆定理:如果三角形的三边长a ,b ,c 满足 ,那么这个三角形是 三角形.3. ①直角三角形斜边上的中线等于 ;②如果一个三角形 ,那么这个三角形是直角三角形.4. ①30°角所对的直角边是 ;②在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于 .5. 常用直角三角形的三边关系A C B45°1130°234211BCA BCAB CA6. 等面积法ABCC B Aa 2+b 2=c2ABC C BAβαC A B 30°CB A CBA2mmD h C BAc bay x二、精讲精练1. 下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边(x >y ),下列四个说法:①x 2+y 2=49,②x -y =2,③2xy +4=49,④x +y =9.其中说法正确的是( ) A .①③ B .①②③ C .②④ D .①②③④2. 如图,在正方形ABCD 中,E 是DC 的中点,F 为BC 上的一点且BC =4CF ,试说明△AEF 是直角三角形.3. 如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB =∠ECD =90°,D 为AB 边上一点,求证:AD 2+DB 2=DE 2.ABCDE4. 在△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长是_______.FE DC B A5.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()A.10 B.45C.10或45D.10或2176.直角三角形斜边上的中线长是6.5,一条直角边长是5,则另一直角边长等于()A.13 B.12 C.10 D.57.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为()A.3B.3.5C.4D.4.58.△ABC周长是24,M是AB的中点,MC=MA=5,则△ABC的面积是.9.如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为()A.3B.23C.33D.43EDCBAPDCB A23423410. 如图,四边形ABCD 中,∠DAB =∠DCB =90o ,点M 、N 分别是BD 、AC 的中点.MN 、AC 的位置关系如何?证明你的猜想.11. 如图,在Rt △ABC 中,AC ≠AB ,AD 是斜边BC 上的高,DE⊥AC ,DF ⊥AB ,垂足分别为E 、F ,则图中与∠C (除∠C 外)相等的角的个数是( ) A .2 B .3 C .4 D .512. 如图,已知DE =m ,BC =n ,∠EBC 与∠DCB 互余,求BD 2+CE 2的值.BCDE13. 在△ABC 中,∠C =90°,AB =6,∠B =30°,点P 是BC 边上的动点,则AP 长不可能是( )A .3.5B .4.2C .5.8D .214. 如图,在Rt △ABC 中,∠A =30°,DE 垂直平分斜边AC ,交AB 于D ,E 是垂足,连接CD ,若BD =1,则AC 的长是( ) A .23 B .2 C .43 D .4NMCD BAFEDCB AEDA15. 某市在旧城改造中,计划在一块如图所示的△ABC 空地上种植草皮以美化环境,已知∠A =150°,这种草皮每平方米售价a 元,则购买这种草皮至少需要( ) A .300a 元 B .150a 元 C .450a 元 D .225a 元CBA30m20m16. 放风筝是大家喜爱的一种运动.星期天的上午小明在绿城广场上放风筝,如图他在A 处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D 处,此时风筝线AD 与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了离A 处6米的B 处,此时风筝线BD 与水平线的夹角为45°.已知点A 、B 、C 在同一条直线上,∠ACD =90°.求DC 的长度.ABCD30°45°17. 已知,在△ABC 中,∠A =45°,AC =2,AB =3+1,则边BC 的长为 .CBAP CBA18. 在Rt △ABC 中,∠C =90°,AC =9,BC =12,则点C 到AB 的距离是( )A .365B .1225C .94D .33419. 如图所示,等边△ABC 内一点P 到三边距离分别为h 1,h 2,h 3,且h 1+h 2+h 3=3,其中PD =h 1,PE =h 2,PF =h 3,则△ABC 的面积S △ABC =( )A .23B .33C .103D .12320. 如图,△ABC 中,∠C =90°,两直角边AC =8,BC =6,在三角形内有一点P ,它到各边的距离相等,则这个距离是( ) A .1 B .2 C .3 D .无法确定21. 在直线l 上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4=_______.l321S 4S 3S 2S 1P FEDCBACBA22. 如图,△ABC 中,∠ACB =90°,点E 为AB 的中点,点D 在BC 上,且AD =BD ,AD 、CE 相交于点F ,若∠B =20°,则∠DFE 等于( ) A .70° B .60° C .50° D .40°23. 在锐角△ABC 中,∠BAC =60°,BN 、CM 为高,P 为BC 的中点,连接MN 、MP 、NP ,则结论:①NP =MP ;②当∠ABC =60°时,MN ∥BC ;③BN =2AN ;④::AN AB =AM AC ,一定正确的有( )A .1个B .2个C .3个D .4个三、回顾与思考______________________________________________________ ______________________________________________________ ______________________________________________________【参考答案】 一、 知识点睛1.互余,斜边长2.平方和,平方,a 2+b 2=c 2,直角3.斜边的一半,一边上的中线等于这边的一半4.斜边的一半,30°二、精讲精练1.B 2.(略) 3.(略) 4. 42或32 5.C 6.B 7.A 8.24 9.D 10.MN ⊥AC ,证明(略) 11.BABCD EFPNM CBA12.m2+n2,证明(略)13.D14.A15.B 16.8m,求解(略)17.2 18.A19.B20.B 21.4 22.B 23.C。
八年级数学直角三角形(学生讲义)

直角三角形一、直角三角形的性质重点:直角三角形的性质定理及其推论:①直角三角形的性质,在直角三角形中,斜边上的中线等于斜边的一半;②推论:(1)在直角三角形中,如果一个锐角等于30°,则它所对的直角边等于斜边的一半;(2)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为30°.难点:1.性质定理的证明方法.2.性质定理及其推论在解题中的应用.二、直角三角形全等的判断重点:掌握直角三角形全等的判定定理:斜边、直角边公理:斜边和一条直角边对应相等的两个直角三角形全等(HL)难点:创建全等条件与三角形中各定理联系解综合问题。
三、角平分线的性质定理1.角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.定理的数学表示:如图4,∵ OE是∠AOB的平分线,F是OE上一点,且CF⊥OA于点C,DF⊥OB于点D,∴ CF=DF.定理的作用:①证明两条线段相等;②用于几何作图问题;角是一个轴对称图形,它的对称轴是角平分线所在的直线.2.关于三角形三条角平分线的定理:(1)关于三角形三条角平分线交点的定理:三角形三条角平分线相交于一点,并且这一点到三边的距离相等.定理的数学表示:如图6,如果AP、BQ、CR分别是△ABC的内角∠BAC、∠ ABC、∠ACB的平分线,那么:① AP、BQ、CR相交于一点I;②若ID、IE、IF分别垂直于BC、CA、AB于点D、E、F,则DI=EI=FI.定理的作用:①用于证明三角形内的线段相等;②用于实际中的几何作图问题.(2)三角形三条角平分线的交点位置与三角形形状的关系:三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心(即内切圆的圆心).3.关于线段的垂直平分线和角平分线的作图:(1)会作已知线段的垂直平分线;(2)会作已知角的角平分线;(3)会作与线段垂直平分线和角平分线有关的简单综合问题的图形.四、勾股定理的证明及应用图4内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方 2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c ,b ,a ②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题 5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数: 221,2,1n n n -+(2,n ≥n 为正整数);cbaHG F EDCBAbacbac cabcab a bcc baE D CBA2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解. 8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.常见图形:ABC30°D C BA ADB C10、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。
等腰三角形与直角三角形讲义

等腰三角形与直角三角形讲义一、等腰三角形(一)等腰三角形的定义有两边相等的三角形叫做等腰三角形。
相等的两条边称为腰,另一条边称为底边。
两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
(二)等腰三角形的性质1、等腰三角形的两个底角相等(简写成“等边对等角”)。
2、等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)。
例如,在等腰三角形 ABC 中,AB = AC,如果 AD 是顶角∠BAC 的平分线,那么 AD 也是底边 BC 上的中线和高;如果 AD 是底边 BC 上的中线,那么 AD 也是顶角∠BAC 的平分线和底边 BC 上的高;如果 AD 是底边 BC 上的高,那么 AD 也是顶角∠BAC 的平分线和底边BC 上的中线。
(三)等腰三角形的判定1、如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
2、有两条边相等的三角形是等腰三角形。
(四)等腰三角形的周长和面积1、周长:等腰三角形的周长=腰长×2 +底边长度。
2、面积:等腰三角形的面积=底×高÷2。
(五)等腰三角形的常见题型1、利用等腰三角形的性质求角度。
比如,已知等腰三角形的一个底角为 70°,求顶角的度数。
因为等腰三角形的两个底角相等,所以另一个底角也是 70°,根据三角形内角和为 180°,顶角的度数为 180° 70°×2 = 40°。
2、利用等腰三角形的判定证明三角形是等腰三角形。
给定一个三角形,已知其中两个角相等,证明它是等腰三角形。
3、利用等腰三角形的周长和面积解决实际问题。
例如,要制作一个等腰三角形的招牌,已知腰长为 5 米,底边长为6 米,求制作这个招牌需要多少材料(即求周长),以及招牌的面积是多少。
二、直角三角形(一)直角三角形的定义有一个角为 90°的三角形,叫做直角三角形。
直角三角形的边角关系的讲义

直角三角形的边角关系的讲义(一)知识点梳理: 1、正切的定义的对边与邻边的比便随之确定,这个比叫做∠A 的正切,记作例1:已知在Rt △ABC 中,∠C=90°,CD ⊥AB ,AD=8,BD=4,求tanA 的值。
2、坡度的定义及表示例题2:如图,水坝的横断面为梯形ABCD ,迎水坡BC 的坡角∠B 为300,背水坡AD 的坡度为65,坝顶宽DC =2.5m ,坝高CF =4.5m ,求:(1)迎水坡BC 的长;(2)坝底AB 的长(精确到0.1m ).3、正弦、余弦的定义例3:在△ABC中,∠C=90°,BC=1,AC=2,求sinA、sinB、cosA、cosB的值。
通过计算你有什么发现?请加以证明。
4、三角函数的定义例:∠C=90°,点D在BC上,BD=6,AD=BC,cos∠ADC=,求CD的长。
55、30°,45°,60°角的三角函数值 1、30°,45°,60°角的三角函数值例:求下列各式的值。
(1)︒︒-︒60tan 30sin 60sin ; (2)︒-+︒-︒45sin 22460tan 460tan 2。
精选试题练习: 一、选择填空。
1.把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦函数值( ) A .不变 B .缩小为原来的13C .扩大为原来的3倍D .不能确定 2.在△ABC 中,∠A =120°,AB =4,AC =2,则sinB 的值是( )CB AA .1475 B .53C .721 D .1421 3. 如图,在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE=60°,BD=4,CE=43,则△ABC 的面积为( ) A.B .15C.D.BACDE4. 如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB,垂AC=则sin ∠足为D.若ACD 的值为( )C. D. 235.如图,在等腰Rt △ABC 中,∠C =90o ,AC =6,D 是AC 上一点,若tan ∠DBA =51,则AD 的长为 ( ) (A ) 2 (B )3 (C )2(D )16.如图,在梯形ABCD 中,AD//BC ,AC ⊥AB ,AD=CD54cos =∠DCA ,BC=10,则AB 的值是( )A .9B .8C .6D .37.如图,已知梯形ABCD 中,AD ∥BC ,∠B =30°,∠C =60°,AD =4,AB =,则下底BC 的长为 __________.8.如图,已知Rt ΔABC 中,斜边BC 上的高AD=4,cosB=54,则AC= . 9.如图,已知直线1l ∥2l ∥3l ∥4l ,相邻两条平行直线间的距离都是1,如果正方形ABCD 的四个顶点分别在四条直线上,则sin α= .60°30°D CBA10. 如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A 、B 两岛的视角∠ACB= 11.如图,在Rt △ABC 中,∠ABC=90°,∠ACB=30°,将△ABC 绕点A 按逆时针方向旋转15°后得到△AB 1C 1,B 1C 1交AC 于点D ,如果AD=△ABC 的周长等于 .二、解答题。
初中数学直角三角形边角关系讲义初稿

直角三角形边角关系讲义(初稿)一、 概念部份 一、大体概念 正弦:在Rt ∆ABC (如图),锐角A 的对边与斜边的比叫做A ∠的正弦,记为A sin ,caA A =∠=斜边的对边sin 。
余弦:在Rt ∆ABC (如图),锐角A的余弦,记为A cos ,cbA A =∠=斜边的邻边cos 。
正切:在Rt ∆ABC (如图),锐角A 的对边与邻边的比叫做A ∠的正切,记为A tan ,baA A A =∠∠=的邻边的对边tan 。
余切:在Rt ∆ABC (如图),锐角A 的邻边与对边的比叫做A ∠的余切,记为A cot ,abA A A =∠∠=的对边的邻边cot 。
二、巧记概念:按正弦、余弦、正切、余切的顺序记八个字:对斜邻斜对邻邻对。
3、依照正弦、余弦、正切、余切的概念,在Rt ∆ABC 中, 90=∠C ,有sinA=cosB ,sinB=cosA ,tanA=cotB ,tanB=cotA 。
4、正弦、余弦、正切的值与梯子倾斜程度之间的关系:sinA 的值越大,梯子越陡; cosA 的值越小,梯子越陡; tanA 的值越大,梯子越陡。
五、在Rt ∆ABC 中,︒=∠90C ,a 、b 、c 别离是A ∠、B ∠、C ∠的对边,那么caA =sin , c b A =cos , b a A =tan , abA =cot 能够变形为A c a sin •=,A c b cos •=,A b a tan •=或A a c sin =,Abc cos =等等,在解题中能够依照条件正确选用。
六、注意:①、在初中,正弦、余弦、正切、余切的概念都是在直角三角形中给出的,不能在任意三角形中套用概念。
②、sinA 、cosA 、tanA 、cotA 别离表示正弦、余弦、正切、余切的数学表达符号,是一个整体,不能明白得为sin 与A 、cos 与A 、tan 与A 、cot 与A 的乘积。
③sinA 、cosA 、tanA 、cotA 是一个完整的符号,它表示A ∠的正弦、余弦、正切、余切,记号里适应省去角的符号“∠”,但当角用三个大写字母或数字表示时,角的符号“∠”不能省略。
等边三角形直角三角形讲义

等边三角形直角三角形讲义关键信息项1、协议目的:明确等边三角形和直角三角形的相关知识和教学要点。
2、适用范围:适用于数学教学、学术研究等领域。
3、协议有效期:自签订之日起X年内有效。
4、知识要点涵盖:等边三角形和直角三角形的定义、性质、判定方法等。
5、教学方法与资源:包括讲解示例、练习题目、多媒体资料等。
6、考核与评估方式:如考试、作业、课堂表现等。
7、版权与使用权限:明确讲义的版权归属和使用限制。
8、协议变更与终止条件:规定在何种情况下可以变更或终止协议。
11 等边三角形的定义等边三角形是指三条边长度相等的三角形。
111 等边三角形的性质1、等边三角形的三个内角相等,均为 60°。
2、等边三角形是轴对称图形,有三条对称轴。
3、等边三角形的中线、高线和角平分线三线合一。
112 等边三角形的判定方法1、三条边都相等的三角形是等边三角形。
2、三个角都相等的三角形是等边三角形。
3、有一个角是 60°的等腰三角形是等边三角形。
12 直角三角形的定义直角三角形是指其中一个角为 90°的三角形。
121 直角三角形的性质1、直角三角形的两个锐角互余。
2、直角三角形斜边上的中线等于斜边的一半。
3、直角三角形中,30°角所对的直角边等于斜边的一半。
4、勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
122 直角三角形的判定方法1、有一个角为 90°的三角形是直角三角形。
2、若一个三角形的两条边的平方和等于第三边的平方,则这个三角形是直角三角形。
13 等边三角形与直角三角形的关系1、等边三角形不可能是直角三角形,因为等边三角形的三个角均为 60°。
2、直角三角形中,如果一个锐角为 60°,另一个锐角为 30°,则三条边的长度关系满足特定比例。
14 教学方法141 理论讲解通过课堂讲解,让学生理解等边三角形和直角三角形的定义、性质和判定方法。
解直角三角形-特殊角的三角函数值讲义

三角函数 正弦sinα 锐角α
余弦 cosα
正切 tanα
300 450
600
1 2 2 2 3 2
3 2 2 2 1 2
ห้องสมุดไป่ตู้
3 3
1
3
1 2 3 2 2 2
1 3 1 1 3
例1、求下列各式的值:
(1). 1-2sin30 +cos30°
(2). 3tan30 -tan45 +2sin60°
B
1 2
sin30°=
C
30.0
A
A的 对 边 1 斜边 2
A的 邻 边 3 斜边 2
3
cos30°=
A的 对 边 3 tan30°= A的 邻 边 3
新知探索:45°角的三角函数值
B
2
1
45.0
A的 对 边 2 sin45°= 斜边 2
A
1
C
cos45°= A的 邻 边 2
特殊角的三角函数值
请同学们拿出 自己的学习工具— 1 —一副三角尺,思 考并回答下列问题:
1
1
2
2
3
45° 45°
1、这两块三角尺各有几个锐角?它们分别等于多少度? 30° 60°
2、每块三角尺的三边之间有怎样的特殊关系?如 果设每块三角尺较短的边长为1,请你说出未知边 的长度。
新知探索:30°角的三角函数值
o
2
3
2 2
1 (2)如果∠A为锐角,且 cos A 5,那么(
)
A.0°< A ≤ 30° B.30°< A ≤ 45°
C.45°< A ≤ 60°
D.60°< A < 90°
《直角三角形全等的判定》 讲义

《直角三角形全等的判定》讲义一、直角三角形全等的概念在平面几何中,如果两个直角三角形能够完全重合,那么它们就是全等的。
全等的直角三角形具有相同的形状和大小,对应的边和角都相等。
二、直角三角形全等的判定方法1、 SSS(边边边)如果两个直角三角形的三条边分别对应相等,那么这两个直角三角形全等。
2、 SAS(边角边)如果两个直角三角形的两条边及其夹角分别对应相等,那么这两个直角三角形全等。
3、 ASA(角边角)如果两个直角三角形的两个角及其夹边分别对应相等,那么这两个直角三角形全等。
4、 AAS(角角边)如果两个直角三角形的两个角和其中一个角的对边分别对应相等,那么这两个直角三角形全等。
5、 HL(斜边、直角边)如果两个直角三角形的斜边和一条直角边分别对应相等,那么这两个直角三角形全等。
这是直角三角形全等特有的判定方法。
因为在直角三角形中,斜边是最长的边,当斜边和一条直角边对应相等时,由勾股定理可以推出另一条直角边也对应相等,从而满足边边边(SSS)的判定条件。
三、HL 判定方法的证明已知:在 Rt△ABC 和 Rt△A'B'C' 中,∠C =∠C' = 90°,AB =A'B',AC = A'C' 。
求证:Rt△ABC ≌ Rt△A'B'C'证明:在 Rt△ABC 中,根据勾股定理:BC²= AB² AC²在 Rt△A'B'C' 中,根据勾股定理:B'C'²= A'B'² A'C'²因为 AB = A'B',AC = A'C' ,所以 BC = B'C'因为 AB = A'B',AC = A'C' ,BC = B'C' ,所以 Rt△ABC ≌Rt△A'B'C'(SSS)四、直角三角形全等判定方法的应用1、证明线段相等例如,已知两个直角三角形全等,那么它们对应的边相等,从而可以证明某些线段相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直角三角形性质应用
➢ 课前预习
1. 根据图中给出的边长及角度信息,在横线上补全下列直角三角形的边长.
1
1
45°
30°
2
30°
45°
23
2. 下列是不完整的弦图结构,请补全弦图.
➢ 知识点睛
直角三角形性质梳理:
1. 从边与角的角度来考虑
①直角三角形两锐角_______,且任一直角边长小于_______.
②勾股定理:直角三角形两直角边的______等于斜边的____; 勾股定理逆定理:如果三角形两边的______等于__________,那么这个三角形是_______三角形.
2. 添加一些特殊的元素(中线或30°角)
①直角三角形斜边上的中线等于______________; 如果一个三角形____________________________,那么这个三角形是直角三角形.
②30°角所对的直角边是_____________________;
在直角三角形中,如果一条直角边等于斜边的一半,那么这 条直角边所对的锐角等于_____________.
3. 特殊的直角三角形
A
C B 45°
1
130°
2
3
4
2
1
1
C
A
B
C
A B C
A
4. 垂直(多个)
①等面积法
a 2+
b 2=c
2
C
B
A
C B A
β
α
C
A A B
C
A
B
C C
B
A
2m
m
A
B
C
30°
ab=ch
D h C B
A
c b
a
h h=h 1+h 2+h 3
h 3
h 2h 1
A
C
B
②弦图结构
外弦图(赵爽弦图) 内弦图(毕达哥拉斯图)
➢ 精讲精练
1. 如图,在Rt △ABE 中,∠B =90°,延长BE 到C ,使EC =AB ,分别过点C ,E 作
BC ,AE 的垂线,两线相交于点D ,连接AD .若AB =3,DC =4,则AD 的长为___________.
E D
C B
A
A
E
D
C
B
第1题图 第2题图
2. 如图,在△ABC 中,点D ,E 分别在AC ,AB 边上,若DE =m ,BC =n ,且∠EBC
与∠DCB 互余,则BD 2+CE 2=__________(用含m ,n 的式子表示).
3. 如图,在△ABC 中,∠C =2∠B ,点D 是BC 上一点,AD =5,且AD ⊥AB ,点E
是BD 的中点,AC =6.5,则AB 的长为______.
A
B
C F
E
C B A
第3题图 第4题图
4. 如图,在△ABC 中,∠ACB =90°,点E 为AB 的中点,点D 在BC 上,且AD =BD ,
AD ,CE 相交于点F .若∠B =20°,则∠DFE 等于( ) A .70°
B .60°
C .50°
D .40°
5. 已知△ABC 的周长是24,M 是AB 的中点,MC =MA =5,则△ABC 的面积是
__________.
6. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的
连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2,4,3,则原直角三角形纸片的斜边长是( ) A .10
B
.C .10
或
D .10
或
4
3
2
4
32
7. 如图,在Rt △ABC 中,∠C =90°,AC =BC ,点D 在AC 上,若∠CBD =30°,则
AD
DC
=_________. D
C
B A
8. Rt △ABC 和Rt △DEF 按如图方式放置,A ,B ,D 在同一直线上,EF ∥AD ,∠
CAB =∠EDF =90°,∠C =45°,DE =8,EF =16,则BD =__________.
C
B
A
E
D
F
A D
B
E
C
第8题图 第9题图
9. 如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,
∠BDA =90°,∠CBE =30°,∠CEB =45°,AE =4EC ,BC =2,则BE =__________,CD =__________.
10. 如图,在Rt △ABC 中,∠ABC =90°,AB =2,BC =3,以斜边AC 为边作正方形
ACDE ,连接BE ,则BE 的长为________.
E
D
C
B A
E
D
C B
A
O
第10题图 第11题图
11. 如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 为边向外作正方形ABDE ,且
正方形的对角线交于点O ,连接OC ,已知AC =5,OC
=,则另一直角边BC 的长为__________.
12. 如图,以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCDE ,设正方
形的中心为O ,连接AO ,如果AB =4,AO
=那么AC 的长为__________.
【参考答案】
➢ 课前预习
1.
3
,3
;2
,2
;3
2. 略
➢ 知识点睛
1. ①互余,斜边长
②平方和,平方;平方和,第三边的平方,直角 2. ①斜边的一半,一边上的中线等于这边长的一半
②斜边的一半;30°
3.
①11:
12
,12:345:: ➢ 精讲精练
1.
2. 22m n +
3. 12
4. B
5. 24
6.
C
7.
1-+8.
12-9.
1+
10.
11. 7 12. 8
直角三角形性质应用(随堂测试)
1. 如图,在Rt △ABC 中,AC ⊥BC ,AD 平分∠BAC ,交BC 于点D ,DE ⊥AD ,交
AB 于点E ,M 为AE 的中点,连接DM .若AD
=CD
,则DM 的长为_____________.
第1题图 第2题图
2. 如图,在Rt △ABC 中,∠ACB =90°,以Rt △ABC 的斜边
AB 为一边在△ABC 的同侧作正方形ABDE ,对角线AD ,
O
D
C
E
A
M
E C
B A
BE相交于点O,连接OC.若AC=5,AB=13,则OC的长为___________.
【参考答案】
1. 2
2.。
