平面四杆机构设计(解析法)
综合运用解析法和实验法设计平面四杆机构

三 对 对 应 位 置 ( . ) ( , ) ( , ) 则 有 下 列 、 、 也 ,
关 系 :
C8 : O + o ( ) P 0 咖】 S c s 妇一 + 2 c s>- 0 Pl 8 如一她) P o 4F 8 c ( 0 + 2 C 8 o c s 只c s 如一 ) O 也t o + o ( + P,
al 、 / 、 c 根 据 实 际 需 要 决 定 构 件 的 长 度 c 其 c b c d, 再 , 余 构 件 的 长 度 。 6、 便 可 最 后 确 定 。 、 d 然 而 , 生 产 实 践 中 , 常 要 求 原 动 件 和 从 动 在 常
件 之 间 能 实 现 三对 以 上 或 更 多 的 对 应 位 置 关 系 。根
在 生 产 实 践 中 , 常 要 求 平 面 四 杆 机 构 的 原 动 常 件 和 从 动 件 之 间 能 实 现 三 对 以 上 或 更 多 对 对 应 的 位 置 关 系 。 解 析 法 只 能 准 确 实 现 原 动 件 和 从 动 件 之
间 的 三 对 对 应 位 置 关 系 ,实 验 法 虽 然 能 近 似 地 解 决
其 中 、 、 同前 。 只
( 4)
显 然 . 要 知 道 原 动 件 和 从 动 件 的 四对 对 应 位 其 置 关 系 , 可 以 求 出 : 、 / 、 / 和 0 然 后 . 据 实 就 6 ca da 。 根
际 需 要 确 定 构 件 AB的 长 度 口 从 而 即 可 确 定 机 构 其 ,
若 以 构 件 C 的 长 度 c 基 准 , 按 方 程 ( ) ( ) D 为 1 、2 、 ( ) 确 定 , 3可 , ,进 而 求 解 出其 余 的 相 对 长 度
第8章 第5讲 平面四杆机构的设计——解析法

第5讲平面四杆机构的设计(二)
8.5.1 解析法设计的基本思想
8.5.2 平面四杆机构的解析设计
8.5.1 解析法设计的基本思想
在用解析法设计四杆机构时,首先需建立包含机构各尺度参数和运动变量在内的解析式,然后根据已知的运动变量求机构的尺度参数。
方法特点:
可借助于计算器或计算机求解,计算精度高,适应于对三个或三个以上位置设计的求解,尤其是对机构进行优化设计和精度分析十分有利。
8.5.2 平面四杆机构的解析设计
1. 按预定的连杆位置设计四杆机构
2. 按预定的运动轨迹设计四杆机构
3. 按预定的连架杆运动规律设计四杆机构
(1)按预定的两连架杆对应位置设计
(2)按期望函数设计
(3)按给定的急回运动要求设计
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)。
平面四杆机构的设计

以A为圆心、 l1为半径作圆, 交C1A的延长线于
B1, 交C2A于B2, 即可得连杆的长度l2=B1C1=B2C2
以及机架的长度l4=AD。 机构AB1C1D即为该机构在
极限位置时的运动简图。
返回
机械设计基础
cos l2 cos l4 l3 cos
sin l2 sin l3 sin
机械设计基础
Machine Design Foundation
平面四杆机构的设计
该机构的四个杆组成封闭多边形。取各杆在坐标轴 x和y上的投影,可得以下关系式:
将cosφ和sinφ平移到等式右边,再把等式两边平
机械设计基础
Machine Design Foundation
平面四杆机构的设计
1.3 按给定的行程速度变化系数设计
在设计具有急回特性的平面四杆机构时, 通常 按照实际的工作需要, 先确定行程速度变化系数K的
数值, 并按式(6 - 2)计算出极位夹角θ, 然后利用
机构在极限位置时几何关系, 再结合其它有关的附加 条件进行四杆机构的设计, 从而求出机构中各个构件 的尺寸参数。
P
平面四杆机构的设计
NM
图6- 25 按K值设计曲柄摇杆机构
机械设计基础
Machine Design Foundation
平面四杆机构的设计
解 设计的实质就是确定曲柄与机架组成的固定
铰链中心A的位置, 并求出机构中其余三个构件的长 度l1、 l2和l4。
其设计步骤如下:
(1) 计算极位夹角θ。
根据给定的行程速度变化系数K, 由式(4 - 9)计
解 设计的实质就是确定连架杆与机架组成的固定
铰链中心A和D的位置, 并由此求出机构中其余三个构 件的长度l1、 l3和l4。
平面四杆机构的设计

一.按给定的行程速比系数设计四杆机构
设计具有 急回特性 的四杆机 构,关键 是要抓住 机构处于 极限位置 时的几何 关系,必 要时还应 考虑其他 辅助条件。
例:已知摇杆长度L=100,摆角 =50 和行程速比 系数k=1.4,试设计曲柄摇杆机构。
K 1 解: 由给定的行程速比系 180 = 30 数求出极位夹角 : K 1
2-4平面四杆机构的设计
设计类型 :
1.实现给定的运动规律:给定行程速 比系数以实现预期的急回特性、实现 连杆的几组给定位置等。 2.实现给定的运动轨迹:要求连杆上 某点沿着给定轨迹运动等。
设计目标 :
根据给定的运动条件,选定机构的类 型,确定机构中各构件的尺寸参数。
设计方法 :图解法、实验法和解析法等。
有无穷多个解。实际上,还应考虑几何、动力等辅助条 件,例如各杆所允许的尺寸范围、最小传动角或其他结 构上的要求,就可以合理选定A、D两点的位置而得到确 定的解。 如果给定连杆三个、四个或五个位置呢?
例:设计一铰链四杆 机构作为加热炉炉门 的启闭机构。已知炉 门上两活动铰链B、C 的中心距为50。要求 炉门打开后成水平位 置,且热面朝下(如 虚线所示)。如果规 定铰链A、D安装在炉 体的y-y坚直线上, 其相关尺寸如图所示。 用图解法求此铰链四 杆机构其余三杆的尺 寸。
C1 90- E l4
C2
A B1
B2 D
以A为圆心,AC1为 半径作圆弧交A与 E,平分EC2得曲柄 长度 AB 。再以A 为圆心, AB 为 半径作圆,交C1A 的延长线和C2A于 B1和B2,连杆长度
BC B 1 C 1 B 2 C 2
.
分析机械原理四连杆机构的图解法与解析法的优缺点

分析机械原理四连杆机构的图解法与解析法的优缺点摘要:铰链四杆机构是机械设备中最基本的机构类型之一,文中以它为研究对象建立数学模型,应用MATLAB编程与ADMAS建模分别
对四杆机构进行仿真分析,获得各点的运动曲线,进行对比,两种方法各有所长,分析结果显示直观。
平面四杆机构是连杆机构中最常见的机构组成,由于其结构简单,可承受载荷大,连杆曲线具有多样性等优点,它在工程中得到广泛的运用,设计四杆机构的方法有很多,比如解析法、作图法、实验法,但这些方法都存在一定的缺点,图解法精度差,解析法的计算工作量大,不直观使其在工程运用中受到约束,如果设计平面四杆机构时能显示其运动轨迹从而将图示结果与设计要求进行对比,可以使设计显得更加直观,提高工作效率。
本文以MATLAB、ADMAS为平台,开发了一个平面四杆机构运动轨迹仿真系统,模拟四杆机构的运动仿真,并获得各点的运动轨迹坐标,使设计显得直观,更好的帮助了工程技术人员在机构分析与设计过程中进行优化,提高了工作效率,降低产品开发成本。
机械原理NO[1].12 8-3 平面四杆机构的基本知识--2
![机械原理NO[1].12 8-3 平面四杆机构的基本知识--2](https://img.taocdn.com/s3/m/f4a7b4b6e87101f69f319596.png)
工程上也常利用死点来工作。
夹具
机械原理
第8章 平面连杆机构及其设计
四、铰链四杆机构的连杆曲线 Coupler-curve of four-bar linkages
在四杆机构运动时,其连杆平面上的每一点均描绘出一条曲线, 称为连杆曲线(coupler curves)
B型
水滴型
面包型
瘦长型
伪椭圆型
三角型
机构尺寸: 各运动副之间的相对位置尺寸(或
角度)以及描绘连杆上某点(该点实现 给定运动轨迹)的位置参数等。
平面连杆机构设计的基本要求:
1。要求从动件满足预定的运动规律要求(函数生成问题); 2。满足预定的连杆位置要求(刚体导引问题); 3。满足预定的轨迹要求(轨迹生成问题)。
机械原理
第8章 平面连杆机构及其设计
最多能解五个精确位置,多于五个位置只能近似求解,少于五个位置可有无穷解。
机械原理
第8章 平面连杆机构及其设计
2。按预定的运动规律设计四杆机构(函数综合)
1)按预定的两连架杆对应位置设计四杆机构:
要求: 3i f (1i ) , i =1、2、…、k
(已知条件)
取杆长的相对变量 a/a=1 , b/a=l, c/a=m , d/a=n 为设计参数,不影响各构件的相对 转角关系,故杆长的设计变量为l、m、 n ,再加上0 、0共5个设计变量。
• (2)改变运动副的尺寸;
• (3)选不同的构件为机架;
• (4)运动副元素的逆换。
机械原理
第8章 平面连杆机构及其设计
• 4.平面四杆机构有曲柄的条件: • (1)各杆长满足杆长条件:最短杆与最长杆的长度之和
应小于或等于其余两杆长度之和; • (2)最短杆为连架杆或机架。 • 5.急回运动及行程速度变化系数: • (1) 急回运动: • 当连机构的主动件为等速回转时,从动件空回行程的平
第8章第5讲平面四杆机构的设计——解析法

第8章第5讲平面四杆机构的设计——解析法平面四杆机构是机械工程中常用的一种机构,它由4个连接杆组成,通过连接杆与铰链的连接方式,能够实现不同形式的运动。
平面四杆机构的设计可以采用解析法,该方法通过解析机构的运动学性质和机构参数,来确定机构的设计参数和结构尺寸。
在平面四杆机构的解析法设计中,首先需要确定机构的运动类型。
根据机构的运动要求和工作环境,可以选择不同的运动类型,如平行移动、旋转、复杂曲线轨迹等。
运动类型的选择将对机构的结构设计和参数确定产生重要影响。
接下来,需要确定机构的工作原理和结构特点。
根据机构的运动类型,可以选择不同的结构形式,如平行四杆机构、向心四杆机构、菱形四杆机构等。
不同的结构形式具有不同的运动学特性和工作原理,需要根据实际需求进行选择。
确定机构的杆件长度和角度。
在机构设计中,杆件的长度和角度是关键的设计参数。
杆件的长度决定了机构的尺寸和工作范围,而杆件的角度决定了机构的运动轨迹和运动特性。
通过分析机构的运动学方程和几何方程,可以确定机构的杆件长度和角度。
确定机构的铰链位置。
铰链的位置决定了杆件之间的连接方式和机构的运动特性。
通过分析机构的力学平衡条件和运动学方程,可以确定机构的铰链位置,使机构能够实现所需要的运动要求。
最后,进行机构的参数优化和结构优化。
根据机构的运动学性能和工作要求,可以对机构的结构参数进行优化,使机构的运动特性更加优秀。
同时,还需要对机构的结构进行优化,提高机构的强度和刚度,确保机构在工作过程中的可靠性和稳定性。
通过解析法进行平面四杆机构的设计,可以使机构的结构和性能更加合理和可靠。
这种设计方法具有简单易行、工程实用性强的特点,是一种常用的机构设计方法。
在实际的机械设计中,可以根据具体的需求和实际情况,采用解析法进行平面四杆机构的设计,以提高机构的性能和工作效果。
机械设计基础(高教版第五版)精品教案:第2章平面四杆机构
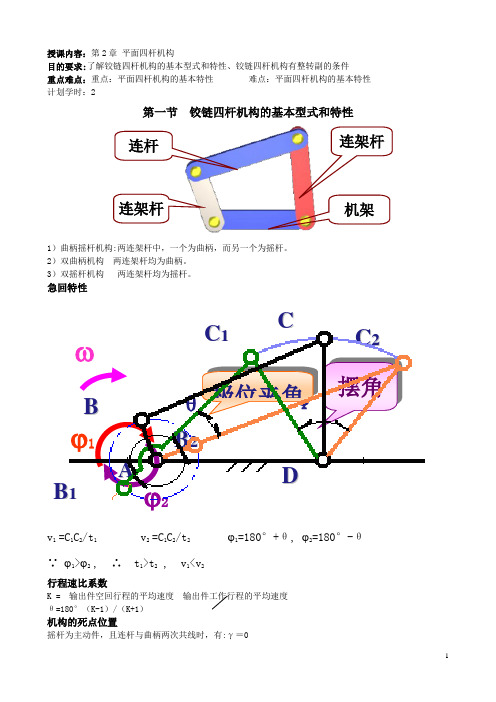
授课内容:第2章 平面四杆机构目的要求:了解铰链四杆机构的基本型式和特性、铰链四杆机构有整转副的条件重点难点:重点:平面四杆机构的基本特性 难点:平面四杆机构的基本特性 计划学时:2第一节 铰链四杆机构的基本型式和特性1)曲柄摇杆机构:两连架杆中,一个为曲柄,而另一个为摇杆。
2)双曲柄机构 两连架杆均为曲柄。
3)双摇杆机构 两连架杆均为摇杆。
急回特性v 1 =C 1C 2/t 1 v 2 =C 1C 2/t 2 ϕ1=180°+θ, ϕ2=180°-θ ∵ ϕ1>ϕ2 , ∴ t 1>t 2 , v 1<v 2行程速比系数K = 输出件空回行程的平均速度 输出件工作行程的平均速度θ=180°(K-1)/(K+1)机构的死点位置摇杆为主动件,且连杆与曲柄两次共线时,有:γ=0连架杆连杆连架杆机架摆角 θψ C 1C 2DAB 1B 2Bϕ1Cωϕ2极位夹角此时机构不能运动,称此位置为:“死点”避免措施:两组机构错开排列,如火车轮机构;靠飞轮的惯性第二节 铰链四杆机构有整转副的条件平面四杆机构具有整转副可能存在曲柄整转副存在的条件最长杆与最短杆的长度之和应≤其他两杆长度之和整转副是由最短杆(曲柄)与其邻边组成的当满足杆长条件时,说明存在整转副,当选择不同的构件作为机架时,可得不同的机构。
如 曲柄摇杆1 、曲柄摇杆2 、双曲柄、 双摇杆机构F’’’’ B CA BE FD CGA B CDl 1l 2 l 3 l 4授课内容:第2章平面四杆机构(§2.3—§2.4)目的要求:了解铰链四杆机构的基本型式和特性、铰链四杆机构有整转副的条件重点难点:重点:平面四杆机构的基本特性难点:平面四杆机构的基本特性计划学时:22.3 铰链四杆机构的演化通过前面的学习,我们知道在铰链四杆机构中,可根据两连架杆是曲柄还是摇杆,把铰链四杆机构分为三种基本形式——曲柄摇杆机构、双曲柄机构、双摇杆机构,而后两种可视为曲柄摇杆机构取不同构件作为机架的演变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
按行程速比系数K设计
• 极位夹角θ和近极位传动角γ1为 • 环路AC1D投影方程
(b a) cos( 0 ) 1 c cos( 1 0 ) (b a) sin( 0 ) c sin( 1 0 )
1 2 K 1 180 K 1
• 由上式解出
2 2 2 2 ( y2 y1 )( y3 y12 x3 x12 ) ( y3 y1 )( y2 y12 x2 x12 ) x 2( x3 x1 )( y2 y1 ) ( x2 x1 )( y3 y1 ) 2 2 y2 y12 x2 x12 ( x2 x1 ) x y 2( y2 y1 ) ( y2 y1 )
按连杆给定位置设计
• 连架杆的杆长和方位角
l ( x x1 ) 2 ( y y1 ) 2
y yi i arctan xx i
按行程速比系数K设计
• 给定行程速比系数K、执行构件摆角ψ和机构远 极位传动角γ2
y C2 C1 θ A B1 a θ0 γ1 B2 d ψ D x b γ2 c
平面四杆机构设计(解析法)
1. 按连杆给定位置设计 2. 按行程速比系数置设计四杆机构
• 问题实质:求固定支座A、D的坐标值
C1 C2
b B2 B3
c
C3
B1
D a A d α4
按连杆给定位置设计
• 由某点的三个位置坐标求其转动中心坐标
( x1 x) 2 ( y1 y ) 2 ( x2 x) 2 ( y2 y ) 2 ( x1 x) 2 ( y1 y ) 2 ( x3 x) 2 ( y3 y ) 2
y C2 C1 θ γ1 B2 d ψ D x b γ2 c
• 环路AC2D投影方程
(b a) cos 0 1 c cos( 2 0 ) (b a) sin 0 c sin( 2 0 )
A B1 a θ0
按行程速比系数K设计
• 变换得
tan 0 sin 2 sin (sin 1 sin 2 cos ) a ( A B ) N y b ( A B) N c sin 0 sin 2
C2 C1 γ1 B2 d ψ D x b γ2 c
• 其中
A cos( 0 ) sin( 2 0 ) B sin 2 sin 0 cos( 1 0 ) N 2 sin cos( ) 2 0
B1
θ A a θ0
