2020年高考理科数学 《二项式定理》题型归纳与训练及参考答案
二项式定理高考真题

二项式定理常考点:1、二项式定理:2、几个基本概念(1)二项展开式:右边的多项式叫做的二项展开式(2)项数:二项展开式中共有项(3)二项式系数:叫做二项展开式中第项的二项式系数(4)通项:展开式的第项,即(5)二项式系数的和:(6)各项式系数之和:3.二项式系数的性质:(1)对称性:在二项展开式中,与首末两端等距离的任意两项的二项式系数相等(2)增减性与最值二项式系数先增后减且在中间取得最大值当是偶数时,中间一项取得最大值当是奇数时,中间两项相等且同时取得最大值=(3)奇数项的二项式系数的和等于偶数项的二项式系数和基本题型(一)通项公式的应用的展开式中第三项的二项式系数为________;第三项的系数为_______;常数项为_______;含的项为______。
(二)二项式系数的最值的展开式中二项式系数最大的是第____项;的展开式中二项式系数最大的是第____项(三)展开式中各项系数和问题已知,求一.选择题1.在(x-)的展开公式中,x的系数为( )A.-120B.120C.-15D.152.8x y项的系数是()x的展开式中62()A.56 B.56-- C.28 D.283.二项式的展开式中系数为有理数的项共有()A.6项B.7项C.8项D.9项4.已知(x-)8展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是( )A.28B.38C.1或38D.1或285.(+)n展开式中存在常数项,则n的值可以是()A.8B.9C.10D.126.(2x3-)7的展开式中常数项是()A.14B.-14C.42D.-427.若的展开式中的系数是( )A. B. C. D.8.在()n的二项展开式中,若常数项为60,则n等于( )A.3B.6C.9D.129.的值为()A.61 B.62 C.63 D.64 10.若(ax-1)5的展开式中x3的系数是80,则实数a的值是( )A.-2 B.2 C. D.211.的展开式中各项系数之和为64,则展开式的常数项为( )A.-540B.-162C.162D.54012.若对于任意的实数x ,有x 3=a 0+a 1(x -2)+a 2(x -2)2+a 3(x -2)3,则a 2的值为( )A.3B.6C.9D.1 13.在的二项展开式中,若只有的系数最大,则( )A.8B. 9C. 10D.11 14.已知(+)n 展开式中,各项系数的和与其各项二项式系数的和之比为64,则n 等于( )A.4B.5C.6D.715.设(x 2+1)(2x +1)9=a 0+a 1(x +2)+a 2(x +2)2+…+a 11(x +2)11,则a 0+a 1+a 2+…+a 11的值为( )A.-2B.-1C.1D.2 16.设则中奇数的个数为( )A .2B .3C .4D .5 二.填空题17.已知a 为如图所示的程序框图中输出的结果,求二项式6(的展开式中含x 2项的系数18. 72x x x ⎛⎫- ⎪⎝⎭的展开式中,4x 的系数是19.展开式中的常数项是20.若(1-2x )2004=a 0+a 1x +a 2x 2+…+a 2004x 2004(x ∈R ),则(a 0+a 1)+(a 0+a 2)+(a 0+a 3)+…+(a 0+a 2004)=21.已知(1+kx 2)6(k 是正整数)的展开式中,x 8的系数小于120,k=____________参考答案CADCC ABBBD ABCCAA17.-19218.8419.21020.200421.1。
《二项式定理》知识点总结+典型例题+练习(含答案)

二项式定理考纲要求1.了解二项式定理的概念.2.二项展开式的特征及其通项公式.3.会区别二项式系数和系数.4.了解二项式定理及简单应用,并运用二项式定理进行有关的计算和证明. 知识点一:二项式定理设a , b 是任意实数,n 是任意给定的正整数,则0011222333110()n n n n n m n m m n n n nn n n n n n n a b C a b C a b C a b C a b C a b C ab C a b------+=++++⋅⋅⋅++⋅⋅⋅++这个公式所表示的定理叫做二项式定理,其中右边的多项式叫的二项式展开式,每项的0n C ,1n C , 2n C ⋅⋅⋅ n n C 叫做该项的二项式系数.注意:二项式具有以下特征:1.展开式中共有1n +项,n 为正整数.2.各项中a 与b 的指数和为n ,并且第一个字母a 依次降幂排列,第二个字母b 依次升幂排列.3.各项的二项式系数依次为0n C , 1n C , 2n C ⋅⋅⋅ nn C . 知识点二:二项展开式通项公式二项展开式中的m n m mn C a b -叫做二项式的通项, 记作 1m T +. 即二项展开式的通项为 1m n m mm n T C a b -+=.注意:该项为二项展开式的第1m +项,而不是第m 项. 知识点三:二项式系数的性质二项式展开式的二项式系数是0n C , 1n C , 2n C ⋅⋅⋅ nn C .1.在二项展开式中,与首末两端距离相等的两项的二项式系数相等,即m n mn n C C -=.2.如果二项式()na b +的幂指数n 是偶数,那么它的展开式中间一项的二项式系数最大即12n+项的二项式系数最大. 3.如果二项式()na b +的幂指数n 是奇数,那么它的展开式中间两项的二项式系数最大,并且相等,即第12n +项和第32n +项的二项式系数最大且相等.4.二项式()na b +的展开式中,所有二项式系数的和为01232m nn n n n n n n C C C C C C ++++⋅⋅⋅++⋅⋅⋅+=.5.二项式()na b +的展开式中奇数项和偶数项的二项式系数和相等即02413512n n n n n n n C C C C C C -+++⋅⋅⋅=+++⋅⋅⋅=.知识点四:二项式系数与系数的区别 1.二项展开式中各项的二项式系数: mn C .2.二项展开式中各项的系数:除了字母外所有的数字因数的积. 题型一 二项式定理 例1 求51(2)x x-的展开式. 分析:熟记二项式定理.解答:51(2)x x-=05014123232355551111(2)()(2)()(2)()(2)()C x C x C x C x x x x x -+-+-+-4145055511(2)()(2)()C x C x x x+-+-533540101328080x x x x x x=-+-+-题型二 二项展开式通项公式 例2 求91(3)9x x+的展开式中第3项. 分析:灵活运用通项公式. 解答:272532191(3)()9729T T C x x x+===, 所以第3项为5972x . 题型三 二项式系数的性质例3 求7(2)x +的展开式中二项式系数最大的项.分析:根据二项式()na b +的幂指数n 是奇数,那么它的展开式中间两项的二项式系数最大,并且相等,即第12n +项和第32n +项的二项式系数最大且相等.先求出二项式最大项的项数,再利用通项公式计算.解答:由于7为奇数,所以第4项和第5项的二项式系数最大.即3733343172560T T C x x -+=== 4744454172280T T C x x -+===题型四 二项式系数与系数的区别例4 二项式9(12)x -的二项式系数之和为 . 分析:二项式()na b +的展开式中,所有二项式系数的和为01232m n n n n n n n n C C C C C C ++++⋅⋅⋅++⋅⋅⋅+=。
2020年高考山东版高考理科数学 11.2 二项式定理

考向突破
考向1 求二项展开式中的项或项的系数
例1
已知在
3
x
1 23 x
n
的展开式中,第6项为常数项.
(1)求n;
(2)求含x2的项的系数;
(3)求展开式中所有的有理项.
解析
(1)通项公式为Tr+1= Crn
nr
x 3
1 2
r
r
x 3
=
Crn
n
2
2
项
的二项式系数最大,最大值为⑤
n
Cn2 ;
当n为奇数时,中间两项 第
n
1 项和第 2
n
2
3
项
的二项式系数相等,且同时
n1
n1
取得最大值,最大值为⑥
或 Cn2
Cn2
.
5.各二项式系数的和: (a+b)n的展开式的各个二项式系数的和等于2n,即 C0n + C1n + C2n +…+ Cnn =2n. 二项展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的 和,即 C0n + C2n + C4n +…= C1n + C3n + C5n +…=2n-1.
数项系数之和为a0+a2+a4+…= f (1) f (1) ,偶数项系数之和为a1+a3+a5+
2
…= f (1) f (1) .
2
例2
(1)(2017湖南三湘名校联盟三模,7)在(x2-4)· x
1 x
9
高三数学二项式定理与性质试题答案及解析

高三数学二项式定理与性质试题答案及解析1.在二项式的展开式中,含的项的系数是()A.B.C.D.【答案】A【解析】由二项式定理可知,展开式的通项为,则令得,所以含项的系数为,故选【考点】二项式定理.2.已知(1+x)10=a0+a1(1-x)+a2(1-x)2+…+a10(1-x)10,则a8等于()A.180B.90C.-5D.5【答案】A【解析】(1+x)10=[2-(1-x)]10,其通项公式为Tr+1=210-r·(-1)r(1-x)r,a8是r=8时,第9项的系数.∴a8=22(-1)8=180.故选A.3.二项式(2-)6的展开式中所有有理项的系数和等于________.(用数字作答)【答案】365【解析】Tr+1=·(2)6-r·(-1)r·x-r=(-1)r·26-r,r=0,1,2,3,4,5,6,当r=0,2,4,6时,Tr+1=(-1)r26-r为有理项,则所有有理项的系数和为26+24+22+20=365.4.已知(1+kx2)6(k是正整数)的展开式中,x8的系数小于120,则k=________.【答案】1【解析】由Tr+1= (kx2)6-r=k6-r x2(6-r),得x8的系数为k4=15k4,由15k4<120得k4<8,因为k为正整数,所以k=1.5.的展开式中,的系数为15,则a=________.(用数字填写答案)【答案】【解析】因为,所以令,解得,所以=15,解得.【考点】本小题主要考查二项式定理的通项公式,求特定项的系数,题目难度不大,属于中低档. 6.的二项展开式中,的系数等于.【答案】15【解析】,时,,此时的系数等于.【考点】二项式系数7.二项式的展开式中系数最大的项是第项.【答案】9【解析】因为,而组合数中最大,所以展开式中系数最大的是,即第9项.【考点】组合数性质8.若(的展开式中第2项与第4项的二项式系数相等,则直线y=nx与曲线y=x2围成的封闭区域面积为()A.B.12C.D.36【答案】C【解析】展开式中第二项与第四项的二项式系数相等,所以,那么,与围成的封闭图形区域为,故选C.【考点】1.二项式系数;2.定积分.9.的展开式中各项系数的和为2,则该展开式中常数项为A.-40B.-20C.20D.40【答案】D【解析】令x=1得a=1.故原式=。
二项式定理经典题型及详细答案

二项式定理经典考点例析考点1:二项式系数与项的系数1、在28(2x -的展开式中,求: (1)第5项的二项式系数及第5项的系数.(2)2x 的系数.2.若1()nx x+展开式中第2项与第6项的系数相同,则展开式的中间一项的系数为___________.3.已知二项式102)3x求 (1)第四项(2)展开式第四项的二项式系数(3)展开式第四项的系数考点2:二项式定理逆用1、5432(1)5(1)10(1)10(1)5(1)x x x x x -+-+-+-+-=_____________2、5432)12()12(5)12(10)12(10)12(51+-+++-+++-x x x x x =_____________考点3:求二项式展开式中的特定项、某一项【例题】 1、二项式3522()x x-的展开式中5x 的系数___________;2. 二项式43(1)(1x -的展开式中2x 的系数是___________.3.若4(1a +=+(,a b 为有理数),则a b +=___________.4.二项式8(2-展开式中不含4x 项的系数的和为___________.5、二项式53)31()21(x x -+的展开式中4x 的系数___________.【练习】1.二项式4(1)x +的展开式中2x 的系数为___________..2.二项式210(1)x -的展开式中,4x 的系数为___________.3.二项式6展开式中含2x 项的系数为___________. 4.二项式533)1()21(x x -+的展开式中x 的系数___________.、常数项和有理项【例题】 1. 二项式61(2)2x x-的展开式的常数项是___________.2、二项式100的展开式中x 的系数为有理数的项的个数___________.3. 二项式261(1)()x x x x++-的展开式中的常数项为___________.4.二项式5)12(++xx 的展开式中常数项是___________. 【练习】1.8(2x -的展开式中的常数项___________. 2.在261()x x+的展开式中,常数项是___________.3.二项式5)44(++xx 的展开式中常数项是___________. 4.二项式54)31()21(xx -+的展开式中常数项是___________. 考点4:求展开式中的各项系数之和的问题1、已知7270127(12)...x a a x a x a x -=++++.求:(1)0a ; (2)763210a a a a a a ++++++ ;(3)763210a a a a a a -++-+-(4)6420a a a a +++;(5)7531a a a a +++;(6)2753126420)()(a a a a a a a a +++-+++. (7)||||||||||||763210a a a a a a ++++++ .(8)7766321022842a a a a a a ++++++ ;(9)7766321022842a a a a a a ++++++; 2.在二项式9(23)x y -的展开式中,求:(1)二项式系数之和;(2)各项系数之和;(3)所有奇数项系数之和;(4)所有项的系数的绝对值之和.3.利用二项式nn n n n n n n x C x C x C x C C x +++++=+ 432210)1(展开式nn n n n n n n n nn n n n n n n n n n n n n nn n n n n C C C C C C C C C C C C C C C C C C C C C 32842)4(2)3(0)1()2(2)1(3210153142032103210=+++++=+++=+++=-++-+-=+++++-考点5:多项式的展开式最大项问题【例题】1、二项式9)21(x +展开式中,(1)二项式系数的最大项 (2)系数的最大项 2、二项式12)21(x -展开式中(1)求展开式中系数的绝对值最大的项.(2)求展开式中系数最大的项.(3)求展开式中系数最小的项.3、已知()(1)(12)(,)m n f x x x m n N +=+++∈的展开式中含x 项系数为11,求()f x 展开式中2x 项系数的最小值.4、n xx )1(4+展开式中含x 的整数次幂的项的系数之和为__________.【练习】1、2102()x x+的展开式中系数最大的项; 2、求7(12)x -展开式中系数最大的项.3、设x =50(1)x +展开式中第几项最大?4、已知()nx x 2323+展开式中各项系数的和比各项的二项式系数的和大992,(1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项.考点6:含参二次函数求解【例题】1.【特征项】在二项式25()a x x-的展开式中x 的系数是-10,则实数a 的值是___________.2.【常数项】若n的展开式中存在常数项,则n 的值可以是___________.3.【有理项】已知n的展开式中,前三项的系数成等差数列,展开式中的所有有理项________. 4.【特征项】在210(1)x px ++的展开式中,试求使4x 项的系数最小时p 的值.5.【系数最大】已知1(2)2nx +的展开式中,第5项、第6项、第7项的二项式系数成等差数列,求展开式中二项式系数最大的项. 【练习】1.若9()a x x-的展开式中3x 的系数是-84,则a =___________.2.已知2)n x的展开式中第5项系数与第3项的系数比56:3,则该项展开式中2x 的系数_____. 3.若二项式22()nx x-的展开式中二项式系数之和是64,则展开式中的常数项为___________ 4.已知(13)nx +的展开式中,末三项的二项式系数的和等于121,求展开式中系数最大的项.考点7:求解某些整除性问题或余数问题1. 求证22*389()n n n N +--∈能被64整除.2. 9291被100整除所得的余数为_________ 3. 设21(*)n k k N =-∈,则11221777...7nn n n n n n C C C ---+⋅+⋅++⋅被9除所得的余数为_________4. 求证:(1)51511-能被7整除;(2)2332437n n +-+能被64整除.5. 如果今天是星期一,那么对于任意的自然数n ,经过33(275)n n +++天是星期几?考点8:计算近似值1、求60.998的近似值,使误差小于0.001. 2、求51.997精确到的近似值.考点9:有关等式与不等式的证明化简问题1、求121010101010124...2C C C ++++的值. 2、化简:1231248...(2)nnn n n n C C C C -+-++-. 3、求证:01121*(2)!...()(1)!(1)!n nn n n n n n n C C C C C C n N n n -+++=∈-+.4、证明下列等式与不等式(1)123123 (2)nn n n n n C C C nC n -++++=⋅.(2)设,,a b c 是互不相等的正数,且,,a b c 成等差数列,*n N ∈,求证2nnna cb +>. 【练习】1、=++++nn n n n n C C C C 2222210 ;2、=-++-+-nn n n n n n n C C C C C 2)1(22232210 ; 3、求证:12122-⋅=+++n n n n n n nC C C4、求证:nn n n n n n C C C C C 22222120)()()()(=++++5、已知7292222210=++++nn n n n n C C C C ,求n n n n C C C +++ 21考点10:创新型题目1、对于二项式(1-x)1999,有下列四个命题:①展开式中T 1000= -C 19991000x999;②展开式中非常数项的系数和是1;③展开式中系数最大的项是第1000项和第1001项;④当x=2000时,(1-x)1999除以2000的余数是1.其中正确命题的序号是__________.(把你认为正确的命题序号都填上) 2、规定!)1()1(m m x x x C m x +--=,其中x ∈R,m 是正整数,且10=x C ,这是组合数m n C (n 、m 是正整数,且m ≤n )的一种推广.(1) 求315-C的值;(2) 设x >0,当x 为何值时,213)(xxC C 取得最小值(3) 组合数的两个性质;①m n n m n C C -=. ②mn m n m n C C C 11+-=+.是否都能推广到mx C (x ∈R,m 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.3、对于任意正整数,定义“n的双阶乘n!!”如下:对于n是偶数时,n!!=n·(n-2)·(n-4)……6×4×2;对于n是奇数时,n!!=n·(n-2)·(n-4)……5×3×1.现有如下四个命题:①(2005!!)·(2006!!)=2006!;②2006!!=21003·1003!;③2006!!的个位数是0;④2005!!的个位数是5.正确的命题是________.。
高中试卷-6.3 二项式定理(精讲)(含答案)
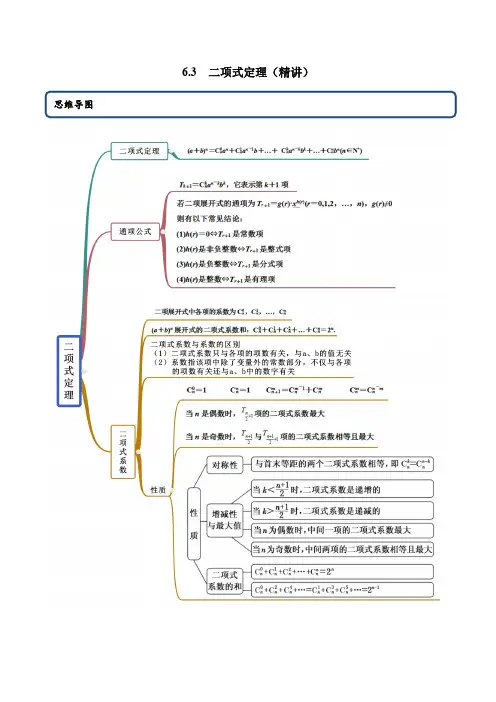
6.3 二项式定理(精讲)考法一 二项式定理展开式【例1】(1)求4+的展开式为 .(2)(2020·江苏省太湖高级中学高二期中)已知012233444(1)4729nnnn n n n n C C C C C -+-++-=L ,则n 的值为【答案】(1)1x 2+12x+54+108x +81x 2【解析】(1)方法一 (14=4+C 143·1)+C 2421)2+C 341)3+C41)4=81x 2+108x +54+12x+1x2.方法二 (14=3x +14=1x 2(1+3x )4=1x 2·[1+C 14·3x +C 24(3x )2+C 34(3x )3+C 4(3x )4]=1x2(1+12x +54x 2+108x 3+81x 4)=1x2+12x+54+108x +81x 2.(2)由012233444(1)4729n n nn n n n n C C C C C-+-++-=L 得()()()()()0120312312301414141414729nn n n n n n n n n n C C C C C ---××-+××-××-+××-×-+++=×L 则()12479n-=,即()()672933n =-=-,解得6n =.【一隅三反】1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )A .(2x+2)5B .2x 5C .(2x-1)5D .32x 5【答案】D【解析】依题意可知,多项式的每一项都可看作()()55211rrr C x -+-,故为()5211x éù+-ëû的展开式,化简()()555211232x x x éù+-==ëû.故选D.2.(2020·江苏宿迁市·宿迁中学高二期中)化简:2012222412333...3n n n n n n n n C C C C ---×+×+×++×=_________.【答案】101n -【解析】()()()()011020201211212(31)3131...3131n n n n n nn n n n n C C C C ----+=´´+´´++´´+´´则2012222412233331(31)10n n n n n nn n n n C C C C ---×+×+×++×+=+=L 所以2012222412333...3101nn n n n n n n n C C C C ---×+×+×++×=-故答案为:101n -.考法二 二项式指定项的系数与二项式系数【例2】(1)(2020·全国高二单元测试)在(x 10的展开式中,x 6的系数是(2)(2020·广东佛山市·高二期末)二项式81x x æö+ç÷èø的展开式中常数项是______(用数字作答)(3)(2020·安徽省蚌埠第三中学高二月考)30的有理项共有 项【答案】(1)9410C (2)70(3)6【解析】(1)由T k +1=10kC x 10-k k ,令10-k =6,解得k =4,∴系数为)4410C =9410C (2)二项式81x x æö+ç÷èø的展开式的通项公式8821881r r r rr r T C x C x x --+==,令820r -=,得4r =,则常数项为4588765==704321T C ´´´=´´´,故答案为:70(3)30的通项公式为:53010613030rrrrr r T C C x--+==,061051730300,,6,r T x r T x C C ====,12180513********,,18,r T x r T x C C -====,243010152531303024,,30,r T x r T x C C --====,所以有理项共有6项,故选:C 【一隅三反】1.(2020·北京市鲁迅中学高二月考)二项式261(2)x x-的展开式中的常数项是_______.(用数字作答)【答案】60【解析】有题意可得,二项式展开式的通项为:()62612316612(1)2rrr r r r rr T C xC xx ---+æö=-=-ç÷èø令1230r -=可得4r = ,此时2456260T C ==.2.(2021·上海青浦区)在6212x x æö+ç÷èø二项展开式中,常数项是_______.【答案】60【解析】展开式的通项公式是()626123166122rrrr r r r T C xC x x ---+æö=××=××ç÷èø,当1230r -=时,4r = 24416260T C +=×=.故答案为603..(2020·青海西宁市)若8x æ+çè的展开式中4x 的系数为7,则实数a =______.【答案】12【解析】根据二项展开式的通项公式可得:4888331888=rr r r r r r r r r r T C x C a x C a x ----+==,令4843r -=,可得3r =,3388==7r r C a C a ,解得:12a =,故答案为:124.(2020·梁河县)已知31(2)nx x+的展开式的常数项是第7项,则n =________.【答案】8【解析】根据题意,可知第7项为()666366324122n n n nn C xC x x ---æö××=××ç÷èø,而常数项是第7项,则3240n -=,故8n =.故答案为:8.考法三 多项式系数或二项式系数【例3】(1)(2020·福建三明市·高二期末)52212x x æö+-ç÷èø的展开式中常数项是( )A .-252B .-220C .220D .252(2).(2021·四川成都市)若5(2)a x x x æö+-ç÷èø的展开式中常数项为80-,则a =( )A .2B .1C .2-D .1-【答案】(1)A (2)C 【解析】(1)由2510211(2)()x x x x+-=-,可得二项式101()x x-的展开式通项为10102110101()(1)rrr r r r r T C xC x x--+=-=-,令1020r -=,解得=5r ,所以展开式的常数项为5510(1)252C -=-.故选:A.(2)Q 5a x x æö-ç÷èø的展开式的通项公式为:55251(1)r r r r r T C a x --+=×××-,显然,25r -为奇数,Q 若求5(2)a x x x æö+-ç÷èø展开式的常数项,251r \-=-,解得2r =故5(2)a x x x æö+-ç÷èø的展开式的常数项等于:23580C a ×=-2a \=-故选:C.【一隅三反】1.(2020·全国高三专题练习)4211x x æö+-ç÷èø展开式中常数项为( ).A .11B .11-C .8D .7-【答案】B【解析】将21x x +看成一个整体,展开得到:41421()(1)r r rr T C x x-+=+- 421(r x x-+的展开式为:4243144m r m m m r mm r r T C x x C x -----+--=×=取430r m --= 当0m =时,4r = 系数为:4440(1)1C C ´´-= 当1m =时,1r = 系数为:11143(1)12C C ´´-=- 常数项为11211-=- 故答案选B2.(2020·全国高三专题练习)52431x x x ææö-+ç÷çèøè的展开式中常数项为( )A .30-B .30C .25-D .25【答案】C【解析】51æçè 的通项为15(1)r r r r T C +=-, 55224311x x x x æææö-+=-ç÷ççèøèè 554311x x ææ-+ççèè,根据式子可知当4r = 或2r = 时有常数项,令4r = 41455(1)T C Þ=- ; 令232352(1)r T C =Þ=-;故所求常数项为13553C C -´ 53025=-=- ,故选C.3.(2020·河南商丘市)()64111x x æö++ç÷èø的展开式的常数项为( )A .6B .10C .15D .16【答案】D【解析】由题意得611x æö+ç÷èø的展开式的通项为()160,1,2,,6r r r T C x r -+=×=×××,令4r =,则4615C =,所以()64111x x æö++ç÷èø的展开式的常数项为11516+=.故选:D.4.(2020·枣庄市第三中学高二月考)在1020201(1)x x++的展开式中,x 2项的系数为( )A .30B .45C .60D .90【答案】B 【解析】在1020201(1)x x++的展开式中,通项公式为T r +110rC=•20201rx x æö+ç÷èø.对于20201rx x æö+ç÷èø,通项公式为T k +1kr C =•x r ﹣2021k ,k ≤r ,r 、k ∈N ,r ≤10.令r ﹣2021k =2,可得r =2+2021k ,故k =0,r =2,故x 2项的系数为210C •02C =45,故选:B .5.(2020·全国高二专题练习)若()1021x a x x æö-+ç÷èø的展开式中6x 的系数为30,则a 等于( )A .13B .12C .1D .2【答案】D【解析】将题中所给式子可化为()10101022111x a x x x a x x x x æöæöæö-+=+-+ç÷ç÷ç÷èøèøèø根据二项式定理展开式通项为1C rn rrr nT a b -+=,101x x æö+ç÷èø的通项为10102110101rr r r r r T C x C x x --+æö=×=ç÷èø令1024r-= 解得3r =所以6x 的项为234610120x C xx ×=令1026r -=解得2r =所以6x 的项为2661045a C x ax -×=-综上可知, 6x 的系数为1204530a -= 解得2a = 故选:D考法四 二项式定理的性质【例2】(1)(多选)(2020·全国高二单元测试)111x x æö-ç÷èø的展开式中二项式系数最大的项是( )A .第5项B .第6项C .第7项D .第8项(2)(2020·山东省桓台第一中学高二期中)(多选)二项式1121x x æö+ç÷èø的展开式中,系数最大的项为( ).A .第五项B .第六项C .第七项D .第八项(3)(2020·绵阳市·四川省绵阳江油中学高二开学考试)若1nx x æö-ç÷èø的展开式中只有第7项的二项式系数最大,则展开式中含2x 项的系数是A .462-B .462C .792D .792-【答案】(1)BC (2)BC (3)D【解析】(1)因为n =11为奇数,所以展开式中第1112+项和第11112++项,即第6项和第7项的二项式系数相等,且最大.故选:BC(2)二项式1121x x æö+ç÷èø的展开式中,每项的系数与二项式系数相等,共有12项所以系数最大的项为第六项和第七项故选:BC(3)∵1nx x æö-ç÷èø的展开式中只有第7项的二项式系数最大,∴n 为偶数,展开式共有13项,则12n =.121x x æö-ç÷èø的展开式的通项公式为()1212211C r r r r T x -+=-,令1222r -=,得5r =.∴展开式中含2x 项的系数是()12551C 792-=-,故选D .【一隅三反】1.(2020·辽宁沈阳市·高二期中)在()()1nx n N +-Î的二项展开式中,若只有第5项的二项式系数最大,则næçè的二项展开式中的常数项为( )A .960B .1120C .-560D .-960【答案】B【解析】在(x ﹣1)n (n ∈N +)的二项展开式中,若只有第5项的二项式系数最大,则n=8,则n =8æ-çè的二项展开式的通项公式为T r+1=8r C •28﹣r •(﹣1)r •x 4﹣r ,令4﹣r=0,求得r=4,可得展开式中的常数项为48C •24•(﹣1)4=1120,故选B .2.(2021·湖南常德市)(ax +1x )(2x ―1)5的展开式中各项系数的和为2,则该展开式中常数项为( )A .B .C .10D .20【答案】C【解析】由已知,当x =1时,(a +11)(2―1)5=2,即a =1,所以(x +1x )(2x ―1)5展开式中常数项为1x ×C 452x ×(―1)4=10,故选C .3.(多选)(2020·三亚华侨学校高二开学考试)已知()na b +的展开式中第5项的二项式系数最大,则n 的值可以为( )A .7B .8C .9D .10【答案】ABC【解析】∵已知()na b +的展开式中第5项的二项式系数4n C 最大,则7n =或n =8或n =9故选:ABC .4.(2020·全国高二课时练习)已知6(31)x +展开式中各项系数的和为m ,且2log n m =,求2nx ö-÷ø展开式中二项式系数最大的项的系数 .【答案】59136【解析】设6260126(31)x a a x a x a x +=++++L ,令1x =,得6612(31)42m =+==,所以2log 12n m ==,则122x ö÷ø展开式中有13项,且中间一项(第7项)的二项式系数最大,该项为6666633712122(2)59136T C C x x x --æö=-=-=ç÷èø.故所求的系数为59136.5.(2020·重庆市第七中学校高二月考)二项式()*122nx n N x æö-Îç÷èø的展开式中,二项式系数最大的项是第4项,则其展开式中的常数项是_________.【答案】-20【解析】由题意知,展开式中有7项,6n =.因为()661122rrrTr C x x -æö+=-ç÷èø()6262612r r r r C x --=-令620r -=,得3r =,所以常数项为()336120C -=-.考法五 二项式系数或系数和【例5】(2020·安徽省泗县)若2701277()(12)f x x a a x a x a x =+=++++L .求:(1)017a a a ++¼+;(2)1357a a a a +++;(3)0127a a a a ++++L .【答案】(1)27;(2)14;(3)27.【解析】(1)令1x =,可得301235674()3271f a a a a a a a a ==+++++++=,∴4012356727a a a a a a a a ++++++=+.①(2)令1x =-可得301235674(1)(1)f a a a a a a a a -=-=-+-+-+-,∴401235671a a a a a a a a +-+-+-=--.②由①-②得13572()28a a a a +++=,∴135714a a a a +++=.(3)由题意得二项式7(12)x +展开式的通项为177(2)2rrrr rr T C x C x +==,∴每项的系数0(0,1,2,,7)i a i >=L ,∴01235017647227a a a a a a a a a a a a ++++=++++++=+L .【一隅三反】1.(2020·北京朝阳区·高二期末)在5(21)x +的二项展开式中,二项式系数之和为___________;所有项的系数之和为_______.【答案】32 243【解析】根据二项展开式的性质,展开式的二项式系数之和为52232n ==,令1x =可得所有项的系数之和为55(211)3243==´+,故答案为:32,2432.(2020·全国高二单元测试)若-x )10=a 0+a 1x +a 2x 2+…+a 10x 10,则(a 0+a 2+…+a 10)2-(a 1+a 3+…+a 9)2= 【答案】1【解析】令1x =,得)1001101a a a +++=-L ,令1x =-,得)100123101a a a a a -+-++=+L ,()()220210139a a a a a a +++-+++L L ()()0110012310a a a a a a a a =+++-+-++L L))1010111==.故选:A.3.(2020·福建厦门市·厦门双十中学高二期中)已知()1121011012101112x a a x a x a x a x +=+++++L ,则12101121011a a a a -+-+=L _____.【答案】22【解析】对等式112012(12)x a a x a x +=++10111011a x a x +++L 两边求导,得101222(12)2x a a x +=+91010111011a x a x +++L ,令1x =-,则1210112101122a a a a -+-+=L .4.(2020·宁县第二中学高二期中)设2012(21)n n n x a a x a x a x -=++++L 展开式中只有第1010项的二项式系数最大.(1)求n ;(2)求012n a a a a ++++L ;(3)求.312232222n na a a a ++++L .【答案】(1)2018;(2)20183;(3)-1.【解析】(1)由二项式系数的对称性,1101020182n n +=\= (2)201801220180122018=3a a a a a a a a ++++-+++=L L (3)令0x = ,得20180(10)1a =-=,令12x =,得21232018232018(11)02222a a a a ++++=-=L ,故3201812023201812222a a a a a +++=-=-.考法六 二项式定理运用【例6】(1)(2020·上海市七宝中学高二期中)7271除以100的余数是________(2)(2020·全国高二单元测试)6(1.05)的计算结果精确到0.01的近似值是_________【答案】(1)41(2)1.34【解析】(1)()727217172727270727127270170177070C C C C +==++++L 21072701()m m N =+´+Îg 2105041m =+g 即7271除以100的余数为41.故答案为:41.(2)()()66122661.0510.051+0.05+0.05+1+0.3+0.0375=1.3375 1.34C C =+=××»»L 故答案为:1.34【一隅三反】1.(2020·四川棠湖中学高二月考)已知202074a +能够被15整除,则a =________.【答案】14【解析】由题可知,()0202020275714=-Q ()()()()0120192020020201201920191202002020202020202020751751751751C C C C =-+-++-+-L 0202012019201912020202020207575751C C C =-+-+L 所以0202012019201912020202022020200775754751C C C a a =-++-++L ,而75能被15整除,要使202074a +能够被15整除,只需1a +能被15整除即可,所以115a +=,解得:14a =.故答案为:14.2.(2020·江苏泰州市·泰州中学高二期中)83被5除所得的余数是_____________.【答案】1【解析】因为883(52)=-0817********8888855(2)5(2)5(2)5(2)C C C C C =×+×´-+×´-++×´-+×´-K 071625277808888885(55(2)5(2)(2))5(2)C C C C C =×+×´-+×´-++-+×´-K ,所以转化为求80885(2)256C ×´-=被5除所得的余数,因为2565151=´+,所以83被5除所得的余数是1,故答案为:13.(2021·河北保定市)60.99的计算结果精确到0.001的近似值是【答案】0.941【解析】()()()()6620126666330.9910.0110.010.010.01...C C C C =-=´-´+´-´ 10.060.00150.00002...=-+- 0.941»故选B。
(完整版)二项式定理公式、各种例题讲解及练习
二项式定理例题讲解分 类 计 数 原 理分 步 计 数 原理做一件事,完成它有n 类不同的办法.第一类办法中有m1种方法,第二类办法中有m2种方法……,第n 类办法中有mn 种方法,则完成这件事共有:N=m1+m2+…+mn 种方法。
做一件事,完成它需要分成n 个步骤。
第一步中有m1种方法,第二步中有m2种方法……,第n 步中有mn 种方法,则完成这件事共有:N=m1 m2 … mn 种方法。
注意:处理实际问题时,要善于区分是用分类计数原理还是分步计数原理,这两个原理的标志是“分类”还是“分步骤”。
排列组合从n 个不同的元素中取m (m≤n)个元素,按照一定的顺序排成一排,叫做从n 个不同的元素中取m 个元素的排列。
从n 个不同的元素中,任取m(m≤n)个元素并成一组,叫做从n 个不同的元素中取m 个元素的组合。
排列数组合数从n 个不同的元素中取m(m≤n)个元素的所有排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,记为Pnm从n 个不同的元素中取m(m≤n)个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,记为Cnm选排列数全排列数二项式定理二项展开式的性质(1)项数:n+1项(2)指数:各项中的a 的指数由n 起依次减少1,直至0为止;b 的指出从0起依次增加1,直至n 为止.而每项中a 与b 的指数之和均等于n 。
(3)二项式系数:各奇数项的二项式数之和等于各偶数项的二项式的系数之和例1.试求:(1)(x 3-22x )5的展开式中x 5的系数; (2)(2x 2-x 1)6的展开式中的常数项;(3)(x -1)9的展开式中系数最大的项;(4)在1003)23(+x 的展开式中,系数为有理数的项的个数.解:(1)T r +1=rr r r r rx C xx C 51552535)2()2()(---=-依题意15-5r =5,解得r =2故(-2)2rC 5=40为所求x 5的系数(2)T r +1=rC 6(2x 2)6- rr x)1(-=(-1)r ·26- r ·r r x C 3126- 依题意12-3r =0,解得r =4故4)1(-·2226C =60为所求的常数项.(3)T r +1=r )1(-r r x C -99∵1265949==C C ,而(-1)4=1,(-1)5=-1∴ T 5=126x 5是所求系数最大的项(4)T r +1=r r rrr r r x C x C ---⋅⋅=1003250100310010023)2()3(,要使x 的系数为有理数,指数50-2r与3r 都必须是整数, 因此r 应是6的倍数,即r =6k (k ∈Z ), 又0≤6k ≤100,解得0≤k ≤1632(k ∈Z ) ∴x 的系数为有理数的项共有17项.评述 求二项展开式中具有某特定性质的项,关键是确定r 的值或取值范围.应当注意的是二项式系数与二项展开式中各项的系数不是同一概念,要加以区分.例2.试求:(1)(x +2)10(x 2-1)的展开式中x 10的系数;(2)(x -1)-(x -1)2+(x -1)3-(x -1)4+(x -1)5的展开式中x 2的系数;(3)321⎪⎪⎭⎫ ⎝⎛-+x x 的展开式中的常数项。
二项式定理(题型及答案)
⼆项式定理(题型及答案)1、(1) 已知92-x x a 的展开式中3x 的系数为49,常数a 的值为___________. (2)设k=1,2,3,4,5,则的展开式中的系数不可能是()A. 10B. 40C. 50D. 80(3)若展开式中含项的系数与含项的系数之⽐为-5,则n 等于()A. 4B. 6C. 8D. 102、求值: (1) =-++?-?+-nn n n n C C C 3)1(333133221(2) S=(x-1)4+4(x-1)3+6(x-1)2+4(x-1)+1= (3)=3、试求下列⼆项展开式中指定项的系数:(1)(a+b+c)10的展开式中,含a 5b 3c 2的系数为_________(2)求的常数项(3) 的展开式中项的系数(4) 的展开式中项的系数(5) 的展开式中项的系数(6) 的展开式中x 项的系数(7) 的展开式中项的系数(8)5)12)((xx x a x -+的展开式中各项系数的和为2,则该展开式中常数项为。
,其中b 0+b 1+b 2+……+b n =62, 则n=_________(Ⅱ)如果的展开式中各项系数之和为128,则展开式中的系数是()A. 7B. –7C. 21D. –21(Ⅲ)已知(1)求a 0, (2)求a 1+a 2+a 3+a 4+a 5(3)求(a 0+a 2+a 4)2-(a 1+a 3+a 5)2(4)求a 1+a 3+a 5 (5)|a 0|+|a 1|+……+|a 5|5、已知⼆项式展开式中,末三项的系数依次成等差数列,求此展开式中所有的有理项。
~6、已知nx x )3(232 的展开式各项系数和⽐它的⼆项式系数和⼤992. (1)展开式中⼆项式系数最⼤的项 (2)求展开式中系数最⼤的项.]*7、已知的展开式中奇数项的⼆项式系数之和等于512,试求:(1)⼆项式系数最⼤的项;(2)系数的绝对值最⼤的项;(3)系数最⼤的项。
二项式定理训练题(含答案)
⼆项式定理训练题(含答案)⼆项式定理训练题⼀、单选题(共4题;共8分)1.若⼆项式的展开式中各项的系数和为243,则该展开式中含x项的系数为()A. 1B. 5C. 10D. 202.已知⼆项式的展开式中第2项与第3项的⼆项式系数之⽐是2︰5,则的系数为()A. 14B.C. 240D.3.若,则的值为()A. B. C. D.4.在(x2﹣x﹣2)5的展开式中,x3的系数为()A. ﹣40B. 160C. 120D. 200⼆、填空题(共13题;共15分)5.⼆项式的展开式中常数项为________.6.展开式中常数项为________.7.的展开式中,x3的系数为________.8.已知的展开式中各项系数和为2,则其展开式中常数项是________.9.的⼆项展开式中,含项的系数为________.10.若,则的展开式的第4项的系数为________.(⽤数字作答)11.⼆项式的展开式的各项系数之和为________,的系数为________.12.已知的展开式中的系数为108,则实数________.13.的展开式中,的系数是20,则________.14.展开式中的系数是15,则展开式的常数项为________,展开式中有理项的⼆项式系数和为________.15.在的展开式中,的系数是________.16.的展开式中的系数为________.17.在的展开式中,的系数为15,则实数________.三、解答题(共3题;共25分)18.已知展开式中各项系数和⽐它的⼆项式系数和⼤992,其中.(Ⅰ)求的值;(Ⅱ)求其展开式中的有理项.19.设.(1)求;(2)求及关于的表达式.20.已知⼆项式的⼆项展开式中所有奇数项的⼆项式系数之和为128.(1)求的展开式中的常数项;(2)在(1+x)+(1+x)2+(1+x)3+(1+x)4+…+(1+x) 的展开式中,求项的系数.(结果⽤数字作答)答案解析部分⼀、单选题1.【答案】C【解析】【解答】由令得,解得,⼆项式展开式的通项公式为,令,解得,故展开式中含x项的系数为.故答案为:C.【分析】令,结合展开式中各项的系数和为234列⽅程,求得n的值,再利⽤⼆项式展开式的通项公式,即可求得含x项的系数.2.【答案】C【解析】【解答】⼆项展开式的第项的通项公式为由展开式中第2项与第3项的⼆项式系数之⽐是2︰5,可得:.解得:.所以令,解得:,所以的系数为故答案为:C【分析】由⼆项展开式的通项公式为及展开式中第2项与第3项的⼆项式系数之⽐是2︰5可得:,令展开式通项中x的指数为3,即可求得,问题得解.3.【答案】C【解析】【解答】展开式的通项为:,故,,根据对称性知:.故答案为:C.【分析】计算,根据⼆项式系数的对称性即可得到答案.4.【答案】C【解析】【解答】∵(x2﹣x﹣2)5=(x+1)5(x﹣2)5,∴x3的系数为.故答案为:C.【分析】先把(x2﹣x﹣2)5变形为(x+1)5(x﹣2)5,再利⽤⼆项式定理中的通项公式求出结果.⼆、填空题5.【答案】60【解析】【解答】⼆项式的展开式的通项公式为,令,解得,所以该⼆项式展开式中常数项为,故答案为:60。
(完整版)二项式定理知识点和各种题型归纳带答案
二项式定理1.二项式定理:(a b)n C n0a n C1n a n 1b L C n r a n r b r L C n n b n (n N ),2.基本概念:①二项式展开式:右边的多项式叫做(a b)n的二项展开式。
②二项式系数:展开式中各项的系数C n r (r 0,1,2, ,n) .③项数:共(r 1)项,是关于a与b的齐次多项式④通项:展开式中的第r 1项C n r a n r b r叫做二项式展开式的通项。
用T r 1 C n r a n r b r表示。
3.注意关键点:①项数:展开式中总共有(n 1) 项。
②顺序:注意正确选择a, b ,其顺序不能更改。
(a b)n与(b a)n是不同的。
③指数:a 的指数从n 逐项减到0,是降幂排列。
b的指数从0逐项减到n ,是升幂排列。
各项的次数和等于n .④系数:注意正确区分二项式系数与项的系数,二项式系数依次是数是a与b 的系数(包括二项式系数) 。
4.常用的结论:令a 1,b x, (1 x)n C n0C n1x C n2x2L C n r x r L C n n x n(n N )5.性质:①二项式系数的对称性:与首末两端“对距离” 的两个二项式系数相等,即C n0 C n n,···C n k C n k 1②二项式系数和:令a b 1, 则二项式系数的和为C n0C n1C n2L C n r L C n n2n,变形式C1n C n2 L C n r L C n n2n 1 。
③奇数项的二项式系数和=偶数项的二项式系数和:在二项式定理中,令a1,b 1 ,则C n0 C n1 C n2C n3 L ( 1)n C n n (1 1)n 0 ,从而得到:C n0 C n2C n4C n2r C n1 C n3 L 2r 1Cn12n2n 1 2④奇数项的系数和与偶数项的系数和:C n,C n,C n , ,C n, ,C n .项的系令a 1,b x, (1 x)n C n0 C1n x C n2x2 L C n r x r L ( 1)n C n n x n (n N )n 2 2解:由条件知 C n n 2 45 ,即 C n 2 45 , 2n 2 n 90 0 ,解得 n9(舍去 )或n 10 ,由(a x)nC n 0a n0xC n 1a n 1xC n 2a n 22 x L n 0 n 1 C n a x a 0 a 1x 2na 2x La n x(x a)nC n 0a0nx 1C n axn1C n 2a 2 n2xLn n 0 nC n a x a n x L21 a 2x a 1x a令x 1, 则 a 0 a 1 a 2a 3Lan(a 1)n①令x 1,则a 0a1a2a3L a n (a 1)n②① ②得,a 0 a2a 4L an(a1)n (a 2 1)(奇数项的系数和 )①②得,a 1a3a 5La n(a 1)n (a21)(偶数项的系数和)n⑤二项式系数的最大项: 如果二项式的幂指数 n 是偶数时,则中间一项的二项式系数 C n 2 取得最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年高考理科数学 《二项式定理》题型归纳与训练
【题型归纳】
题型一 二项式定理展开的特殊项
例 在二项式5
21⎪⎭⎫ ⎝⎛-x x 的展开式中,含4x 的项的系数是( ) A .10- B .10
C .5-
D .5
【答案】B
【解析】对于()()r r r r
r r r x C x x
C T 3105525111--+-=⎪⎭⎫ ⎝⎛-=,对于2,4310=∴=-r r ,则4x 的项的系数是()101225=-C 【易错点】公式记错,计算错误。
【思维点拨】本题主要考查二项式定理的展开公式,知道什么是系数,会求每一项的系数.
题型二 求参数的值
例 若二项式n x x ⎪⎭⎫ ⎝
⎛+21的展开式中,第4项与第7项的二项式系数相等,则展开式6x 的系数为________.(用数字作答)
【答案】9
【解析】根据已知条件可得: 96363=+=⇒=n C C n n , 所以n
x x ⎪⎭⎫ ⎝
⎛+21的展开式的通项为23999912121C r r r
r r x C x x T --+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=,令26239=⇒=-r r ,所以所求系数为921292=⎪⎭⎫ ⎝⎛C . 【易错点】分数指数幂的计算
【思维点拨】本题主要考查二项式定理的展开公式,并用其公式求参数的值.
题型三 展开项的系数和
例 已知()()()()10
102210101...111x a x a x a a x -++-+-+=+,则8a 等于( ) A .180-
B .180
C .45
D .45-
【答案】B
【解析】由于()()[]1010121x x --=+,又()[]10
12x --的展开式的通项公式为: ()[]()()r
r r r r r r r x C x C T -⋅⋅⋅-=--⋅⋅=--+12112101010101,在展开式中8a 是()81x -的系数,所以应取8=r ,
∴()1802128108
8=⋅⋅-=C a . 【易错点】对二项式的整体理解
【思维点拨】本题主要对二项式定理展开式的综合考查,学会构建模型
题型四 二项式定理中的赋值
二项式()932y x -的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和.
【答案】(1)9
2 (2)-1 (3)2
159- 【解析】设()9927281909...32y a y x a y x a x a y x ++++=+ (1)二项式系数之和为9992919
092...=++++C C C C . (2)各项系数之和为()132 (9)
9210-=-=++++a a a a (3)由(2)知1...9210-=++++a a a a ,令1,1-==y x ,得992105...=++++a a a a ,将两式相加,得2
15986420-=++++a a a a a ,即为所有奇数项系数之和. 【思维点拨】本题主要学会赋值法求二项式系数和、系数和,难点在于赋值
【巩固训练】
题型一 二项式定理展开的特殊项
1.在 ()10
2-x 的展开式中,6x 的系数为( ) A .41016C B .41032C C .6108C - D .61016C -
【答案】A
【解析】解:()4,610,210101==-∴-=-+r r x C T r r r r ,6x 的系数为()4104
410162C C =- 2.8
22⎪⎭⎫ ⎝⎛+x x 的展开式中4x 的系数是________ 【答案】1120
【解析】解:r r r r r r r x C x
x C T 316--88281+2=)2()(=,4=316∴r -,解得4=r ,所以4x 的系数为11202484=C
3.在()()6
321x x +-的展开式中,5x 的系数是________ . (用数字作答) 【答案】228-
【解析】解:()()6
321x x +-的展开式中,5x 的系数是2282226456-=-C C 题型二 求参数的值
1.已知()n
x 31+的展开式中含有2x 的系数是54,则n =________ . 【答案】4
【解析】解:()n x 31+的展开式中通项公式:()r
r n r n r x C T 311-+= ∵含有2x 的系数是54,∴r =2. ∴ 54322=n C ,可得 62=n
C ,∴()*,621N n n n ∈=÷- ,解得4=n . 2.在 6
⎪⎭⎫ ⎝⎛+x a x ()0>a 的展开式中常数项的系数是60,则a 的值为________ . 【答案】2
【解析】解:r r r r r r
r x C a x a x C T 2336661+=)()(=--,令0=2
33r -,解得r=2. ∴ 60262=C a ,a >0,解得a=2.
3.在()52x +的展开式中,3x 的系数为 .(用数字作答)
【答案】40
【解析】利用通项公式,,2551r r r r x C T -+=,令3=r ,得出3x 的系数为40235
2=C
题型三 展开项的系数和
1.在 n x x ⎪⎭⎫ ⎝
⎛+3的展开式中,各项系数和与二项式系数和之比为64,则 的系数为( )
A .135
B .405
C .15
D .45
【答案】A 【解析】由题意可得6424=n n ,6=∴n 。
r r r r r r r x C x x C T 2366661+3=)3(=--,32
36=-∴r ,2=r ,则3x 的系数为1353262=C
2.若二项式n
x x ⎪⎭⎫ ⎝⎛+1的展开式中各项的系数和为32,则该展开式中含x 的系数为( ) A .1 B .5 C .10 D .20
【答案】B
【解析】解:令1=x ,则5,322==n n , ∴r r r r r r x C x
x C T 23255551+=)1()(=-- 令
1,12
325==-r r ,.∴该展开式中含x 的系数为515=C 3.n x x ⎪⎭⎫ ⎝
⎛-2 的二项展开式中第五项和第六项的二项式系数最大,则各项的系数和为________ .
【答案】-1
【解析】解:因为n
x x ⎪⎭⎫ ⎝
⎛-2的展开式中第五项和第六项的二项式系数最大 所以n =9 令()121,19-=-=x
题型四 二项式定理中的赋值
1.已知()6626
...1211x a bx x ax ++++=+,则实数b 的值为( )
A .15
B .20
C .40
D .60
【答案】D
【解析】解:其展开式的通项为()r
r r ax C T 61=+ , 则x 的系数为12116=a C ,解得2=a , 则602226==C b
2.若()6622106
...1x a x a x a a mx ++++=+,且63...621=+++a a a ,则实数m 的值为 ( ) A .1或3
B .-3
C .1
D .1或-3
【答案】D 【解析】令x =0,得()10160=+=a ,令x =1,得()62106
...1a a a a m ++++=+,又64...6210=++++a a a a ,∴()66
2641==+m ,∴m =1或m =-3. 3.的展开式中x 的奇数次幂项的系数之和为32,则__________.
【答案】3
【解析】由已知得()432446411x x x x x ++++=+,故()()4
1x x a ++的展开式中x 的奇数次冥项分别为533,6,,4,4x x x ax ax ,其系数之和为3216144=++++a a ,解得a =3
4()(1)a x x ++a =。
