进制转换计算+ASCII表
16进制转换ascii码表
16进制转换ascii码表摘要：1.16 进制转换概述2.ASCII 码表简介3.16 进制与ASCII 码表的转换方法4.实例解析5.总结正文：一、16 进制转换概述16 进制，又称十六进制，是一种计数方法，它的基数为16。
在计算机领域，16 进制广泛应用于数据的存储和传输。
为了将16 进制的数据转换为ASCII 码表中的字符，我们需要了解它们之间的对应关系。
二、ASCII 码表简介ASCII 码表（American Standard Code for Information Interchange）是美国标准信息交换码的简称，是一种将字符与二进制数相对应的编码方式。
ASCII 码表包含128 个字符，包括大小写字母、数字和一些特殊符号。
三、16 进制与ASCII 码表的转换方法将16 进制数据转换为ASCII 码表中的字符，我们需要按照以下步骤进行：1.首先，将16 进制数按照四位一组划分，不足四位的，在左侧用0 补足。
例如，将十六进制数2A3B 划分为0x2A 0x3B。
2.然后，将每一组16 进制数转换为相应的十进制数。
例如，0x2A 转换为42，0x3B 转换为59。
3.接着，将十进制数转换为ASCII 码表中的字符。
例如，42 对应的字符是"B"，59 对应的字符是""；"。
4.最后，将得到的字符按照顺序拼接在一起，得到最终的ASCII 码表字符。
例如，0x2A3B 转换为ASCII 码表字符为"B"。
四、实例解析假设我们有一个16 进制数0x1F3A，我们需要将其转换为ASCII 码表中的字符。
按照上述步骤，我们可以得到：1.划分为0x1F 0x3A2.转换为十进制数，得到25 583.转换为ASCII 码表字符，得到"[" "；"4.拼接字符，得到"【；"因此，0x1F3A 转换为ASCII 码表字符为"【；"。
ASCII码与16进制的互相转换（表）
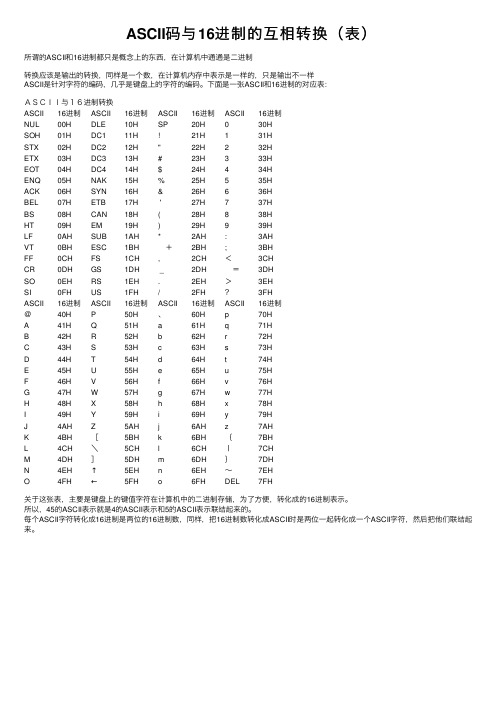
ASCII码与16进制的互相转换（表）所谓的ASCII和16进制都只是概念上的东西，在计算机中通通是⼆进制转换应该是输出的转换，同样是⼀个数，在计算机内存中表⽰是⼀样的，只是输出不⼀样ASCII是针对字符的编码，⼏乎是键盘上的字符的编码。
下⾯是⼀张ASCII和16进制的对应表：ＡＳＣＩＩ与１６进制转换ASCII16进制ASCII16进制ASCII16进制ASCII16进制NUL00H DLE10H SP20H030HSOH01H DC111H!21H131HSTX02H DC212H"22H232HETX03H DC313H#23H333HEOT04H DC414H$24H434HENQ05H NAK15H%25H535HACK06H SYN16H&26H636HBEL07H ETB17H '27H737HBS08H CAN18H(28H838HHT09H EM19H)29H939HLF0AH SUB1AH*2AH:3AHVT0BH ESC1BH ＋2BH;3BHFF0CH FS1CH,2CH＜3CHCR0DH GS1DH _2DH ＝3DHSO0EH RS1EH.2EH＞3EHSI0FH US1FH/2FH？3FHASCII16进制ASCII16进制ASCII16进制ASCII16进制＠40H P50H、60H p70HA41H Q51H a61H q71HB42H R52H b62H r72HC43H S53H c63H s73HD44H T54H d64H t74HE45H U55H e65H u75HF46H V56H f66H v76HG47H W57H g67H w77HH48H X58H h68H x78HI49H Y59H i69H y79HJ4AH Z5AH j6AH z7AHK4BH［5BH k6BH｛7BHL4CH＼5CH l6CHㄧ7CHM4DH］5DH m6DH｝7DHN4EH↑5EH n6EH～7EHO4FH←5FH o6FH DEL7FH关于这张表，主要是键盘上的键值字符在计算机中的⼆进制存储，为了⽅便，转化成的16进制表⽰。
ASCII码与16进制转换对照表
n
小写字母n
6F
o
小写字母o
70
p
小写字母p
71
q
小写字母q
72
r
小写字母r
73
s
小写字母s
74
t
小写字母t
75
u
小写字母u
76
v
小写字母v
77
w
小写字母w
78
x
小写字母x
79
y
小写字母y
7A
z
小写字母z
7B
{
左大括号
7C
|
垂直线
7D
}
右大括号(ALTMODE)
7E
~
代字号(ALTMODE)
7F
5A
Z
大写字母Z
5B
[
左中括号
5C
\
反斜杠
5D
]
右中括号
5E
^
音调符号
5F
_
下划线
60
`
重音符
61
a
小写字母a
62
b
小写字母b
63
c
小写字母c
64
d
小写字母d
65
e
小写字母e
66
f
小写字母f
67
g
小写字母g
68
h
小写字母h
69
i
小写字母i
6A
j
小写字母j
6B
k
小写字母k
6C
l
小写字母l
6D
m
小写字母m
E7
ç
带变音符号的小写字母c
E8
è
ASCII代码转换表
ASCII求助编辑ASCII（American Standard Code for Information Interchange，美国信息互换标准代码）是基于拉丁字母的一套电脑编码系统。
它主要用于显示现代英语和其他西欧语言。
它是现今最通用的单字节编码系统，并等同于国际标准ISO/IEC 646。
目录展开编辑本段名称美国信息交换标准代码( American Standard Code for Information Interchange, ASCII ) 编辑本段产生编辑本段常见ASCII码的大小规则0~9＜A~Z＜a~z1）数字比字母要小。
如“7”＜“F”；2）数字0比数字9要小，并按0到9顺序递增。
如“3”＜“8” ；3）字母A比字母Z要小，并按A到Z顺序递增。
如“A”＜“Z” ；4）同个字母的大写字母比小写字母要小32。
如“A”＜“a” 。
记住几个常见字母的ASCII码大小：换行LF为0x0A；回车CR为0x0D；空格为0x20；“0”为0x30；“A”为0x41；“a”为0x61。
另外还有128-255的ASCII字符编辑本段查询ASCII技巧方便查询ASCII码对应的字符：新建一个文本文档，按住ALT+要查询的码值（注意，这里是十进制）松开即可显示出对应字符。
例如：按住ALT+97,则会显示出‘a’。
编辑本段字符集简史6000年前象形文字3000年前字母表1838年到1854年 Samuel F. B. Morse发明了电报,字母表中的每个字符对应于一系列短的和长的脉冲1821年到1824年 Louis Braille发明盲文，6位代码，它把字符、常用字母组合、常用单字和标点进行编码。
一个特殊的escape代码表示后续的字符代码应解释为大写。
一个特殊的shift代码允许后续代码被解释为数字。
1931年 CCITT标准化Telex代码，包括Baudot #2的代码，都是包括字符和数字的5位代码。
进制转换(附ASCII码表)
一、十进制与二进制之间的转换二、 （1）十进制转换为二进制，分为整数部分和小数部分三、①整数部分方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。
下面举例： 例：将十进制的168转换为二进制得出结果将十进制的168转换为二进制，（10101000）2 分析:第一步，将168除以2,商84,余数为0。
第二步，将商84除以2，商42余数为0。
第三步，将商42除以2，商21余数为0。
第四步，将商21除以2，商10余数为1。
第五步，将商10除以2，商5余数为0。
第六步，将商5除以2，商2余数为1。
第七步，将商2除以2，商1余数为0。
第八步，将商1除以2，商0余数为1。
第九步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000（2）小数部分 方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分 为零为止。
如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数，下面举例： 例1：将0.125换算为二进制 得出结果：将0.125换算为二进制（0.001）2 分析：第一步，将0.125乘以2，得0.25,则整数部分为0,小数部分为0.25; 第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5; 第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0; 第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制（保留到小数点第四位）大家从上面步骤可以看出，当第五次做乘法时候，得到的结果是0.4，那么小数部分继续乘以2，得0.8，0.8又乘以2的，到1.6这样一直乘下去，最后不可能得到小数部分为零，因此，这个时候只好学习十进制的方法进行四舍五入了，但是二进制只有0和1两个，于是就出现0舍1入。
码制转换十二进制数ASCII码之间的互相转换BCD
MOV SS,AX
MOV SP,TOP
LEA BX,STRING ;取变量偏址
PUSH BX
;将偏址压栈
PUSH NUM
;将变量压栈
堆栈
AF 25 02 00
0060H 0062H 0064H
26
CALL BINHEX
;(SP)=005EH
CS:0113 LEA DX,STRING ;(DX)=0002H
;若(CL)=0,转NEXT2 ;取字符 ;转换成BCD码 ;加到中间结果上
10
MOV MUL INC JMP NEXT2: MOV AND ADD CMP JNZ NEG NEXT3: MOV RET
DX,10 DX BX SHORT LP1 DL,[BX] DL,0FH AX,DX CH,’-’ NEXT3 AX [DI],AX
(AX)+1000(AX) DL存至缓冲区 令(DL)＝0
求100的个数，结构同上
A
(AX)-10
Y
<0?
N
(DL)+1
(AX)+10(AX) 存DL 存AL
返回DOS
15
汇编程序如下：
DATA SEGMENT BNUM DB 270FH DNUM DB 4 DUP(?) ;存放BCD码的缓冲区 DATA ENDS CODE SEGMENT
STR1
0A
02
32
36
0D …
STR2
0A
02
33 33
0D …
NUM
1A
00
21
00
SUM
3B
00
OVER
‘O’
…
…
16进制和ascii码的转换表
16进制和ascii码的转换表摘要：一、16进制转换简介1.16进制数的表示方法2.16进制与ASCII码的关系二、ASCII码转换简介1.ASCII码的表示方法2.ASCII码与16进制数的转换三、16进制与ASCII码转换表1.16进制转ASCII码2.ASCII码转16进制正文：一、16进制转换简介16进制数是一种以16为基数的数制表示方法，它的每一位数都可以由0-9和A-F这16个数字表示。
在计算机科学中，16进制数常用于简化二进制数，使得人们更容易理解和操作。
同时，16进制数与ASCII码有着密切的关系，因为ASCII码中的字符也可以用16进制数来表示。
2.16进制与ASCII码的关系在计算机中，字符和数字都以二进制数的形式存储。
为了方便表示和处理这些二进制数，人们将它们转换成16进制数。
同时，由于ASCII码是一种将字符与数字相互转换的编码方式，因此16进制数与ASCII码之间的转换就变得尤为重要。
二、ASCII码转换简介1.ASCII码的表示方法ASCII码是一种将字符和数字用7位二进制数表示的编码方式。
在ASCII 码中，每个字符都有一个对应的整数值，范围从0到127。
这种编码方式使得计算机能够识别和处理各种英文字母、数字和一些符号。
2.ASCII码与16进制数的转换由于16进制数可以简化二进制数的表示，因此将ASCII码转换成16进制数是一种非常实用的方法。
通常，我们可以将7位二进制数转换成1位16进制数。
例如，二进制数"01100001"可以转换成16进制数"A"。
三、16进制与ASCII码转换表为了方便进行16进制与ASCII码之间的转换，我们可以制作一个转换表。
十六进制转ascii码对照表
十六进制转ascii码对照表十六进制转ASCII码对照表1. 引言在计算机科学中，十六进制和ASCII码是两个经常被使用的概念。
十六进制是一种表示数字的方法，而ASCII码则用于表示字符。
本文将介绍十六进制转ASCII码对照表，帮助读者更好地理解十六进制和ASCII码之间的关系。
2. 十六进制的基本概念十六进制是一种使用16个数字（0-9和A-F）来表示数值的系统。
在计算机领域中，经常使用十六进制来表示内存地址、颜色值等。
例如，十六进制数值0x1A表示十进制的26。
3. ASCII码的基本概念ASCII码是一种将字符映射为数字的编码系统。
每个字符都有一个对应的ASCII码值。
例如，字符'A'的ASCII码为65，字符'Z'的ASCII码为90。
通过ASCII码，计算机可以识别和处理各种字符。
4. 十六进制转ASCII码对照表下面是一个简单的十六进制转ASCII码对照表：十六进制 ASCII码0x01 SOH 0x02 STX 0x03 ETX 0x04 EOT 0x05 ENQ 0x06 ACK 0x07 BEL 0x08 BS 0x09 HT 0x0A LF 0x0B VT 0x0C FF 0x0D CR 0x0E SO 0x0F SI 0x10 DLE 0x11 DC1 0x12 DC2 0x13 DC3 0x14 DC4 0x15 NAK0x17 ETB0x18 CAN0x19 EM0x1A SUB0x1B ESC0x1C FS0x1D GS0x1E RS0x1F US5. 结论通过十六进制转ASCII码对照表，我们可以轻松地将十六进制数值转换为对应的ASCII字符。
这对于计算机科学的学习和应用非常重要。
希望本文能够帮助读者更好地理解和应用十六进制和ASCII码。
让我们一起探索计算机科学的奥秘吧！。
ASCII码和16进制转换对照表
ç
带变音符号的小写字母c
E8
è
带重音符的小写字母e
E9
é
带尖锐重音的小写字母e
EA
ê
带音调符号的小写字母e
EB
ë
带元音变音(分音符号)的小写字母e
EC
ì
带重音符的小写字母i
ED
í
带尖锐重音的小写字母i
EE
î
带音调符号的小写字母i
EF
ï
带元音变音(分音符号)的小写字母i
F0
[保留]2
F1
ñ
带代字号的小写字母n
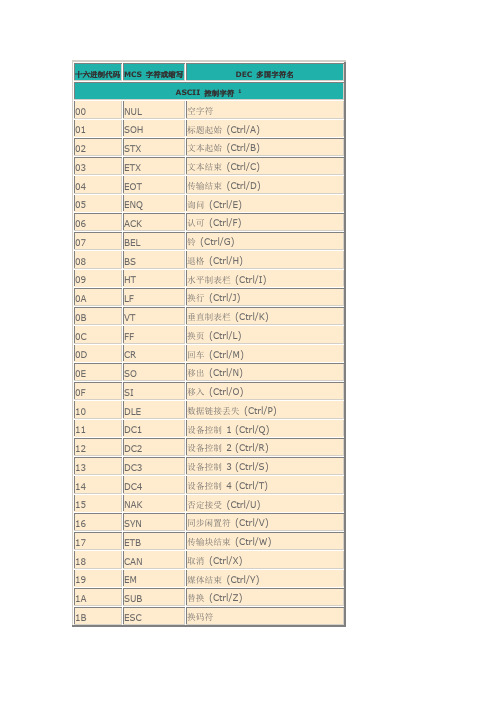
十六进制代码
MCS字符或缩写
DEC多国字符名
ASCII控制字符1
00
NUL
空字符
01
SOH
标题起始(Ctrl/A)
02
STX
文本起始(Ctrl/B)
03
ETX
文本结束(Ctrl/C)
04
EOT
传输结束(Ctrl/D)
05
ENQ
询问(Ctrl/E)
06
ACK
认可(Ctrl/F)
07
BEL
铃(Ctrl/G)
2E
.
句点或小数点
2F
/
斜杠
30
0
零
31
1
1
32
2
2
33
3
3
34
4
4
35
5
5
36
6
6
37
7
7
38
8
8
39
9
9
3A
:
冒号
3B
;
分号
3C
ASCII码与16进制转换对照表
ESC
换码符
1C
FS
文件分隔符
1D
GS
组分隔符
1E
RS
记录分隔符
1F
US
单位分隔符
ASCII特殊和数字字符
20
SP
空格
21
!
感叹号
22
1!
引号（双引号）
23
#
数字符号
24
$
美兀符
25
%
百分号
26
&
和号
27
1!
省略号（单引号）
28
(
左圆括号
29
)
右圆括号
2A
*
星号
2B
加号
2C
逗号
2D
--
连字号或减号
大写字母G
48
H
大写字母H
49
I
大写字母1
4A
J
大写字母J
4B
K
大写字母K
4C
L
大写字母L
4D
M
大写字母M
4E
N
大写字母N
4F
O
大写字母0
50
P
大写字母P
51
Q
大写字母Q
52
R
大写字母R
53
S
大写字母S
54
T
大写字母T
55
U
大写字母U
56
V
大写字母V
57
W
大写字母W
58
X
大写字母X
59
Y
大写字母Y
5A
12
DC2
设备控制2（Ctrl/R）
ASCII码和进制转换对照表
ASCII码和进制转换对照表十六进制代码M CS 字符或缩写DEC 多国字符名ASCII 控制字符100 NUL 空字符01 SOH 标题起始(Ctrl/A)02 STX 文本起始(Ctrl/B)03 ETX 文本结束(Ctrl/C)04 EOT 传输结束(Ctrl/D)05 ENQ 询问(Ctrl/E)06 ACK 认可(Ctrl/F)07 BEL 铃(Ctrl/G)08 BS 退格(Ctrl/H)09 HT 水平制表栏(Ctrl/I)0A LF 换行(Ctrl/J)0B VT 垂直制表栏(Ctrl/K)0C FF 换页(Ctrl/L)0D CR 回车(Ctrl/M)0E SO 移出(Ctrl/N)0F SI 移入(Ctrl/O)10 DLE 数据链接丢失(Ctrl/P)11 DC1 设备控制 1 (Ctrl/Q)12 DC2 设备控制 2 (Ctrl/R)13 DC3 设备控制 3 (Ctrl/S)14 DC4 设备控制 4 (Ctrl/T)15 NAK 否定接受(Ctrl/U)16 SYN 同步闲置符(Ctrl/V)17 ETB 传输块结束(Ctrl/W)18 CAN 取消(Ctrl/X)19 EM 媒体结束(Ctrl/Y)1A SUB 替换(Ctrl/Z) 1B ESC 换码符1C FS 文件分隔符1D GS 组分隔符1E RS 记录分隔符1F US 单位分隔符ASCII 特殊和数字字符20 SP 空格21 ! 感叹号22 " 引号(双引号)23 # 数字符号24 $ 美元符25 % 百分号26 & 和号27 " 省略号(单引号)28 ( 左圆括号29 ) 右圆括号2A * 星号2B 加号2C , 逗号2D -- 连字号或减号2E . 句点或小数点2F / 斜杠30 0 零31 1 132 2 233 3 334 4 435 5 536 6 637 7 738 8 839 9 93A : 冒号3B ; 分号3C < 小于3D = 等于3E > 大于3F ? 问号ASCII 字母字符40 @ 商业at 符号41 A 大写字母 A42 B 大写字母 B43 C 大写字母 C44 D 大写字母 D45 E 大写字母 E46 F 大写字母 F47 G 大写字母G48 H 大写字母H49 I 大写字母I 4A J 大写字母J 4B K 大写字母K 4C L 大写字母L 4D M 大写字母M 4E N 大写字母N 4F O 大写字母O50 P 大写字母P51 Q 大写字母Q52 R 大写字母R53 S 大写字母S54 T 大写字母T55 U 大写字母U56 V 大写字母V57 W 大写字母W58 X 大写字母X59 Y 大写字母Y 5A Z 大写字母Z 5B [ 左中括号5C \ 反斜杠5D ] 右中括号5E ^ 音调符号5F _ 下划线60 ` 重音符61 a 小写字母 a62 b 小写字母 b63 c 小写字母 c64 d 小写字母 d65 e 小写字母 e66 f 小写字母 f67 g 小写字母g68 h 小写字母h69 i 小写字母i 6A j 小写字母j 6B k 小写字母k 6C l 小写字母l 6D m 小写字母m 6E n 小写字母n 6F o 小写字母o70 p 小写字母p71 q 小写字母q72 r 小写字母r73 s 小写字母s74 t 小写字母t75 u 小写字母u76 v 小写字母v77 w 小写字母w78 x 小写字母x79 y 小写字母y7A z 小写字母z7B { 左大括号7C | 垂直线7D } 右大括号(ALTMODE) 7E ~ 代字号(ALTMODE)7F DEL 擦掉(DELETE)控制字符80 [保留]81 [保留]82 [保留]83 [保留]84 IND 索引85 NEL 下一行86 SSA 被选区域起始87 ESA 被选区域结束88 HTS 水平制表符集89 HTJ 对齐的水平制表符集8A VTS 垂直制表符集8B PLD 部分行向下8C PLU 部分行向上8D RI 反向索引8E SS2 单移 28F SS3 单移 390 DCS 设备控制字符串91 PU1 专用 192 PU2 专用 293 STS 设置传输状态94 CCH 取消字符95 MW 消息等待96 SPA 保护区起始97 EPA 保护区结束98 [保留]99 [保留]9A [保留]9B CSI 控制序列引导符9C ST 字符串终止符9D OSC 操作系统命令9E PM 秘密消息9F APC 应用程序其他字符A0 [保留] 2A1 ? 反向感叹号A2 ￠分币符A3 ￡英磅符A4 [保留] 2A5 ￥人民币符A6 [保留] 2A7 §章节符A8 ¤通用货币符号2 A9 ? 版权符号AA a 阴性顺序指示符AB ? 左角引号AC [保留] 2AD [保留] 2AE [保留] 2AF [保留] 2B0 °温度符B1 ±加/减号B2 2 上标 2B3 3 上标 3B4 [保留] 2B5 μ微符B6 ? 段落符，pilcrowB7 ·中点B8 [保留] 2B9 1 上标 1BA o 阳性顺序指示符BB ? 右角引号BC ? 分数四分之一BD ? 分数二分之一BE [保留] 2BF ? 反向问号C0 à带重音符的大写字母 AC1 á带尖锐重音的大写字母 AC2 ? 带音调符号的大写字母 AC3 ? 带代字号的大写字母 AC4 ? 带元音变音(分音符号) 的大写字母 A C5 ? 带铃声的大写字母AC6 ? 大写字母AE 双重元音C7 ? 带变音符号的大写字母 CC8 è带重音符的大写字母 EC9 é带尖锐重音的大写字母 ECA ê带音调符号的大写字母 ECB ? 带元音变音(分音符号) 的大写字母 ECC ì带重音符的大写字母ICD í带尖锐重音的大写字母ICE ? 带音调符号的大写字母ICF ? 带元音变音(分音符号) 的大写字母I D0 [保留] 2D1 ? 带代字号的大写字母ND2 ò带重音符的大写字母OD3 ó带尖锐重音的大写字母OD4 ? 带音调符号的大写字母OD5 ? 带代字号的大写字母OD6 ? 带元音变音(分音符号) 的大写字母O D7 OE 大写字母OE 连字2D8 ? 带斜杠的大写字母OD9 ù带重音符的大写字母UDA ú带尖锐重音的大写字母UDC ü带元音变音(分音符号) 的大写字母U DD Y 带元音变音(分音符号) 的大写字母Y DE [保留] 2DF ? 德语高调小写字母sE0 à带重音符的小写字母 aE1 á带尖锐重音的小写字母 aE2 a 带音调符号的小写字母 aE3 ? 带代字号的小写字母 aE4 ? 带元音变音(分音符号) 的小写字母 a E5 ? 带铃声的小写字母aE6 ? 小写字母ae 双重元音E7 ? 带变音符号的小写字母 cE8 è带重音符的小写字母 eE9 é带尖锐重音的小写字母 eEA ê带音调符号的小写字母 eEB ? 带元音变音(分音符号) 的小写字母e EC ì带重音符的小写字母iED í带尖锐重音的小写字母iEE ? 带音调符号的小写字母iEF ? 带元音变音(分音符号) 的小写字母i F0 [保留] 2F1 ? 带代字号的小写字母nF2 ò带重音符的小写字母oF3 ó带尖锐重音的小写字母oF4 ? 带音调符号的小写字母oF5 ? 带代字号的小写字母oF6 ? 带元音变音(分音符号) 的小写字母o F7 oe 小写字母oe 连字2F8 ? 带斜杠的小写字母oF9 ù带重音符的小写字母uFA ú带尖锐重音的小写字母uFC ü带元音变音(分音符号) 的小写字母u FD ? 带元音变音(分音符号) 的小写字母y 2 FE [保留] 2FF [保留] 2。
进制转换计算+ASCII表
一、二进制转化成其他进制例子1：将二进制数（10010）2转化成八进制数。
（10010）2=（010 010）2=（2 2）8=（22）8例子2：将二进制数（0.1010）2转化为八进制数。
（0.10101）2=（0. 101 010）2=（0. 5 2）8=（0.52）8诀窍：因为每三位二进制数对应一位八进制数，所以，以小数点为界，整数位则将二进制数从右向左每3位一隔开，不足3位的在左边用0填补即可；小数位则将二进制数从左向右每3位一隔开，不足3位的在右边用0填补即可。
例子1：将二进制数（10010）2转化成十进制数。
（10010）2=（1x24+0x23+0x22+1x21+0x20）10=（16+0+0+2+0）10=(18) 10例子2：将二进制数（0.10101）2转化为十进制数。
（0.10101）2=（0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5）10=（0+0.5+0.25+0.125+0.0625+0.03125）10=（0.96875）10诀窍：以小数点为界，整数位从最后一位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0或1）乘以2的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3……..n，然后将第n位的数（0或1）乘以2的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。
例子1：将二进制数（10010）2转化成十六进制数。
（10010）2=（0001 0010）2=（1 2）16=(12) 16例子2：将二进制数（0.1010）2转化为十六进制数。
（0.10101）2=（0. 1010 1000）2=（0. A 8）16=（0.A8）16诀窍：因为每四位二进制数对应一位十六进制数，所以，以小数点为界，整数位则将二进制数从右向左每4位一隔开，不足4位的在左边用0填补即可；小数位则将二进制数从左向右每4位一隔开，不足4位的在右边用0填补即可。
16进制转换ascii码表
16进制转换ascii码表ASCII码表将十六进制数映射到对应的ASCII字符。
以下是ASCII 码表的一部分，显示了十六进制数到ASCII字符的转换：十六进制 ASCII字符--------- ----------00 NUL (空字符)01 SOH (标题开始)02 STX (正文开始)03 ETX (正文结束)04 EOT (传输结束)05 ENQ (请求)06 ACK (确认)07 BEL (响铃)08 BS (退格)09 HT (水平制表符)0A LF (换行)0B VT (垂直制表符)0C FF (换页)0D CR (回车)0E SO (移位输出)0F SI (移位输入)10 DLE (数据链路逃逸)11 DC1 (设备控制1)12 DC2 (设备控制2)13 DC3 (设备控制3)14 DC4 (设备控制4)15 NAK (否定确认)16 SYN (同步空闲)17 ETB (结束传输块)18 CAN (取消)19 EM (媒介结束) 1A SUB (替代)1B ESC (转义)1C FS (文件分隔符) 1D GS (组分隔符) 1E RS (记录分隔符) 1F US (单元分隔符)20 (空格)21 !22 "23 #...2D -2E .2F /30 031 1...39 93A :3B ;3C <...5A Z5B [ 5C \ 5D ] 5E ^5F _60 `61 a...7A z7B {7C |7D }7E ~7F DEL (删除)在ASCII码表中，每个ASCII字符都与一个唯一的十六进制数对应。
你可以通过查阅ASCII码表将十六进制数转换为对应的ASCII字符。
这只是一个简要的展示，完整的ASCII码表包括了更多的字符和控制字符。
ASCII码与16进制转换对照表
大写字母C
44
D
大写字母D
45
E
大写字母E
46
F
大写字母F
47
G
大写字母G
48
H
大写字母H
49
I
大写字母I
4A
J
大写字母J
4B
K
大写字母K
4C
L
大写字母L
4D
M
大写字母M
4E
N
大写字母N
4F
O
大写字母O
50
P
大写字母P
51
Q
大写字母Q
52
R
大写字母R
53
S
大写字母S
54
T
大写字母T
55
U
大写字母U
9D
OSC
操作系统命令
9E
PM
秘密消息
9F
APC
应用程序
其他字符
A0
[保留]2
A1
¡
反向感叹号
A2
¢
分币符
A3
£
英磅符
A4
[保留]2
A5
¥
人民币符
A6
[保留]2
A7
§
章节符
A8
¤
通用A
ª
阴性顺序指示符
AB
«
左角引号
AC
[保留]2
AD
[保留]2
AE
[保留]2
AF
[保留]2
B0
°
温度符
B1
±
加/减号
B2
²
上标2
B3
³
上标3
B4
[保留]2
ASCII码与16进制转换对照表
08
BS
退格 (Ctrl/H)
09
HT
程度制表栏 (Ctrl/I)
0A
LF
换行 (Ctrl/J)
0B
VT
垂直制表栏 (Ctrl/K)
0C
FF
换页 (Ctrl/L)
0D
CR
回车 (Ctrl/M)
0E
SO
移出 (Ctrl/N)
0F
SI
移入 (Ctrl/O)
10
DLE
数据链接丧掉 (Ctrl/P)
(
左圆括号
29
)
右圆括号
2A
*
星号
2B
加号
2C
,
逗号
2D
--
连字号或减号
2E
.
句点或小数点
2F
/
斜杠
30
0
零
31
1
1
32
2
2
33
3
3
34
4
4
35
5
5
36
6
6
37
7
7
38
8
8
39
9
9
3A
:
冒号
3B
;
分号
3C
<
小于
3D
=
等于
3E
>
大于
3F
?
问号
ASCII 字母字符
40
@
贸易 at 符号
41
A
大写字母 A
76
v
小写字母 v
77
w
小写字母 w
78
x
进制转换计算+ASCII表
一、二进制转化成其他进制1。
二进制（BINARY）——>八进制（OCTAL）例子1：将二进制数（10010）2转化成八进制数。
(10010)2=（010 010)2=(2 2）8=(22）8例子2：将二进制数（0。
1010）2转化为八进制数。
（0.10101)2=（0. 101 010）2=（0。
5 2)8=(0。
52）8诀窍：因为每三位二进制数对应一位八进制数,所以，以小数点为界，整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可；小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2。
二进制(BINARY）-—>十进制（DECIMAL）例子1：将二进制数(10010）2转化成十进制数。
(10010）2=(1x24+0x23+0x22+1x21+0x20)10=（16+0+0+2+0)10=（18) 10例子2:将二进制数(0。
10101）2转化为十进制数。
（0。
10101）2=（0+1x2—1+0x2—2+1x2-3+0x2—4+1x2—5)10=(0+0。
5+0。
25+0.125+0.0625+0。
03125）10=（0。
96875）10诀窍：以小数点为界，整数位从最后一位（从右向左)开始算，依次列为第0、1、2、3………n，然后将第n位的数（0或1)乘以2的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3……。
n，然后将第n位的数(0或1）乘以2的—n次方，然后相加即可得到小数位的十进制数（按权相加法）。
3。
二进制（BINARY）—-〉十六进制(HEX)例子1：将二进制数（10010）2转化成十六进制数。
（10010）2=（0001 0010）2=（1 2)16=(12）16例子2:将二进制数(0。
1010）2转化为十六进制数.（0.10101）2=（0。
1010 1000)2=（0. A 8)16=(0.A8）16诀窍：因为每四位二进制数对应一位十六进制数，所以，以小数点为界，整数位则将二进制数从右向左每4位一隔开，不足4位的在左边用0填补即可；小数位则将二进制数从左向右每4位一隔开，不足4位的在右边用0填补即可。
将ASCII码表示的十进制数转换为二进制数
一、实验内容:实验1：将ASCII码表示的十进制数转换为二进制数二、实验步骤：1、从键盘输入五位的十进制数，保存在地址为3500H的存储单元2、把这个十进制数转换为十六进制数，所得结果保存在地址为3510H的存储单元中3、把这个十六进制的结果的每位取出来，转换为ACSII码值，存储在地址为3514H的存储单元中4、把以3514H为起始地址的字符串输出到屏幕，即可得到5位十进制数转换为二进制数的结果三、程序代码：DATA SEGMENTORG 34FEHBUF DB 10DB?DB 10 DUP(?)ORG 3510HBBF DB 20 DUP(?),0DH,0AH,'$'IBF DB'Please input one number:',0DH,0AH,'$'ICF DB 0DH,0AH,'The result is:',0DH,0AH,'$'DATA ENDSSTACK SEGMENT STACK 'STACK'STACK ENDSCODE SEGMENTASSUME CS:CODE,DS:DATA,SS:STACKSTART:MOV AX,DATAMOV DS,AXMOV DX,OFFSET IBFMOV AH,9INT 21HMOV DX,0MOV AH,0AHLEA DX,BUFINT 21HMOV SI,3500HMOV DX,0MOV CX,04HMOV BX,000AHMOV AH,00HCIRCLE:MOV AL,[SI]SUB AL,30HADD AX,DXMUL BXMOV DX,AXINC SIMOV AH,0LOOP CIRCLEMOV AL,[SI]SUB AL,30HADD AX,DXLEA SI,BBFMOV [SI],AXMOV DX,AXMOV CH,04HMOV CL,04HMOV BX,3514HNEXT:ROL AX,CLMOV DL,ALAND DL,0FHCMP DL,09HJBE PLADD DL,07HPL: ADD DL,30HMOV [BX],DLINC BXDEC CHJNZ NEXTMOV DX,OFFSET ICFMOV AH,9INT 21HMOV AH,09HMOV DX,3514HINT 21HMOV AH,4CHINT 21HCODE ENDSEND START四、代码运算过程：实验2：将从键盘输入的五位十进制数的ASCII码已存在3500起始的内存单元中。
C语言-ASCII与十六进制互相转换
C语⾔-ASCII与⼗六进制互相转换0.简介写⼀个关于ASCII与⼗六进制转换的函数实现吧，年纪⼤了，记性不好，有时候总是得翻⼀翻看看怎么实现的，现在记⼀下，以后好找。
如有什么不⾜，⼤家可以提意见，相互学习，进步。
1.概述与其说是记不住，其实还是⾃⼰没有理解透彻ASCII与⼗六进制之间的关系，所以在写函数实现的时候，不知道如何下⼿，下表是ASCII与⼗六进制的对照表，可以好好记记，记住了，以后代码实现就信⼿拈来了ASCII⼗六进制030131232333434535636737838939A41B42C43D44E45F46a61b62c63d64e65f66根据对照表，加减相应的值，就可以实现ASCII与⼗六进制的互相转换。
2.ASCII转⼗六进制实现uint8_t char_2_hex(uint8_t *src){uint8_t desc;if((*src >= '0') && (*src <= '9'))desc = *src - 0x30;else if((*src >= 'a') && (*src <= 'f'))desc = *src - 0x57;else if((*src >= 'A') && (*src <= 'F'))desc = *src - 0x37;return desc;}3.⼗六进制转ASCII实现uint8_t hex_2_char(uint8_t *src){uint8_t desc;if((*src >= 0) && (*src <= 9))desc = *src + 0x30;else if((*src >= 0xA) && (*src <= 0xF)) desc = *src + 0x37;return desc;}。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、二进制转化成其他进制1. 二进制（BINARY）——>八进制（OCTAL）例子1：将二进制数（10010）2转化成八进制数。
（10010）2=（010 010）2=（2 2）8=（22）8例子2：将二进制数（）2转化为八进制数。
（）2=（0. 101 010）2=（0. 5 2）8=（）8诀窍：因为每三位二进制数对应一位八进制数，所以，以小数点为界，整数位则将二进制数从右向左每3位一隔开，不足3位的在左边用0填补即可；小数位则将二进制数从左向右每3位一隔开，不足3位的在右边用0填补即可。
2. 二进制（BINARY）——>十进制（DECIMAL）例子1：将二进制数（10010）2转化成十进制数。
（10010）2=（1x24+0x23+0x22+1x21+0x20）10=（16+0+0+2+0）10=(18) 10例子2：将二进制数（）2转化为十进制数。
（）2=（0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5）10=（0+++++）10=（）10诀窍：以小数点为界，整数位从最后一位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0或1）乘以2的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3……..n，然后将第n位的数（0或1）乘以2的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。
3. 二进制（BINARY）——>十六进制（HEX）例子1：将二进制数（10010）2转化成十六进制数。
（10010）2=（0001 0010）2=（1 2）16=(12) 16例子2：将二进制数（）2转化为十六进制数。
（）2=（0. 1010 1000）2=（0. A 8）16=（）16诀窍：因为每四位二进制数对应一位十六进制数，所以，以小数点为界，整数位则将二进制数从右向左每4位一隔开，不足4位的在左边用0填补即可；小数位则将二进制数从左向右每4位一隔开，不足4位的在右边用0填补即可。
（10010）2=（22）8=(18) 10=(12)16（）2=（）8=（）10=（）16二、八进制转化成其他进制1. 八进制（OCTAL）——>二进制（BINARY）例子1：将八进制数（751）8转换成二进制数。
（751）8=（7 5 1）8=（111 101 001）2=（1）2例子2：将八进制数（）8转换成二进制数。
（）8=（0. 1 6）8=（0. 001 110）2=（）2诀窍：八进制转换成二进制与二进制转换成八进制相反。
2. 八进制（OCTAL）——>十进制（DECIMAL）例子1：将八进制数（751）8转换成十进制数。
（751）8=（7x82+5x81+1x80）10=（448+40+1）10=（489）10例子2：将八进制数（）8转换成十进制数。
（）8=（0+1x8-1+6x8-2）10=（0++）10=（）10诀窍：方法同二进制转换成十进制。
以小数点为界，整数位从最后一位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0-7）乘以8的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3……..n，然后将第n位的数（0-7）乘以8的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。
3. 八进制（OCTAL）——>十六进制（HEX）例子1：将八进制数（751）8转换成十六进制数。
（751）8=（1）2=（0001 1110 1001）2=（1 E 9）16=（1E9）16例子2：将八进制数（）8转换成十六进制数。
（）8=（）2=（0. 0011 1000）2=（）16诀窍：八进制直接转换成十六进制比较费力，因此，最好先将八进制转换成二进制，然后再转换成十六进制。
（751）8=（1）2=（489）10=（1E9）16（）8=（）2=（）10=（）16三、十进制转化成其他进制1. 十进制（DECIMAL）——>二进制（BINARY）例子1：将十进制数（93）10转换成二进制数。
93/2=46 (1)46/2=23 023/2=11 (1)11/2=5 (1)5/2=2 (1)2/2=1 0（93）10=（1011101）2例子2：将十进制数（）10转换成二进制数。
= 0 . 625= 1 .25= 0 .5= 1 .0（）10=（）2诀窍：以小数点为界，整数部分除以2，然后取每次得到的商和余数，用商继续和2相除，直到商小于2。
然后把第一次得到的余数作为二进制的个位，第二次得到的余数作为二进制的十位，依次类推，最后一次得到的小于2的商作为二进制的最高位，这样由商+余数组成的数字就是转换后二进制的值（整数部分用除2取余法）；小数部分则先乘2，然后获得运算结果的整数部分，将结果中的小数部分再次乘2，直到小数部分为零。
然后把第一次得到的整数部分作为二进制小数的最高位，后续的整数部分依次作为低位，这样由各整数部分组成的数字就是转化后二进制小数的值（小数部分用乘2取整法）。
需要说明的是，有些十进制小数无法准确的用二进制进行表达，所以转换时符合一定的精度即可，这也是为什么计算机的浮点数运算不准确的原因。
2. 十进制（DECIMAL）——>八进制（OCTAL）例子1：将十进制数（93）10转换成八进制数。
93/8=11 (5)11/8=1 (3)（93）10=（135）8例子2: 将十进制数（）10转换成八进制数。
= 2 .5= 4 .0（）10=（）8诀窍：方法同十进制转化成二进制。
以小数点为界，整数部分除以8，然后取每次得到的商和余数，用商继续和8相除，直到商小于8。
然后把第一次得到的余数作为八进制的个位，第二次得到的余数作为八进制的十位，依次类推，最后一次得到的小于8的商作为八进制的最高位，这样由商+余数组成的数字就是转换后八进制的值（整数部分用除8取余法）；小数部分则先乘8，然后获得运算结果的整数部分，将结果中的小数部分再次乘8，直到小数部分为零。
然后把第一次得到的整数部分作为八进制小数的最高位，后续的整数部分依次作为低位，这样由各整数部分组成的数字就是转化后八进制小数的值（小数部分用乘8取整法）。
3. 十进制（DECIMAL）——>十六进制（HEX）例子1：将十进制数（93）10转换成十六进制数。
93/16=5……..13（D）（93）10=（5D）16例子2: 将十进制数（）10转换成十六进制数。
= 5.0（）10=（）16诀窍：方法同十进制转化成二进制。
以小数点为界，整数部分除以16，然后取每次得到的商和余数，用商继续和16相除，直到商小于16。
然后把第一次得到的余数作为十六进制的个位，第二次得到的余数作为十六进制的十位，依次类推，最后一次得到的小于16的商作为十六进制的最高位，这样由商+余数组成的数字就是转换后十六进制的值（整数部分用除16取余法）；小数部分则先乘16，然后获得运算结果的整数部分，将结果中的小数部分再次乘16，直到小数部分为零。
然后把第一次得到的整数部分作为十六进制小数的最高位，后续的整数部分依次作为低位，这样由各整数部分组成的数字就是转化后十六进制小数的值（小数部分用乘16取整法）。
（93）10=（1011101）2=（135）8=（5D）16（）10=（）2=（）8=（）16四、十六进制转换成其他进制1. 十六进制（HEX）——>二进制（BINARY）例子1：将十六进制数（A7）16转换成二进制数。
（A7）16=（A 7）16=（1010 0111）2=（）2例子2：将十六进制数（）16转换成二进制数。
（）16=（0. D 4）16=（0. 1101 0100）2=（）2诀窍：十六进制转换成二进制与二进制转换成十六进制相反。
2. 十六进制（HEX）——>八进制（OCTAL）例子1：将十六进制数（A7）16转换成八进制数。
（A7）16=（）2=（010 100 111）8=（247）8例子2：将十六进制数（）16转换成八进制数。
（）16=（）2=（0. 110 101）8=（）8诀窍：十六进制直接转换成八进制比较费力，因此，最好先将十六进制转换成二进制，然后再转换成八进制。
3. 十六进制（HEX）——>十进制（DECIMAL）例子1：将十六进制数（A7）16转换成十进制数。
（A7）16=（10x161+7x160）10=（160+7）10=（167）10例子2：将十六进制数（）16转换成十进制数。
（）16=（0+13x16-1+4x16-2）10=（0++）10=（）10诀窍：方法同二进制转换成十进制。
以小数点为界，整数位从最后一位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0-9，A-F）乘以16的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3……..n，然后将第n位的数（0-9，A-F）乘以16的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。
（A7）16=（）2=（247）8=（167）10（）16=（）2=（）8=（）10五、总结1. 其他进制转十进制：将二进制数、八进制数、十六进制数的各位数字分别乘以各自基数的(N-1)次方，其相加之和便是相应的十进制数，这是按权相加法。
2. 十进制转其他进制：整数部分用除基取余法，小数部分用乘基取整法，然后将整数与小数部分拼接成一个数作为转换的最后结果。
3. 二进制转八进制：从小数点位置开始，整数部分向左，小数部分向右，每三位二进制为一组用一位八进制的数字来表示，不足三位的用0补足。
4. 八进制转二进制：与二进制转八进制相反。
5. 二进制转十六进制：从小数点位置开始，整数部分向左，小数部分向右，每四位二进制为一组用一位十六进制的数字来表示，不足四位的用0补足。
6. 十六进制转二进制：与二进制转十六进制相反。
7. 八进制转十六进制：通常将八进制转换成二进制，然后通过二进制再转换成十六进制。
8. 十六进制转八进制：通常将十六进制转换成二进制，然后通过二进制再转换成八进制ASCIIAmerican Standard Code for Information Interchange，美国信息互换标准代码是基于拉丁字母的一套电脑编码系统。
它主要用于显示现代英语和其他西欧语言。
它是现今最通用的单字节编码系统，并等同于国际标准ISO/IEC 646。
ASCII十进制十六进制八进制二进制空0000报头开始1111文本开始22210文本结束33311传送结束444100询问555101受理666110响铃777111ASCII十进制十六进制八进制二进制退格符88101000水平制表符99111001换行符10A121010垂直制表符11B131011换页12C141100回车符13D151101移出14E161110移入15F171111数据连接转义字符16102010000设备控制 1/Xon17112110001设备控制 218122210010设备控制 3/Xoff19132310011设备控制 420142410100拒绝受理21152510101同步空闲22162610110传输块结束23172710111取消24183011000媒体结束25193111001文件／替换结束261A3211010ASCII十进制十六进制八进制二进制转义271B3311011文件分隔符281C3411100组分隔符291D3511101记录分隔符301E3611110单元分隔符311F3711111空格322040100000 !332141100001 "342242100010 #352343100011 $362444100100 %372545100101 &382646100110 '392747100111 (402850101000 )412951101001 *422A52101010 +432B53101011 ,442C54101100 -452D55101101ASCII十进制十六进制八进制二进制.462E56101110 /472F57101111 0483060110000 1493161110001 2503262110010 3513363110011 4523464110100 5533565110101 6543666110110 7553767110111 8563870111000 9573971111001 :583A72111010 ;593B73111011 <603C74111100 =613D75111101 >623E76111110 ?633F77111111 @64401001000000ASCII十进制十六进制八进制二进制A65411011000001 B66421021000010 C67431031000011 D68441041000100 E69451051000101 F70461061000110 G71471071000111 H72481101001000 I73491111001001 J744A1121001010 K754B1131001011 L764C1141001100 M774D1151001101 N784E1161001110 O794F1171001111 P80501201010000 Q81511211010001 R82521221010010 S83531231010011ASCII十进制十六进制八进制二进制T84541241010100 U85551251010101 V86561261010110 W87571271010111 X88581301011000 Y89591311011001 Z905A1321011010 [915B1331011011 \925C1341011100 ]935D1351011101 ^945E1361011110 _955F1371011111 `96601401100000 a97611411100001 b98621421100010 c99631431100011 d100641441100100 e101651451100101 f102661461100110ASCII十进制十六进制八进制二进制g103671471100111 h104681501101000 i105691511101001 j1066A1521101010 k1076B1531101011 l1086C1541101100 m1096D1551101101 n1106E1561101110 o1116F1571101111 p112701********* q113711********* r114721********* s115731********* t116741********* u117751********* v118761********* w119771********* x120781********* y121791*********ASCII十进制十六进制八进制二进制z1227A1721111010 {1237B1731111011 |1247C1741111100 }1257D1751111101 ~1267E1761111110 DEL1277F1771111111128802001298120113082202131832031328420413385205134862061358720713688210137892111388A2121398B2131408C214ASCII十进制十六进制八进制二进制1418D2151428E2161438F217144902201459122114692222147932231489422414995225150962261519722715298230153992311549A2321559B2331569C2341579D2351589E2361599F237ASCII十进制十六进制八进制二进制160A0240161A1241162A2242163A3243164A4244165A5245166A6246167A7247168A8250169A9251170AA252171AB253172AC254173AD255174AE256175AF257176B0260177B1261178B2262ASCII十进制十六进制八进制二进制179B3263180B4264181B5265182B6266183B7267184B8270185B9271。