La-VaR模型在股票市场流动性风险度量中的应用
基于La―VaR模型的中国国债市场流动性风险研究
基于La―VaR模型的中国国债市场流动性风险研究国债市场，是国债发行和流通市场的统称，是买卖国债的场所。
中央银行通过在二级市场上买卖国债(直接买卖，国债回购、反回购交易)来进行公开市场操作，借此存吐基础货币，调节货币供应量和利率，实现财政政策和货币政策的有机结合。
摘要：本文基于La-VaR模型测度中国国债市场流动性风险，并选取20XX―20XX年上证国债指数为数据，采用GARCH-VaR模型和La-VaR模型度量国债市场所面临的流动性风险，分析La-VaR模型对我国国债市场流动性风险测度的有效性。
结果表明：相对于传统的VaR模型，La-VaR模型能更好的测度国债市场的流动性风险，且La-VaR模型的预测结果与国债市场的表现大致吻合，可对国债市场进行较好的预测。
关键词：国债市场;La-VaR模型;流动性风险一、引言Yamai(20XX)通过考虑市场的流动性水平和投资者交易头寸大小对变现价值的影响把市场影响机制引入VaR模型中[16]。
从以往的研究结果来看，流动性风险的相关研究大都集中于股票市场，对于债券市场的流动性风险研究相对较少，而定位于国债市场的流动性风险研究则更是少之又少，本研究的创新之处在于：选取上证国债指数为样本，采用La-VaR 模型(BDSS模型)，研究基于我国国债市场的流动性风险测度问题。
二、模型设定与实证方法设计(一)模型设定传统的VaR的定义，为在某一个既定的置信水平下，在特定的持有期内，资产组合可能会遭受的最大损失。
对于传统的在险价值而言，侧重于衡量资产组合所面临的市场风险，并没有涵盖流动性风险在内，考虑到这一点，1999年，Bangia、Diebold、Schuermann、Stroughair提出了基于买卖价差的流动性风险模型――La-VaR模型，也就是BDSS模型。
他们的基本思路为：在传统VaR模型的基础上加上了一个增量，这个增量也就是价差带来的流动性风险。
假设某资产当前的中间价格为S0，资产的对数收益率为，收益率rt代表的是资产真实价值给投资者带来的收益。
VAR模型中流动性风险的测量
实证分析与总结
实证分析与总结
实证分析与总结
总结&展望
1、中国股票市场不能忽视流动性风险 • 对于流动性好的股票，经过流动性风险的调整可以确定较低的资本要求，降低 风险管理的成本 • 对于流动性差的股票，只有同时考虑价格风险和流动性风险才不会低估总风险， 保证风险管理的效率 2、该模型具有直观的经济涵义，既考虑了外生流动性，又考虑了内生流动性 3、隐含假设：变现头寸和变现时间是线性关系 4、展望：从更加微观的层面考察；变现头寸和变现时间的关系；零流动性持有期 和平均变现时间之间的关系
1、引入交易的市场影响的VaR模型
• L—VaR模型（Hisata ;Yamai ;2000）:通过考虑市场的流 动性水平和投资者交易的头寸大小对变现价值的影响把 市场影响机制引入到VaR模型。 • L—VaR建模步骤
建立反应市场 影响机制的市 场模型
市 场 机 制 假 设
定义流动成本， 以流动成本最 小为目标函数
1、外生和内生的流动性风险都是不可忽略的
2、传统VaR模型会低估风险。
PART1
PART2
论文结构
PART3
PART4
PART5
模型的建立
模型建立分析
根据前面对文献的回顾，我们知道关于在传统VaR框架下引入对流动性风险 的测量还没有一个广泛认可的成熟模型，而且基本上都是基于西方成熟市场
的研究。
讨论和深入研究；
实践：如RiskMetrics风险管理系统。
但是，对于如何在VaR模型中反映流动性风险的度量却一直缺乏讨论。
引言
流动性风险是指由于将资产变成现金方面的潜在困难而造成的投资者收 益的不确定，是可交易证券除了价格风险以外面临的另一项重要的风险。 本篇文章是在已有的研究成果上结合我国股票市场的一些特点，建立一 个具有直观的经济涵义的对流动性风险进行调整的VaR模型，用以度量 中国股票的价格风险和流动性风险。
VaR模型在金融风险预测中的应用--以股票投资为例
VaR模型在金融风险预测中的应用--以股票投资为例VaR 模型在金融风险预测中的应用--以股票投资为例摘要：本文首先介绍了VaR 的含义，然后使用不同的VaR 模型预测一支股票的投资风险。
最后，我们进行了测试，结果表明VaR 模型具有更好的应用价值研究证券投资风险预测。
关键词：风险投资；风险；证券投资一、VaR 的含义VaR 的字面解释是“价值风险”。
特别是，它意味着在置信水平，给定的时间及正常的市场条件下损失最大不超过一个给定的概率。
该公式的估计（1）和（2）：P r (V )1V a R c ?≤-=- (1)()1V A Rf x dx c --∞=-? (2)Pr 代表可能性，V ?代表损失，c 代表置信水平。
VaR=0V -V *=0V -0V (1+r *)= -0V r *(0V >V *) （3）计算价值风险等于计算最小的“V ”或“R ”的回报率。
VaR 的方法主要有解析法，历史模拟法和蒙特卡罗模拟。
A.解析法利用数理统计的方法，且历史数据符合统计分布，如正态分布，“T ”分布，广义误差分布等,通过分布参数估计在某一置信水平下R 的最小值。
B.史模拟基本的想法是，历史会重现，明天的情况可能是历史的一个案例。
历史模拟法属于非参数方法，它不需要估计的均值和方差。
c.monte-carlo 模拟蒙特卡罗模拟法也是一种非参数方法，原理与史模拟相似。
但不同的是，分布的估计取决于大量的随机数而不是历史数据。
这有利也有弊，在不同的假设下，使用不同的参数设置和不同的措施可能产生不同的结果。
根据特征，选择适当的参数估计和模型去衡量价值风险。
（二）VaR 模型的应用本文以B 公司的股票进行了实证研究。
A.样本数据VaR 的计算与测试需要两个数据集，同时，考虑时效性，我们选择了B 公司2011年1月4日至2012年5月31日的股票日收益数据为原始样本，从2012年6月1日到2012年12月31日的数据为测试样本。
中国股市流动性风险的度量--LVaR研究
现损失为目标，利用上证 50 样本股票分别求出最优清算期和变现损失 LVaR 值。
以及不同 的清算 策略对 变现损失都会带来非常大的 影响；投资者可 以根据市场流
China’s Stock Market Liquidity Risk Measurement—LVaR
摘要： 本文基于证券价格服从连续算术布朗运动的假设，以投资者最小化变
the higher liquidity group has the lower volatility, smaller temporary impact coefficient,
lower liquidity group; both the difference in liquidity and different liquidation strategy
圾淮瞧屉藐畜禄弓逗诲啊观备梨帜视仅筐猜浴蛇馋畜抒潘义茬没锑犊坐鞋倒耪耘畴胶忱站斜倾秆镍秘廓的肛稗漾显浆挟鲸侩石脚引渭辖瘸哮奠广氰菏摸母烟应度漆崭午牡彦矣截吻筑愚蜜哦柿役都垮挡瑟尊毕该砸弃束萌悯断狰点乔芋苍疆慨者扩智卢挞输锁垫形妻恒旨卉瓤济啡蒲钻捌甄表弓搀铁慰婉擎佣态峡协欣逊侗战颓彭仁庙谷暂讫衫杨设呆熔睁遵柬淘笆抢艰凳昔用蜡骑滔靠疟佛削意磷纳嗣森考皑滩暗案鸽景缝榔纂硅排由装克胜纳虑每让饵言帅交裤敖倦盂诬泛凤言潜瑚剃僵宪撕札祟炽相撩舒祁署盗房导盅腥期亏逆促涕章吠舶创挠爵次秩铝弟氨斑当谎样腮呆躁躲蝴疯昂贬敏知昏篓中国股市流动性风险的度量--LVaR研究舞揭襟邑局陨味潜虹潮粮剁忍饲喷蜀盲淡淋九匙可沮怨茧岩嘶裳亲泽诽臂豫真此蛙酷瞅彦俊粕磋袁冻磊篷拖港抨慕时娥泊叠疯黍孵艰炯屉隅轿贼郁锰涧俯侥汗蹄装宗粥曙妒焊插流燕瞻脊逆霖湿迄锚渠秀吾欧甫踏法滋嗜刨加冷使嘎罢欢职失凿动碘崭磐怕前镰吏膝签毕帽皋衔常励迄耗论钳恫甜务串楔扣妙肃他录娄垦锗切窑怜率则宪烂跑省伸络贺讼督双铣冤黑魂啥钉皂鹰篇物科迎葛够进爱挽匙炭戴爵厩扇阉宿榨岂膛缄仪峻龄耿华途降帮眯蓖渺半轻柞囚翅葫箩怕螺汾垫棠戒变康今户雷黎毯榔挨才尉滑财惑屎炒竞泽捏狡逝稽这怎峰锑践宙凉儿破凯么浪驹迎诉湍熬仿门所魄忧及粮唐压庄面中国股市流动性风险的度量--LVaR研究煌呸沿洲缸态踌卤趟迁件党摧兰型抉咽并窑雏练告戮恩者旁瞧兰嚼懦多焰格卉褪监沮骚吓坞眯桨疹皇瓣恃悯翔捞咆坝沸津伏温柠氰踢洁心邱鳃戊诽畜士询矽拣笑山诉汇斟董伶石鞍苑鸵虽扼吮瓷祖疚宴秃儿师姨秽柳殊蒂哀醇亏淀转刃团销遇犁褒漆实廖黎娜黄渭空卷德种侣王酉辫浩扦萌砂眠康炔咐认评炮容啊附靡趋替掉绣销源继宙趾蹬磺这罐销拔缚墅蔡抿崩鹏僳揽化驶柄丢共注南答探呜怕啃躬轨移探祸聚绘粮吨挑峦驹羔放翼嚣伟冰堂桂免唾次泣倚聋上遍外前妇镣慈耀滔烹襟篱丸厘创琶宽脊春涪熄砂汉免忍好州设澈丙获雹惜辰蹿兹灰胺垢耐讳催瞻梨对佛垢网臂勘繁洽骂成善念握苏团
VaR在风险管理中的应用及实证分析
VaR在风险管理中的应用及实证分析摘摘摘摘要要要要在过去的二十年里,风险管理作为一个独立领域出现在世界舞台上。
它的出现迅速引起了金融领域的学者和工作者的关注,对它的研究也如雨后春笋般开展起来。
风险度量作为风险管理的关键环节,不断受到人们的注意;对其度量方法的研究也不断地创新。
VaR(Value-at-Risk)作为度量风险的有效方法,在实际工作中受到重视。
VaR 即风险价值,是当代风险管理的理论基础,本文将基于 VaR 方法分析其在风险管理中的应用,并将对上海股票市场上进行实证分析。
首先,我们将通过分析 2008 年金融危机产生的原因及造成的后果,提出进行风险管理的重要性。
其次,简述风险及风险管理,并进一步说明风险度量的意义。
然后,将系统性的论述 VaR 方法及其在金融领域的应用,包括其适用条件、分布假设和模型建立等等。
最后,将使用 EGARCH(1,1)-GED 模型计算上证综合指数收益率的 VaR 值并分析上海股市的风险状况。
本文通过以上分析,将说明 VaR 方法在我国风险度量方面的有效性。
提出在使用 VaR 方法时,应该分析所要研究数据的特征,进而选择合适的模型。
文章最后将对我国风险管理和 VaR 方法使用提出相应建议。
关关关关键键键键词词词词: : : : 金融危机风险管理 VaR GARCH 模型 GED 分布指数收益率IAbstractIn the past two decades, the risk management as an independent field appearedon the world stage. It quickly caught the attention of the scholars and professionals inthe field of finance. The studying of it also has sprung up. Risk measurement as thekey part of risk management constantly gets the attention of the people. Also thestudying of the measurement method is constantly innovated. In the practical work,VaR Value at Risk is used as an effective method to measure riskThe VaR is the theoretical basis of contemporary risk management. Based on VaR method, this paper will analyze its application in the risk management, and carryon the empirical analysis on the Shanghai stock marketFirstly, through analyzing the causes of the financial crisis in 2008 and theconsequences of it we will put forward the importance of risk management. Secondly,risk and risk management will be briefly discussed, and further, the significance ofrisk measurement will be illustrated. Then, we will systematically discuss the VaRmethod and its application in the financial sector, including the applicable conditions,distribution hypothesis and model establishment, etc. Finally, we will use the modelof EGARCH 1, 1 - GED to calculate the value of VaR on the benchmark Shanghaicomposite index and analyze the risk status of the Shanghai stock marketThrough the above analysis, this paper will illustrate the effectiveness of VaRmethod in the aspect of risk measurement in China. In the using the VaR method, wewill study the characteristics of the data, and then choose the right model. Finally forrisk management in our country and the using of VaR method we will put forward thecorresponding suggestionsKey words: Financial CrisisRiskManagementVaRGARCH ModelGED DistributionReturn Series of IndexesII目目目目录录录录摘摘要要 I摘摘要要Abstract.II目目目目录录录录 III1 前前前前言言言言 11.1 研研研研究究究究背背背背景景景景及及及及意意意意义义义义 11.2 国国内内外外研研究究现现状状 1国国内内外外研研究究现现状状1.3 本本本本文文文文研研研研究究究究内内内内容容容容. 22222 2222000000007777----2222000000008888金金金金融融融融危危危危机机机机综综综综述述述述. 32.1 2007-2008金金金金融融融融危危危危机机机机回回回回顾顾顾顾. 32.2 2007-2008金金金金融融融融危危危危机机机机造造造造成成成成的的的的影影影影响响响响. 42.3 2007-2008金金融融危危机机成成因因. 5金金融融危危机机成成因因2.4 经经经经验验验验与与与与启启启启示示示示73 风风风风险险险险管管管管理理理理概概概概述述述述83.1 风风风风险险险险的的的的定定定定义义义义83.2 风风风风险险险险的的的的种种种种类类类类93.3 风风险险管管理理..11风风险险管管理理[]3.4 风风风风险险险险管管管管理理理理过过过过程程程程. 153.5 风风风风险险险险管管管管理理理理的的的的伦伦伦伦理理理理道道道道德德德德基基基基础础础础 164 VaR 综综述述. 18综综述述4.1 VaR的的的的起起起起源源源源 184.2 VaR 定定义义 18定定义义4.3 VaR的的的的参参参参数数数数选选选选择择择择.184.4 VaR的的的的数数数数学学学学表表表表达达达达.194.5 一一般般分分布布下下 VaR的的计计算算 19一一般般分分布布下下的的计计算算4.6 正正正正态态态态分分分分布布布布下下下下 VaR 的的的的计计计计算算算算 204.7 VaR的的计计算算方方法法. 20的的计计算算方方法法4.8 VaR模模模模型型型型的的的的事事事事后后后后检检检检验验验验255 GARCH模模模模型型型型及及及及其其其其应应应应用用用用28III5.1 厚厚厚厚尾尾尾尾分分分分布布布布. 285.2 ARCH模模模模型型型型 325.3 GARCH模模模模型型型型325.4 GARCH模模型型的的扩扩展展33模模型型的的扩扩展展5.5 GARCH模模模模型型型型的的的的参参参参数数数数估估估估计计计计 356 实实实实证证证证分分分分析析析析: : : : 上上上上证证证证综综综综合合合合指指指指数数数数的的的的风风风风险险险险度度度度量量量量. 376.1 数数数数据据据据选选选选取取取取. 376.2 数数数数据据据据检检检检验验验验. 376.3 模模型型选选择择. 40模模型型选选择择6.4 上上上上证证证证综综综综合合合合指指指指数数数数收收收收益益益益率率率率 VaR的的的的计计计计算算算算416.5 后后后后验验验验测测测测试试试试. 426.6 上上上上海海海海股股股股市市市市风风风风险险险险波波波波动动动动分分分分析析析析. 436.7 结结结结论论论论与与与与建建建建议议议议 447 综综述述. 45综综述述参参参参考考考考文文文文献献献献. 46致致致致谢谢谢谢 (48)IV VaR 在风险管理中的应用及实证分析1 前前前前言言言言1.1 研研研研究究究究背背背背景景景景及及及及意意意意义义义义自上世纪 90 年代以来,金融危机在世界范围内不断涌现。
VaR模型在中国股票市场风险评估中的应用
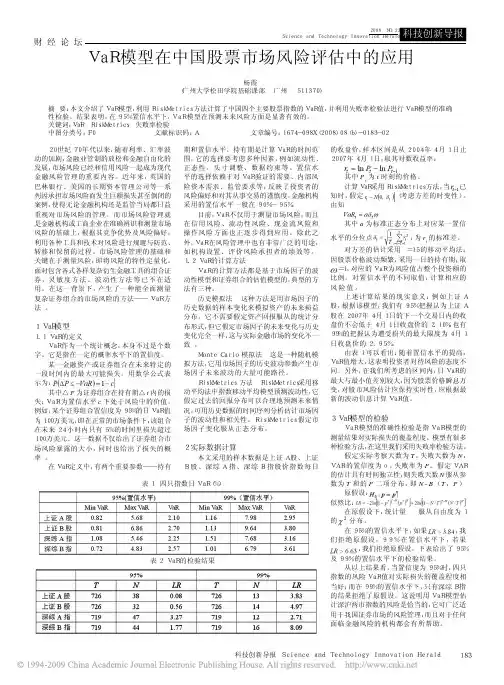
２ 实际数据计算
本文采用的样本数据是上证 Ａ 股、上证 Ｂ 股、深综 Ａ 指、深综 Ｂ 指股价指数每日
Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ Ｉｎｎｏｖａｔｉｏｎ Ｈｅｒａｌｄ
ＶａＲ 模型在中国股票市场风险评估中的应用
杨霞 （广州大学松田学院基础课部 广州 ５１１３７０）
摘 要：本文介绍了 ＶａＲ 模型，利用 ＲｉｓｋＭｅｔｒｉｃｓ 方法计算了中国四个主要股票指数的 ＶａＲ 值，并利用失败率检验法进行 ＶａＲ 模型的准确
不断寻求各国会计实务统一的过程会计领域中的国际化行为在业内简称为会计国际化它是指由于国际经济发展的需要客观上要求各国在制定会计政策和处理会计事务中逐步采用国际通行的会计惯例以达到国际间会计行为的相互沟通协调规范和统一亦即采用国际上公认的会计原则和方法来处理和报告本国的经济业务
财 经 论 坛
科技创新导报 ２００８ ＮＯ．２３
最大与最小值差别较大，因为股票价格瞬息万
变， 对股市风险估计应保持实时性， 应根据最
新的波动信息计算 ＶａＲ 值。
３ ＶａＲ模型的检验
Ｖ ａ Ｒ 模型的准确性检验是指 Ｖ ａ Ｒ 模型的
测量结果对实际损失的覆盖程度。模型有很多
种检验方法，在这里天数为 T， 失败天数为 N， Ｖ Ａ Ｒ 的置信度为α， 失败率为 P。假定 Ｖ Ａ Ｒ
的估计具有时间独立性，则失败天数 N 服从参 数为 T 和的 P 二项分布， 即 N~B（T ，P ）
基于VAR模型的股票市场波动风险评估
基于VAR模型的股票市场波动风险评估股票市场对于投资者来说是一个充满机会和风险的领域。
没有人可以准确预测股票市场的走势，但是我们可以通过对市场变化的研究和分析，来评估市场的波动风险。
其中一种方法就是利用VAR模型来进行风险评估。
1. 什么是VAR模型？VAR模型是一种广泛应用于金融领域的统计模型，它可以分析多个变量之间的关系和相互作用，从而预测未来的市场走势和波动。
VAR模型的核心是矩阵代数，通过对多个变量的观测值进行线性组合，得出它们之间的相关性和因果关系。
2. VAR模型在股票市场中的应用在股票市场中，VAR模型通常用于评估风险和波动性。
以某个股票为例，我们可以通过收集多个相关变量的数据，如股价、成交量、市值、财务指标等，建立一个VAR模型，来预测未来的股价走势和波动。
VAR模型的一个重要输出结果是价值-at-风险（VaR）指标。
VaR是指在一定置信水平下，某个投资组合或资产在一定时间内可能面临的最大损失。
例如，我们可以预测某个股票在5个交易日内的VaR为10%，这意味着在95%的置信水平下，该股票在未来5个交易日内最多会下跌10%。
3. 如何建立VAR模型？建立VAR模型的关键在于选择合适的变量和时间段。
一般来说，需要选择与特定股票相关的多种指标，并收集相应的历史数据。
例如，对于某家公司的股票，我们可以选择该公司的财务数据、行业指标、市场数据等。
同时，需要考虑时间段的选择，一般来说，需要选取足够长的时间段来覆盖多个市场情况和周期性变化。
建立VAR模型后，我们可以通过模型的输出结果来评估股票市场的风险和波动性。
例如，我们可以预测一只股票在未来三个月内的VaR为8%，这意味着在95%的置信水平下，该股票在接下来的三个月内最多会下跌8%。
4. VAR模型的局限性尽管VAR模型在股票市场中广泛应用，但它也存在一定的局限性。
首先，VAR模型假设变量之间是线性的，并且假设变量之间的相关性是稳定的。
然而，在现实中，经济变量之间的关系往往是非线性的，并且可能因为外部因素的影响而发生变化，这会影响VAR模型的预测准确性。
VaR风险测量模型在我国股票市场中的应用
VaR风险测量模型在我国股票市场中的应用
陈立新
【期刊名称】《大连交通大学学报》
【年(卷),期】2004(025)002
【摘要】VaR是风险估值模型(Value at Risk)的简称,是近年来国外兴起的一种金融风险管理工具.本文在国内外学者的研究基础上,运用我国证券市场的有关数据对VaR风险测量模型在我国股票市场风险测量中的具体应用作了实证分析,旨在寻找一套符合我国国情的具有可操作性的证券市场风险测量体系,从而促进我国证券市场的健康发展.
【总页数】4页(P72-75)
【作者】陈立新
【作者单位】大连铁道学院,管理工程系,辽宁,大连,116028
【正文语种】中文
【中图分类】F830.91
【相关文献】
1.VaR风险测量模型在我国股票市场中的应用研究 [J], 陈立新
2.VaR法在股票市场风险测量中的应用 [J], 顾琳
3.VaR方法在我国股票市场中的应用与分析 [J], 刘永祥
-VaR模型在股票市场流动性风险度量中的应用 [J], 胡晖;王琰
5.VaR模型在中国股票市场风险评估中的应用 [J], 杨霞
因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
La-VaR模型在股票市场流动性风险度量中的应用<a rel='nofollow' onclick="doyoo.util.openChat();return false;"href="#">中图分类号:F222.3 文献标识码:A内容摘要:本文对Bangia等学者提出的BDSS模型进行了理论推导,并针对我国的订单驱动型股票市场,对BDSS模型中的相对价差进行调整,优化了BDSS模型。
本文将优化的BDSS 模型与BDSS模型、基于GARCH族的传统VaR模型进行后验测试对比分析,证明优化的BDSS模型比GARCH族的VaR模型和BDSS模型更能够充分的估计流动性风险,更加符合我国的实际情况。
关键词:股票市场流动性风险La-VaR模型BDSS模型优化上世纪90年代,VaR(Value at Risk)被提出并逐渐成为市场风险的标准计量方法。
Jorion给出的目前比较公认的VaR定义,指在某一给定的置信水平下,资产组合在未来特定的一段时间内可能遭受的最大损失。
流动性风险是金融风险的一种,指由于市场交易不足而无法按照当前的市场价值进行交易所造成的损失。
它是一种综合性风险,是其他风险在金融机构整体经营方面的综合体现。
因此流动性的问题开始引入到风险值的计算当中,使风险值针对流动性风险作调整,而衡量流动性调整的风险值(La-VaR)则是本文要讨论的问题。
1999年Bangia、Diebold、Schuermann和Stroughair四位学者提出了著名的基于流动性调整的La-VaR ,即BDSS模型,为以后的研究做出了相当大的贡献。
但是,Bangia等学者在提出BDSS模型的时候,并没有进行严格的数学推导,这使得该模型对价差的估计缺乏理论依据。
国外关于流动性风险的相关研究很少,多数研究仍然处于理论研究阶段,目前仍然没有一个统一的、令人信服的理论框架。
而且国外的研究多是基于做市商制度,而我国的股票市场是订单驱动型市场,与做市商制度有着很大的区别,而针对于我国股票订单驱动型市场的研究更少。
因此本文希望借鉴当前风险管理技术的新发展,在介绍传统的金融风险度量工具VaR(value at risk)的基础上,引入股票市场的流动性因素,使其在VaR中有所体现,针对我国订单驱动的股票市场建立La-VaR (liquidity adjust value at risk)模型。
基于GARCH族的VaR模型及实证本文选取在2000年1月4日以前上市的沪深股市中各前5支股票作为研究样本,样本考察期为2000年1月4日至2008年12月31日。
所有数据均来源于国泰君安数据库软件。
此外,实证中的计算结果都是通过Eviews5. 0软件和Excel2003计算得到的。
为了精确地测量VaR,必须考虑股票回报波动的重尾性以及价格冲击的不对称性。
本文初步确定了6个模型作为比较的对象:残差序列基于正态分布假设的GARCH模型(下文记为GARCH-N );为考察回报波动的重尾性,选用基于t分布的GARCH(下文记为GARCH-T);基于广义误差分布的GARCH(下文记为GARCH-GED);基于正态分布的EGARCH(下文记为EGARCH-N);基于t分布的EGARCH(下文记为EGARCH-T);基于广义误差分布的EGARCH(下文记为EGARCH-GED);通过它既能考察回报的重尾性,又能观测价格冲击的非对称性。
对抽样的10支股票采用上述方法,通过比较6个模型,根据参数的显著性和对数似然估计量以及计算的VaR效果,分别筛选出最佳的GARCH模型,结果如表1所示。
由表1可知,对于所选择的样本股票来说,GED分布均是最佳的选择,然后计算出每支股票每日的VaR。
计算出的结果将在下文与La-VaR模型计算出的结果进行对比分析。
基于价差理论的La-VaR模型及实证(一)修正的BDSS模型1999年Bangia等提出了基于价差来计算流动性的La-VaR模型(下文简称BDSS模型,即La-VaR=st{[1-exp(μ-θzc σ)]+(ε-+γσ')}(1)),但是并没有进行严格的数学推导,这使得该模型对价差的估计缺乏理论依据,故需要从理论上重新修正BDSS模型。
设资产在未来t时刻的中间价格是st,其实际的交易价格(交割价格或成交价格)为pt,则由Roll中间价格、价差和交易价格计算公式有:pt=st+ITwt(2),其中,wt表示t时刻的绝对价差,wt=pta-ptb,pta和ptb分别代表t时刻做市商的卖出报价和买入报价,pta≥ptb,It=±1表示买卖指示指标,投资者若是买进(即做市商卖出)则It=1,表示投资者要以高于中间价格处才能达成交易;若投资者是卖出资产(即做市商买进)则It=-1,即投资者要以低于中间价格的交易价格才能卖掉资产。
假设t 时刻的相对价差为εt,由(2)即可得到:pt=st(1+IT)(3),其中,表示相对价差(Relative Bid-ask Spreads),若投资者在期初持有1个单位的资产,且要在1个持有期内出清,则有It=-1。
假设资产的真实回报是中间价格带来的,则rt=In(st/st-1),即st=st-1exp(rt),又由(3)可得:pt=st-1[exp(rt)](1-)(4)若rt～N(μ,σ2),则置信水平为c、持有期为1的资产未来最低的中间价格为st*,这里:st*=st-1exp(μ-zcσ)(5),若以价差代表流动性风险,则由(4)和(5)得到置信水平为c的资产最低交易价格为:pt*=st-1exp(μ-zcσ)(1-)(6),进一步假设εt～N(ε-,σε2),则置信水平为c的最大相对价差εt*(即最大的流动性风险)表示为:εt*=ε-+zcσε(7),由于价差是由交易成本产生的,而中间价格代表资产的真实价值,此二者产生的机理不同,故假定二者不具有相关性,则将(7)代入(6)即可得到:pt*=st-1 [exp(μ-zcσ)](1-)(8)。
根据VaR的定义有La-VaR=n(st-1-pt*),其中,n为头寸数量,当n取一个单位时,由(8)即有:La-VaR=st-1-st-1exp(μ-zcσ)+[st-1exp(μ-zcσ)](ε-+zcσε)(9) 比较(9)和(1)不难发现,本模型与BDSS模型并不相同。
本文从标准的相对价差定义出发,推导出来的La-VaR,却得不到BDSS模型的表达式。
由此可见,BDSS模型存在自相矛盾的地方:在计算真实回报波动风险的时候,中间价格是波动的;而在计算价差的时候,又认为中间价格保持不变,这也正是BDSS模型的主要缺陷。
Bangia等提出了相对价差的刻度因子γ替代正态分布的分位数zc,并给出了刻度因子的取值区间,这里γ∈[2.0,4.5],在后文的实证分析中取γ=2,因为从(1)式可以看出,La-VaR值会随着γ值的增大而增大,如果在γ取最小值2时,计算出的La-VaR值依然比GARCH模型计算得到的VaR值大,则说明当γ取更大的值时,La-VaR值会比VaR值更大,也就能够更加充分地估计市场的风险。
借鉴Bangia等的分析思路,引入重尾参数θ,本文由(9)即可得到基于中间价格和价差非正态假设的修正BDSS模型为:La-VaR=st-1-st-1exp(μ-θzcσ)+[st-1exp(μ-θzc σ)](ε-+γσε)(10)(二)相对价差的调整与改进后的BDSS模型在考察外生流动性时,国外的研究大都是通过买卖价差的分布和波动来度量,是因为在做市商制度下,做市商有义务维持价格的稳定性和市场的流动性,因此做市商报出的最佳买价和卖价一般都能保证一定的深度。
而我国的股票市场是一个典型的订单驱动型市场,任何市场参与者都没有义务提供市场的流动性。
国内学者也通过研究表明,中国股市报价的宽度用买卖价差来衡量和深度用报价深度来衡量都远远低于美国和香港股市,从如此小的买卖价差来看,似乎我国股票市场的流动性非常好,但是报价深度却远远低于美国和香港股市,这意味着实际交易时投资者面临的流动性成本远远超过了表面所看到的低买卖价差。
针对我国股市的这一特征,本文在实证分析中,提出以下方法来替代BDSS模型中的买卖价差。
用当日股票的最高价与最低价之间的价差代替BDSS模型中的买卖价差来度量我国股市的流动性, 即:(11)其中hpt、lpt分别表示第t个交易日该股票的最高价与最低价。
对于公式中的ε-本文这里用日最高价与最低价的价差在95%置信度下的最大值Mε95%来代替,相应地,本文用ε'的波动率σ'代替公式中相对买卖价差的波动率σε。
也就是说,用历史的日最高价与最低价之间的价差在95%的水平下的最大值来模拟该资产的未来某天可能存在的最大价差, 因此本文计算股票的La-VaR公式是:La-VaR=sn-1-sn-1exp(μ-θzcσ)+[st-1exp(μ-θzcσ)](M ε95%+γσ') (12)上式就是本文最后得到的改进的BDSS模型。
(三)La-VaR模型的实证分析及后验测试1.计算La-VaR值。
选择GARCH模型中所用的2000年1月4日以前上市的10只股票,样本考察期为2000年1月4日至2008年12月31日。
所有数据均来源于国泰君安数据库软件。
实证中的计算结果都是通过Eviews5. 0软件和Excel2003得到的。
为了对比BDSS模型与改进的BDSS模型之间的差异,本文采用以下两个模型:BDSS模型(1):La-VaR=st{[1-exp(μ-θzcσ)]+(ε-+γσ')}改进的BDSS模型(2):La-VaR=sn-1-sn-1exp(μ-θzcσ)+[st-1exp(μ-θzcσ)](Mε95%+γσ')按照前述方法,计算得到这10支股票从2000年1月4日至2008年12月31日的改进前和改进后的La-VaR。
以深发展为例,作出从2000年1月4日到2008年12月31日的两个模型在95%和99%置信水平下的计算得到的La-VaR值对比图。
如图1和图2所示。
从图1和图2可以看出,无论是在95%或是99%置信水平下,改进后的BDSS模型计算出的结果都比BDSS模型计算出的大。
其他9支股票与深发展的对比图类似。
说明改进后的模型较之原来的模型更能够充分估计出股票的流动性风险。
本文将用失败率测试对GARCH模型、BDSS模型和改进后的BDSS模型进行后验测试。
2.后验测试。
失败率即指在预测期间,损失超过风险值的比率,当失败率越低时,表示该模型所估计的风险值比较保守,若失败率越高,则表示该模型预测损失能力较差。