八年级数学每日一题
初二数学上基础练习计算题
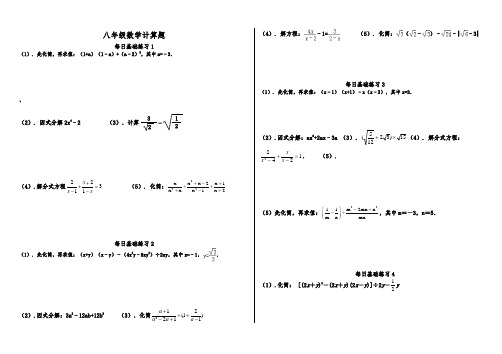
八年级数学计算题每日基础练习1(1). 先化简,再求值:(1+a )(1﹣a )+(a ﹣2)2,其中a=﹣3.、(2). 因式分解2x 4﹣2 (3).计算3 2-12(4).解分式方程22311x x x(5). 化简:222x x x 2x 1x x x 1x 2+-+÷++-+每日基础练习2(1). 先化简,再求值:(x+y )(x ﹣y )﹣(4x 3y ﹣8xy 3)÷2xy,其中x=﹣1,.(2).因式分解:3a 2﹣12ab+12b 2 (3).化简212(1)211a a a a +÷+-+- (4). 解方程:﹣1= (5). 化简:(﹣)﹣﹣|﹣3|每日基础练习3(1). 先化简,再求值:(x ﹣1)(x+1)﹣x (x ﹣3),其中x=3.(2).因式分解:ax 2+2ax ﹣3a (3).15)32125(⨯+(4). 解分式方程:12422=-+-x xx . (5).(5)先化简,再求值:2211m 2mn nm n mn -+⎛⎫-÷ ⎪⎝⎭,其中m =-3,n =5.每日基础练习4(1).化简: [(2x +y )2-(2x +y )(2x -y )]÷2y -21y(2).因式分解:a ab ab 442+- (3).(827-53)· 6(4).解方程:. (5). 化简求值: 221m 2m 11m 2m 4++⎛⎫-÷ ⎪+-⎝⎭,其中m =1。
每日基础练习5(1). 先化简,再求值:[(5x +2y )(3x +2y )+(x +2y )(x -2y )]÷4x ,其中x=2,y=-3.(2).因式分解:()()a a a 322+-+ (3).12)323242731(⋅--(4).解方程:. (5).化简求值:22312x x x 1x x 2x 1-⎛⎫-÷⎪+++⎝⎭,其中x=1.每日基础练习6(1). 化简求值:(a 2+3)(a -2)-a (a 2-2a -2),其中a=122- (2)因式分解:x 2-4(x -1) (3).化简:,(5).解方程:23112x x x x -=-+-. (4)每日基础练习7(1). 化简:(x ―1)2+(x +3)(x ―3)+(x ―3)(x ―1); (2).因式分解:22)3(4)2(--+m m(3).先化简,再求值:,其中.(4). 方程(5).12(75+313-48)每日基础练习81121231548333(1). 22)1)2)(2(+-+-x x x x -( (2).因式分解:14-x ;(3).先化简,再求值.,其中m=2.(4). )解方程:. (5). )632)(632()232)(3(2-+-+每日基础练习9 班级 姓名(1). 化简:[(x +y )2-y (2x +y )-8x ]÷2x . (2). 因式分解:a a a 81721623+-(3).先化简,再求值:(1﹣)÷,其中a=﹣2.(4). 13321++=+x x x x (5). 2)153()347)(347(---+每日基础练习10(1). 化简求值:()()()()[]x xy y y x y x y x 3442323÷--+-+-,其中2=x ,31=y .(2). 因式分解: 432244y xy y x +- (3).)62)(2332(-+(4).解方程:311(1)(2)x x x x -=--+ (5). 先化简,再求值:x 23x 1x 1x 1-⎛⎫÷+- ⎪--⎝⎭,其中x 3-2.每日基础练习11(1).化简求值:.2)3)(3()2)(3(2-=-+-+-aaaxx其中,x=1(2).因式分解: 9a2(x-y)+4b2(y-x)(3).计算:1)21(248-+-(4).解方程:32211xx x+=-+(5). 化简求值:x35x2x2x2-⎛⎫÷+-⎪--⎝⎭,其中x3-每日基础练习12(1). 解不等式:(x+3)(x-7)+8>(x+5)(x-1). (2).因式分解:aaa1812223-+-(3).)先简化,再求值:x25x32x6x3--⎛⎫÷--⎪--⎝⎭,其中x2=-(4).解方程:2227611x x x x x-=+--(5).⎛÷⎝每日基础练习13(1). 先化简,再求值:2(2)(21)(21)4(1)x x x x x+++--+,其中x=(2).因式分解: 16-24(a-b)+9(a-b)(3).(4).解方程:22510x x x x -=+-(5). 先化简,再求值:÷(x+1﹣),其中x=﹣2每日基础练习14(1). 22))(()32(y y x y x x --+-- (2). 因式分解:22)23()32(y x y x --+(3).先简化,再求值:21x 2x 11x x -⎛⎫-÷ ⎪⎝⎭+,其中x 2=.(4).解方程: 114112=---+x x x (5). 26)1(30--+-π每日基础练习15(1). 解方程(3x -2)(2x -3)=(6x +5)(x -1)+15. (2). 因式分解:2442x y x y -(3).先化简:,再求值,其中a=.(4). 解方程:14143=-+--x x x (5). 11181222-⎛⎫++ ⎪⎝⎭每日基础练习16(1). 化简求值:x (x -1)+2x (x +1)-(3x -1)(2x -5), (2).171372222--+=--+x x x x x x 其中x =2.(3).先化简,再求值:232224x x x x x x ⎛⎫-÷ ⎪-+-⎝⎭,其中x 取一个你喜欢的值求值(4).分解因式:am 2﹣4an 2 (5). )52)(103(-+ (6).因式分解:4x 3﹣36x(7). 22- 3 -12 +( 3 +1) (8). 22 -(3 -2)0+20(9).)32)(532(+-(10). )32)(532(+- (11).(231⎛+ ⎝二次根式50道典型计算题1. 2484554+-+2. 2332326--3. 21418122-+- 4. 3)154276485(÷+-5.已知: 的值。
八年级数学每日一题

每日一题初中数学【每日一题】(第 1 期)1、如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A2,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=答案:n=9初中数学【每日一题】(第 2 期)2、已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B 两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),当t为时,△PBQ是直角三角形.答案:t=1秒或t=2秒初中数学【每日一题】(第 3 期)水滴石穿!3、如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是__°.答案:50°【解析】试题分析:设∠A=x°,根据MN为中垂线可得:∠ABD=∠A=x°,则∠ABC=(x+15)°,根据AB=AC可得:∠C=∠ABC=(x+15)°,则根据△ABC的内角和定理可得:x+x+15+x+15=180°,解得:x=50°.初中数学【每日一题】(第 4 期)锲而不舍,金石可镂!如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长是_________.答案:11【解析】试题分析:根据题意可得:△BDO和△COE是等腰三角形,OD=BD,OE=EC,则△ADE的周长=AD+DE+AE=AD+DO+OE+AE=AD+BD+AE+CE=AB+AC=6+5=11.考点:(1)、角平分线的性质;(2)、等腰三角形的性质.初中数学【每日一题】(第 5 期)小水长流,则能穿石!如图所示,三角形ABC的面积为1.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是.【解析】试题分析:过点P作PE⊥BP,垂足为P,交BC于点E,由角平分线的定义可知∠ABP=∠EBP,结合BP=BP以及∠APB=∠EPB=90°即可证出△ABP≌△EBP (ASA),进而可得出AP=EP,根据三角形的面积即可得出,再根据=.故答案为:.考点:等腰三角形的判定与性质;角平分线的定义;三角形的面积;全等三角形的判定与性质.初中数学【每日一题】(第 6 期)立志不坚,终不济事!如图,△ABC是等腰直角三角形,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.(1)求证:BF=2AD;(2)若CE=,求AC的长试题解析:(1)证明:∵△ABC是等腰直角三角形,∴AC=BC,∠FCB=∠ECA=90°,∵AC⊥BE,BD⊥AE,∴∠CBF+∠CFB=90°,∠DAF+∠AFD=90°,∵∠CFB=∠AFD,∴∠CBF=∠CAE,在△BCF与△ACE中,,∴△BCF≌△ACE,∴AE=BF,∵BE=BA,BD⊥AE,∴AD=ED,即AE=2AD,∴BF=2AD;(2)由(1)知△BCF≌△ACE,∴CF=CE=,∴在Rt△CEF中,EF==2,∵BD⊥AE,AD=ED,∴AF=FE=2,∴AC=AF+CF=2+.考点:全等三角形的判定与性质;勾股定理初中数学【每日一题】(第 7 期)已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,求证:BP=2PQ.试题解析:∵△ABC是等边三角形,∴AB=AC,∠BAE=∠C=60°,在△ABE和△CAD中,AB=AC,∠BAE=∠C=60°,AE=CD,∴△ABE≌△CAD(SAS),∴∠1=∠2,∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,∵BQ⊥AD,∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,∴BP=2PQ.考点:全等三角形的判定与性质;等边三角形的性质;含30度角的直角三角形.初中数学【每日一题】(第 8 期)如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC. 若AC=4,BC=3,AB=5,则OC的长度的最大值是.【解析】试题分析:取AB中点E,连接OE、CE,在直角三角形AOB中,OE=AB,利用勾股定理的逆定理可得△ACB是直角三角形,所以CE=AB,利用OE+CE≥OC,所以OC的最大值为OE+CE,即OC的最大值=AB=5.考点:勾股定理的逆定理初中数学【每日一题】(第 9 期)精诚所至,金石为开!著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B 能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为cm.试题解析:连接OP,∵△AOB是直角三角形,P为斜边AB的中点,∴OP=AB,∵AB=20cm,∴OP=10cm,考点:直角三角形斜边上的中线.初中数学【每日一题】(第 10 期)最可怕的是比你优秀的人还比你努力!如图,在△ABC中,AB=AC,点E为BC边上一动点(不与点B、C重合),过点E作射线EF交AC于点F,使∠AEF=∠B.(1)判断∠BAE与∠CEF的大小关系,并说明理由;(2)请你探索:当△AEF为直角三角形时,求∠AEF与∠BAE的数量关系.【解析】(1)∠BAE=∠FEC;理由如下:∵∠B+∠BAE=∠AEC,∠AEF=∠B,∴∠BAE=∠FEC;(2)如图1,当∠AFE=90°时,∵∠B+∠BAE=∠AEF+∠CEF,∠B=∠AEF=∠C,∴∠BAE=∠CEF,∵∠C+∠CEF=90°,∴∠BAE+∠AEF=90°,即∠AEF与∠BAE的数量关系是互余;如图2,当∠EAF=90°时,∵∠B+∠BAE=∠AEF+∠1,∠B=∠AEF=∠C,∴∠BAE=∠1,∵∠C+∠1+∠AEF=90°,∴2∠AEF+∠1=90°,即2∠AEF与∠BAE的数量关系是互余.【点评】此题考查了等腰三角形的性质以及外角的性质,此题难度适中,注意掌握分类讨论思想的应用.初中数学【每日一题】(第 11 期)耐心是一切聪明才智的基础!如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则::等于.试题分析:由角平分线的性质可得,点O到三角形三边的距离相等,即三个三角形的AB、BC、CA的高相等,利用面积公式即可求解.过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,∵O是三角形三条角平分线的交点,∴OD=OE=OF,∵AB=20,BC=30,AC=40,∴::=2:3:4.故答案为:2:3:4.考点:角平分线的性质;三角形的面积.初中数学【每日一题】(第 12 期)如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM= .解:过P作PC⊥MN∵PM=PN∴C为MN中点在Rt△OPC中,∠AOB=60°,∴∠OPC=30°,∴2OC=OP=8,∴OC=4则OM=OC﹣MC=4﹣1=3,初中数学【每日一题】(第 13 期)能坚持别人不能坚持的,才能拥有别人不能拥有的如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为()A.①②④B.①②③C.②③D.①③∵∠B和∠ACD都是∠CAB的余角,∴∠ACD=∠B,故①正确;∵CD⊥AB,EF⊥AB,∴EF∥CD,∴∠AEF=∠CHE,∴∠CEH=∠CHE,∴CH=CE=EF,故②正确;∵角平分线AE交CD于H,∴∠CAE=∠BAE,∴△ACE≌△AFE(AAS),∴AC=AF,故③正确;CH=CE=EF>HD,故④错误.故:正确答案选 B初中数学【每日一题】(第 14 期)如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,则DE与DF的数量关系是_______如图,连接CD.∵BC=AC,∠BCA=90°∴△ABC是等腰直角三角形∵D为AB中点∴BD=CD=AD,CD平分∠BCA,CD⊥AB∵∠A+∠ACD=∠ACD+∠FCD=90°∴∠A=∠FCD∵∠CDF+∠CDE=90°∠CDE+∠ADE=90°∴∠ADE=∠CDF,在△ADE和△CFD中∵∠A=∠FCD,AD=CD,∠ADE=∠CDF∴△ADE≌△CFD(ASA)∴DE=DF.初中数学【每日一题】(第 15 期)耐心和恒心总会得到报酬的。
八上数学每日一练:扇形统计图练习题及答案_2020年综合题版

八上数学每日一练:扇形统计图练习题及答案_2020年综合题版答案解析答案解析2020年八上数学:统计与概率_数据收集与处理_扇形统计图练习题1.(2020牡丹.八上期末) 某校300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A :4棵;B :5棵:C :6棵:D :7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2)回答下列问题:(1) 在这次调查中D 类型有多少名学生?(2) 写出被调查学生每人植树量的众数中位数(3) 求被调查学生每人植树量的平均数,并估计这300名学生共植树多少棵?考点: 用样本估计总体;扇形统计图;条形统计图;中位数;众数;2.(2020天桥.八上期末) 为宣传6月6日世界海洋日,某校八年级举行了主题为“珍海洋资源,保护海洋生物多科性“的知识党春活动,为了解此次宛赛成镇(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图):请根据图表信息解答以下问题:(1) 本次调查一共随机抽取了个参赛学生的成绩;(2) a =,b =.(3) 所抽取的参赛学生的成绩的中位数落在的“组别”是(4) 请你估计,该校八年级全年级有500名学生,竞赛成绩达到80分以上(含80分)的学生约有多少人?考点: 用样本估计总体;扇形统计图;频数与频率;3.(2020历下.八上期末) 某校对全校3000名学生本学期参加艺术学习活动的情况进行评价,其中甲班学生本学期参观美术馆的次数以及艺术评价等级和艺术赋分的统计情况,如下表所示:(1) 甲班学生总数为人,表格中 的值为;(2) 甲班学生艺术赋分的平均分是分;答案解析答案解析答案解析(3) 根据统计结果,估计全校3000名学生艺术评价等级为级的人数是多少?考点: 用样本估计总体;统计表;扇形统计图;4.(2020洛宁.八上期末) 某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m 名学生,并将其结果绘制成如下不完整的条形图和扇形图.请结合以上信息解答下列问题:(1)m=;(2)请补全上面的条形统计图;(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为;(4)已知该校共有1200名学生,请你估计该校约有名学生最喜爱足球活动.考点: 用样本估计总体;扇形统计图;条形统计图;5.(2019农安.八上期末) 某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,按A,B ,C ,D 四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.(1) 求抽取了多少份作品;(2) 求此次抽取的作品中等级为B 的作品的数量,并补全条形统计图;(3) 若该校共征集到800份作品,请估计等级为A 的作品约有多少份.考点: 用样本估计总体;扇形统计图;条形统计图;2020年八上数学:统计与概率_数据收集与处理_扇形统计图练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
(文末带答案)八年级数学勾股定理经典大题例题

(每日一练)(文末带答案)八年级数学勾股定理经典大题例题单选题1、若△ABC三边长a,b,c满足√a+b−25+|b−a−1|+(c−5)2=0,则△ABC是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形2、如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,,则BC的长是()折痕现交于点F,已知EF=32A.3√2B.3√2C.3D.3√323、如图,在△ABC中,点D是线段AB上的一点,过点D作DE∥AC交BC于点E,将△BDE沿DE翻折,得到△B'DE,若点C恰好在线段B'D上,若∠BCD=90°,DC:CB'=3:2,AB=16√2,则CE的长度为()A.2√2B.4C.3√2D.64、勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是()A .B .C .D .5、如图,在Rt △ABC 中,∠ACB =90°,BC =3,AB =5,角平分线CD 交AB 于点D ,则点D 到AC 的距离是( )A .127B .2C .157D .3 6、如图,正方形ABCD 的边长为9,将正方形折叠,使顶点D 落在BC 边上的点E 处,折痕为GH,若BE:EC=2:1,则线段CH 的长是( )A .3B .4C .5D .67、有一个直角三角形的两边长分别为3和4,则第三边的长为( )A .5B .√7C .√5D .5或√78、已知Rt △ABC 中,∠C =90°,若a +b =14cm ,c =10cm ,则Rt △ABC 的面积是( )A .24cm 2B .36cm 2C .48cm 2D .60cm 2填空题9、在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.则旗杆的高度______.10、如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为____.11、如图,在四边形ABCD中,∠ABC=∠ADC=90°,分别以四边向外做正方形甲、乙、丙、丁,若甲的面积为30,乙的面积为16,丙的面积为17,则丁的面积为______.12、正方形ABCD的边长是4,点P是AD边的中点,点E是正方形边上的一点,若△PBE是等腰三角形,则腰长为________.13、已知一直角三角形的两条直角边分别为6cm、8cm,则此直角三角形斜边上的高为____.解答题14、如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.(1)求证:∠ADC=90°;(2)求图中阴影部分土地的面积.15、勾股定理是人类最伟大的十个科学发现之一,在《周髀算经》中就有“若勾三,股四,则弦五”的记载,汉代数学家赵爽为证明勾股定理创制的“赵爽弦图”也流传至今.迄今为止己有400多种证明勾股定理的方法.下面是数学课上创新小组验证过程的一部分.请认真阅读并根据他们的思路将后续的过程补充完整:将两张全等的直角三角形纸片按图所示摆放,其中b>a,点E在线段AC上,点B、D在边AC两侧,试证明:a2+b2=c2.(文末带答案)八年级数学勾股定理_007参考答案1、答案:C解析:根据非负数的性质求得a、b、c的值,再根据勾股定理的逆定理即可解答.解:∵√a+b−25+|b-a-1|+(c-5)2=0,∴a+b-25=0,b-a-1=0,c-5=0,∴a=12,b=13,c=5,∵a2+c2=b2=169,∴△ABC是直角三角形.故选C.小提示:本题考查了非负数的性质及勾股定理的逆定理,根据非负数的性质求得a、b、c的值是解决问题的关键.2、答案:B解析:折叠的性质主要有:1.重叠部分全等;2.折痕是对称轴,对称点的连线被对称轴垂直平分. 由折叠的性质可知AB,所以AB=AC,的长可求,再利∠B=∠EAF=45°,所以可求出∠AFB=90°,再直角三角形的性质可知EF=12用勾股定理即可求出BC的长.解:∵沿过点E的直线折叠,使点B与点A重合,∴∠B=∠EAF=45°,∴∠AFB=90°,∵点E为AB中点,且∠AFB=90°,∴EF=12AB,∵EF=32,∴AB=2EF=32×2=3,在ΔRtABC中, AB=AC,AB=3,∴BC=√AB2+AC2=√32+32=3√2,故选B.小提示:本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用,求出∠AFB=90°是解题的关键.3、答案:C解析:设DC=3x,CB′=2x,则DB'=5x,由折叠的性质得出DB=DB',∠BDE=∠B'DE,BE=B'E,由勾股定理求出BC =8√2,设CE=a,则BE=8√2﹣a=B'E,由勾股定理得出方程求出a的值,则可得出答案.解:设DC=3x,CB'=2x,则DB'=5x,∵将△BDE沿DE翻折,得到△B'DE,∴DB'=DB,∠BDE=∠B'DE,BE=B'E,∵DE∥AC,∴∠A=∠BDE,∠ACD=∠CDE,∴∠A=∠ACD,∴CD=AD=3x,∴AB=AD+DB=8x=16√2,∴x=2√2,∴CD=6√2,BD=10√2,B'C=4√2,∴BC=√BD2−CD2=8√2,设CE=a,则BE=8√2﹣a=B'E,∵CE2+B'C2=B'E2,∴a2+32=(8√2﹣a)2,解得a=3√2,∴CE=3√2,故选:C.小提示:本题考查了折叠的性质,勾股定理,平行线的性质,等腰三角形的性质与判定,熟练掌握折叠的性质是解题的关键.4、答案:D解析:利用两个以a和b为直角边三角形面积与一个直角边为c的等腰直角三角形面积和等于上底为a,下第为b,高为(a+b)的梯形面积推导勾股定理可判断A,利用以a与b为两直角边四个全等三角形面积与边长为c的小正方形面积和等于以a+b的和为边正方形面积推导勾股定理可判断B,利用以a与(a+b)为两直角边四个全等三角形面积与边长为b的小正方形面积和等于以c为边正方形面积推导勾股定理可判断C,利用四个小图形面积和等于大正方形面积推导完全平方公式可判断D.解: A、两个以a和b为直角边三角形面积与一个直角边为c的等腰直角三角形面积和等于上底为a,下第为b,高为(a+b)的梯形面积,故12ab+12ab+12c2=12(a+b)2,整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;B、以a与b为两直角边四个全等三角形面积与边长为c的小正方形面积和等于以a+b的和为边正方形面积,故4×12ab+c2=(a+b)2,整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;C、以a与(a+b)为两直角边四个全等三角形面积与边长为b的小正方形面积和等于以c为边正方形面积,4×12a(a+b)+b2=c2,整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;D、四个小图形面积和等于大正方形面积,2ab+a2+b2=(a+b)2,根据图形证明完全平方公式,不能证明勾股定理,故本选项符合题意;故选:D.小提示:本题考查利用面积推导勾股定理与完全平方公式,掌握利用面积推导勾股定理与完全平方公公式是关键.5、答案:A解析:作DE⊥AC于E,作DF⊥BC于F,根据勾股定理可求AC,根据角平分线的性质可得DE=DF,再根据三角形面积公式即可求解.解:作DE⊥AC于E,作DF⊥BC于F,在Rt△ACB中,AC=√AB2−BC2=√52−32=4,∵CD是角平分线,∴DE=DF,∴12AC⋅DE+12BC⋅DF=12AC⋅BC,即12×4×DE+12×3×DE=12×4×3,解得DE=127.故点D到AC的距离是127.故选:A.小提示:本题考查了勾股定理,角平分线的性质,关键是熟悉勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方;角平分线的性质:角的平分线上的点到角的两边的距离相等.6、答案:B解析:试题分析:设CH=x,因为BE:EC=2:1,BC=9,所以,EC=3,由折叠知,EH=DH=9-x,在Rt△ECH中,由勾股定理,得:(9−x)2=32+x2,解得:x=4,即CH=4考点:(1)图形的折叠;(2)勾股定理7、答案:D解析:分4是直角边、4是斜边两种情况考虑,再根据勾股定理计算即可.解:当4是直角边时,斜边=√32+42=5;当4是斜边时,另一条直角边=√42−32=√7;故选:D.小提示:本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.8、答案:A解析:根据∠C=90°确定直角边为a、b,对式子a+b=14两边平方,再根据勾股定理得到ab的值,即可求解.解:根据∠C=90°确定直角边为a、b,∴a2+b2=c2=100∵a+b=14∴(a+b)2=142,即a2+2ab+b2=196∴2ab=96∴S△ABC=1ab=24cm22故选A小提示:此题考查了勾股定理的应用,涉及了完全平方公式,解题的关键是根据所给式子确定ab的值.9、答案:12米解析:设旗杆的高度是x米,绳子长为(x+1)米,旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求出x的值,从而求出旗杆的高度.解:设旗杆的高度为x米,根据题意可得:(x+1)2=x2+52,解得:x=12,答:旗杆的高度为12米.所以答案是:12米.小提示:本题考查勾股定理的应用,关键看到旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求解.10、答案:45°解析:利用勾股定理可求出AB2,AC2,BC2的长,进而可得出AB2=AC2+BC2,AC=BC,利用勾股定理的逆定理可得出△ABC 为等腰直角三角形,再利用等腰直角三角形的性质,可得出∠ABC=45°.解:连接AC,根据题意,可知:BC2=12+22=5,AC2=12+22=5,AB2=12+32=10.∴AB2=AC2+BC2,AC=BC,∴△ABC为等腰直角三角形,∴∠ABC=45°.所以答案是:45°.小提示:本题考查了勾股定理的逆定理、勾股定理以及等腰直角三角形的性质,利用勾股定理的逆定理及AC=BC,找出△ABC为等腰直角三角形是解题的关键.11、答案:29解析:如图(见解析),先根据正方形的面积公式可得AB2=30,BC2=16,CD2=17,再利用勾股定理可得AD2的值,由此即可得出答案.如图,连接AC,由题意得:AB2=30,BC2=16,CD2=17,∵在△ABC中,∠ABC=90°,∴AC2=AB2+BC2=46,∵在△ACD中,∠ADC=90°,∴AD2=AC2−CD2=29,则正方形丁的面积为AD2=29,所以答案是:29.小提示:本题考查了勾股定理的应用,熟练掌握勾股定理是解题关键.12、答案:2√5或52或√652 解析:分情况讨论:(1)当PB 为腰时,若P 为顶点,则E 点与C 点重合,如图1所示:∵四边形ABCD 是正方形,∴AB=BC=CD=AD=4,∠A=∠C=∠D=90°,∵P 是AD 的中点,∴AP=DP=2,根据勾股定理得:BP=√AB 2+AP 2=√42+22=2√5;若B 为顶点,则根据PB=BE′得,E′为CD 中点,此时腰长PB=2√5;(2)当PB 为底边时,E 在BP 的垂直平分线上,与正方形的边交于两点,即为点E ;①当E 在AB 上时,如图2所示:则BM=12BP=√5,∵∠BME=∠A=90°,∠MEB=∠ABP ,∴△BME ∽△BAP ,∴BE BP =BM BA ,即2√5=√54,∴BE=52;②当E 在CD 上时,如图3所示:设CE=x ,则DE=4−x ,根据勾股定理得:BE 2=BC 2+CE 2,PE 2=DP 2+DE 2,∴42+x 2=22+(4−x)2,解得:x=12,∴CE=12,∴BE=√BC 2+CE 2 =√42+(12)2=√652;综上所述:腰长为:2√5,或52,或√652; 故答案为2√5,或52,或√652. 点睛:本题考查了正方形的性质、等腰三角形的判定、勾股定理;熟练掌握正方形的性质并能进行推理计算是解决问题的关键.13、答案:4.8cm.解析:根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.∵直角三角形的两条直角边分别为6cm ,8cm ,∴斜边为√62+82 =10(cm),设斜边上的高为h ,则直角三角形的面积为12×6×8=12×10h , 解得:h=4.8cm ,这个直角三角形斜边上的高为4.8cm.故答案为4.8cm.小提示:此题考查勾股定理,解题关键在于列出方程.14、答案:(1)见解析;(2)24解析:(1)根据勾股定理求出AC 的长,再根据勾股定理的逆定理证明∠ADC=90°;(2)利用△ABC 的面积减去△ACD 的面积即可.解:(1)∵∠ACB=90°,BC=12,AB=13,∴AC=√AB2−BC2=5,∵32+42=52,即AD2+CD2=AC2,∴∠ADC=90°;(2)S阴影=S△ABC-S△ACD=1 2×AC×BC−12×CD×AD=1 2×5×12−12×3×4=24.小提示:本题考查的是勾股定理在实际生活中的应用以及勾股定理的逆定理,有利于培养学生生活联系实际的能力.15、答案:见解析.解析:首先连结BD,作DF⊥BC延长线于F,则AE=b−a,根据RtΔABC≅RtΔDAE,易证∠DAB=90°,再根据S四边形ADFB =SΔADE+SΔABC+S四边形DFCE,S四边形ADFB=SΔADB+SΔDFB,两者相等,整理即可得证.证明:连结BD,作DF⊥BC延长线于F,则AE=b−aS四边形ADFB =SΔADE+SΔABC+S四边形DFCE=12ab+12ab+(b−a)⋅b =ab+b2−ab=b2∵RtΔABC≅RtΔDAE ∴AB=AD=c∴∠ADE=∠BAC∵∠ADE+∠DAE=90°∴∠BAC+∠DAE=90°即∠DAB=90°,∴AD⊥AB∴S四边形ADFB=SΔADB+SΔDFB=12c2+12(a+b)⋅(b−a) =12c2+12b2−12a2即有:b2=12c2+12b2−12a2∴a2+b2=c2小提示:本题考查了勾股定理的证明,用两种方法表示出四边形ADFB的面积是解本题的关键.。
八年级上册每日一练习题

八年级上册每日一练习题一、选择题(每题3分,共30分)1. 下列关于二次根式的说法正确的是()A. √9 = 3B. √9 = 3C. √9 = 3D. √9 = 32. 下列等式中,正确的是()A. (a + b)² = a² + b²B. (a b)² = a² b²C. (a + b)² = a² + 2ab + b²D. (a b)² = a² 2ab + b²3. 下列关于平行四边形的性质,错误的是()A. 对边平行且相等B. 对角相等C. 对角线互相平分D. 邻角互补4. 已知a = 3,b = 4,则a² + b²的值为()A. 7B. 12C. 25D. 95. 下列关于圆的性质,正确的是()A. 圆的半径等于直径的一半B. 圆的直径等于半径的两倍C. 圆的周长等于半径的两倍D. 圆的面积等于半径的平方6. 下列关于函数的说法,错误的是()A. 函数是一种特殊的映射关系B. 函数的定义域是自变量的取值范围C. 函数的值域是因变量的取值范围D. 函数的图像是一条直线7. 下列关于概率的说法,正确的是()A. 概率是描述事件发生可能性的数值B. 概率的取值范围是0到1C. 概率等于事件发生的次数除以总次数D. 概率等于事件不发生的次数除以总次数8. 下列关于二次函数的说法,错误的是()A. 二次函数的图像是抛物线B. 二次函数的对称轴是x轴C. 二次函数的顶点坐标为(h,k)D. 二次函数的系数a决定了抛物线的开口方向9. 下列关于几何图形的变换,错误的是()A. 平移变换不改变图形的形状和大小B. 旋转变换不改变图形的形状和大小C. 对称变换不改变图形的形状和大小D. 缩放变换改变图形的形状和大小10. 下列关于概率的公式,正确的是()A. P(A∪B) = P(A) + P(B)B. P(A∪B) = P(A) P(B)C. P(A∪B) = P(A) + P(B) P(A∩B)D. P(A∪B) = P(A) P(B) + P(A∩B)二、填空题(每题3分,共30分)11. 若a² = 9,则a的值为______。
人教版数学八年级上册每日一练

如图所示,点M、N分别是正五边形ABCDE的边BC、CD 上的点,且BM=CN,AM交BN于点P, (1)求证:△ABM≌△BCN (2)求∠APN得度数
90≤分数
每日一练 11.4
如图,已知D是等腰三角形ABC底边BC上一点,它到两腰 AB,AC的距离分别为DE,DF,探索DE,DF与等腰三角 形ABC的高的关系。
11月5日
分数<40
每日一练 11.5
已知:AB=AC=BC , 求证:∠A= ∠ B=∠C= 60°
40≤分数<60
每日一练 11.5
80≤分数<100
每日一练 11.8
如图所示,△ACB和△ADE均为等边三角形,点C、E、D 在同一直线上,在△ACD中,线段AE是CD边上的中线, 连接BD.求证:CD=2BD.
100≤分数
二选一
每日一练 11.8
如图所示,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点, CE⊥BD于E.过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关 系,并证明你的猜想.
11月8日
分数<40
每日一练 11.8
如图所示,在△ABC中,AB=AC,点D在AC上,且 BD=BC=AD,求三角形ABC各角的度数
40≤分数<60
每日一练 11.8
如图所示,∠1=∠2,∠ACE=∠ADB,AC=AD,求证: AB=AE
60≤分数<80
每日一练 11.8
如图所示,在△ABC中,D是BC边上一点,AD=BD, AB=AC=CD,求∠BAC的度数
11月7日
分数<40
每日一练 11.7
已知点A(m+2,3)与B(-4,n+5)关于y轴对称,试求m+n 的值
八年级数学题100道(含答案)

八年级数学题100道带答案1) 66x+17y=396725x+y=1200答案:x=48 y=47(2) 18x+23y=230374x-y=1998答案:x=27 y=79(3) 44x+90y=779644x+y=3476答案:x=79 y=48(4) 76x-66y=408230x-y=2940答案:x=98 y=51(5) 67x+54y=854671x-y=5680答案:x=80 y=59(6) 42x-95y=-141021x-y=1575答案:x=75 y=48(7) 47x-40y=85334x-y=2006答案:x=59 y=48(8) 19x-32y=-1786 75x+y=4950答案:x=66 y=95 (9) 97x+24y=7202 58x-y=2900答案:x=50 y=98 (10) 42x+85y=6362 63x-y=1638答案:x=26 y=62 (11) 85x-92y=-2518 27x-y=486答案:x=18 y=44 (12) 79x+40y=2419 56x-y=1176答案:x=21 y=19 (13) 80x-87y=2156 22x-y=880答案:x=40 y=12 (14) 32x+62y=5134 57x+y=2850答案:x=50 y=57 (15) 83x-49y=8259x+y=2183答案:x=37 y=61 (16) 91x+70y=5845 95x-y=4275答案:x=45 y=25 (17) 29x+44y=5281 88x-y=3608答案:x=41 y=93 (18) 25x-95y=-4355 40x-y=2000答案:x=50 y=59 (19) 54x+68y=3284 78x+y=1404答案:x=18 y=34 (20) 70x+13y=3520 52x+y=2132答案:x=41 y=50 (21) 48x-54y=-3186 24x+y=1080答案:x=45 y=99 (22) 36x+77y=7619 47x-y=799答案:x=17 y=91 (23) 13x-42y=-2717 31x-y=1333答案:x=43 y=78 (24) 28x+28y=3332 52x-y=4628答案:x=89 y=30 (25) 62x-98y=-2564 46x-y=2024答案:x=44 y=54 (26) 79x-76y=-4388 26x-y=832答案:x=32 y=91 (27) 63x-40y=-821 42x-y=546答案:x=13 y=41 (28) 69x-96y=-1209 42x+y=3822答案:x=91 y=78 (29) 85x+67y=7338 11x+y=308答案:x=28 y=74(30) 78x+74y=12928 14x+y=1218答案:x=87 y=83 (31) 39x+42y=5331 59x-y=5841答案:x=99 y=35 (32) 29x+18y=1916 58x+y=2320答案:x=40 y=42 (33) 40x+31y=6043 45x-y=3555答案:x=79 y=93 (34) 47x+50y=8598 45x+y=3780答案:x=84 y=93 (35) 45x-30y=-1455 29x-y=725答案:x=25 y=86 (36) 11x-43y=-1361 47x+y=799答案:x=17 y=36 (37) 33x+59y=325494x+y=1034答案:x=11 y=49 (38) 89x-74y=-2735 68x+y=1020答案:x=15 y=55 (39) 94x+71y=7517 78x+y=3822答案:x=49 y=41 (40) 28x-62y=-4934 46x+y=552答案:x=12 y=85 (41) 75x+43y=8472 17x-y=1394答案:x=82 y=54 (42) 41x-38y=-1180 29x+y=1450答案:x=50 y=85 (43) 22x-59y=824 63x+y=4725答案:x=75 y=14 (44) 95x-56y=-401 90x+y=1530(45) 93x-52y=-852 29x+y=464答案:x=16 y=45 (46) 93x+12y=8823 54x+y=4914答案:x=91 y=30 (47) 21x-63y=84 20x+y=1880答案:x=94 y=30 (48) 48x+93y=9756 38x-y=950答案:x=25 y=92 (49) 99x-67y=4011 75x-y=5475答案:x=73 y=48 (50) 83x+64y=9291 90x-y=3690答案:x=41 y=92(51) 17x+62y=3216 75x-y=7350(52) 77x+67y=2739 14x-y=364答案:x=26 y=11 (53) 20x-68y=-4596 14x-y=924答案:x=66 y=87 (54) 23x+87y=4110 83x-y=5727答案:x=69 y=29 (55) 22x-38y=804 86x+y=6708答案:x=78 y=24 (56) 20x-45y=-3520 56x+y=728答案:x=13 y=84 (57) 46x+37y=7085 61x-y=4636答案:x=76 y=97 (58) 17x+61y=4088 71x+y=5609答案:x=79 y=45(59) 51x-61y=-1907 89x-y=2314答案:x=26 y=53 (60) 69x-98y=-2404 21x+y=1386答案:x=66 y=71 (61) 15x-41y=754 74x-y=6956答案:x=94 y=16 (62) 78x-55y=656 89x+y=5518答案:x=62 y=76 (63) 29x+21y=1633 31x-y=713答案:x=23 y=46 (64) 58x-28y=2724 35x+y=3080答案:x=88 y=85 (65) 28x-63y=-2254 88x-y=2024答案:x=23 y=46 (66) 43x+50y=706485x+y=8330答案:x=98 y=57 (67) 58x-77y=1170 38x-y=2280答案:x=60 y=30 (68) 92x+83y=11586 43x+y=3010答案:x=70 y=62 (69) 99x+82y=6055 52x-y=1716答案:x=33 y=34 (70) 15x+26y=1729 94x+y=8554答案:x=91 y=14 (71) 64x+32y=3552 56x-y=2296答案:x=41 y=29 (72) 94x+66y=10524 84x-y=7812答案:x=93 y=27 (73) 65x-79y=-5815 89x+y=2314答案:x=26 y=95 (74) 96x+54y=6216 63x-y=1953答案:x=31 y=60 (75) 60x-44y=-352 33x-y=1452答案:x=44 y=68 (76) 79x-45y=510 14x-y=840答案:x=60 y=94 (77) 29x-35y=-218 59x-y=4897答案:x=83 y=75 (78) 33x-24y=1905 30x+y=2670答案:x=89 y=43 (79) 61x+94y=11800 93x+y=5952答案:x=64 y=84 (80) 61x+90y=5001 48x+y=2448答案:x=51 y=21(81) 93x-19y=286x-y=1548答案:x=18 y=88 (82) 19x-96y=-5910 30x-y=2340答案:x=78 y=77 (83) 80x+74y=8088 96x-y=8640答案:x=90 y=12 (84) 53x-94y=1946 45x+y=2610答案:x=58 y=12 (85) 93x+12y=9117 28x-y=2492答案:x=89 y=70 (86) 66x-71y=-1673 99x-y=7821答案:x=79 y=97 (87) 43x-52y=-1742 76x+y=1976答案:x=26 y=55 (88) 70x+35y=829540x+y=2920答案:x=73 y=91 (89) 43x+82y=4757 11x+y=231答案:x=21 y=47 (90) 12x-19y=236 95x-y=7885答案:x=83 y=40 (91) 51x+99y=8031 71x-y=2911答案:x=41 y=60 (92) 37x+74y=4403 69x-y=6003答案:x=87 y=16 (93) 46x+34y=4820 71x-y=5183答案:x=73 y=43 (94) 47x+98y=5861 55x-y=4565答案:x=83 y=20 (95) 30x-17y=239 28x+y=1064答案:x=38 y=53 (96) 55x-12y=4112 79x-y=7268答案:x=92 y=79 (97) 27x-24y=-450 67x-y=3886答案:x=58 y=84 (98) 97x+23y=8119 14x+y=966答案:x=69 y=62 (99) 84x+53y=11275 70x+y=6790答案:x=97 y=59 (100) 51x-97y=297 19x-y=1520答案:x=80 y=39。
初二期末每日一练习题

初二期末每日一练习题第一题:小明有一束蓝色的气球,他将气球上升5米,然后又下降3米,再上升4米,最后再下降2米。
请问气球现在高于原来位置多少米?解析:首先,小明将气球上升了5米,再下降3米,所以气球的高度是5-3=2米。
然后,小明又将气球上升了4米,再下降了2米,所以气球的高度现在是2+4-2=4米。
因此,气球现在高于原来位置3米。
第二题:小华有25个苹果,她将其中的1/5分给了小明,然后又将剩下的3/5分给了小李。
请问小明和小李各分到了多少个苹果?解析:首先,小华将25个苹果的1/5分给了小明,所以小明共分到了25*(1/5)=5个苹果。
然后,小华剩下的苹果有25-5=20个。
再将这20个苹果的3/5分给了小李,所以小李共分到了20*(3/5)=12个苹果。
因此,小明分到了5个苹果,小李分到了12个苹果。
第三题:小明去商店买了一本参考书,原价100元,现在打8折,请问小明需要支付多少钱?解析:打8折表示购买时只需要支付原价的80%,所以小明需要支付的钱数为100*80%=80元。
第四题:甲、乙、丙三人共做了一个项目,甲做了总工作量的1/4,乙做了总工作量的1/3,那么丙做了剩下的工作量的多少?解析:甲做了总工作量的1/4,乙做了总工作量的1/3,所以甲和乙两人总共做了1/4+1/3=7/12的工作量。
剩下的工作量为1-7/12=5/12,所以丙做了剩下工作量的5/12。
第五题:小华的身高是150厘米,大于她的人有50人,小于她的人有60人,请问和小华一样高的人有多少人?解析:身高大于小华的人有50人,小于小华的人有60人,所以不包括小华在内的这110人中,和小华一样高的人有110-50-60=0人。
因此,和小华一样高的人有0人。
通过以上题目的解答,我们可以练习和巩固初二期末的数学知识。
希望同学们多做类似的练习题,提高自己的数学能力。
加油!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
每日一题初中数学【每日一题】(第 1 期)1、如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB 于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A2,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=答案:n=9初中数学【每日一题】(第 2 期)2、已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B 两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),当t为时,△PBQ是直角三角形.答案:t=1秒或t=2秒初中数学【每日一题】(第 3 期)水滴石穿!3、如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 __°.答案:50°【解析】试题分析:设∠A=x°,根据MN为中垂线可得:∠ABD=∠A=x°,则∠ABC=(x+15)°,根据AB=AC可得:∠C=∠ABC=(x+15)°,则根据△ABC的内角和定理可得:x+x+15+x+15=180°,解得:x=50°.初中数学【每日一题】(第 4 期)锲而不舍,金石可镂!如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长是_________.答案:11【解析】试题分析:根据题意可得:△BDO和△COE是等腰三角形,OD=BD,OE=EC,则△ADE 的周长=AD+DE+AE=AD+DO+OE+AE=AD+BD+AE+CE=AB+AC=6+5=11.考点:(1)、角平分线的性质;(2)、等腰三角形的性质.初中数学【每日一题】(第 5 期)小水长流,则能穿石!如图所示,三角形ABC的面积为1.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是.【解析】试题分析:过点P作PE⊥BP,垂足为P,交BC于点E,由角平分线的定义可知∠ABP=∠EBP,结合BP=BP以及∠APB=∠EPB=90°即可证出△ABP≌△EBP (ASA),进而可得出AP=EP,根据三角形的面积即可得出,再根据=.故答案为:.考点:等腰三角形的判定与性质;角平分线的定义;三角形的面积;全等三角形的判定与性质.初中数学【每日一题】(第 6 期)立志不坚,终不济事!如图,△ABC是等腰直角三角形,延长BC至E使BE=BA,过点B作BD⊥AE 于点D,BD与AC交于点F,连接EF.(1)求证:BF=2AD;(2)若CE=,求AC的长试题解析:(1)证明:∵△ABC是等腰直角三角形,∴AC=BC,∠FCB=∠ECA=90°,∵AC⊥BE,BD⊥AE,∴∠CBF+∠CFB=90°,∠DAF+∠AFD=90°,∵∠CFB=∠AFD,∴∠CBF=∠CAE,在△BCF与△ACE中,,∴△BCF≌△ACE,∴AE=BF,∵BE=BA,BD⊥AE,∴AD=ED,即AE=2AD,∴BF=2AD;(2)由(1)知△BCF≌△ACE,∴CF=CE=,∴在Rt△CEF中,EF==2,∵BD⊥AE,AD=ED,∴AF=FE=2,∴AC=AF+CF=2+.考点:全等三角形的判定与性质;勾股定理初中数学【每日一题】(第 7 期)已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,求证:BP=2PQ.试题解析:∵△ABC是等边三角形,∴AB=AC,∠BAE=∠C=60°,在△ABE和△CAD中,AB=AC,∠BAE=∠C=60°,AE=CD,∴△ABE≌△CAD(SAS),∴∠1=∠2,∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,∵BQ⊥AD,∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,∴BP=2PQ.考点:全等三角形的判定与性质;等边三角形的性质;含30度角的直角三角形.初中数学【每日一题】(第 8 期)如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC. 若AC=4,BC=3,AB=5,则OC的长度的最大值是.【解析】试题分析:取AB中点E,连接OE、CE,在直角三角形AOB中,OE=AB,利用勾股定理的逆定理可得△ACB是直角三角形,所以CE=AB,利用OE+CE≥OC,所以OC的最大值为OE+CE,即OC的最大值=AB=5.考点:勾股定理的逆定理初中数学【每日一题】(第 9 期)精诚所至,金石为开!著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为cm.试题解析:连接OP,∵△AOB是直角三角形,P为斜边AB的中点,∴OP=AB,∵AB=20cm,∴OP=10cm,考点:直角三角形斜边上的中线.初中数学【每日一题】(第 10 期)最可怕的是比你优秀的人还比你努力!如图,在△ABC中,AB=AC,点E为BC边上一动点(不与点B、C重合),过点E作射线EF交AC于点F,使∠AEF=∠B.(1)判断∠BAE与∠CEF的大小关系,并说明理由;(2)请你探索:当△AEF为直角三角形时,求∠AEF与∠BAE的数量关系.【解析】(1)∠BAE=∠FEC;理由如下:∵∠B+∠BAE=∠AEC,∠AEF=∠B,∴∠BAE=∠FEC;(2)如图1,当∠AFE=90°时,∵∠B+∠BAE=∠AEF+∠CEF,∠B=∠AEF=∠C,∴∠BAE=∠CEF,∵∠C+∠CEF=90°,∴∠BAE+∠AEF=90°,即∠AEF与∠BAE的数量关系是互余;如图2,当∠EAF=90°时,∵∠B+∠BAE=∠AEF+∠1,∠B=∠AEF=∠C,∴∠BAE=∠1,∵∠C+∠1+∠AEF=90°,∴2∠AEF+∠1=90°,即2∠AEF与∠BAE的数量关系是互余.【点评】此题考查了等腰三角形的性质以及外角的性质,此题难度适中,注意掌握分类讨论思想的应用.初中数学【每日一题】(第 11 期)耐心是一切聪明才智的基础!如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则::等于.试题分析:由角平分线的性质可得,点O到三角形三边的距离相等,即三个三角形的AB、BC、CA的高相等,利用面积公式即可求解.过点O作OD⊥AC 于D,OE⊥AB于E,OF⊥BC于F,∵O是三角形三条角平分线的交点,∴OD=OE=OF,∵AB=20,BC=30,AC=40,∴::=2:3:4.故答案为:2:3:4.考点:角平分线的性质;三角形的面积.初中数学【每日一题】(第 12 期)如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM= .解:过P作PC⊥MN∵PM=PN∴C为MN中点在Rt△OPC中,∠AOB=60°,∴∠OPC=30°,∴2OC=OP=8,∴OC=4则OM=OC﹣MC=4﹣1=3,初中数学【每日一题】(第 13 期)能坚持别人不能坚持的,才能拥有别人不能拥有的如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD 于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为()A.①②④B.①②③C.②③D.①③∵∠B和∠ACD都是∠CAB的余角,∴∠ACD=∠B,故①正确;∵CD⊥AB,EF⊥AB,∴EF∥CD,∴∠AEF=∠CHE,∴∠CEH=∠CHE,∴CH=CE=EF,故②正确;∵角平分线AE交CD于H,∴∠CAE=∠BAE,∴△ACE≌△AFE(AAS),∴AC=AF,故③正确;CH=CE=EF>HD,故④错误.故:正确答案选 B初中数学【每日一题】(第 14 期)如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F 分别在AC,BC上,则DE与DF的数量关系是_______如图,连接CD.∵BC=AC,∠BCA=90°∴△ABC是等腰直角三角形∵D为AB中点∴BD=CD=AD,CD平分∠BCA,CD⊥AB∵∠A+∠ACD=∠ACD+∠FCD=90°∴∠A=∠FCD∵∠CDF+∠CDE=90°∠CDE+∠ADE=90°∴∠ADE=∠CDF,在△ADE和△CFD中∵∠A=∠FCD,AD=CD,∠ADE=∠CDF∴△ADE≌△CFD(ASA)∴DE=DF.初中数学【每日一题】(第 15 期)耐心和恒心总会得到报酬的。
如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)请求出何时△PBQ是直角三角形?初中数学【每日一题】(第 16 期)守其初心,始终不变!解:(1)不变,∠CMQ=60°.∵△ABC是等边三角形,∴等边三角形中,AB=AC,∠B=∠CAP=60°又∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.∴AP=BQ,∴△ABQ≌△CAP(SAS),∴∠BAQ=∠ACP,∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;(2)设时间为t秒,则AP=BQ=tcm,PB=(4﹣t)cm,当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,即4﹣t=2t,t=当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4﹣t),t=∴当第秒或第秒时,△PBQ为直角三角形.初中数学【每日一题】(第 16 期)守其初心,始终不变!已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.①证明:连结CD,∵D在BC的中垂线上∴BD=CD∵DE⊥AB,DF⊥ACAD平分∠BAC∴DE=DF∠BED=∠DCF=90°在RT△BDE和RT△CDF中,∴RT△BDE≌RT△CDF(HL),∴BE=CF;②解:由(HL)可得,Rt△ADE≌Rt△ADF,∴AE=AF=5,∴△ABC的周长=AB+BC+AC,=(AE+BE)+BC+(AF﹣CF)=5+6+5=16.初中数学【每日一题】(第 17 期)逝者如斯夫,不舍昼夜!如图,在Rt△ABC中,∠B=90°,∠C=30°BC=5 .点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;(2)当t为何值时,△DEF为直角三角形?请说明理由.(1)证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF=t.又∵AE=t,∴AE=DF;(2)①∠EDF=90°时,四边形EBFD为矩形.在Rt△AED中,∠ADE=∠C=30°,∴AD=2AE.即10-2t=2t,∴t=;②∠DEF=90°时,由(2)知EF∥AD,∴∠ADE=∠DEF=90°.∵∠A=90°-∠C=60°,∴AD=AE.即10-2t=t,∴t=4;③∠EFD=90°时,此种情况不存在;综上所述,当t=或4时,△DEF为直角三角形.初中数学【每日一题】(第 18 期)有梦想,才有远方!如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为()初中数学【每日一题】(第19 期)坚持,就会改变!如果不等式(1+a)x>1+a的解集为x<1,那么a的取值范围是() A. a>0 B. a<0 C. a>-1 D. a<-1初中数学【每日一题】(第20期)对于有恒心的的旅人,不存在遥远的途程。
