中考专题二次函数题型分类总结

合集下载

中考数学专题复习《二次函数综合题》知识点梳理及典例讲解课件

时，S有最大值，最大值为，此时点P的坐标为（3; ＝－ m2＋9m＝－（m2－6m）＝－（m－3）2＋ .

∵－＜0，∴ 当m＝3
类型二面积问题
典例2 （2023·
湘潭）如图，二次函数y＝x2＋bx＋c 的图象与x轴交于点
∴ 设M（t，－t2＋2t＋3）（0＜t＜3），则Q（t，－t＋3）.∴ MQ
＝－t2＋3t.过点Q作QD⊥OC，垂足为D，则易得△CDQ是等腰直
角三角形.∴ CQ＝ t.
∴ MQ＋ CQ＝－t2＋3t＋2t＝－t2＋5t＝－

−
＋ .∴

时，MQ＋ CQ 有最大值，此时点M的坐标为
式，当x＝1时求出y的值，从而求出点P的坐标，此时PA＋PC的最
小值就是BC的长，利用勾股定理求解即可；（3）由抛物线与直线
BC对应的函数解析式，分别设出点M，Q的坐标，过点Q作
QD⊥OC，垂足为D，将MQ＋ 2CQ用含参数的代数式表示出来，
再结合二次函数的性质求解问题.
解：（1） ∵ 抛物线y＝ax2＋bx＋3（a≠0）的对称轴是直线x＝1，点A的坐标为（－
1，0），∴ 由抛物线的对称性，可知点B的坐标为（3，0）.
（2）由题意，可知抛物线对应的函数解析式为y＝a（x＋1）（x－
3）＝a（x2－2x－3）.∵ 抛物线y＝ax2＋bx＋3（a≠0）与y轴交于点
C，
∴ 易得C（0，3）.将C（0，3）代入y＝a（x2－2x－3），得－3a＝
3，解得a＝－1.∴ 抛物线对应的函数解析式为y＝－x2＋2x＋3.如图

二次函数题型分类总结

二次函数题型分类总结一、顶点在坐标轴上的二次函数方程当二次函数的顶点坐标为（0，a）或（b，0）时，可以得到以下两种形式的二次函数方程。

1. 顶点在y轴上的二次函数方程：y = ax^2这种形式的二次函数方程对称轴为y轴，开口向上或向下。

当a > 0时，抛物线开口向上；当a < 0时，抛物线开口向下。

2. 顶点在x轴上的二次函数方程：y = a(x-b)^2这种形式的二次函数方程对称轴为x = b，开口向上或向下。

当a > 0时，抛物线开口向上；当a < 0时，抛物线开口向下。

二、顶点不在坐标轴上的二次函数方程当二次函数的顶点坐标为（h，k）时，可以得到以下两种形式的二次函数方程。

1. 一般形式的二次函数方程：y = ax^2 + bx + c这种形式的二次函数方程对称轴为x = -b/2a，开口向上或向下。

根据a的正负值可知抛物线的开口方向。

2. 完全平方形式的二次函数方程：y = a(x-h)^2 + k这种形式的二次函数方程对称轴为x = h，开口向上或向下。

根据a的正负值可知抛物线的开口方向。

三、特殊形式的二次函数方程除了以上分类外，还存在一些特殊形式的二次函数方程。

1. 平移后的二次函数方程：y = a(x-p)(x-q)在一般形式的二次函数方程中，平移抛物线的顶点至（p，q）处即可得到平移后的二次函数方程。

2. 平方差公式：y = (x-h)^2 - k^2这种形式的二次函数方程本质上是一个完全平方公式，可利用平方差公式进行求解。

其对称轴为x = h，开口向上或向下。

四、应用题型除了基本形式的二次函数方程外，还存在一些应用题型，需要根据题目给出的条件进行分析和求解。

1. 求最值问题：通过求二次函数的极值点来解决。

2. 求交点问题：将两个二次函数方程相等，解方程得到交点坐标。

3. 求解区间问题：通过对二次函数方程进行开口方向和对称轴的分析，确定函数的定义域或值域。

二次函数中考题型总结

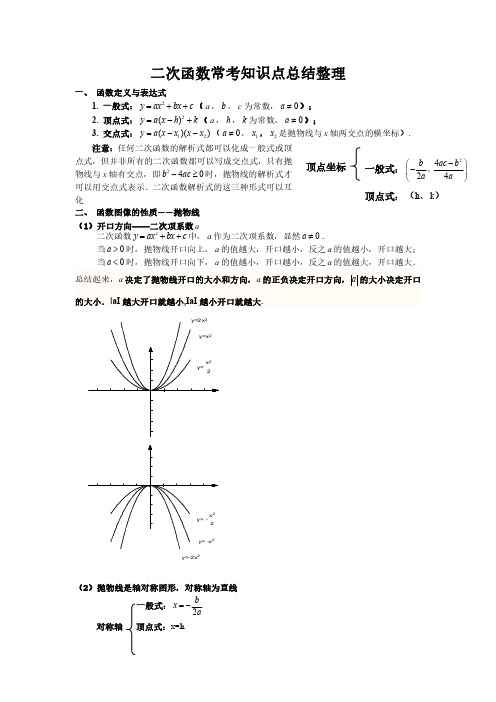
二次函数常考知识点总结整理一、函数定义与表达式1.一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2.顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3.交点式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化二、函数图像的性质——抛物线（1）开口方向——二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大；（2）抛物线是轴对称图形，对称轴为直线一般式：2bx a=-对称轴顶点式：x=h一般式：2424b ac b aa ⎛⎫-- ⎪⎝⎭，顶点式：（h、k）顶点坐标y=-2x 2两根式：x=221x x +（3）对称轴位置一次项系数b 和二次项系数a 共同决定对称轴的位置。

（“左同右异”）a 与b 同号（即ab ＞0）对称轴在y 轴左侧a 与b 异号（即ab ＜0）对称轴在y 轴右侧（4）增减性，最大或最小值当a>0时，在对称轴左侧（当2bx a<-时），y 随着x 的增大而减少；在对称轴右侧（当2bx a<-时），y 随着x 的增大而增大；当a<0时，在对称轴左侧（当2bx a<-时），y 随着x 的增大而增大；在对称轴右侧（当2bx a<-时），y 随着x 的增大而减少；当a>0时，函数有最小值，并且当x=a b2-，2min 44ac b y a -=；当a<0时，函数有最大值，并且当x=ab2-，2max 44ac b y a -=；（5）常数项c常数项c 决定抛物线与y 轴交点。

二次函数中考常见题型

二次函数中考常见题型二次函数中考常见题型二次函数作为数学中比较重要的一章，其考试题型也会经常出现在中考中。

在备考阶段，要注意哪些题型是重点，做好相应的准备。

以下为二次函数中考常见题型：一、教材基础部分1. 含义理解：定义、性质、图像等。

2. 根的求法：公式法、配方法、图像法等。

3. 解析式的求法：从图像入手，按照标准式来确定。

二、与之相关的几何问题1. 抛物线上某点的切线问题。

2. 对称轴问题：如已知抛物线的顶点，求其对称轴方程等。

3. 根与系数问题：如已知根，求系数等。

三、实际问题与抛物线模型1. 炮弹轨迹问题。

2. 喷水池设计问题。

3. 碗碟生产成本分析问题。

四、考点分类综合练习通过以上几个方面的题型练习，这里特意准备了几道综合练习题，读者可以将所学知识综合运用，巩固自己的学习成果。

1. (2018·江苏镇江) 根据题意，列方程解析式，并画出抛物线的图像。

现已知一条水泄水道曲线，用实验室的计算仪器测试，得到其一些关键点坐标。

当流量为 4L/s 时，水面高度为 200 cm，当流量为 9L/s 时，水面高度为 260 cm。

(1) 请根据已知数据，列出方程。

(2) 请用解析式画出此抛物线的图像。

2. (2019·辽宁大连) 已知 y=ax²+bx+c 是顶点为 (1，4)，且过点 (2，2)、(6，-8) 的抛物线。

(1) 求出该抛物线解析式。

(2) 求出 a，b，c 的值。

(3) 给出该抛物线的图像。

以上就是二次函数中考常见题型的总结，考生可根据此文进行重复梳理与练习。

希望各位在中考中能够取得好成绩！。

中考二次函数压轴题题型总结(一)

中考二次函数压轴题题型总结(一)中考二次函数压轴题题型总结前言二次函数作为中考数学的重要内容之一，经常作为压轴题出现。

对于考生来说，熟练掌握二次函数的基本知识和解题方法是非常重要的。

本文将对中考二次函数压轴题题型进行总结，帮助考生更好地备考。

一、基本概念回顾1.二次函数的标准形式：y=ax2+bx+c2.二次函数的图像特征：–开口方向（参数a的正负）–顶点坐标（x=−b2a ,y=−D4a）–对称轴方程（x=−b2a）–判别式（D=b2−4ac）二、题型分析与解题技巧1. 求解二次函数的解•求解二次函数的零点：–根据方程y=0，列出二次方程并求解；–利用零点和对称轴的关系求解。

2. 求解二次函数图像的特征•开口方向：–根据参数a的正负判断开口方向；–利用顶点和对称轴的关系判断开口方向。

•顶点坐标：求解。

–利用x=−b2a•对称轴方程：求解。

–利用x=−b2a3. 利用图像解题•区间范围：–根据图像的开口方向确定y的取值范围。

•最值问题：–利用顶点坐标求解函数的最值。

通过以上总结，我们可以看出，二次函数压轴题在中考中占据了重要的位置。

对于考生来说，熟练掌握二次函数的基本概念和解题技巧是提高数学成绩的关键。

希望本文能对考生复习备考有所帮助。

4. 利用判别式解二次函数的性质•判别式D=b2−4ac可以判断二次函数的根的情况：–当D>0时，方程有两个不相等的实根；–当D=0时，方程有两个相等的实根；–当D<0时，方程没有实根。

•利用判别式的性质解题：–求解满足条件的参数；–求解满足条件的x的取值范围。

5. 利用二次函数的性质解实际问题•利用二次函数的最值性质解实际问题：–求解物体的最高点、最低点等位置；–求解时间、速度、距离等相关问题。

通过本文的总结，我们可以看出，在中考二次函数压轴题中，考察的内容主要包括基本概念、解题技巧、图像特征、判别式和实际问题的应用。

考生在备考时应该注重理解二次函数的概念和性质，掌握解题的方法和技巧，加强对图像特征和判别式的理解和应用，同时培养解实际问题的能力。

二次函数的图象与性质大题(五大题型)—2024年中考数学(全国通用)解析版

二次函数的图象与性质大题（五大题型）通用的解题思路：题型一．二次函数的性质二次函数y＝ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x＝﹣，二次函数y＝ax2+bx+c （a≠0）的图象具有如下性质：①当a＞0时，抛物线y＝ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x＝﹣时，y取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y＝ax2+bx+c（a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x＝﹣时，y取得最大值，即顶点是抛物线的最高点．③抛物线y＝ax2+bx+c（a≠0）的图象可由抛物线y＝ax2的图象向右或向左平移|﹣|个单位，再向上或向下平移||个单位得到的．题型二．二次函数图象与系数的关系二次函数y＝ax2+bx+c（a≠0）①二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|还可以决定开口大小，|a|越大开口就越小．②一次项系数b和二次项系数a共同决定对称轴的位置．当a与b同号时（即ab＞0），对称轴在y轴左侧；当a与b异号时（即ab＜0），对称轴在y轴右侧．（简称：左同右异）③．常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．④抛物线与x轴交点个数．△＝b2﹣4ac＞0时，抛物线与x轴有2个交点；△＝b2﹣4ac＝0时，抛物线与x轴有1个交点；△＝b2﹣4ac ＜0时，抛物线与x轴没有交点．题型三．待定系数法求二次函数解析式（1）二次函数的解析式有三种常见形式：①一般式：y＝ax2+bx+c（a，b，c是常数，a≠0）；②顶点式：y＝a（x﹣h）2+k（a，h，k是常数，a≠0），其中（h，k）为顶点坐标；③交点式：y＝a（x﹣x1）（x﹣x2）（a，b，c是常数，a≠0）；（2）用待定系数法求二次函数的解析式．在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．题型四．抛物线与x轴的交点求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y＝0，即ax2+bx+c＝0，解关于x 的一元二次方程即可求得交点横坐标．（1）二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c＝0根之间的关系．△＝b2﹣4ac决定抛物线与x轴的交点个数．△＝b2﹣4ac＞0时，抛物线与x轴有2个交点；△＝b2﹣4ac＝0时，抛物线与x轴有1个交点；△＝b2﹣4ac＜0时，抛物线与x轴没有交点．（2）二次函数的交点式：y＝a（x1）（x﹣x2）（a，b，c是常数，a≠0），可直接得到抛物线与x轴的交点坐标（x1，0），（x2，0）．题型五．二次函数综合题（1）二次函数图象与其他函数图象相结合问题解决此类问题时，先根据给定的函数或函数图象判断出系数的符号，然后判断新的函数关系式中系数的符号，再根据系数与图象的位置关系判断出图象特征，则符合所有特征的图象即为正确选项．（2）二次函数与方程、几何知识的综合应用将函数知识与方程、几何知识有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．（3）二次函数在实际生活中的应用题从实际问题中分析变量之间的关系，建立二次函数模型．关键在于观察、分析、创建，建立直角坐标系下的二次函数图象，然后数形结合解决问题，需要我们注意的是自变量及函数的取值范围要使实际问题有意义．题型一．二次函数的性质（共3小题）1．（2024•石景山区校级模拟）在平面直角坐标系xOy 中，1(A x ，1)y ，2(B x ，2)y 是抛物线2(0)y x bx b =−+≠上任意两点，设抛物线的对称轴为直线x h =．（1）若抛物线经过点(2,0)，求h 的值；（2）若对于11x h =−，22x h =，都有12y y >，求h 的取值范围；（3）若对于121h x h −+……，221x −−……，存在12y y <，直接写出h 的取值范围．【分析】（1）根据对称轴2bx a=−进行计算，得2b h =，再把(2,0)代入2(0)y x bx b =−+≠，即可作答．（2）因为1(A x ，1)y ，2(B x ，2)y 是抛物线2(0)y x bx b =−+≠上的点，所以把11x h =−，22x h =分别代入，得出对应的1y ，2y ，再根据12y y >联立式子化简，计算即可作答；（3）根据121h x h −+……，221x −−……，存在12y y <，得出当221h −<−<−或者211h −<+<−，即可作答．【解答】解：（1）抛物线的对称轴为直线x h =， 22b bh ∴=−=−，即2b h =，∴抛物线22y x hx =−+，把(2,0)代入22y x hx =−+，得0422h =−+⨯，解得1h =；（2）由（1）知抛物线22y x hx =−+，1(A x ，1)y ，2(B x ，2)y 是抛物线22y x hx =−+上任意两点，221(1)2(1)1y h h h h ∴=−−+−=−，22(2)220y h h h =−+⨯=，对于11x h =−，22x h =，都有12y y >， 210h ∴−>，解得1h >或1h <−；（3）1(A x ，1)y ，2(B x ，2)y 是抛物线22y x hx =−+上任意两点，对于121h x h −+……，221x −−……，存在12y y <，且1(2,)h y −关于直线x h =的对称点为1(2,)h y +，1(1,)h y +关于直线x h =的对称点为1(1,)h y −，∴当221h −<−<−时，存在12y y <，解得01h <<，当221h −<+<−时，存在12y y <，解得43h −<<−，当211h −<+<−时，存在12y y <，解得32h −<<−，当211h −<−<−时，存在12y y <，解得10h −<<，综上，满足h 的取值范围为41h −<<且0h ≠．【点评】本题考查了二次函数的图象性质、增减性，熟练掌握二次函数的图象和性质是解决本题的关键． 2．（2024•鹿城区校级一模）已知二次函数223y x tx =−++．（1）若它的图象经过点(1,3)，求该函数的对称轴．（2）若04x ……时，y 的最小值为1，求出t 的值．（3）如果(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上，直线2y mx a =+与该二次函数交于1(M x ，1)y ，2(N x ，2)y 两点，则12x x +是否为定值？若是，请求出该定值；若不是，请说明理由．【分析】（1）把(1,3)代入解析式求出12t =，再根据对称轴公式求出对称轴；（2）根据抛物线开口向下，以及0x =时3y =，由函数的性质可知，当4x =时，y 的最小值为1，然后求t 即可；（3）(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上，有对称轴公式得出1m t −=，再令2232x tx mx a −++=+，并转化为一般式，然后由根与系数的关系求出122x x +=−．【解答】解：（1）将(1,3)代入二次函数223y x tx =−++，得3123t =−++，解得12t =， ∴对称轴直线为21122t x t =−==−⨯；（2）当0x =时，3y =，抛物线开口向下，对称轴为直线x t =， ∴当x t =时，y 有最大值，04x ……时，y 的最小值为1，∴当4x =时，16831y t =−++=，解得74t =；（3）12x x +是定值，理由：(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上， 212m mx t m −+∴===−， 1m t ∴−=，令2232x tx mx a −++=+，整理得：22()30x m t x a +−+−=，直线2y mx a =+与该二次函数交于1(M x ，1)y ，2(N x ，2)y 两点， 1x ∴，2x 是方程22()30x m t x a +−+−=的两个根，122()2()21m t x x m t −∴+=−=−−=−是定值．【点评】本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识，关键是掌握二次函数的性质． 3．（2024•拱墅区一模）在平面直角坐标系中，抛物线2(2)2y ax a x =−++经过点(2,)A t −，(,)B m p ．（1）若0t =，①求此抛物线的对称轴；②当p t <时，直接写出m 的取值范围；（2）若0t <，点(,)C n q 在该抛物线上，m n <且5513m n +<−，请比较p ，q 的大小，并说明理由．【分析】（1）①当0t =时，点A 的坐标为(2,0)−，将其代入函数解析式中解得1a =−，则函数解析式为抛物线的解析式为22y x x =−−+，再根据求对称轴的公式2bx a=−即可求解； ②令0y =，求出抛物线与x 轴交于(2,0)−和(1,0)，由题意可得0p <，则点B 在x 轴的下方，以此即可解答；（2）将点A 坐标代入函数解析式，通过0t <可得a 的取值范围，从而可得抛物线开口方向及对称轴，根据点B ，C 到对称轴的距离大小关系求解．【解答】解：（1）①当0t =时，点A 的坐标为(2,0)−，抛物线2(2)2y ax a x =−++经过点(2,0)A −， 42(2)20a a ∴+++=，1a ∴=−，∴抛物线的解析式为22y x x =−−+， ∴抛物线的对称轴为直线112(1)2x −=−=−⨯−；②令0y =，则220x x −−+=，解得：11x =，22x =−，∴抛物线与x 轴交于(2,0)−和(1,0)，点(2,0)A −，(,)B m p ，且0p <， ∴点(,)B m p 在x 轴的下方，2m ∴<−或1m >．（2）p q <，理由如下：将(2,)t −代入2(2)2y ax a x =−++得42(2)266t a a a =+++=+，0t <， 660a ∴+<， 1a ∴<−，∴抛物线开口向下，抛物线对称轴为直线(2)1122a x a a −+=−=+， 1a <−，110a∴−<<， 1111222a ∴−<+<， m n <且5513m n +<−，∴1312102m n +<−<−， ∴点(,)B m p 到对称轴的距离大于点(,)C n q 到对称轴的距离，p q ∴<．【点评】本题考查二次函数的综合应用，解题关键是掌握二次函数的性质，掌握二次函数与方程及不等式的关系．题型二．二次函数图象与系数的关系（共8小题）4．（2023•南京）已知二次函数223(y ax ax a =−+为常数，0)a ≠．（1）若0a <，求证：该函数的图象与x 轴有两个公共点．（2）若1a =−，求证：当10x −<<时，0y >．（3）若该函数的图象与x 轴有两个公共点1(x ，0)，2(x ，0)，且1214x x −<<<，则a 的取值范围是．【分析】（1）证明240b ac −>即可解决问题．（2）将1a =−代入函数解析式，进行证明即可．（3）对0a >和0a <进行分类讨论即可．【解答】证明：（1）因为22(2)43412a a a a −−⨯⨯=−，又因为0a <，所以40a <，30a −<，所以24124(3)0a a a a −=−>，所以该函数的图象与x 轴有两个公共点．（2）将1a =−代入函数解析式得，2223(1)4y x x x =−++=−−+，所以抛物线的对称轴为直线1x =，开口向下．则当10x −<<时，y 随x 的增大而增大，又因为当1x =−时，0y =，所以0y >．（3）因为抛物线的对称轴为直线212ax a−=−=，且过定点(0,3)，又因为该函数的图象与x 轴有两个公共点1(x ，0)，2(x ，0)，且1214x x −<<<，所以当0a >时，230a a −+<，解得3a >，故3a >．当0a <时，230a a ++<，解得1a <−，故1a <−．综上所述，3a >或1a <−．故答案为：3a >或1a <−．【点评】本题考查二次函数的图象和性质，熟知二次函数的图象和性质是解题的关键．5．（2024•南京模拟）在平面直角坐标系xOy 中，点1(1,)y ，2(3,)y 在抛物线222y x mx m =−+上．（1）求抛物线的顶点(,0)m ；（2）若12y y <，求m 的取值范围；（3）若点0(x ，0)y 在抛物线上，若存在010x −<<，使102y y y <<成立，求m 的取值范围．【分析】（1）利用配方法将已知抛物线解析式转化为顶点式，可直接得到答案；（2）由12y y <，得到221296m m m m −+<−+，解不等式即可；（3）由题意可知012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩，解不等式组即可．【解答】解：（1）抛物线222()y x mx m x m =−+=−． ∴抛物线的顶点坐标为(,0)m ．故答案为：(,0)m ；（2）点1(1,)y ，2(3,)y 在抛物线222y x mx m =−+上，且12y y <， 221296m m m m ∴−+<−+，2m ∴<；（3）点0(x ，0)y 在抛物线上，存在010x −<<，使102y y y <<成立， ∴012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩，解得302m <<．【点评】本题考查了二次函数与系数的关系，二次函数图象上点的坐标特征，熟知二次函数的性质是解题的关键．6．（2024•北京一模）在平面直角坐标系中，已知抛物线23y ax bx =++经过点(2,3)a −．（1）求该抛物线的对称轴（用含有a 的代数式表示）；（2）点(2,)M t m −，(2,)N t n +，(,)P t p −为该抛物线上的三个点，若存在实数t ，使得m n p >>，求a 的取值范围．【分析】（1）将点(2,3)a −代入抛物线23y ax bx =++中，然后根据二次函数的对称轴公式代入数值，即可得出答案；（2）分类讨论当0a >和0a <，利用数形结合以及二次函数的性质就可以得出a 的取值范围．【解答】解（1）抛物线23y ax bx =++经过点(2,3)a −， ∴把(2,3)a −代入23y ax bx =++得2(2)233a a ab ⨯−−+=，22b a ∴=，2223y ax a x ∴=++，∴抛物线的对称轴222a x a a=−=−，答：抛物线的对称轴为：x a =−；（2）①当0a >时，抛物线开口方向向上，对称轴0x a =−<，在x 轴的负半轴上，所以越靠近对称轴函数值越小， ∴当0t <时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+，∴此时p m n >>与题干m n p >>相矛盾，故舍去， ∴当0t >时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+，∴此时m n <与题干m n p >>相矛盾，故舍去；②当0a <时，抛物线开口方向向下，对称轴0x a =−>，在x 轴的正半轴上，所以越靠近对称轴函数值越大， ∴当0t >时，点M 、N 分别在对称轴同侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+， .m n p >>，∴此时02a t <−<−，即20t a −<<，2t ∴>，∴当0t >时，点M 、N 分别在对称轴两侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，p m n ∴>>与题干m n p >>相矛盾，故舍去，∴当0t <时，且点M 、N 分别在对称轴两侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，n m ∴>与题干m n p >>相矛盾，故舍去，当0t <时，且点M 、N 分别在对称轴同侧时， (2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，n m ∴>与题干m n p >>相矛盾，故舍去，答：a 的取值范围为20(2)t a t −<<>．7．（2024•张家口一模）某课外小组利用几何画板来研究二次函数的图象，给出二次函数解析式2y x bx c =++，通过输入不同的b ，c 的值，在几何画板的展示区内得到对应的图象．（1）若输入2b =，3c =−，得到如图①所示的图象，求顶点C 的坐标及抛物线与x 轴的交点A ，B 的坐标；（2）已知点(1,10)P −，(4,0)Q ．①若输入b ，c 的值后，得到如图②的图象恰好经过P ，Q 两点，求出b ，c 的值；②淇淇输入b ，嘉嘉输入1c =−，若得到二次函数的图象与线段PQ 有公共点，求淇淇输入b 的取值范围．【分析】（1）将2b =，3c =−，代入函数解析式，进行求解即可；（2）①待定系数法进行求解即可；②将1c =−代入解析式，得到抛物线必过点(0,1)−，求出1x =−和4x =的函数值，根据抛物线与线段PQ 有公共点，列出不等式进行求解即可．【解答】解：（1）2y x bx c =++，解：当2b =，3c =−时，2223(1)4y x x x =+−=+−， ∴顶点C 的坐标为：(1,4)−−；当0y =时，2230x x +−=，即(3)(1)0x x +−=，解得：13x =−，21x =， (3,0)A ∴−，(1,0)B ；（2）①抛物线恰好经过P ，Q则：1101640b c b c −+=⎧⎨++=⎩，解得：54b c =−⎧⎨=⎩；②当1c =−时，21y x bx =+−，当0x =时，1y =−， ∴抛物线过(0,1)−，当1x =−时，11y b b =−−=−，当点(1,)b −−在点P 上方，或与点P 重合时，抛物线与线段PQ 有公共点，即：10b −…，解得：10b −…；当4x =时，1641415y b b =+−=+，当点(4,154)b +在点Q 上方，或与点Q 重合时，抛物线与线段PQ 有公共点，即：1540b +…，154b ≥−；综上：10b −…或154b ≥−．【点评】本题考查二次函数的综合应用．正确的求出函数解析式，熟练掌握二次函数的图象和性质是解题的关键．8．（2024•浙江模拟）设二次函数24(y ax ax c a =−+，c 均为常数，0)a ≠，已知函数值y 和自变量x 的部分对应取值如下表所示：（1）判断m ，n 的大小关系，并说明理由；（2）若328m n −=，求p 的值；（3）若在m ，n ，p 这三个数中，只有一个数是负数，求a 的取值范围．【分析】（1）根据所给函数解析式，可得出抛物线的对称轴为直线2x =，据此可解决问题．（2）根据（1）中发现的关系，可求出m 的值，据此即可解决问题．（3）根据m 和n 相等，所以三个数中的负数只能为p ，据此可解决问题．【解答】解：（1）m n =．因为二次函数的解析式为24y ax c =+，所以抛物线的对称轴为直线422ax a−=−=，又因为1522−+=，所以点(1,)m −与(5,)n 关于抛物线的对称轴对称，故m n =．（2）因为m n =，328m n −=，所以8m =．将(0,3)和(1,8)−代入函数解析式得：348c a a c =⎧⎨++=⎩，解得13a c =⎧⎨=⎩所以二次函数的解析式为243y x x =−+．将2x =代入函数解析式得，224231p =−⨯+=−．（3）由（1）知，m n =，所以m ，n ，p 中只能p 为负数．将(0,3)代入函数解析式得，3c =，所以二次函数解析式为243y ax ax =−+．将1x =−代入函数解析式得，53m a =+．将2x =代入函数解析式得，43p a =−+．则430530a a −+<⎧⎨+≥⎩，解得34a >，所以a 的取值范围是34a >．【点评】本题考查二次函数图象与系数的关系及二次函数图象上点的坐标特征，熟知二次函数的图象和性质是解题的关键．9．（2024•北京模拟）在平面直角坐标系xOy 中，抛物线2(26)1y x m x =+−+经过点1(,)m y −，2(,)m y ，3(2,)m y +．（1）若13y y =，求抛物线的对称轴；（2）若231y y y <<，求m 的取值范围．【分析】（1）利用对称轴意义即可求解；（2m 的不等式组，解不等式组即可．【解答】解：（1）抛物线2(26)1y x m x =+−+经过点1(,)m y −，2(,)m y ，3(2,)m y +，13y y =， ∴该抛物线的对称轴为：直线22m m x −++=，即直线1x =；（2）当0m >时，可知点1(,)m y −，2(,)m y ，3(2,)m y +从左至右分布， 231y y y <<，∴232232m m m m m m ++⎧−<⎪⎪⎨−++⎪−>⎪⎩，解得12m <<；当0m <时，3m m m ∴<−<−+，21y y ∴>，不合题意，综上，m 的取值范围是12m <<．【点评】本题考查了二次函数图象上点的坐标特征，二次函数的性质，熟练掌握二次函数的性质是解题的关键．10．（2024•浙江模拟）在平面直角坐标系xOy 中，抛物线2(y ax bx c a =++，b ，c 为常数，且0)a ≠经过(2,4)A −−和(3,1)B 两点．（1）求b 和c 的值（用含a 的代数式表示）；（2）若该抛物线开口向下，且经过(23,)C m n −，(72,)D m n −两点，当33k x k −<<+时，y 随x 的增大而减小，求k 的取值范围；（3）已知点(6,5)M −，(2,5)N ，若该抛物线与线段MN 恰有一个公共点时，结合函数图象，求a 的取值范围．【分析】（1）把(2,4)A −−和(3,1)B 代入2y ax bx c =++，即可求解；（2）先求出对称轴为：直线2x =，结合开口方向和增减性列出不等式即可求解；（3）分0a >时，0a <时，结合图象即可求解．【解答】解：（1）把(2,4)A −−和(3,1)B 代入2y ax bx c =++，得：424931a b c a b c −+=−⎧⎨++=⎩，解得：162b a c a =−⎧⎨=−−⎩；（2）抛物线经过(23,)C m n −，2,)m n −两点， ∴抛物线的对称轴为：直线237222m mx −+−==，抛物线开口向下，当33k x k −<<+时，y 随x 的增大而减小，32k ∴−…，即5k …；（3）①当0a >时，6x =−，5y …，即2(6)(1)(6)625a a a ⨯−+−⨯−−−…，解得：1336a …，抛物线不经过点N ，如图①，抛物线与线段MN 只有一个交点，结合图象可知：1336a …；②当0a <时，若抛物线的顶点在线段MN 上时，则2244(62)(1)544ac b a a a a a−−−−−==，解得：11a =−，2125a =−，当11a =−时，111112222(1)a −=−=⨯−，此时，定点横坐标满足116222a−−……，符合题意；当11a =−时，如图②，抛物线与线段MN 只有一个交点，如图③，当2125a =−时，11111312222()25a −=−=⨯−，此时顶点横坐标不满足116222a−−……，不符合题意，舍去；若抛物线与线段MN 有两个交点，且其中一个交点恰好为点N 时，把(2,5)N 代入2(1)62y ax a x a =+−−−，得：252(1)262a a a =⨯+−⨯−−，解得：54a =−，当54a =−时，如图④，抛物线和线段MN 有两个交点，且其中一个交点恰好为点N ，结合图象可知：54a <−时，抛物线与线段MN 有一个交点，综上所述：a 的取值范围为：1336a …或1a =−或54a <−．【点评】本题考查二次函数的性质和图象，根据题意画出图象，分类讨论是解题的关键．11．（2024•海淀区校级模拟）在平面直角坐标系xOy 中，点(0,3)，1(6,)y 在抛物线2(0)y ax bx c a =++≠上．（1）当13y =时，求抛物线的对称轴；（2）若抛物线2(0)y ax bx c a =++≠经过点(1,1)−−，当自变量x 的值满足12x −……时，y 随x 的增大而增大，求a 的取值范围；（3）当0a >时，点2(4,)m y −，2(,)m y 在抛物线2y ax bx c =++上．若21y y c <<，请直接写出m 的取值范围．【分析】（1）当13y =时，(0,3)，(6,3)为抛物线上的对称点，根据对称性求出对称轴；（2）把(0,3)，(1,1)−−代入抛物线解析式得出a ，b 的关系，然后求出对称轴，再分0a >和0a <，由函数的增减性求出a 的取值范围；（3）先画出函数图象，再根据21y y c <<确定m 的取值范围．【解答】解：（1）当13y =时，(0,3)，(6,3)为抛物线上的对称点， 0632x +∴==， ∴抛物线的对称轴为直线3x =；（2）2(0)y ax bx c a =++≠过(0,3)，(1,1)−−，3c ∴=，31a b −+=−， 4b a =+，∴对称轴为直线422b a x a a+=−=−，①当0a >时，12x −……时，y 随x 的增大而增大，∴412a a+−−…，解得4a …，04a ∴<…；②当0a <时，12x −……时，y 随x 的增大而增大，∴422a a+−…，解得45a −…， ∴405a −<…，综上：a 的取值范围是405a −<… 或04a <…；（3）点(0,3)在抛物线2y ax bx c =++上，3c ∴=，点2(4,)m y −，2(,)m y 在抛物线2y ax bx c =++上， ∴对称轴为直线422m mx m −+==−， ①如图所示：21y y c <<，6m ∴<且06232m +−>=， 56m ∴<<；②如图所示：21y y c <<，46m ∴−>， 10m ∴>，综上所述，m 的取值范围为56m <<或10m >．【点评】本题考查二次函数图象与系数的关系以及二次函数图象上点的坐标特征，关键是利用数形结合和分类讨论的思想进行解答．题型三．待定系数法求二次函数解析式（共3小题）12．（2024•保山一模）如图，抛物线2y ax bx c =++过(2,0)A −，(3,0)B ，(0,6)C 三点；点P 是第一象限内抛物线上的动点，点P 的横坐标是m ，且132m <<．（1）试求抛物线的表达式；（2）过点P 作PN x ⊥轴并交BC 于点N ，作PM y ⊥轴并交抛物线的对称轴于点M ，若12PM PN =，求m 的值．【分析】（1）将A ，B ，C 三点坐标代入函数解析式即可解决问题．（2）用m 表示出PM 和PN ，建立关于m 的方程即可解决问题．【解答】解：（1）由题知，将A ，B ，C 三点坐标代入函数解析式得，4209306a b c a b c c −+=⎧⎪++=⎨⎪=⎩，解得116a b c =−⎧⎪=⎨⎪=⎩，所以抛物线的表达式为26y x x =−++．（2）将x m =代入抛物线得表达式得，26y m m =−++，所以点P 的坐标为2(,6)m m m −++．令直线BC 的函数解析式为y px q =+，则306p q q +=⎧⎨=⎩，解得26p q =−⎧⎨=⎩，所以直线BC 的函数解析式为26y x =−+．因为132m <<，且抛物线的对称轴为直线12x =，所以12PM m =−．又因为点N 坐标为(,26)m m −+，所以226(26)3PN m m m m m =−++−−+=−+．因为12PM PN =，所以211(3)22m m m −=−+，解得m =，又因为132m <<，所以m =．【点评】本题考查待定系数法求二次函数解析式及二次函数的图象和性质，熟知待定系数法及二次函数的图象和性质是解题的关键．13．（2024•东营区校级一模）如图，在平面直角坐标系xOy 中，直线28y x =−+与抛物线2y x bx c =−++交于A ，B 两点，点B 在x 轴上，点A 在y 轴上．（1）求抛物线的函数表达式；（2）点C 是直线AB 上方抛物线上一点，过点C 分别作x 轴，y 轴的平行线，交直线AB 于点D ，E ．当38DE AB =时，求点C 的坐标．【分析】（1）根据一次函数解析式求出A ，B 两点坐标，再将A ，B 两点坐标代入二次函数解析式即可解决问题．（2）根据AOB ECD ∆∆∽得到CD 与OB 的关系，建立方程即可解决问题．【解答】解：（1）令0x =得，8y =，所以点A 的坐标为(0,8)；令0y =得，4x =，所以点B 的坐标为(4,0)；将A ，B 两点坐标代入二次函数解析式得，81640c b c =⎧⎨−++=⎩，解得28b c =⎧⎨=⎩，所以抛物线的函数表达式为228y x x =−++．（2）因为//CD x 轴，//CE y 轴，所以AOB ECD ∆∆∽，则CD DEOB AB=．因为38DE AB =，4OB =，所以32CD =．令点C 坐标为2(,28)m m m −++，则点D 坐标为21(2m m −，228)m m −++所以2211()222CD m m m m m =−−=−+，则213222m m −+=，解得1m =或3．当1m =时，2289m m −++=；当3m =时，2285m m −++=；所以点C 的坐标为(1,9)或(3,5)．【点评】本题考查待定系数法求二次函数解析式及二次函数图象上点的坐标特征，熟知待定系数法及二次函数的图象和性质是解题的关键．14．（2024•南关区校级二模）已知二次函数2y x bx c =++的图象经过点(0,3)A −，(3,0)B ．点P 在抛物线2y x bx c =++上，其横坐标为m ．（1）求抛物线的解析式；（2）当23x −<<时，求y 的取值范围；（3）当抛物线2y x bx c =++上P 、A 两点之间部分的最大值与最小值的差为34时，求m 的值；（4）点M 在抛物线2y x bx c =++上，其横坐标为1m −．过点P 作PQ y ⊥轴于点Q ，过点M 作MN x ⊥轴于点N ，分别连结PM ，PN ，QM ，当PQM ∆与PNM ∆的面积相等时，直接写出m 的值．【分析】（1）依据题意，将A 、B 两点代入解析式求出b ，c 即可得解；（2）依据题意，结合（1）所求解析式，再配方可得抛物线的最值，进而由23x −<<可以判断得解；（3）依据题意，分类讨论计算可以得解；（4）分别写出P 、Q 、M 、N 的坐标，PQM ∆与PNM ∆的面积相等，所以Q 到PM 的距离等于N 到PM 的距离，可得m 的值．【解答】解：（1）由题意，将(0,3)A −，(3,0)B 代入解析式2y x bx c =++得，3c =−，930b c ++=，2b ∴=−，3c =−，∴抛物线的解析式为223y x x =−−；（2）由题意，抛物线2223(1)4y x x x =−−=−−，∴抛物线223y x x =−−开口向上，当1x =时，y 有最小值为4−，当2x =−时，5y =；当3x =时，0y =， ∴当23x −<<时，45y −<…；（3）由题意得，2(,23)P m m m −−，(0,3)A −，①当0m <时，P 、A 两点之间部分的最大值为223m m −−，最小值为3−， 2323(3)4m m ∴−−−−=，解得：1m =−②当02m ……时，P 、A 两点之间部分的最大值为3−，最小值为223m m −−或4−，显然最小值是4−时不合题意， ∴最小值为223m m −−， 233(23)4m m ∴−−−−=，解得：32m =或12m =， 32m =时，P 、A 两点之间部分的最小值为4−，故舍去， ③当2m <时，P 、A 两点之间部分的最大值为223m m −−，最小值为4−， 2323(4)4m m ∴−−−−=，解得：1m =+，12+<，故舍去，综上，满足题意得m 的值为：1或12；（4）由题意得，2(1,4)M m m −−，(1,0)N m −，2(0,23)Q m m −−，设PM y kx b =+，代入P 、M 两点， 2223(1)4mk b m m m k b m ⎧+=−−⎨−+=−⎩，解得：1k =−，23b m m =−−，23PM y x m m =−+−−，PQM ∆与PNM ∆的面积相等，Q ∴到23PM y x m m =−+−−的距离与N 到23PM y x m m =−+−−的距离相等，Q 到23PM y x m m =−+−−的距离=，N 到23PMy x m m =−+−−的距离=， 2|||4|m m ∴−=−+，当2m <−时，24m m −=−，解得：m =，当20m −……时，24m m −=−，解得：m =，当02m <…时，24m m =−，解得：m =当2m <时，24m m =−，解得：m =综上，满足题意得m ．【点评】本题考查了二次函数，关键是注意分类讨论．题型四．抛物线与x 轴的交点（共14小题）15．（2024•秦淮区校级模拟）已知函数2(2)2(y mx m x m =−−−为常数）．（1）求证：不论m 为何值，该函数的图象与x 轴总有公共点．（2）不论m ．（3）在22x −……的范围中，y 的最大值是2，直接写出m 的值．【分析】（1）分两种情况讨论，利用判别式证明即可；（2）当1x =时，0y =，当0x =时，2y =−，即可得到定点坐标；（3）利用抛物线过两个定点，得到函数y 随x 增大而增大，代入解析式求出m 值即可．【解答】解：（1）①当0m =时，函数解析式为22y x =−，此一次函数与x 轴有交点； ②当0m ≠时，函数解析式为2(2)2y mx m x =−−−，令0y =，则有2(2)20mx m x −−−=，△2222(2)4(2)44844(2)0m m m m m m m m =−−⨯−=−++=++=+…． ∴不论m 为何值，该函数的图象与x 轴总有公共点．（2）222(2)222()22y mx m x mx mx x m x x x =−−−=−+−=−+−，当1x =时，0y =，当0x =时，2y =−，∴不论m 为何值，该函数的图象经过的定点坐标是(1,0)．(0,2)−故答案为：(1,0)，(0,2)−，（3）若0m =，函数22y x =−，y 随x 增大而增大，当2x =时，2y =，与题干条件符；当0m ≠时，函数2(2)2y mx m x =−−−是二次函数，①当0m >时，抛物线过(1,0)，(0,2)−两点，当22x −……的范围中时，y 随x 的增大而增大， ∴当2x =时，2y =，即242(2)2m m =−−−，解得0m =（舍去）．②当0m <时，抛物线过(1,0)，(0,2)−两点，其增减性依旧是y 随x 的增大而增大和①相同．综上分析，0m =．【点评】本题考查了二次函数的图象与性质，熟练掌握二次函数的性质是解答本题的关键．16．（2024•柳州模拟）如图，在平面直角坐标系中，二次函数2y x bx c =++的图象与x 轴交于A ，B 两点，B 点的坐标为(3,0)，与y 轴交于点(0,3)C −，点D 为抛物线的顶点．（1）求这个二次函数的解析式；（2）求ABD ∆的面积【分析】（1）利用待定系数法求解即可；（2）先求出点A 和点D 坐标，再根据||2D ABD AB y S ∆⋅=解析求解即可．【解答】解：（1）将(3,0)B ，(0,3)C −代入2y x bx c =++得0933b c c =++⎧⎨=−⎩，解得23b c =−⎧⎨=−⎩，∴二次函数的解析式为：223y x x =−−；（2）将223y x x =−−配方得顶点式2(1)4y x =−−， ∴顶点(1,4)D −，在223y x x =−−中，当2230y x x =−−=时，解得1x =−或3x =， (1,0)A ∴−，4AB ∴=， ∴||44822D ABD AB y S ∆⋅⨯===．【点评】本题主要考查了抛物线与x 轴的交点，二次函数的性质，二次函数图象上点的坐标特征，待定系数法求二次函数解析式，熟练掌握二次函数的性质是解答本题的关键．17．（2024•安阳模拟）如图，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同，且与x 轴交于点(1,0)−和(4,0)．直线2y kx =+分别与x 轴、y 轴交于点A ，B ，交抛物线2y ax bx c =++于点C ，D （点C 在点D 的左侧）．（1）求抛物线的解析式；（2）点P 是直线2y kx =+上方抛物线上的任意一点，当2k =时，求PCD ∆面积的最大值；（3）若抛物线2y ax bx c =++与线段AB 有公共点，结合函数图象请直接写出k 的取值范围．【分析】（1）根据题意直接求出二次函数解析式即可；（2）求出直线与抛物线的交点C ，D 坐标，过点P 作y 轴的平行线交CD 于点H ，交x 轴于点G ，设点P坐标为(m ，234)(12)m m m −++−<<，则点(,22)H m m +，求出PH ，由三角形的面积公式求出关于m 的函数解析式，再根据函数的性质求最值；（3）分0k >和0k <两种情况讨论即可．【解答】解：（1）抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同，1a ∴=−，抛物线2y ax bx c =++与x 轴交于点(1,0)−和(4,0)， ∴抛物线的解析式为2(1)(4)34y x x x x =−+−=−++；（2）当2k =时，联立方程组22234y x y x x =+⎧⎨=−++⎩，解得10x y =−⎧⎨=⎩或26x y =⎧⎨=⎩， (1,0)C ∴−，(2,6)D ，过点P 作y 轴的平行线交CD 于点H ，交x 轴于点G ，如图，设点P 坐标为(m ，234)(12)m m m −++−<<， ∴点(,22)H m m +，2234(22)2PH m m m m m ∴=−++−+=−++，221331273(2)()22228PCD S PH m m m ∆∴=⨯=−++=−−+， 302−<，12m −<<， ∴当12m =时，S 有最大值，最大值为278． PCD ∴∆面积的最大值为278；（3）令0x =，则2y =， ∴点B 坐标为(0,2)，令0y =，则20kx +=，解得2x k=−，∴点A 坐标为2(k−，0)，若抛物线2y ax bx c =++与线段AB 有公共点，当0k >时，如图所示，则21k−<−，解得02k <<；当0k <时，如图所示：则24k−>，解得102k −<<；综上所述，k 的取值范围为02k <<或102k −<<．【点评】本题考查抛物线与x 轴的交点，待定系数法求函数解析式，二次函数图象上点的坐标特征，一次函数图象上点的坐标特征，二次函数的最值等知识，关键是对这些知识的掌握和运用．18．（2024•西湖区校级模拟）已知21()y ax a b x b =+++和22()(y bx a b x a a b =+++≠且0)ab ≠是同一直角坐标系中的两条抛物线．（1）当1a =，3b =−时，求抛物线21()y ax a b x b =+++的顶点坐标；（2）判断这两条抛物线与x 轴的交点的总个数，并说明理由；（3）如果对于抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…．当20y …时，求自变量x 的取值范围．【分析】（1）把a ，b 的值代入配方找顶点即可解题；（2）分别令10y =，20y =，解方程求出方程的解，然后根据条件确定交点的个数即可解题；（3）现根据题意得到0a <，且24()224ab a b a b a−+=+，然后得到30b a =−>，借助图象求出不等式的解集即可．【解答】解：（1）当1a =，3b =−时，2221()23(1)4y ax a b x b x x x =+++=−−=−−， ∴顶点坐标为(1,4)−；（2）3个，理由为：令10y =，则2()0ax a b x b +++=，即()(1)0ax b x ++=，解得：1bx a=−，21x =−，令20y =，则2()0bx a b x a +++=，即()(1)0bx a x ++=，解得：1ax b=−，21x =−，又a b ≠且0ab ≠，∴两条抛物线与x 轴的交点总个数为3个；（3）抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…，0a ∴<，且24()224ab a b a b a−+=+，整理得：30b a =−>，∴22()y bx a b x a =+++的开口向上，且抛物线与x 轴交点的横坐标为113x =，21x =−，如图所示，借助图象可知当13x …或1x −…时，20y …．【点评】本题考查二次函数的图象和性质，掌握配方法求顶点坐标，二次函数和一元二次方程的关系是解题的关键．19．（2024•三元区一模）抛物线23y ax bx =++与x 轴相交于点(1,0)A ，(3,0)B ，与y 轴正半轴相交于点C ．（1）求抛物线的解析式；（2）点1(M x ，1)y ，2(N x ，2)y 是抛物线上不同的两点． ①当1x ，2x 满足什么数量关系时，12y y =； ②若12122()x x x x +=−，求12y y −的最小值．【分析】（1）用待定系数法即可求解；（2）①若12y y =，则M 、N 关于抛物线对称轴对称，即可求解；②22121122121212(43)(43)()()4()y y x x x x x x x x x x −=−+−−+=+−+−，而12122()x x x x +=−，得到12y y −的函数表达式，进而求解．【解答】解：（1）设抛物线的表达式为：12()()y a x x x x =−−，即2(1)(3)(43)y a x x a x x =−−=−+，即33a =，解得：1a =，故抛物线的表达式为：243y x x =−+；（2）如图，。

二次函数题型分类总结

二次函数题型分类总结二次函数是高中数学中一个重要的内容，也是学生们经常接触到的数学题型之一。

在学习二次函数的过程中，我们会遇到各种不同类型的题目，这些题目涵盖了二次函数的基本概念、性质、图像、方程、不等式等多个方面。

为了帮助大家更好地理解和掌握二次函数的相关知识，本文将对二次函数题型进行分类总结，以便学生们能够更系统地学习和应用这一知识点。

一、基本概念题型。

1. 求二次函数的顶点、对称轴、开口方向等基本性质；2. 确定二次函数的增减性、最值等相关问题；3. 根据二次函数的图像特点进行分析和判断。

二、方程与不等式题型。

1. 解二次函数的方程，包括一元二次方程和二元二次方程；2. 求二次函数不等式的解集，包括一元二次不等式和二元二次不等式。

三、图像与性质题型。

1. 根据给定的二次函数，绘制其图像；2. 根据图像，确定二次函数的各种性质，如开口方向、顶点坐标、对称轴等；3. 利用二次函数的图像进行相关问题的分析和解决。

四、应用题型。

1. 利用二次函数解决实际问题，如抛物线运动、优化问题等；2. 利用二次函数的性质解决相关的数学问题，如几何问题、物理问题等。

五、综合题型。

1. 将多个知识点进行综合运用，解决复杂的二次函数问题；2. 考察学生对二次函数整体理解和运用能力的题目。

通过以上分类总结，我们可以清晰地了解到二次函数题型的多样性和复杂性。

在学习和解答二次函数题目时，我们需要全面掌握二次函数的基本概念和性质，灵活运用相关的解题方法，善于将不同的知识点进行整合和应用。

同时，我们也要注重实际问题的应用，将抽象的数学知识与实际生活相结合，更好地理解和掌握二次函数的相关内容。

希望通过本文的总结，能够帮助大家更好地理解和掌握二次函数的相关知识，提高解答二次函数题目的能力和水平。

同时，也希望大家能够在学习数学的过程中保持耐心和积极性，不断提升自己的数学素养，为将来的学习和发展打下坚实的数学基础。

中考数学二次函数题型总结一网打尽

中考数学二次函数题型总结一网打尽
二次函数在历年中考中均为压轴题，区分度较大，通常为三小问，每小问4分，共计11-12分。

第一问较为基础，通常为求，点坐标或函数解析式(二次函数、一次函数)，以及判断三角形形状（通常为判断直角三角形）和求线段长度，求解比较容易。

第二问为动，点双最值问题，难度中上。

通常为“面积最值+线段和差最值”或“线段和差积最值+线段和差最值”组合形式，即先求出使得某三角或四边形面积最大时的动点位置，在此基础上再求相关线段和差最值，如两线段差值最大或线段和最小（如某三角形或四边形周长最小等），计算量偏大，易出错。

常要利用第一问中的条件或结论进行求解。

第三问多为动态背景下的存在性问题，常为两类。

一类是动点，一类是动线（线段运动或是抛物线运动），在此背景下讨论特殊几何图形(等腰三角形、等边三角形、直角三角形、平行四边形、矩形、菱形等)的存在性问题，综合性强，难度大。

历来以等腰三角形考察居多。

666。

中考压轴题-二次函数综合(八大题型+解题方法)——冲刺2024年中考数学考点押题(全国通用)(解析)

中考压轴题-二次函数综合（八大题型+解题方法）1、求证“两线段相等”的问题：借助于函数解析式,先把动点坐标用一个字母表示出来；然后看两线段的长度是什么距离即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴y 轴的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等;2、“平行于y 轴的动线段长度的最大值”的问题：由于平行于y 轴的线段上各个点的横坐标相等常设为t,借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标;3、求一个已知点关于一条已知直线的对称点的坐标问题：先用点斜式或称K ,且与已知直线垂直的直线解析式,再求出两直线的交点坐标,最后用中点坐标公式即可;4、“抛物线上是否存在一点,使之到定直线的距离最大”的问题：方法1先求出定直线的斜率,由此可设出与定直线平行且与抛物线相切的直线的解析式注意该直线与定直线的斜率相等,因为平行直线斜率k 相等,再由该直线与抛物线的解析式组成方程组,用代入法把字母y 消掉,得到一个关于x 的的一元二次方程,由题有△=2b -4ac=0因为该直线与抛物线相切,只有一个交点,所以2b -4ac=0从而就可求出该切线的解析式,再把该切线解析式与抛物线的解析式组成方程组,求出x 、y 的值,即为切点坐标,然后再利用点到直线的距离公式,计算该切点到定直线的距离,即为最大距离; 方法2该问题等价于相应动三角形的面积最大问题,从而可先求出该三角形取得最大面积时,动点的坐标,再用点到直线的距离公式,求出其最大距离;方法3先把抛物线的方程对自变量求导,运用导数的几何意义,当该导数等于定直线的斜率时,求出的点的坐标即为符合题意的点,其最大距离运用点到直线的距离公式可以轻松求出;5、常数问题：1点到直线的距离中的常数问题：“抛物线上是否存在一点,使之到定直线的距离等于一个固定常数”的问题：先借助于抛物线的解析式,把动点坐标用一个字母表示出来,再利用点到直线的距离公式建立一个方程,解此方程,即可求出动点的横坐标,进而利用抛物线解析式,求出动点的纵坐标,从而抛物线上的动点坐标就求出来了;2三角形面积中的常数问题：“抛物线上是否存在一点,使之与定线段构成的动三角形的面积等于一个定常数”的问题：先求出定线段的长度,再表示出动点其坐标需用一个字母表示到定直线的距离,再运用三角形的面积公式建立方程,解此方程,即可求出动点的横坐标,再利用抛物线的解析式,可求出动点纵坐标,从而抛物线上的动点坐标就求出来了;3几条线段的齐次幂的商为常数的问题：用K 点法设出直线方程,求出与抛物线或其它直线的交点坐标,再运用两点间的距离公式和根与系数的关系,把问题中的所有线段表示出来,并化解即可;6、“在定直线常为抛物线的对称轴,或x 轴或y 轴或其它的定直线上是否存在一点,使之到两定点的距离之和最小”的问题：先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出利用求交点坐标的方法;7、三角形周长的“最值最大值或最小值”问题：① “在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题简称“一边固定两边动的问题：由于有两个定点,所以该三角形有一定边其长度可利用两点间距离公式计算,只需另两边的和最小即可;② “在抛物线上是否存在一点,使之到定直线的垂线,与y 轴的平行线和定直线,这三线构成的动直角三角形的周长最大”的问题简称“三边均动的问题：在图中寻找一个和动直角三角形相似的定直角三角形,在动点坐标一母示后,运用=C C 动动定定斜边斜边,把动三角形的周长转化为一个开口向下的抛物线来破解;8、三角形面积的最大值问题：① “抛物线上是否存在一点,使之和一条定线段构成的三角形面积最大”的问题简称“一边固定两边动的问题”：方法1：先利用两点间的距离公式求出定线段的长度；然后再利用上面３的方法,求出抛物线上的动点到该定直线的最大距离;最后利用三角形的面积公式= 12底×高;即可求出该三角形面积的最大值,同时在求解过程中,切点即为符合题意要求的点;方法2：过动点向y 轴作平行线找到与定线段或所在直线的交点,从而把动三角形分割成两个基本模型的三角形,动点坐标一母示后,进一步可得到）（）（左（定）右（定）下（动）上（动）动三角形x x y y 21−⋅−=S ,转化为一个开口向下的二次函数问题来求出最大值;②“三边均动的动三角形面积最大”的问题简称“三边均动”的问题：先把动三角形分割成两个基本模型的三角形有一边在x 轴或y 轴上的三角形,或者有一边平行于x 轴或y 轴的三角形,称为基本模型的三角形面积之差,设出动点在x 轴或y 轴上的点的坐标,而此类题型,题中一定含有一组平行线,从而可以得出分割后的一个三角形与图中另一个三角形相似常为图中最大的那一个三角形;利用相似三角形的性质对应边的比等于对应高的比可表示出分割后的一个三角形的高;从而可以表示出动三角形的面积的一个开口向下的二次函数关系式,相应问题也就轻松解决了;9、“一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”：由于该四边形有三个定点,,即可得到一个定三角形的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与7相同;10、“定四边形面积的求解”问题：有两种常见解决的方案：方案一：连接一条对角线,分成两个三角形面积之和；方案二：过不在x 轴或y 轴上的四边形的一个顶点,向x 轴或y 轴作垂线,或者把该点与原点连结起来,分割成一个梯形常为直角梯形和一些三角形的面积之和或差,或几个基本模型的三角形面积的和差11、“两个三角形相似”的问题：两个定三角形是否相似：（1）已知有一个角相等的情形：运用两点间的距离公式求出已知角的两条夹边,看看是否成比例若成比例,则相似;否则不相似;（2）不知道是否有一个角相等的情形：运用两点间的距离公式求出两个三角形各边的长,看看是否成比例若成比例,则相似;否则不相似;一个定三角形和动三角形相似：（1）已知有一个角相等的情形：先借助于相应的函数关系式,把动点坐标表示出来一母示,然后把两个目标三角形题中要相似的那两个三角形中相等的那个已知角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那两边对应成比例要注意是否有两种情况,列出方程,解此方程即可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点;2不知道是否有一个角相等的情形：这种情形在相似性中属于高端问题,破解方法是,在定三角形中,由各个顶点坐标求出定三角形三边的长度,用观察法得出某一个角可能是特殊角,再为该角寻找一个直角三角形,用三角函数的方法得出特殊角的度数,在动点坐标“一母示”后,分析在动三角形中哪个角可以和定三角形中的那个特殊角相等,借助于特殊角,为动点寻找一个直角三角形,求出动点坐标,从而转化为已知有一个角相等的两个定三角形是否相似的问题了,只需再验证已知角的两边是否成比例若成比例,则所求动点坐标符合题意,否则这样的点不存在;简称“找特角,求动点标,再验证”;或称为“一找角,二求标,三验证”;12、“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题：首先弄清题中是否规定了哪个点为等腰三角形的顶点;若某边底,则只有一种情况；若某边为腰,有两种情况；若只说该三点构成等腰三角形则有三种情况;先借助于动点所在图象的解析式,表示出动点的坐标一母示,按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程;解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点就是不能构成三角形这个题意;13、“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题：这类问题,在题中的四个点中,至少有两个定点,用动点坐标“一母示”分别设出余下所有动点的坐标若有两个动点,显然每个动点应各选用一个参数字母来“一母示”出动点坐标,任选一个已知点作为对角线的起点,列出所有可能的对角线显然最多有3条,此时与之对应的另一条对角线也就确定了,然后运用中点坐标公式,求出每一种情况两条对角线的中点坐标,由平行四边形的判定定理可知,两中点重合,其坐标对应相等,列出两个方程,求解即可;进一步有：①若是否存在这样的动点构成矩形呢先让动点构成平行四边形,再验证两条对角线相等否若相等,则所求动点能构成矩形,否则这样的动点不存在;②若是否存在这样的动点构成棱形呢先让动点构成平行四边形,再验证任意一组邻边相等否若相等,则所求动点能构成棱形,否则这样的动点不存在;③若是否存在这样的动点构成正方形呢先让动点构成平行四边形,再验证任意一组邻边是否相等和两条对角线是否相等若都相等,则所求动点能构成正方形,否则这样的动点不存在;14、“抛物线上是否存在一点,使两个图形的面积之间存在和差倍分关系”的问题：此为“单动问题”〈即定解析式和动图形相结合的问题〉,后面的19实为本类型的特殊情形;先用动点坐标“一母示”的方法设出直接动点坐标,分别表示如果图形是动图形就只能表示出其面积或计算如果图形是定图形就计算出它的具体面积,然后由题意建立两个图形面积关系的一个方程,解之即可;注意去掉不合题意的点,如果问题中求的是间接动点坐标,那么在求出直接动点坐标后,再往下继续求解即可;15、“某图形〈直线或抛物线〉上是否存在一点,使之与另两定点构成直角三角形”的问题：若夹直角的两边与y轴都不平行：先设出动点坐标一母示,视题目分类的情况,分别用斜率公式算出夹直角的两边的斜率,再运用两直线没有与y轴平行的直线垂直的斜率结论两直线的斜率相乘等于-1,得到一个方程,解之即可;若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式;补救措施是：过余下的那一个点没在平行于y轴的那条直线上的点直接向平行于y的直线作垂线或过直角点作平行于y轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定;16、“某图象上是否存在一点,使之与另两定点构成等腰直角三角形”的问题;①若定点为直角顶点,先用k点法求出另一直角边所在直线的解析式如斜率不存在,根据定直角点,可以直接写出另一直角边所在直线的方程,利用该解析式与所求点所在的图象的解析式组成方程组,求出交点坐标,再用两点间的距离公式计算出两条直角边等否若等,该交点合题,反之不合题,舍去;②若动点为直角顶点：先利用k点法求出定线段的中垂线的解析式,再把该解析式与所求点所在图象的解析式组成方程组,求出交点坐标,再分别计算出该点与两定点所在的两条直线的斜率,把这两个斜率相乘,看其结果是否为-1 若为-1,则就说明所求交点合题；反之,舍去;17、“题中含有两角相等,求相关点的坐标或线段长度”等的问题：题中含有两角相等,则意味着应该运用三角形相似来解决,此时寻找三角形相似中的基本模型“A”或“X”是关键和突破口;18、“在相关函数的解析式已知或易求出的情况下,题中又含有某动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或线段长”的问题：此为“单动问题”〈即定解析式和动图形相结合的问题〉,本类型实际上是前面14的特殊情形;先把动图形化为一些直角梯形或基本模型的三角形有一边在x 轴或ｙ轴上,或者有一边平行于x 轴或y 轴面积的和或差,设出相关点的坐标一母示,按化分后的图形建立一个面积关系的方程,解之即可;一句话,该问题简称“单动问题”,解题方法是“设点动点标,图形转化分割,列出面积方程”;19、“在相关函数解析式不确定系数中还含有某一个参数字母的情况下,题中又含有动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或参数的值”的问题：此为“双动问题”即动解析式和动图形相结合的问题;如果动图形不是基本模型,就先把动图形的面积进行转化或分割转化或分割后的图形须为基本模型,设出动点坐标一母示,利用转化或分割后的图形建立面积关系的方程或方程组;解此方程,求出相应点的横坐标,再利用该点所在函数图象的解析式,表示出该点的纵坐标注意,此时,一定不能把该点坐标再代入对应函数图象的解析式,这样会把所有字母消掉;再注意图中另一个点与该点的位置关系或其它关系,方法是常由已知或利用2问的结论,从几何知识的角度进行判断,表示出另一个点的坐标,最后把刚表示出来的这个点的坐标再代入相应解析式,得到仅含一个字母的方程,解之即可;如果动图形是基本模型,就无须分割或转化了,直接先设出动点坐标一母式,然后列出面积方程,往下操作方式就与不是基本模型的情况完全相同;一句话,该问题简称“双动问题”,解题方法是“转化分割,设点标,建方程,再代入,得结论”;常用公式或结论：1横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长=纵标之差的绝对值=-y y 大小=-y y 下上 2点轴距离：点P 0x ,0y 到X 轴的距离为0y ,到Y 轴的距离为o x ; 3两点间的距离公式：若A 11,x y ,B 2,2x y , 则AB=目录：题型1：存在性问题题型2：最值问题题型3：定值问题题型4：定点问题题型5：动点问题综合题型6：对称问题题型7：新定义题题型8：二次函数与圆题型1：存在性问题1．（2024·四川广安·二模）如图，抛物线2y x bx c =−++交x 轴于()4,0A −，B 两点，交y 轴于点()0,4C ．(1)求抛物线的函数解析式．(2)点D 在线段OA 上运动，过点D 作x 轴的垂线，与AC 交于点Q ，与抛物线交于点P ，连接AP 、CP ，求四边形AOCP 的面积的最大值．(3)在抛物线的对称轴上是否存在点M ，使得以点A 、C 、M 为顶点的三角形是直角三角形？若存在，请求出点M【答案】(1)234y x x =−−+；(2)四边形AOCP 的面积最大为16；(3)点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭．【分析】本题主要考查了二次函数综合，熟练掌握用待定系数法求解函数解析式的方法和步骤，以及二次函数的图象和性质，是解题的关键．（1）把()4,0A −，()0,4C 代入2y x bx c =−++，求出b 和c 的值，即可得出函数解析式；（2）易得182AOCSOA OC =⋅=，设()2,34P t t t −−+，则(),4Q t t +，求出24PQ t t =−−，则()()212282ACP C A S PQ x x t =⋅−=−++，根据四边形AOCP 的面积()22216ACP AOCS St =+=−++，结合二次函数的增减性，即可解答；（3）设3,2M m ⎛⎫− ⎪⎝⎭，根据两点之间距离公式得出232AC =，22254AM m =+，229(4)4CM m =+−，然后分情况根据勾股定理列出方程求解即可．【解析】（1）解：把()4,0A −，()0,4C 代入2y x bx c =−++得：01644b c c =−−+⎧⎨=⎩，解得：34b c =−⎧⎨=⎩，∴该二次函数的解析式234y x x =−−+；（2）解：∵()4,0A −，()0,4C ，∴4,4OA OC ==，∴1144822AOC S OA OC =⋅=⨯⨯=△，设直线AC 的解析式为4y kx =+，代入()4,0A −得，044k =−+，解得1k =，∴直线AC 的解析式为4y x =+，设()2,34P t t t −−+，则(),4Q t t +，∴()223444PQ t t t t t=−−+−+=−−∴()()()22114422822ACPC A SPQ x x t t t =⋅−=−−⨯=−++，∴四边形AOCP 的面积()22216ACP AOCSSt =+=−++，∵20−<，∴当2t =−时，四边形AOCP 的面积最大为16；（3）解：设3,2M m ⎛⎫− ⎪⎝⎭，∵()4,0A −，()0,4C ，∴2224432AC =+=，2222325424AM m m ⎛⎫=−++=+ ⎪⎝⎭，()()2222394424CM m m ⎛⎫=−+−=+− ⎪⎝⎭，当斜边为AC 时，AM CM AC 222+=，即()2225943244m m +++−=，整理得：24150m m ++=，无解；当斜边为AM 时，222AC CM AM +=，即2292532(4)44m m ++−=+，解得：112m =；∴311,22M ⎛⎫− ⎪⎝⎭当斜边为CM 时，222AC AM CM +=，即2225932(4)44m m ++=+−，解得：52m =−；∴35,22M ⎛⎫−− ⎪⎝⎭综上：点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭．2．（2024·内蒙古乌海·模拟预测）如图（1），在平面直角坐标系中，抛物线()240y ax bx a =+−≠与x 轴交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于点C ，点A 的坐标为()1,0−，且OC OB =，点D 和点C 关于抛物线的对称轴对称．(1)分别求出a ，b 的值和直线AD 的解析式；(2)直线AD 下方的抛物线上有一点P ，过点P 作PH AD ⊥于点H ，作PM 平行于y 轴交直线AD 于点M ，交x 轴于点E ，求PHM 的周长的最大值；(3)在（2）的条件下，如图2，在直线EP 的右侧、x 轴下方的抛物线上是否存在点N ，过点N 作NG x ⊥轴交x 轴于点G ，使得以点E 、N 、G 为顶点的三角形与AOC 相似？如果存在，请直接写出点G 的坐标；如果不存在，请说明理由．【答案】(1)1a =，3b =−，=1y x −−(2)4+(3)存在，点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】本题主要考查的是二次函数的综合应用，掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式，列出PM 的长与a 的函数关系式是解题的关键．（1）先求得C 的坐标，从而得到点B 的坐标，设抛物线的解析式为()()14y a x x =+−，将点C 的坐标代入求解即可；先求得抛物线的对称轴，从而得到点()3,4D −，然后可求得直线AD 的解析式=1y x −−；（2）求得45BAD ∠=︒，接下来证明PMD △为等腰直角三角形，所当PM 有最大值时三角形的周长最大，设()2,34P a a a −−，()1M a −−，则223PM aa =−++，然后利用配方可求得PM 的最大值，最后根据MPH△的周长(1PM=求解即可；（3）当90EGN ∠=︒时，如果OA EG OC GN = 或OA GNOC EN =时，则AOC ∽EGN △，设点G 的坐标为(),0a ，则()2,34N a a a −−，则1EG a =−，234NG aa =−++，然后根据题意列方程求解即可．【解析】（1）点A 的坐标为()1,0−，1OA ∴=．令0x =，则4y =−，()0,4C ∴−，4OC =，OC OB =Q ， 4OB ∴=，()4,0B ∴，设抛物线的解析式为()()14y a x x =+−，将0x =，4y =−代入得：44a −=−，解得1a =，∴抛物线的解析式为234y x x =−−；1a ∴=，3b =−；抛物线的对称轴为33212x −=−=⨯，()0,4C −，点D 和点C 关于抛物线的对称轴对称，()3,4D ∴−；设直线AD 的解析式为y kx b =+．将()1,0A −、()3,4D −代入得：034k b k b −+=⎧⎨+=−⎩，解得1k =−，1b =-，∴直线AD 的解析式=1y x −−；（2）直线AD 的解析式=1y x −−，∴直线AD 的一次项系数1k =−，45BAD ∴∠=︒． PM 平行于y 轴，90AEP ∴∠=︒，45PMH AME ∴∠=∠=︒．MPH ∴的周长(122PM MH PH PM MP PM PM =++=++=．设()2,34P a a a −−，则(),1M a a −−，则()22213423(1)4PM a a a a a a =−−−−−=−++=−−+．∴当1a =时，PM 有最大值，最大值为4．MPH ∴的周长的最大值(414=⨯=+（3）在直线EP 的右侧、x 轴下方的抛物线上存在点N ，过点N 作NG x ⊥轴交x 轴于点G ，使得以点E 、N 、G 为顶点的三角形与AOC 相似；理由如下：设点G 的坐标为(),0a ，则()2,34N a a a −−①如图2.1，若OA EG OC GN = 时，AOC ∽EGN △．则 211344a a a −=−++，整理得：280a a +−=．得：a =负值舍去)，∴点G为⎫⎪⎪⎝⎭； ②如图2.2，若OA GN OC EN =时，AOC ∽NGE ，则21434a a a −=−++，整理得：2411170a a −−=，得：a =负值舍去)，∴点G为⎫⎪⎪⎝⎭，综上所述，点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭． 3．（2024·重庆·一模）如图，在平面直角坐标系中，抛物线2y ax bx =+x 轴交于点()1,0A −，()5,0B ，与y 轴交于点C ，连接BC ，AC ．(1)求抛物线的表达式；(2)P 为直线BC 上方抛物线上一点，过点P 作PD BC ⊥于点D ，过点P 作PE x 轴交抛物线于点E，求4+PD PE 的最大值及此时点P 的坐标； (3)点C 关于抛物线对称轴对称的点为Q ，将抛物线沿射线CAy '，新抛物线y '与y 轴交于点M ，新抛物线y '的对称轴与x 轴交于点N ，连接AM ，MN ，点R 在直线BC 上，连接QR ．当QR 与AMN 一边平行时，直接写出点R 的坐标，并写出其中一种符合条件的解答过程．【答案】(1)2y x x =++(2)当154t =时，PE的最大值，15,416P ⎛ ⎝⎭， (3)R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(．【分析】（1）利用待定系数法求抛物线解析式即可；（2）先求得2y x =2x =，过点P 作PG x ⊥轴交BC 于点F ，利用勾股定理求得BC ==DPF OBC ∽，得PF DP BC OB =即PF PD=，从而得PF =，求出设直线BC的解析式后，设2,P t ⎛+ ⎝，则,F t ⎛+ ⎝，从而2PF =+，当点P在E 点右侧时()424PE t t t =−−=−，从而得2154t ⎫=−⎪⎝⎭，利用二次函数的性质即可求解；当点P 在E 点左侧时：442PE t t t =−−=−时，同理可求．然后比较4+PE 的最大值即可得出答案. （3）先求得1OA=，OC AC =设抛物线2y =H ⎛ ⎝⎭平移后为P ，过点P 作PW ⊥直线2x =，则AOC PWH ∽，得1OA OC AC WP HW PH ====，进而得平移后的抛物线2y x +'=，从而求得()1,0N，M ⎛ ⎝⎭，然后分QR AM ∥，QR MN ∥，QR AN ∥三种情况，利用二次函数的性质及一次函数的与二元一次方程的关系求解即可得解．【解析】（1）解：∵抛物线2y ax bx =+x 轴交于点()1,0A −，()5,0B 两点，代入坐标得：02550a b a b ⎧−=⎪⎨+=⎪⎩，解得：a b ⎧=⎪⎪⎨⎪=⎪⎩，∴抛物线的函数表达式为255y x x =−++（2）解：∵)2225555y x x x =−+=−−+，∴2y x =2x=，顶点为⎛ ⎝⎭ 过点P 作PG x ⊥轴交BC 于点F ，当0x =时，200y =∴(C ∵()5,0B ∴BC ==∵PG x ⊥轴，PD BC ⊥，x 轴y ⊥轴，∴909090CBO BFG DPF PFD PDF BOC ∠∠∠∠∠∠+=︒+=︒==︒，，∵PFD BFG ∠∠=∴DPF CBO ∠∠=∴DPF OBC ∽，∴PF DP BC OB =即PF PD =，∴PF PD =∴44+PD PE =PF +PE ，设直线BC ：y kx b =+，把(C ，()5,0B 代入得：05k b b =+⎧⎪=，解得5k b ⎧=−⎪⎨⎪=⎩， ∴直线BC：y =设2,P t ⎛ ⎝，则,F t ⎛+ ⎝，∴22PF ⎛⎛=−+=+ ⎝⎝，∵2y x =2x =，PE x 轴，∴24,E t ⎛−+ ⎝当点P 在E 点右侧时：()424PE t t t =−−=−，当24PE t =−时：∴+PD PE =PF +()221524545416t t ⎛⎫=−+−=−−+ ⎪⎝⎭ ∴当154t =时，的最大值∴2151544⎛⎫= ⎪⎝⎭，∴154P ⎛ ⎝⎭；当点P 在E 点左侧时：442PE t t t =−−=−时，∴+PD PE =PF +()225424t t ⎫=−=−⎪⎝⎭， ∴当54t =时，的最大值．2,55P t ⎛−+ ⎝∴25544⎛⎫ ⎪⎝⎭∴5,416P ⎛ ⎝⎭，∵> 综上所诉，当点P 在E 点右侧时：即154t =时，的最大值，154P ⎛ ⎝⎭，（3）解：设直线AC ：y mx n =+，把()1,0A −，(C ， ∴1OA =，OC =∴AC ==设抛物线2y x =H ⎛ ⎝⎭平移后为P ，过点P 作PW ⊥直线2x =，则AOC PWH ∽，∴1OA OC AC WP HW PH ====∴1PW =，HW=∴21,5P ⎛−⎝即1,5P ⎛ ⎝⎭，∴平移后的抛物线)22155555y x x x =−−+=−++'， ∴()1,0N令0x =，y '=，∴M ⎛ ⎝⎭ 如图，当QR AM ∥时，设直线AM 的解析式为：y px q =+，把M ⎛ ⎝⎭，()1,0A −代入得：0p q q =−+⎧=解得p q ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线AM的解析式为：y =， ∴设直线QR的解析式为：y x n =∵(C ，Q 和C 关于2x =对称，∴(Q把(Q代入5y x n =+45n +，解得n =，∴直线QR的解析式为：y = 联立直线QR的解析式y =与直线BC：y x =+55y x y x ⎧=−⎪⎪⎨⎪=⎪⎩，解得3x y =⎧⎪⎨=⎪⎩，∴R ⎛ ⎝⎭ 同理可得：当QR MN ∥时，6,5R ⎛− ⎝⎭ 当QR AN ∥时，(R所有符合条件的R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(．【点睛】本题考查待定系数法求抛物线解析式，勾股定理，抛物线的性质，抛物线平移，一次函数的平移，相似三角形的判定及性质，图形与坐标，掌握待定系数法求抛物线解析式，抛物线的性质，抛物线平移，相似三角形的判定及性质，图形与坐标，利用辅助线画出准确图形是解题关键．题型2：最值问题4．（2024·安徽合肥·二模）在平面直角坐标系中，O 为坐标原点，抛物线23y ax bx =+−与x 轴交于()1,0A −，()3,0B 两点，与y 轴交于点C ，连接BC ．(1)求a ，b 的值；(2)点M 为线段BC 上一动点（不与B ，C 重合），过点M 作MP x ⊥轴于点P ，交抛物线于点N ．（ⅰ）如图1，当3PA PB=时，求线段MN 的长；（ⅱ）如图2，在抛物线上找一点Q ，连接AM ，QN ，QP ，使得PQN V 与APM △的面积相等，当线段NQ 的长度最小时，求点M 的横坐标m 的值．【答案】(1)1a =，2b =−(2)（ⅰ）2MN =；（ⅱ）m 的值为32或12【分析】本题考查诶粗函数的图象和性质，掌握待定系数法和利用函数性质求面积是解题的关键．（1）运用待定系数法求函数解析式即可；（2）（ⅰ）先计算BC 的解析式，然后设(),3M m m −，则3PM PB m ==−，1PA m =+，根据题意得到方程133m m +=−求出m 值，即可求出MN 的长；（ⅱ）作QR PN ⊥于点R ，由（ⅰ）可得1PA m =+，3PB PM m =−−，223PN m m =−++，然后分为点Q 在PN 的左侧和点Q 在PN 的右侧两种情况，根据勾股定理解题即可．【解析】（1）由题意得309330a b a b −−=⎧⎨+−=⎩，解得12a b =⎧⎨=−⎩；（2）（ⅰ）当0x =时，3y =−，∴()0,3C −，设直线BC 为3y kx =−，∵点()3,0B ，∴330k −=，解得1k =，∴直线BC 为3y x =−，设(),3M m m −，则3PM PB m ==−，1PA m =+， ∵3PA PB =， ∴133m m +=−，解得2m =，经检验2m =符合题意，当2m =时，222233y =−⨯−=−， ∴3PN =，31PM PB m ==−=，∴2MN =；（ⅱ）作QR PN ⊥于点R ，由（ⅰ）可得1PA m =+，3PB PM m =−−，223PN m m =−++，PQN V 的面积为()21232m m QR −++⋅，APM △的面积为()()1312m m −+，∴()()()211233122m m QR m m −++⋅=−+，解得1QR =；当点Q 在PN 的左侧时，如图1，Q 点的横坐标为1m QR m −=−，纵坐标为()()2212134m m m m −−⨯−−=−，∴R 点的坐标为()2,4m mm−，∵N 点坐标为()2,23m mm −−，∴32RN m =−，∴()22231NQ m =−+，∴当32m =时，NQ 取最小值；当点Q 在PN 的右侧时，如图2，Q 点的横坐标为1m QR m +=+，纵坐标为()()2212134m m m +−⨯+−=−，∴R 点的坐标为()2,4m m−，∵N 点的坐标为()2,23m mm −−，∴21RN m =−， ∴()222211NQ m =−+，∴当12m =时，NQ 取最小值．综上，m 的值为32或12．。

中考复习二次函数题型分类总结

中考复习二次函数题型分类总结优秀资料！【二次函数的定义】（考点：二次函数的二次项系数不为0，且二次函数的表达式必须为整式）1、下列函数中，是二次函数的是.y=_24_ ；y=2_2；y=2_2 4_；y=3_；y=2_；y=m_2 n_ p；y=(4,_)；y=5_。

2、在一定条件下，若物体运动的路程s（米）与时间t（秒）的关系式为s=5t2 2t，则t4秒时，该物体所经过的路程为。

3、若函数y=(m2 2m7)_2 4_ 5是关于_的二次函数，则m的取值范围为。

、若函数m2是关于_的二次函数，则的值为。

4y=(m2)_ 5_ m6、已知函数y=(m)_m2 5_3是二次函数，求m的值。

【二次函数的对称轴、顶点、最值】（技法：如果解析式为顶点式y=a(_h)2 k，则最值为k；如果解析式为一般式24ac-b2y=a_ b_ c，则最值为4a22。

抛物线y=2_ 4_ mm经过坐标原点，则m的值为2抛物y=_2 b_ c线的顶点坐标为（，3），则b，c.3抛物线y_23_的顶点在A.第一象限B.第二象限C.第三象限D.第四象限4若抛物线ya_26_经过点(2，0)，则抛物线顶点到坐标原点的距离为A.3B.0C.5D.45若直线ya_b不经过二、四象限，则抛物线ya_2b_cA.开口向上，对称轴是y轴B.开口向下，对称轴是y轴C.开口向下，对称轴平行于y轴D.开口向上，对称轴平行于y轴26已知抛物线y_(m)_4的顶点的横坐标是2，则m的值是_.7抛物线y=_2 2_3的对称轴是。

8若二次函数y=3_2 m_3的对称轴是直线_，则m。

9当n_，m_时，函数y(mn)_n(mn)_的图象是抛物线，且其顶点在原点，此抛物线的开口_.0已知二次函数y=_22a_ 2a 3，当a=时，该函数y的最小值为0.优秀资料！已知二次函数y=m_2 (m)_ m有最小值为0，则m_。

2已知二次函数y=_24_ m3的最小值为3，则m。

(完整版)中考数学二次函数压轴题题型归纳

中考二次函数综合压轴题型归类一、常考点汇总1、两点间的距离公式：()()22B A B A x x y y AB -+-=2、中点坐标：线段AB 的中点C 的坐标为：⎪⎭⎫⎝⎛++22B A B A y y x x ，直线11b x k y +=（01≠k ）与22b x k y +=（02≠k ）的位置关系：（1）两直线平行⇔21k k =且21b b ≠ （2）两直线相交⇔21k k ≠ （3）两直线重合⇔21k k =且21b b = （4）两直线垂直⇔121-=k k3、一元二次方程有整数根问题，解题步骤如下：① 用∆和参数的其他要求确定参数的取值范围；② 解方程，求出方程的根；（两种形式：分式、二次根式）③ 分析求解：若是分式，分母是分子的因数；若是二次根式，被开方式是完全平方式。

例：关于x 的一元二次方程()01222＝－m x m x ++有两个整数根，5＜m 且m 为整数，求m 的值。

4、二次函数与x 轴的交点为整数点问题。

（方法同上）例：若抛物线()3132+++=x m mx y 与x 轴交于两个不同的整数点，且m 为正整数，试确定此抛物线的解析式。

5、方程总有固定根问题，可以通过解方程的方法求出该固定根。

举例如下：已知关于x 的方程23(1)230mx m x m --+-=（m 为实数），求证：无论m 为何值，方程总有一个固定的根。

解：当0=m 时，1=x ；当0≠m 时，()032≥-=∆m ，()m m x 213∆±-=，mx 321-=、12=x ；综上所述：无论m 为何值，方程总有一个固定的根是1。

6、函数过固定点问题，举例如下：已知抛物线22-+-=m mx x y （m 是常数），求证：不论m 为何值，该抛物线总经过一个解：把原解析式变形为关于m 的方程()x m x y -=+-122；∴ ⎩⎨⎧=-=+-01 02 2x x y ，解得：⎩⎨⎧=-=1 1 x y ；∴ 抛物线总经过一个固定的点（1，－1）。

中考二次函数常见题型

中考二次函数常见题型
中考二次函数常见题型包括：
1. 确定二次函数的表达式：根据已知条件，如顶点坐标、与x轴的交点坐标等，使用待定系数法求出二次函数的表达式。

2. 二次函数与一元一次方程的关系：根据二次函数图象与x轴的交点，求得一元二次方程的根。

3. 二次函数的增减性：根据二次函数的开口方向以及对称轴，判断函数的增减性。

4. 二次函数图象的平移：通过平移规则，将一个二次函数图象平移到指定位置，再根据平移后的顶点坐标求得新的二次函数表达式。

5. 二次函数的最值问题：根据二次函数的顶点和开口方向，求得函数的最大值或最小值。

6. 二次函数与几何图形的综合题：例如，已知抛物线与x轴交于A、B两点，与y轴交于点C，点P是抛物线上的动点，探究四边形ABCP的面积的最大值等。

这些题型涵盖了中考中二次函数的主要考点，可以通过针对性的练习加以掌握。

二次函数10大专题，40种类型！必考突破中考最后一关！。

学生、家长留言即送，机构老师请转载。

下载方式见私信。

专题1：二次函数基础上的数学建模类（部分内容）
专题2：二次函数与营销问题（部分内容）
专题3：二次函数背景下的图形变换
专题4：二次函数背景下的面积探究
专题5：特殊三角形存在性判定
专题6：二次函数背景下特殊四边形存在性讨论
专题7：二次函数背景下的三角形相似（全等）
专题8：二次函数背景下的线段和差倍分最值问题
专题9：二次函数背景下的动点问题
专题10：二次函数背景下与圆的综合
以上为部分截图，全部资料10个专题40余种类型，共100余页。

全部看完，学懂。

二次函数压轴题应该就不是问题。

初中中考二次函数压轴题分类突破之专题(一)数学建模类(附答案解析)

专题01 二次函数基础上的数学建模类【方法综述】此类问题以实际问题为背景，一般解答方法是先按照题目要求利用各种数学知识，构造二次函数的数学模型，再通过将临界点带入讨论或者通过考察二次函数最值讨论解决实际问题。

【典例示范】类型一临界点讨论例1：（2019河北石家庄毕业班教学质量检测）跳绳是大家喜闻乐见的一项体育运动,集体跳绳时,需要两人同频甩动绳子,当绳子甩到最高处时,其形状可近似看作抛物线,下图是小明和小亮甩绳子到最高处时的示意图,两人拿绳子的手之间的距离为4m,离地面的高度为1m,以小明的手所在位置为原点建立平面直角坐标系.(1)当身高为15m的小红站在绳子的正下方,且距小明拿绳子手的右侧1m处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;(2)若身高为1.65m的小丽也站在绳子的正下方.①当小丽在距小亮拿绳子手的左侧1.5m处时,绳子能碰到小丽的头吗?请说明理由；②设小丽与小亮拿绳子手之间的水平距离为dm,为保证绳子不碰到小丽的头顶,求d的取值范围.(参考数据: √10取3.16)【答案】（1）y=−16x2+23x；（2）①绳子能碰到小丽的头，理由见解析；②1.684⩽d⩽2.316.【思路引导】（1）因为抛物线过原点，可设抛物线的解析式为：y=ax2+bx（a≠0），把小亮拿绳子的手的坐标（4，0），以及小红头顶坐标（1，1.5-1）代入，得到二元一次方程组，解方程组便可；（2）①由自变量的值求出函数值，再比较便可；①由y=0.65时求出其自变量的值，便可确定d的取值范围．【解析】（1）根据题意,设绳子所对应的抛物线的表达式为y=ax2+bx(a≠0)∵1.5-1=0.5，∴抛物线经过点(4,0)和点(1,0.5) ∴{16a +4b =0a +b =0.5 ，解得{a =−16b =23∴绳子对应的抛物线表达式为y =−16x 2+23x （2）①绳子能碰到小丽的头理由如下：∵小丽在距小亮拿绳子手的左侧1.5m 处， ∴小丽所在位置与原点距离为4-1.5=2.5(m )，∴当x =2.5时，y =−16x 2+23x =−16×2.52+23×2.5=0.625∵1+0.625=1.625<1.65 ∴绳子能碰到小丽的头.②∵1.65-1=0.65，∴当y =0.65时，0.65=−16x 2+23x即10x 2−40x +39=0，解得：x =20±√1010∵√10取3.16 ∴x 1=20+3.1610=2.316，x 2=20−3.1610=1.684，∴4−2.316=1.684，4−1.684=2.316， ∴1.684≤d ≤2.316. 【方法总结】本题是二次函数的应用，主要考查了待定系数法求二次函数的解析式，应用二次函数的解析式由自变量求函数值，由函数值确定自变量等知识判定实际问题，关键是确定抛物线上点的坐标，和应用二次函数解析式解决实际问题．针对训练1．（2017内蒙古鄂尔多斯市东胜区）如图，排球运动员站在点O 处练习发球，将球从O 点正上方2m 的A 处发出，把球看成点，其运行的高度y （m ）与运行的水平距离x （m ）满足关系式y =a(x −6)2+ℎ，已知球网与O 点的水平距离为9m ，高度为3m ，球场的边界距O 点的水平距离为14m. （1）当h=4时，求y 与x 的关系式（不要求写出自变量x 的取值范围）（2）当h=4时，球能否越过球网？球会不会出界？请说明理由；（3）若球一定能越过球网，又不出边界，求h 的取值范围.【答案】(1) y =−118(x −6)2+4 ;(2)见解析;(3) h≥327.【解析】分析：（1）运用待定系数法求二次函数解析式；（2）由（1）可得函数解析式，当x =9时y=3.5,由此可判定球能越过网，令y =0时，求得x =6+6√2,所以球会出界;(3)把两临界值求出来即可. 详解：（1）当h=4时，y =a(x −6)2+4 ∵它过（0,2）， ∴2=a(0−6)2+4 ∵a =−118∴y =−118(x −6)2+4；（2）答：球能越过球网且球会出界理由如下：由（1）可知， y =−118(x −6)2+4令x=9得y=3.5， ∵3.5＞3 ∴球能越过球网; 令y=0得x=6+6√2， ∵6+6√2＞14 ∴球会出界（3）当球过球网时y =a(x −6)2+ℎ过（0，2）和（9,3） {36a +ℎ=29a +ℎ=3 解得：{a =−127ℎ=103 ∴-h≥103 当球到界时，y =a(x −6)2+ℎ过（0，2）和（14,0）{36a +ℎ=264a +ℎ=0 解得：{a =−114ℎ=327 ∴-h≥327 ∴h≥327时球一定能越过球网，又不出边界.2．（2018•河北）如图是轮滑场地的截面示意图，平台AB 距x 轴（水平）18米，与y 轴交于点B ，与滑道y=kx （x≥1）交于点A ，且AB=1米．运动员（看成点）在BA 方向获得速度v 米/秒后，从A 处向右下飞向滑道，点M 是下落路线的某位置．忽略空气阻力，实验表明：M ，A 的竖直距离h （米）与飞出时间t （秒）的平方成正比，且t=1时h=5，M ，A 的水平距离是vt 米．（1）求k ，并用t 表示h ；（2）设v=5．用t 表示点M 的横坐标x 和纵坐标y ，并求y 与x 的关系式（不写x 的取值范围），及y=13时运动员与正下方滑道的竖直距离；（3）若运动员甲、乙同时从A 处飞出，速度分别是5米/秒、v 乙米/秒．当甲距x 轴1.8米，且乙位于甲右侧超过4.5米的位置时，直接写出t 的值及v 乙的范围．【答案】（1）k=18，h=5t 2；（2）x=5t+1，y=﹣5t 2+18，y=−15x 2+25x +895，当y=13时，运动员在与正下方滑道的竖直距离是10米；（3）t=1.8，v 乙＞7.5 解：（1）由题意，点A （1，18）代入y=kx ，得：18=k1，∴k=18，设h=at 2，把t=1，h=5代入， ∴a=5， ∴h=5t 2；（2）∵v=5，AB=1， ∴x=5t+1， ∵h=5t 2，OB=18，∴y=﹣5t 2+18，由x=5t+1，则t=15（x -1），∴y=﹣15（x -1）2+18=−15x 2+25x +895，当y=13时，13=﹣15（x -1）2+18，解得x=6或﹣4， ∵x≥1， ∴x=6，把x=6代入y=18x ， y=3，∴运动员在与正下方滑道的竖直距离是13﹣3=10（米）；（3）把y=1.8代入y=﹣5t 2+18 得t 2=8125，解得t=1.8或﹣1.8（负值舍去） ∴x=10∴甲坐标为（10，1.8）恰号落在滑道y=18x 上，此时，乙的坐标为（1+1.8v 乙，1.8），由题意：1+1.8v 乙﹣（1+5×1.8）＞4.5， ∴v 乙＞7.5.3．（2019盘锦双台子区）一位运动员在距篮下4米处跳起投篮，篮球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮筐。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、二次函数的定义1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．练习：1、下列函数中，是二次函数的是 .①y=x 2－4x+1； ②y=2x 2； ③y=2x 2+4x ； ④y=－3x ；⑤y=－2x －1； ⑥y=mx 2+nx+p ； ⑦y =(4,x) ；⑧y=－5x 。

2、在一定条件下，若物体运动的路程s （米）与时间t （秒）的关系式为s=5t 2+2t ，则t ＝4秒时，该物体所经过的路程为。

3、若函数y=(m 2+2m －7)x 2+4x+5是关于x 的二次函数，则m 的取值范围为。

4、若函数y=(m －2)xm －2+5x+1是关于x 的二次函数，则m 的值为。

6、已知函数y=(m －1)x m2 +1+5x －3是二次函数，求m 的值。

二、二次函数的对称轴、顶点、最值1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a-．练习：1．抛物线y=2x 2+4x+m 2－m 经过坐标原点，则m 的值为。

2．抛物y=x2+bx+c线的顶点坐标为（1，3），则b＝，c＝ .3．抛物线y＝x2＋3x的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限4．若抛物线y＝ax2－6x经过点(2，0)，则抛物线顶点到坐标原点的距离为( )B.5．若直线y＝ax＋b不经过二、四象限，则抛物线y＝ax2＋bx＋c( )A.开口向上，对称轴是y轴B.开口向下，对称轴是y轴C.开口向下，对称轴平行于y轴D.开口向上，对称轴平行于y轴6．已知抛物线y＝x2＋(m－1)x－14的顶点的横坐标是2，则m的值是_ .7．抛物线y=x2+2x－3的对称轴是。

8．若二次函数y=3x2+mx－3的对称轴是直线x＝1，则m＝。

9．当n＝______，m＝______时，函数y＝(m＋n)x n＋(m－n)x的图象是抛物线，且其顶点在原点，此抛物线的开口________.10．已知二次函数y=x2－2ax+2a+3，当a= 时，该函数y的最小值为0.11．已知二次函数y=mx2+(m－1)x+m－1有最小值为0，则m＝ ______ 。

12．已知二次函数y=x2－4x+m－3的最小值为3，则m＝。

三、函数y=ax2+bx+c的图象和性质练习：1．抛物线y=x 2+4x+9的对称轴是。

2．抛物线y=2x 2－12x+25的开口方向是，顶点坐标是。

3．试写出一个开口方向向上，对称轴为直线x ＝－2，且与y 轴的交点坐标为（0，3）的抛物线的解析式。

4.二次函数y=3x 2－6x+5，当x>1时，y 随x 的增大而；当x<1时，y 随x 的增大而；当x=1时，函数有最值是。

5.已知函数y=4x 2－mx+5，当x> －2时,y 随x 的增大而增大；当x< －2时，y 随x 的增大而减少；则x ＝1时,y 的值为。

6.已知二次函数y=x 2－(m+1)x+1，当x ≥1时，y 随x 的增大而增大，则m 的取值范围是 .7.已知二次函数y=－12 x 2+3x+52 的图象上有三点A(x 1,y 1),B(x 2,y 2),C(x 3,y 3)且3<x 1<x 2<x 3，则y 1,y 2,y 3的大小关系为 .8．通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）y=12 x 2－2x+1 ；（2）y=－3x 2+8x －2；（3）y=－14 x 2+x －49.如图，如果函数b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（）10．试说明函数y=12 (x －3)2 的图象特点及性质（开口、对称轴、顶点坐标、增减性、最值）。

11．某商场以每台2500元进口一批彩电。

如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？四、二次函数图象的平移及二次函数基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：上加下减。

3. ()2y a x h =-的性质：左加右减。

4.()2y a x h k =-+的性质：2、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）练习：1．填表：2．已知函数y=2x 2,y=2(x －4)2，和y=2(x+1)2。

（1）分别说出各个函数图象的开口方、对称轴和顶点坐标。

（2）分析分别通过怎样的平移。

可以由抛物线y=2x 2得到抛物线y=2(x －4)2和y=2(x+1)2？3．试写出抛物线y=3x 2经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标。

（1）右移2个单位；（2）左移23 个单位；（3）先左移1个单位，再右移4个单位。

5．把抛物线y=x 2+bx+c 的图象向右平移3个单位，在向下平移2个单位，所得图象的解析式是y=x 2－3x+5，试求b 、c 的值。

6．把抛物线y=－2x 2+4x+1沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值，若有，求出该最大值；若没有，说明理由。

7.抛物线y= －32 x 2向左平移3个单位，再向下平移4个单位，所得到的抛物线的关系式为。

8.抛物线y= 2x 2，，可以得到y=2(x+4}2－3。

9.将抛物线y=x 2+1向左平移2个单位，再向下平移3个单位，所得到的抛物线的关系式为。

10.如果将抛物线y=2x 2－1的图象向右平移3个单位，所得到的抛物线的关系式为。

11.将抛物线y=ax 2+bx+c 向上平移1个单位，再向右平移1个单位，得到y=2x 2－4x －1则a ＝，b ＝，c ＝ . 12.将抛物线y ＝ax 2向右平移2个单位，再向上平移3个单位，移动后的抛物线经过点(3，－1)，那么移动后的抛物线的关系式为 _.五、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．这两点间的距离2214b acAB x x a-=-=.② 当0∆=时，图象与x 轴只有一个交点； ③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2'当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <．2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；3. 二次函数常用解题方法总结：⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程；⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式； ⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的符号判断图象的位置，要数形结合；⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标.下面以0a >时为例，揭示二次函数和一元二次方程之间的内在联系：练习：1. 如果二次函数y ＝x 2＋4x ＋c 图象与x 轴没有交点，其中c 为整数，则c ＝（写一个即可）2. 二次函数y ＝x 2-2x-3图象与x 轴交点之间的距离为3. 抛物线y ＝－3x 2＋2x －1的图象与x 轴交点的个数是( ) A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点4. 如图所示，二次函数y ＝x 2－4x ＋3的图象交x 轴于A 、B 两点，交y 轴于点C ，则△ABC的面积为( ) A.6 B.4C.3D.15. 已知抛物线y ＝5x 2＋(m －1)x ＋m 与x 轴的两个交点在y 轴同侧，它们的距离平方等于为4925，则m 的值为( ) A.－2 B.12C.24D.486. 若二次函数y ＝(m+5)x 2+2(m+1)x+m 的图象全部在x 轴的上方，则m 的取值范围是7. 1.抛物线y=x 2+7x+3与直线y=2x+9的交点坐标为。

8. 2.直线y=7x+1与抛物线y=x 2+3x+5的图象有个交点。