(整理)光量子学习题答案
习题解答(光学篇和量子物理篇)
第14章习题解答1．某单色光从空气射入水中，其频率、波速、波长是否变化?怎样变化?解: υ不变，为波源的振动频率；nn 空λλ=变小；υλn u =变小．2．什么是光程? 在不同的均匀介质中，若单色光通过的光程相等时，其几何路程是否相同?其所需时间是否相同？在光程差与相位差的关系式2πϕδλ∆=中，光波的波长要用真空中波长，为什么？解:nr δ=．不同媒质若光程相等，则其几何路程定不相同；其所需时间相同，为t C δ∆=．因为δ中已经将光在介质中的路程折算为光在真空中所走的路程。
3．在杨氏双缝实验中，作如下调节时，屏幕上的干涉条纹将如何变化？试说明理由。
(1)使两缝之间的距离变小；(2)保持双缝间距不变，使双缝与屏幕间的距离变小； (3)整个装置的结构不变，全部浸入水中；(4)光源作平行于1S 、2S 连线方向的上下微小移动； (5)用一块透明的薄云母片盖住下面的一条缝。
解: 由λdDx =∆知，(1)条纹变疏；(2)条纹变密；(3)条纹变密；(4)零级明纹在屏幕上作相反方向的上下移动；(5)零级明纹向下移动．4．在空气劈尖中，充入折射率为n 的某种液体，干涉条纹将如何变化？ 解：干涉条纹将向劈尖棱边方向移动，并且条纹间距变小。
5．当将牛顿环装置中的平凸透镜向上移动时，干涉图样有何变化？解：透镜向上移动时，因相应条纹的膜厚k e 位置向中心移动，故条纹向中心收缩。
6．杨氏双缝干涉实验中，双缝中心距离为0.60mm ，紧靠双缝的凸透镜焦距为2.5m ，焦平面处有一观察屏。
（1）用单色光垂直照射双缝，测得屏上条纹间距为2.3mm ，求入射光波长。
（2）当用波长为480nm 和600nm 的两种光时，它们的第三级明纹相距多远？ 解：（1）由条纹间距公式λdDx =∆，得 332.3100.6105522.5x d nm D λ--∆⋅⨯⨯⨯===（2）由明纹公式Dx k d λ=，得92132.5()3(600480)10 1.50.610D x k mm d λλ--∆=-=⨯⨯-⨯=⨯ 7．在杨氏双缝实验中，双缝间距d =0.20mm ，缝屏间距D ＝1.0m 。
光量子学习题答案
《光量子学基础》习题答案（沈建其提供，2009年6月）说明：习题难度非常低，大多习题均可以在ppt 中直接找到答案。
第一次习题：1．计算（1）：de Broglie 波长均为5埃（Å）的电子、中子与光子的动量与能量各为多少？答：这三种粒子的动量都是3424106.6310 1.3310510p h λ---⨯===⨯⨯Kg ·m/s (或241.310-⨯ Kg ·m/s)。
电子的动能 ()224218300 1.33100.96510220.91110k pE m ---⨯===⨯⨯⨯J 6.03=eV （或6eV ） （1电子伏特＝191.6010-⨯焦耳）中子的动能 ()224221270 1.33100.5261022 1.6710k p E m ---⨯===⨯⨯⨯J 20.33010-=⨯eV 以上使用牛顿力学的动能公式（6.03eV 远比电子的静止能量20m c 约0.5MeV 小，0.0033eV 远比中子的静止能量20m c 约990MeV 小，说明没有必要使用相对论来计算） 但光子是相对论性粒子，必须用相对论来计算：光子动能（总能）2481.3310 3.0010k E pc -==⨯⨯⨯J ＝4.001610-⨯J=2.50310⨯eV 。
说明：虽然以上问题中，牛顿力学的动能公式是非常良好的近似，但使用相对论亦可。
有的学生计算了动能部分，有的学生计算了总能量2E mc =，答案是开明的，都属对，但要知道2E mc =与动能22p m 之间如下关系：粒子总能量2E mc =，动质量m =2E mc =可以用泰勒展开：2246001...2E m c m v av bv =++++，其中20m c 为静止能量（rest energy ）, 2012m v 为牛顿动能（它只是2E mc =的一部分）。
只有当低速的时候，220012m c m v +才重要，其中2012m v更重要。
第二章习题答案量子光学（中科院研究生院）
(∆X1)n
=
n m=0
: (∆X1)m :
n!
1
m!(
n−m 2
)!
8
n−m 2
.
由于对于相干态，如果 m = 0，则 : ∆X1m : = 0，所以上式右边在相干态下不为零的 展开项仅为首项
(∆X1)n
=
n!
(
n 2
)!8n/2
=
1·2·3····n
1
·
2
·
3
·
·
·
·
n 2
·
8n/2
=
1·2·3····n
ν π
1/2
exp
−ν
q2 − 2qq0 cos νt + q02 cos2 νt
ν π
1/2
exp
− ν (q − q0 cos νt)2
.
习题 2.4.
习题 2.5.
Y1
=
1 2
Y2
=
1 2i
e−i
θ 2
a
+
ei
θ 2
a†
e−i
θ 2
a
−
ei
θ 2
a†
(∆Y1)2 = Y12 − Y1 2 由此可得
a cosh r − a†eiθ sinh r
a cosh r − a†eiθ sinh r
e−iθ a† cosh r − ae−iθ sinh r a† cosh r − ae−iθ sinh r
a† cosh r − ae−iθ sinh r a cosh r − a†eiθ sinh r
a cosh r − a†eiθ sinh r a† cosh r − ae−iθ sinh r |0
量子力学课后习题答案
Wnl (r)dr Rnl2 (r)r 2dr
例如：对于基态 n 1, l 0
W10 (r) R102 (r)r 2
4 a03
r e2 2r / a0
求最可几半径
R e 2 r / a0
10
a03 / 2
dW10 (r) 4 (2r 2 r 2 )e2r / a0
x)
k
2
2
(
x)
0
其解为 2 (x) Asin kx B cos kx
根据波函数的标准条件确定系数A、B，由连续性条件，得
2 (0) 1(0) B 0
2 (a) 3 (a) Asin ka 0
A0
sin ka 0
ka n
(n 1, 2, 3,)
[1 r
eikr
r
(1 r
eikr )
1 r
eikr
r
(1 r
eikr )]er
i1 1 11 1 1
2
[ r
(
r2
ik
) r
r
(
r2
ik
r )]er
k
r2
er
J1与er 同向。 1 表示向外传播的球面波。
习题
(2)
J2
i
2
(
2
* 2
2*
解：U (x)与t 无关，是定态问题
薛定谔方程为
2
2
d2 dx2
(x) U (x) (x)
E (x)
在各区域的具体形式为：
x0
量子力学作业及参考答案
15-1 将星球看做绝对黑体，利用维恩位移定律测量m λ便可求得T ．这是测量星球表面温度的方法之一．设测得：太阳的m 55.0m μλ=，北极星的m 35.0m μλ=，天狼星的m 29.0m μλ=，试求这些星球的表面温度．解：将这些星球看成绝对黑体，则按维恩位移定律：K m 10897.2,3⋅⨯==-b b T m λ对太阳： K 103.51055.010897.236311⨯=⨯⨯==--mbT λ对北极星：K 103.81035.010897.236322⨯=⨯⨯==--mbT λ对天狼星：K 100.11029.010897.246333⨯=⨯⨯==--mbT λ15-3 从铝中移出一个电子需要4.2 eV 的能量，今有波长为2000οA 的光投射到铝表面．试问：(1)由此发射出来的光电子的最大动能是多少?(2)遏止电势差为多大?(3)铝的截止(红限)波长有多大?解：(1)已知逸出功eV 2.4=A 据光电效应公式221m mv hv =A +则光电子最大动能：A hcA h mv E m -=-==λυ2max k 21eV0.2J 1023.3106.12.41020001031063.6191910834=⨯=⨯⨯-⨯⨯⨯⨯=----m2max k 21)2(mvE eUa==∴遏止电势差 V 0.2106.11023.31919=⨯⨯=--a U(3)红限频率0υ,∴000,λυυcA h ==又∴截止波长 1983401060.12.41031063.6--⨯⨯⨯⨯⨯==Ahc λm 0.296m 1096.27μ=⨯=-15-4 在一定条件下，人眼视网膜能够对5个蓝绿光光子(m 105.0-7⨯=λ)产生光的感觉．此时视网膜上接收到光的能量为多少?如果每秒钟都能吸收5个这样的光子，则到 达眼睛的功率为多大? 解：5个兰绿光子的能量J1099.1100.51031063.65187834---⨯=⨯⨯⨯⨯⨯===λυhcn nh E功率 W 1099.118-⨯==tE15-5 设太阳照射到地球上光的强度为8 J ·s -1·m -2，如果平均波长为5000οA ，则每秒钟落到地面上1m 2的光子数量是多少?若人眼瞳孔直径为3mm ，每秒钟进入人眼的光子数是多少? 解：一个光子能量 λυhch E ==1秒钟落到2m 1地面上的光子数为21198347ms1001.21031063.6105888----⋅⨯=⨯⨯⨯⨯⨯===hcEn λ每秒进入人眼的光子数为11462192s1042.14/10314.31001.24--⨯=⨯⨯⨯⨯==dnN π15-6若一个光子的能量等于一个电子的静能，试求该光子的频率、波长、动量．解：电子的静止质量S J 1063.6,kg 1011.934310⋅⨯=⨯=--h m 当 20c m h =υ时，则Hz10236.11063.6)103(1011.92034283120⨯=⨯⨯⨯⨯==--hc m υο12A 02.0m 104271.2=⨯==-υλc122831020122sm kg 1073.21031011.9sm kg 1073.2-----⋅⋅⨯=⨯⨯⨯=====⋅⋅⨯==c m cc m c E p cpE hp 或λ15-7 光电效应和康普顿效应都包含了电子和光子的相互作用，试问这两个过程有什么不同? 答：光电效应是指金属中的电子吸收了光子的全部能量而逸出金属表面，是电子处于原子中束缚态时所发生的现象．遵守能量守恒定律．而康普顿效应则是光子与自由电子(或准自由电子)的弹性碰撞，同时遵守能量与动量守恒定律．15-8 在康普顿效应的实验中，若散射光波长是入射光波长的1.2倍，则散射光子的能量ε与反冲电子的动能k E 之比k E /ε等于多少? 解：由 2200mc h c m hv +=+υ)(00202υυυυ-=-=-=h h h cm mcE kυεh =∴5)(00=-=-=υυυυυυεh h E k已知2.10=λλ由2.10=∴=υυλυc2.11=υυ则52.0112.110==-=-υυυ15-10 已知X 光光子的能量为0.60 MeV ，在康普顿散射之后波长变化了20%，求反冲电子的能量．解：已知X 射线的初能量,MeV 6.00=ε又有00,ελλεhchc =∴=经散射后 000020.1020.0λλλλ∆λλ=+=+= 此时能量为 002.112.1ελλε===hc hc反冲电子能量 MeV 10.060.0)2.111(0=⨯-=-=εεE15-11 在康普顿散射中，入射光子的波长为0.030 οA ，反冲电子的速度为0.60c ，求散射光子的波长及散射角． 解：反冲电子的能量增量为202022020225.06.01c m cm cm cm mcE =--=-=∆由能量守恒定律，电子增加的能量等于光子损失的能量， 故有 20025.0c m hchc=-λλ散射光子波长ο121083134103400A043.0m 103.410030.0103101.925.01063.610030.01063.625.0=⨯=⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯=-=------λλλc m h h由康普顿散射公式2sin0243.022sin22200ϕϕλλλ∆⨯==-=cm h可得 2675.00243.02030.0043.02sin2=⨯-=ϕ散射角为 7162'=οϕ15-12 实验发现基态氢原子可吸收能量为12.75eV 的光子． (1)试问氢原子吸收光子后将被激发到哪个能级?(2)受激发的氢原子向低能级跃迁时，可发出哪几条谱线?请将这些跃迁画在能级图上． 解：(1)2eV 6.13eV 85.0eV 75.12eV 6.13n -=-=+-解得 4=n 或者 )111(22n Rhc E -=∆75.12)11.(1362=-=n解出 4=n题15-12图 题15-13图(2)可发出谱线赖曼系3条，巴尔末系2条，帕邢系1条，共计6条.15-13 以动能12.5eV 的电子通过碰撞使氢原子激发时，最高能激发到哪一能级?当回到基态时能产生哪些谱线?解：设氢原子全部吸收eV 5.12能量后，最高能激发到第n 个能级，则]11[6.135.12,eV 6.13],111[2221nRhc nRhc E E n -==-=-即得5.3=n ，只能取整数，∴ 最高激发到3=n ，当然也能激发到2=n 的能级．于是ο322ο222ο771221A 6563536,3653121~:23A 121634,432111~:12A1026m 10026.110097.18989,983111~:13===⎥⎦⎤⎢⎣⎡-=→===⎥⎦⎤⎢⎣⎡-=→=⨯=⨯⨯===⎥⎦⎤⎢⎣⎡-=→-R R R n R R R n RR R n λυλυλυ从从从可以发出以上三条谱线．题15-14图15-14 处于基态的氢原子被外来单色光激发后发出巴尔末线系中只有两条谱线，试求这两 条谱线的波长及外来光的频率．解：巴尔末系是由2>n 的高能级跃迁到2=n 的能级发出的谱线．只有二条谱线说明激发后最高能级是4=n 的激发态．ο1983424ο101983423222324A4872106.1)85.04.3(1031063.6A6573m 1065731060.1)51.14.3(10331063.6e 4.326.13e 51.136.13e 85.046.13=⨯⨯-⨯⨯⨯=-==⨯=⨯⨯-⨯⨯⨯⨯=-=∴-=∴-==-=-=-=-=-=-=-----E E hc E E hcE E hc E E hch VE V E V E a mn mn βλλλλυ基态氢原子吸收一个光子υh 被激发到4=n 的能态 ∴ λυhcE E h =-=14Hz 1008.310626.6106.1)85.06.13(15341914⨯=⨯⨯⨯-=-=--hE E υ15-15 当基态氢原子被12.09eV 的光子激发后，其电子的轨道半径将增加多少倍? 解： eV 09.12]11[6.1321=-=-nE E n 26.1309.126.13n =-51.16.1309.12.1366.132=-=n , 3=n12r n r n =,92=n,19r r n =轨道半径增加到9倍.15-16德布罗意波的波函数与经典波的波函数的本质区别是什么?答：德布罗意波是概率波，波函数不表示实在的物理量在空间的波动，其振幅无实在的物理意义,2φ仅表示粒子某时刻在空间的概率密度．15-17 为使电子的德布罗意波长为1οA ，需要多大的加速电压? 解： ooA 1A 25.12==uλ 25.12=U∴ 加速电压 150=U 伏15-18 具有能量15eV 的光子，被氢原子中处于第一玻尔轨道的电子所吸收，形成一个 光电子．问此光电子远离质子时的速度为多大?它的德布罗意波长是多少?解：使处于基态的电子电离所需能量为eV 6.13，因此，该电子远离质子时的动能为eV 4.16.13152112=-=+==E E mvE k φ它的速度为31191011.9106.14.122--⨯⨯⨯⨯==mE v k -15s m 100.7⋅⨯=其德布罗意波长为：o953134A 10.4m 1004.1100.71011.91063.6=⨯=⨯⨯⨯⨯==---mvh λ15-19 光子与电子的波长都是2.0οA ，它们的动量和总能量各为多少? 解：由德布罗意关系：2mc E =，λhmv p ==波长相同它们的动量相等．1-241034s m kg 103.3100.21063.6⋅⋅⨯=⨯⨯==---λhp光子的能量eV 102.6J 109.9103103.3316824⨯=⨯=⨯⨯⨯====--pc hch λυε电子的总能量 2202)()(c m cp E +=,eV 102.63⨯=cp而 eV 100.51MeV 51.0620⨯==c m∴ cp c m >>2∴ MeV 51.0)()(202202==+=c m c m cp E15-20 已知中子的质量kg 1067.127n -⨯=m ，当中子的动能等于温度300K 的热平衡中子气体的平均动能时，其德布罗意波长为多少? 解：kg 1067.127n -⨯=m ,S J 1063.634⋅⨯=-h ,-123K J 1038.1⋅⨯=-k中子的平均动能 mpKT E k 2232==德布罗意波长 oA 456.13===mkTh phλ15-21 一个质量为m 的粒子，约束在长度为L 的一维线段上．试根据测不准关系估算这个粒子所具有的最小能量的值．解：按测不准关系，h p x x ≥∆∆，x x v m p ∆=∆，则h v x m x ≥∆∆,xm h v x ∆≥∆这粒子最小动能应满足222222min 22)(21)(21mLhxm hxm h m v m E x =∆=∆≥∆=15-22 从某激发能级向基态跃迁而产生的谱线波长为4000οA ，测得谱线宽度为10-4οA ，求该激发能级的平均寿命． 解：光子的能量 λυhch E ==由于激发能级有一定的宽度E ∆，造成谱线也有一定宽度λ∆，两者之间的关系为： λλ∆=∆2hcE由测不准关系，h t E ≥∆⋅∆，平均寿命t ∆=τ，则λλτ∆=∆=∆=c Eh t 2s 103.51010103)104000(81048210----⨯=⨯⨯⨯⨯=15-23 一波长为3000οA 的光子，假定其波长的测量精度为百万分之一，求该光子位置的测不准量．解： 光子λhp =，λλλλ∆=∆-=∆22hhp由测不准关系，光子位置的不准确量为cm 30A 103103000o962=⨯=====-λλ∆λλ∆λ∆∆p h x。
量子光学答案
量子光学答案一 1：单模光场相干态定义为光子湮灭算符的本征态，即a ααα=。
相干态的三个主要性质：（1） 相干态是非正交和超完备的； （2） 相干态是最小测不准量子态，因而也是量子理论所容许的最接近经典极限的量子态；（3） 相干态下能量的起伏最小，即零点能。
任何相干态的量子起伏都相等，相干态的量子起伏实质上是真空的起伏。
2： 通常引用密度算符来统一地描述量子系统中两类性质不同的系统状态（纯态和混合态）的统计平均。
n n n nP ρψψ≡∑密度算符的物理含义：密度算符ρ包含了有关此系统的所有物理上有意义的信息。
求解量子力学的问题实际上归结为求出系统的密度算符ρ。
3： 压缩态是一类最小测不准态，但在某一正交分量上具有更小的起伏噪音（小于真空起伏）。
两个正交相位算符的均方起伏乘积为最小，但不相等的态称为压缩相干态，俗称压缩态。
4： 利用相干态的对角化矩阵可以将密度算符表示为：*2(,)P d ρααααα=⎰上式中分布函数称*(,)P αα为 Glauber-Sudarshan 表示，即 密度算符的P 表示。
在分布函数的积分形式中，存在以下傅里叶变换形式：22***221(,)P eeed αββαβαααβρββπ--=-⎰其中积分2**221ee d ββαβαβρββπ--⎰存在奇异性，通过比较βρβ-与2eβ-的下降速度的快慢，即可以判断场所处的状态（经典态、纯量子态、相干态）。
由此可见，密度算符的P 表示可以作为非经典场的判据。
5： HBT 实验原理如下图所示：SMP1P2相关器t图 实验HBT来自光源S 的光束经一半透半反的分束器M 后，分成两束光，并分别用两个光电探测器P1和P2测量，探测器输出的光电信号被反馈到一个相关器（符合计数器），其中一路光电信号经过了τ时间的延迟器。
这个装置测量的是在两个不同时空点光场强度的起伏I ∆的关联，而不再是以往光学实验所测量的场本身的关联。
相关器测量到得物理量是在P1和P2处强度起伏的关联。
量子力学练习题答案
Wmk =| am (t) |2
∫ ∫ 其中
am
(t)
=
1 i=
t 0
eiωmkτ
H
′
mk
dτ
，
H
′
mk
=
ϕm* Hl ′(t)ϕkdτ ，ωmk = (Em − Ek ) / =
二、 证明题 1． 证明黑体辐射的辐射本领 E(ν ,T ) 与 E(λ,T ) 之间的关系。 证明：黑体的辐射本领是指辐射体单位面积在单位时间辐射出来的、单位 频率间隔内的能量，用 E(ν ,T ) 表示。由于ν = c / λ ，所以黑体的辐射本领也 可以表示成 E(λ,T ) 。由定义得单位面积、单位时间内辐射的能量为
的同时决定，也使得它们的分布同时制约，这种制约就是不确定性原理，
它是任何两个力学量在任何状态下的涨落（用均方差表示）必须满足的相
互制约关系，公式表示为
ΔA⋅ ΔB ≥ 1 ⋅ [lA, Bl] 2
23． 如果算符 Aˆ 的本征值分别为 A1, A2, A3,"，在算符 Aˆ 的自身表象中写出
算符 Aˆ 的矩阵形式。
下，所有力学量的概率分布不随时间改变；在一切状态下，守恒量的概率
分布不随时间改变。
25． 在 Sz 表象下，写出算符 Sˆz 及其本征态|↑〉 和|↓〉 的矩阵表达式。
答：在 Sz 表象下，算符 Sˆz 的矩阵表达式为
Sz
=
= ⎛1
2
⎜ ⎝
0
0⎞ − 1⎟⎠
其本征态|↑〉 和|↓〉 的矩阵表达式分别为
v∫ 答： pkdqk = nkh (nk = 1, 2,3,")
其中 (qk , pk ) 代表一对共轭的正则坐标和动量。 7． 利用光波的双缝干涉实验，说明 Born 的概率波解释。 答：Born 认为，微观粒子的运动状态用“波函数”来描述，粒子通过双缝 时，每一个缝都有一个所谓的“波”通过，只不过与经典波的强度对应的， 是粒子在某点附近出现的相对概率。对通过双缝的粒子，其概率“分成” 了两束（波动性），但对某个具体的粒子，它只能通过其中的一个缝（粒子
量子习题解答
n 0,1,2,3...
8、氢原子： 氢原子能级：
me4 1 1 En 2 13.6 2 (e V) 2 2 2 (4 0 ) n n
轨道角动量
L l (l 1)
轨道角动量沿磁场方向分量：Lz m 主量子数 轨道量子数 轨道磁量子数
n=1,2,3…
l=0,1,2,3…,n-1 ml=-l,-(l-1),…,0,1,..,l
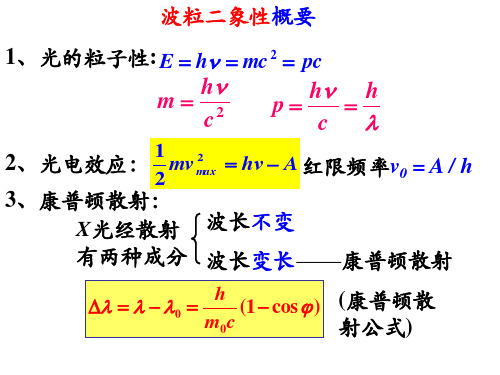
h 0 ( 1 cos ) m0 c
4、不确定关系(1927)：
h 2
x p x (或, 或h) 位臵动量不确定关系： 2
能量时间不确定关系：Et / 2
5、氢原子光谱(1913) 谱线的波数
1 1 R ( 2 2 ) T ( m) T ( n) m n
玻尔磁子
电子自旋磁矩在磁场中的能量 Es B B
e B 9.27 10 24 J / T 2me
10、多电子原子的电子组态 电子的状态用4 个量子数n,l,ml,ms确定。n相同 的状态组成一壳层，可容纳2n2个电子；l相同 的状态组成一次壳层，可容纳2（2l+1)个电子。 基态原子电子组态遵循两个规律： （1）能量最低原理，即电子总处于可能最 低的能级。一般n越大，l越大，能量就越高。 （2）泡利不相容原理(1921)，不可能有两个 或两个以上的电子处在同一量子状态。即不 能有两个电子具有相同的n, l, ml , ms。
解： 光子的散射角 θ π 时电子获得的能量最大， v 电子的反冲速度沿入射光子的运动方向.设 为入 pe 射光的频率，为散射光的频率， 为反冲电子的动 v 量。 1 由能量守恒有： h(v v) Ek
由动量守恒有: 2 式得 由1 、
量子力学习题集及答案
量子力学习题集及答案09光信息量子力研究题集一、填空题1.__________2.设电子能量为4电子伏，其德布罗意波长为6.125A。
XXX的量子化条件为∫pdq=nh，应用这量子化条件求得一维谐振子的能级En=(nωℏ)。
3.XXX假说的正确性，在1927年为XXX和革末所做的电子衍射实验所证实，德布罗意关系为E=ωℏ和p=ℏk。
4.ψ(r)=(三维空间自由粒子的归一化波函数为e^(ip·r/ℏ))，其中p为动量算符的归一化本征态。
5.∫ψ*(r)ψ(r)dτ=(δ(p'-p))，其中δ为狄拉克函数。
6.t=0时体系的状态为ψ(x,0)=ψ_n(x)+2ψ_2(x)，其中ψ_n(x)为一维线性谐振子的定态波函数，则ψ(x,t)=(ψ(x)e^(-iωt/2)+2ψ_2(x)e^(-5iωt/2))。
7.按照量子力学理论，微观粒子的几率密度w=(|Ψ|^2)，几率流密度j=(iℏ/2μ)(Ψ*∇Ψ-Ψ∇Ψ*)。
其中Ψ(r)描写粒子的状态，Ψ(r)是粒子的几率密度，在Ψ(r)中F(x)的平均值为F=(∫Ψ*F(x)Ψdx)/(∫Ψ*Ψdx)。
8.波函数Ψ和cΨ是描写同一状态，Ψe^(iδ)中的e^(iδ)称为相因子，e^(iδ)不影响波函数Ψ的归一化，因为e^(iδ)=1.9.定态是指能量具有确定值的状态，束缚态是指无穷远处波函数为零的状态。
10.E1=E2时，Ψ(x,t)=Ψ_1(x)exp(-iE1t)+Ψ_2(x)exp(-iE2t)是定态的条件。
11.这时几率密度和几率流密度都与时间无关。
12.粒子在能量小于势垒高度时仍能贯穿势垒的现象称为隧道效应。
13.无穷远处波函数为零的状态称为束缚态，其能量一般为分立谱。
14.ψ(x,t)=(ψ(x)e^(-iωt/2)+ψ_3(x)e^(-7iωt/2))。
2.15.在一维无限深势阱中，粒子处于位置区间x a，第一激发态的能量为1/13（22222/2ma2），第一激发态的波函数为sin（n x/a）（n=2）/a。
量子力学总结习题考卷及答案
量⼦⼒学总结习题考卷及答案第⼀章⒈玻尔的量⼦化条件，索末菲的量⼦化条件。
⒉⿊体：能吸收射到其上的全部辐射的物体，这种物体就称为绝对⿊体，简称⿊体。
⒎普朗克量⼦假说：表述1：对于⼀定频率ν的辐射，物体只能以hν为能量单位吸收或发射电磁辐射。
表述2：物体吸收或发射电磁辐射时，只能以量⼦的⽅式进⾏，每个量⼦的能量为：ε=h ν。
表述3：物体吸收或发射电磁辐射时，只能以能量ε的整数倍来实现，即ε，2ε，3ε，…。
⒏光电效应：光照射到⾦属上，有电⼦从⾦属上逸出的现象。
这种电⼦称之为光电⼦。
⒐光电效应有两个突出的特点：①存在临界频率ν0：只有当光的频率⼤于⼀定值v0 时，才有光电⼦发射出来。
若光频率⼩于该值时，则不论光强度多⼤，照射时间多长，都没有光电⼦产⽣。
②光电⼦的能量只与光的频率有关，与光的强度⽆关。
光的强度只决定光电⼦数⽬的多少。
⒑爱因斯坦光量⼦假说：光(电磁辐射)不仅在发射和吸收时以能量E= hν的微粒形式出现，⽽且以这种形式在空间以光速C 传播，这种粒⼦叫做光量⼦，或光⼦。
爱因斯坦⽅程⒒光电效应机理：当光射到⾦属表⾯上时，能量为E= hν的光⼦⽴刻被电⼦所吸收，电⼦把这能量的⼀部分⽤来克服⾦属表⾯对它的吸引，另⼀部分就是电⼦离开⾦属表⾯后的动能。
⒓解释光电效应的两个典型特点：①存在临界频率v0：由上式明显看出，当hν- W0≤0时，即ν≤ν0 = W0 / h时，电⼦不能脱出⾦属表⾯，从⽽没有光电⼦产⽣。
②光电⼦动能只决定于光⼦的频率：上式表明光电⼦的能量只与光的频率ν有关，⽽与光的强度⽆关。
⒔康普顿效应：⾼频率的X射线被轻元素如⽩蜡、⽯墨中的电⼦散射后出现的效应。
⒕康普顿效应的实验规律：①散射光中，除了原来X光的波长λ外，增加了⼀个新的波长为λ'的X光，且λ' >λ；②波长增量Δλ=λ-λ随散射⾓增⼤⽽增⼤。
⒖量⼦现象凡是普朗克常数h在其中起重要作⽤的现象⒗光具有微粒和波动的双重性质，这种性质称为光的波粒⼆象性⒘与运动粒⼦相联系的波称为德布罗意波或物质波。
量子力学习题集及答案
09光信息量子力学习题集一、填空题1． 设电子能量为4电子伏，其德布罗意波长为（ 6.125A ）。
2．索末菲的量子化条件为（ ⎰=nh pdq ），应用这量子化条件求得一维谐振子的能级=n E （ ωn ）。
3．德布罗意假说的正确性，在1927年为戴维孙和革末所做的（ 电 ）子衍射实验所证实，德布罗意关系（公式）为（ ω=E ）和（ k p= ）。
4．三维空间自由粒子的归一化波函数为()r pψ=（ r p i e⋅2/3)2(1π ）， ()()=⎰+∞∞-*'τψψd r r p p （ )(p p-'δ ）。
5．动量算符的归一化本征态=)(r p ψ（r p i e⋅2/3)2(1π ），='∞⎰τψψd r r p p )()(* （ )(p p-'δ ）。
6．t=0时体系的状态为()()()x x x 2020,ψψψ+=，其中()x n ψ为一维线性谐振子的定态波函数，则()=t x ,ψ（ t i t iex ex ωωψψ25220)(2)(--+ ）。
7． 按照量子力学理论，微观粒子的几率密度w =2），几率流密度=（()**2ψ∇ψ-ψ∇ψμi ）。
8．设)(r ψ描写粒子的状态，2)(r ψ是（ 粒子的几率密度 ），在)(r ψ中Fˆ的平均值为F =（ ⎰⎰dx dx F ψψψψ**ˆ ）。
9．波函数ψ和ψc 是描写（ 同一 ）状态，δψi e 中的δi e 称为（ 相因子 ），δi e 不影响波函数ψ1=δi ）。
10． 定态是指（ 能量具有确定值 ）的状态，束缚态是指（无穷远处波函数为零）的状态。
11．)i ex p()()i ex p()(),(2211t Ex t E x t x-+-=ψψψ是定态的条件是（ 21E E = ），这时几率密度和（ 几率密度 ）都与时间无关。
12． （ 粒子在能量小于势垒高度时仍能贯穿势垒的现象 ）称为隧道效应。
量子力学课后习题答案
量子力学课后习题答案量子力学是物理学中一门重要的学科，它描述了微观粒子的行为和性质。
在学习量子力学的过程中，习题是不可或缺的一部分，通过解答习题可以巩固对该学科的理解和应用。
本文将为大家提供一些量子力学课后习题的答案，希望能对大家的学习有所帮助。
1. 请解释什么是量子力学中的“叠加态”？在量子力学中，叠加态是指一个量子系统处于多个可能状态的线性组合。
这意味着在特定的测量之前，量子系统可以同时处于多个不同的状态。
例如，一个电子可以处于自旋向上和自旋向下的叠加态。
只有在进行测量时，才会决定电子的自旋是向上还是向下。
2. 什么是量子力学中的“测量”？在量子力学中，测量是指对量子系统进行观察并获取其性质或状态的过程。
量子力学的基本原理之一是测量会导致量子系统的状态塌缩到一个确定的状态。
例如，在测量一个电子的自旋时，我们只能观察到它的自旋向上或自旋向下，而不是同时观察到两个状态。
3. 请解释什么是量子力学中的“不确定性原理”？不确定性原理是量子力学的一个基本原理，由海森堡提出。
它指出，在某些物理量（如位置和动量、能量和时间等）之间存在一种固有的不确定性关系，无法同时准确测量这些物理量的值。
换句话说，我们无法同时精确地知道一个粒子的位置和动量，或者一个系统的能量和时间。
4. 请解释什么是量子力学中的“波粒二象性”？波粒二象性是指微观粒子既可以表现出粒子性质，又可以表现出波动性质。
根据波动性，微观粒子可以像波一样传播，并且存在干涉和衍射现象。
根据粒子性，微观粒子具有离散的能量和动量，并且在测量时表现出局部性。
5. 请解释什么是量子力学中的“量子纠缠”？量子纠缠是指两个或多个量子系统之间存在一种特殊的关联关系，使得它们的状态无法独立描述。
当两个量子系统纠缠在一起时，它们的状态会相互依赖，无论它们之间的距离有多远。
这种纠缠关系在量子通信和量子计算中具有重要的应用。
以上是对一些量子力学课后习题的简要答案。
通过解答这些习题，我们可以更好地理解和应用量子力学的概念和原理。
量子力学答案
量子力学习题及解答 第一章量子理论基础1. 1由黑体辐射公式导出维恩位移定律：能量密度极大值所对应的波长 比，即m T=b并近似计算b 的数值，准确到二位有效数字。
解根据普朗克的黑体辐射公式hc如果令x=，则上述方程为kT以及这里的 本题关注的是入取何值时， 由此可求得相应的入的值，记作 处的取值是否小于零，如果小于零,v dv8 hv 33~cv vdvhve kTc ,vd ,1 -dv , 1(1) (2) (3)dvd v ()v ()8 hc 5 的物理意义是黑体内波长介于入与入 取得极大值，因此，就得要求m 。
但要注意的是， 那么前面求得的1 hc 11 +d 入之间的辐射能量密度。
对入的一阶导数为零， 还需要验证 对入的二阶导数在 m m 就是要求的，具体如下：hc~6~1hce kT1hc kT hc 1讦丁kT5(11 ehc肓)hc kTm 与温度T 成反（常量）；5（1 这是一个超越方程。
首先，易知此方程有解： 个解可以通过逐步近似法或者数值计算法获得： 样则有X) X但经过验证，此解是平庸的；另外的一 e x=0, x=4.97，经过验证，此解正是所要求的，这mThc xk把x以及三个物理常量代入到上式便知m T 2.9 103 4 5m K这便是维恩位移定律。
据此，我们知识物体温度升高的话，辐射的能量分布的峰值向较短波长方面移动，这样便会根据热物体（如遥远星体）的发光颜色来判定温度的高低。
1. 2在0K附近，钠的价电子能量约为解根据德布罗意波粒二象性的关系,E=hv,e c 2),那么2p如果我们考察的是相对性的光子，那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV，远远小于电子的质量与光速平方的乘积, 6即0.51 10 eV，因此利用非相对论性的电子的能量一一动量关系式，这样，便有P_h_H Ehc1.24 102 0.51 106 730.71 10 9m0.71 nm在这里，利用了以及最后，对hc2 e C2E作一点讨论，从上式可以看出，当粒子的质量越大时，这个粒子的波长就越短，因而这个粒子的波动性较弱，而粒子性较强；同样的，当粒子的动能越大时，这个粒子的波长就越短，因而这个粒子的波动性较弱，而粒子性较强，由于宏观世界的物体质量普遍很大，因而波动31. 3氦原子的动能是E -kT （k为玻耳兹曼常数），求T=1K时，氦原子的德布罗意波2长。
量子力学练习一+解答
量子力学练习一1．爱因斯坦在解释光电效应时，提出 概念；爱因斯坦光电效应方程为 ；电子的康普顿波长为 。
光量子（光子）21v 2h m A ν=+ 20 2.4310Ac h m cλ-==⨯ 2．玻尔氢原子理论的三个基本假设是：（1）（2） （3） 。
定态假设 跃迁假设 角动量量子化假设3．能量为100eV 的电子，其德布罗意物质波的波长为 。
101.210m -⨯4．在量子力学中，描述系统的运动状态用波函数()r ψ，一般要求波函数满足三个条件即 ； ； 。
根据玻恩对波函数的统计解释，电子呈现的波动性只是反映客体运动的一种统计规律，称为 波，波函数模的平方()2r ψ表示粒子在空间的几率分布，称为 。
而()2r d ψτ表示 ，要表示粒子出现的绝对几率，波函数必须 。
单值的、连续的、平方可积的；几率或概率 几率密度或概率密度；在空间体积d τ中找到粒子的几率或概率；归一化 5．测不准关系/2x x p ∆∆≥ 表明，微观粒子的位置（坐标）和动量 ，这是 的反映，当0→ 时，量子力学将回到经典力学，或者说 可以忽略。
而/2E t ∆∆≥ 说明原子处于激发态时有一定的时间限制，则原子激发能级有一定 ，这是原子光谱存在 的根源。
不能同时具有完全确定的值 粒子的波动－粒子两重性 量子效应 宽度 自然宽度6．在量子力学中，力学量通常用算符表示，在坐标表象中，动量变为动量算符即ˆp = ，在动量表象中，坐标变为坐标算符，即ˆr=。
i -∇ p i ∇7．设波函数()22xx Aeαψ-=，α为常数，求归一化常数A()222222222*21x x x x dx A e Ae dx Ae dx Aαααψ∞∞∞----∞-∞-∞====⎰⎰⎰其中利用2xe dx ∞--∞=⎰A ＝1/41/22απ⎛⎫⎪⎝⎭8．已知做直线运动的粒子处于状态()11x ixψ=- （1）将()x ψ归一化；（2）求出粒子坐标取值几率为最大处的位置和最大几率密度。
量子力学所有简答题答案
简答题1．什么是光电效应？光电效应有什么规律？爱因斯坦是如何解释光电效应的？答：光照射到*些物质上，引起物质的电性质发生变化，也就是光能量转换成电能。
这类光致电变的现象被人们统称为光电效应。
或光照射到金属上，引起物质的电性质发生变化。
这类光变致电的现象被人们统称为光电效应。
光电效应规律如下：1．每一种金属在产生光电效应时都存在一极限频率〔或称截止频率〕，即照射光的频率不能低于*一临界值。
当入射光的频率低于极限频率时，无论多强的光都无法使电子逸出。
2．光电效应中产生的光电子的速度与光的频率有关，而与光强无关。
3．光电效应的瞬时性。
实验发现，只要光的频率高于金属的极限频率，光的亮度无论强弱，光子的产生都几乎是瞬时的。
4.入射光的强度只影响光电流的强弱，即只影响在单位时间内由单位面积是逸出的光电子数目。
爱因斯坦认为：(1)电磁波能量被集中在光子身上，而不是象波那样散布在空间中，所以电子可以集中地、一次性地吸收光子能量，所以对应弛豫时间应很短，是瞬间完成的。
(2)所有同频率光子具有一样能量，光强则对应于光子的数目，光强越大，光子数目越多，所以遏止电压与光强无关，饱和电流与光强成正比。
(3)光子能量与其频率成正比，频率越高，对应光子能量越大，所以光电效应也容易发生，光子能量小于逸出功时，则无法激发光电子。
逸出电子的动能、光子能量和逸出功之间的关系可以表示成：221mv A h +=ν这就是爱因斯坦光电效应方程。
其中，h 是普朗克常数；f 是入射光子的频率。
2．写出德布罗意假设和德布罗意公式。
德布罗意假设：实物粒子具有波粒二象性。
德布罗意公式：νωh E == λhk P ==3．简述波函数的统计解释，为什么说波函数可以完全描述微观体系的状态。
几率波满足的条件。
波函数在空间中*一点的强度和在该点找到粒子的几率成正比。
因为它能根据现在的状态预知未来的状态。
波函数满足归一化条件。
4．以微观粒子的双缝干预实验为例，说明态的叠加原理。
量子光学习题解答
e e =e e e 令 λ =1，即 e = e e e = e ee A ↔ B ，则有 e = e ee 。
A+ B
=e
λA
λB
−1 λ 2C 2
−1 λ 2C 2
A B
λA
λB
−1 C 2
−1 [ A, B ] 2
A
B
A+ B
1 [ A, B ] 2
B
A
1.3
α 为参数，A,B 不对易，求证
∴e
−α a + a
f ( a , a + )e
α a +a
= f (ae , a + e ) 。
α
−α
（c）的另一种证法： 由 1.2 题的（1）式，易得 [a + , a n ] = −na n −1 ， [a , a + n ] = na + n −1 ∴[a + a, a n ] = − na n ， [aa + , a + n ] = na + n 由 1.3 题结果，易得 e
1 ∂2 A =0 2 c ∂t 2
（1 ）
(i = x , y , z )
在直角坐标系中，分离变量
Ai ( r , t ) = Ai ( r ) Ai (t )
（2）
代入（1）式，有
∇2 Ai ( r ) Ai ( r )
2
=
1 ∂ 2 Ai ( t ) c2 ∂t 2 Ai ( t )
2
= −k 2
+ + + + + + + + + + +
30道量子力学知识选择题和答案
30道量子力学知识选择题和答案1. 关于量子态，以下说法正确的是（）A. 量子态是可连续变化的B. 量子态是离散的答案：B2. 量子叠加原理是指（）A. 多个量子态可以同时存在B. 量子态只能有一个答案：A3. 量子纠缠现象说明了（）A. 量子之间存在相互作用B. 量子之间存在非定域性关联答案：B4. 在量子力学中，测量会导致（）A. 量子态的改变B. 量子态的保持不变答案：A5. 关于波函数，以下说法正确的是（）A. 描述了量子系统的状态B. 是一个实数函数答案：A6. 海森堡不确定性原理涉及到哪两个物理量的不确定性（）A. 位置和动量B. 能量和时间答案：A7. 量子力学中的算符表示（）A. 物理量B. 对量子态的操作答案：B8. 泡利不相容原理适用于（）A. 电子B. 所有费米子答案：B9. 以下哪种现象与量子力学有关（）A. 黑体辐射B. 光电效应答案：B10. 在量子力学中，能量的量子化表现为（）A. 能量只能取特定的值B. 能量可以连续变化答案：A11. 关于量子隧道效应，以下说法正确的是（）A. 粒子可以穿过势垒B. 粒子不能穿过势垒答案：A12. 量子力学中的可观测量对应的是（）A. 厄米算符B. 非厄米算符答案：A13. 狄拉克方程描述的是（）A. 电子的运动B. 所有粒子的运动答案：B14. 关于量子力学的诠释，以下说法正确的是（）A. 只有一种诠释是正确的B. 有多种诠释，且都有实验支持答案：B15. 量子力学中的全同粒子（）A. 是完全相同的B. 可以区分答案：A16. 关于量子力学的基本假设，以下说法错误的是（）A. 物理量都可以用实数来描述B. 量子态的演化是确定性的答案：AB17. 量子力学中的概率幅表示（）A. 概率的大小B. 概率的相位答案：B18. 以下哪种实验验证了量子力学的基本原理（）A. 双缝干涉实验B. 迈克尔逊-莫雷实验答案：A19. 量子力学中的守恒量对应的是（）A. 不变的物理量B. 随时间变化的物理量答案：A20. 关于量子力学中的对称性，以下说法正确的是（）A. 存在多种对称性B. 对称性与物理规律无关答案：A21. 量子力学中的密度算符描述的是（）A. 量子系统的概率分布B. 量子系统的能量分布答案：A22. 以下哪种量子系统具有简并性（）A. 氢原子B. 自由粒子答案：A23. 量子力学中的散射理论主要研究（）A. 粒子的碰撞过程B. 粒子的传播过程答案：A24. 关于量子力学中的表象，以下说法正确的是（）A. 有多种表象可以选择B. 表象是唯一确定的答案：A25. 量子力学中的时间演化算符描述的是（）A. 量子态随时间的变化B. 物理量随时间的变化答案：A26. 以下哪种量子系统的能级是分立的（）A. 谐振子B. 自由电子答案：A27. 量子力学中的角动量算符具有（）A. 分立的本征值B. 连续的本征值答案：A28. 关于量子力学中的路径积分表述，以下说法正确的是（）A. 是一种量子力学的表述方式B. 与薛定谔方程等价答案：AB29. 量子力学中的对称性破缺会导致（）A. 新的物理现象B. 物理规律的改变答案：A30. 以下哪种量子系统的波函数可以用球谐函数来描述（）A. 氢原子B. 原子核答案：A。
量子力学作业答案精选全文完整版
可编辑修改精选全文完整版量子力学课后习题答案2.1证明在定态中，概率流密度与时间无关。
证：对于定态，可令)]r ()r ()r ()r ([m2i ]e )r (e )r (e )r (e )r ([m2i )(m 2i J e)r ( )t (f )r ()t r (**Et iEt i **Et i Et i **Etiψψψψψψψψψψψψψψψ∇-∇=∇-∇=∇-∇===-----）（）（，可见t J 与无关。
2.2 由下列定态波函数计算几率流密度： ikr ikr e re r -==1)2( 1)1(21ψψ 从所得结果说明1ψ表示向外传播的球面波，2ψ表示向内(即向原点) 传播的球面波。
解：分量只有和r J J 21在球坐标中 ϕθθϕθ∂∂+∂∂+∂∂=∇sin r 1e r 1e r r 0 r m r k r m r k r r ik r r r ik r r m i r e rr e r e r r e r m i mi J ikr ikr ikr ikr30202201*1*111 )]11(1)11(1[2 )]1(1)1(1[2 )(2 )1(==+----=∂∂-∂∂=∇-∇=--ψψψψ r J 1与同向。
表示向外传播的球面波。
rm r k r m r k r r ik r r r ik r r m i r e r r e r e r r e r m i mi J ikr ikr ikr ikr3020220*2*222 )]11(1)11(1[2 )]1(1)1(1[2 )(2 )2(-=-=---+-=∂∂-∂∂=∇-∇=--ψψψψ可见，r J与2反向。
表示向内(即向原点) 传播的球面波。
2.3 一粒子在一维势场⎪⎩⎪⎨⎧>∞≤≤<∞=a x a x x x U ，，，0 00)( 中运动，求粒子的能级和对应的波函数。
解：t x U 与)(无关，是定态问题。
2019年光量子学习题答案.doc
《光量子学基础》习题答案（沈建其提供，2009年6月）说明：习题难度非常低，大多习题均可以在ppt 中直接找到答案。
第一次习题：1．计算（1）：de Broglie 波长均为5埃（Å）的电子、中子与光子的动量与能量各为多少？答：这三种粒子的动量都是3424106.6310 1.3310510p h λ---⨯===⨯⨯Kg ·m/s (或241.310-⨯ Kg ·m/s)。
电子的动能 ()224218300 1.33100.96510220.91110k pE m ---⨯===⨯⨯⨯J 6.03=eV （或6eV ） （1电子伏特＝191.6010-⨯焦耳）中子的动能 ()224221270 1.33100.5261022 1.6710k p E m ---⨯===⨯⨯⨯J 20.33010-=⨯eV 以上使用牛顿力学的动能公式（6.03eV 远比电子的静止能量20m c 约0.5MeV 小，0.0033eV 远比中子的静止能量20m c 约990MeV 小，说明没有必要使用相对论来计算） 但光子是相对论性粒子，必须用相对论来计算：光子动能（总能）2481.3310 3.0010k E pc -==⨯⨯⨯J ＝4.001610-⨯J=2.50310⨯eV 。
说明：虽然以上问题中，牛顿力学的动能公式是非常良好的近似，但使用相对论亦可。
有的学生计算了动能部分，有的学生计算了总能量2E mc =，答案是开明的，都属对，但要知道2E mc =与动能22p m 之间如下关系：粒子总能量2E mc =，动质量m =2E mc =可以用泰勒展开：2246001...2E m c m v av bv =++++，其中20m c 为静止能量（rest energy ）, 2012m v 为牛顿动能（它只是2E mc =的一部分）。
只有当低速的时候，220012m c m v +才重要，其中2012m v更重要。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《光量子学基础》习题答案（沈建其提供，2009年6月）说明：习题难度非常低，大多习题均可以在ppt 中直接找到答案。
第一次习题：1．计算（1）：de Broglie 波长均为5埃（Å）的电子、中子与光子的动量与能量各为多少？答：这三种粒子的动量都是3424106.6310 1.3310510p h λ---⨯===⨯⨯Kg ·m/s (或241.310-⨯ Kg ·m/s)。
电子的动能 ()224218300 1.33100.96510220.91110k pE m ---⨯===⨯⨯⨯J 6.03=eV （或6eV ） （1电子伏特＝191.6010-⨯焦耳）中子的动能 ()224221270 1.33100.5261022 1.6710k p E m ---⨯===⨯⨯⨯J 20.33010-=⨯eV 以上使用牛顿力学的动能公式（6.03eV 远比电子的静止能量20m c 约0.5MeV 小，0.0033eV 远比中子的静止能量20m c 约990MeV 小，说明没有必要使用相对论来计算） 但光子是相对论性粒子，必须用相对论来计算：光子动能（总能）2481.3310 3.0010k E pc -==⨯⨯⨯J ＝4.001610-⨯J=2.50310⨯eV 。
说明：虽然以上问题中，牛顿力学的动能公式是非常良好的近似，但使用相对论亦可。
有的学生计算了动能部分，有的学生计算了总能量2E mc =，答案是开明的，都属对，但要知道2E mc =与动能22p m 之间如下关系：粒子总能量2E mc =，动质量m =2E mc =可以用泰勒展开：2246001...2E m c m v av bv =++++，其中20m c 为静止能量（rest energy ）, 2012m v 为牛顿动能（它只是2E mc =的一部分）。
只有当低速的时候，220012m c m v +才重要，其中2012m v更重要。
当高速的时候，2012m v 不再重要。
此时应该用2E mc =等来计算。
因此，本习题求中子与电子的动能时，可以用如下两法：①使用p =求出速度v ，代入2E =，求出总能量E, 再减去静止能量20m c ，即是动能。
② 利用动量p 的数值，使用222240E p c m c =+，求出总能量E, 再减去静止能量20m c ，即是动能。
以上两法是等价的。
以上两法对于光电系学生不作要求，但还是有不少学生就使用了以上两法，说明他们对于普通物理掌握得不错。
值得赞赏！！计算（2）：当电子与中子的速度都为1000m/s 时，它们的物质波（de Broglie波）波长各为多少？当它们通过一个宽度为10nm 的细缝时，谁的衍射效应强？哪者需要使用量子论研究，哪者可以近似用牛顿力学处理？普朗克常数346.6310h -=⨯J ·s, 约化（reduced ）普朗克常数341.05102hπ-==⨯J ·s, 电子质量300.91110-⨯Kg, 质子与中子质量接近，可以取271.6710-⨯Kg 。
答： 电子的物质波波长347306.63107.30100.911101000h p λ---⨯===⨯⨯⨯m ＝730nm ， 中子的物质波波长3410276.6310 3.97101.67101000h p λ---⨯===⨯⨯⨯m ＝0.4nm ， 根据衍射理论，屏幕上衍射暗条纹之间的距离为/L a λ （L 为细缝与屏幕 之间的垂直距离，a 为缝宽）。
波长越短，粒子性越强；波长越长，波动性越明显，衍射效应越强。
电子的衍射效应强，电子需要使用量子论研究，本例中子可以近似用牛顿力学处理。
2． 根据“1-量子力学的提出.ppt ”中的内容，把Compton （康普顿）散射理论独立推导一遍，体会光子的确具有客观实在性，同时锻炼自学能力。
答：略3． 根据“1-量子力学的提出.ppt ”中的内容，把Bohr （波尔）的氢原子结构理论的数学独立推导一遍，体会Bohr 创建原子模型的心路历程，同时锻炼自学能力。
答：略第二次习题：1．下面各个状态中，哪个与1ψ描写同一个状态？理由是？2/2/3/1232/(2)/2/456,,,,3,(42).i x i x i x i x i x i x e e e e e i e πψψψψψψ--+====-==+答：146(),(),()x x x ψψψ描述同一个状态（差别仅在于无关紧要的常数系数，它们可以通过归一化手续去掉）。
2．有两个波函数12sin()||()1,2,3,20||sin()||()1,2,3,20||n A x a x a x n ax a n A x a x a x n ax aπψπψ⎧-≤⎪==±±±⎨⎪>⎩⎧+≤⎪==±±±⎨⎪>⎩1()x ψ与2()x ψ是否等价？理由是？对1()x ψ中，2n =±的两个波函数，是否等价？理由是？ 答：()()12sinsin sin cos cos sin ;2222222sin sin sin cos cos sin 2222222n n n n n n n A x a A x A x A x a aa a n n n n n n n A x a A x A x A x a a a a πππππππψπππππππψ⎛⎫⎛⎫⎛⎫=-=-=-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭可以看出：当n 是偶数的时候， sin 02n π⎛⎫±= ⎪⎝⎭，1()x ψ与2()x ψ等价。
当n 是奇数的时候，cos 02n π⎛⎫±= ⎪⎝⎭，1()x ψ与2()x ψ等价。
说明：我们也可以使用如下更为方便且严密的做法：即把1ψ用2ψ表示出来。
()()()222222422222222222222211sin 2221122sin sin22n n nn n n i x a i x a i x i x i i a a a a n n n n n n n n n n i x i x i x i x i i i i i i a a a a n n iin x a e e e e e e a i i e e e e e e e e e e i i n n n x e eaππππππππππππππππππππππ---------⎡⎤⎡⎤-=-=-⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦⎛⎫=+= ⎪⎝⎭()2x a a+ 其中第三等号后使用了关系421n ie π=。
以上看出，1ψ与2ψ可以互相表示，它们只相差一个常数系数22n i eπ（常数系数之间的差别可以通过归一化手续去掉，所以1ψ与2ψ等价）。
（说明：这里，22(1)n i n e π=-）对1()x ψ中，2n =±的两个波函数，()1sin sin sin cos 22222n n n n n A x a A x A x a a a πππππψ⎛⎫⎛⎫=-=-=-⎪ ⎪⎝⎭⎝⎭，2n =±，它们等价。
3．由薛定谔方程22[]2iV t μ∂ψ=-∇+ψ∂证明：2[]2i t μ***∂ψψ=∇⋅ψ∇ψ-ψ∇ψ∂（）， 并与粒子数守恒公式（连续性方程）0J tω∂+∇⋅=∂比较：如果粒子数密度ω定义为*ψψ，那么流密度J 的表达式是什么？答：见PPT 讲义或曾谨言的《量子力学教程》（2003年出版）（有扫描电子版）p.17.4．一维谐振子处于状态22()exp(/2)x A x ψα=-。
求：归一化系数A （请用α表示）。
答：假设归一化系数A 为实数。
由归一化条件，可得*222()()1exp()1.x x dx A x dx ψψα+∞-∞=⇒-=⎰⎰由数学用表可以查得：22exp()x dx α+∞-∞-=⎰那么21A =，所以A = 说明：如果没有数学用表，我们也可以自己计算22exp()x dx α+∞-∞-⎰（是某一年的数学考研填空题），方法如下：设2222exp()exp()I x dx y dy αα+∞+∞-∞-∞=-=-⎰⎰，()()()22222202222202exp exp 2exp I x y dxdy r rdr r d rααππαααπα+∞-∞∞∞⎡⎤=-+⎣⎦⎡⎤=-⋅⎣⎦=-=⎰⎰⎰那么，I α=。
那么21A α=，所以A = 注意：以上把,x y 看作直角坐标，2dxdy rdr π=是直角坐标与二维极坐标面积微元之间的转换。
第三次习题：1．一维无限深势阱，其势能分布是：,00,0,x V x a x a ⎧+∞<⎪=≤≤⎨⎪+∞>⎩求势阱中的粒子波函数（包括归一化系数）与对应的能量本征值。
答：答案见曾谨言的《量子力学教程》（2003年出版）（有扫描电子版）p.32-33.2．大学生应该有相当高的自学能力。
根据 “4-力学量的算符表示与氢原子.ppt ”角动量算符（自学部分），独立推导出如下的角动量算符三个分量公式以及角动量算符平方公式（需要比较高的忍耐力。
也有助于理解直角坐标系与球坐标系之间的关系，此训练具普适性）： ˆ[sin cot cos ]ˆ[cos cot sin ]xy L i L i φθφθφφθφθφ⎧∂∂=+⎪∂∂⎪⎪∂∂⎪=-+⎨∂∂2222211ˆ[(sin )]sin sin L θθθθθφ∂∂∂=-+∂∂∂答：球坐标与直角坐标之间的换算关系式是：)()arctan,arctan /r z y x θϕ===。
利用多元函数求偏微分法则，直角坐标偏导数可以用球坐标偏导数表示：2222,,r x y x x r x x r r x y r y x y y r y y r r x y r z z z r z z r r θϕθϕϕθϕθϕϕθϕθϕ∂∂∂∂∂∂∂∂∂=++=+∂∂∂∂∂∂∂∂+∂∂∂∂∂∂∂∂∂∂=++=+∂∂∂∂∂∂∂∂+∂∂∂∂∂∂∂∂∂=++=∂∂∂∂∂∂∂∂ 在ˆx L i y z z y⎛⎫∂∂=-- ⎪∂∂⎝⎭中，我们有 yz y z rr ∂∂=∂∂ 222zy zx z y r r x y ϕ∂∂∂=++∂∂+∂， 所以，x 分量角动量2222ˆsin cot cos ;x zx L i i x y x y ϕθϕθϕθϕ⎛⎫⎛⎫∂∂∂ ⎪=---=+⎪ ⎪∂+∂∂∂+⎝⎭⎝⎭ 在ˆy L i z x xz ∂∂⎛⎫=-- ⎪∂∂⎝⎭中，我们有222zx zy z x r r x y ϕ∂∂∂=∂∂+∂， xz x z r r ∂∂=∂∂， 所以，y 分量角动量2222ˆcos cot sin ;y zy L i i x y x y ϕθϕθϕθϕ⎛⎫⎛⎫∂∂∂ ⎪=--=-+ ⎪ ⎪∂+∂∂∂+⎝⎭⎝⎭在ˆz L i x y y x ⎛⎫∂∂=-- ⎪∂∂⎝⎭中，我们有 222xy x x y r r x y ϕ∂∂∂=++∂∂+∂，222yx yyx r r x yϕ∂∂∂=∂∂+∂，显然，z分量角动量ˆzL iϕ∂=-∂。