理论力学--第3章解剖

合集下载

理论力学第三章.ppt

MB MB (F ) Fd
2、平面任意力系向作用面内一点简化·主矢和主矩
F1' F1 F2' F2
M1 Mo (F1) M2 Mo (F2 )

Fn' Fn Mn Mo (Fn )
FR Fi Fi

MO Mi MO (Fi )
求： A ,C支座处约束力. 解：取整体，受力图能否这样画？
取整体，画受力图.
求: A,B处的约束力.
解: 取整体,画受力图.
M A 0 12FBy 10P 6P1 4P2 2P 5F 0
解得
FBy 77.5kN
Fiy 0 FAy FBy 2P P1 P2 0
解得
FAy 72.5kN
取吊车梁,画受力图.
MD 0
求:
DC=CE=CA=CB=2l,R=2r=l, 450,
P, 各构件自重不计.
A,E支座处约束力及BD杆受力.
解: 取整体,画受力图.
ME 0
5
FA
2 2l P l 0 2
பைடு நூலகம்
解得
FA

52 8
P
Fix 0
FEx FA cos 450 0
解得
FEx
Fy 0

M A 0

M M
A B

0 0
各力不得与投影轴垂直 A, B 两点连线不得与各力平行
例3-3 已知： P1 700kN, P2 200kN, 尺寸如图；
求：（1）起重机满载和空载时不翻倒，平衡载重P3；

理论力学教学课程第3章

上一页下一页返回
第一节平面静定桁架
• 2 ．截面法 • 当桁架中的杆件比较多，而只需计算其中某几个杆件的内力时，应用
节点法往往比较麻烦，这时采用截面法。截面法是适当选取一截面，假想地将桁架截开，选取其中的一部分作为研究对象。作用在这部分桁架上的外力与被截断杆件的内力构成平面一般力系，应用平面一般力系的平衡条件，可求解三个未知量。因此，在应用截面法时，一般截断的未知内力的杆件数应不多于三根。假想截面的形状可任意选择，既可以是平面，也可以是曲面。
• 所有杆件都在同一平面内的桁架，称为平面桁架。桁架中杆件与杆件的连接处称为节点，节点的构造通常使用铆接、焊接或螺栓连接等形式。如图 3-2 所示，由基本三角形结构出发，通过增加杆件延拓而成的平面桁架称为平面简单桁架，图 3-2 （ a ）和（ b ）分别为屋架和桥梁结构的平面简单桁架。这种结构是静定的几何不变系统。本节只讨论平面简单桁架的内力计算问题。
• 二、桁架内力的计算方法
• 计算平面简单桁架的内力有两种方法：节点法和截面法。在求解桁架内力之前，通常先选取整体为研究对象，求出桁架支座的约束力。
• 1 ．节点法 • 节点法求解桁架内力是以桁架的节点为研究对象的。平面桁架的每个
节点都受平面汇交力系的作用，可用平面汇交力系的平衡方程求解。对于每个节点只能列两个独立的平衡方程，求解两个未知量。因此，在采用节点法时，选取的节点的未知量应不超过两个。
• Fd=f dFN （ 3-3 ） • 式中： f d 称为动摩擦系数，它与接触物的材料、表面粗糙度及相对
滑动速度等因素有关，其值略小于静摩擦系数，即 f d < f s 。 • 2 ．摩擦角与自锁现象 • 1 ）摩擦角 • 摩擦角是对静摩擦系数的几何描述。

理论力学第三章刚体力学 ppt课件

正常转动，赝张量的变换多出一个负号。
对于张量，可定义如下运算：
1）相等。
设A和B为两个同阶张量，如果它们的所有分量相等，
即
A ... B ... ，则称它们相等，记为A = B.
2）加法。
两个同阶张量A和B的和定义为 C ...＝A ...＋B ... 它仍为一个张量，记为 C＝A＋B

L
a

L
a AL L )(a L
a L
a

B L
L

)

a L aa L a AL L BL L (a a )
a L aa L a ( AL L BL L )
nr nr nr nr
1）转动前： rr 2）转动nr 后：rr nr rr
3）再rr 转动nr rrnr后nr：rr nr rr
不计二阶微量，则有
rr rr nr rr nrrr
交换转动次序，则有
rr rr nrrr nr rr 已知对线位移，有 rr rr rr rr 可得 nr rr nrrr nrrr nr rr
§3.1 刚体运动的分析 §3.2 角速度矢量 §3.3 欧勒角 §3.4 刚体运动方程与平衡方程 §3.5 转动惯量 §3.6 刚体的平动与绕固定轴的转动
§3.7 刚体的平面平行运动 §3.8 刚体绕固定点的运动 §3.9 重刚体绕固定点转动的解 §3.10 拉莫尔进动
§3.1 刚体运动的分析
1. 描写刚体位置的独立变量
将两个矢量Av和Bv按顺序并在一起，不作任何运算
得到的量称为并矢，记为
vv AB

A
B ev ev

理论力学第3章-力偶系

例 3-1 图示机构，各杆自重不计，在两力偶作用下处于平衡。已知：M1 = 100 N · m，O1A = 40 cm，O2B = 60 cm。试求力偶矩M2的大小。 B A FB F B FA
30 o
B
O1
B
A FA M2
M1 FO1 O1 A M1
M
2
O2
O2
FO2
解：取O1A杆为研究对象，受力如图所示，
若两个力偶对刚体的作用效应相同，则称这二力偶等效。
两力偶的等效条件：力偶矩矢相等，即
M1 M2
(3-2) FR'
B'
证明：
A'
FR F1 FR F'
A B
FR' F1'
F
力偶(FR，FR' ) 代了原力偶(F，F' ) 并与原力偶等效。
A'
FR
FR'
B'
D F' C
比较(F,F')和(FR,FR')可得 M(F,F')=2△ABD=M(FR,FR') =2 △ABC
合力偶矩矢的大小和方向余弦为
M ( M x )2 ( M y )2 ( M z )2 (280)2 1602 (800)2 862.55 kN m
M cos( M , i )
280 0.3246 M 862.55 My 160 cos( M , j ) 0.1855 M 862.55
1 3 200 280kN m 5 5 4 M y M y M 1 y M 2 y 0 200 160kN m 5 2 M z M z M1z M 2 z 400 5 0 800kN m 5 M x M x M1x M 2 x 400 5

理论力学第三章课件

例6：起重机自重 P1=700kN, 作用线过塔
M A (F ) 0 :
FAy–P–Fcos600=0
MA–M–Fql+Fcos600l+Fsin6003l=0 解得：FAx=316.4kN； FAy=300kN
MA=–1188kN.m (与图示转向相反）
Fq FAy FAx MA
静力学/第三章：平面任意力系
■ 平衡方程的其它形式 1 二矩式：
Y 0
FAy FB Fq F 0
1 M 1 FB (3F qa ) 2 a 2
1 M 5 FAy ( F qa ) 2 a 2
静力学/第三章：平面任意力系
例3 ：已知有一平面任意力系，满足 X ≠ 0, Y = 0,
y
b B

A为x轴上的点，B为y轴上的点，OB=b, 角已知。求：OA=？
二矩式成立
充分性即: 二矩式成立
由：
则：力系不可能合成为合力偶，
只可能合成为合力或平衡。
静力学/第三章：平面任意力系
由由
又因： X= 0
若有合力，则合力作用线过A点。
若有合力，则合力作用线过B点。
B A
x
合力作用线过 AB
且 x 轴不与AB连线垂直
故必有：合力为零，即力系平衡。
合力
合力偶 MO = M
O
Mo
作用于O点
静力学/第三章：平面任意力系
2、力系的主矢和主矩
力系的主矢：对O点的主矩：
M o M o (F )
F FR
■力系主矢的特点： * 对于给定的力系，主矢唯一；

理论力学周衍柏第三章

一、基础知识 1. 力系：作用于刚体上里的集合. 平衡系：使静止刚体不产生任何运动的力系. 等效系：二力系对刚体产生的运动效果相同. 二、公理： 1）二力平衡原理：自由刚体在等大、反向、共线二力作用下必呈平衡。 2）加减平衡力学原理：任意力系加减平衡体系,不改变原力系的运动效应。 3）力的可传性原理：力沿作用线滑移，幵不改变其作用效果，F与F’等效。注：1）以上公理适用于刚体, 2) 力的作用线不可随便平移
(e) dT Fi dri
(e) 若 Fi dri dV 则 T V E
为辅助方程，可代替上述6个方程中任何一个
§3.5 转动惯量
一、刚体的动量矩 1. 某时刻刚体绕瞬轴OO’转动,则pi点的速度为
vi rii
动量矩为 2. 坐标表示
R Fi Fi 0 M M i ri Fi 0
2. 几种特例 1）汇交力系（力的作用线汇交于一点）：取汇交点为简化中心，则
Fix 0 R Fi 0 Fiy 0 Fiz 0
三、力偶力偶矩 1. 力偶：等大、反向、不共线的两个力组成的利系。
力偶所在平面角力偶面. 2. 力偶矩: 对任意一点O M rA F rB F (rA rB ) F r F M Fd
方向 : 右手法则上式表明:
J z x mi zi xi y mi zi yi z mi ( xi2 yi2 )
I yy mi ( zi2 源自xi2 ) I zy mi zi yi I yz mi yi zi I xz mi xi zi
I zz mi ( xi2 yi2 )

理论力学课件受力分析与受力图、第三章

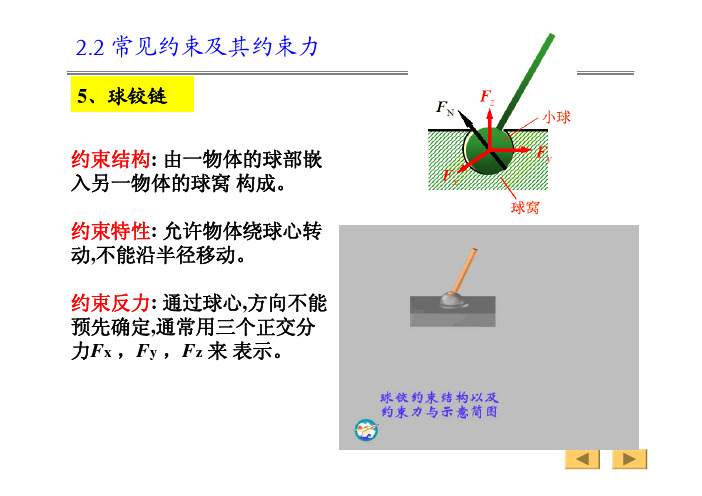
5、球铰链
约束结构: 由一物体的球部嵌入另一物体的球窝构成。

约束特性: 允许物体绕球心转动,不能沿半径移动。

约束反力: 通过球心,方向不能预先确定,通常用三个正交分力F x，F y，F z来表示。

人造髋关节
二力杆工程实例
固定端约束除了加约束力，还要加上约束力偶。

运动学角度：固定端既限制线位移，又限制角位移，如果只有约束力，则构件将转动。

必须有约束力偶才行。

力系简化角度：固定端所受的力是一个复杂的平面任意力系，力系向端部某点简化的结果是一力和一力偶。

CD是不是二力
杆？
2.3 受力分析与受力图
刚化原理：若变形体在某一力系作用下处于平衡，则将此变形体刚化为刚体，其平衡状态保持不变。

只有刚化原理没有软化原理。

1. 右拱BC 的受力图。

C
B
解：
F C
F B
2. 左拱AC 的受力图。

A C
F
F Ax C F
F Ay。

理论力学-第3章

M Oy M Oy Fi 0
略去所有表达式中的下标 i ，空间任意力系平
F F F
x y
0 0 0
z
M F 0 M F 0 M F 0
x y z

任意力系的平衡方程
平衡方程的一般形式
F F F
x y
0 0 0
平衡方程的一般形式
对于作用在刚体或刚体系统上的任意力系，平
衡条件的投影形式为
z
F2 M2
FRx Fix 0 FRz Fiz 0
FRy Fiy 0
M Ox M Ox Fi 0 M Oz M Oz Fi 0
F1
M1
O y
Mn
l
l
A C
第三种情形
l
B
FP
D

平衡方程的应用
例题 1
图示结构，若 FP 和 l 已知，确定四种情形下的约束力
l
l
A C
第三种情形
l
B
FP
D
FA
l
A C B
l
FP
D
l
FCx
FCy

平衡方程的应用
例题 1
图示结构，若 FP 和 l 已知，确定四种情形下的约束力 MA ( F ) = 0 :
平衡方程的应用
例题 1
图示结构，若 FP 和 l 已知，确定四种情形下的约束力
l
l
B D
FP
FAy FAx A
l
A C
l
d C
B FBC
l
FP
D
第一种情形
l

理论力学第三章

注意结果中“ - ‖的含意 !!!
END
例3-2 已知：小车匀速上升，P = 10kN。α=30o y 求：拉力T 和轨道给车轮的约束反力。解：1) 取小车为分离体; a=0.75m; b=0.3m T b 画受力图： 2) 列平衡方程：
X 0 : T P sin 0 3)解：T = Psin30o = 5 kN
X 0 : X A T cos 30 0
XA = Tcos30o = 15.01 kN
P Q
Y 0 : YA T sin 30 P Q 0
YA = P + Q－Tcos30o = 5.33 kN
M A 0 : T 6 sin 30 P 3 Q 4 0
END
例3-3 已知：P = 20 kN, m = 16 kN· qa = 20 kN/m, a = 0.8 m m, q
求：A、B的支反力。
解：1)取AB梁为分离体；画受力图如右图示： 2)列平衡方程：
XA
YA
YB
X 0：
Y 0：
XA 0
YA YB qa P 0
小结
1) 力的平移定理：条件、结论及其应用 2) 力矩与附加力偶：概念、区别及其特性
3) 平面任意力系的简化：
概念 —— 合成与分解结果 —— 主矢与主矩
应用 —— 求合力或受力分析
3.4 平面任意力系的平衡条件与平衡方程
1) 平面任意力系的平衡条件与平衡方程从上节可知平面任意力系平衡的充要条件是：而
1
3
2)平面汇交力系、平面平行力系：2 所以：当独立方程的数目“n”≥未知数的数目“m‖时，就是静定问题(即可以由静力学平衡方程完全确定的问题)。

理论力学(郝桐生)第三版第3单元课件

动画
力线平移定理
参见动画：平面力线平移定理
2021/10/10
5
参见动画：钳工用丝锥攻螺纹(断)
为什么如此攻螺纹会断？
参见动画：力线平移实例
2021/10/10
6
二、平面任意力系向作用面内一点简化‧主矢和主矩
参见动画：平面任意力系向平面内任一点的简化
2021/10/10 称点O为简化中心
7
平面力系向作用面内一点简化
30
例题
平面任意力系
例题5
解： 1. 取T 字形刚架为研究对象，受力分析如图。
l
60
F
B
l
D
M
l
F 60
B
y l
D M
3l
G
A
q
2021/10/10
F1
G
l MA FAy
x
A FAx 31
例题
平面任意力系
例题5
2. 按图示坐标，列写平衡方程。
y
l
l
F 60
Fx 0,
FAx F1 F sin 60 0
FR (Fx)2(Fy)2
coF sR (,i)FFRx ,
co(F sR , j)FFRy
原力系的主矢与简化中心O的位置无关
主矩：原力系中各力对简化中心O之矩的代数和称为原力
系对点O的主矩。
n
M O M O (F1) M O (F2 ) ...... M O (Fn ) M o (Fi )
M O (FR ) FRd M O
n
而 M O M o (Fi )
n
i 1
M O (FR ) M o (Fi ) 合力矩定理得证

理论力学静力学第三章

∑MA = 0 4aFAx + 8.5aP − F a = 0 T
解得
FAx = −20kN
∑ FAx + F = 0 Cx
解得
F = 20kN Cx
取BDC杆（带着轮）
∑MB = 0
解得
4aF + F ⋅ 3a + F 1 ⋅ a − F ⋅ 4a = 0 Cy T T Cx
F =15kN Cy
FBy = 0
取ADB杆，画受力图取DEF杆，画受力图
∑MD = 0
FE sin45 ⋅ a − F ⋅ 2a = 0
得
FE sin45 = 2F
∑F = 0 ix
得
' FE cos45 − FDx = 0
' FDx = FE cos45 = 2F
' FDx ⋅ a − F ⋅ 2a = 0
∑MB = o
可否列下面的方程：
∑F = 0 ix
∑MA = 0 ∑MB = 0 ∑ F = 0 ix ∑MA = 0 ∑M = 0 B
FAx − F cos300 = 0 T
F sin300 ⋅ 6 − 4P − 3P = 0 2 1 T
−6FAy + 3P + 2P = 0 1 2
FAx − F cos30 = 0 T F sin30 ⋅ 6 + 4P −3P = 0 T 2 1 − 6FAy + 3P + 2P = 0 1 2
。 D
L
L
L
L
∑M (F)=0,
C
FBsin60°•L-q•L/2-Fcos30°•2L=0 FB=45.77kN
(a)

理论力学3章

习题3-1 台阶形鼓轮装在水平轴上，小头重量为2Q ，大头重量为1Q ，半径分别为2r 和1r ，分别挂一重物，物体A 重为2P ，物体重B 为1P ，且12P P >。

如3-1题图所示，求鼓轮的角加速度。

解：本题有明显的转轴o ，因而可以用角动量定理求解。

系统只有一个转轴，求运动而不求内力，所以取质心为研究对象。

因重力12,P P对轴o 的力矩不为零，可得：01122()L PQ PQ k =-质心系的动量距为：21202OQ OP OP k J J J J =+++2212121212211()22Q Q p p r r v v r k g g g gωωω=+++ 另外还有运动学补充方程：1122v r v r ωω==所以22220112211221(22)2J Q r Q r Pr P r k gω=+++应用角动量定理由 0i d J L dt =∑得 222211*********(22)2d Q r Q r Pr P r Pr g dtω+++=+11Pr 又 d dt ωε= 则有 11222222112211222()22Pr P r g Q r Q r Pr P r ε-=⋅+++答案：()12112222221122122d d 22Pr -P r g t Q r +Q r +Pr +P r ω=。

3-2 如图所示，两根等长等重的均匀细杆AC 和BC ，在C 点用光滑铰链连接，铅直放在光滑水平面上，设两杆由初速度为零开始运动。

试求C 点着地时的速度。

解：系统在水平方向上受力为零，角动量守恒有2211222h mv m ω+⨯2（I ）=2g其中 002/2vv l l ω==0v 为C 点着地时A 点速度002c v v v ===答案：c v =3-3 半径为a ，质量为M 的薄圆片，绕垂直于圆片并通过圆心的竖直轴以匀角速度ω转动，求绕此轴的角动量。

3-2题图3-1题图解由题意作图如图所示由某一质点组对某个固定轴的动量矩1ni i i i J r m v==⨯∑20adm rd dr rdr d πρθρθ==⎰⎰其中2Ma ρπ=故 223001()2a J r dmv d r dr Ma πθρωω=⨯==⎰⎰⎰⎰答案：212J Ma ω=3-4 一半径为r ，重量为P 的水平台，以初角速度0ω绕一通过中心o 的铅直轴旋转；一重量为Q 的人A 沿半径B o 行走，在开始时，A 在平台中心。

【理论力学2】第三章分析力学基础

n xi yi z i ( Fxi Fyi Fzi )q k 0 q k q k q k k 1 i 1
（3－6）
如令
Qk ( Fxi
i 1 n
xi y z Fyi i Fzi i ) (k 1 ， 2，，N ) （3－7） qk qk qk
如图所示
由式（b）的变分
可得一组虚位移 y A y B a sin 11 ，xB a cos11 则对应于 1的广义力为
Q1
（e ）
W1 FAy A Fy B Fx B 1 1
将式（e）代入上式得保持 1不变只有2 时如图所示由式（b）的变分可得另一组虚位移 y A 0 ，y B b sin 2 2 ，xB b cos 2 2 代入对应于 2 的广义力表达式得
W A FAx A PC yC ( FA PC )x A
对应广义坐标 x A 的广义力为 WA 1 QxA PC FA x A 2
1 2
（a）
再令y B向下 x A 0
同理可解得（b）
1 PC 2 P ，FA PC P 2 因此平衡时要求物块与台面间静摩擦因数 FA f 0.5 2P 如果作用在质点系上的主动力都是有势力则势能应为各点坐标的函数记为
（3－13）
这样由广义坐标表示的平衡条件可写成如下形式 V Qk 0 (k 1 ， 2，，N ) （3－14） qk 即在势力场中具有理想约束的质点系的平衡条件是势能对于每个广义坐标的偏导数分别等于零稳定平衡不稳定平衡在稳定平衡的平衡位置处系统势能具有极小值在不平衡位置上系统势能具有极大值对于随遇平衡系统在某位置附近其势能是不变的所以其附近任何可能位置都是平衡位置

理论力学第三章

1静力学第三章平面任意力系第三章平面任意力系若所有力的作用线都在同一平面内，且它们既不相交于一点，又不平行，此力系称为平面任意力系，简称平面力系。

本章将研究该力系的简化与平衡问题，这是静力学的重点之一。

本章还介绍平面简单桁架的内力计算。

2静力学第三章平面任意力系§3-1 平面任意力系向作用面内一点简化要研究一个力系的平衡，首先要研究它的简化。

力系简化的理论基础是力线平移定理。

1．力线平移定理作用在刚体上点A的力F 可以平行移动（简称平移）到任一点O上，但必须同时附加一个力偶，此附加力偶的矩等于原来力F 对新作用点B的矩。

3静力学第三章平面任意力系请看动画4静力学第三章平面任意力系5静力学第三章平面任意力系2．平面任意力系向作用面内一点简化 • 主矢与主矩设刚体上有一平面任意力系F1，F2，…，Fn，如图（a）。

应用力线平移定理，得一作用在点O的汇交力系F1′，F2′，…， Fn′以及相应的附加平面力偶系M1，M2，…，Mn，如图（b）。

再将平面汇交力系进一步合成过点O的一个力FRˊ，如图（c）,即′ FR =  Fi′ =  Fii =1 i =1nn(c)6静力学第三章平面任意力系平面力偶系进一步合成为对点O的一个力偶MO，即MO = Mi = MO (Fi )i =1 i =1nnFRˊ是平面汇交力系的合力，它的大小和方向称为原力系的主矢。

MO为平面力偶系的合力偶，但它是原力系的主矩。

主矢与简化中心无关，而主矩一般与简化中心有关，故必须指明力系是对于哪一点的主矩。

结论：平面任意力系向作用面内任一点O简化。

可得一个作用线通过简化中心的与主矢相等的力和一个相对于简化中心的主矩。

该主矩等于原力系对简化中心的矩。

它们的解析表达式为7静力学第三章平面任意力系′ ′ ′ FR = FRx + FRy =  Fx i +  Fy j大小方向余弦′ FR = ( Fx ) + ( Fy )22F cos( F ′ , i ) =Rx′ FR,nF cos( F ′ , j ) =Ry′ FR主矩M O =  M O (Fi ) =  ( xi Fyi − yi Fxi )i =1 i =1n8静力学第三章平面任意力系3．固定端约束及其约束力在工程实际中，有一种约束称为固定端（或插入端）支座，如电线杆的支座，阳台的支座等约束，使被约束物体既不能移动也不能转动。

大学本科理论力学课程第3章力矩与平面力偶理论

理论力学电子教程
O2
第三章力矩与平面力偶理论
A D
FB B
O1
E
F
H
FC AC
C
理论力学电子教程
第A三章力矩与平面力偶理论
O
O1
FD 沿O1DO2
F
E
D
H
FE AC
O2 A
FA 沿AO2， AC
FD 沿O2DO1 D
D
FB B
A
FA 沿AO2， AC
O2
FB
B
E
F
D
FD
理论力学电子教程
第三章力矩与平面力偶理论
思考题不计自重的三杆组成系统，判断固定铰支座B和C处约束反力方向（即画整体受力图）
A
a D
a B
E
F
H
C
a
a
理论力学电子教程
第三章力矩与平面力偶理论
A O1
D
E
F
H
O2
FB B
C
（1）分析整体，FC的作用点为C，故无论其方向如何FC与F二者的力的作用线必交于C点，利用三力平衡汇交原理判断固定铰支座对 DB处提供的约束反力合力的方位（沿BC）指向待定，FC的方向待定。
H
FC AC
C
O1
E FE AC FC A
C
理论力学电子教程
第三章力矩与平面力偶理论
第三章力矩与平面力偶理论
§3－1力矩的概念与计算 §3－2力偶及平面力偶系
理论力学电子教程
第三章力矩与平面力偶理论
力对物体作用时可以产生移动和转动两种效应。力的移动效应取决于力的大小和方向；为了度量力的转动效应，需引入力矩的概念。

理论力学第三章刚体力学-3

3、求 a1 （转动加速度） d总 a1 r dt d总 d di 其中， (ctgi ) ctg
dt
h h 2 ctg cos 2k ctg sin 2i cos cos 2h (cos2k sin 2i ) sin
1
1 I mR 2 2
平行轴定理
I I c md
2
叙述：刚体对某一轴线的转动惯量，等于对通过质心的平行轴的转动惯量加上刚体的质量与两轴间垂直距离平方的乘积。
2、对定点转动惯性的大小，由于转轴的方向不断变化，要用一个张量才能描述。 z
I xx 1 惯量张量： I yx I zx I xy I yy I zy I xz I yz I zz

N
O
y

x
§3.7 转动惯量
一、定点转动刚体的动量矩动坐标系oxyz
z
i
设 Pi 为刚体上任一质点，该质点对定点 o的动量矩为

i
ri mii
整个刚体对同一点o的动量矩为
n J ri mii
i 1 n
o
x
ri
y
mi ri ri
2
h 2 h 2 2 大小： a1 ( ) [cos 2 sin 2 ] sin sin
2 2
2h 所以： a1 sin
3、求 a2（向轴加速度）
a2 总 (总 r )
h h 其中，总 r ctgi ( cos 2i sin 2k ) cos cos h ctg sin 2j cos cos h 2 sin cosj sin cos 2h cosj a2 总 (总 r ) (ctgi ) (2h cosj ) 2 2 cos 2 h k sin 2 cos 2 所以： a2 a2 2 h sin

理论力学三-PPT精品

q q qq qq q 1 q 2 1 e 1 d1 e 2 d2 d1 d2(e 1 e 2) d1 d2 e 1e 2 q q q q 1 e 1 d1 e 2 d2 q 2 q 1 2 (e 1 d1 e 2 d2)
• 因此，无穷小角度旋转是可交换的，且能表示为转轴方向的大小为dq的矢量，并满足合成法则。
ω j θψ

R(y
,
e(3) z
)R(q
,
e(2) x
)[je(z1)
]

R(y
,
e(3) z
)[qe(x2)
]

[y
e(3) z
]
cosy

siny
0
siny cosy
0
0 1 0 ( 0 1 0
0
cosq sinq
0 0 q 0
四元数表示旋转
• 转动可以用一个归一化的4元数来表示。 r xiyjzk, eexiey jezk, ee* 1
qcosqesinq, q* cosqesinq, qq* 1 rqrq* (rq2sinqer)q* r2sinq(er)q* r2sinq[cosqer(er)esinq] rsin2qer(cos2q1)[r(re)e] cos2q(r(re)e)ersin2q(re)e
sinq

0

0
)

0

cosq j 0 y
r(rez)ezco sq(r(rez)ez)sinqez r
zez(xco sqysinq)ex(xsinqyco sq)ey
• 变换矩阵为
cosq sinq 0x

理论力学--第3章解剖

理论力学第三章.ppt

理 论 力 学 教学 课程第3章

理论力学第三章刚体力学 ppt课件

理论力学第3章-力偶系

理论力学第三章课件

理论力学周衍柏第三章

理论力学课件 受力分析与受力图、第三章

理论力学-第3章

理论力学第三章

理论力学(郝桐生)第三版第3单元课件

理论力学 静力学第三章

理论力学3章

【理论力学2】第三章分析力学基础

理论力学第三章

大学本科理论力学课程第3章力矩与平面力偶理论

理论力学第三章 刚体力学-3

理论力学三-PPT精品

理论力学教学课程第3章

理论力学课件受力分析与受力图、第三章

理论力学静力学第三章

理论力学第三章刚体力学-3