哈工大理论力学(第七版)第三章§1-3
哈工大第七版 理论力学

F1
FR
F1 F2
FR
F2
☆ 公理2
二力平衡条件
作用在 刚 体 上的两个力,使刚体保持平衡 的充分必要条件是:这两个力大小相等,方向相 反,且在同一直线上 即 F1 = - F2
F1
F2
☆ 公理3
加减平衡力系原理
在已知力系上加上或减去任意的平衡力系,不改变原力 系对刚体的作用。(效应不变)
力可分为两类:主动力和被动力。 把受力体从施力体中分离出来,单独画简图的过 程叫取研究对象或取分离体。
把受力体所受的所有力(外力)全画出来的图称 为受力图。
• 受力图举例
例1-1
F F
试画出图示重为P的石磙的受力图。
A
B
FA
p
A B
FB
P F B A
例1-2
试画出图示自重为 P,AC 边承受均 布风力 (单位长度上的力的载荷集度为 q)的 屋架的受力图。
光滑铰链的特点是只限制两物体径向 的相对位移,而不限制两物体绕铰链 中心的相对转动及沿轴向的位移。
4. 其它约束
(1) 滚动支座(辊轴支座) 约束力 实物简图
(2)球铰链
Fz
Fy
Fx
约束力 实物简图
(3)止推轴承
√ ×
实物简图
Fz Fy Fx
约束力
§1-4 物体的受力分析和受力图
在求解之前,首先要确定构件受几个力,及其位 置和作用方向。此过程称为物体的受力分析。
C
A
B
铰链和固定铰支的构造
C
C
销钉A
A A
销钉C
B
B
销钉B
固定在地面上的支架
哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-空间力系(圣才出品)
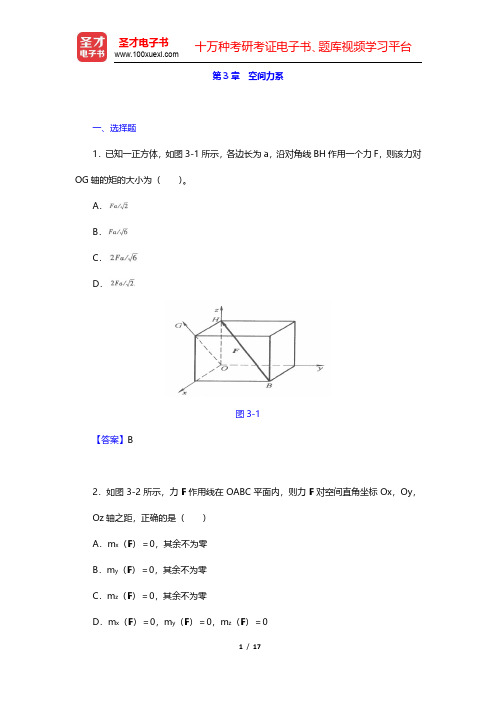
矩。已知:F=1kN,a=18cm,b=c=10cm。
图 3-6 解:解法一:利用力对点之矩与力对轴之矩的关系定理来计算。由于 CD 轴和 CE 轴均 过 C 点,因此可以先计算力对 C 点之矩,再将其分别向 CD 轴和 CE 轴投影来求解。
4 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
1 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 3-2 【答案】C 【解析】先计算 F 在各轴上的投影大小
Fx = −F cos30。cos 60。, Fy = −F cos30。sin 60。, Fz = F sin 30。
再计算对各轴的矩
3.有重力为 W、边长为 a 的均质正方形薄板,与—重力为 0.75W、边长分别为 a 和 2a 的直角均质三角形薄板组成的梯形板,如图 3-3 所示。其重心的坐标(xc,yc)为( )。
A. B. C. D.
2 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
【答案】B
图 3-3
二、填空题 1.空间力系若不平衡,其简化的最后结果:或者是一个力,或者是______;或者是 ______。 【答案】一个力偶;一个力螺旋 【解析】空间任意力系简化的最终结果有 4 种情况:合力、合力偶、力螺旋和平衡。当 主矢不为零,主矩为零或主矩不为零但主矢主矩垂直时,最终结果为合力;当主矢主矩均不 为零,主矢与主矩平行或成任意角(不包括垂直角度时),最终结果为力螺旋;当主矢为零 主矩不为零时,最终结果为合力偶;当主矢主矩均为零时,力系平衡。
(1)先将力 F 分解为沿坐标轴的三个分力如图 3-6(b)所示,其中有
代入数据可计算出
(2)计算力对过 C 点的三根正交轴之矩,因为有
理论力学(第七版)课后题答案哈工大

x
F1 40° F2
O
b
40° F2
a F1
θ
FR
O
F3 y
(a) 图 2-2 (b)
F3 c
(c)
解 (1)解析法 建立如图 2-2b 所示的直角坐标系 Oxy。
∑ Fx = F1 + F2 cos 40° = 2 000 N + 2 500 N ⋅ cos 40° =3 915 N
9
∑ Fy = F3 + F2 sin 40° = 1 500 N + 2 500 N ⋅ sin 40° =3 107 N FR = (∑ Fx ) 2 + (∑ Fy ) 2 =
第1章 静力学公理和物体的受力分析
1-1 画出下列各图中物体 A,ABC 或构件 AB,AC 的受力图。未画重力的各物体的自 重不计,所有接触处均为光滑接触。
FN 1
A
P FN 2
(a)
(a1)
FT A P FN
(b)
A
(b1)
FN1
P
B FN 3
FN 2
(c)
(c1)
FT B
FAy
P1 A P2
FAx
B
A
F Ax
C
FC
(d)
F Ay
(d1)
q
FDy
D
q
FB B
A
F Ax
C
FDx D FC
′ FDx ′ FDy
(d3)
(d2)
FAy FAx A
FCy
q
FAy
B P C
FCx
′ FBx
B
′ FBy
q
B FBy
理论力学(哈工第七版) 课后练习答案 第三部分
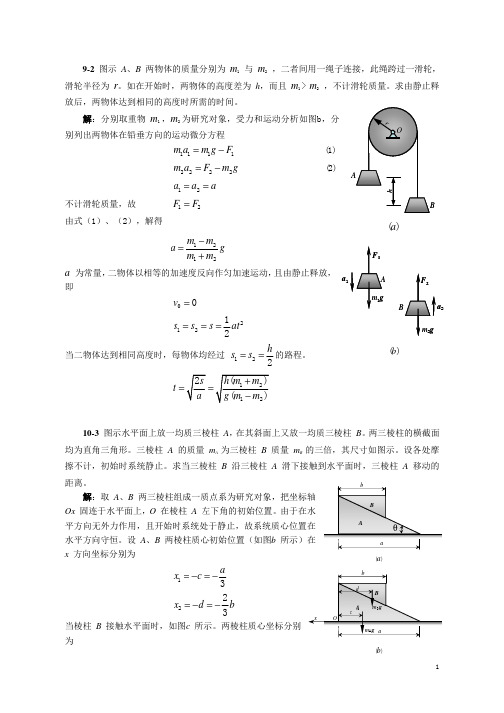
b A d B mBg mAg a (c)
x
c O
a 2 mA (− ) + mB (− b) 3 3 = − mA a + 2mB b xc = mA + mB 3(mA + mB )
棱柱 B 接触水平面时系统质心坐标
a b mA (l − ) + mB [l − (a − )] ' 3 3 = 3(mA + mB )l − a (mA + 3mB ) + mB b xc = 3(mA + mB ) mA + mB
用矢量表示有
v v v v v v v v & + myj & ) = ( xmy & − ymx & )k LO = r × mv = ( xi + yj ) × (mxi
&,y & 由式(1)确定。 其中 x
3
11-2 无重杆 OA 以角速度 ωo 绕轴 O 转动,质量 m = 25 kg,半径 R = 200 mm 的均质圆 盘以三种方式安装于杆 OA 的点 A, 如图所示。 在图a 中, 圆盘与杆 OA 焊接在一起, 在图b 中, 圆盘与杆 OA 在点 A 铰接,且相对杆 OA 以角速度 ωr 逆时针向转动。在图c 中,圆盘相对杆 OA 以角速度 ωr 顺时针向转动。 已知 ωO =ωr =4 rad/s , 计算在此三种情况下, 圆盘对轴 O 的 动量矩。
α1 =
11-12 重物 A 质量为 m1, 系在绳子上, 绳子跨过不计质量的固定滑轮 D, 并绕在鼓轮 B 上, 如图a 所示。由于重物下降,带动了轮 C,使它沿水平轨道只滚不滑。设鼓轮半径为 r,轮 C 的 半径为 R,两者固结在一起,总质量为 m2,对于其水平轴 O 的回转半径为 ρ 。求重物 A 的加 速度。 解:分别取重物 A 和鼓轮 B 为研究对象,其受力和运动 分析如图b、c 所示。重物 A 的运动微分方程:
哈尔滨工业大学理论力学第七版第II篇 第3章 碰撞

害的一面: 鸟祸、机械、仪器及其它物品由于碰撞损坏等。
利的一面:利用碰撞进行工作,如锻打金属,用锤打桩等。 研究碰撞现象,就是为了掌握其规律,以利用其有利的一 面,而避免其危害。
§3-2
用于碰撞过程的基本定理
由于碰撞过程时间短、碰撞力变化规律复杂,因此只分 析碰撞前、后运动的变化。 碰撞过程中有机械能的损失,难以用力的功来计算,因 此一般采用动量定理和动量矩定理的积分形式来确定力 的作用和运动变化的关系。 1. 用于碰撞过程的动量定理—冲量定理
t 对于质点: mv mv Fdt I 0 I 称为碰撞冲量,普通力的冲量忽略不计
§3-3
§3-4
质点对固定面的碰撞 · 恢复因数
碰撞问题举例
§3-5
碰撞冲量对绕定轴转动刚体的作用
· 撞击中心
§3-1
碰撞的分类 · 碰撞问题的简化
1. 碰撞的分类
碰撞时两物体间的相互作用力,称为碰撞力。
(1)两个物体相碰时,按其相处位置,可分为 对心碰撞 ---- 碰撞力的作用线通过两物体的质心。 否则称为偏心碰撞 偏心碰撞 正碰撞 斜碰撞 ---- 碰撞时各自质心的速度均沿着公法线。 否则称为斜碰撞
(i ) Ii 0
n i 1
冲量定理:质点系在碰撞开始和结束时动量的变化,等于作 用于质点系的外碰撞冲量的主矢。
(e ) mvC mvC I i
2. 用于碰撞过程的动量矩定理—冲量矩定理
n n (e) d (e) LO M O ( Fi ) ri Fi dt i 1 i 1 n n (e) (e) dLO ri Fi dt ri dI i i 1 i 1
理论力学第7版(哈工大)第3章习题

《理论力学》第二章作业习题2-1解:根据题意,取滑轮B 为研究对象,其受力情况如上图所示:物体对其有一铅直向下的拉力P , 沿DB 有一与物体重量相等的拉力P,拉杆AB 的作用力A B F 和支杆CB 的作用力C B F。
建立图示坐标系,列平衡方程0X YF F ⎧=⎪⎨=⎪⎩∑∑co s 30sin 300sin 30co s 300o oA B C B o oC B F F P P F P ⎧++=⎨++=⎩解之得54.64()74.64()A B C B F kN F kN =⎧⎨=-⎩答:拉杆AB 和支杆CB 所受的的力分别为54.64kN (拉)和74.64 kN (压)。
习题2-6解:(1) 取构件BC 为研究对象,其受力情况如上图(a)所示:由于其主动力仅有一个力偶M ,那末B 、C 处所受的约束力BF、CF 必定形成一个阻力偶与之平衡。
列平衡方程()0B M F =∑C M F l -=所以C M F l=(2) 取构件ACD 为研究对象,其受力情况如上图(b)所示:C 处有一约束力C F '与BC 构件所受的约束力C F 互为作用力与反作用力关系,在D 处有一约束力D F,方向向上;在A 处有一约束力A F,其方向可根据三力汇交定理确定,根据构件尺寸,A F与水平方向成45度角。
列平衡方程X F =∑sin 450oA C F F '-=所以222A C C M F F F l'===答:支座A的约束力为2M l,其方向如上图(b)所示。
习题2-9解:主矢RF在各坐标轴上的投影:)(6.4375210121321N F F F F x -=---=∑)(6.1615110321321N F F F F y -=+--=∑力系对O 点的主矩:).(42.21439805120021100)(31mm N F F F F MMOO=-+==∑由于主矢在各坐标轴上的投影均为负值而主矩为正值,合力的作用线应在原点O的左侧且方向向左下方,其大小为()())(5.46622N F F F YXR =+=∑∑其与O 点的距离为:)(96.455.46642.21439mm F M d R O=='=答:力系向O点简化的结果得一方向向左下方的主矢ji F R6.1616.437--='和一沿顺时针方向的力偶,力偶矩为21439.42Nmm; 力系的合力的大小为466.5N ,处于原点O 的左侧且与O 点的距离为45.96mm (如图)。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题(第1~3章)【圣才出品】

圣才电子书 十万种考研考证电子书、题库视频学习平台
图 2-3 答:支座约束力不相同,如图 2-4 所示。
图 1-4
图 1-5
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它 们的力学简图及受力图。
(1)用两根细绳将日光灯吊挂在天花板上; (2)水面上的一块浮冰; (3)一本打开的书静止于桌面上; (4)一个人坐在一只足球上。
3 / 142
圣才电子书
答:如图 1-8 所示。
图 1-7
4 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-8 二、习题 1-1 画出图 1-1 各图中物体 A、ABC 或构件 AB、AC 的受力图。未画重力的各物体 的自重不计,所有接触处均为光滑接触。
5 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
6 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-1 解:各物体的受力图如图 1-2 所示。
7 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
13 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
14 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
FD
图 1-4 1-3 画出图 1-5 中每个标注字符的物体的受力图,各题的整体受力图。未画重力的物 体的自量均不计,所有接触处均为光滑接触。
15 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
哈工大理论力学第七版第1章-课件

(3)止推轴承
约束特点: 止推轴承比径向轴承多一个轴
向的位移限制.
约束力:比径向轴承多一个轴向的约束力,亦有三个正交 分力 FAx , FAy., FAz
第28页/共46页
总结
(1)光滑面约束——法向约束力 FN
(2)柔索约束——张力 FT
(3)光滑铰链—— FAy , FAx
画出左、右拱 AB,C的B受力图与
系统整体受力图.
解:
右拱 C为B二力构件,其受力图
如图(b)所示
第35页/共46页
取左拱 AC,其受力图如图 (c)所示
系统整体受力图如图 (d)所示
第36页/共46页
考虑到左拱 AC三个力作用下平
衡,也可按三力平衡汇交定理
画出左拱 的AC受力图,如图
(e)所示
合力(合力的大小与方向) FR F(1矢量F2和)
亦可用力三角形求得合力矢
第8页/共46页
公理2 二力平衡条件 作用在刚体上的两个力,使刚体保持平衡的必要和充分条件 是:这两个力的大小相等,方向相反,且作用在同一直线上。
使刚体平衡的充分必要条件
F1பைடு நூலகம் F2
最简单力系的平衡条件
第9页/共46页
第42页/共46页
在建立力学模型时,要抓住关键、本质的方面,忽略 次要的方面。
例如:
忽略变形
三维问题 几何形状 重力P 和力F 的简化
A,B处约束力的简化
刚体
平面问题
圆形 作用在圆心 点接触 光滑接触
力学模型
第43页/共46页
理论力学中力学模型常遇到的几个方面
材料假设为均匀; 将物体视为刚体; 几何形状简化为圆柱、圆盘、板、杆及由它们组成的简单 形状; 受力简化为集中力、分布力; 接触简化为光滑铰链、光滑接触、柔索等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M x Mix
M y Miy
M z Miz
M x Mix
M y Miy
M z Miz
合力偶矩矢的大小和方向余弦 大 小
M ( M x ) 2 ( M y ) 2 ( M z ) 2
方向余弦
(2) 平衡
Mx cos q M
cos b
z
Fz F cosg
Fxy F sin g
第二次投影
Fz
F
g
Fy
Fx F sin g cos
O
y
Fx
x
Fy F sin g sin
Fxy
例3-1
已知: Fn , b ,
求:力 Fn 在三个坐标轴上的投影.
Fn F xy y F y b
z F z
x
F x
F Az F Bz
F Ax
F Bx
M x 0 F2 0.4 FBz 0.8 0
M z 0 F1 0.4 FBx 0.8 0
0.4 F1 0.4 3 FAx FBx 1.5( N ) 0.8 0.8 0.4 F2 0.4 5 FAz FBz 2.5( N ) 0.8 0.8
My M
Mz cos g M
空间力偶系平衡的充分必要条件是 :合力偶矩矢等于零,即 M M xi M y j M z k 0
M
ix
0
M
iy
0
M
iz
0
--称为空间力偶系的平衡方程.
例3-5 已知:在工件四个面上同时钻5个孔,每个孔所受切削 力偶矩均为80N· m。求:工件所受合力偶矩在x,y,z轴上的投影. 解: 把力偶用力偶矩 矢表示,平行移 到点A 。
Fz 0 F1 cos 45 sin 30 F2 cos 45 sin 30 FA cos 30 P 0
F1 F2 3.54kN
FA 8.66kN
§3–2
力对点的矩和力对轴的矩
一.力对点的矩以矢量表示 ——力矩矢 MO(F )=r×F 其中
z B F
r= xi + yj + zk
例3-2
已知:物重 P=10kN, q =30°;CE=EB=DE=a。 求:杆受力及绳拉力。
解: 画受力图,列平衡方程
Fx 0 F1 sin 45 F2 sin 45 0
Fy 0 FA sin 30 F1 cos 45 cos 30
F2 cos 45 cos 30 0
M O ( F ) xFy yFx M z ( F ) z
例3-4
已知:F,l,a,q。求:M x ( F )
a l
q
M y (F )
M z (F )
解:
把力 F 分解如图
Fx F sin q
Fz F cosq
M x (F ) M x (Fz ) (l a) F cosq M y ( F ) M y ( Fz ) l F cosq M z (F ) M z (Fx ) (l a) F sin q
§3–3
空间力偶
一.力偶矩以矢量表示——力偶矩矢
M rBA F
M1
F2 F1 ' F2
M2
' F1
F1 F1 F2 F2
空间力偶 的三要素
M1 M 2
M1 M 2
(1) 大小:力与力偶臂的乘积;
(2) 方向:转动方向; (3) 作用面:力偶作用面。
二.力偶的等效定理 实例
空间力偶的等效定理:作用在同一刚体上的两个力偶, 如果其力偶矩相等,则它们彼此等效。
空间力偶可以平移到与其作用面平行的任意平面上而不 改变力偶对刚体的作用效果. 只要保持力偶矩不变,力偶 可在其作用面内任意移转,且可
以同时改变力偶中力的大小与力
偶臂的长短,对刚体的作用效果 不变. 力偶矩矢是自由矢量
FR ( Fx )2 ( Fy )2 ( Fz )2
Fx
方向余弦 cos( FR , i )
FR
cos( FR , j )
Fy
FR
cos( FR , k )
Fz
FR
空间汇交力系的合力等于各分力的矢量和,合力的作用 线通过汇交点。
FR Fi F1 F2 Fn
FA= FB= F1= F2 杆AA1受拉,BB1受压。
y
M1
x
(c)
3—6,9 ,12
i i 0 i j k j i k
i i 1
z
k
i j 0
x
O
i
j
y
F2
M
M
x
0
M 1 M 3 cos 45 0
E
D
O C
FB
B
y
0 M 2 M 3 sin 45 0
FA
A
F2' x
y
M1 M 2
设正方体边长为 a ,有
M1 F1 a M 2 F2 a
有
F1'
M3
O A
F1 (b)
B M2
F1 F2
M3 FA 2a
F n
F z
x
F xy F y
b
F xy
F x
y
解:
Fz Fn sin
Fxy Fn cos
Fx Fxy sin β Fn cos α sin β Fy Fxy cos b Fn cos cos b
二、空间汇交力系的合力与平衡条件 空间汇交力系的合力
空间汇交力系平衡的充分必要条件是: 该力系的合力等于零,即 FR 0
F1
Fn
x
z
F2
FR (Fx ) (Fy ) (Fz ) 0
2 2 2
Fi
FR F3 F4
y
F
x
0
F
y
0
--称为空间汇交力系的平衡方程
空间汇交力系平衡的充要条件:该力系中所有各力在三 个坐标轴上的投影的代数和分别为零。
M O ( F ) yFz zFy x
M O ( F ) zFx xFz y
M O ( F ) xFy yFx z
M O ( F ) yFz zFy M x ( F ) x
M O ( F ) zFx xFz M y ( F ) y
§3–1
空间汇交力系
当空间力系中各力作用线汇交于一点时,称其为空间汇交力系。
一.力在直角坐标轴上的投影 1.直接投影法
z
F F
Fz
由、b、g 三个方向角确定
F
g
o
b Fy
y
投影
Fx F cos Fy F cos b Fz F cos g
Fx
x
2.间接(二次)投影法 第一次投影
FR F1 F2 F3 Fi
FRx Fix Fx
F1
Fn
x
z
F2
合矢量(合力)投影定理
FRy Fiy Fy
Fi
FR F3 y F4
FRz Fiz Fz
合力的大小
例
已知:正方体上作用两个力偶 ( F 1, F 1 ), ( F 2, F 2 ),
CD // AE ,不计正方体和直杆自重.
求:正方体平衡时,力 F1 , F2 的关系和两根杆受力.
F2
A1 A B1 D B
E
F2' x
C
O
y
F1'
F1
(a)
解: 两杆为二力杆,取正方体,画受力图建坐标系如图(b) 以矢量表示力偶,如图(c)
三.力偶系的合成与平衡条件 (1) 合成
Fn Mn Fn
M1
y
M
Mn
F1
F1
F2
F2
=
M1 M2
=
zHale Waihona Puke M2xO
M1 r1 F1
M 2 r2 F2
M n rn Fn
M M i 为合力偶矩矢,等于各分力偶矩矢的矢量和.
MO(F )
k
三要素:
(1)大小:力 F 与力臂的乘积
(2)方向:转动方向 (3)作用面:力矩作用面.
x
O
i
r
j
A(x,y,z ) y
r xi yj zk
F Fx i Fy j Fz k
M O ( F ) (r F ) ( xi yj zk ) ( Fxi Fy j Fz k )
二.力对轴的矩
M z ( F ) M O ( Fxy ) Fxy h
力对轴的矩是代数量
力与轴相交或与轴平行(力与轴在同一平面内),力对该轴 的矩为零.
三.力对点的矩与力对过该点的轴的矩的关系 M x ( F ) M x ( Fx ) M x ( Fy ) M x ( Fz ) yFz zFy M y ( F ) M y ( Fx ) M y ( Fy ) M y ( Fz ) zFx xFz M z ( F ) xFy yFx
