数学必修2直线与方程练习题(新)
(word完整版)高中数学必修二直线与方程及圆与方程测试题.docx
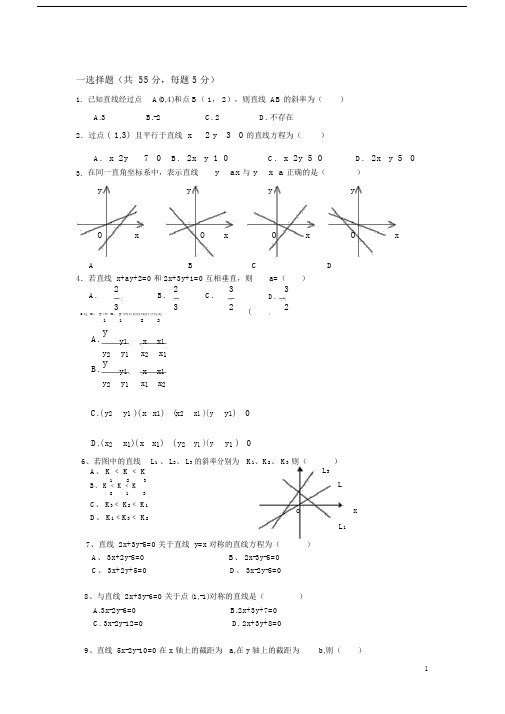
一选择题(共 55 分,每题 5 分)1. 已知直线经过点A(0,4)和点 B ( 1, 2),则直线 AB 的斜率为( )A.3B.-2C. 2D. 不存在2.过点 ( 1,3) 且平行于直线 x2 y3 0 的直线方程为()A . x 2y7 0 B . 2x y 1 0 C . x 2y 5 0 D . 2x y 5 0 3. 在同一直角坐标系中,表示直线y ax 与 yx a 正确的是()yyyyOxOxOxO xABCD4.若直线 x+ay+2=0 和 2x+3y+1=0 互相垂直,则a=()A .2B .2 C .33332D .(25.过 (x , y )和 (x , y )两点的直线的方程是)11 22A. yy 1 x x 1 y 2y 1 x 2 x 1 B.yy 1 x x 1 y 2 y 1x 1 x 2C.( y 2 y 1 )( x x 1) (x 2 x 1 )( y y 1) 0D.( x 2x 1)( x x 1) ( y 2 y 1 )( yy 1 ) 06、若图中的直线 L 1 、 L 2、 L 3 的斜率分别为 K 1、K 2、 K 3 则()A 、 K ﹤ K ﹤ KL 3123LB 、 K ﹤ K ﹤ K2 1 3C 、 K 3﹤ K 2﹤ K 1oxD 、 K 1﹤K 3﹤ K 2L 17、直线 2x+3y-5=0 关于直线 y=x 对称的直线方程为( )A 、 3x+2y-5=0B 、 2x-3y-5=0C 、 3x+2y+5=0D 、 3x-2y-5=08、与直线 2x+3y-6=0 关于点 (1,-1)对称的直线是()A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=0A.a=2,b=5;B.a=2,b= 5 ;C.a= 2 ,b=5;D.a= 2 ,b= 5 .10、直线 2x-y=7 与直线 3x+2y-7=0 的交点是()A (3,-1)B (-1,3)C (-3,-1)D (3,1)11、过点 P(4,-1)且与直线 3x-4y+6=0垂直的直线方程是()A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=0二填空题(共20 分,每题 5 分)12.过点(1,2)且在两坐标轴上的截距相等的直线的方程_ __________;13 两直线 2x+3y- k=0 和 x- ky+12=0 的交点在y 轴上,则k 的值是14、两平行直线x 3y 4 0与 2x 6 y 9 0 的距离是。
必修二直线与方程试题三套含答案

3.3.1 两条直线的交点坐标练习一一、 选择题 1、点(a , b )到直线0x yb a+=的距离是(A(B(C(D2、已知M (sin α, cos α), N (cos α, sin α),直线l : x cos α+y sin α+p =0 (p <–1),若M , N 到l 的距离分别为m , n ,则(A )m ≥n (B )m ≤n (C )m ≠n (D )以上都不对3、已知A , B , C 为三角形的三个内角,它们的对边长分别为a , b , c ,已知直线x sin A +y sin B +sin C =0到原点的距离大于1,则此三角形为(A )锐角三角形 (B )直角三角形 (C )钝角三角形 (D )不能确定4、过两直线x –3y +1=0和3x +y –3=0的交点,并与原点的距离等于1的直线共有 (A )0条 (B )1条 (C )2条 (D )3条5、与直线2x +3y –6=0关于点(1, –1)对称的直线是(A )3x –2y +2=0 (B )2x +3y +7=0 (C )3x –2y –12=0 (D )2x +3y +8=0 6、若直线y =ax +2与直线y =3x –b 关于直线y =x 对称,则(A )a =31, b =6 (B )a =31, b =–2 (C )a =3, b =–2 (D )a =3, b =67、不论m 取何值,直线(2m –1)x –(m +3)y –(m –11)=0恒过的定点的坐标是 (A )(3, 2) (B )(2, –3) (C )(2, 3) (D )(–2, 3)8、已知函数f (x )=x +1,则与曲线y =f (x +1)关于直线l : x +1=0成轴对称图形的曲线方程是 (A )y =–x (B )y =–x –4 (C )y =–x +2 (D )y =x9、方程2x 2+9xy +10y 2–7x –15y +k =0表示两条直线,则过这两直线的交点且与x –y +2=0垂直的直线方程是 (A )x +y –1=0 (B )x +y –2=0 (C )x +y +1=0 (D )x +y +2=0二、填空题10、若点P 在直线x +3y =0上,且它到原点的距离与到直线x +3y –2=0的距离相等,则点P 的坐标是 .11、若两平行直线3x –2y –1=0和6x +ay +c =0之间的距离是,则2c a +的值为 .12、直线y =2x +1关于直线y +2=0对称的直线方程是 .13、直线l 过点A (0, 1),且点B (2, –1)到l 的距离是点C (1, 2)到l 的距离的2倍,则直线l 的方程是 . 14、11.给出下列五个命题:① 过点(–1, 2)的直线方程一定可以表示为y –2=k (x +1);② 过点(–1, 2)且在x 轴、y 轴截距相等的的直线方程是x +y –1=0; ③ 过点M (–1, 2)且与直线l : Ax +By +C =0(AB ≠0)垂直的直线方程是B (x +1)+A (y –2)=0;④ 设点M (–1, 2)不在直线l : Ax +By +C =0(AB ≠0)上,则过点M 且与l 平行的直线方程是A (x +1)+B (y –2)=0;⑤ 点P (–1, 2)到直线ax +y +a 2+a =0的距离不小于2,以上命题中,正确的序号是 。
最新高中数学必修2直线与方程单元测试试题及答案

精品文档 2第三章《直线与方程》单元测试题必修姓名班别 50分)小题,每小题5分,共一、选择题(本大题共10(4,2+),则此直线的倾斜角是()1.若直线过点(1,2),3A30°B45°C60°D90°2. 如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a=23、、 DA、 -3 B、-6 C?323.点P(-1,2)到直线8x-6y+15=0的距离为()17)(D (C)2 (A)(B)1 224. 点M(4,m)关于点N(n, - 3)的对称点为P(6,-9),则()A m=-3,n=10B m=3,n=10C m=-3,n=5D m=3,n=55.以A(1,3),B(-5,1)为端点的线段的垂直平分线方程是()A 3x-y-8=0 B 3x+y+4=0 C 3x-y+6=0 D 3x+y+2=06.过点M(2,1)的直线与X轴,Y轴分别交于P,Q两点,且|MP|=|MQ|,则L的方程是()A x-2y+3=0 B 2x-y-3=0 C 2x+y-5=0 D x+2y-4=07. 直线mx-y+2m+1=0经过一定点,则该点的坐标是A(-2,1) B (2,1) C (1,-2) D (1,2)8. 直线的位置关系是0?n?x?0和?2y2x?y?m(A)平行(B)垂直(C)相交但不垂直(D)不能确定x?y?2≤0,?y?y,x则的取值范围是(满足约束条件9. 已知变量)x≥1,?x?,07≤x?y??9??9????????,??6,??3,6,[36]...DC B.A6??,??,????55????10.已知A (1,2)、B(-1,4)、C(5,2),则ΔABC的边AB上的中线所在的直线方程为()(A)x+5y-15=0 (B)x=3 (C) x-y+1=0 (D)y-3=0选择题答题表精品文档.精品文档分)4分,共20二、填空题(本大题共5小题,每小题 . 的距离相等的直线方程为和则过点且与11.已知点B,A)1,B(3,2),2C(?,A(?54). .过点P(1,2)且在X轴,Y轴上截距相等的直线方程是12 . 的距离是与直线10x+24y+5=013.直线5x+12y+3=0 . ,则直线L的方程为14.原点O在直线L上的射影为点H(-2,1)03??x?y??0y?x?________yx,y满足约束条件的最小值为,则2x+15.已设变量??3x??2??分)10分,共30(本大题共三、解答题3小题,每小题2x+3my+2m=0)(m-2直线17.x+my+6=0与直线16. ①求平行于直线3x+4y-12=0,且与它的.的值;没有公共点,求实数m距离是7的直线的方程P(-1,0)且与点②求垂直于直线x+3y-5=0,3的直线的方程.的距离是105l0??6?3xy03??yx和3?,且直3被两平行直线*18.已知直线所截得的线段长为精品文档.精品文档l的方程.),求直线线过点(1,0参考答案:1.A;2.B;3.B;4.D;5.B;6.D;7.A;8.C;9. ;10.A.1;14.2x-y+5=0; 或2x-y=0;13.11.x+4y-7=0或x=-1;12.x+y-3=02615. (1)3x+4y+23=0或3x+4y-47=0;(2)3x-y+9=0或3x-y-3=0.16.m=0或m=-1;17.x=1或3x-4y-3=0.精品文档.。
人教版数学必修2直线与方程单元测试题(最新整理)

⎥ 第三章《直线与方程》单元测试题一、选择题1. 直线l 经过原点和点(-1,1) ,则它的倾斜角是( )A.3π B. 5 π π 5 C. 或 π D. - π 4 4 4 4 42. 斜率为2 的直线过(3,5),( a ,7),(-1, b )三点,则a , b 的值是( )A. a = 4 , b = 0 C. a = 4 , b = -3 B. a = -4 , b = -3 D. a = -4 , b = 33. 设点 A (2,- 3) , B (-3,- 2) ,直线过 P (1,1) 且与线段 AB 相交,则l 的斜率 k 的取值范围是 ()A. k ≥ 3 4 或k ≤ -4 B. -4 ≤ k ≤ 3 4 C. - 3 ≤ k ≤ 4 4 D.以上都不对4. 直线(a + 2)x + (1- a ) y - 3 = 0 与直线(a -1)x + (2a + 3) y + 2 = 0 互相垂直,则a = ( )A. -1B.1C. ±1D. - 325. 直线l 过点 A (1,2) ,且不过第四象限,那么直线l 的斜率的取值范围是()A. [0,2] B. [0,1] C. ⎡0 1 ⎤D. ⎛ 0 1 ⎫, ⎣ 2 ⎦, ⎪ ⎝ 2 ⎭6. 到两条直线3x - 4 y + 5 = 0 与5x -12 y +13 = 0 的距离相等的点 P (x ,y ) 必定满足方程()A. x - 4 y + 4 = 0B. 7x + 4 y = 0C. x - 4 y + 4 = 0 或4x - 8 y + 9 = 0D. 7x + 4 y = 0 或32x - 56 y + 65 = 07. 已知直线3x + 2 y - 3 = 0 和6x + my +1 = 0 互相平行,则它们之间的距离是()A. 4B.2 1313C. 5 1326 D. 7 13268.已知等腰直角三角形 ABC 的斜边所在的直线是3x - y + 2 = 0 ,直角顶点是C (3,- 2) ,则两条直角边 AC , BC 的方程是( )A. 3x - y + 5 = 0 , x + 2 y - 7 = 0B. 2x + y - 4 = 0 , x - 2 y - 7 = 0C. 2x - y + 4 = 0 , 2x + y - 7 = 0D. 3x - 2 y - 2 = 0 , 2x - y + 2 = 09. 入射光线线在直线l 1 : 2x - y - 3 = 0 上,经过 x 轴反射到直线l 2 上,再经过 y 轴反射到直线l 3 上,则直线l 3 的方程为( )⎢3⎨ ⎩ ⎨ ⎩ A. x - 2 y + 3 = 0 B. 2x - y + 3 = 0 C. 2x + y - 3 = 0 D. 2x - y + 6 = 0⎧x - y + 5 ≥ 0 10. 已知 x ,y 满足⎪x ≤ 3 ⎪x + y + k ≥ 0,且 z =2x +4y 的最小值为-6,则常数 k =()A.2B.9C. D.0二、填空题 11. 已知三点(2,- 3) , (4,3) 及(5 k ) 在同一条直线上,则k 的值是., 2 12. 在 y 轴上有一点 m , 它与点 (- 为.3,1) 连成的直线的倾斜角为 120þ , 则点 m 的坐标13. 设点 P 在直线 x + 3y = 0 上,且 P 到原点的距离与 P 到直线 x + 3y - 2 = 0 的距离相等,则点 P 坐标是 .14. 直线l 过直线2x - y + 4 = 0 与 x - 3y + 5 = 0 的交点,且垂直于直线 y = 1x ,则直线l 的方程2是 . ⎧x + y - 3 ≥ 0 15. 若 x ,y 满足⎪x - y + 1 ≥ 0 ⎪3x - y - 5 ≤ 0,设 y = kx ,则 k 的取值范围是 .三、解答题16. 已知 ∆ABC 中, 点 A(1,2), AB 边和 AC 边上的中线方程分别是 5x - 3y - 3 = 0 和7x - 3y - 5 = 0 ,求 BC 所在的直线方程的一般式。
必修2---直线与圆

《直线与方程》练习题一、选择题1、若直线1=x 的倾斜角为α,则=α( )A 、ο0B 、ο45C 、ο90D 、不存在2、经过两点)3,2(),12,4(-+B y A 的直线的倾斜角为ο135,则y 的值等于( )A 、1-B 、3-C 、0D 、23、过点(1-,4)作直线l 使点M (1,2)到直线l 距离最大,则直线l 的方程为( )A 、03=-+y xB 、05=++y xC 、01=+-y xD 、05=+-y x4、如果0<ac 且0<bc ,那么直线0=++c by ax 不通过( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限5、经过点A (1,2),且在两坐标轴上的截距相等的直线共有( )A 、1条B 、2条C 、3条D 、4条6、已知直线012)4()4(2=++++--m y m x m m 的倾斜角为ο135,则m 的值是( )A 、2-或4B 、4-或2C 、4或0D 、0或2-7、直线l 与直线0632=-+y x 关于点)1,1(-对称,则直线l 的方程是( )A 、0223=+-y xB 、0732=++y xC 、01223=--y xD 、0832=++y x8、方程2240x y -=表示的图形是( )A 、两条相交而不垂直的直线B 、一个点C 、两条垂直直线D 、两条平行直线9、下列说法正确的是A 、 若直线1l 与2l 的斜率相等,则1l ∥2l ;B 、若直线1l ∥2l ,则1l 与2l 的斜率相等;C 、若一条直线的斜率存在,另一条直线的斜率不存在,则它们一定相交;D 、若直线1l 与2l 的斜率都不存在,则1l ∥2l10、到直线0143=+-y x 的距离为3,且与此直线平行的直线方程为 ( )A 、0443=+-y xB 、02430443=--=+-y x y x 或C 、01643=+-y xD 、0144301643=--=+-y x y x 或11、若直线y x k =+与曲线21y x -=恰有一个公共点,则k 的取值范围是( )A 、;2±=kB 、;22-≤≥k k 或C 、;22<<-kD 、;112≤<--=k k 或12、若直线0ax by c ++=过第一、二、三象限,则a 、b 、c 应满足的条件是A、0,0ab bc >> B 、0,0ab bc <> C 、 0,0ab bc >< D 、0,0ab bc <<二、填空题13、如果直线l 与直线x +y -1=0关于y 轴对称,则直线l 的方程是 。
高一数学必修二直线与直线方程习题

高一数学必修二直线与直线方程习题1、已知点A(1,3)、B(2,6)、C(5,m)在同一条直线上,那么实数m的值为________、2、直线mx-y+2m+1=0经过一定点,则该点的坐标是 A(-2,1) B (2,1) C (1,-2) D (1,2)3、已知m≠0,则过点(1,-1)的直线ax+3my+2a=0的斜率为________【提升】XXXXX:4、若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则+的值等于、5、已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:mx+y-m=0与线段PQ有交点,求m的范围、二:截距问题:6、已知,则直线通过()A、一、二、三象限B、一、二、四象限C、一、三、四象限D、二、三、四象限7、过点P(1,2)且在x轴,y轴上截距相等的直线方程是、8、过点P(1,2)且在x轴,y轴上截距之和为6的直线方程是_________9、过点作一直线使它与两坐标轴相交且与两轴所围成的三角形面积为5、三:对称问题10、(04吉林)已知点A(1,2),(3,1),则线段的垂直平分线的方程为()A、4x+2y=5B、4x-2y=5C、x+2y=5D、x-2y=511、点关于直线对称的点的坐标是()、A、B、C、D、12、(07浙江)直线关于直线对称的直线方程是()A、B、C、D、四:平行垂直:13、(05全国)已知过点和的直线与直线平行,则m的值A 、B、 C 、D、14、(07上海)若直线与直线平行,则m=___ (若垂直呢)15、过点且垂直于直线的直线方程为()五:交点问题:16、求经过直线的交点且平行于直线的直线方程、(若条件改为垂直那直线方程又是多少呢?)17、若直线l:y=kx-1与直线x+y-1=0的交点位于第一象限,则实数k的取值范围是A、(-∞,-1)B、(-∞,-1]C、(1,+∞)D、[1,+∞)【提升】XXXXX:18:过直线x+2y-3=0,和直线2x-y-1=0的交点,且和点(0,1)距离等于1的直线方程六:距离问题19、已知点到直线的距离等于1,则()、A、B、C、D、或20、已知直线和互相平行,则它们之间的距离是()21、①求平行于直线3x+4y-12=0,且与它的距离是7的直线的方程; ②求垂直于直线x+3y-5=0, 且与点P(-1,0)的距离是的直线的方程、22、过点A(1,2)且与原点距离最大的直线方程是()A、B、 CD、23、过点M(2,1)的直线与x轴,y轴分别交于P,Q两点,且|MP|=|MQ|,则l的方程是()Ax-2y+3=0 B2x-y-3=0 C2x+y-5=0 D x+2y-4=024、若动点到点和直线的距离相等,则点的轨迹方程为A、B、C、D、25、已知点,,点在直线上,求取得最小值时点的坐标。
《必修2》第三章“直线与方程”测试题(含答案)

《必修2》第三章“直线与方程”测试题(含答案)《必修2》第三章“直线与方程”测试题一.选择题:1. 在同一直角坐标系中,表示直线y ax =与y x a =+正确的是( )x y O x y O x y O xyOA B C D2.若直线20x ay ++=和2310x y ++=互相垂直,则a =( )A .32-B .32C .23- D .23 3.过11(,)x y 和22(,)x y 两点的直线的方程是( )111121212112211211211211...()()()()0.()()()()0y y x x y y x x A B y y x x y y x x C y y x x x x y y D x x x x y y y y ----==---------=-----=4.直线2350x y +-=关于直线y x =对称的直线方程为( ) A 、3x+2y-5=0 B 、2x-3y-5=0C 、3x+2y+5=0D 、3x-2y-5=05 如果直线l 沿x 轴负方向平移3个单位再沿y 轴正方向平移1个单位后,又回到原来的位置,那么直线l 的斜率是( )23-二.填空题:11. 过点(1,2)且在两坐标轴上的截距相等的直线的方程方程1=+y x 表示的图形所围成的封闭区域的面积为_________13 点(,)P x y 在直线40x y +-=上,则22xy +的最小值是________14 直线10x y -+=上一点P 的横坐标是3,若该直线绕点P 逆时针旋转090得直线l ,则直线l 的方程是15 已知直线,32:1+=x y l若2l 与1l 关于y 轴对称,则2l 的方程为__________;23y x =-+三、解答题16.求过点(5,4)A --的直线l ,使它与两坐标轴相交且与两轴所围成的三角形面积为517. 一直线被两直线0653:,064:21=--=++y x l y x l 截得线段的中点是P 点,当P 点为(0,0)时,求此直线方程18.直线313y x =-+和x 轴,y 轴分别交于点,A B ,在线段AB为边在第一象限内作等边△ABC ,如果在第一象限内有一点1(,)2P m 使得△ABP 和△ABC 的面积相等, 求m 的值19.已知三角形ABC的顶点坐标为A(-1,5)、B (-2,-1)、C(4,3),M是BC边上的中点。
高中数学必修二直线与方程单元练习题(精选.)

直线与方程练习一、填空题(5分*18=90分)1.若直线过点(、后,一3)且倾斜角为30。
,则该直线的方程为;2.如果4(3,1)、8(-2,k)、H8, 11),在同一直线上,那么A的值是;3.两条直线3x + 2y + /〃 = 0和+ l)x - 3y + 2 - =0的位置关系是;4.直线X-2),+。
=。
与两坐标轴所围成的三角形的面积不大于1 ,那么〃的取值范围是5.经过点(-2,—3),在x轴、y轴上截距相等的直线方程是;6.已知直线至互相平行,则它们之间的距离是: 7、过点A (1,2)且与原点距离最大的直线方程是:8.三直线aw+2y+8=0, 4x+3y=10, 2x—y=10相交于一点,则a的值是:9.已知点A(—1,2), B(2-2), C(0,3),若点M(a,b) (a # 0)是线段AB上的一点,则直线CM的斜率的取值范围是:10.若动点4匹,y )、5(巧,当)分别在直线11: 1 + 又-7 =0和-:x+y-5 = 0上移动,则中点M 到原点距离的最小值为:11.与点A(l,2)距离为1,且与点B(3,l)距离为2的直线有条.12.直线/过原点,且平分68CD的面积,若8(1, 4)、D(5,0),则直线/的方程是.13.当Ovkv;时,两条直线&X—丁 =攵-1、ky —工=2攵的交点在象限.14.过点(1, 2)且在两坐标轴上的截距相等的直线的方程;15.直线y=1x关于直线x=l对称的直线方程是;16.已知43,1)、5(-1,2),若NAC5的平分线在_y=x+l上,则AC所在直线方程是.”.光线从点A(2,3)射出在直线/: x + y +1 = 0上,反射光线经过点8(11),则反射光线所在直线的方程18.点A (1, 3), B(5, -2),点P在x轴上使|AP|-18Pl最大,则P的坐标为:二懈答题(1。
分*4+15分*2=70分)19.已知直线/: Ax-y+l+M=O伏WR).(1)证明:直线/过定点;(2)若直线/不经过第四象限,求上的取值范围;(3)若直线,交x轴负半轴于点A,交y轴正半轴于点B, O为坐标原点,设ZvlOB的面积为4,求直线,的方程.20. (1)要使直线Zi: (2〃/+机- 3)x + (〃J 一机)y = 2〃?与直线A: x-y=l平行,求m的值.(2)直线Z” ax+(l-a)y=3与直线心:(a-l)x+(2a+3)y=2互相垂直,求a的值.21.已知“fits中,41,3),48、加边上的中线所在直线方程分别为八^^+4=€和y—1=0,求"ec 各边所在直线方程.22.Z\48C中,A (3, -1), 48边上的中线CM所在直线方程为:6x+10y-59=0, N8的平分线方程BT为:x-4y+10=0,求直线8c的方程.f(x) = x + -,、/(2) = 2 + —23.已知函数X的定义域为(仇+8),且 2 .设点P是函数图象上的任意一点, 过点P分别作直线>'=工和>轴的垂线,垂足分别为M、N.(1)求〃的值;(2)问:是否为定值?若是,则求出该定值,若不是,则说明理由;(3)设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学练习题
一、选择题
1、如果直线220ax y ++=与直线320x y --=平行,则系数a =()
A .3-
B .6-
C .32
- D .23 2、点()1,2P -到直线86150x y -+=的距离为()
A .
3、点A .C .4A 5、若CD ;
③A. 6、若a A. 7( A.
8 A. 9、点A )
10 A. 13 B. 13 C. 26 D. 26
11、直线0632=-+y x 关于点(1,-1)对称的直线方程是( )
A 、0223=+-y x
B 、0732=++y x
C 、01223=--y x
D 、0832=++y x
12、已知A (7,1),B (1,4),直线y =12ax 与线段AB 交于点C ,且AC =2CB ,则a 等于( )
A .2
B .1 C.45 D.53
13、已知点A (-3,-4),B (6,3)到直线l :ax +y +1=0的距离相等,则实数a 的值等于( )
A.79 B .-13 C .-79或-13 D.79或13
14、若直线l 1:y =kx +k +2与l 2:y =-2x +4的交点在第一象限,则实数k 的取值范围是( )
A .k >-23
B .k <2
C .-23<k <2
D .k <-23
或k >2 二、填空题:
15、倾斜角是135,在y 轴上的截距是3的直线方程是 .
16、过两点(5,7)和(1,3)的直线一般式方程为 ;若点(a ,12)在此直
线上,则a = 10 .
17、已知点P (2,-4)与Q (0,8)关于直线l 对称,则直线l 的方程为
18、过点)3,2(P ,且在两坐标轴上的截距互为相反数的直线方程是 。
三、解答题:
19、求适合下列条件的直线方程:
(1)经过点P (3,2),且在两坐标轴上的截距相等;
(2)经过点A (-1,-3),倾斜角等于直线y=3x 的倾斜角的2倍.
20、直线l 经过点P (3,2)且与x ,y 轴的正半轴分别交于A 、B 两点,△OAB 的面积为12,求直线l 的方程.
21、已知点(1,3),(3,1),(1,0)A B C -,求△ABC 的面积.
.
22、已知(1,0)(1,0)M N -、,点P 为直线210x y --=上的动点.求22PM PN +的最小值,
及取最小值时点P 的坐标.
1.B
2.C
3.A 5.B 6.C 7.A 8.C 9.A 10.D 11.D
12解析:设点C (x ,y ),由于AC =2CB ,
所以(x -7,y -1)=2(1-x,4-y ),
所以有⎩⎪⎨⎪⎧ x -7=2-2x y -1=8-2y ⇒⎩⎪⎨⎪⎧ x =3y =3
, 又点C 在直线y =12ax 上,所以有3=32
a ,a =2. 答案:A
13解析:由题意知|6a +3+1|a 2+1=|-3a -4+1|a 2+1
, 解得a =-13或a =-79
. 答案:C
14.解析:由⎩⎪⎨⎪⎧ y =kx +k +2
y =-2x +4得⎩⎪⎨⎪⎧ x =2-k
k +2y =6k +4
k +2,
由⎩⎪⎨⎪⎧2-k
k +2>0
6k +4k +2>0得⎩⎪⎨⎪⎧ -2<k <2,k <-2或k >-2
3,
∴-23<k <2. 答案:C
(2)由已知:设直线y=3x 的倾斜角为α,
则所求直线的倾斜角为2α.
∵tan α=3,∴tan2α=αα2tan 1tan 2-=-43
.
又直线经过点A (-1,-3),
因此所求直线方程为y+3=-43
(x+1),
即3x+4y+15=0.
20.解 方法一 设直线l 的方程为1=+b y
a x (a >0,
b >0),
∴A(a,0),B(0,b),
∴⎪⎩⎪⎨⎧=+=.12
3,
24b a ab 解得⎩⎨⎧==.4,
6b a
∴所求的直线方程为46y
x +=1,
即2x+3y-12=0.
方法二 设直线l 的方程为y-2=k(x-3),
令y=0,得直线l 在x 轴上的截距a=3-k 2
,
令x=0,得直线l 在y 轴上的截距b=2-3k.
∴⎪⎭⎫
⎝⎛-k 23(2-3k)=24.解得k=-32.
∴所求直线方程为y-2=-32
(x-3).
即2x+3y-12=0.
21.解:设AB 边上的高为h ,则1
2ABC S AB h ∆=⋅.
22(31)(13)22AB =-+-=,
AB 边上的高为h 就是点C 到AB 的距离.
AB 边所在的直线方程为31
1331y x
--=--,
即40x y +-=.
点(1,0)C -到40x y +-=的距离
221045211h -+-==+因此,15
225
22ABC S ∆=⨯⨯=
22.最小值12/5, 点P 的坐标(2/5 ,-1/5)。
