第十一章 连续分段独立一体化积分法
11-3曲面解析
L AO ( x 2 3 y ) d x ( y 2 x) d y OA
( x 2 3 y ) d x ( y 2 x) d y
D
4 2 x dx 0
4 d xd y
64 8 3
y
L D
o
Ax
例 3 计算 L 2xydx x2dy 其中 L 为抛物线
1 1 ONA xdy ydx AMO xdy ydx 2 2
1 AMO xdy ydx 2
1 0 a a x( 1)dx ( ax x )dx 2 2 ax
a a 1 2 0 xdx 6 a . 4
M
A(a ,0)
N
三、平面上曲线积分与路径无关的条件
取 P y, Q x, 得 2
dxdy xdy ydx
L D
二、格林公式的应用
1.简化曲线积分
例 1 计算
AB
y
A
D
xdy,其中曲线
x
AB 是半径为 r 的圆在第一 象限部分.
o
L
B
解
引入辅助曲线 L,
L OA AB BO 应用格林公式, P 0, Q x 有
第十一章 曲线积分
第三节 格林公式及其应用
一、格林公式
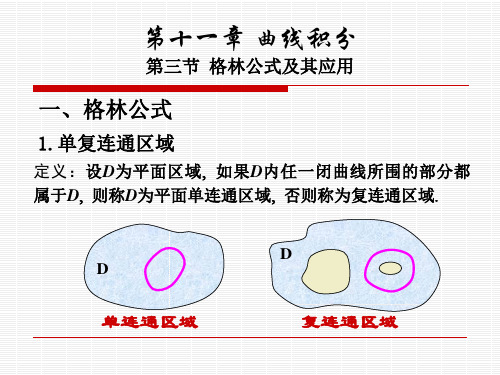
1.单复连通区域
定义:设D为平面区域 如果D内任一闭曲线所围的部分都 属于D 则称D为平面单连通区域 否则称为复连通区域
D D
单连通区域
复连通区域
2.边界曲线的方向
定义:当观察者沿区域D的边界曲线L行走时 如果左手在区
域D内 则行走方向是L的正向
P Q , y x 原积分与路径无关
zhongke积分学共43页

1.3.2 定积分
1、定积分定义:
b f ( x)dx a
I
n
lim 0 i1
f (i )xi.
2、定积分的性质
b
b
b
性质1 a [f(x ) g (x )d ] x af(x ) d x a g (x ) dx
性质2
a b k(x f ) d x k a b f(x ) dx k (为 常 数 )
例5 设f(x)在(,)内有一阶,导数
1
F(x)x x f(t)d, t 求 F(x). 0
解 F ( : x )0 1 xf(t)d tx(f 1 x )(x 1 2)
1 x
f(t)dt1
f(1)
0
xx
F (x ) x 1 2f(1 x ) 1 x f(1 x ) ( x 1 2 ) x 1 3f(1 x )
4、牛顿—莱布尼茨公式
如果F ( x)是连续函数 f ( x)在区间[a, b]上的一
个原函数,则
b
a f ( x)dx F(b) F(a)
也可写成 abf(x)dx [F(x)b a].
牛顿—莱布尼茨公式
表明 :一个连续函[a数 ,b]上 在的 区定 间积分 它的任一原函 [a,b]数 上在 的区 增 . 间 量
2x3x 32x 22x
dx
1 ((3232))x2dxadxx axlnadx
1
ln
2 3
d(32)x 1 (32)2 x
arctan32)(x C ln2ln3
第二类换元的解题思路为 (t)f[(t) ](t)
x(t)
f (x)dx f[(t)](t)dt
(t)C [1(x)]C
《分部积分法》ppt课件

cos sin
x x
dx
cos x sin x
dx
cos x sin x
dx
1,
1
cos sin
x x
dx
得0=1
ln sin x C
答: 不定积分是原函数族 , 相减不应为 0 . 求此积分的正确作法是用换元法 .
21
P191 1 2
22
x)
C
说明: 1。也可设
为三角函数 , 但两次所设类型
必须一致 .
2.有些不定积分经过分部积分后,虽未能求出该积分,
但又出现了与所求积分相同的形式,这时可以从等式中
象解代数方程那样解出所求的积分来。
14
把被积函数视为两个函数之积 ,
按 “ 反对幂指三” 的顺 前者为 u 后者为 v.
序, 反: 反三角函数 对: 对数函数 幂: 幂函数 指: 指数函数 三: 三角函数
幂函数的幂次降低一次。即在
Pn (x)exdx Pn (x)sin xdx Pn (x)cos xdx
中,总令
Pn (x) u
7
(ax b)sin xcos xdx
解:原式
(ax
b)
1 2
sin
2xdx
1 4
(ax
b)
sin
2xd
2x
1 4
(ax
b)d
cos
2x
1 4
(ax
b)
cos 2 x
xarccosx 1 x2 C
10
x arctan x dx.
解: 原式
x2 arctanx d .
2
1 x2 arctanx 1
2
2
《分部积分法》课件

02
分部积分法的计算步确定积分区间和积分变量,以 便确定被积函数。
VS
确定函数
根据题目要求,确定需要计算的函数。
确定分部函数和被积函数
分部函数的选择
根据被积函数的性质,选择适当的分部函数 。
被积函数的确定
根据题目要求和分部函数的性质,确定被积 函数。
计算积分结果
注意积分的范围和上下限
总结词
确定积分的范围和上下限是分部积分法中至关重要的 一步,错误的设定可能导致结果错误或无法计算。
详细描述
在应用分部积分法时,应根据函数的具体形式和积分的 原函数,准确设定积分的上下限,以避免计算中出现符 号错误或无法收敛的情况。同时,要注意上下限之间的 逻辑关系和连续性。
注意计算过程中的符号和单位问题
《分部积分法》ppt课件
目录 CONTENTS
• 分部积分法概述 • 分部积分法的计算步骤 • 分部积分法的实例解析 • 分部积分法的注意事项 • 分部积分法与其他积分方法的比较
01
分部积分法概述
分部积分法的定义
总结词
分部积分法是一种求解积分的方法, 通过将积分拆分为两个或多个部分的 乘积,再分别对各部分进行积分,最 终求得原积分的结果。
与直接积分法的比较
适用范围
直接积分法适用于简单的积分,如 $int x^n dx$;分部积分法适用于被 积函数为两个函数的乘积或商的情况 ,如$int frac{x^2}{x+1} dx$。
操作步骤
直接积分法是通过凑微分来完成的; 分部积分法是通过将被积函数拆分为 两个函数的乘积,然后分别积分,最 后相减来完成的。
与换元积分法的比较
适用范围
换元积分法适用于被积函数为复合函数或三角函数的情况;分部积分法适用于被积函数为两个函数的 乘积或商的情况。
高等数学教材部分积分法

高等数学教材部分积分法在高等数学教材中,积分法是求解定积分的重要方法之一。
其中,部分积分法是一种常用而且灵活的积分法。
本文将介绍部分积分法的基本原理、步骤以及一些典型的应用。
一、部分积分法的基本原理部分积分法是基于积分运算中的乘法法则。
根据积分的定义,定积分可以理解为曲线与坐标轴之间所夹的面积。
而部分积分法能够将一个较复杂的积分转化成一个相对简单的积分,从而更容易求解。
二、部分积分法的步骤部分积分法的求解步骤如下:1. 根据乘法法则,将要求解的积分中的函数分为两部分:一部分为求导容易,另一部分为求积容易。
2. 对分部后的两部分进行求导和求积。
3. 利用部分积分公式进行积分化简。
4. 若未达到最终的简化形式,可考虑再次应用部分积分法,直至达到求解目标为止。
三、部分积分法的应用举例举例一:计算积分∫ xe^x dx。
解:设 u = x,dv = e^x dx,则 du = dx,v = ∫e^x dx = e^x。
根据部分积分法公式∫u dv = uv - ∫ v du,代入相应的值:∫xe^x dx = x * e^x - ∫e^x dx = x * e^x - e^x + C。
所以,积分∫ xe^x dx = x * e^x - e^x + C。
举例二:计算积分∫ ln x dx。
解:设 u = ln x,dv = dx,则 du = 1/x dx,v = x。
根据部分积分法公式∫u dv = uv - ∫v du,代入相应的值:∫ln x dx = x * ln x - ∫x * (1/x) dx = x * ln x - ∫ dx = x * ln x - x + C。
所以,积分∫ ln x dx = x * ln x - x + C。
综上所述,部分积分法是高等数学教材中重要的积分方法之一。
通过将复杂的积分转化为相对简单的积分,部分积分法能够简化求解过程。
在实际应用中,我们可以根据具体的问题选择合适的函数进行分部积分,从而提高解题效率。
高数同济第七版-高数第十一章重点内容

第十一章基本知识点1. 对弧长的曲线积分的定义、性质(P188起)2. 对弧长的曲线积分的计算:(1) 对光滑曲线弧,)(,)(,)(:βαψφ≤≤==t t y t x L⎰L s y x f d ),(⎰=βαψφ)](),([t t f t t t d )()(22ψφ'+'(2) • 对光滑曲线弧,)()(:b x a x y L ≤≤=φ⎰L s y x f d ),(⎰=ba x x f ))(,(φx x d )('12φ+(3) • 对光滑曲线弧),()(:βθαθ≤≤=r r L ⎰Ls y x f d ),( ⎰=βαθθθθ)sin )(,cos )((r r f θθθd )()(22r r '+3. 对坐标的曲线积分的定义、性质(P194起)4. 对坐标的曲线积分的计算(P197起)注意:L - 表示 L 的反向弧:⎰-+L y y x Q x y x P d ),(d ),(⎰+-=Ly y x Q x y x P d ),(d ),( 对坐标的曲线积分必须注意积分弧段的方向!5. 两类曲线积分的联系:⎰+L y Q xP d d {}s Q P L d cos cos βα+=⎰ z R y Q x P d d d ++⎰Γ{}s R Q P d cos cos cos γβα++=⎰Γ6. 格林公式:⎰+L y Q x P d d y x yP x Q D d d )(⎰⎰∂∂-∂∂= 7. 四个等价条件:设 P , Q 在 D 内具有一阶连续偏导数, 则有⎰+L y Q x P d d 在 D 内与路径无关. 等价于:对 D 内任意闭曲线 L 有0d d =+⎰L y Q x P等价于:在 D 内有yP x Q ∂∂=∂∂ 等价于:在 D 内有y Q x P u d d d +=8. 对面积的曲面积分的计算法⎰⎰∑S z y x f d ),,(y x y x z y x z y x z y x f y x D y x d d ),(),(1)),(,,(22++=⎰⎰ 如果曲面方程为:z y D z y z y x x ∈=),(),,(z x D z x z x y y ∈=),(),,(或 公式类似9. 对坐标的曲面积分的计算法 ⎰⎰∑yx z y x R d d ),,(y x y x z y x R yx D d )d ),(,,(⎰⎰=(取上侧) 10. 两类曲面积分及其联系 ⎰⎰∑++y x R x z Q zy P d d d d d d S R Q P d )cos cos cos (⎰⎰∑++=γβα11. 高斯公式⎰⎰⎰Ω∂∂+∂∂+∂∂z y x z R y Q x P d d d )(⎰⎰∑++=y x R x z Q z y P d d d d d d (∑ 取外侧)12. 斯托克斯公式(P240起)。
分部积分法定积分

分部积分法定积分
分部积分法是定积分中比较常见的解决方法之一,也叫做间断积分法,是把一个复杂的定积分分解成若干个相对简单的和关系容易求得的定积分,最后把每一部分的积分值相加,得到总的积分值的方法。
下面以定积分[abx^2e^x/(1-e^2x)]dx为例,来讲解下分部积分法是怎么实现的。
首先,把复杂的定积分分解成几个容易求解的简单积分,比如
([a/2]*x^3+[b/3]*x^4+[d/4]*x^5+[e]*x^2) dx,最后通过对这几个简单积分求解,求出每
一部分的积分值,然后将每一部分的积分值相加即可得到最终的结果。
其次,经过分部积分法处理后,你可以看到,原来复杂的积分变得更加简单,所以可以看
出分部积分法可以帮助我们把复杂的定积分分解成相对简单和容易求解的定积分,从而大
大简化解题的步骤,获得更准确、更快捷的定积分结果。
最后,分部积分法为我们提供了一种解决复杂定积分问题的新思路,从减少计算步骤入手,把复杂的定积分分解为几个比较简单的定积分,没有太多时间和精力来完成一个复杂的定积分,都可以利用分部积分法来辅助传统的积分方法,来实现快速有效的积分解答。
《分部积分法》课件

实例三:求解二重积分
总结词
通过分部积分法求解二重积分
详细描述
二重积分是多元函数积分的常见形式 之一。在实例中,我们将展示如何使 用分部积分法求解一些常见的二重积 分问题,并给出相应的计算过程和结 果。
04
分部积分法的注意事项
BIG DATA EMPOWERS TO CREATE A NEW
ERA
正确选择u和v函数
总结词
在应用分部积分法时,选择合适的u和v 函数是至关重要的,因为它们将直接影 响积分的计算结果。
VS
详细描述
选择u和v函数时,应确保它们在积分区 间内具有明确的表达式,并且易于计算。 此外,u和v函数的选择应与被积函数的 原函数有关,以便简化计算过程。
注意积分的上下限
总结词
在应用分部积分法时,上下限的确定也是关 键的一步。
v函数
选择一个与u函数相乘后能够简化积分 的函数作为v函数。
计算积分
计算v函数的定积分。 利用分部积分公式计算u和v函数的乘积的积分,得到结果。
验证结果
• 将计算结果与原函数进行比较,验证结果的正确 性。
03
分部积分法的实例解析
BIG DATA EMPOWERS TO CREATE A NEW
分部积分法的应用场景
总结词
分部积分法适用于求解形如∫u(x)v'(x)dx的 积分问题,特别是当u(x)和v(x)都是多项式 、三角函数、指数函数等基本初等函数时。
详细描述
分部积分法适用于求解形如∫u(x)v'(x)dx的 积分问题,其中u(x)和v(x)都是可微的函数 。在具体应用中,我们通常选择u(x)和v(x) 为易于计算导数和积分的函数,如多项式、 三角函数、指数函数等基本初等函数。通过 合理选择u(x)和v(x),我们可以将复杂积分 问题转化为多个简单积分问题的和或差,从
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近似微分方程如下:
d4v1 dx4
0, 0
x
L
(1a)
d4v2 dx4
q EI
,L
x
2L
(1b)
d4v3 dx4
2q EI
,2L
x
3L
(1c)
第二步:对(1)式各段的挠曲线近似微分方程分别 积分四次,得到剪力、弯矩、转角和挠度的通解。 在通解中,包含有12个积分常数 Ci i 1,2,L ,12。
####################################### #子曰:“我非生而知之者,好古敏以求之者也。# #######################################
第11章电脑求解弯曲变形 的一种快速解析法
提出了一种求解复杂载荷作用下梁弯曲变形
问题的连续分段独立一体化积分法。连续分段独 立一体化积分法首先将梁进行分段,独立建立具 有4阶导数的挠曲线近似微分方程,然后分段独 立积分4次,得到挠度的通解。根据边界条件和 连续性条件,确定积分常数,得到剪力、弯矩、 转角和挠度的解析函数,同时绘出剪力图、弯矩 图、转角图和挠度图。工程实例表明,连续分段 独立一体化积分法建立方程简单,计算编程程式化, 利用计算机求解速度快,与有限元法相比其优点 是可以得到精确的解析解。
积分四次,得到挠度方程通解
i 1, 2,L , n
(11-4)viຫໍສະໝຸດ qi xEi Ii
dx
dx
dx
dx
1 6
Ci,1x3
1 2
Ci
,2
x2
Ci ,3 x
Ci,4
i 1,2,L ,n
(11-5)
(iii)利用位移边界条件、力边界条件和连续性条件建立 4n
个边界条件约束方程
f Ci, j 0 i 1,2,L ,n, j 1,2,3,4
2. 复杂载荷作用下的悬臂梁
例11-2悬臂梁的载荷和尺寸如图11-2所示,弯曲刚度 EI
为常数,试利用计算机求解剪力、弯矩、转角和挠度
的函数表达式。已知:
F
2 3
q,L
L 5m ,
q 3kN/m 。
图11-2复杂载荷作用下的悬臂梁
解:利用连续分段独立一体化积分法求解步骤为
第一步:本题分为三段 n 3 ,各段的挠曲线
i 1, 2,L , n
(11-2)
积分两次,得到弯矩方程通解
d2vi
dx2
qi x
Ei Ii
dx
dx
Ci,1x
Ci
,2
i 1,2,L ,n
(11-3)
积分三次,得到转角方程通解
dvi
dx
qi x
Ei Ii
dx
dx
dx
1 2
Ci ,1 x 2
Ci,2
x
Ci,3
(11-6)
(iv)将积分常数 Ci, j i 1, 2,L , n, j 1, 2,3, 4
代入(11-2)~(11-5)式就可得到剪力、弯矩、转角和挠度 的解析表达式。
11.2静定梁的快速解析法
11.2.1等截面梁的快速解析法
1. 复杂载荷作用下的简支梁 例11-1简支梁的载荷和尺寸如图11-1所示,弯曲刚度 EI 为常数,试利用计算机求解剪力、弯矩、转角和 挠度的最大值。 已知: L 5m ,Me 80kN m ,F 15kN ,q 5kN/m 。
8个积分常数 Ci i 1,2,L ,8。
第三步:利用如下的位移边界条件、力边界条件和连续性条件
v1 0 0 , EIv10 Me
(2a)
v1 L v2 L , v1L v2 L
(2b)
EIv1 L EIv2 L , EIv1L EIv2L F
(2c)
v2 2L 0 , EIv22L 0
第三步:利用如下的位移边界条件、力边界条件和连续性条件
EIv10 0
, EIv10 F
(2a)
v1 L v2 L
, v1L v2 L
(2b)
EIv1 L EIv2 L , EIv1L EIv2L
(2c)
v2 2L v3 2L ,
v2 2L v3 2L
(2d)
EIv2 2L EIv3 2L , EIv22L EIv32L
(2e)
v3 3L 0
, v3 3L 0
(2f)
联立解方程组(2)式,得出12个积分常数 Ci i 1,2,L ,12
。
第四步:将积分常数 Ci i 1,2,L ,12 代入剪力、弯矩、转角 和挠度的通解得到剪力、弯矩、转角和挠度的
解析表达得到剪力、弯矩、转角和挠度的解析
表达式如下:
剪力函数:
FS1
max
0.7225
qL3 EI
(
x 0 ),
max
0.5508
qL3 EI
( x 2L);
挠度最大值:vmax
0.3647
qL4 EI
(
x 0.9624L
)。
第六步:利用支座约束力与剪力函数的关系:
FAy FS1 0, FB FS2 2L 。
可以得到支座约束力:
FAx 0 , FAy 5.75kN, FB 34.25kN 。
图11-1复杂载荷作用下的简支梁
解:利用连续分段独立一体化积分法求解步骤为:
第一步:本题分为两段 n 2,各段的挠曲线近似微分方程如下:
d4v1 dx4
0, 0
x
L
(1a)
d4v2 dx4
q EI
,L
x
2L
(1b)
第二步:对(1)式各段的挠曲线近似微分方程分别积分四次, 得到剪力、弯矩、转角和挠度的通解。在通解中,包含有
11.1连续分段独立一体化积分法
连续分段独立一体化积分法的解题步骤如下:
(i)首先把梁在突变处自然分成 n 段,
建立独立的四阶导数挠曲线微分方程
d4vi qi x
dx4 Ei Ii
i 1, 2,L , n
(11-1)
(ii)积分一次,得到剪力方程通解
d3vi
dx3
qi
xdx
Ei Ii
Ci,1
解得 x 0.963L ,代入第一段挠度函数 v1 x ,
即得最大挠度。
求出剪力、弯矩、转角和挠度的最大值如下:
剪力最大值:
F S,max
5.75kN
(
x 0),
F S,max
34.25kN
(
x 10m);
弯矩最大值: Mmax 108.8kN m ( x 5m );
转角最大值:
(2d)
联立解方程组(2)式,得出8个积分常数 Ci i 1,2,L ,8。
第四步:将积分常数 Ci i 1,2,L ,8 代入剪力、弯矩、转角和
挠度的通解得到剪力、弯矩、转角和挠度的解析表达式
第五步:通过观察图形与解析求解相结合的方法,
最大挠度位置发生在第一段转角为零的位置,即
1 x 0
(3)
