截长补短法
八年级上册数学截长补短法

八年级上册数学截长补短法一、截长补短法的概念。
1. 定义。
- 截长补短法是几何证明题中一种常用的辅助线添加方法。
“截长”就是将一条较长的线段截成两段或几段,使得其中的一段或几段与已知线段相等;“补短”就是将一条较短的线段延长,使得延长后的线段与已知的较长线段相等。
- 例如,在三角形ABC中,要证明AB = AC+CD(假设AB>AC),“截长”的做法可以是在AB上截取AE = AC,然后去证明BE=CD;“补短”的做法可以是延长AC到F,使CF = CD,然后去证明AB = AF。
2. 适用情况。
- 当题目中出现证明两条线段之和等于第三条线段或者两条线段之差等于第三条线段等类型的问题时,常常考虑使用截长补短法。
- 比如在四边形或者三角形的边的关系证明中经常用到。
如在等腰三角形的相关证明中,如果要证明等腰三角形腰长与底边一部分线段的关系时,可能就需要用到这种方法。
二、截长补短法的解题步骤。
1. 截长法解题步骤。
- 第一步:观察图形和已知条件,确定要截的线段。
一般选择较长的那条线段进行截取。
- 第二步:根据已知条件截取合适的长度,使得截取后的线段与其他已知线段有一定的联系。
例如,在三角形中,如果有角平分线的条件,可能会截取与角平分线到角两边距离相等的线段。
- 第三步:连接截取点与其他点,构造全等三角形或者其他特殊的几何关系。
- 第四步:利用全等三角形的性质或者其他几何定理进行推理,得出要证明的结论。
- 例如:在三角形ABC中,AD是∠BAC的角平分线,∠C = 2∠B,求证:AB = AC+CD。
- 证明(截长法):在AB上截取AE = AC,连接DE。
- 因为AD是角平分线,所以∠EAD = ∠CAD。
- 在△AED和△ACD中,AE = AC,∠EAD = ∠CAD,AD = AD,根据SAS(边角边)定理,△AED≌△ACD。
- 所以∠AED = ∠C,CD = ED。
- 又因为∠C = 2∠B,∠AED = ∠B + ∠EDB,所以∠B = ∠EDB。
特殊平行四边形截长补短法的运用

截长补短法截长补短法是几何证明题中十分重要的方法。
往常来证明几条线段的数目关系。
截长补短法有多种方法。
截长法:(1)过某一点作长边的垂线(2)在长边上截取一条与某一短边同样的线段,再证剩下的线段与另一短边相等。
补短法(1)延伸短边。
(2)经过旋转等方式使两短边拼合到一同。
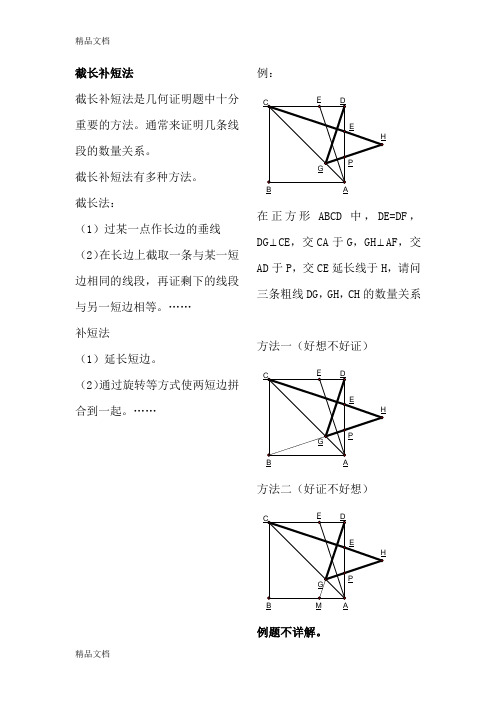
例1:在正方形 ABCD中, DE=DF, DG CE,交 CA于 G, GH AF,交 AD于 P,交 CE延伸线于 H,请问三条粗线 DG, GH,CH的数目关系。
C FDEHPGB A 方法一(好想不好证)方法二(好证不好想)(1)正方形ABCD中,点 E 在 CD上,点 F 在 BC上,EAF=45o。
求证: EF=DE+BF。
A BFD CE(1)变形 a正方形 ABCD中,点 E 在 CD延伸线上,点F 在 BC延伸线上,EAF=45o。
请问此刻 EF、 DE、BF 又有什么数目关系?A BE D CF(1)变形 b正方形 ABCD中,点 E 在 DC延伸线上,点F 在 CB延伸线上,EAF=45o。
请问此刻 EF、 DE、BF 又有什么数目关系?FA BD C E(1)变形 c正三角形 ABC中, E在 AB上, F 在AC上EDF=45o。
DB=DC,BDC=120o。
请问此刻EF、 BE、 CF又有什么数目关系?AFEBj CD(1)变形 d正方形ABCD中,点E 在CD上,点F 在 BC上,EAD=15o,FAB=30o ,AD= 3求AEF的面积.A BFD CE(1)变形 e如图,在正方形ABCD中, M是 AB的中点, DM⊥MN, BN均分∠ CBE。
求证: DM=MN.(1) 变形 f如图,在正方形ABCD中, E是 BC的中点,AE⊥EF,一种正确的解题思路:取AB的中点 M,连结 ME,则CF 均分∠ DCG,经过思虑,小明展现了AM=EC,易证△≌△AME ECF ,所以 AE EF .在此基础上,同学们作了进一步的研究:(1)小颖提出:如图 2,假如把“点E是边BC的中点”改为“点E是边BC上(除B,C 外)的随意一点”,其余条件不变,那么结论“AE=EF”仍旧建立,你以为小颖的看法正确吗?假如正确,写出证明过程;假如不正确,请说明原因;(2)小华提出:如图 3,点E是BC的延伸线上(除C点外)的随意一点,其余条件不变,结论“ AE=EF”仍旧建立.你以为小华的看法正确吗?假如正确,写出证明过程;假如不正确,请说明原因.A D A DF A DF FB ECG B ECG BC E G图 1 图 2 图 3(2)正方形 ABCD中,对角线 AC与 BD交于 O,点 E 在 BD上, AE均分DAC。
经典截长补短法巧解资料讲解
截长补短法截长补短法是几何证明题中十分重要的方法。
通常来证明几条线段的数量关系。
截长补短法有多种方法。
截长法:(1)过某一点作长边的垂线(2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
……补短法(1)延长短边。
(2)通过旋转等方式使两短边拼合到一起。
……例:HPGFB AC DE在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系方法一(好想不好证)HPGFB AC DE方法二(好证不好想)HMPGFB AC DE例题不详解。
(第2页题目答案见第3、4页)FEDCAB(1)正方形ABCD 中,点E 在CD 上,点F 在BC 上,∠EAF=45o 。
求证:EF=DE+BF(1)变形aEFD CAB正方形ABCD 中,点E 在CD 延长线上,点F 在BC 延长线上,∠EAF=45o 。
请问现在EF 、DE 、BF 又有什么数量关系?(1)变形bEFD C AB正方形ABCD 中,点E 在DC 延长线上,点F 在CB 延长线上,∠EAF=45o 。
请问现在EF 、DE 、BF 又有什么数量关系?(1)变形cj FEABCD正三角形ABC 中,E 在AB 上,F 在AC 上∠EDF=45o 。
DB=DC ,∠BDC=120o 。
请问现在EF 、BE 、CF 又有什么数量关系?(1)变形 dFEDCAB正方形ABCD 中,点E 在CD 上,点F 在BC 上,∠EAD=15o ,∠FAB=30o 。
AD=3求∆AEF 的面积(1)解:(简单思路)GFEDCA B延长CD 到点G ,使得DG=BF ,连接AG 。
由四边形ABCD 是正方形得∠ADG=∠ABF=90o AD=AB 又DG=BF所以∆ADG ≅∆ABF (SAS ) ∠GAD=∠FAB AG=AF由四边形ABCD 是正方形得∠DAB=90o =∠DAF+∠FAB =∠DAF+∠GAD=∠GAF所以∠GAE=∠GAF-∠EAF =90o -45o =45o∠GAE=∠FAE=45o 又AG=AF AE=AE所以∆EAG ≅∆EAF (SAS ) EF=GE=GD+DE=BF+DE变形a 解:(简单思路)GEFD CABEF= BF-DE在BC 上截取BG ,使得BG=DF ,连接AG 。
线段和差处理技巧截长补短法

线段和差处理技巧截长补短法线段的和差处理技巧是数学中非常重要的一个概念。
在数学中,线段和差处理可以通过截长补短法来实现。
所谓截长补短,就是在两个线段之间找到一个公共的部分,然后通过截取和补足的方式实现线段的和差处理。
以下是线段和差处理技巧截长补短法的详细介绍。
在讨论线段和差处理之前,我们先来了解一下什么是线段。
线段是数学中的一个基本概念,是一个有两个端点的连续部分。
线段一般用两个点表示,比如用A和B表示一个线段AB。
线段的长度等于两个端点之间的距离。
线段的和差处理是指在给定的线段AB和线段CD的情况下,通过截长补短的方法计算出线段AB和线段CD的和或差。
具体来说,截长补短法可以分为两种情况:一种是线段AB和线段CD的起点和终点相同,另一种是线段AB和线段CD的起点和终点不同。
第一种情况下,如果线段AB和线段CD的起点和终点相同,那么它们可以看作是同一个线段。
在这种情况下,线段AB和线段CD的和差就是线段AB(或CD)的两倍。
更具体地说,如果我们要计算线段AB和线段CD的和,那么和的长度等于线段AB的长度加上线段CD的长度;如果我们要计算线段AB和线段CD的差,那么差的长度等于线段AB的长度减去线段CD的长度。
第二种情况下,如果线段AB和线段CD的起点和终点不同,那么它们不可以看作是同一个线段。
在这种情况下,我们需要找到线段AB和线段CD的一个公共部分,并将其截取下来。
具体来说,我们可以通过以下步骤实现线段和差的处理:1.先找到线段AB和线段CD的一个公共的端点。
这个公共端点可以是线段AB的起点或终点,也可以是线段CD的起点或终点。
2.从线段AB的起点开始,沿着线段AB的方向,截取和线段CD长度相等的一段线段。
这段线段的长度等于线段CD的长度。
3.将截取下来的线段与线段CD的起点相连。
这样我们就得到了一条新的线段EF,其中E是线段AB的起点,F是线段CD的起点。
4.线段EF就是线段AB和线段CD的和。
《截长补短法》课件

04
截长补短法的实例
实例一:几何图形
总结词
通过图形直观展示
详细描述
在PPT中,我们可以使用几何图形来展示截长补短法的应用。例如,在平面几何中,我们可以通过将一个不规则 图形切割成几个规则图形,然后进行补充,从而得到一个新的规则图形。这种方法可以帮助学生更好地理解几何 图形的性质和特点。
实例二:数据可视化
原理的数学解释
截长补短法是一种基于几何和代数知识 的解题方法,其原理可以通过数学公式
和定理进行解释。
在几何学中,截长补短法可以用于证明 一些线段或角度的性质和关系,例如通 过截取线段来证明两个三角形相似或通 过补全角度来证明一个四边形是平行四
边形。
在代数中,截长补短法可以用于解决一 些方程和不等式问题,例如通过将一个 复杂的多项式方程进行截取和补全,来
索其在其他领域的应用。
拓展应用范围
尝试将截长补短法与其他几何 作图方法结合,拓展其应用范 围,解决更多复杂的几何问题 。
提高教学水平
在数学教学中,加强对截长补 短法的介绍和讲解,帮助学生 更好地理解和掌握该方法。
激发学习兴趣
通过引导学生运用截长补短法 解决实际问题,激发他们对数
学学习的兴趣和热情。
THANKS
简单、更易于解决的小问题。
补全短线段
补全短线段是指在解题过程中,将一些较短的线段或步骤进行补充和整合,使其形 成一个完整的解决方案。
通过补全短线段,可以将零散的信息和步骤整合起来,形成一个完整的知识体系或 解决方案。
在数学问题中,补全短线段通常用于将一些分散的条件和信息整合起来,形成一个 完整的证明或解题过程。
找到满足条件的解。
03
截长补短法的步骤
截长补短法证明题课件

THANKS
谢谢
总结词:梯形中位线定理 详细描述
1. 定义梯形中位线为AD, 并设梯形两底分别为AB和 CD。
2. 通过梯形中位线的定义, 我们知道AD是AB和CD的组 合线段。
3. 根据组合线段的性质, AD等于两底AB和CD的平均 值。
4. 因此,AD等于 (AB+CD)/2,即梯形的中位 线等于两底和的一半。
02
CHAPTER
截长补短法的基础知识
平行线定理与推论
平行线定理
两条平行线被第三条直线所截,截得的对应线段成比例。
推论
如果一条直线截三角形的两边或其延长线,都使得两对边成 比例,那么这条直线一定与三角形相交。
三角形中位线定理
定理
三角形的中位线平行于第三边,并且等于第三边的一半。
应用
通过证明三角形中位线定理,可以得出四边形可以被分割成若干个三角形,从 而利用三角形面积公式求解四边形面积。
05
CHAPTER
截长补短法的实际应用
在几何作图中的应用
总结词
截长补短法在几何作图中应用广泛,是解决 作图题的重要方法。
详细描述
在几何作图中,常常需要将一条线段分成两 段或几段,然后利用这些线段构造新的图形 。截长补短法通过将长线段截取成若干段, 或补短线段以形成所需的新图形,从而实现 作图目标。
截长补短法证明题课件
目录
CONTENTS
• 截长补短法概述 • 截长补短法的基础知识 • 截长补短法的证明技巧 • 截长补短法经典例题解析 • 截长补短法的实际应用 • 截长补短法的进一步研究与探讨
01
CHAPTER
截长补短法概述
定义与特点
定义
截长补短法是一种证明几何命题 的技巧,通过将较长的线段截取 一部分,用来补足较短线段的不 足,从而使命题得证。
截长补短法构造全等三角形

截长补短法构造全等三角形
截长补短法(SSS)是指通过修改三角形的边长,在保持三个边长之和不变的情况下,改变三角形的形状,使其与另一个三角形完全相同。
下面是一个使用截长补短法构造全等三角形的示例:
给定三角形ABC和DEF,其中AB=6cm,BC=5cm,AC=7cm,DE=5cm,EF=6cm,DF=7cm。
我们需要使用截长补短法构造一个与ABC全等的三角形。
步骤如下:
1. 在BC的中点G处,画一条平行于AC的直线,并延长到交DE延长线于点H。
2. 在AC的中点I处,画一条平行于BC的直线,并延长到交EF延长线于点J。
3. 连接BH和CJ,将四边形BCHJ分成两个三角形。
4. 证明三角形ABH和DEF全等,由于BH=DE=5cm,AB和DF都平行于HJ,AH和DE都平行于BC,因此根据副角定理和平行线性质可知,两个三角形全等。
5. 证明三角形ACJ和DEF全等,AC=DF=7cm,AC和DF都平行于CJ,AJ 和DE都平行于BC,因此根据副角定理和平行线性质可知,两个三角形全等。
因此,三角形ABC和DEF是全等的,且可以通过截长补短法构造。
76 截长补短模型证明问题-【初中数学】120个题型大招!冲刺满分秘籍!

截长补短模型证明问题【专题说明】截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a+b=c时,用截长补短.【知识总结】1、补短法:通过添加辅助线“构造”一条线段使其为求证中的两条线段之和,在证所构造的线段和求证中那一条线段相等;2、截长法:通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段,在证明截剩部分与线段中的另一段相等。
3、截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明,这种做法一般遇到证明三条线段之间关系是常用.如图1,若证明线段AB,CD,EF之间存在EF=AB+CD,可以考虑截长补短法.截长法:如图2,在EF上截取EG=AB,在证明GF=CD即可;补短法:如图3,延长AB至H点,使BH=CD,再证明AH=EF即可.【类型】一、截长“截长”是指在较长的线段上截取另外两条较短的线段,截取的作法不同,涉及四种方法。
方法一:如图2所示,在BF上截取BM=DF,易证△BMC≌△DFC(SAS),则MC=FC=FG,∠BCM=∠DCF,可得△MCF为等腰直角三角形,又可证∠CFE=45°,∠CFG=90°,∠CFG=∠MCF,FG∥CM,可得四边形CGFM为平行四边形,则CG=MF,于是BF=BM+MF=DF+CG.图2方法二:如图2所示,在BF上截取FM=GC,可证四边形GCFM为平行四边形,可得CM=FG=CF;可得∠BFC=∠BDC=45°,得∠MCF=90°;又得∠BMC=∠DFC=135°,于是△BMC≌△DFC(AAS),BM=DF,于是BF=FM+BM=CG+DF.上述两种方法中都利用了两个共顶点的等腰Rt△BCD和△MCF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
。C
M
T
.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
证法3: 延长MC到T,使CT=BM, 则∠ACT=∠ABM, A 。 连结AT. ∵AC=AB=BC, ∴△MAB≌△TAC, ∠ABC=60°, 。C B ∴MA=TA. M ∵∠AMC=∠ABC=60°,
圆里的 截长补短
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠BAC=60°, °A 分析:
把已知条件及可得结论 标在图上:
60° °
。
.
Hale Waihona Puke B.60° ° 。C 60°60° ° °
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠BAC=60°, °A 分析:
.
.
∴MA=MS=AS, ∴MA=MB+MC.
延长 分析3:补短法 MC到T, A 使CT=BM, 。 连结AT. MA=MT, ∠AMC=60°, MA=MT=AT, MA=AT, △MA?≌△TA? B △MAB≌△TAC, AB=AC, BM=CT, ∠ABM=∠ACT,
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠ACT=∠ABM,
。 使MN=CM, 连结CN.△CMN是等边三角形, MA=NB,
.
△MA?≌△NB? △MAC≌△NBC, 。C B AC=BC, ∠MAC=∠NBC, M N ∠AMC=∠BNC, ∠AMC=60°, ∠CMN=∠BAC=60°, ∠BNC=60°, △CMN是等边三角形,
.
证法1: 延长BM到N,使MN=CM, CN. 连结 ∵AB=BC=CA, A ∴∠BAC=∠ABC=60°. 。 ∵∠CMN=∠BAC=60°, ∴△CMN是等边三角形, ∴∠BNC=60°. ∵∠AMC=∠ABC=60°, 。C B ∴∠AMC=∠BNC. ∵∠MAC=∠NBC, AC=BC, M N ∴△MAC≌△NBC, ∴MA=NB, ∴MA=MB+MC.
证法9: 由托勒密定理得 BCMA =ACMB+ABMC. ∵BC=AC=AB, ∴MA=MB+MC.
B
A
C M
证法10:记MA交BC于点P.
∴AC =AB, ∵AC=AB, P ∴∠AMC=∠AMB . 。C B ∵∠BCM=∠BAM , M ∴△MCP ∽△MAB , MC CP MB BP ∴MA = AB ; 同理,MA = AC . MB MC BP CP ∵BC=AC=AB, MA + MA = AC + AB =1, ∴ ∴MA=MB+MC.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
.
.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠ABS=∠ACM, °A 延长 分析2:补短法 MB到S, ∠BAC=60°,
使BS=MC, 连结AS. MA=MS, ∠AMB=60°, S MA=AS, MA=MS=AS, △MAC≌△SAB, △MA?≌△SA? AC=AB, MC=SB, ∠ACM=∠ABS,
.
T
.
∴MA=MT=AT, ∴MA=MB+MC.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ° A 延长 分析4:补短法 CM到F, ∠BAC=60°,
。 使MF=BM, 连结BF. △BFM是等边三角形, MA=FC,
.
△MA?≌△FC? △MAB≌△FCB, B AB=CB, ∠ABM=∠CBF, BM=BF,
.
.
在MA 分析8:截长法 上截取MH=MB, AH=MC, 连结BH. A △HBM是等边三角形. 。 △AH?≌△CM? △AHB≌△CMB, H AB=CB, ∠BAH=∠BCM, ∠ABH=∠CBM, ∠ABC=60°, B ∠HBM=60°, △HBM是等边三角形.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
把已知条件及可得结论 标在图上: 把能表示的60°角 用圆弧表示:
。
.
B
.
60° °
。C
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠BAC=60°, °A 分析:
把已知条件及可得结论 标在图上: 把能表示的60°角 用圆弧表示:
。
.
B
.
M
。C
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. °A 延长 分析1:补短法 BM到N, ∠BAC=60°,
A
.
.
在AM 分析5:截长法 上截取AE=MC, ME=MB, A ∠AMB=60°, 。 连结BE. E MB=EB, ME=MB=BE, △MB?≌△EB? △MBC≌△EBA, B BC=BA, ∠BCM=∠BAM, CM=AE,
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
把已知条件及可得结论 标在图上: 把能表示的60°角 用圆弧表示:
60° °
。
.
B
.
60° ° 。C 60°60° ° °
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠BAC=60°, °A 分析:
把已知条件及可得结论 标在图上: 把能表示的60°角 用圆弧表示:
.
.
△KCM是等边三角形.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
证法6: MA上截取MK=MC, 连结KC. 在 ∵AC=BC=AB, A ∴∠ABC=∠ACB=60°, ∴∠AMC=∠ABC=60°, AMC= ABC=60 ∠AMB=∠ACB=60°, ∴∠BMC=120°, K △KCM是等边三角形, B C ∴∠AKC=120°=∠BMC, M ∵∠KAC=∠MBC, ∴△AKC≌△BMC, ∴AK=MB,∴MA=AK+MK=MB+MC.
F
.
M
。C
△BFM是等边三角形, ∠BMF=∠BAC=60°,
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
证法4: ∵AB=AC=CB, 。 ∴∠BAC=∠ABC=60°. 延长CM到F,使MF=BM, 则∠BMF=∠BAC=60°, 。C 连结BF, B 则△BFM是等边三角形, M BM=BF, ∴∠FMB=∠FBM=60°, ∴∠ABM=∠CBF, F ∴△MAB≌△FCB, ∴MA=FC, ∴MA=MB+MC.
.
.
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. 在AM 分析7:截长法 上截取AD=MB, A
MD=MC, 连结DC. ∠DMC=60°, MD=MC=DC, MC=DC, △MCB≌△DCA, △MC?≌△DC? B CB=CA, ∠MBC=∠DAC, BM=AD,
。
.
B
.
M
。C
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
证法2: 延长MB到S,使BS=MC, A 则∠ABS=∠ACM. 。 连结AS. ∵AC=AB=BC, ∴△MAC≌△SAB, S 。C B ∠ACB=60°, ∴MA=SA. M ∵∠AMB=∠ACB=60°,
。C
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
证法5: AM上截取AE=MC, 在 连结BE.
A ∵BC=BA=AC, 。 ∴∠ACB=60°. E ∵∠BCM=∠BAE, CM=AE, ∴△MBC≌△EBA, 。C B ∴ME=MB; M ∵∠AMB=∠ACB=60°, ∴ME=MB=BE,∴MA=ME+AE=MB+MC.
在MA 分析6:截长法 上截取MK=MC, A AK=MB, 连结KC. △KCM是等边三角形, △AK?≌△BM? △AKC≌△BMC, AC=BC, ∠KAC=∠MBC, K ∠AKC=∠BMC, C B ∠BMC=120°, M ∠AKC=120°,
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
“截长补短”是初中平面几何中化难为易 的一种常用解题思想。 本题是一道典型例题。 这里表现 8 种证法,是要说明实际解题 时怎么补、怎么截。在作好辅助线后要及时 看到所产生的辅助条件,结合已知条件打通 思路。 本题的其它证法附于后面。
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
。
.
B
.
60° ° 。C 60°60° ° °
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠BAC=60°, °A 分析:
把已知条件及可得结论 标在图上: 把能表示的60°角 用圆弧表示:
。
.
B
.
60°60° ° °
。C
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC. ∠BAC=60°, °A 分析:
。C
M
题目: 如图,M是等边△ABC的外接圆BC上的一点, 求证:MA = MB+MC.
