第10章能量法
《结构力学》习题集及答案(下册)第十章结构弹性稳定计算
第十章 结构弹性稳定计算一、判断题:1、稳定方程即是根据稳定平衡状态建立的平衡方程。
2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。
3、在稳定分析中,有n 个稳定自由度的结构具有n 个临界荷载。
4、两类稳定问题的主要区别是:荷载—位移曲线上是否出现分支点。
5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。
6、能量法确定临界荷载的依据是势能驻值原理。
二、计算题:7、用静力法推导求临界荷载cr P 的稳定方程。
PE I ,l8、写出图示体系失稳时的特征方程。
k lEIk AB P9、求刚架在反对称失稳时的稳定方程。
n 为常数。
l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。
转动刚度kl k r 2=,k 为弹簧刚度。
P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。
已知弹簧刚度l EI k 33= 。
PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。
PEI l13、用静力法求图示结构的临界荷载cr P ,欲使B 铰不发生水平移动,求弹性支承的最小刚度k 值。
PlEI A Bk14、用静力法确定图示具有下端固定铰,上端滑动支承压杆的临界荷载crP。
P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。
设失稳时两柱的变形曲线均为余弦曲线:yxh=-δπ(cos).12提示:cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。
PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆,AB段失稳时变形曲线设为:()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。
l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ,设变形曲线为正弦曲线。
第10章 杆件稳定性
a
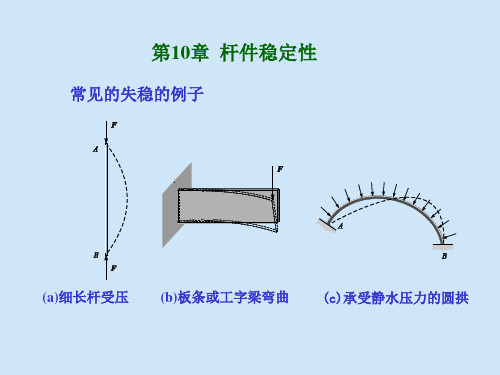
II (大 挠 度 理 论) II (小 挠 度 理 论)
Fcr
B I (稳 定)
D'
O
a)
b)
第10章
两条平衡路径Ⅰ 的交点为分支点 分支点 B 将 分支点。 两条平衡路径 Ⅰ和 Ⅱ 的交点为 分支点 。
10.1 稳定性概念
原始的平衡路径Ⅰ分为两段:前段 OB 上的点属于稳定 原始的平衡路径Ⅰ 分为两段: 平衡, 上的点属于不稳定平衡。 平衡 , 而后段 BC 上的点属于不稳定平衡 。 具有这种特 征的失稳形式称为分支点失稳形式。 征的失稳形式称为 分支点失稳形式。 分支点失稳形式
θ
例10.2
第10章
考虑如图(a)的单自由度非完善体 考虑如图(a)的单自由度非完善体 (a)
F k
B B'
系,刚性杆AB有初倾角 ε 。 刚性杆 有初倾角
k
10.1 稳定性概念
l
l
A
A
(a) )
(b) )
解:在图(b)中,平衡条件(水平方向)为 在图(b)中 平衡条件(水平方向) (b)
F tan(θ + ε ) − kl[sin(θ + ε ) − sin ε ] = 0 sin ε F = kl cos(θ + ε )[1 − ] sin(θ + ε )
第10章
例10.5
10.1 稳定性概念
如图所示, 如图所示,由三根相同的刚性杆组
成的系统,一端作用外力 ,铰结处B、 都是弹性 成的系统,一端作用外力F,铰结处 、C都是弹性 系数为k的弹性支座。试用两种方法求临界载荷。 系数为 的弹性支座。试用两种方法求临界载荷。 的弹性支座
第10章动载荷与交变载荷

4、振动问题: 求解方法很多。
4
工 程 力 学§10-2 构件作等加速直线运动
时的动应力计算
钢索起吊重物,W、a, 求:钢索 d
钢索具有a,不为平衡状态,不能用平
衡方程求内力。
kd
动荷因数
kd
FNd Fst
d st
d st
结论:只要将静载下的应力,变形,乘以动荷系数Kd即得 动载下的应力与变形。
6
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
冲击荷载问题的动响应
方法原理:能量法 ( 机械能守恒 )
在冲击物与受冲构件的接触区域内,应力状态异常复杂, 且冲击持续时间非常短促,接触力随时间的变化难以准确分析, 放弃动静法。工程中通常采用能量法来解决冲击问题,即在若 干假设的基础上,根据能量守恒定律对受冲击构件的应力与变 形进行偏于安全的简化计算。
7
工 程 力 学§10-3 构件受冲击载荷作用件受冲击载荷作用时
的动应力计算
9
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
10
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
在冲击过程中,运动中的物体称为冲击物。 阻止冲击物运动的构件,称为被冲击物。
(3)、构件在交变应力作用下发生破坏需要经历一定数量的应 力循环,其循环次数与应力的大小有关。应力愈大,循环次数 愈少。
实验表明在静载荷下服从胡克定律的材料,只要应力不超 过比例极限 ,在动载荷下虎克定律仍成立且E静=E动.
动荷因数:
动响应 Kd 静响应
第十章-动载荷

2
2 动载荷问题分类 1) 构件有加速度时旳应力计算; 2) 冲击问题; 3) 振动问题; 4) 交变载荷。
3
§10. 2 动静法旳应用
1 动静法
即为理论力学中简介旳达朗伯原理。
2 匀加速平动构件中旳动应力分析
例子 设杆以匀加速度a作平动,
b
R
aR
截面积为A,比重为 。
加上惯性力系。
3 求解冲击问题旳能量法 线弹性系统
任一线弹性杆件或构造都可简化为线性弹簧。 15
3 求解冲击问题旳能量法 线弹性系统
任一线弹性杆件或构造都可简化为线性弹簧。
l Pl EA
P EA l l
等价弹簧旳弹性
系数 k EA
l
16
l Pl EA
等价弹簧旳弹性系数 能量法
P EA l l
k EA l
工程实例 气缸
在满足刚度和强度要求旳前提下
28
冲击问题旳一般解题环节
1) 判断是垂直冲击还是水平冲击;
2) 求 △st ; 3) 求 Kd ;
4) 计算静应力 st ; 5) 计算动应力 d = Kd st .
注意
1) 对于不是垂直冲击或水平冲击问题,或不满 足条件(冲击前无应力和变形),则需要应
a g
)
记: 若忽视自重,则
对线性系统
a
Kd Kd
1 a
g
g
动荷系数
内力、应力、应变和变形都与外力成线性关系。
动载荷问题旳求解 1) 求出动荷系数; 2) 按静载荷求解应力、应变、变形等; 3) 将所得成果乘以动荷系数 Kd 即可。 6
动载荷问题旳求解
1) 求出动荷系数;
材料力学第十章杆件计算的能量法

T
T
A
T
l
o
B
3.梁弯曲时的应变能
3.1 纯弯曲梁
l Ml
M
EI
W
1 2
M e
Vε
W
1 2
M
e
M 2l 2EI
M
l
3.2 剪切弯曲梁
弯矩M:
dVε M
M (x)2 dx 2EI
M (x)2 dx
Vε M l 2EI
剪力FQ:
6FQ
h2 (
y2)
0 2EI
l
2EI
FA
4
F2 A
l
3
F
l2 3
5FA Fl3
3EI 6EI 6EI
3.位移
Δ A
Vε FA
0
FA
5 16
F
例 求如图所示简支梁截面A的转角,设梁EI的为常数。
Mo A
M B
l
解:为了求A截面的转角A,可在A端加一虚力偶M0,如
图所示。则按卡氏第二定理,A截面的转角:
§10-2 杆件的弹性应变能
一、杆在基本变形下的应变能
1.杆在轴向拉伸(压缩)时的应变能
F
F
A
l l1
Vε
1 2
FN l
FN2l 2EA
dF F1 F
o
d(△l) △l1
B △l
2.圆杆扭转时的应变能
W 1 T
2
Mx T
M xl
GIP
材料力学习题

材料力学作业册学院:专业:年级:班级:学号:姓名:前言本作业题册是为适应当前我校教学特色而统一筛选出来的题集,入选题目共计72个,教师可根据学时情况有选择性的布置作业。
本题册中列出的题目仅是学习课程的最基本的作业要求,老师根据情况可适当增加部分作业,部分学生如果有考研或者其他方面更高的学习要求,请继续训练其他题目。
本题册仅用于学生课程训练之练习,任何人不得将其用于商业目的,违者将追究其法律责任。
由于时间仓促,并限于编者水平有限,缺点和错误在所难免,恳请大家提出修改建议。
王钦亭wangqt@ 2013年2月27日目录第一章绪论 (1)第二章拉伸与压缩 (2)第三章扭转 (7)第四章弯曲应力 (11)第五章弯曲变形 (18)第六章简单超静定问题 (20)第七章应力状态与强度理论 (25)第八章组合变形与连接件计算 (32)第九章压杆稳定 (36)第十章能量法 (41)第十一章动荷载.交变应力 (49)附录I 截面的几何性质 (53)第一章绪论1-1 材料力学的中所讲的构件失效是指哪三方面的失效?1-2 可变形固体的基本假设有哪些?1-3 材料力学中研究的“杆”,有什么样的几何特征?1-4 材料力学中,杆件的基本变形有哪些?第二章 拉伸与压缩2-1(SXFV5-2-1)试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
2-2(SXFV5-2-2)一打入地基内的木桩如图所示,沿杆轴单位长度的摩擦力为2f kx (k 为常数),试作木桩的轴力图。
A2-3(SXFV5-2-3)石砌桥墩的墩身高=10 m l ,其横截面尺寸如图所示。
荷载 1 000 kN F =,材料的密度33=2.3510 kg/m ρ⨯。
试求墩身底部横截面上的压应力。
2-4(SXFV5-2-6)一木桩受力如图所示。
柱的横截面为边长200 mm 的正方形,材料可认为符合胡克定律,其纵向弹性模量10 GPa E =。
如不计柱的自重,试求: (1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4)柱端A 的位移。
弹塑性力学第十章

( V
ijui),jdV V
i,jj
uidV
Snjijuid SVi,jjuidV
代入原虚位移方程
2019/10/27
34
§10-4 虚位移原理和最小势能原 理
代入原虚位移方程
V (i,jj fi)u id V S (X i n j i) ju id S 0
各向同性线性材料的应力应变关系
ijE 1(1)ijk kij
代入Uc表达式
Uc
1 2
VijijdV
1
U c2EV
(1)i2 j
kklldV
2019/10/27
10
§10-1 几个基本概念和术语
应变能、应变余能的计算举例
l
P
o
x
l
P
o
x
U
2P3l 3E2 A2
P 3l 3E 2A2
2019/10/27
14
§10-1 几个基本概念和术语
作业:图示结构各杆等截
面杆,截面面积为A,结点 A
C承受荷载P作用,材料应
力—应变关系分别为(1) l
y
=E ,(2) =E 1/2 。
试计算结构的应变能U 和 B
应变余能Uc。
2019/10/27
27
§10-3 功的互等定理
对于线弹性体本构关系
ij Eijkl kl
Eij kl kijli2j W k likjlEk lij
dVE dV (1) (2)
V ij ij
(1) (2) V ijkl kl ij
4
§10-1 几个基本概念和术语
能量法

第十章能量法承载的构件或结构发生变形时,加力点的位置都要发生变化,从而使载荷位能减少。
如果不考虑加载过程中其他形式的能量损耗,根据机械能守恒定律,减少了的载荷位能将全部转变为应变能储存于构件或结构内。
据此,通过计算构件或结构的应变能,可以确定构件或结构加力点处沿加力方向的位移。
但是,机械能守恒定律难以确定构件或结构上任意点沿任意方向的位移,也不能确定构件或结构上各点的位移函数。
应用更广泛的能量方法,不仅可以确定构件或结构上加力点处沿加力方向的位移,而且可以确定构件或结构上任意点沿任意方向的位移;不仅可以确定特定点的位移,而且可以确定梁的位移函数。
本章介绍的是:用应变能的概念,根据能量守恒原理来解决与弹性结构或构件变形有关问题的一般方法,这种方法称为能量法。
能量法既可用于计算构件或结构位移;也可用以解决静不定问题及其它一些问题;本章只讨论用能量方法计算位移。
§10.1 杆件的应变能计算前面我们曾讨论过拉伸(压缩)、扭转或弯曲时的变形计算。
但是在工程上还常遇到比较复杂的结构,例如图10-1中所示的桁架、刚架——是指由直杆组成的具有刚性结点的结构、拱——是指杆轴为曲线而且在铅垂载荷作用下会产生水平支座反力的结构等。
在计算这些结构上某一点或某一截面的位移时,能量法是比较简单的方法。
通过拉伸(压缩)、扭转、弯曲时的应变能分析,可见:杆件在受力变形后,都储藏有应变能。
若不计杆件变形过程中少量的热能等损失,则杆件能量守恒,外力在弹性体变形过程中所作的功W应等于杆件内储藏的应变能Vε,即Vε=W。
在第七章我们曾经分别得到等截面杆各横截面上的内力为常量时,拉伸(压缩)、扭转、弯曲(参看图10-2)时的应变能表达式如下拉伸(压缩)时2122NPF lV F lEAε=∆=此处F N=F P(10-1)圆轴扭转时 2122x P PM l V M GI εϕ== 此处M x =M P (10-2)平面弯曲时 2122P M lV M EIεθ== 此处M =M P (10-3)综合以上三个表达式中外力表达的部分,可以把应变能概括地写为12V W F εδ==(10-4) 式中 F ——在拉伸(压缩)时表示拉力(压力),在扭转或弯曲时表示集中力偶,所以此处F 称为广义力;δ——在广义力作用处与广义力F 相应的位移,称为广义位移,在拉伸(压缩)时它是与拉力(压力)相应的位移l ∆,在扭转时它是与扭转力偶矩相应的转角φ,在平面弯曲时它是与弯曲力偶矩相应的截面转角θ(如图2所示)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ddF
非线性 u*? ??0 1?d?
§10-3 互等定理
一、功和位移互等定理
1.推导:以简支梁为例
1)先加F1再加F2 ,二 力作的总功为
F1
F2
d11
d21
d12
d22
U
1
?
W1
?
1 2
F1d11?
12F2d
22
?
F1d12
2)同时加F1和F2 ,二
力作的总功为
F1 d11+d12
?U
i?1
i
?
?i?n12TGi2Ilpi i
b)为杆长x的函数
U
?
?0ldU
?
?0l 2TG2Ip(
x) (x
dx )
2)比能
u?
dU dV
?
0.5(?A)(?
dV
d
x
)
? ?? ? ? 2 ? G? 2
2 2G 2
? A
?
dx
? dx
§10-2 弹性应变能的计算
3.弯、杆件应变能的计算
1.轴向拉伸或压缩
l
1)应变能
U ?W ? 12FDl ?
U ? FN2l 2 EA
F Dl
若轴力FN或截面面积A为变量时
a)分段变化
b)为杆长x的函数
U
?
n
?U
i?1
i
?
?i?n12FEN2iAlii
U
?
?0ldU
?
?0l
FN2 ( x) dx 2EA( x)
2)比能
u?
dU dV
§10-1 概 述
一、功能原理
U ?W:应变能?无?能量??损失? 外力功
二、能量法
用功能原理求解结构位移、变形等力学问题的方法
三、重要性
1.解题简单、适用性广; 2.不受材料和形状限制,适用于线弹性、非线性和塑性
问题; 3.可求解静定与非静定问题; 4.学习后续课程的基础。
§10-2 弹性应变能的计算
2)组合变形的应变能
dU ? FN2 ( x )dx
M(x)
2 EA
? M 2 ( x )dx 2 EI z
? T 2 ( x)dx 2GIp
FN(x)
T(x) T (x) dx
M(x) FN(x)
U
?
?l
F
2 N
(
x
) dx
2 EA
?
?l
M2(x 2EI z
)d
x
?
?l
T 2 ( x)dx 2GIp
(
Fx 2
)2
dx
?
F 2l3 96 EI
U
?
U
弯
?
U剪
?
F 2l 3 96EI
?
?F 2l
8GA
U
剪
?
2
?0l
/2
?(
2GA
F 2
)
2
dx
?
?F 2l
8GA
U
剪
:U
弯
?
12EI?
GAl2
? 152(1??
)(
h l
)2
矩形截面梁:? ? 6/5,I / A? h2 /12,G? E /[2(1?? )]
第十章 能 量 法
? §10-1 概 述 ? §10-2 弹性应变能的计算 ? §10-3 互等定理 ? §10-4 卡氏第二定理 ? §10-5 虚功原理*
第十章 能 量 法
? §10-6 单位载荷法 ? §10-7 图乘法(维利沙金法 ) ? §10-8 瑞利—李兹法* ? §10-9 超静定结构的基本解法 ? §10-10 力法 正则方程* ?小 结
上式指圆截面情况。若截面并非圆形,则右第三
项中的Ip应为It。
§10-2 弹性应变能的计算
例10-1 图示矩形梁,比较弯曲
l/2
F l/2
和剪切两种应变能,并
求中点C的挠度。
C
h
解:1)将M(x)=Fx/2和
x
b
FQ(x)=F/2代入弯曲和 剪切应变能公式,并考虑对称性
U
弯
?
2 ?0l /
2
2
1 EI
U
?
?0ldU
?
?0l?
FQ2 dx 2GA
dx
? dx
FQ——横截面剪力,A——横截面面积。
? ——截面系数,
矩形:? =6/5;实心圆: ? =10/9;薄圆环:? =2。
3)注意:在细长梁中,剪切应变能远小于弯曲应变 能,通常忽略不计。
§10-2 弹性应变能的计算
5.组合变形下的应变能
1)各广义力只在自己相应广义位移上做功,互不相干;
取? =0.3,h/l=0.1,上述比值为0.0312。可见对长梁可不考虑剪
切应变能。
2)求C点挠度:由外力功等于应变能(W=U),并忽略剪切应变能有
W
?
1 2
Ff
C
?
U
弯
?
F 2l3 96 EI
?
f
C
?
Fl 3 48EI
§10-2 弹性应变能的计算
三、非线性固体的应变能
1.应变能 与比能
F 非线性 U*
c)外力总功
W?
?dW ? (?
Fidi
)?01bdb
??
(
1 2
Fid
i
)
d)弹性体中的应变能
U
?W
?
?
(
1 2
Fi
di
)
克拉贝依隆原理:线弹性体应变能等于每一广义外力
与其产生广义位移乘积二分之一的总和。
§10-2 弹性应变能的计算
3)弹性应变能可以表达成外力或位移的唯一表达式, 称为外力的二次齐函数或位移的二次齐函数。
§10-2 弹性应变能的计算
2)弹性应变能
a)等比例加载,使Fi同时由零到终值,则d i也同时由零 到终值;
b)引进参数b (0~1),则有b Fi和与之对应的bd i,给b 一个增量db,则位移有相应的增量dbd i。 外力在位移增量上作的功为
dW ? ? (bFi ? dbFi )?(dbdi ) ? (? Fidi )bdb
? [FN2 ( x)dx]/[2EA( x)] A( x )dx
?
F
2 N
(
x
)
2EA2 ( x)
? ? 2 ? 1??
2E 2
? 1 E? 2
2
§10-2 弹性应变能的计算
2.扭转圆轴
1)应变能
U
?
W
?
1 2
Me?
?
U ? T2l 2GIp
若扭矩或截面直径为变量时
Me ?
?
l
a)分段变化
U
?
n
线性
? 非线性 u*
线性
2.余能与 F1 余比能
?1 U
d
u ?
d1
?1
应变能:线弹性
U
?
W
?
1 2
F1d1
非线性 U ?W ? ?d01 Fdd
比能:线弹性
u?
1?
2
1?1
非线性 u? ?0?1? d?
余能:线弹性
U*?U ?
1 2
F1d1
余比能:线弹性
u*?
u?
1?
2
1?1
非线性
U
*?
?F1 0
一、弹性应变能的一般公式 广义力与广义位移
1.广义力和广义位移
1)广义力泛指力与力矩; 广义位移为广义力所 F1 d1 直接产生的位移和转 角,如力产生位移, 力矩产生转角;
d2 F2
d3 F3
2)线弹性情况下,广义力与 广义位移成线性关系。
2.弹性应变能
1)弹性体中的应变能只决定于外力和位移的最终值, 与加力的次序无关;
?
1 2
M
(
x
)d?
?
1 2
M
(
x
)d?x
M(x)
M(x)
? M 2 ( x)dx
2 EI
2)l 段应变能
dx
U
?
?0ldU
?
?0l
M2(x 2 EI
)dx
§10-2 弹性应变能的计算
4.剪切
1)dx段应变能
dU
?
1(?A)(?d x)? ?
2
2 d xA ??
2G
FQ2dx 2GA
? A
?
2)l 段应变能
