第10章 能量法
《结构力学》习题集及答案(下册)第十章结构弹性稳定计算
第十章 结构弹性稳定计算一、判断题:1、稳定方程即是根据稳定平衡状态建立的平衡方程。
2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。
3、在稳定分析中,有n 个稳定自由度的结构具有n 个临界荷载。
4、两类稳定问题的主要区别是:荷载—位移曲线上是否出现分支点。
5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。
6、能量法确定临界荷载的依据是势能驻值原理。
二、计算题:7、用静力法推导求临界荷载cr P 的稳定方程。
PE I ,l8、写出图示体系失稳时的特征方程。
k lEIk AB P9、求刚架在反对称失稳时的稳定方程。
n 为常数。
l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。
转动刚度kl k r 2=,k 为弹簧刚度。
P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。
已知弹簧刚度l EI k 33= 。
PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。
PEI l13、用静力法求图示结构的临界荷载cr P ,欲使B 铰不发生水平移动,求弹性支承的最小刚度k 值。
PlEI A Bk14、用静力法确定图示具有下端固定铰,上端滑动支承压杆的临界荷载crP。
P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。
设失稳时两柱的变形曲线均为余弦曲线:yxh=-δπ(cos).12提示:cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。
PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆,AB段失稳时变形曲线设为:()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。
l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ,设变形曲线为正弦曲线。
第10章 杆件稳定性
a
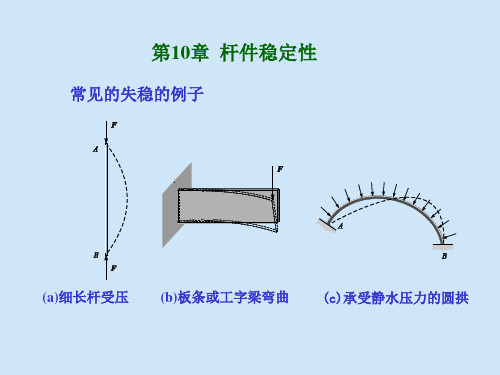
II (大 挠 度 理 论) II (小 挠 度 理 论)
Fcr
B I (稳 定)
D'
O
a)
b)
第10章
两条平衡路径Ⅰ 的交点为分支点 分支点 B 将 分支点。 两条平衡路径 Ⅰ和 Ⅱ 的交点为 分支点 。
10.1 稳定性概念
原始的平衡路径Ⅰ分为两段:前段 OB 上的点属于稳定 原始的平衡路径Ⅰ 分为两段: 平衡, 上的点属于不稳定平衡。 平衡 , 而后段 BC 上的点属于不稳定平衡 。 具有这种特 征的失稳形式称为分支点失稳形式。 征的失稳形式称为 分支点失稳形式。 分支点失稳形式
θ
例10.2
第10章
考虑如图(a)的单自由度非完善体 考虑如图(a)的单自由度非完善体 (a)
F k
B B'
系,刚性杆AB有初倾角 ε 。 刚性杆 有初倾角
k
10.1 稳定性概念
l
l
A
A
(a) )
(b) )
解:在图(b)中,平衡条件(水平方向)为 在图(b)中 平衡条件(水平方向) (b)
F tan(θ + ε ) − kl[sin(θ + ε ) − sin ε ] = 0 sin ε F = kl cos(θ + ε )[1 − ] sin(θ + ε )
第10章
例10.5
10.1 稳定性概念
如图所示, 如图所示,由三根相同的刚性杆组
成的系统,一端作用外力 ,铰结处B、 都是弹性 成的系统,一端作用外力F,铰结处 、C都是弹性 系数为k的弹性支座。试用两种方法求临界载荷。 系数为 的弹性支座。试用两种方法求临界载荷。 的弹性支座
第10章 结构动力计算基础

m
1
k
k
k
根据功的互等定理,有:
11 k
1 k
二、自由振动微分方程的解
2 y 单自由度体系自由振动微分方程写为: y 0
(10-2)
二阶齐次线性常微分方程 式中: 其通解为: 当初始条件
2
k 1 m m
y(t ) C1 sin t C 2 cost
t 简谐荷载(按正余弦规律变化) 一般周期荷载
t
(2)非周期荷载 冲击荷载:在很短时间内,荷载值急剧增大或减小,如各种爆炸荷载、 打桩机的锤头对桩柱的冲击等。
突加荷载:突然施加在结构上并保持不变的荷载,如施工中吊起重物的 卷扬机突然开动时施加于钢丝绳上的荷载。
P(t) P
P(t)
P(t)
P tr t
四、自由振动和强迫振动
自由振动:结构在没有动荷载作用时,由初速度、初位移所引起的 振动。研究结构的自由振动,可得到结构的自振频率、 振型和阻尼参数。 强迫振动:结构在动荷载作用下产生的振动。研究结构的强迫振 动,可得到结构的动力反应。
五、动力计算中体系的自由度
1.动力自由度的定义 动力问题的基本特征是需要考虑惯性力,根据达朗伯原理,惯性力 与质量和加速度有关,这就要求分析质量分布和质量位移,所以, 动力学一般将质量位移作为基本未知量。 确定体系运动过程中任一时刻全部质量位臵所需的独立几何参数 数目,称为体系的动力自由度。
§10.1 动力计算的特点和动力自由度
一、动力荷载的概念及分类 1.动力荷载与静力荷载 是指大小、方向和作用位臵不随时间变化或变化 很小的荷载。这类荷载对结构产生的惯性力较小 因而可以忽略不计,由它所引起的内力和变形都 是确定的。
材料力学重点

吉林大学材料力学考试大纲
(此为总括版,详细版可以加QQ809856869,希望对要考吉大的师弟师妹有帮助)
要考的章数为1-14章。
第3章第9节不考弹簧应力和变形不考。
第4章第6节叠加法做弯矩图不考。
第5章第5节弯曲理论对某些问题的扩充不考。
第6章叠加法求弯曲变形不考。
第7章第10节莫尔强度理论和双剪理论不考。
第9章不考。
第10章第3节不考虚功原理不考。
第12章第5节不考。
第13章8节不考弯曲组合构件交变力计算知道公式推算不必计算。
第14章5、6、7节不考。
考试重点
一:画内力图(轴力•剪力•弯矩)
二:组合变形(拉•扭)静不
定
三:压杆稳定,弯曲应力
四:应力状态•强度稳定
五:能量法•求位移,变形
六:冲击,动载荷
七:疲劳
八:求变形能(10章能量法)(非必考)(拉分题)(变形能基本公式推倒)九:推倒公式(拉分题)
十:广义胡克定律
注:考试重点内容考的机率很大。
另外除了考试重点和不考范围之外的内容也要看,只是考的机率没那么大,但并非不考。
材料力学第十章杆件计算的能量法

T
T
A
T
l
o
B
3.梁弯曲时的应变能
3.1 纯弯曲梁
l Ml
M
EI
W
1 2
M e
Vε
W
1 2
M
e
M 2l 2EI
M
l
3.2 剪切弯曲梁
弯矩M:
dVε M
M (x)2 dx 2EI
M (x)2 dx
Vε M l 2EI
剪力FQ:
6FQ
h2 (
y2)
0 2EI
l
2EI
FA
4
F2 A
l
3
F
l2 3
5FA Fl3
3EI 6EI 6EI
3.位移
Δ A
Vε FA
0
FA
5 16
F
例 求如图所示简支梁截面A的转角,设梁EI的为常数。
Mo A
M B
l
解:为了求A截面的转角A,可在A端加一虚力偶M0,如
图所示。则按卡氏第二定理,A截面的转角:
§10-2 杆件的弹性应变能
一、杆在基本变形下的应变能
1.杆在轴向拉伸(压缩)时的应变能
F
F
A
l l1
Vε
1 2
FN l
FN2l 2EA
dF F1 F
o
d(△l) △l1
B △l
2.圆杆扭转时的应变能
W 1 T
2
Mx T
M xl
GIP
材料力学习题

材料力学作业册学院:专业:年级:班级:学号:姓名:前言本作业题册是为适应当前我校教学特色而统一筛选出来的题集,入选题目共计72个,教师可根据学时情况有选择性的布置作业。
本题册中列出的题目仅是学习课程的最基本的作业要求,老师根据情况可适当增加部分作业,部分学生如果有考研或者其他方面更高的学习要求,请继续训练其他题目。
本题册仅用于学生课程训练之练习,任何人不得将其用于商业目的,违者将追究其法律责任。
由于时间仓促,并限于编者水平有限,缺点和错误在所难免,恳请大家提出修改建议。
王钦亭wangqt@ 2013年2月27日目录第一章绪论 (1)第二章拉伸与压缩 (2)第三章扭转 (7)第四章弯曲应力 (11)第五章弯曲变形 (18)第六章简单超静定问题 (20)第七章应力状态与强度理论 (25)第八章组合变形与连接件计算 (32)第九章压杆稳定 (36)第十章能量法 (41)第十一章动荷载.交变应力 (49)附录I 截面的几何性质 (53)第一章绪论1-1 材料力学的中所讲的构件失效是指哪三方面的失效?1-2 可变形固体的基本假设有哪些?1-3 材料力学中研究的“杆”,有什么样的几何特征?1-4 材料力学中,杆件的基本变形有哪些?第二章 拉伸与压缩2-1(SXFV5-2-1)试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
2-2(SXFV5-2-2)一打入地基内的木桩如图所示,沿杆轴单位长度的摩擦力为2f kx (k 为常数),试作木桩的轴力图。
A2-3(SXFV5-2-3)石砌桥墩的墩身高=10 m l ,其横截面尺寸如图所示。
荷载 1 000 kN F =,材料的密度33=2.3510 kg/m ρ⨯。
试求墩身底部横截面上的压应力。
2-4(SXFV5-2-6)一木桩受力如图所示。
柱的横截面为边长200 mm 的正方形,材料可认为符合胡克定律,其纵向弹性模量10 GPa E =。
如不计柱的自重,试求: (1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4)柱端A 的位移。
能量法

第十章能量法承载的构件或结构发生变形时,加力点的位置都要发生变化,从而使载荷位能减少。
如果不考虑加载过程中其他形式的能量损耗,根据机械能守恒定律,减少了的载荷位能将全部转变为应变能储存于构件或结构内。
据此,通过计算构件或结构的应变能,可以确定构件或结构加力点处沿加力方向的位移。
但是,机械能守恒定律难以确定构件或结构上任意点沿任意方向的位移,也不能确定构件或结构上各点的位移函数。
应用更广泛的能量方法,不仅可以确定构件或结构上加力点处沿加力方向的位移,而且可以确定构件或结构上任意点沿任意方向的位移;不仅可以确定特定点的位移,而且可以确定梁的位移函数。
本章介绍的是:用应变能的概念,根据能量守恒原理来解决与弹性结构或构件变形有关问题的一般方法,这种方法称为能量法。
能量法既可用于计算构件或结构位移;也可用以解决静不定问题及其它一些问题;本章只讨论用能量方法计算位移。
§10.1 杆件的应变能计算前面我们曾讨论过拉伸(压缩)、扭转或弯曲时的变形计算。
但是在工程上还常遇到比较复杂的结构,例如图10-1中所示的桁架、刚架——是指由直杆组成的具有刚性结点的结构、拱——是指杆轴为曲线而且在铅垂载荷作用下会产生水平支座反力的结构等。
在计算这些结构上某一点或某一截面的位移时,能量法是比较简单的方法。
通过拉伸(压缩)、扭转、弯曲时的应变能分析,可见:杆件在受力变形后,都储藏有应变能。
若不计杆件变形过程中少量的热能等损失,则杆件能量守恒,外力在弹性体变形过程中所作的功W应等于杆件内储藏的应变能Vε,即Vε=W。
在第七章我们曾经分别得到等截面杆各横截面上的内力为常量时,拉伸(压缩)、扭转、弯曲(参看图10-2)时的应变能表达式如下拉伸(压缩)时2122NPF lV F lEAε=∆=此处F N=F P(10-1)圆轴扭转时 2122x P PM l V M GI εϕ== 此处M x =M P (10-2)平面弯曲时 2122P M lV M EIεθ== 此处M =M P (10-3)综合以上三个表达式中外力表达的部分,可以把应变能概括地写为12V W F εδ==(10-4) 式中 F ——在拉伸(压缩)时表示拉力(压力),在扭转或弯曲时表示集中力偶,所以此处F 称为广义力;δ——在广义力作用处与广义力F 相应的位移,称为广义位移,在拉伸(压缩)时它是与拉力(压力)相应的位移l ∆,在扭转时它是与扭转力偶矩相应的转角φ,在平面弯曲时它是与弯曲力偶矩相应的截面转角θ(如图2所示)。
第10章 能量法

EI L x
2
P A O
U =
∫
[M n ( x)]
L
2 EI
P 2 L2 dx = 6 EI
∂U PL3 = ③求位移 δ A = ∂P 3EI
例5(续): 求 A点的转角 解: ①求弯矩 M n ( x) = −(M 0 + Px) ②求变形能
U =
EI L x
P A O
N1 = N 2 cos α = Pctgα , N 2 =
对每个杆内能
2 2
P sin α
2
L
A N1 α
2
P
U =∫
L
[ N ( x)] dx + [ M T ( x)] dx + [ M n ( x)] dx = N
2 EA
∫
L
2GI p
∫
L
2 EI
L 2 EA
C
对整个杆系内能 N 12 l1 N 22 l 2 1 U = + = W = P yc 2 E A1 2 E A2 2 1 ( Pctg α ) 2 l1 l2 P 2 Py c = + ( ) 2 2 EA 1 2 EA 2 sin α
δ1 δi δn
δ2
Fi
Fn
1 n U = ∑ Fiδ i 2 i =1
二. 互等定理
1.功互等定理 Fi δ′ = Fjδ′ji ij
i 力在 j 力引起的位移δ’ij上 做的功等于j 力在 i 力引起 的位移δ’ji上做的功。
Fi
δ i′
i
0 Fj j
δ i′
i Fi
0
δ ij ′
δ j′
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 能量法10-1 图示桁架,已知各杆的EA 相等,试求在载荷F 作用下桁架的应变能。
解:1.支反力∑=0x F :0=-Ax F F F F Ax =∑=0B M :02=⨯-⨯l F l F Ay ,2F F Ay =∑=0y F :0=-By Ay F F ,2F F By = 2.各杆的轴力由结点A 的平衡可求得 2N FF AC =,2N F F AD =由结点B 的平衡可求得2N F F BC -=,2N F F BD = 由结点D 的平衡可求得 0N =CD F3.桁架的应变能[]()EAl F l l F l F l F l F EA l F l F l F l F l F EAEA l F U CDCD BD BD AD AD BC BC AC AC ii 4122 022222221 21 2222222N 2N 2N 2N 2N 2N +=⎥⎥⎦⎤⎢⎢⎣⎡⨯+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎪⎭⎫ ⎝⎛-+⨯⎪⎪⎭⎫ ⎝⎛=++++==∑10-2 图示传动轴,已知轴的直径m m 40=d ,材料的弹性模量GPa 210=E ,切变模量GPa 80=G 。
试求轴的应变能。
解:4444p cm 8cm 32432πππ=⨯==d I 4p cm 42π==I I作用在轮上的合力为:kN 06.1kN 36.0122=+=F()()m N m 4.02.0 4.0530m2.00 035⋅⎩⎨⎧≤≤-≤≤=x x x x x M ()m N m 4.02.0 80m2.00 0⋅⎩⎨⎧<<<≤=x x x T ()()m m N 8.31m N 108108022.04.080 d 80212d 892.40 .20 2p p2⋅=⋅⨯⨯⨯⨯-⨯===-⎰⎰πxGI GI x x T U l T()()m mN 4.28m N 1041021032.0530 d 53012d 8932.20 02 2⋅=⋅⨯⨯⨯⨯===-⎰⎰πx x EI EI x x M U l M∴ 轴的应变能:m m N 2.60⋅=+=T M U U U10-3 图示桁架,各杆的EA 相等。
试求结点C 的水平位移和垂解:用单位载荷法求解。
如图所示,在结点C 分别沿水平和垂直方向杆件杆长i l 由F 、所引起的轴力i F N 由单位水平力所引起的轴力i F N 由单位竖直力所引起的轴力i F N ' AB l F 2-0 0 BC lF 0CD l F1-1-AD l0 ACl 2 F 2- 2结点C 处的水平位移:()22151N N EAFlEA l F F i i i i CH +==∑=δ 垂直位移:)( 51NN ↑='=∑=EAFl EA l F F i i i i CV δEI 为常数)。
解:用卡氏定理求解1.求截面B 的挠度,在截面B 作用零值附加力s F当0≤x ≤a ,()()()x l F x a q x M ----=s 22,()()x l F x M --=∂∂s 当a ≤x ≤l ,()()x l F x M --=s , ()()x l F x M --=∂∂s()()()EIa l qa dx x l x a EI q x F x M x M EI F U y a l F F B 244)()(2 d 1302 0 0s 0s ss -=--=⎥⎦⎤⎢⎣⎡∂∂=⎪⎪⎭⎫ ⎝⎛∂∂=⎰⎰==2.求截面B 的转角,在截面B 作用零值附加力偶es M当0≤x ≤a ,()()es 22M x a q x M ---=,()1es -=∂∂M x M当a ≤x ≤l ,()es M x M -=,()1es-=∂∂M x M ()()EI qa x M x M x M EI M U l M M B 6d 130 0es 0es es es =⎥⎦⎤⎢⎣⎡∂∂=⎪⎪⎭⎫ ⎝⎛∂∂=⎰==θEI解:用单位载荷法求解如图所示,在截面A 处分别作用一水平方向单位力、铅垂方向单位力和一顺时针方向单位力偶,并分别求出由荷载F 以及单位力和单位力偶所引起的内力,列表计算如下:杆段 由载荷F 所引起的弯矩()i x M 由水平单位力所引起的弯矩()i x M 1 由铅垂单位力所引起的弯矩()i x M 2 由单位力偶所引起的弯矩()i x M 3 AB 1Fx - 01x - 1- BCFl -2x -l -1-截面A 的水平位移: 2d 120 22EIFlhx Flx EI hAH ==⎰δ 截面A 的竖直位移:() 33d d 12 0 0 22121EI h l Fl x Fl x Fx EI l h AV+=⎥⎦⎤⎢⎣⎡+=⎰⎰δ截面A 转 角:()EIh l Fl x Fl x Fx EI l h A 22d d 1 0 0 211+=⎥⎦⎤⎢⎣⎡+=⎰⎰θEI 相等。
试求截面A 和B 的位移。
解:用单位载荷法求解 在A 、B 点分别作用一铅垂方向与水平方向的单位力,如图所示,并分别求出由荷载q 以及单位力所引起的内力,列表计算如下:杆段 由q 所引起的弯矩()i x M由A 竖直单位力所引起的弯矩()i x M 由B 水平单位力所引起的弯矩()i x M 'DE 01x DA 22222qx qlx - 22x h利用对称性截面A 的竖铅垂位移:)( 3845d 222242 0 22222↓=⎪⎪⎭⎫ ⎝⎛-=⎰EI ql x x qx qlx EI l AV δ 截面B 的水平位移:)( 12d 22232 0 2222→=⎪⎪⎭⎫ ⎝⎛-=⎰EI h ql x h qx qlx EI l BH δ截面A 的水平位移:)( 24213→==EIh ql BH AH δδ10-7 图示刚架,各杆的EI 相等。
试求在一对力F 的作用下截面A 和B 之间的相对位移和相对转角。
解:用单位载荷法求解由于结构和载荷的对称性,取刚架对称轴的一侧来求解AB δ和AB θ在A 截面分别作用一水平单位力和一单位力偶,如图所示,列表计算如下:杆段 由载荷F 所引起的弯矩()i x M由水平单位力所引起的弯矩()i x M 由单位力偶所引起的弯矩()i x M 'AC 1Fx - 1x - -1 CEFh -h --1A 、B 两点之间的相对位移:⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+==⎰⎰a h EI Fh x Fh x Fx EI h aA AB 32d d 222 020 22121δδ A 、B 两截面的相对转角:()a h EI Fh x Fh x Fx EI h a A AB +=⎪⎪⎭⎫ ⎝⎛+==⎰⎰ 0 2 0 211d d 22θθ10-8 图示细圆环,平均半径为R ,抗弯刚度为EI ,在切口处嵌解:在块体嵌入后,块体与切口截面之间产生水平作用力F ,两切口截面之间产生水平相对位移e 任意一θ截面的弯矩为 ()()θθcos 1-=FR M()()θθcos 1-=∂∂R FM 根据卡氏定理切口处两截面之间的水平相对位移()()()EIFR EI FR s F M EI M e l 320 3 3d cos 12d πθθθθπ=-=∂∂=⎰⎰由此可求得33ReEIF π= ∴ ()2max 322ReEI FR M M ππ===10-9 图示外伸梁,抗弯刚度为EI 。
不计弯曲剪力的影响,试用图乘法求自由端A 的挠度和支座C 截面的转角。
解:用叠加法作梁在F 和q 共同作用下的M 图,并作梁仅在A 、C 处分别作用一竖直单位力和一单位力偶时的的M 和'M 图,如图所示。
由图乘法求得()()()⎪⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-⨯⨯⨯+⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯-⨯+⎪⎭⎫ ⎝⎛-⨯⨯-⨯=++=832832 3221322111323222332211l l a a EI qa a l ql a l qa a a qa EI M M M EI y C C C A ωωω()()()EI l a ql l ql l qa EI M M EIC C C 2442183231211 122223322-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯⨯+⎪⎭⎫ ⎝⎛-⨯⨯-⨯=+=ωωθ10-10 试求图示超静定梁的支反力。
设固定端沿梁轴线的反力可以忽略。
解:为二次超静定问题。
由对称性可得:2qlF F By Ay ==,B A M M = 化为一次超静定问题。
以A M 为多余约束,取静定基如图所示()AAAy Mx lx q M qx x F x M --=--=)(22122()1-=∂∂A M x M 由卡氏定理()()0121 d )(21d 130 2=⎪⎪⎭⎫ ⎝⎛--=⎥⎦⎤⎢⎣⎡---=∂∂=⎰⎰A ll A A M ql EI x M x lx qEIx x x M x M EIθ可得:122ql M A =10-11解:为一次超静定问题。
1.用卡氏定理求多余约束力,以C 截面处的约束为多余约束AB 段:()11x F x M C =,()11x F x M C =∂∂ BC 段:()22Fx a F x M C -=,()a F x M C =∂∂2 由卡氏定理()()()()()0234 d d 1 d d 3 0 22 0 121 0222 0111=⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡-+=∂∂+∂∂=∂∂=⎰⎰⎰⎰F F EI a x a Fx a F x x F EI x F x M EIx Mx F x M EIx M F U y C a C a C a Ca CCC可求得:83F F C =2.作刚架的内力图10-12 图示杆系,各杆的EA 相等。
试用力法求各杆的内力。
(a)(d )解:为一次超静定问题。
1. 求多余约束力以C 处约束为多余约束,得到静定基,如图(b)所示,力法正则方程为0111=∆+F C F δ分别求出静定基在F 作用下(图(c ))在单位力作用下(图(d ))各杆的内力i F N 和i F N ,列表计算如下(根据对称性,32N N F F =)i i N i N ① l1 ②③αcos l αcos 2Fαcos 21-α331N N 1cos 2EA FlEA l F F i i i i F -==∆∑= ⎪⎭⎫⎝⎛+==∑=1cos 21331N N 11αδEA l EA l F F i i i i ∴ αδ3111cos 21+=∆-=FF F C2. 求各杆的内力α31N cos 21+==FF F C取结点D 为研究对象(图(a ))0=∑yF: 0cos 22N 1N =-+F F F α由此求得ααα321N 2N cos 21cos cos 2+=-=F F F F10-13 图示结构,AB 梁和梁CD 的抗弯刚度均为26m N 1024⋅⨯=EI ,2mm =a 。
