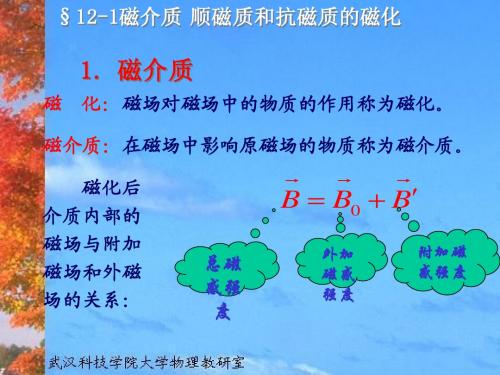
磁介质
磁介质及其分类

4
第15章 物质的磁性
3) 原子核的磁矩
整个原子核的自旋磁矩
r Pg
e
r I
2mp
r I
为核的自旋角动量, 因子g由原子核决定。
由上可知,核磁矩远小于电子磁矩。
4) 分子磁矩和分子电流
I分
电子轨道磁矩
电子自旋磁矩
分子磁矩
r P分
等效
S分 r P分
分子电流I分
原子核的磁矩
5
第15章 物质的磁性
2. 磁介质的磁化
rr
B r B0
μr ─相对磁导率
rr r B B0 B
B0 B
I0
长直密绕螺线管
▲ 弱磁质, r 1
•顺磁质
r 1
如:Mn ,Al,O2,N2 ,…
g,Cl2,H2, …
▲ 铁磁质 r 1 如:Fe,Co,Ni, …
2
第15章 物质的磁性
二、 磁介质的磁化
第 i 个电子受的磁力矩 rr r Mi Pm,i B0
电子轨道磁矩受磁力矩方向垂直纸面向内
r
Mi
r
电子轨道角动量增量
rr
r
Li
d Li Mi dt Li
轨道角动量绕磁场旋进
∴ 电子旋进,它引起的感应
r
r
r
磁矩 Δ Pm,i 反平行于 B0
Pm,i
这种效应在顺磁质中也有,不过与分
子固有磁矩的转向效应相比弱得多。
电子轨道半径不变
当外场方向与原子磁矩反方向时
f Pm (Pm )
7
第15章 物质的磁性
B0
Pm
o
r
e
f
Pm
v
磁介质(Magnetic materials)

1/ 2
于顺外场的增加。 在(i)、(ii)两种情形,电子都获得一个逆外场方向的诱导磁矩(induced 101
5.1 磁化(Magnetization) moment), 用到式(5.2),有 e e minduced = L= ⋅m r 2 。 2 me 2 me e L 将 L 的表达式代入,得到诱导磁矩的矢量式为 e2 r2 m induced =− B (5.6) 4 me 原子序数为 Z 的原子有 Z 个电子,其轨道半径各不相同,相对于外场 的倾角也各不相同。取平均值,得到每个原子的有效(effective)诱导磁 矩为 e2 m =− Zr 2 B (5.7) 6 me 0 物质的磁化强度(magnetization)为 Ne2 2 M =− Zr B (5.8) 6 me 0
•
•
•
磁化强度(magnetization): 设物质中的原子在外磁场中磁化后的磁矩为 m。对大量原子的磁矩取平均, 其平均值记为 m 。 定义:磁化强度为单位体积中的原子磁矩的矢量和。 M = N m 。 (5.1) 其中,N 为单位体积中的原子数。磁化强度是描述物质磁化性质的量。
5.1.5 抗磁性(Diamagnetism)
•
原子在外场中的诱导磁矩(induced magnetic moments):
•
电子的固有角速度(angular velocity): 设电子在半径 r 的圆轨道以角速度 0 运动。向心加速度为 2 0r , 2 2 向心力为 Ze / 4 0 r ,故有 2 2 2 m e 0 r = Ze / 4 0 r 从而有 Ze2 0= 4 0 me r 3
104
第五章 磁介质(Magnetic materials) 向减少,合成效果为向下的净磁化电流(net magnetic current)。如 Figure 5.8 所示。 如 Figure 5.9, 在磁化体中取一个体积元 = x y z , 其中心点的坐标为 (x, y, z)。类似于螺线管中介质的 M 与 I 的关系 I M = M ,磁化强度矢量 M 的 x, y, z 分量,分别对应于环绕电流 I1, I2, I3。即,将积元 中磁偶极矩 矢量 M , 分解为 x, y, z 分量,与环绕电流 I1, I2, I3 的对应关系分别为 I 1 y z =M x 即 I 1= M x x . (5.16a) 同理,有 I 2= M y y , (5.16b) I 3= M z z . (5.16c) 合成的磁化电流密度 jM,其 z 分量由 I1,I2 贡献而得。如果 I2 沿 x 轴方向变
磁介质

µ = µ0 µr叫磁介质的磁导率。 H 叫磁场强度。 叫磁介质的磁导率。 叫磁场强度。
的环路积分: 考虑 H 的环路积分
H ⋅ dl = ∫ ∫
L
B
µ0 µ r L
⋅ dl =
1
µ0
∫µ
L
B
r
⋅ dl
=
1
µ0
∫B
L
0
⋅ dl = I 0,int
∫ H ⋅ dl = I
L
0 ,int
H 的环路定理
B = B0 + B′ > B0
µr > 1
磁化电流 Is 可产生附加磁场,但无热效应,因为 可产生附加磁场,但无热效应, 无宏观电荷的移动,磁化电流束缚在介质表面上, 无宏观电荷的移动,磁化电流束缚在介质表面上,不 可引出,因此,磁化电流也称为束缚电流 束缚电流。 可引出,因此,磁化电流也称为束缚电流。
µ 当磁介质为铁磁质时, 当磁介质为铁磁质时, r
j' = (µr −1)nI
管内磁场基本上由束缚电流产生, 管内磁场基本上由束缚电流产生,这时的自由电流 往往被叫做励磁电流 励磁电流。 往往被叫做励磁电流。
3.磁场强度矢量及其环路定理。 3.磁场强度矢量及其环路定理。 磁场强度矢量及其环路定理 在真空中的安培环路定理中: 在真空中的安培环路定理中:
2)抗磁质的磁化机制 对抗磁介质来说,无外磁场时, 对抗磁介质来说,无外磁场时, 各电子的磁矩矢量和为 0,分子磁 分子不显磁性。 矩 分子不显磁性。 ∑ m,= 0
B0
ω
v
f核
fL
i
加外磁场后,电子受的向心力 加外磁场后, 为核力和洛仑兹力的叠加, 为核力和洛仑兹力的叠加,
磁介质
B=B+(ralative8以电子的轨道运动为例,第i 个电子受的磁力矩B m M i i v vv ×=电子轨道角动量增量ii i L t M L v v v ⊥=d d ∴电子旋进,它引起的感应磁矩反平行于。
i m Δv0B v 这种效应在顺磁质中也有,不过与分子固有磁矩的转向效应相比弱得多。
m im i11由于介质磁化而出现的一些等效的附加电流分布。
2. 磁化电流如上图,磁介质均匀被磁化,内部各点处的分子电流会相互抵消;表面上的小分子电流没有抵消,它们方向相同,等效为表面上有一层面束缚电流。
Si m v v=分子以顺磁质为例:由于分子的热运动,每个磁极子的取向不断在变化,但从统计平均的角度,每个磁极子对磁化强度的贡献是一样的, 将这个贡献等效为一分子磁矩,设分子m vM v在磁场中发生磁化,磁化强度MSNΔP m分m r ΔiS Ni分m r 顺磁质抗磁质2rS S i m π=v v 图示为顺磁质情形Mnm VM Vm n VMmM V V V ˆΔˆΔlim limΔ)ˆ(lim0ΔΔ0Δ分分分====→→→∑v14现为面束缚电流。
磁化n rM rt M r lrd SI ′d θ与电介质极化电荷面密度nP ˆ⋅v设:二、环路定理的应用举例[例1]书P171:无限长直螺线管充以磁介质[例2]书P172: 长同轴电缆充以磁介质19SΔS ΔSS Δ<<Δ侧lΔlΔ<<δ(2(当tg tg 211=θμμθ23* 静磁屏蔽铁磁材料的闭合壳体置于外磁场中,壳内口腔中磁感应强度大大削弱的现象。
应用:精密探头、显象管…都需要磁屏蔽。
*铁磁质具有把磁感应线聚集于自己内部的特性(磁感应线沿铁走)部分磁屏蔽25§19.4 铁磁质(ferromagnetic substance)一、磁畴(magnetic domain )自发磁化的小区域─磁畴实验研究表明:铁磁质内部存在一个个小区域,小区域内,分子磁矩有序排列(自发磁化)。
磁场中磁介质

磁介质的分类
顺磁性介质
抗磁性介质
铁磁性介质
反铁磁性介质
在磁场中容易被磁化的 物质,如铝、铂等。
在磁场中不容易被磁化 的物质,如铜、金等。
在磁场中极易被磁化的 物质,如铁、钴、镍等。
在磁场中具有反铁磁性 的物质,如锰、铬等。
02
磁场对磁介质的影响
磁场对磁介质的作用
磁化现象
磁场对磁介质产生作用,使其内 部磁矩定向排列,形成磁化现象。
剩余磁化强度
当磁场去除后,磁介质仍会保留一部分磁化强度, 称为剩余磁化强度。
磁介质的磁导率
相对磁导率
描述磁介质在磁场中的导磁能力与真空导磁能 力的比值。
最大磁导率
在一定磁场强度下,磁介质的磁导率达到最大 值。
温度系数
表示磁导率随温度变化的系数,某些材料的温度系数较大,对温度变化较为敏 感。
03
磁介质的性质与特点
磁滞现象
磁介质在磁化过程中会出现滞后现 象,即当磁场反向时,磁介质的磁 化强度不会立即消失,而是逐渐减 小。
磁损耗
在交变磁场中,磁介质会因为磁滞 现象和涡流效应产生能量损耗。
磁介质的磁化过程
起始磁化
磁介质在磁场中开始被磁化的过程,起始磁化曲 线通常是非线性的。
磁饱和
随着磁场强度的增加,磁介质的磁化强度逐渐达 到饱和状态,此时磁导率不再变化。
3
磁滞损耗
由于磁滞现象产生的能量损耗,通常表现为热量。
磁介质的损耗特性
介电损耗
01
由于电场作用在磁介质上产生的能量损耗,通常表现为热量。
涡流损耗
02
由于磁场变化产生的涡旋电流在磁介质中产生的能量损耗,通
常表现为热量。
磁介质

Ze2 2 e rB m r 2 4 0 r
v
' m
同向时
当B不太大时,
0 , 0 20
2 2
eB 由此解得 2m
当 // B 时,也可以得到上述表达式
即 的方向总是与外磁场 B的方向相同。
0 B H M
M ) dl I
L
0
0 S ( 0 E P ) dS q S D 0E P
S
0
L H dl I
L
D dS e dV
S V
B , H , M 之间的关系
(4)超导体
r 0
B0
1933年,迈斯纳和奥克森菲尔德两位科学家发现,如果把超 导体放在磁场中冷却,则在材料电阻消失的同时,磁感应线将 从超导体中排出,不能通过超导体,这种现象称为抗磁性。
由于 r 与1相差甚微,为使用方便,故引入磁介 质的磁化率 m
r 1 m
r 1 e
L
B dl 0 I 0 I s
L L
磁介质中的 安培环路定理
电介质中的 高斯定理
L B dl 0 I 0 L M dl
L ( B
L
1 ' S E dS (q qi ) 0 S 1 1 S E dS q S P dS
Is
I0
Is——磁化电流 js——沿轴线单位长度上的磁 化电流(磁化面电流密度)
3、磁化强度和磁化电流密度之间的关系:
以长直螺线管中的圆柱形磁介质来说明它们的关系。
第十二章 磁介质
B B0 顺磁质(锰、铬、铂、氧、氮等)
B B0 抗磁质(铜、铋、硫、氢、银等)
B B0 铁磁质(铁、钴、镍等)
在介质均匀充满 磁场的情况下
定义
r
B B0
r
1 1 1
顺磁质 抗磁质 铁磁质
相对 磁导率
2. 分子电流和分子磁矩
分子电流:把分子或原子看作一个整体,分子 或原子中各个电子对外界所产生磁效应的总和,可 用一个等效的圆电流表示,统称为分子电流。 分子磁矩:把分子所具有的磁矩统称为分子磁 矩,用符号 pm 表示。 子中和每个电子相联系的磁矩都受到磁力矩的作用, 由于分子或原子中的电子以一定的角动量作高速转 动,这时,每个电子除了保持环绕原子核的运动和 电子本身的自旋以外,还要附加电子磁矩以外磁场 方向为轴线的转动,称为电子的进动。
或
(
B
0
M ) dl
I
磁介质中的安培环路定理
定义 H
M为磁场强度 0 B ( M ) dl
B
0
I
有磁介质时的 安培环路定理
则
H dl
I
磁介质中的安培环路定理: 磁场强度沿任
意闭合路径的线积分等于穿过该路径的所有传导电 流的代数和,而与磁化电流无关。 表明:磁场强度矢量的环流和传导电流I有关, 而在形式上与磁介质的磁性无关。其单位在国际单 位制中是A/m.
m
§12-2 磁化强度 1. 磁化强度
磁化电流
反映磁介质磁化程度(大小与方向)的物理量。 磁化强度:单位体积内所有分子固有磁矩的 矢量和 p 加上附加磁矩的矢量和 p ,称为磁 化强度,用 M表示。
m m
第15章磁介质

第15章磁介质一、物质的磁化1、磁介质中的磁场设真空中的磁感应强度为的磁场中,放进了某种磁介质,在磁场和磁介质的相互作用下,磁介质产生了附加磁场,这时磁场中任意一点处的磁感应强度2、磁导率由于磁介质产生了附加磁场磁介质中的磁场不再等于原来真空中的磁场,定义和的比值为相对磁导率:介质中的磁导率:式中为真空中的磁导率3、三种磁介质(1)顺磁质:顺磁质产生的与方向相同,且。
略大于1(2)抗磁质:抗磁质产生的与方向相反,且。
略小于1(3)铁磁质:铁磁质产生的与方向相同,且。
远大于1二、磁化强度1、磁化强度定义为单位体积中分子磁矩的矢量和即:2、磁化强度与分子面电流密度的关系:式中为磁介质外法线方向上的单位矢量。
3、磁化强度的环流即磁化强度对闭合回路的线积分等于通过回路所包围面积内的总分子电流三、磁介质中的安培环路定律1、安培环流定律在有磁介质条件下的应用即:2、磁场强度定义为:3、磁介质中的安培环路定律:4、应用磁介质中的安培环路定律的注意点:(1)的环流只与传导电流有关,与介质(或分子电流)无关。
(2)的本身()既有传导电流也与分子电流有关。
既描写了传导电流磁场的性质也描写了介质对磁场的影响。
(3)要应用磁介质中的安培环路定律来计算磁场强度时,传导电流和磁介质的分布都必须具有特殊的对称性。
5、磁介质中的几个参量间的关系:(1)磁化率(2)与的关系(3)与等之间的关系四、磁场的边界条件(界面上无传导电流)ေ、壁介蔨分界面伤边磁感应强度的法向分量连廭,即Ҩ2、磁介谨分界面两龹的磁场强嚦纄切向分量连续,即:Ƞ3 磃感应线的折射定律ā*怎义如图15-1所示)五、铁磁物贩q、磁畴:电子ꇪ旋磁矩取向相同的對区域。
2、磁化曲线(图55-2中曲线)ေ磁导率曲线(图15-2中??曲线)4、磁滞回线ေ图17耩3)图中乺矫끽嚛㠂5、铁磁质与非铁㳁质的主要区别:铁磁物质产生的附加磁场错误!未定义书签。
的比原来真空中的磁场大得多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 磁介质
§1.分子电流观点 (P560习题)
3.附图所示是一根沿轴向均匀磁化的细长永磁棒,磁化强度为M ,求图中标出各点的B 和H 。
解:在磁棒内外,B B B '+=0,M B H -=
μ.
无传导电流,00=B .对细长永磁棒,在两端的4、5、6、7点M B 02
1μ≈
',在中点1,
M B 0μ≈',在棒外的2、3点0='B ,所以
M B 01μ= 032==B B M B B B B 076542
1μ====
注意到在磁棒内M=常数,在磁棒外M=0,根据M B
H -=
μ立即可得:
0321===H H H M H H 2
174== M H H 2
165-
==
4.附图所示是一个带有很窄缝隙的永磁环,磁化强度为M,求图中所标各点的B 和H. 解: 由B B B '+=0, 其中00=B ,因缝隙很窄, M i B B B 00321μμ='='='=' 故 B B B 0
321μ===
由M B
H -=
μ注意到在环内M=常数,在缝隙中M=0, 所以 M H =1,032==H H
§3.介质的磁化规律 (P605习题)
1.一环形铁芯横截面的直径为4.0毫米,环的平均半径R=15毫米,环上密绕着200匝线圈(见附图),当线圈导线通有25毫安的电流时,铁芯的(相对)磁导率300=μ求通过铁芯横截面的磁通量φ. 解: 由S
nI BS 00ημφ
==,其中 3
2
1012.210
5.12200⨯=⨯⨯=
-πn 米1
-,所以
7
6
233710
5.210
44
10251012.2104300----⨯=⨯⨯⨯
⨯⨯⨯⨯⨯⨯=ππφ韦伯
4.一无穷长圆柱形直导线外包一层磁导率为μ的圆筒形磁介质,导线半径为1R ,磁介质的外半径为2R (见附图),导线内有电流I 通过.(1)求介质内、外的磁场强度和磁感应强度的分布,并画r H - 、r B =曲线;(2) 介质内、外表面的束缚面电流密度i ';(3) 从磁荷观点来看,介质表面有无磁荷?
解: (1)在横截面内分别在导线内外取以导线轴线为中心的圆形回路,应用安培环路定理可得
2
7
4
212/R Ir H π=, )(1R r <, r I H π2/=, )(21R r R <<
r I H π2/= )(2R r > 再由
H B 0μμ=可得 21
02/R Ir B πμ= )(1R r < r
I
B πμμ20= )(
21R r R <<
)R (r 2/20>=r I B πμ
(2) 由n M i ⨯=', 在 1R r =处,
n 指向内,
12/)1(R I H x M i m πμ-==='在2R r =处, n 指向外, 22/)1(R I H x M i m πμ-=-=-=' (3)按磁荷观点, n m n
n m H x M J 00μμσ===,在介质内外表面,H 和表面相切,0=n H ,
故 0=m
σ
.
§3.边界条件 磁路定理 (P621习题) 11.证明两磁路并联时的磁阻服从下列公式:
2
1
111m m m
R R R +
=
解:参见附图,设总磁通为0B φ,并联支路的磁通为1B φ和2B φ;并联磁路的磁阻分别为1m R 和
2m R ,总磁阻为m R .按磁路定理:
,11m B m R φε= 22m B m R φε=
,/ 1B1m m R εφ=∴ ,/ 2B2m m R εφ=
又 021B B B φφφ=+
m m B m m R R R /)/ ()/( 02m 1m εφεε==+∴
21/1/1/1m m m R R R +=
12.一电磁铁铁芯的形状如附图所示,线圈的匝为1000,空气隙长度0.2=l 毫米.磁路的、、、c b a 三段长度与截面都相等,,气隙的磁阻比它们每个大30倍,当线圈中有电流I=1.8安培时,气隙中的磁场强度为多少奥斯特?
解: 参看附图,设各支路中的磁通为Ba φ、Bb φ和Bc φ气隙中的磁场强度为H,气隙磁阻为0m R ,磁路总磁阻为m R ,按磁阻串并联的公式
1
2
1
2
2
m R
1
m R
)/()(00m ma mb m ma mb mc m R R R R R R R R ++++= 又 30/0m mc mb ma R R R R === 所以 960/630m m R R = 按磁路定理 m BC R NI φ= (1)
)(0m ma Ba mb Bb R R R +=φφ (2)
又 Bc Bb Ba φφφ=+ (3)
SH Ba 0μφ= (4)
联立(1)-(4)式.解得:
奥斯特
米安3
5
3
3
000
104.5/ 103.410
2638.1103063306330⨯=⨯=⨯⨯⨯⨯=
=
=
⋅
++=
-l
NI SR NI SR NI
R R R R H m m
m mb ma mb
μμ
§5.磁场的能量和能量密度 (P631习题)
2.利用高磁导率的铁磁体,在实验室产生B=5000高斯的磁场并不空难.(1) 求这磁场的能量密度m w ; (2) 要想产生能量密度等于这个值的电场,问电场强度E 的值应为多少? 这在实验上容易作到吗?
解: (1) 按 02
2/2/)(μB H B w m =⋅=
得: 3
572/101)108/(5.0米焦耳⨯=⨯=-πm w
(2) 按 3
520/1012/米焦耳⨯==E w e ε
得: 8
12
5105.110
85.8/102⨯=⨯⨯=-E 伏/米
显然这个场强在实验室中是较难实现的.
6.一根长直导线载有电流I, I 均匀分布在它的横截面上.证明:这导线内部单位长度的磁场能量为:
π
μ162
0I .
证: 因在电流密度均匀分布的长直导线内部
)R I r /(2H
),2/()(2
20ππμ==R Ir B 其中R 为导线的半径,所以 )8/2/)(4
2220R r I H B w m πμ=⋅=, 单位长导线内的总磁能为
π
μπ1622
00
I rdr w W R
m m =
⋅=
⎰
.。
