光电子技术第三版安毓英刘继芳等著习题答案完整版
光电子技术安毓英第五章课后习题参考答案1
5.1以图中p型半导体器件为例，栅极加正电压超过MOS晶体管的开启电压时，在半导体金属界面会形成深度耗尽层，称为电子的势阱。
当有光照时，光生电子会聚集在势阱中，形成电荷存储。
以图中三相CCD结构为例，相邻三个栅极电压从高电平依次降低到低电平，为一个周期。
每个栅极电压降低过程与下一个栅极高电平重合。
这样三个栅极位置的电子势阱会依次减小，消失与出现。
存储电子会随着势阱位置的移动发生转移。
电荷输出：外加放大电路，利用电荷电势进行放大，输出信号CCD输出信号的特点：1.信号电压是在浮置电平基础上的负电压2.每个电荷包的输出占有一定的时间长度3.在输出信号总叠加有复位期间的高电平脉冲根据这些特点，对CCD的输出进行处理时，较多地采用了取样技术，以去除浮置电平，复位高脉冲及抑制噪声。
5.2光电成像系统利用的都是帧扫描方式，完成一帧扫描所需要的时间称为帧时T，单位时间完成的帧数称为帧速 F, 它们的关系是T=1/F5.3(1)F=0.3m(2) W=n*α=128*a/f=128x100um/0.3m=4.26x10-2 rad5.5从目标调制度（对比度）到人眼观察到，总的调制函数为各个调制函数的乘积，光学体统调制传递函数为MTF O, 人眼能感知的极限调制度为0.026，则0.5×MTF O×0.9×0.5×0.95×0.5≥0.026MTF O≥0.245.7(1)像增强器CCD (ICCD)可以探测微光图像，但是其内经过光子-电子的多次转换，图像质量会有损失，光锥中光纤光栅干涉波纹，折断和耦合损失都将使ICCD输出噪声增加，对比度下降，动态范围减小，影响成像质量。
（2）薄型背向CCD器件灵敏度高，噪声低，但当照度低于10-6 lx 时，只能依赖图像增强来提高增益，克服噪音（3）电子轰击型CCD简化了光子多次转换过程，信噪比大大提高，与ICCD相比，电子轰击型CCD具有体积小，重量轻，可靠性高，分辨率高及对比度好等优点。
最新光电子技术(安毓英)习题课后答案
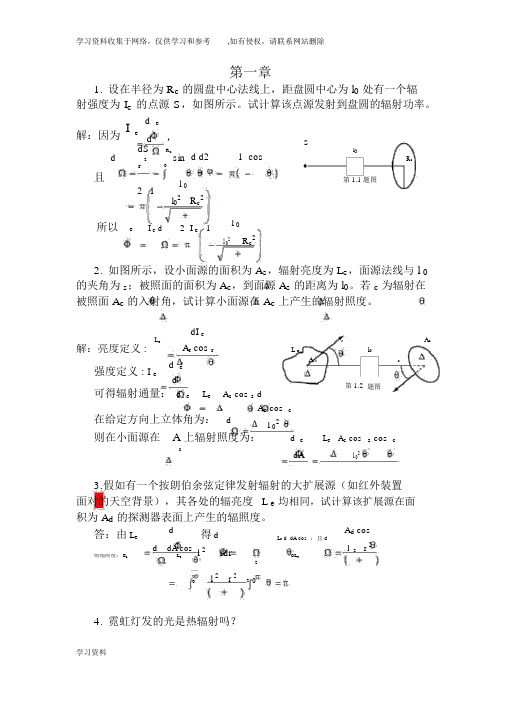
第一章1. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：因为，且()⎪⎪⎭⎫ ⎝⎛+-=-===Ω⎰22000212cos 12sin c R R l l d d rdS d c πθπϕθθ 所以⎪⎪⎭⎫ ⎝⎛+-=Ω=Φ220012c e e e R l lI d I π2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：亮度定义:强度定义:ΩΦ=d d I ee 可得辐射通量：Ω∆=Φd A L d s s e e θcos 在给定方向上立体角为：2cos l A d cc θ∆=Ω 则在小面源在∆A c 上辐射照度为：20cos cos l A L dA d E cs s e e e θθ∆=Φ=ΩΦd d ee I =r r ee A dI L θ∆cos =3.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度L e 均相同，试计算该扩展源在面积为A d 的探测器表面上产生的辐照度。
答：由θcos dA d d L e ΩΦ=得θcos dA d L d e Ω=Φ，且()22cos rl A d d +=Ωθ 则辐照度：()e e e L d rlrdrl L E πθπ=+=⎰⎰∞20022224. 霓虹灯发的光是热辐射吗？不是热辐射。
霓虹灯发的光是电致发光，在两端放置有电极的真空充入氖或氩等惰性气体，当两极间的电压增加到一定数值时，气体中的原子或离子受到被电场加速的电子的轰击，使原子中的电子受到激发。
当它由激发状态回复到正常状态会发光，这一过程称为电致发光过程。
光电子技术第三版安毓英刘继芳等著习题答案完整版
学习资料收集于网络，仅供学习和参考 ,如有侵权，请联系网站删除第一章1. 设在半径为 R c 的圆盘中心法线上，距盘圆中心为 l 0 处有一个辐射强度为 I e 的点源 S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：因为 Ie d ed，SdSR c d d21 cosl 0d2sin R cr且l 0第 1.1 题图2 1l 02R c 2所以 eI e d2 I e 1l 0R c 2l 022. 如图所示，设小面源的面积为 A s ，辐射亮度为 L e ，面源法线与 l 0 的夹角为 s ；被照面的面积为 A c ，到面源 A s 的距离为 l 0。
若 c 为辐射在被照面 A c 的入射角，试计算小面源在 A c 上产生的辐射照度。
dI e L e A r cos rsA c解：亮度定义 :L el 0强度定义 : I ed e A scd第 1.2 题图可得辐射通量： d e L e A s cos s d在给定方向上立体角为： A c cos cdl 02则在小面源在 A 上辐射照度为：d eL e A s cos s cos ccdAl 023.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度 L e 均相同，试计算该扩展源在面 积为 A d 的探测器表面上产生的辐照度。
答：由 L ed得 dA d cosdA cosL e d dA cos ，且 d2 r 2d l2rdrl 则辐照度： E eL ed L e2l 2 r 22 04. 霓虹灯发的光是热辐射吗？学习资料收集于网络，仅供学习和参考,如有侵权，请联系网站删除不是热辐射。
霓虹灯发的光是电致发光，在两端放置有电极的真空充入氖或氩等惰性气体，当两极间的电压增加到一定数值时，气体中的原子或离子受到被电场加速的电子的轰击，使原子中的电子受到激发。
当它由激发状态回复到正常状态会发光，这一过程称为电致发光过程。
〖电工电子技术〗(第三版) 高等教育出版社习题解答
〖电工电子技术〗（第三版）主编刘蕴陶习题解答（仅供参考）2 0 1 4 . 8习 题 一1-1电流I 1、I 2实际方向与图示参考方向一致I 3实际方向与图示参考方向相反电压U 1、U 2、U 3实际方向与图示参考方向一致U 4实际方向与图示参考方向相反电流I 1与U 4、I 2与U 2、I 3与U 3为关联参考方向 I 1与U 1为非关联参考方向1-2(a)图 P =20W 吸收 (b) 图 P =20W 提供(c)图 P =(－10)×(－2)=20W 吸收 (d) 图 P =10×(－2)=－20W 吸收1-3 （a ） U =IR =2×1.5=3V （b ） U =－IR =－（－2）×1.5=3V1-4 (b)U =10V 不变 (1) U －7+2.5×2=0 U =2V (2) 电流源 P 1=2.5×2=5W 吸收电压源 P 2=2.5×7=17.5W 提供 1-6(1) 电流 A 25.131==II =I 1+3=5A恒流源端电压 U =1.5I 1－3×1=1.5×2－3=0(2) 电压源 P 1=3I =3×5=15W 提供 电流源 P 2=01Ω电阻 W 91323=⨯=P 吸收+ + － － － － U =10V U =10V U =－10V U =10V － +U+ U U 1-- + －U1．5Ω电阻 W 65.1224=⨯=P 吸收 功率平衡1-7 I 1+I 2－I 3－I 4=0I 4=I 1+I 2－I 3=1.5+(－2.5)－3=－4A1-8I R =－I 1+I 2+I 3=－（－4）+3.5+1=8.5AI 5=I R +I 4=8.5+（－8）=0.5A1-9电流参考方向如图所示KVL 方程212211E E R I R I -=+1-10 (a) (b)U =E －IR U =－E+IR 1-11 mA 4.22312311=+=+=R R U ImA 8.08712422=+=+=R R U IU AB =I 2R 2﹣I 1R 1=0.8×7－2.4×3=－1.6V1-12KVL 方程01122S =---R I U R I U1-13 电源电动势 E = U O = 49.44V 电流 A 4.22048===R U IEE E2E 1 UR 2R 4I SR E内阻 Ω==-=-=6.04.244.14.24844.49O I U E R1-14 短路电流 A 4.826.044.49O ===R E I sh 6.2044.82N Sh ==I I （倍）1-15U 1=U －U N =120－110=10V 分压电阻 Ω===52101N I U R1-16 2W 、5k Ω电阻器额定电流 mA 2010523=⨯==R P I (1) 两个0.5W 、2.5k Ω电阻器串联，等效电阻5k Ω，满足阻值要求。
光电子技术安毓英第一章课后习题参考答案1
(t)
2
− A21t
20
20 − s
因此
s
=
1 A 21
1.19 该电矢量方程写成实数形式：
E=(-2i+2 3 j) cos (6x108t-(- 3 x-y)
E0= (-2, 2 3 , 0), k=(- 3 , -1, 0), = 6108
平面波电矢量的振动方向为 X 和 Y 轴面内, 一，三象限内，与 X 轴成 60°角 传播方向为与 X 和 Y 轴平面内，第三象限，与 X 轴成 30°角负向传播
类似于一个完全吸收的黑体，所以室外看窗口感觉较黑。
1.8 （1）根据维恩位移定律：
m
=
2897.9m 3K
K
= 966m
（2）根据斯忒潘-波尔兹曼定律，黑体的辐射出射度为
Meb (T ) = T 4 = 5.67 10−8 J （/ m2 s K4）T 4
所以 3K 辐射背景的辐射出射度为：
s
1 ln10
=
4.80 3 103 K ln10
=
6254K
1.13 证明：自发辐射，一个原子由高能级 自发跃迁到 ，单位时间内能级 减少的粒子数为：
dn2 =−( dn21) dt dt
sp
自发跃迁几率
A21
=(
dn21) dt
1 n2
sp
可得：
dn2 dt
=−
A21
n2
t
n =n e n e 解得：
r sin
hr
Le
=
dIe ds cos
,
dIe = Le ds cos
,
ds = rd r sin d cos
光电子技术安毓英习题答案全
第一章IRI，如图1.设在半径为的点源的圆盘中心法线上，距盘圆中心为为ec o所示。
试计算该点源发射到盘圆的辐射功率。
____ e d 解：因为，s dS i R c0上为辐射在被照面，到面源的距离为。
若的入射角，试计算小面源在面积为cccsc o产生的辐射照度。
dI e | __________ e cOsA:解：亮度定义I :强度定c---------------------2I0 cosd cOsL A一 cssee E A上辐射照度为：则在小面源在__________________________________________ e2dA|0,其各处的假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景） 3.的探测器表面上产生的辐照度。
L均相同，试计算该扩展源在面积为A辐亮度de cosA d d L cosdAd Ld d答：由，且得_____________________________ ee 22cOsddA「1旳「2 2 LEdLI 则辐照度：------------------ e ee20022- I 霓虹灯发的光是热辐射吗？ 4.在两端放置有电极的真空充入氖或氩等惰性气体，霓虹灯发的光是电致发光,cosld d d 2sin R 2 c r o 且i.i题图第I o 1 222R I co | 0I1 Id 2 所以eee22R|cOLIA ；被照面的，面源法线与, 辐射亮度为的夹角为 2.如图所示，设小面源的面积为sse o A AAAIS处有一个辐射强度d e Ie L d I e 0 A s cOsAdd L c可得辐射通量：sees cos A cc d 在给定方向上立体角为:图1.2第 _______________不是热辐射。
使原子中气体中的原子或离子受到被电场加速的电子的轰击,当两极间的电压增加到一定数值时,的电子受到激发。
当它由激发状态回复到正常状态会发光，这一过程称为电致发光过程。
光电子技术(安毓英)习题答案
课后题答案1.1设半径为 艮的圆盘中心发现上， 距圆盘中心为l 0处有一辐射强度为I e 的点源S ,如F图所示。
试计算该点光源发射到圆盘的辐射功率。
pl思路分析：要求 e 由公式E e 丄，l edA-都和e 有关，根据条件，都可求出。
解题过程如下:d e dARfE e dA试计算小面源在 A c 上产生的辐射照度。
题过程如下:解:E e又:E el ei o 2代入上式可得:l o法二:l el e dl e R 2lo1.2如下图所示，设小面源的面积为辐射亮度为L e ，面源法线与l 0的夹角为s ；被照面的面积为A ，到面源 A s 的距离为|0。
若c 为辐射在被照面A c 的入射角,E e故:思路分析：若求辐射照度 E e ，则应考虑公式E e卡。
又题目可知缺少"，则该考虑如何求I e 。
通过课本上的知识可以想到公式L edl e ，通过积分则可出I e 。
解dScos亠. dj由L e e可得dScosAI e s L e cos dSe0 e=L e cos A，故:E土L e COS A se—\0—1.3假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐射亮度L.均相同。
试计算该扩展源在面积为A的探测器表面上产生的辐射照度。
思路分析：题目中明确给出扩展源是按朗伯余弦定律发射辐射的，且要求辐射照度dEe，由公式E e 亠可知，要解此题需求出d e，而朗伯体的辐射通量为dAd e L e dS cos d L e dS,此题可解。
解题过程如下：解：E d ee dAd e L e dS cos d L e dSE e L e dS L ee dA e1.4霓虹灯发的光是热辐射吗?答：霓虹灯发光是以原子辐射产生的光辐射，属于气体放电，放电原理后面章节会涉及到。
而热辐射是指由于物体中的分子、原子受到热激发而发射电磁波的现象。
因此霓虹灯放电不属于热辐射。
光电子技术(第三版)课后习题答案《电子工业出版社》.pdf
思路分析：由公式 (z) 0
1 ( z )2 可知，若求 需找出 f，解出 f，代入公式 f
R1
z0
f2 z0
0.3 0.42 0.3
0.83 即可求出结果。解题过程如下：
解：
f L 0.4m 2
(0.3) 0
1 ( 0.3) 2 1.2 10 3 f
1 ( 0.3) 2 1.5 mm 0.4
V000 。 由于f和 w0 是一一对应的，因而也可以用作为表征共焦腔高斯
光束的参数，试以 w0 表示f、 wz ， Rz，V000 。
解答：
w0
f
w wz w0
1
z f
2
V000
1 2
Lw02s
L2 , 2
f
L 2
Rz
z
f2 z
f
z f
f z
1.15 今有一球面腔，R1=1.5m，R2=-1m，L=0.8m。试证明该腔为稳定腔。
1.7 黑体辐射曲线下的面积等于在相应温度下黑体的辐射出射度 M。试普朗克热辐射公
式导出 M 与温度的四次方成正比，即
M=常数 T 4
这一关系称为斯忒藩——波尔兹曼定律，其中常数为 5.67 108W / (m2 K 4)
思路分析：对公式 M e (T )
C1 5
1 eC2 T
进行积分即可证明。
1
1.8 宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于 3K 黑体辐射，此辐射的单体辐
射出射度在什么波长下有极大值？
思路分析：通过 1.6 题不难看出，对于黑体辐射，当辐射出射度取最大值时，波长和温
度 T 有关系，且乘积为常数，此题便可利用这个关系直接求解。解题过程如下：
光电子技术安毓英第四章课后习题参考答案
4.1 比较光子探测器和光热探测器在作用机理、性能及应用特点等方面的差异。
答：光子效应是指单个光子的性质对产生的光电子起直接作用的一类光电效应。
探测器吸收光子后，直接引起原子或分子的内部电子状态的改变。
光子能量的大小，直接影响内部电子状态改变的大小。
因为，光子能量是hν，h是普朗克常数, ν是光波频率，所以，光子效应就对光波频率表现出选择性，在光子直接与电子相互作用的情况下，其响应速度一般比较快。
光热效应和光子效应完全不同。
探测元件吸收光辐射能量后，并不直接引起内部电子状态的改变，而是把吸收的光能变为晶格的热运动能量，引起探测元件温度上升,温度上升的结果又使探测元件的电学性质或其他物理性质发生变化。
所以，光热效应与单光子能量h的大小没有直接关系。
原则上，光热效应对光波频率没有选择性。
只是在红外波段上，材料吸收率高，光热效应也就更强烈，所以广泛用于对红外线辐射的探测。
因为温度升高是热积累的作用，所以光热效应的响应速度一般比较慢，而且容易受环境温度变化的影响。
值得注意的是，以后将要介绍一种所谓热释电效应是响应于材料的温度变化率，比其他光热效应的响应速度要快得多，并已获得日益广泛的应用。
4.3 用光敏电阻设计路灯自动点亮器本题为开放式。
可能有不同答案。
有设计图都算，无明显错误，都算对4.4 已知Si 光电池光敏面积为5×10mm2, 在1000W/m2光照下，开路电压u∞=0.55V，光电流iφ=12mA。
试求:（1）在（200 ~ 700）W/m2光照下,保证线性电压输出的负载电阻和电压变化值;（2）如果希望输出电压变化量为0.5V，怎么办？解：（1）不同的光照强度下，光电池的开路电压有变化，由（4 -115）式得到开路电压变化值：2222222'200/,' 2.610ln('/)' 2.610ln(200/1000)0.55 2.610ln(0.2)0.51'700/' 2.610ln(700/1000)0.55 2.610ln(0.7)0.54oc oc oc oc oc oc p W m u u P P u u Vp W m u u V−−−−−==+⨯=+⨯=+⨯===+⨯=+⨯=电压输出工作在光电池的光电流区域，在该区域光电流与光照功率成正比，所以短路电流为：22'''''200'200/,'12 2.41000'700'700/,'128.41000i P P i i i P PP p W m i i mA mA P P p W m i i mA mA P ϕϕϕϕϕϕϕϕ=∴==⇒==⨯==⇒==⨯=， 根据P140页关于“保证光电池线性工作的负载电阻R L 的选取原则”的分析和讨论，为保证线性电压输出，负载电阻应该用（4 -123）式确定。
光电子技术安毓英版答案
习 题11. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：I ∆A s，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：用定义e L =3.，其各处的辐亮度e L 均相同。
试计算该扩展源在面积为d A 的探测器表面上产生的辐照度。
解：辐射亮度定义为面辐射源在某一给定方向上的辐射通量，因为余弦辐射体的辐射亮度为 得到余弦辐射体的面元dS 向半空间的辐射通量为又因为在辐射接收面上的辐射照度e E 定义为照射在面元上的辐射通量e d Φ与该面元的面积dA 之比，即ee d E dAΦ=所以该扩展源在面积为d A 的探测器表面上产生的辐照度为e e dL dS E A π=单位是2/W m 4. 霓虹灯发的光是热辐射吗？ 解： 不是热辐射。
5刚粉刷完的房间从房外远处看，它的窗口总显得特别黑暗，这是为什么？解：因为刚粉刷完的房间需要吸收光线，故从房外远处看它的窗口总显得特别黑暗6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
试由普朗克热辐射公式导出常数=T m λ。
这一关系式称为维恩位移定律，其中常数为2.898⨯10-3m ∙K 。
解：普朗克热辐射公式求一阶导数，令其等于0，即可求的。
7.黑体辐射曲线下的面积等于在相应温度下黑体的辐射出射度M 。
试由普朗克热辐射公式导出M 与温度T 的四次方成正比，即这一关系式被称为斯忒藩—玻尔兹曼定律，其中常数为-85.67*10W(24m K ⋅)。
解：黑体处于温度T 时，在波长λ处的单色辐射出射度有普朗克公式给出：式中h 为普朗克常数，c 为真空中光速，B k 为玻尔兹曼常数。
光电子技术安毓英习题答案(完整版)
第一章2.如图所示，设小面源的面积为 JA ,辐射亮度为L e ,面源法线与I o 的夹角为 舛 被照面的面积为「A ，至U 面源 A S 的距离为I 。
若氏为辐射 在被照面 A C 的入射角，试计算小面源在 A 上产生的辐射照度。
强度定义：I e =仏d Ω可得辐射通量：d^e = LjA S COSd S dl I 在给定方向上立体角为：A C COSr C3.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对 的天空背景），其各处的辐亮度L e 均相同，试计算该扩展源在面积为 A d 的 探测器表面上产生的辐照度。
7.黑体辐射曲线下的面积等于等于在相应温度下黑体的辐射出射度 M L试有普朗克的辐射公式导出 M⅛温度T 的四次方成正比，即 M=常数T 4这一关系式称斯特藩-波耳兹曼定律，其中常数为5.67 1O -8W∕n 2K 4 解答：教材P9,对公式M e.（T ）=C ; C 1进行积分即可证明。
丸 e %T —1第二章3.对于3m 晶体LiNbo3,试求外场分别加在x,y 和Z 轴方向的感应主 折射率及相应的相位延迟（这里只求外场加在 X 方向上）解：铌酸锂晶体是负单轴晶体，即 n x =n y =n o 、n z = n e 。
它所属的三方晶 系3m 点群电光系数有四个，即丫 22、Y 烬Y 33、Y 51。
电光系数矩阵为：解：亮度定义：5dlA r COSr r则在小面源在 A C 上辐射照度为:E ed ”e L eL A S COSd SCOS ； C ^d^ ^ ∣H答：由 L e=贏A 乔得 ^=L e dIdACO-， 且 d ι 1二A d COSr I 2 r 2则辐照度: E e= Le 0rdrIr 2 2- 00 0 0 γ 51γ-22γ一22γ220 γ510 013球方程为:1 (-2 - 22E^ 15E n o )x 2(n 2由此可得铌酸锂晶体在外加电场后的折射率椭22E y -113E z )y 2(-733E z )z 22 51 (E z yz E X XZ) - 2 22 E X Xy = In e通常情况下， 向通光，即有 E Z =E y =0,且£ ≠ 0。
光电技术习题解
教材：安毓英，刘继芳，李庆辉编著《光电子技术》，北京：电子工业出版社，2002《光电子技术》习题解答习 题11.1 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解答：根据辐射功率的定义及立体角的计算公式：ΩΦd d ee I =，202πd l R c =Ω 202e πd d l R I I c e e ==ΩΦ1.2 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
第1题图第2题图用定义rr ee A dI L θ∆cos =和A E ee d d Φ=求解。
1.4 霓虹灯发的光是热辐射吗？ 不是热辐射。
是电致发光。
1.6 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
试由普朗克热辐射公式导出常数=T m λ。
这一关系式称为维恩位移定律，其中常数为2.898⨯10-3m •K 。
解答：普朗克热辐射公式求一阶导数，令其等于0，即可求的。
教材P81.7 黑体辐射曲线下的面积等于等于在相应温度下黑体的辐射出射度M 。
试有普朗克的辐射公式导出M 与温度T 的四次方成正比，即4T ⨯=常数M这一关系式称斯特藩-波耳兹曼定律，其中常数为5.67⨯10-8W/m 2K 4 解答：教材P9，并参见大学物理相关内容。
1.9常用的彩色胶卷一般分为日光型和灯光型。
你知道这是按什么区分的吗？按色温区分。
1.10 dv v ρ为频率在dv v v +~间黑体辐射能量密度，λρλd 为波长在λλλd +~ 间黑体辐射能量密度。
已知 ()[]1exp 833-=T k hv c hv B v πρ ，试求λρ。
光电子技术课后答案资料
安毓英光电子技术教材课后习题答案详解习 题11. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c4. 霓虹灯发的光是热辐射吗？不是热辐射。
6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
试由普朗克热辐射公式导出常数=T m λ。
这一关系式称为维恩位移定律，其中常数为2.898⨯10-3m ∙K 。
普朗克热辐射公式求一阶导数，令其等于0，即可求的。
9. 常用的彩色胶卷一般分为日光型和灯光型。
你知道这是按什么区分的吗？按色温区分。
习 题21. 何为大气窗口，试分析光谱位于大气窗口内的光辐射的大气衰减因素。
对某些特定的波长，大气呈现出极为强烈的吸收。
光波几乎无法通过。
根据大气的这种选择吸收特性，一般把近红外区分成八个区段，将透过率较高的波段称为大气窗口。
第1题图2. 何为大气湍流效应，大气湍流对光束的传播产生哪些影响？是一种无规则的漩涡流动，流体质点的运动轨迹十分复杂，既有横向运动，又有纵向运动，空间每一点的运动速度围绕某一平均值随机起伏。
这种湍流状态将使激光辐射在传播过程中随机地改变其光波参量，使光束质量受到严重影响，出现所谓光束截面内的强度闪烁、光束的弯曲和漂移（亦称方向抖动）、光束弥散畸变以及空间相干性退化等现象，统称为大气湍流效应。
5. 何为电光晶体的半波电压？半波电压由晶体的那些参数决定？当光波的两个垂直分量E x'，E y'的光程差为半个波长（相应的相位差为π）时所需要加的电压，称为半波电压。
7. 若取v s=616m/s，n=2.35，f s=10MHz，λ0=0.6328μm，试估算发生拉曼-纳斯衍射所允许的最大晶体长度L max=?10. 一束线偏振光经过长L=25cm，直径D=1cm的实心玻璃，玻璃外绕N=250匝导线，通有电流I=5A。
光电子技术答案解析
光电子技术练习及思考题解答（收集整理版）配套光电子技术（第3版）安毓英刘继芳李庆辉冯喆珺编著电子工业出版社由于水平有限，练习及思考题解答难免有错误之处，敬请指正。
欢迎大家交流学习习 题11. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：ΩΦd d e e I =， 202πd l R c =Ω202e πd d l R I I c e e ==ΩΦ2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：用定义rr ee A dI L θ∆cos =和A E e e d d Φ=求解。
3.假设有一个按郎伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度e L 均相同。
试计算该扩展源在面积为d A 的探测器表面上产生的辐照度。
解：辐射亮度定义为面辐射源在某一给定方向上的辐射通量，因为余弦辐射体的辐射亮度为eoe eo dI L L dS== 得到余弦辐射体的面元dS 向半空间的辐射通量为 0e e e d L dS L dS ππΦ==又因为在辐射接收面上的辐射照度e E 定义为照射在面元上的辐射通量e d Φ与该面元的面积dA 之比，即ee d E dAΦ=第1题图第2题图所以该扩展源在面积为d A 的探测器表面上产生的辐照度为e e dL dSE A π=单位是2/W m4. 霓虹灯发的光是热辐射吗？ 解： 不是热辐射。
5刚粉刷完的房间从房外远处看，它的窗口总显得特别黑暗，这是为什么？解：因为刚粉刷完的房间需要吸收光线，故从房外远处看它的窗口总显得特别黑暗 6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章1. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：因为ΩΦd d ee I =， 且 ()⎪⎪⎭⎫ ⎝⎛+-=-===Ω⎰22000212cos 12sin c R R l l d d rdSd c πθπϕθθ 所以⎪⎪⎭⎫ ⎝⎛+-=Ω=Φ220012c e e e R l l I d I π2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：亮度定义:r r ee A dI L θ∆cos =强度定义:ΩΦ=d d I ee可得辐射通量：Ω∆=Φd A L d s s e e θcos在给定方向上立体角为：20cos l A d c c θ∆=Ω则在小面源在∆A c 上辐射照度为：20cos cos l A L dA d E cs s e e e θθ∆=Φ=3.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度L e 均相同，试计算该扩展源在面积为A d 的探测器表面上产生的辐照度。
答：由θcos dA d d L e ΩΦ=得θcos dA d L d e Ω=Φ，且()22cos rl A d d +=Ωθ 则辐照度：()e e e L d rlrdrl L E πθπ=+=⎰⎰∞20022224. 霓虹灯发的光是热辐射吗？第1.1题图第1.2题图不是热辐射。
霓虹灯发的光是电致发光，在两端放置有电极的真空充入氖或氩等惰性气体，当两极间的电压增加到一定数值时，气体中的原子或离子受到被电场加速的电子的轰击，使原子中的电子受到激发。
当它由激发状态回复到正常状态会发光，这一过程称为电致发光过程。
6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
试由普朗克热辐射公式导出常数=T m λ。
答：这一关系式称为维恩位移定律，其中常数为2.898⨯10-3m •K 。
普朗克热辐射公式求一阶导数，令其等于0，即可求的。
7.黑体辐射曲线下的面积等于等于在相应温度下黑体的辐射出射度M 。
试有普朗克的辐射公式导出M 与温度T 的四次方成正比，即4T ⨯=常数M这一关系式称斯特藩-波耳兹曼定律，其中常数为5.67⨯10-8W/m 2K 4 解答：教材P9，并参见大学物理相关内容。
9. 常用的彩色胶卷一般分为日光型和灯光型。
你知道这是按什么区分的吗？按色温区分。
10 dv v ρ为频率在dv v v +~间黑体辐射能量密度，λρλd 为波长在λλλd +~ 间黑体辐射能量密度。
已知 ()[]1exp 833-=T k hv c hv B v πρ ，试求λρ。
解答：由C =λυ，通过全微分进行计算。
11 如果激光器和微波器分别在λ=10μm ，λ=500nm 和ν=3000MHz 输出一瓦的连续功率，问每秒钟从激光上能级向下能级跃迁的粒子数分别是多少？ 解答： Nhv P =，λhCNP =12 设一对激光能级为E 2和E 1（g 2=g 1），相应的频率为ν（波长为λ），各能级上的粒子数为n 2和n 1。
求（1）当ν=3000MHz ，T=300K 时，n 2/n 1=？ （2）当λ=1μm ，T=300K 时，n 2/n 1=？ （3）当λ=1μm ，n 2/n 1=0.1 温度T=？。
解答：Chv E E e g g n n kTE E ==-=--λν,,1212121213 试证明，由于自发辐射，原子在E 2能级的平均寿命211A s =τ。
解答： 参见教材P1214 焦距f 是共焦腔光束特性的重要参数，试以f 表示w ，z w ，()z R ，000V 。
由于f 和0w 是一一对应的，因而也可以用作为表征共焦腔高斯光束的参数，试以0w 表示f 、z w ，()z R ，000V 。
解答：πλfw =()201⎪⎪⎭⎫⎝⎛+==f z w z w w2,221220000L f L w L V s ===λπ()⎪⎪⎭⎫ ⎝⎛+=+=z f f z f z f z z R 215 今有一球面腔，R 1=1.5m ，R 2=-1m ，L=0.8m 。
试证明该腔为稳定腔；并求出它的等价共焦腔的参数。
解答：221111R Lg R L g -=-=稳定强条件：1021<<g g ，求出g 1和g 2为腔参数。
16 某高斯光束w =1.2mm ，求与束腰相距0.3m ，10m 和1000m 远处的光斑w 的大小及波前曲率半径R 。
解答：πλfw =()201⎪⎪⎭⎫⎝⎛+==f z w z w w()⎪⎪⎭⎫ ⎝⎛+=+=z f f z f z f z z R 2第二章1. 何为大气窗口，试分析光谱位于大气窗口内的光辐射的大气衰减因素。
答：对某些特定的波长，大气呈现出极为强烈的吸收。
光波几乎无法通过。
根据大气的这种选择吸收特性，一般把近红外区分成八个区段，将透过率较高的波段称为大气窗口。
2. 何为大气湍流效应，大气湍流对光束的传播产生哪些影响？ 答：是一种无规则的漩涡流动，流体质点的运动轨迹十分复杂，既有横向运动，又有纵向运动，空间每一点的运动速度围绕某一平均值随机起伏。
这种湍流状态将使激光辐射在传播过程中随机地改变其光波参量，使光束质量受到严重影响，出现所谓光束截面内的强度闪烁、光束的弯曲和漂移（亦称方向抖动）、光束弥散畸变以及空间相干性退化等现象，统称为大气湍流效应。
3．对于3m 晶体LiNbO3，试求外场分别加在x,y 和z 轴方向的感应主折射率及相应的相位延迟（这里只求外场加在x 方向上）解：铌酸锂晶体是负单轴晶体，即n x =n y =n 0、n z ＝n e 。
它所属的三方晶系3m 点群电光系数有四个，即γ22、γ13、γ33、γ51。
电光系数矩阵为：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=0000000002251513313221322γγγγγγγγγij 由此可得铌酸锂晶体在外加电场后的折射率椭球方程为：12)(2)1()1()1(2251233121322202152220=-++++++++-xy E xz E yz E z E n y E E n x E E n x x z z ez y z y γγγγγγγ （1）通常情况下，铌酸锂晶体采用450－z 切割，沿x 轴或y 轴加压，z 轴方向通光，即有E z =E y =0,且E x ≠0。
晶体主轴x,y 要发生旋转，上式变为：1222251222222=-+++xy E xz E n z n y n x x x zy x γγ （2）因151〈〈x E γ，且光传播方向平行于z 轴，故对应项可为零。
将坐标轴绕z 轴旋转角度α得到新坐标轴，使椭圆方程不含交叉项，新坐标轴取为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡''cos sin sin cos y x y x αααα，z=z ’ （3） 将上式代入2式，取o 45=α消除交叉项，得新坐标轴下的椭球方程为：1''1'1222222022220=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛-e x x n z y E n x E n γγ （4） 可求出三个感应主轴x ’、y ’、z ’（仍在z 方向上）上的主折射率变成：ez x y xx n n E n n n E n n n =-=+='22300'22300'2121γγ （5）可见，在x 方向电场作用下，铌酸锂晶体变为双轴晶体，其折射率椭球z 轴的方向和长度基本保持不变，而x,y 截面由半径为n 0变为椭圆，椭圆的长短轴方向x ’ y ’相对原来的x y 轴旋转了450，转角的大小与外加电场的大小无关，而椭圆的长度n x ，n y 的大小与外加电场E x 成线性关系。
当光沿晶体光轴z 方向传播时，经过长度为l 的晶体后，由于晶体的横向电光效应（x-z ），两个正交的偏振分量将产生位相差：l E n l n n x y x 22302)''(2γλπλπϕ=-=∆ （6）若d 为晶体在x 方向的横向尺寸，d E V x x =为加在晶体x 方向两端面间的电压。
通过晶体使光波两分量产生相位差π（光程差λ/2）所需的电压x V ，称为“半波电压”，以πV 表示。
由上式可得出铌酸锂晶体在以（x-z ）方式运用时的半波电压表示式：ldn V 22302γλπ=（7） 由（7）式可以看出，铌酸锂晶体横向电光效应产生的位相差不仅与外加电压称正比，还与晶体长度比l /d 有关系。
因此，实际运用中，为了减小外加电压，通常使l /d 有较大值，即晶体通常被加工成细长的扁长方体。
4．一块45度-z 切割的GaAs 晶体，长度为L ，电场沿z 方向，证明纵向运用时的相位延迟为EL r n 4132λπϕ=∆。
解：GaAs 晶体为各向同性晶体，其电光张量为：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=41414163000000000000000γγγγ （1） z 轴加电场时，E z ＝E ，E x =E y =0。
晶体折射率椭球方程为：1241222222=+++xy E n z n y n x γ （2） 经坐标变换，坐标轴绕z 轴旋转45度后得新坐标轴，方程变为：1''1'12224122412=+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+n z y E n x E n γγ （3） 可求出三个感应主轴x ’、y ’、z ’（仍在z 方向上）上的主折射率变成：nn E n n n En n n z y x =+=-='413'413'2121γγ （4）纵向应用时，经过长度为L 的晶体后，两个正交的偏振分量将产生位相差：EL n L n n y x 4132)''(2γλπλπϕ=-=∆ （5）5. 何为电光晶体的半波电压？半波电压由晶体的那些参数决定？答：当光波的两个垂直分量E x '，E y '的光程差为半个波长（相应的相位差为π）时所需要加的电压，称为半波电压。
6．在电光晶体的纵向应用中，如果光波偏离z 轴一个远小于1的角度传播，证明由于自然双折射引起的相位延迟为2220012θωϕ⎪⎪⎭⎫ ⎝⎛-=∆e n n n c L，式中L 为晶体长度。