七年级数学下册压轴题(汇编)
完整版七年级下册数学压轴题集锦

、2如图,已知(A0,a),B(0,b),C(m,b)且(a-4)+b+3=0,S=14.1ABCV(1)求C点坐标o。
90DFE=为?AED的平分线,且?点,(2)作DE?DC,交y轴于EEF求证:FD平分?ADO;(3)E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分∠AEC,且PM⊥EM,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程?MPQ中,?ECA的大小是否发生变化,若不变,求出其值。
y yA A ND F oQ D x oxE MC CB PE1 2=2∠∠、如图1,AB//EF,2FCE;FEC=∠(1)证明∠NMC,则∠FNM=∠FMNN为AC上一点,为FE延长线上一点,且∠M(2)如图2,有何数量关系,并证明。
与∠CFMAN1MEE2CCB BFF2 1 图图1(1)如图,∠ABC的平分线与∠ADC的平分线交于点E,试问BE与DE有何位置关系?说明你的理由。
(2)如图,试问∠ABC的平分线BE与∠ADC的外角平分线DF有何位置关系?说明你的理由。
(3)如图,若∠ABC的外角平分线与∠ADC的外角平分线交于点E,试问BE与DE有何位置关系?说明你的理由。
N G DE D DM BF C B BC C EA A EA,B=60∠°DCE的平分线交于点F,∠1()如图,点E在AC的延长线上,BAC与∠6. BDC的度数。
F=56°,求∠∠FBDEC、试问∠F的平分线交于点与∠ADEF,∠E2()如图,点在CD的延长线上,BAD 之间有何数量关系?为什么?和∠∠BC ABFECD。
的平分线交于点与∠已知∠7.ABCADCE3(1)如图,试探究∠E、∠A与∠C之间的数量关系,并说明理由。
AEDCB(2)如图,是探究∠E、∠A与∠C之间的数量关系,并说明理由。
DAECB的反向延MF,若点G恰好在MF)如图,点E是AB上方一点,平分∠AME8.(1 互余,求∠AME的大小。
压轴题02:相交线与平行线综合专练20题(解析版)-年七年级数学下学期期末精选题汇编(北师大版)
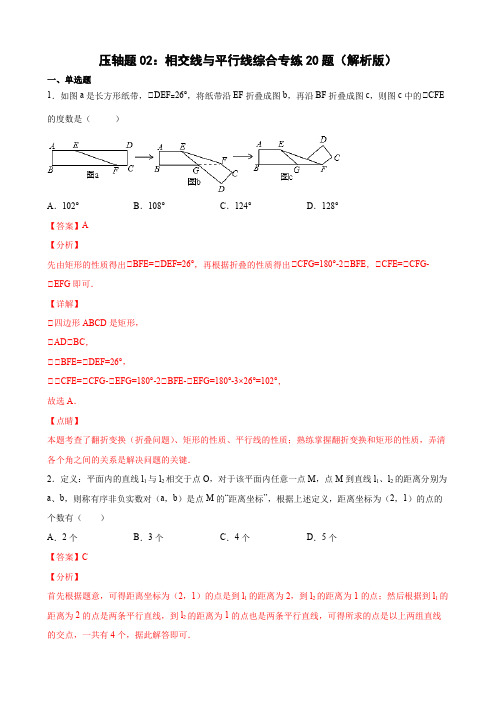
压轴题02:相交线与平行线综合专练20题(解析版)一、单选题1.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE 的度数是()A.102°B.108°C.124°D.128°【答案】A【分析】先由矩形的性质得出∠BFE=∠DEF=26°,再根据折叠的性质得出∠CFG=180°-2∠BFE,∠CFE=∠CFG-∠EFG即可.【详解】∠四边形ABCD是矩形,∠AD∠BC,∠∠BFE=∠DEF=26°,∠∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,故选A.【点睛】本题考查了翻折变换(折叠问题)、矩形的性质、平行线的性质;熟练掌握翻折变换和矩形的性质,弄清各个角之间的关系是解决问题的关键.2.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有()A.2个B.3个C.4个D.5个【答案】C【分析】首先根据题意,可得距离坐标为(2,1)的点是到l1的距离为2,到l2的距离为1的点;然后根据到l1的距离为2的点是两条平行直线,到l2的距离为1的点也是两条平行直线,可得所求的点是以上两组直线的交点,一共有4个,据此解答即可.【详解】解:如图1,,到l 1的距离为2的点是两条平行直线l 3、l 4,到l 2的距离为1的点也是两条平行直线l 5、l 6,∠两组直线的交点一共有4个:A 、B 、C 、D ,∠距离坐标为(2,1)的点的个数有4个.故选C .【点睛】此题主要考查了点的坐标,以及对“距离坐标”的含义的理解和掌握,解答此题的关键是要明确:到l 1的距离为2的点是两条平行直线,到l 2的距离为1的点也是两条平行直线.3.如图1n //AB CB ,则∠1+∠2+∠3+…+∠n=( )A .540°B .180°nC .180°(n-1)D .180°(n+1)【答案】C【分析】 根据题意,作21//DB AB ,31//EB AB ,41//FB AB ,由两直线平行,同旁内角互补,即可求出答案.【详解】解:根据题意,作21//DB AB ,31//EB AB ,41//FB AB ,∠1n //AB CB ,∠121180B B D ∠+∠=︒,2323180DB B B B E ∠+∠=︒,3434180EB B B B F ∠+∠=︒,……∠122323343411803B B D DB B B B E EB B B B F ∠+∠+∠+∠+∠+∠=︒⨯,……∠123180(1)n n ∠+∠+∠++∠=︒⨯-;故选:C .【点睛】本题考查了平行线的性质,解题的关键是正确作出辅助线,熟练运用两直线平行同旁内角互补进行证明.4.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( ) A .50°、130°B .都是10°C .50°、130°或10°、10°D .以上都不对 【答案】C【分析】首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x °,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.【详解】解:∠两个角的两边分别平行,∠这两个角相等或互补.设其中一角为x °,若这两个角相等,则x =3x ﹣20,解得:x =10,∠这两个角的度数是10°和10°;若这两个角互补,则180﹣x =3x ﹣20,解得:x =50,∠这两个角的度数是50°和130°.∠这两个角的度数是50°、130°或10°、10°.故选:C .【点睛】此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.5.如图,已知//AB CD ,M 为平行线之间一点连接AM ,CM ,N 为AB 上方一点,连接AN ,CN ,E 为NA 延长线上一点.若AM ,CM 分别平分BAE ∠,DCN ∠,则M ∠与N ∠的数量关系为( ).A .90M N ∠-∠=︒B .2180M N ∠-∠=︒C .180M N ∠+∠=︒D .2180M N ∠+∠=︒【答案】B【分析】 过点M 作//MO AB ,过点N 作//NP AB ,则//////MO AB CD NP ,根据平行线的性质可得12AMC ∠=∠+∠,223CNE ∠=∠-∠,318021∠=︒-∠,即可得出结论.【详解】解:过点M 作//MO AB ,过点N 作//NP AB ,//AB CD ,//////MO AB CD NP ∴,1AMO ∴∠=∠,OMC MCD ∠=∠, AM ,CM 分别平分BAE ∠,DCN ∠,21BAE ∴∠=∠,22NCD ∠=∠,2MCD ∠=∠,12AMC ∴∠=∠+∠,//CD NP ,22PNC NCD ∴∠=∠=∠,223CNE ∴∠=∠-∠,//NP AB ,∴∠=∠=︒-∠,NAB31802122(18021)2(12)1802180CNE AMC ∴∠=∠-︒-∠=∠+∠-︒=∠-︒,2180AMC CNE ∴∠-∠=︒,故选:B .【点睛】本题考查了平行线的性质,邻补角的定义,解题的关键是熟练掌握平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6.如图,△ABC 中,∠ACB =90°,AC =3,BC =4,AB =5,P 为直线AB 上一动点,连接PC ,则线段PC 的最小值是( )A .3B .2.5C .2.4D .2【答案】C【分析】 当PC ∠AB 时,PC 的值最小,利用面积法求解即可.【详解】解:在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,AB =5,∠当PC ∠AB 时,PC 的值最小,此时:△ABC 的面积=12•AB •PC =12•AC •BC ,∠5PC =3×4,∠PC =2.4,故选:C .【点睛】本题主要考查了垂线段最短和三角形的面积公式,解题的关键是学会利用面积法求高.7.如图,已知直线AB 、CD 被直线AC 所截,//AB CD ,E 是平面内任意一点(点E 不在直线AB 、CD 、AC 上),设BAE α∠=,DCE β∠=.下列各式:∠αβ+,∠αβ-,∠a β-,∠360αβ︒--,AEC ∠的度数可能是( )A.∠∠B.∠∠C.∠∠∠D.∠∠∠∠【答案】D【分析】由题意根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.【详解】解:(1)如图1,由AB∠CD,可得∠AOC=∠DCE1=β,∠∠AOC=∠BAE1+∠AE1C,∠∠AE1C=β-α.(2)如图2,过E2作AB平行线,则由AB∠CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∠∠AE2C=α+β.(3)如图3,由AB∠CD,可得∠BOE3=∠DCE3=β,∠∠BAE3=∠BOE3+∠AE3C,∠∠AE3C=α-β.(4)如图4,由AB∠CD,可得∠BAE4+∠AE4C+∠DCE4=360°,∠∠AE4C=360°-α-β.(5)(6)当点E在CD的下方时,同理可得∠AEC=α-β或β-α.综上所述,∠AEC的度数可能为β-α,α+β,α-β,360°-α-β,即∠∠∠∠.故选:D.【点睛】本题主要考查平行线的性质的运用,解题时注意两直线平行,同位角相等;两直线平行,内错角相等以及分类讨论.8.∠如图1,AB∥CD,则∠A+∠E+∠C=180°;∠如图2,AB∥CD,则∠E=∠A+∠C;∠如图3,AB ∥CD,则∠A+∠E-∠1=180°;∠如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是()A.∠∠∠∠B.∠∠∠C.∠∠∠D.∠∠∠【答案】C【分析】∠过点E作直线EF AB∥,由平行线的性质即可得出结论;∠过点E作直线EF AB∥,由平行线的性质即可得出结论;∠过点E作直线EF AB∥,由平行线的性质可得出∠A+∠E-∠1=180°;∠先过点P作直线PF AB∥,再根据两直线平行,内错角相等和同位角相等即可作出判断.【详解】∥,解:∠过点E作直线EF AB∥∥,∠∠A+∠1=180°,∠2+∠C=180°,∠AB CD∥,∠AB CD EF∠∠A+∠C+∠AEC=360°,故∠错误;∠过点E作直线EF AB∥,∠AB CD∥,∥∥,∠∠A=∠1,∠2=∠C,∠AB CD EF∠∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故∠正确;∠过点E作直线EF AB∥,∥∥,∠∠A+∠3=180°,∠1=∠2,∠AB CD∥,∠AB CD EF∠∠A+∠AEC-∠2=180°,即∠A+∠AEC-∠1=180°,故∠正确;∠如图,过点P作直线PF AB∥,∠AB CD∥∥,∥,∠AB CD PF∠∠1=∠FP A,∠C=∠FPC,∠∠FP A=∠FPC+∠CP A,∠∠1=∠C+∠CP A,∠AB ∠CD ,∠∠A =∠1,即∠A =∠C+∠C P A ,故∠正确.综上所述,正确的小题有∠∠∠.故选:C .【点睛】本题考查的是平行线的性质及平行公理的推论,根据题意作出辅助线是解答此题的关键. 9.如图,//,AD BC D ABC ∠=∠,点E 是边DC 上一点,连接AE 交BC 的延长线于点H ,点F 是边AB 上一点,使得FBE FEB ∠=∠,作FEH ∠的角平分线EG 交BH 于点G ,若100DEH ︒∠=,则BEG ∠的度数是( ).A .30︒B .40︒C .50︒D .60︒【答案】B【分析】 AD ∠BC ,∠D =∠ABC ,则AB ∠CD ,则∠AEF =180°-∠AED -∠BEG =180°-2β,在△AEF 中,100°+2α+180°-2β=180°,故β-α=40°,即可求解.【详解】解:设FBE =∠FEB =α,则∠AFE =2α,∠FEH 的角平分线为EG ,设∠GEH =∠GEF =β,∠AD ∠BC ,∠∠ABC +∠BAD =180°,而∠D =∠ABC ,∠∠D +∠BAD =180°,∠AB ∠CD ,∠DEH=100°,则∠CEH=∠F AE=80°,∠AEF=180°-∠FEG-∠BEG=180°-2β,在∠AEF中,在∠AEF中,80°+2α+180-2β=180°,故β-α=40°,而∠BEG=∠FEG-∠FEB=β-α=40°,故选:B.【点睛】此题考查平行线的性质,解题关键是落脚于∠AEF内角和为180°,即100°+2α+180°-2β=180°,题目难度较大.10.如图,直线AB MN∥,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC 的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令ECMα∠=,用含α的式子表示∠EBC为().A.52αB.10α︒-C.1102α︒-D.1102α-︒【答案】D【分析】先求出∠ABC,再延长CE,交AB于点G,结合平行线的性质表示出∠BCE,然后根据三角形内角和定理表示∠CED,再根据角平分线得定义表示出∠CEB,最后根据三角形内角和定理得出答案.【详解】在∠ABC中,∠CAB=40°,∠ACB=90°,∠∠ABC=50°.延长CE,交AB于点G,∠MN BA∥,∠EGBα∠=,∠ACM=∠BAC=40°,∠∠ACE=α-40°,∠∠BCE=90°-(α-40°)=130°-α.∠∠CEA=180°-∠CAE-∠ACE,∠∠CED=180°-∠CEA=∠CAE+∠ACE=20°+(α-40°)=α-20°.∠EF平分∠CED,∠∠CEF=111022CEDα∠=-︒,∠∠CEB=1110706022αα-︒+︒=+︒,∠∠EBC=11180(60)(130)10 22ααα︒-+︒-︒-=-︒.故选:D.【点睛】本题主要考查了角平分线的定义,三角形内角和定理,平行线的性质,将待求角转化到适合的三角形是解题的关键.二、填空题11.如图,已知,∠ABG为锐角,AH∠BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∠AB交直线AH于点D,CE∠CD交AB于点E,CF∠AD,垂足为F(F不与A重合),若∠ECF =n°,则∠BAF的度数为_____度.(用n来表示)【答案】n或180﹣n【分析】分两种情况讨论:当点M在线段BC上;点C在BM延长线上,根据平行线的性质,即可得到结论.【详解】解:过A作AM∠BC于M,如图1,当点C在BM延长线上时,点F在线段AD上,∠AD∠BC,CF∠AD,∠CF∠BG,∠∠BCF=90°,∠∠BCE+∠ECF=90°,∠CE∠AB,∠∠BEC=90°,∠∠B+∠BCE=90°,∠∠B=∠ECF=n°,∠AD∠BC,∠∠BAF=180°﹣∠B=180°﹣n°,过A作AM∠BC于M,如图2,当点C在线段BM上时,点F在DA延长线上,∠AD∠BC,CF∠AD,∠CF∠BG,∠∠BCF=90°,∠∠BCE+∠ECF=90°,∠CE∠AB,∠∠BEC=90°,∠∠B+∠BCE=90°,∠∠B=∠ECF=n°,∠AD∠BC,∠∠BAF=∠B=n°,综上所述,∠BAF的度数为n°或180°﹣n°,故答案为:n或180﹣n.【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.12.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是.【答案】6秒或19.5秒【分析】设A灯旋转t秒,两灯光束平行,B灯光束第一次到达BQ需要180÷4=45(秒),推出t≤45−12,即t≤33.利用平行线的性质,结合角度间关系,构建方程即可解答.【详解】解:设A灯旋转t秒,两灯的光束平行,B灯光束第一次到达BQ需要180÷4=45(秒),∠t≤45﹣12,即t≤33.由题意,满足以下条件时,两灯的光束能互相平行:∠如图,∠MAM'=∠PBP',12t=4(12+t),解得t=6;∠如图,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;综上所述,满足条件的t的值为6秒或19.5秒.故答案为:6秒或19.5秒.【点睛】本题主要考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠B 的补角,则∠BAH的度数是_____.【答案】60°##60度【分析】首先设∠BAF=x°,∠BCF=y°,过点B作BM AD,过点F作FN AD,根据平行线的性质,可得∠AFC =(x+2y)°,∠ABC=(2x+y)°,又由∠F的余角等于2∠B的补角,可得方程:90﹣(x+2y)=180﹣2(2x+y),继而求得答案.【详解】解:设∠BAF=x°,∠BCF=y°,∠∠BCF=∠BCG,CF与∠BAH的平分线交于点F,∠∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,过点B作BM AD,过点F作FN AD,如图所示:∠AD CE,∠AD FN BM CE ,∠∠AFN =∠HAF =x °,∠CFN =∠GCF =2y °,∠ABM =∠BAH =2x °,∠CBM =∠GCB =y °,∠∠AFC =(x +2y )°,∠ABC =(2x +y )°,∠∠F 的余角等于2∠B 的补角,∠90﹣(x +2y )=180﹣2(2x +y ),解得:x =30,∠∠BAH =60°.故答案为:60°【点睛】此题考查了平行线的性质与判定以及余角、补角的定义.此题难度适中,注意掌握辅助线的作法,掌握数形结合思想与方程思想的应用.14.如图,已知AB //CD ,BE 、DE 的交点为E ,现作如下操作:第一次操作,分别作∠ABE 和∠CDE 的平分线,交点为E 1,第二次操作,分别作∠ABE 1和∠CDE 1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠CDE 2的平分线,交点为E 3,...第n (n ≥2)次操作,分别作∠ABEn ﹣1和∠CDEn ﹣1的平分线,交点为En ,若∠En =α度,则∠BED =___度.【答案】2n a【分析】先过E 作//EF AB ,确定BED ABE CDE ∠=∠+∠,再根据角平分线的性质确定n E ∠与BED ∠的关系,即可求解.【详解】解:如下图,过E 作//EF AB ,∠//AB CD ,∠////AB EF CD ,∠B BEF D DEF ∠=∠∠=∠,,∠BED BEF DEF ∠=∠+∠,∠BED ABE CDE ∠=∠+∠;如下图,∠ABE ∠和CDE ∠的平分线交点为1E ∠111111222DE B ABE CDE ABE CDE BED ∠=∠+∠=∠+∠=∠ ∠1ABE ∠和1CDE ∠的平分线交点为2E , ∠22211111122412BE ABE CDE ABE CD E D E DE B B D ∠=∠+∠=∠+∠∠=∠=; ∠2ABE ∠和2CDE ∠的平分线交点为3E , ∠33322211122812BE ABE CDE ABE CD E D E DE B B D ∠=∠+∠=∠+∠∠=∠=; … 以此类推,12n n E BED ∠=∠ ∠当n E α∠=度时,2n BED α∠=度.故答案为2n α .【点睛】本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,找到角之间的关系.15.如图,直线,,AB CD EF 与直线,,GH IJ KL 分别相交,图中的同位角共有__________对.【答案】156【分析】观察图形,直线 GH,IJ,KL 上,每条直线有5个交点,直线AB,CD,EF 上,每条直线有3个交点,每个交点存在4个角,根据每2个交点可以构成4对同位角,分别求得直线GH,IJ,KL 和AB,CD,EF 上的同位角的对数即可.【详解】观察图形,直线,,GH IJ KL 上,每条直线有5个交点,直线,,AB CD EF 上,每条直线有3个交点,每个交点存在4个角,则直线,,GH IJ KL 上存在的同位角的个数是:5(51)4310434031202-⨯⨯=⨯⨯=⨯=对,同理直线,,AB CD EF 上存在的同位角的个数是:3(31)43362-⨯⨯=对, 则总数是12036156+=对.故答案为:156.【点睛】 本题考查了找同位角,分类讨论是解题的关键.三、解答题16.探究并尝试归纳:(1)如图1,已知直线a 与直线b 平行,夹在平行线间的一条折线形成一个角∠A ,试求∠1+∠2+∠A 的度数,请加以说明.(2)如图2,已知直线a 与直线b 平行,夹在平行线间的一条折线增加一个折,形成两个角∠A 和∠B,请直接写出∠1+∠2+∠A +∠B = 度.(3)如图3,已知直线a 与直线b 平行,夹在平行线间的一条折线每增加一个折,就增加一个角.当形成n 个折时,请归纳并写出所有角与∠1、∠2的总和: 【结果用含有n 的代数式表示,n 是正整数,不用证明】【答案】(1)360°(2)540(3)180(1)n ⋅+︒【分析】(1)过A 作AB //直线a ,再根据平行线的性质即可得到结论;(2)过A 作AC //直线a ,BD //直线a ,则AC//BD //直线b ,根据平行线的性质即可得到结论; (3)根据平行线的性质即可得到结论.(1)解:过A 作AB //直线a ,则AB //直线b ,1342180∴∠+∠=∠+∠=︒,12360MAN ∴∠+∠+∠=︒;(2)解:过A 作AC //直线a ,BD //直线a ,则AC //BD //直线b ,135642180∴∠+∠=∠+∠=∠+∠=︒,12540MAB ABN ∴∠+∠+∠+∠=︒,故答案为:540;(3)解:由(1),(2)知,当形成1个折时,所有角与1∠、2∠的总和180(11)360=⋅+︒=︒,当形成2个折时,所有角与1∠、2∠的总和180(21)540=⋅+︒=︒,当形成n 个折时,所有角与1∠、2∠的总和180(1)n =⋅+︒,故答案为:180(1)n ⋅+︒.【点睛】本题考查了平行线的性质,正确的作出图形是解题的关键.17.如图,已知AB CD ∥,E 、F 分别在AB CD 、上,点G 在AB 、CD 之间,连接GE GF 、.(1)当40BEG ∠=︒时,EP 平分,BEG FP ∠平分DFG ∠;∠如图1,当EG FG ⊥时,则P ∠=______°;∠如图2,在CD 的下方有一点Q ,若EG 恰好平分,BEQ FD ∠恰好平分GFQ ∠,求2Q P ∠+∠的度数;(2)在AB 的上方有一点O ,若FO 平分GFC ∠.线段GE 的延长线平分OEA ∠,则当100EOF EGF ∠+∠=︒时,直接写出OEA ∠与OFC ∠的关系.【答案】(1)∠45;∠140︒(2)3160OEA OFC ∠-∠=︒【分析】(1)根据平行线的性质,以及角平分线的定义即可求解;(2)过点O 作OT AB ∥,则OT CD ∥设OFC OFG ∠=∠β=,OEH HEA α∠=∠=,1802G BEG GFD αβ∠=∠+∠=+︒-,根据平行线的性质求得80αβ+=︒,进而根据()33222160OEA OFC ββαβα∠-∠=--=+=︒即可求解.(1)∠如图,分别过点,G P 作,GN AB PM AB ∥∥,BEG EGN ∴∠=∠,AB CD ∥,NGF GFD ∴∠=∠,EGF BEG GFD ∴∠=∠+∠,同理可得EPF BEP PFD ∠=∠+∠,EG FG ⊥,90EGF ∴∠=︒,EP 平分,BEG FP ∠平分DFG ∠;11,22BEP BEG PFD GFD ∴∠=∠∠=∠, ∴()114522EPP BEG GFD EGF ∠=∠+∠=∠=︒, 故答案为:45,∠如图,过点Q 作QR CD ∥,40BEG ∠=︒,EG 恰好平分,BEQ FD ∠恰好平分GFQ ∠,40GEQ BEG ∴∠=∠=︒,GFQ QFD ∠=∠,设GFQ QFD ∠=∠α=,QR CD ∥,AB CD ∥,1801802100EQR QEB QEG ∴∠=︒-∠=︒-∠=︒,CD QR ∥,180DFQ FQR ∴∠+∠=︒,180FQR α∴+∠=︒,100FQE α∴+∠=︒,100FQE α∴∠=︒-,由(1)可知240G P BEG EFD α∠=∠=∠+∠=︒+,210040140FQE P αα∴∠+∠=︒-+︒+=︒;(2)如图,在AB 的上方有一点O ,若FO 平分GFC ∠,线段GE 的延长线平分OEA ∠,设H 为线段GE 的延长线上一点,则OFC OFG ∠=∠,OEH HEA ∠=∠设OFC OFG ∠=∠β=,OEH HEA α∠=∠=如图,过点O 作OT AB ∥,则OT CD ∥TOF OFC β∴∠=∠=,2TOE OEA α∠=∠=2EOF βα∴∠=-HEA BEG α∠=∠=,1802GFD β∠=︒-由(1)可知1802G BEG GFD αβ∠=∠+∠=+︒-100EOF EGF ∠+∠=︒∴2βα-+1802αβ+︒-100=︒80αβ∴+=︒2,OFC OEA βα∠=-∠=β()33222160OEA OFC ββαβα∴∠-∠=--=+=︒即3160OEA OFC ∠-∠=︒【点睛】本题考查了平行线的性质,以及角平分线的定义,掌握平行线的性质是解题的关键.18.点O 是直线AB 上的一点,射线OC 从OA 出发绕点O 顺时针方向旋转,旋转到OB 停止,设AOC α∠=(0180α︒≤≤︒),射线OD OC ⊥,作射线OE 平分BOD ∠.(1)如图1,若40α=︒,且OD 在直线AB 的上方,求DOE ∠的度数(要求写出简单的几何推理过程).(2)射线OC 顺时针旋转一定的角度得到图2,当射线OD 在直线AB 的下方时,其他条件不变,请你用含α的代数式表示DOE ∠的度数,(要求写出简单的几何推理过程).(3)射线OC 从OA 出发绕点O 顺时针方向旋转到OB ,在旋转过程中你发现DOE ∠与AOC∠(01800180AOC DOB ︒≤∠≤︒︒≤∠≤︒,)之间有怎样的数量关系?请你直接用含α的代数式表示DOE ∠的度数.【答案】(1)25DOE ∠=︒ (2)1452DOE α∠=-︒ (3)1452DOE AOC ∠=︒-∠即1452DOE α∠=︒-或1452DOE AOC ∠=︒+∠即1452DOE α∠=︒+或11352DOE AOC ∠=︒-∠即11352DOE α∠=︒-或1452DOE AOC ∠=∠-︒即1452DOE α∠=-︒ 【分析】(1)根据40α=︒,∠COD =90°,求出∠BOD =50°,根据OE 平分∠BOD ,即可得出结果;(2)先用α表示出∠BOC ,再根据∠COD =90°表示出∠BOD ,根据OE 平分∠BOD ,即可得出结果; (3)分四种情况进行讨论,分别求出∠DOE 与∠AOC 的关系,用含α的代数式表示∠DOE 的度数即可.(1)解:∠OD ∠OC ,∠∠COD =90°,∠40α=︒,即40AOC ∠=︒,∠18050BOD COD AOC ∠=︒-∠-∠=︒,∠OE 平分∠BOD , ∠1252DOE BOD ∠=∠=︒. (2)AOC α∠=,180BOC α∴∠=︒-,∠OD ∠OC ,∠∠COD =90°,∠BOD COD BOC ∠=∠-∠()90180α=︒-︒-90α=-︒∠OE 平分∠BOD , ∠114522DOE BOD α∠=∠=-︒. (3)∠当090AOC ︒≤∠≤︒,OD 在直线AB 的上方时,如图所示:180BOD COD AOC ∠=︒-∠-∠18090AOC =︒-︒-∠90AOC =︒-∠,∠OE 平分∠BOD , ∠114522DOE BOD AOC ∠=∠=︒-∠, 即1452DOE α∠=︒-. ∠当090AOC ︒≤∠≤︒,OD 在直线AB 的下方时,如图所示:∠90AOD COD AOC AOC ∠=∠-∠=︒-∠,∠18090BOD AOD AOC∠=︒-∠=︒+∠,∠OE平分∠BOD,∠114522DOE BOD AOC ∠=∠=︒+∠,即1452 DOEα∠=︒+.∠当90180AOC︒∠≤︒<,OD在直线AB的上方时,如图所示:180BOC AOC∠=︒-∠,BOD DOC BOC∴∠=∠+∠90180AOC=︒+︒-∠270AOC=︒-∠,∠OE平分∠BOD,∠1113522DOE BOD AOC ∠=∠=︒-∠,即11352 DOEα∠=︒-.∠当90180AOC︒∠≤︒<,OD在直线AB的下方时,如图所示:∠180BOC AOC ∠=︒-∠,BOD COD BOC ∴∠=∠-∠()90180AOC =︒-︒-∠90AOC =∠-︒,∠OE 平分∠BOD , ∠114522DOE BOD AOC ∠=∠=∠-︒, 即1452DOE α∠=-︒. 综上分析可知,1452DOE AOC ∠=︒-∠即1452DOE α∠=︒-或1452DOE AOC ∠=︒+∠即1452DOE α∠=︒+或11352DOE AOC ∠=︒-∠即11352DOE α∠=︒-或1452DOE AOC ∠=∠-︒即1452DOE α∠=-︒. 【点睛】本题主要考查了角平分线的定义,垂直的定义,根据α的大小和OD 的位置分类讨论,是解决本题的关键.19.如图,AD //BC ,127DAC ∠=︒,15ACF ∠=︒,142EFC ∠=︒.(1)求证:EF //AD ;(2)连接CE ,若CE 平分∠BCF ,求∠FEC 的度数.【答案】(1)证明见解析(2)19FEC ∠=︒【分析】(1)先根据平行线的性质,得到∠ACB 的度数,进而得出∠FCB 的度数,再根据∠EFC =140°,即可得到∠EFC =142°,即可得到EF ∠BC ,进而得出EF ∠AD ;(2)先根据CE 平分∠BCF ,可得∠BCE =19°,再根据EF ∠BC ,即可得到∠FEC =19°.(1)证明:∠AD BC ∥∠180ACB DAC ∠+∠=︒∠127DAC ∠=︒∠53ACB ∠=︒又∠15ACF ∠=︒∠38FCB ACB ACF ∠=∠-∠=︒∠142EFC ∠=︒∠180FCB EFC ∠+∠=︒∠EF BC ∥又∠AD BC ∥∠EF AD ∥(2)解:∠CF 平分∠BCF ∠1192BCE FCB ∠=∠=︒ ∠EF BC ∥∠19FEC ECB ∠=∠=︒答:∠FEC 的度数19°.【点睛】本题考查平行线的判定,三角形内角和定理,角平分线定义,三角形的外角性质,邻补角定义,能综合运用定理运行推理是解此题的关键,难度适中.20.已知点B ,D 分别在AK 和CF 上,且∥CF AK .(1)如图1,若25CDE ∠=︒,80DEB ∠=︒,则ABE ∠的度数为________;(2)如图2,BG 平分ABE ∠,GB 的延长线与EDF ∠的平分线交于H 点,若DEB ∠比DHB ∠大60︒,求DEB ∠的度数;(3)保持(2)中所求的DEB ∠的度数不变,如图3,BM 平分EBK ∠,DN 平分CDE ∠,作∥BP DN ,则PBM ∠的度数是否改变?若不变,请求值;若改变,请说明理由.【答案】(1)55°(2)100°(3)不变,40°【分析】(1)过点E 作ES CF ,根据∥CF AK ,则ES CF AK ,运用平行线的性质计算即可.(2) 延长DE ,交AB 于点M ,则∠DEB =∠EMB +∠EBM ,利用平行线的性质,角平分线的定义,三角形外角的性质计算即可.(3) 过点E 作EQ DN ,则EQ DN BP ,利用前面的结论和方法,进行等量代换并推理计算即可.(1)解:如图1,过点E 作ES CF ,∠∥CF AK ,∠ES CF AK ,∠∠CDE =∠DES ,∠SEB =∠ABE ,∠∠CDE +∠ABE =∠DES +∠SEB =∠DEB ,∠∠CDE =25°,∠DEB =80°,∠∠ABE =∠DEB -∠CDE =80°-25°=55°.故答案为:55°.(2)解:如图2,延长DE ,交AB 于点M ,则∠DEB =∠EMB +∠EBM ,∠∥CF AK ,BG 平分ABE ∠,∠∠EMB =180°-∠MDF ,∠EBM =2∠ABG =2∠HBN ,∠MDH =∠HDF =∠HNK =12∠MDF ,∠∠HBN +∠DHB =∠HNK ,∠∠DEB =(180°-∠MDF ) +2∠HBN =180°-∠MDF +122MDF DHB ⎛⎫⨯∠-∠ ⎪⎝⎭, ∠∠DEB =180°-∠MDF +∠MDF -2∠DHB =180°-2∠DHB ,∠DEB ∠60DHB -∠=︒,∠∠DEB =180°-2(∠DEB -60°),∠3∠DEB =300°,解得∠DEB =100°.(3)解:过点E作EQ DN,则EQ DN BP,根据(1)得,∠DEB=∠CDE+∠ABE,∠BM平分EBK∠,∠,DN平分CDE∠∠DEB=2∠NDE+180°-2∠EBM,∠∠DEB=100°,∠∠EBM-∠NDE=40°,∠EQ DN,∠∠DEQ=∠NDE,∠∠EBM =40°+∠DEQ,,,∠EQ DN DN BP∠EQ BP,∠∠EBM+∠PBM +∠BEQ =180°,∠40°+∠DEQ+∠PBM +∠BEQ =180°,∠40°+∠DEB+∠PBM =180°,∠∠PBM =180°-100°-40°=40°,∠∠PBM 的度数不变,值为40°.【点睛】本题考查了平行线的判定和性质,三角形外角的性质,角的平分线定义,熟练掌握平行线的判定和性质是解题的关键.。
七年级下数学压轴题

七年级下数学压轴题一、相交线与平行线。
题1:如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE = 4:1,求∠AOF的度数。
解析:设∠BOE = x,因为OE平分∠BOD,所以∠BOD = 2∠BOE=2x。
又因为∠AOD + ∠BOD = 180°,且∠AOD:∠BOE = 4:1,所以∠AOD = 4x。
则4x + 2x=180°,6x = 180°,解得x = 30°。
所以∠COE = 180° - ∠BOE = 150°。
因为OF平分∠COE,所以∠COF=(1)/(2)∠COE = 75°。
∠AOC=∠BOD = 60°,所以∠AOF=∠AOC+∠COF = 60°+ 75°=135°。
题2:已知直线l_1∥ l_2,直线l_3和直线l_1、l_2交于点C和D,在C、D之间有一点P。
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?解析:(1)过点P作PE∥ l_1,因为l_1∥ l_2,所以PE∥ l_2。
∠PAC = ∠APE,∠PBD=∠BPE。
所以∠APB = ∠APE+∠BPE = ∠PAC + ∠PBD。
(2)当点P在l_1上方时,过点P作PF∥ l_1,因为l_1∥ l_2,所以PF∥ l_2。
∠PAC = ∠APF,∠PBD + ∠BPF=180°,所以∠PBD = 180°-(∠APB - ∠PAC),即∠PAC=∠APB + ∠PBD。
当点P在l_2下方时,过点P作PG∥ l_2,同理可得∠PBD = ∠APB+∠PAC。
二、实数。
题3:已知a、b满足√(2a + 8)+| b - √(3)|=0,解关于x的方程(a + 2)x + b^2=a - 1。
初一数学第二学期期中压轴题汇编(人教版)

(3)若方程组
的解是
,求 m 的值,并判断该方程组是否符合(2)中
的规律.
第 3 页(共 50 页)
网校新初二数学赵云辉老师主编
11、△ ABC 中有两个角相等,AD 是它的高,∠CAD=40°,求∠BAD.
12、规定,满足(1)各边互不相等且均为整数,(2)最短边上的高与最长边上的高的比值
为整数 k,这样的三角形称为比高三角形、其中 k 叫做比高系数.根据规定解答下列问题:
第 2 页(共 50 页)
网校新初二数学赵云辉老师主编
8、已知:A(4,0),B(1,﹣x),C(1,3),△ ABC 的面积为 6,求代数式 2x2﹣5x+x2+4x ﹣3x2﹣2 的值.
9、根据下列提供的信息,列方程组,求每支网球拍的单价和每支乒乓球拍的单价,小明带 了 500 元,想买这样的 5 只网球拍,4 只乒乓球拍,能否如愿?
(1)周长为 13 的比高系数 k=
.
(2)写出一个只有 4 个比高系数的比高三角形的周长,周长为
.
(3)比高△ ABC 三边与它的比高系数 k 之间满足 BC﹣AC=AC﹣AB=k2,求△ ABC 的周长.
13、已知△ ABC 中的两角之差为 20°,过△ ABC 顶点的一条直线把这个三角形分成了两个 等腰三角形,写出△ ABC 中最大角.(只写出结果不要求过程)
七年级下册数学几何压轴题

七年级下册数学几何压轴题
1. 把一个长方形沿x轴正方向移动m个单位,求移动前后阴影的面积差。
2. 一个小正方体沿着x轴正方向移动,它的一面在x轴上翻转,求翻转前后阴影的面积比值。
3. 一个方形沿着y轴正方向移动,移动到一个圆的周围,求圆和方形的阴影面积比值。
4. 把一个正方形沿对角线方向移动,它最后完全重合的时候恰好覆盖了一个面积为S的等腰三角形,求三角形面积S。
5. 把一个正方形沿着y轴正方向移动,移动m个单位的时候与另外一个正方形刚好重合,求另外一个正方形的边长。
6. 一个矩形沿x轴正方向移动,移动到另外一个矩形的正上方还有b个单位,求两个矩形的阴影面积比值。
7. 把一个半圆形沿y轴正方向移动,移动到正方形的中心时,求正方形面积和半圆形面积的阴影面积比值。
8. 把一个梯形沿y轴正方向移动,移动到一个与梯形相似的大梯形上面靠着底边的位置,求阴影的面积比值。
9. 把一个正三角形沿着x轴正方向移动,相邻两次的位移满足一个等差数列,第一次移动2个单位,第三次移动8个单位,求正三角形的边长。
10. 一个椭圆形沿y轴正方向移动,移动到一个长方形上方恰好横跨长方形的两个端点,求已经移动了多少个单位。
七年级下册数学的压轴题

1.下面哪个数是 8 和 12 的最小公倍数?
A.24
B.36
C.48
D.60
2.如果 3x - 7 = 11,那么 x 的值是多少?
A. 4
B. 6
C.8
D.9
3.一个三角形的三个内角分别为 50°、60°和多少度?
A.70°
B.80°
C.90°
D.100°
4.一辆汽车以每小时 60 公里的速度行驶,4 小时后行驶了多少公里?
A.120 公里
B.180 公里
C.240 公里
D.300 公里
5.一个正方形的边长是 7 厘米,它的面积是多少平方厘米?
A.49 平方厘米
B.54 平方厘米
C.56 平方厘米
D.63 平方厘米
6.如果一个圆的半径是 5 厘米,则它的直径是多少厘米?
A. 5 厘米
B.10 厘米
C.15 厘米
D.20 厘米
7.下列哪个数是 7 的平方?
A.49
B.56
C.64
D.72
8.一个长方体的长是 8 厘米,宽是 5 厘米,高是 4 厘米,它的体积是多少立方厘米?
A.160 立方厘米
B.180 立方厘米
C.200 立方厘米
D.240 立方厘米
9.如果一个数的 25% 是 15,那么这个数是多少?
A.50
B.60
C.75
D.80。
七年级下册数学期末复习压轴题 解答题试题及答案解答

七年级下册数学期末复习压轴题解答题试题及答案解答1.如图,AB∥CD,点E、F在直线AB上,G在直线CD 上,且∠EGF=90°,∠BFG=140°,求∠XXX的度数.解:由XXX,得∠XXX∠CGE,又∠BFG=140°,所以∠CGE=140°.2.已知x+$\frac{1}{x}$=$\frac{2}{3}$,求值;解:将x+$\frac{1}{x}$=$\frac{2}{3}$两边同时乘以x,得x²+1=$\frac{2}{3}$x,移项化简得3x²-2x-3=0,解得x=1或x=-$\frac{3}{2}$,所以所求值为1或-$\frac{3}{2}$.3.已知关于x、y的二元一次方程组begin{cases} 2x+y=k\\ x+2y=-1 \end{cases}$的解互为相反数,求k的值。
解:设x=-a,y=a,代入方程组得begin{cases} -2a+y=k\\ x-2a=-1 \end{cases}$解得a=$\frac{1}{3}$,y=-$\frac{1}{3}$,k=$\frac{4}{3}$.4.分解因式:1) x²-2xy+xy=x²-xy;2) 9x²-6x(y+1)+(y+1)=(3x-1)(3x-y-1);3) m²(m-1)+4(1-m)=-(m-2)².5.某口罩加工厂有A,B两组工人共150人,A组工人每人每小时可加工口罩70只,B组工人每小时可加工口罩50只,A,B两组工人每小时一共可加工口罩9300只。
1)求A、B两组工人各有多少人?2)由于疫情加重,A、B两组工人均提高了工作效率,一名A组工人和一名B组工人每小时共可生产口罩200只,若A、B两组工人每小时至少加工只口罩,那么A组工人每人每小时至少加工多少只口罩?解:(1)设A组工人有x人,B组工人有150-x人,则70x+50(150-x)=9300解得x=90,150-x=60,所以A组工人有90人,B组工人有60人.2)设A组工人每人每小时可加工a只口罩,B组工人每人每小时可加工b只口罩,则a+b=20070a+50b≥解得a≥100,所以A组工人每人每小时至少加工100只口罩.6.已知下列等式:①32-12=8。
七年级下期末数学压轴题

1.已知三个非负数a 、b 、c 满足325a b c ++=和231a b c +−=,若37m a b c +−,求m 的最大值和最小值.【答案】提示:由已知条件得325213a b c a b c +=−+=+ ,解得73711a c b c =− =− ,则32m c =−,由000a b c≥≥≥得73071100c c c −−≥≥≥,解得37711c ≤≤.故m 的最大值为111−,最小值为57−.2.将若干由l 开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为4537,问删去的那个数是多少?分析 设所写的数为l ,2,…,n ,删去其中的()1a a n ≤≤,则余下的数的平均数为1245317n a n +++−=− ,由1a n ≤≤,建立n 的不等式组.解 1a n ∴≤≤,()()()1231231231111n n n a n n n n ++++−++++−++++−∴<<−−−即()()()1112142253171n n n n n n −+−<<−−,解得1110510777n ≤≤,106n =或107.当106n =时,46a =;当107n =时,a 为非整数,舍去.3.若正数a 、b 、c 满足不等式组1126352351124c a b c a b c a b a c b <+<<+< <+<,则a 、b 、c 的大小关系是( )A .a b c <<B .b c a <<C .c a b <<D .不确定【答案】B 提示:175871581736232436a c a b c c a a b c a b a b c b c <++<<++<<++<>,,,,517734826a c c cbc b b >>>>>,,. 4.玩具厂用于生产的全部劳力为450个工时,原料为400个单位,生产一个小熊要使用15个工时、20个单位的原料,售价为80元;生产一个小猫要使用10个工时、5个单位的原料,售价为45元.在芳力和原料的限制下合理安排生产小熊、小猫的个数,可以使小熊和小猫总售价尽可能高,请用你所学过的数学知识分析,总售价是否可能达到2200元?【答案】提示:设小熊和小猫的个数分别为x y 、,总售价为z ,则()804551691510450205400z x y x y x y x y =+=++ +≤≤.当总售价为2200z =元时,即为1694403290480x y x y x y += + + ≤≤,也即440163909440164809x x x x − + − + ≤≤,解得1414x ≤≤,故14x =.此时24y =,当1424x y ==,时,801445242200z =×+×=(元) 故安排生产小熊14个、小猫24个可达到总售价2200元.5. (l )把26(1)x x −+展开后得121121211210...a x a x a x a x a +++++,则121086420a a a a a a a ++++++=________;(2)已知2232012...(1)(7)(2)(2)x x a a x a x +−=++++++88(2)a x +,则1234567a a a a a a a −+−+−+【答案】(1)365 【提示】令1x =,由已知等式得12112101a a a a a +++++= ① 令1x =−,由已知等式午1211210729a a a a a −++−+=② ①+②得()1210202730a a a a ++++= ,即121020365a a a a ++++= . (2)58− 提示:令3x =−,得01234567832a a a a a a a a a =−+−+−+−+,令2x =−,得027a −=,比较两边x 的最高次项系数可得81a =,原式2713258=−+−=−. 6.已知252000x =,802000y =,则11x y+等于( ). A .2B .1C .12D .32【答案】B 【提示】252000xy y = ①,802000xy x = ②,①×②得()25802000xyx y +×=,得xy x y =+.7.已知252510a b c d ⋅−⋅=,求证:()()()()1111a d b c −−=−−).【提示】由已知有251025a b ⋅==×,得11251a b −−⋅=,故()1111251d a b d −−−−⋅=.同理可得()1111251b c d b −−−−⋅=,从而()()()()()()()()111111112525a d b d c b d b −×−−−−×−−−⋅=⋅,即()()()()111122a d c b −−−−=,故()()()()1111a d c b −−=−−.8.若非零实数a b ,(a b ≠)满足220070a a −+=,220070b b −+=,则11a b+=____________. 【答案】12007【提示】两式相减得1a b +=,两式相加得2007ab =. 9.已知3ax by +=,5ay bx −=,则()()2222a b x y ++的值为_________.【答案】34 【提示】原式()()22ax by ay bx =++−10.若a b 、满足5||7b =,则3||s b =−的取值范围是___________.【答案】211453−s ≤≤【提示】由条件得215191430=+=−s b s ,,则21501430+− s s ≥≥,解得211453−s ≤≤ 11.已知实数m n p 、、满足等式⋅,求p 的值.分析0,a ≥0)挖掘隐含条件. 解 由19901990m n m n −+ −−≥≥得199199m n +≤≤,∴199m n +=①0= 又由非负数性质,得3520230m n p m n p +−−=+−= ① ② 解由①②③联立的方程组得201p =.12.如图,已知B 是线段AC 上的一点,M 是线段AB 的中点,N 是线段AC 的中点,P 为NA的中点,Q 为MA 的中点,则MN PQ ∶等于( ).A .1B .2C .3D .4【答案】B 提示:1()2MN AN AM PQ PA QA AN AM =−=−=−,. 思路点拨 利用中点,设法把MN PQ 、用含相同线段的代数式表示.13.如图,C 是线段AB 的中点,D 是线段AC 的中点,已知图中所有线段的长度之和为23,求线段AC 的长度.【答案】7313 提示:设AC x =,则32222x x AD AB x DC DB x CB x =====,,,,,由题意得:113223222x x x x x x +++++=. 14.平面内有若干条直线,当下列情况时,可将乎面最多分成几部分? (1)有一条直线时,最多可分成2部分. (2)有两条直线时,最多可分成4部分.CB NM P QADCBA(3)有三条直线时,最多可分成____部分. (4)有n 条直线时,最多可分成____部分.【答案】7;222n n ++ 15.把一张长方形纸条按图中那样折叠后,若得到70AOB ∠′=°,则B OG ∠′=______.【答案】55°16. (1)O 为平面上一点,过点O 在这个平面上引2005条不同的直线1l ,2l ,3l ,…,2005l ,则可形成______对以点O 为顶点的对顶角.(2)若平面上4条直线两两相交,且无三线共点,则一共有_____对同旁内角.【答案】(1)设过O 点的n 条不同直线可形成n a 对对顶角,2n =时,223a n ==,时,32224a a n +×,时, 4323...a a =+×,,20052004220042200422003...24232221a a =+×=×+×++×+×+×+×200520044018020=×=.(2)共有12条线段,有21224×=对同旁内角.17.如图,直线AB CD ∥,30EFA ∠°=, 90FGH ∠=°,30HMN ∠=°,50CNP ∠=°,则GHM ∠的大小是______.【答案】40° 提示:过G 作RG ∥AB ,过点H 作HT CD 交MN 于T ,则GHM GHT MHT ∠=∠−∠.18.分解因式:32(21)x a x ++2(21)a a x ++−2(1)a +−.分析 因a 的最高次数低于x 的最高次数,故将原式整理成字母a 的二次三项式.(第3题)B 'C ' GODC BAa 30°50° M GH P N FE DCBA (第14题)解 原式2232(1)(22)(1)x a x x a x x x =+++++−− 22(1)2(1)(1)(1)x a x x a x x =+++++− 22(1)(21)x x ax a =+++− (1)(1)(1)x x a x a =++++−19.分解因式:2(1)(3)(5)12x x x −+++= .【答案】22(43)(41)x x x x +−++ 20.把下列各式分解因式:(1)4271x x −+;(2)42221x x ax a +++−; (3)4322321x x x x ++++.思路点拨 所给多项式,或有两项的平方和、或有两项的积的2倍,只需配上缺项,就能用配方法恰当分解.【答案】(1)原式422222219(1)(3)x x x x x =++−=+−22(31)(31)x x x x =++−+ (2)原式=4222222212(1)()x x x ax a x x a ++−+−=+−−=2(1)x x a ++−2(1)x x a −++ (3)原式=22(1)x x ++21.计算下列各题:(1)(252)(472)(692)(8112)(199419972)(142)(362)(582)(7102)(199319962)++++++++++××××…×××××…×;(2)32322000220001998200020002001−−+−×; (3)4444444444(764)(1564)(2364)(3164)(3964)(364)(1164)(1964)(2764)(3564)++++++++++. 思路点拨 观察分子、分母数字间的特点,用字母表示数,从一般情形考虑,通过分解变形,寻找复杂数值下隐含的规律.对于(3),运用44222222264(1664)16(8)(4)(48)(48)a a a a a a a a a a +=++−=+−=++−+的结果.【答案】()()()()21232312+−=++=++n n n n n n 考虑一般性:()()()()()()()()()()34567891019951996998.2345678919941995×⋅××⋅××=×⋅×××⋅×× 原式=(2)设2000=a ,则原式()()()322322a 2a a 2(a 2)a 1a 21998666.a a (a 1)a 12001667a 1(a 1)−−−−−−=−===+−+++−(3)原式=(378)(7118)(11158)(15198)(35398)(39438)(138)(378)(7118)(11158)(31358)(35398)×+×+×+×+×+×+−×+×+×+×+×+×+39438337138×+=−×+. 22. (1)当x 分别取值12007,12006,…,12,1,2,…,2006,2007时,求出代数式2211x x −+的值,将所得的结果相加,其和等于( ). A .-1 B .1 C .0 D .2007(2)已知0a b c ++=,1114a b c ++=−,那么222111a b c++的值为( ). 思路点拨 对于(1),取值成对互为倒数,不妨先计算2222111111x x x x− − +++ ;对于(2),由222222111111a b c a b c ++=++想到完全平方公式. 【答案】().01111111111 122222222=+−++−=+−++−x x x x x x x x C 提示:选().162161112111 22=++×−= ++− ++abc c b a bc ac ab c b a C 提示:原式=选 23. (1)若x 取整数.则使分式6321x x +−的值为整数的x 的值有 个. (2)求最大的正整数n ,使得3n +100能被n +10整除. 分析 因相关分式中分子的次数大于或等于分母的次数,故可用分离整数法解题.对于(2),通过将整式整除的问题转化为一个分式问题来加以解决. 解 (1)原式=3+621x −,由题意得(21)x −|6,2x -1=±1,±2,±3,±6,只有当2x -1=±1,±3,x 才为整数,即满足条件的x 有4个.(2)∵332100(1000)90090010100101010n n n n n n n ++−==−+−+++为整数, ∴(n +10)|900,从而x 的最大值为890. 24.(1)设a 、b 、c 均为非零实数,并且2()ab a b =+,3()bc b c =+,4()ca c a =+,则a b c ++= ;(2)(上海市竞赛题)计算:222212110050022005000+++−+−+221005000k k k +−+22999999005000−+. 解 (1)对已知三式取倒数,得112()ab a b =+,113()bc b c =+,114()ca c a =+.∴111211131114a b b c c a +=+=+=解得245a =,247b =,24c =.∴24241128245735a b c ++=++=. (2)∵2222(100)1005000(100)100(100)5000n n n n n n −+−+−−−+=222200100001005000n n n n −+−+=2,而225050501005000−×+=1∴原式=49×2+1=99.25.(1)若使分式241312a a a−++没有意义,则a 的值为 .(2)若分式22123b b b −−−的值为0,则b 的值为 .【答案】(1)0或15− (2)126.已知115x y+=,则2522x xy yx xy y −+++= . 【答案】5727.若2310x x −+=,则2421x x x ++的值为 . 【答案】18提示:由条件可得13x x +=. 28.甲、乙两个公司用相同的价格购粮,他们各购两次,已知两次的价格不同,甲公司每次购粮1万千克,乙公司每次用1万元购粮,那么两次平均价格较低的是哪个公司?【答案】这两次购粮的价格分别为x 元/千克和y 元/千克(x y ≠),则甲公司两次购粮的平均价格为:1000010000200002x y x y++=,乙公司两次购粮的平均价格为:2000021000010000xy x y x y =++.因22()022()x y xy x y x y x y +−−=>++,故两次平均价格较低的是乙公司.29. (1)如果242114x x x =++,那么42251553x x x −+= ; (2)若a b c d b c d a ===,则a b c da b c d−+−+−+的值是 .思路点拨 对于(1),由条件出发,先求出221x x +的值;对于(2),引入参数,利用参数寻找a 、b 、c 、d 的关系.【答案】()03)31(5,31122=−+=+x x xx 原式=由条件得. (2)设a b c dk b c d a ====,则2d ak c dk a k ===⋅,,34b c k a k a b k a k =⋅=⋅=⋅=⋅,,得41k =,即1k =±,当1k =时,a b c d ===,原式=0;当1k =−时,原式=2−.30.(1)若关于x 的方程1221(1)(2)x x ax x x x x ++−=+−−+无解,求a 的值. 分析 原方程“无解”内涵丰富:可能是化得的整式方程无解.亦可能是求得的整式方程的解为增根,故须全面讨论. 解 原方程化为(2)3a a +=−, ①∵原方程无解,∴20a +=或10x −=,20x +=, 得2a =−或1,2x x ==−.把1,2x x ==−分别代入①,得15,2a a =−=−, 综上知a =-2,-5或12−.(2)解下列分式方程: ① 18272938x x x x x x x x +++++=+++++; ②222111132567124x x x x x x x ++=+++++++.思路点拨 若去分母化为整式方程,则显然较繁.对于(1),分别计算等号左右两边或分离整数;对于(2),把等号左边的每个分式拆项.【答案】(2)①,811311911211+−++−=+−++−x x x x 原方程化为 即1111-,(x 2)(x 3)(x 8)(x 9),329x 8x x x −=++=++++++进一步化为 11x -. 2=解并检验得 ②111111112,,122334444x x x x x x x x x −++−==+++++++++原方程化为--即 2.x =解并检验得31.已知:1ax by cz ===,求444444111111111111a b c x y z +++++++++++的值. 【答案】由条件有:111x y z a b c===,,,于是 44444441111111111111a a x a a a a +=+=+=++++++,原式=3.32.已知实数p 、q 、r 满足26p q r ++=,11131p q r++=,则p q r p r q p r p r q p +++++= .【答案】803 提示:把条件中的两个等式相乘.33.已知x y z uy z u z u x u x y x y z ===++++++++,求x y y z z u u x z u u x x y y z +++++++++++的值. 【答案】由条件,得.x y z u x y z u x y z u x y z uy z u z u x u x y x y z ++++++++++++===++++++++(1)0,111 1 4x y z u x y z u +++≠===+++若,则由分母推得原式==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AEBDFC七年级数学下册期中压轴题1、如图,一条直线1l ,最多将平面分成两块,两条直线1l 、2l 相交,最多将平面分成4块,三条直线1l 、2l 、3l 最多将平面分成7块,…,则9条直线1l 、2l 、…,9l 最多将平面分成( )块。
A .49 B .48C .47D .462、已知直线AB ∥CD ,交直线EF 于E 、F 两点,点P 为直线EF 右边平面上一点,且∠AEP=160°,∠EPF=45° ,则∠CFP 的度数为 .3、已知如图,△ABC 中,A (m ,n ),B (-4,-1),C (a ,b ),且满足条件22+-=b a ,032=-++n m (本题11分)(1)写出A 、C 的坐标,并画出△ABC. (3分) 1l1l2l1l2l3l(2)P 为坐标轴上一点,且△PBC 的面积等于6,直接写出满足条件的所有P 的坐标,并根据所学过的初一、小学知识选一个P 点坐标写出求解过程.(5分)(3)将AB 平移到A′B′使B′(4,0).现让点C 沿x 轴负方向运动,点N 从点A′出发,沿A′A 方向运动,且点N 的速度比点C 慢.当点C 到达点(-3,0)时,点C 、N 同时停止(自己在坐标系中完成图形). 问:点N 、C 在运动过程中,AB N ACN B CN BAC ''∠+∠'∠+∠的值是否变化?如不变,求其值;如变化,说明理由.(3分)NMH G FE D CBA4、学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( ) ①两直线平行,同位角相等;②两直线平行,内错角相等; ③同位角相等,两直线平行;④内错角相等,两直线平行. A .①② B .②③ C .③④ D .①④5、如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠MND=50°,则∠GHM 的大小是 .6、如图1,已知AB ∥CD ,点M 、N 分别是AB 、CD 上两点,点G 在AB 、CD 之间 (1)求证:∠BMG+∠GND=∠MGN.(2)如图2,点E 是AB 上方一点,MF 平分∠AME ,若点G 恰好在MF 的反向延长线上,且NE 平分∠CNG ,2∠E 与∠G 互余,求∠AME 的大小(3)如图3,在(2)的条件下,若点P 是EM 上一动点,PQ 平分∠MPN ,NH 平分∠PNC ,交AB 于点H ,PJ ∥NH 当点P 在线段EM 上运动时,∠JPQ 的度数是7、在平面直角坐标系中,点B (0,4),C (-5,4),点A 是x 轴负半轴上一点,S 四边形AOBC =24. (1)线段BC 的长为 ,点A 的坐标为 ;GNMDCBAABCDACN(2)如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF ⊥AE 点F ,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)若点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON 平分AOP ∠,BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.8、江汉区某中学组织七年级同学参加校外活动,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车刚好坐满.已知45座和60座客车的租金分别为220元/辆和300元/辆.(1)设原计划租45座客车x 辆,七年级共有学生y 人,则y = (用含x 的式子表示);若租用60座客车,则y = (用含x 的式子表示); (2)七年级共有学生多少人?(3)若同时租用两种型号的客车或只租一种型号的客车,每辆客车恰好坐满并且每个同学都有座位,共有哪几种租车方案?哪种方案更省钱?9、如图1,在平面直角坐标系中,A (a ,0),B (b ,0),C (-1,2),且221(24)0a b a b ++++-=.(1)求a ,b 的值;(2)①在x 轴的正半轴上存在一点M ,使△COM 的面积=12△ABC 的面积,求出点M 的坐标;②在坐标轴的其它位置是否存在点M ,使△COM 的面积=12△ABC 的面积仍然成立,若存在,请直接写出符合条件的点M 的坐标;(3)如图2,过点C 作CD ⊥y 轴交y 轴于点D ,点P 为线段CD 延长线上一动点,连接OP ,OE 平分∠AOP ,OF ⊥OE .当点P 运动时,DOEOPD∠∠的值是否会改变?若不变,求其值;若改变,说明理由.F EDCBA10、已知,四边形ABCD 中,AD ∥BC ,∠A =∠BCD =∠ABD ,DE 平分∠ADB ,下列说法:①AB ∥CD ;② ED ⊥CD ;③S △EDF =S △BCF .其中错误的说法有( )A .0个B .1个C .2个D .3个11、如图,直线EF ∥GH ,点B 、A 分别在直线EF 、GH 上,连接AB ,在AB 左侧作三角形ABC ,其中∠ACB = 90°,且∠DAB =∠BAC ,直线BD 平分∠FBC 交直线GH 于D . (1)若点C 恰在EF 上,如图1,则∠DBA =________.(2)将A 点向左移动,其它条件不变,如图2,则(1)中的结论还成立吗?若成立,证明你的结论;若不成立,说明你的理由. CABDFHEGCBFEGADH图1 图2(3)若将题目条件“∠ACB = 90°”,改为:“∠ACB = 120°”,其它条件不变,那么∠DBA = _________.(直接写出结果,不必证明) (2分)12、如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足02)2(2=-++b a ,过C 作CB ⊥x 轴于B .(1)求三角形ABC的面积.(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等,若存在,求出P 点坐标;若不存在,请说明理由.图1 图2 备用图13、已知∠AOB 与∠BOC 互为邻补角,且∠BOC >∠AOB . OD 平分∠AOB ,射线OE 使12BOE EOC ∠=∠,当∠DOE =72°时,则∠EOC 的度数为( )A .72°B .108°C .72°或108°D .以上都不对14、如图,点E 在直线BH 、DC 之间,点A 为BH 上一点,且AE ⊥CE ,∠DCE-∠HAE=90°.(1)求证:BH ∥CD.(2)如图:直线AF 交DC 于F ,AM 平分∠EAF ,AN 平分∠BAE.试探究∠MAN ,∠AFG 的数量关系. EHA BGC DBAH15、如图,点A(a,6)在第一象限,点B(0,b)在y轴负半轴上,且a,b满足:2a b-++=.(|4|0(1)求△AOB的面积.(2)若线段AB与x轴相交于点C,在点C的右侧,x轴的上是否存在点D,使S△ACD=S△BOC,若存在,求出D点坐标,若不存在,请说明理由.(3)若∠AOx轴=60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线OB绕B 点以每秒10°的速度顺时针旋转到O′B,当OB转动一周时两者都停止运动. 若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥O′B?16、如图:AB ∥CD ,OE 平分∠BOC ,OF ⊥OE ,OP ⊥CD , ∠ABO =40°,则下列结论:①OF 平分∠BOD ②∠POE =∠BOF ③∠BOE =70° ④∠POB =2∠DOF ,其中结论正确的序号是( ) A .①②③④ B .只有①③④ C .只有①②③ D .只有①④17、如图:已知在平面直角坐标系中点A (a ,b )点B (a ,0),且满足+=0.(1)求点A 、B 的坐标.(2)已知点C (0,b ),点P 从点B 出发沿x 轴正方向以1个单位每秒的速度移动,同时点Q 从点C 出发沿y 轴负方向以2个单位每秒的速度移动,某一时刻,如 FPEODCBA图所示且S阴=S四边形OCAB,求点P移动的时间.18、A.64B.49C.100D.811920、21、AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合).∠ABC=n°,∠ADC=80°.(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示);(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.BAEDC22、长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.(1)求点B的坐标;(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标;(3)如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的平分线CD交BM的延长线于点D,在点N运动的过程中,D CNM ∠∠的值是否变化?若不变,求出其值;若变化,请说明理由.图1 图223、24、25、26、精品文档精品文档。
