大连理工大学大二复变函数期末试题
复变函数期末试卷及答案2套

1 复变函数与积分变换(B 卷)(答案写在答题纸上,写在试题纸上无效)一、单项选择题(每小题3分,共30分) 1.设1z =,则( )A .||1,arg 3z z π== B .||2,arg 3z z π==- C .||2,arg 3z z π== D .||4,arg 3z z π==-2.下列等式成立的是( ) A .1i e π=- B .1i eπ--=- C .1i e π-=- D .21ieπ=-3.函数2()||f z z =在复平面上( )A .处处不连续B .处处连续,在点0z =解析C .处处连续,处处不可导D .处处连续,仅在点0z =可导 4.下列复数中为实数的是( )A 3(1)i -B ln iC ii D 5.设C 为从0z =到1z i =+的直线段,则积分Czdz =⎰( )A .-1B .0C .1D .1i +6. 设C 为正向单位圆周||1z =,则积分z Ce dz =⎰( ).A .1B .2πC .0D .2i π7. 设C 是绕点0z 的正向简单闭曲线,则积分53()C z dz z z =-⎰ ( ).A .0B .2i πC .502z i πD .3020z i π8.函数1()2f z z=+ 在点00z =的泰勒展开式为 ( ) A.10(1)2n nnn z +∞=-∑ B. 1(1)2n nn n z ∞+=-∑ C. 02n n n z ∞=∑ D.12nn n z ∞=∑ 9. 0z =是函数3sin ()z zf z z-=的( ) A .本性奇点 B .可去奇点 C .一级极点 D .二级极点课程考试试题学期 学年 拟题学院(系): 适 用 专 业:10.设1()(2)zf z z e =+,则Re [(),0]s f z =( ) A .12 B .32 C .2 D .52二、填空题(每空3分,共15分)1 设复数z 满足(2)3i z +=,则z =__________。
复变函数期末考试及答案(珍藏版)

一、填空题1、设12z =,则||z = 1 ,Argz =2,0,1,3k k ππ-+=± . 2、曲线422=+y x 在映射z1=ω下的象为2214u v +=.(写出象曲线的方程) 3、设(1)(1,2,)4n n ni n n α-+==+ 则lim n n α→∞=i . 4、=Z k k i k ∈+),32sin()32cos(ππ.5、函数()f z 在z 点可导是()f z 在z 点解析的 必要不充分 条件.(填充分必要性)6、若幂级数0n nn c z ∞=∑在12z i =+处收敛,则该级数在2z =处的敛散性为绝对收敛 .7、|2|12zz e dz z -==-⎰22ie π. 8、0=z 是函数5sin )(z z z z f -=的 2 阶极点。
9、若1()sin f z z =,则0Res ()z f z == 1 。
二、计算题1、设C 为连接0到2a π的摆线,(sin ),(1cos )x a y a θθθ=-=-,求积分2(281)C z z dz ++⎰.解:由于函数2281z z ++在整个z 平面上解析,故 2220(281)(281)a C z z dz z z dz π++=++⎰⎰3223320216(4)|16233a a z z z a a a ππππ=++=++2、判别级数∑∞=1n nn i 是否绝对收敛,是否收敛.解:因为:∑∑∞=∞==111||n n n n n i 发散,故级数 ∑∞=1n n n i 不绝对收敛.由于∑∑∑∞=∞=∞=+==11212sin 2cos )(n n n in n n n i n n e n i πππ ∑∑∞=∞=+=112s i n 2c o s n n n n i n n ππ 而∑∞=12cos n n n π,∑∞=12sin n n n π都为收敛级数,所以原级数收敛, 故原级数条件收敛。
(完整word版)《复变函数》考试试题与答案各种总结(2)

《复变函数》考试试题(一)一、 判断题(20分):1.若f(z)在z 0的某个邻域内可导,则函数f (z)在z 0解析. ( ) 2。
有界整函数必在整个复平面为常数. ( ) 3。
若}{n z 收敛,则} {Re n z 与} {Im n z 都收敛。
( )4.若f(z)在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数). ( )5。
若函数f(z)在z 0处解析,则它在该点的某个邻域内可以展开为幂级数。
( ) 6。
若z 0是)(z f 的m 阶零点,则z 0是1/)(z f 的m 阶极点. ( ) 7.若)(lim 0z f z z →存在且有限,则z 0是函数f (z)的可去奇点。
( )8.若函数f(z)在是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠. ( ) 9。
若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f .( )10。
若函数f(z)在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数。
( ) 二.填空题(20分)1、 =-⎰=-1||00)(z z nz z dz__________.(n 为自然数)2。
=+z z 22cos sin _________. 3。
函数z sin 的周期为___________.4。
设11)(2+=z z f ,则)(z f 的孤立奇点有__________。
5。
幂级数0n n nz ∞=∑的收敛半径为__________。
6。
若函数f (z)在整个平面上处处解析,则称它是__________.7.若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________。
8.=)0,(Re n zz e s ________,其中n 为自然数。
9. zz sin 的孤立奇点为________ 。
10.若0z 是)(z f 的极点,则___)(lim 0=→z f z z .三。
复变函数期末试题及答案

复变函数期末试题及答案一、选择题(每题5分,共20分)1. 若复数 \( z = a + bi \)(其中 \( a, b \) 为实数),则\( \bar{z} \) 表示()A. \( a - bi \)B. \( -a + bi \)C. \( -a - bi \)D. \( a + bi \)答案:A2. 对于复变函数 \( f(z) = u(x, y) + iv(x, y) \),以下说法正确的是()A. \( u \) 和 \( v \) 都是调和函数B. \( u \) 和 \( v \) 都是解析函数C. \( u \) 和 \( v \) 都是连续函数D. \( u \) 和 \( v \) 都是可微函数答案:A3. 若 \( f(z) \) 在 \( z_0 \) 处可导,则下列说法中正确的是()A. \( f(z) \) 在 \( z_0 \) 处解析B. \( f(z) \) 在 \( z_0 \) 处连续C. \( f(z) \) 在 \( z_0 \) 处可微D. \( f(z) \) 在 \( z_0 \) 处的导数为0答案:C4. 已知 \( f(z) \) 是解析函数,且 \( f(z) \) 在 \( z_0 \) 处有孤立奇点,则 \( f(z) \) 在 \( z_0 \) 处的留数是()A. 0B. \( \infty \)C. 1D. \( -1 \)答案:A二、填空题(每题5分,共20分)1. 若 \( z = x + yi \),且 \( |z| = 2 \),则 \( x^2 + y^2 = \_\_\_\_\_ \)。
答案:42. 设 \( f(z) = z^2 \),则 \( f(2 + 3i) = \_\_\_\_\_ \)。
答案:-5 + 12i3. 若 \( f(z) \) 在 \( z_0 \) 处解析,则 \( f(z) \) 在 \( z_0 \) 处的导数 \( f'(z_0) \) 等于 \_\_\_\_\_。
复变函数期末考试复习题及答案详解

《复变函数》考试试题(一)三 . 计算题( 40 分):dz1、|z z 0 | 1 ( z z )n__________. ( n 为自然数)f ( z)12.sin 2 z cos 2z _________.3. 函数sin z的周期为 ___________.f (z)14. z 2 1 ,则f ( z)的孤立奇点有 __________.设 5. 幂级数nz n的收敛半径为 __________.n 06. 若函数 f(z) 在整个平面上处处解析,则称它是__________.lim z nlimz 1z 2 ... z n7. 若 n,则 nn ______________.Res(ez8.n,0)z________,其中 n 为自然数 .9.sin z的孤立奇点为 ________ .z10. 若zlimf (z) ___是f (z) 的极点,则z z.1. 设( z 1)( z 2) ,求 f ( z) 在 D { z : 0 | z | 1}内的罗朗展式 .1dz.2.|z| 1cos zf ( z) 3 2 71,其中 C { z :| z |3} ,试求 f '(1 i ).3.d设Czwz 14. 求复数 z 1 的实部与虚部 .四 . 证明题 .(20 分 )1. 函数f (z)在区域 D 内解析 . 证明:如果 | f ( z) |在 D 内为常数, 那么它在 D 内为常数 .2. 试证 :f (z)z(1 z) 在割去线段 0 Re z 1 的 z 平面内能分出两个单值解析分支 , 并求出支割线 0 Re z 1 上岸取正值的那支在 z 1 的值 .《复变函数》考试试题(二)二. 填空题 . (20 分)1.设z i ,则| z |__,arg z__, z__2.设 f ( z)(x2 2 xy) i (1 sin( x2y2 ), z x iy C,则lim f (z)________.z1idz_________. (n为自然数)3.|z z0 |1 ( z z )n4.幂级数nz n的收敛半径为 __________ .n05.若 z0是 f(z) 的 m 阶零点且 m>0,则 z0是f ' ( z)的 _____零点 .6.函数 e z的周期为 __________.7.方程 2z5z33z 8 0 在单位圆内的零点个数为________.18.设 f ( z)1z2,则 f ( z) 的孤立奇点有_________.9.函数 f (z)| z |的不解析点之集为________.10.Res( z41,1)____ . z三.计算题 . (40 分)1.求函数sin(2z3)的幂级数展开式 .2. 在复平面上取上半虚轴作割线 . 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点z i 处的值.计算积分: Ii1)单位圆(| z |1)3.| z | dz,积分路径为(i的右半圆 .sin zdzz22( z)4.求2.四. 证明题 . (20 分)1.设函数 f(z) 在区域 D 内解析,试证:f(z)在 D 内为常数的充要条件是 f ( z)在D内解析.2.试用儒歇定理证明代数基本定理 .《复变函数》考试试题(三)二. 填空题 .(20 分)11.设 f ( z),则f(z)的定义域为___________.z212.函数 e z的周期为_________.3.若 z nn 2 i (1 1 )n,则 lim z n __________.1 nn n4. sin 2 z cos 2z___________.dz5.|z z 0 | 1 ( z z )n_________. ( n 为自然数)6.幂级数nx n的收敛半径为 __________.n 07.设f (z)1,则 f ( z ) 的孤立奇点有 __________.z218. 设ez1,则 z___ .9.若z 0 是 f (z) 的极点,则 limf ( z) ___ .z z 010.Res( e z,0)____.z n三. 计算题 . (40分)11.将函数 f ( z)z 2e z在圆环域 0z内展为 Laurent 级数 .n!n2. 试求幂级数nnz的收敛半径 .n3. 算下列积分:e zdz,其中C 是| z| 1.Cz 2 (z29)4. 求z 9 2z 6z28z 2 0 在 | z |<1内根的个数 .四 . 证明题 . (20 分)1.函数f (z)在区域 D 内解析 . 证明:如果 | f ( z) |在 D 内为常数,那么它在D 内为常数 .2.设f (z) 是一整函数,并且假定存在着一个正整数n ,以及两个正数R 及 M ,使得当| z|R 时| f (z) |M | z |n ,证明f (z) 是一个至多 n 次的多项式或一常数。
大工《复变函数与积分变换》课程考试模拟试卷A答案

机 密★启用前大连理工大学网络教育学院2014年8月份《复变函数与积分变换》课程考试 模拟试卷答案考试形式:闭卷 试卷类型:A一、单项选择题(本大题共10小题,每小题2分,共20分)1、B2、C3、C4、D5、B6、D7、B8、A9、C10、A二、填空题(本大题共10小题,每小题3分,共30分)1、)]5sin(ln )5[cos(ln 5ln i e +2、k ek (22ππ--为整数)3、3,2,1,0)]216sin()216[cos(28=+++k k i k ,ππππ4、2ln5、e i 2-和e i26、07、28、i π29、i π2 10、sin 2三、计算题(本大题共5小题,每小题8分,共40分)1、先把括号中的两个复数化成三角式:)3sin 3(cos231ππi i +=+(1分) ))3sin()3(cos(231ππ-+-=-i i (1分) 再由复数的除法和求乘幂的方法,得1010))3sin()3(cos(2)3sin 3(cos 23131⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-+=⎪⎪⎭⎫⎝⎛-+ππi i i i (2分)10)33sin()33cos(⎥⎦⎤⎢⎣⎡+++=ππππi (2分)ππ320sin 320cos i +=i 2321+-=(2分) 2、22221211)1)(1()1(11n nin n ni ni ni ni ni z n +++-=+-+=-+=(2分)22212,11nn y n n x n n +=+-=(2分) 而0lim ,1lim =-=∞→∞→n n n n y x (2分)因此1lim -=∞→n n z ,即复数列niniz n -+=11收敛于-1(2分) 3、因zz z1sin 1cos1cot =,在πk z =1处,即0),,2,1(1=±±==z k k z kπ处z 1cot 不解析(4分),且 0lim =∞→k k z ,故0不为z1cot 的孤立奇点。
(完整)《复变函数与积分变换》期末考试试卷及答案,推荐文档

(完整)《复变函数与积分变换》期末考试试卷及答案,推荐⽂档23∞ ?复变函数与积分变换?期末试题(A)1.1 -i⼀.填空题(每⼩题3 分,共计15 分)的幅⾓是();2. Ln(-1 +i) 的主值是(1);3.f (z) =1 +z 2,z - sin z f (5)(0) =();f (z) =1,4.z = 0 是z 4 的()极点;5.z Re s[f(z),∞]=();⼆.选择题(每⼩题3 分,共计15 分)1.解析函数f (z) =u(x, y) +iv(x, y) 的导函数为();(A)f '(z) =u x +iu y ;(B)f '(z) =u x-iu y;(C) f '(z) =ux+ivy ;(D) f '(z) =u y +iv x.2.C 是正向圆周z = 3 ,如果函数f (z) =(),则?C f (z)d z = 0 .3;(B)3(z -1);(C)3(z -1);(D)3.n=1(A)z =-2 点条件收敛;(B)z = 2i 点绝对收敛;(C)z = 1 +i 点绝对收敛;(D)z = 1 + 2i 点⼀定发散.4.下列结论正确的是( )(A)如果函数f (z) 在z0点可导,则f (z) 在z0点⼀定解析;得分e(B) 如果 f (z ) 在 C 所围成的区域内解析,则 ?C f (z )dz = 0(C )如果 ?C f (z )dz = 0 ,则函数 f (z ) 在 C 所围成的区域内⼀定解析;(D )函数 f (z ) = u (x , y ) + iv (x , y ) 在区域内解析的充分必要条件是u (x , y ) 、v (x , y ) 在该区域内均为调和函数. 5.下列结论不正确的是().(A) ∞为sin 1的可去奇点 z(B) ∞为sin z 的本性奇点 ∞为 1 的孤⽴奇点; ∞ 1 (C) sin 1z(D) 为的孤⽴奇点. sin z三.按要求完成下列各题(每⼩题 10 分,共计 40 分)(1)设 f (z ) = x 2 + axy + by 2 + i (cx 2 + dxy + y 2 ) 是解析函数,求a ,b ,c ,d .z(2).计算 ?Cz (z - 1)2d z 其中 C 是正向圆周: z = 2 ;得分zd z (3)计算? 15z =3 (1 +z 2 )2 (2 +z 4 )3(sin z )3在扩充复平⾯上有什么类型的奇点?,如果有极点,请指出它的级.四、(本题 14 分)将函数 f (z ) = 1z 2 (z - 1)在以下区域内展开成罗朗级得分数;(1) 0 < z - 1 < 1 ,(2) 0 < z < 1 ,(3)1 < z < ∞五.(本题 10 分)⽤ Laplace 变换求解常微分⽅程定解问题 y (x ) - 5 y '(x ) + 4 y (x ) = e -xy (0) = y '(0) = 1得分六、(本题 6 分)求 f (t) e t(0) 的傅⽴叶变换,并由此证明:costt2 2 d 2 e 0复变函数与积分变换?期末试题(A )答案及评分标准⼀.填空题(每⼩题 3 分,共计 15 分)得分3 的幅⾓是( 2k Ln (-1 + i ) ee 1. 1- i 2 - + , k = 0,±1,±2 );2.的主值是( 31 ln2 +3 24 iz - sin z f (z ) =3.1+ z 2 , f(5)(0) = ( 0),4. z = 0 是1 z4的(⼀级)极点;5. f (z ) = z, R e s [ f (z ),∞] =(-1);⼆.选择题(每题 3 分,共 15 分)1----5B DC B D三.按要求完成下列各题(每⼩题 10 分,共 40 分)(1).设 f (z ) = x 2 + axy + by 2 + i (cx 2 + dxy + y 2 ) 是解析函数,求a ,b ,c ,d .解:因为 f (z ) 解析,由 C-R 条件u = vx y u = -vy x2x + ay = dx + 2y ax + 2by = -2cx - dy ,a = 2, d = 2, , a = -2c ,2b = -d ,c = -1, b = -1,给出 C-R 条件 6 分,正确求导给 2 分,结果正确 2 分。
大学《复变函数》试卷及答案
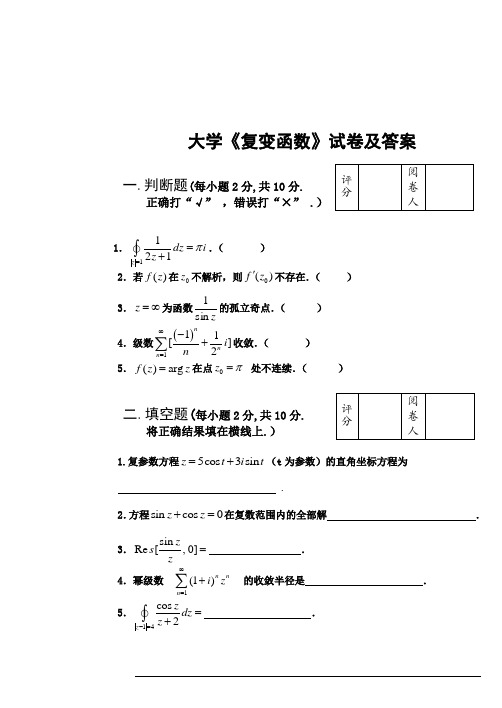
---------------------------- 6分
2.函数 在复平面内何处可导,何处解析,并求
解:设 , 则
.四个偏导数在复平面上都连续,
由C—R方程得: .
故 仅在直线 上可导,在复平面上处处不解析.
--------------------------- 4分
且因为点 在曲线 上,所以 .
大学《复变函数》试卷及答案
一.判断题(每小题2分,共10分.
正确打“√”,错误打“×”.)
评
分
阅
卷
人
1. .()
2.若 在 不解析,则 不存在.()
3. 为函数 的孤立奇点.()
4.级数 收敛.()
5. 在点 处不连续.()
二.填空题(每小题2分,共10分.
将正确结果填在横线上.)
评
分
阅
卷
人
1.复参数方程 (t为参数)的直角坐标方程为
3.下列结论错误的是()
(A) 是函数 的二阶极点.(B) 是函数 的可去奇点.
(C) .(D) 是函数 的本性奇点.
4.下列结论错误的是()
(A)C为不通过原点的简则 也为解析函数.
(C)在点 解析的函数一定可以在点 的邻域内展开成泰勒级数.
(D)对于任意的复数 .
解:由于 在平面上处处解析,所以积分
与路径无关,又 的一个原函数为 ,
---------------------------- 5分
故
= .
------------------------ 7分
2. .
解: 在 内有两个不解析点, 分别为简单极
点、二级极点
,
------------------------ 5分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
_ _
装 订 线
们在D内也处处相等。
2.
复指数函数e z 是单调函数,复三角函数sinz及cosz是无界函数。
3.
因为可微函数的和函数仍是可微函数,所以对于复变函数
f (z) u(x, y) iv(x, y), 当u(x,y)及v(x,y)在点(x,y)可微,则f(z)在点 z=x+iy可微。
三、(8分)设f(z)在C: |z|=1内部解析,且连续到C,在C上|f(z)|<1。试证:在C内部 有且只有一个点z 0 , 使f (z 0 )=z 0 .
A-3
1 四、(10分)将函数 2 在z i的去心邻域展开为洛朗级数,并指出其收敛范围。 2 (z +1)
五、(7分)若f(z)是f(z)是0<|z-a|<R内不恒为常数的解析函数,而且z=a是它的零点 的极限点。 证明:z a是f (z)的本质奇点。
C
无穷可微。
7.复变函数f (z)在点z可微与 f(z)在点 z 解析是等价的。
8.解析函数的虚部和实部互为共轭调和函数。
9.若f(z)在z=0的邻域内可展开为泰勒级数f(z)= cn z n , 则f (z) cn z
n 0 n 0
∞
∞
n
10.若f(z)在z 0的邻域内可展开为泰勒级数f(z)=cn zn , 则f(z) c z
一、计算下列各题(20 分) 。
装 订 线
1. 6 0
2.-i i
3.arccos i
4.(1 i) 20
2 2 二、函数 f (z) x 2 y i 何处连续,何处可导,何处解析(10 分).
B-1
∞ in 三、判断级数 3 的收敛性及绝对收敛性( 10分) . n n 1
B-2
姓名: 学号:
大 连 理 工 大 学
课 程 名 称: 复变函数 试 卷: A 考试形式: 闭卷 试卷共 5 页 总分 100
院系: 级 班
授课院 (系): 数学科学学院 一 标准分 得分 45 二 8 三 8
考试日期:2007 年 6 月 28 日 四 10 五 7 六 12 七 10
一、判断题(45 分) (判断正误(1 分) ,并简单说明理由(2 分) )
四、下列函数在扩充复平面上有哪些奇点,这些奇点的类型是什 么?(10 分)
π z 2 1. cos z
1
2. co s 1
z
五、计算复积分(15 分) 1. c (x iy) dz 其中 c 为从原点到 1-i 的直线段.
2.
e
c
x
dz
其中 c 为以原点为起点,i 为终点的光滑曲线.
B-3
3.
z 2n 1 e z dy (n为正整数)为正向圆周, c z 2. c 1 zn
六、利用留数计算
x sin x dx (12分) 1 x2 ∞
∞
B-4
七、将
1 分别在0< | z | <5,5< | z | <6, 6< | z | < 内展开为洛朗级数. (z 5)(z 6)
B-5
八、设 f(z)在|z-z0|<R 内解析,f(z)在|z-z0|<R 内不恒为零。证明: 存在 r,0<r<R,使 f(z)在 0<|z-z0|<r 内无零点。 (8 分)
B-6
n0
∞
_____
__________ ∞ n n n0
11.函数 f(z)的洛朗展式 cn (z a ) n中的非负幂部分 cn (z a ) n 称为主要部分。
n -∞ n 0
∞
∞
1 12. 在z 0的去心邻域内能展开为洛朗级数。 1 sin z
A-2
二、(8分)讨论复函数f(z)= z 2的单值解析分支情况,并求在z=1取正值的那个分 支在z=i的值。
A-2
n 五、级数 (-1) n 0
∞
1 是否收敛?若收敛,是否绝对收敛? (10分) n
1 六、把 在下列圆环域内展开为洛朗级数 (z-2)(z-3) i)0<|z|<2 ii)2<|z|<3 iii)3<|z|<+∞ iv)0<|z-3|<1
A-3
七、计算下列积分(20分)
2 1.(x +yi)dz,c为起点为0,终点为1+i的有向线段。 c
A-4
姓名: 学号:
大 连 理 工 大 学
课 程 名 称: 复变函数 试 卷: A 考试形式: 闭卷 试卷共 6 页 总 分 100
院系: 级 班
授课院 (系): 数学科学学院
考试日期:2006 年 6 月 24 日
一 标准分 得分 15
二 8
三 10
四 10
五 10
六 12
七 20
八 7
九 8
十 /
4.
在扩充复平面内,单位圆的外部|z|>1是一个单连通区域。
5.
区域D内含有一段实轴,函数u(x,y)+iv(x,y)与u(z,0)+iv(z,0)(z=x+iy)
都在D内解析,则在D内u(x,y)+iv(x,y)=u(z,0)+iv(z,0).
A-1
6. 若f(z)在单连通区域D内连续,且对D内任意周线C有 f (z) dz 0,则f (z)在D内
一、计算下列各题(20 分) 。
1.(1 i)10
装 订 线
2. 3 8
3 .i i
A-1
二、证明sin 2z+cos2 z 1 (8分)
三、判断函数f(z)=x2 y 2 2 xyi的连续性、可导性、解析性。 (10分)
四、已知u (x y)(x 2 4 xy y 2 ), 求v,使f(z)=u+iv在复平面内解析。(10分)
A-4
2.
ex dz , c为正向圆周: |z|=1。 c z2
3. e x dz , c为起点为0,终点为πi的有向光滑曲线。
c
4.
ze x dz , c为正向圆周|z|=2。 c z2 1
A-5
八、若f (z)在开集D内可导,证明: f(z)在D内解析。(7分)
九、设f(z)在复平面内解析,f(z)在复平面内有界。 证明:f(z)在复平面内恒为常数。 (8分)
A-6
姓名: 学号:
Байду номын сангаас
大 连 理 工 大 学
课 程 名 称: 复变函数 试 卷: B 考试形式: 闭卷 试卷共 6 页 总 分 100
院系: 级 班
授课院 (系): 数学科学学院
考试日期:2004 年 1 月 6 日
一 标准分 得分 20
二 10
三 10
四 10
五 15
六 12
七 15
八 8
九 /
十 /
