数字信号处理上机实验(第三版)
《数字信号处理》第三版课后答案(完整版)

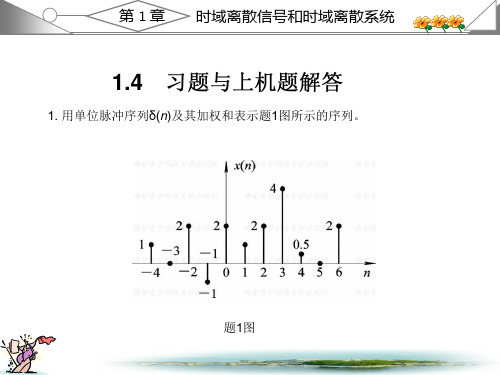
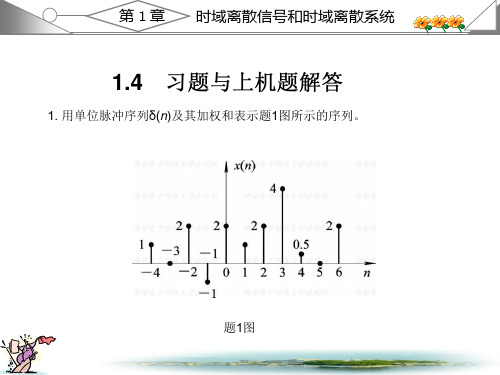
西安电子 ( 高西全丁美玉第三版 ) 数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列 (n) 及其加权和表示 题 1 图所示的序列。
解:x( n)(n4) 2 (n 2) ( n 1)2 (n)(n 1) 2 (n 2) 4 ( n 3)0.5(n 4)2 (n 6)2n 5, 4 n 12. 给定信号: x( n)6,0n 40, 其它(1)画出 x( n) 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示 x(n) 序列;(3)令 x 1( n) 2x(n 2) ,试画出 x 1( n) 波形;(4)令 x 2 (n) 2x(n 2) ,试画出 x 2 (n) 波形;(5)令 x 3 (n) 2x(2 n) ,试画出 x 3 (n) 波形。
解:( 1) x(n) 的波形如 题 2 解图(一) 所示。
( 2)x(n)3 ( n 4)(n 3) (n 2) 3 ( n 1) 6 (n) 6 (n 1)6 ( n 2)6(n 3) 6 (n 4)( 3) x 1 (n) 的波形是 x(n) 的波形右移 2 位,在乘以 2,画出图形如 题 2 解图(二) 所示。
( 4) x 2 (n) 的波形是 x(n) 的波形左移 2 位,在乘以 2,画出图形如 题 2 解图(三) 所示。
( 5)画 x 3 (n) 时,先画 x(-n) 的波形,然后再右移2 位, x3 ( n) 波形如 题 2 解图(四) 所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1) x( n)Acos(3n) ,A 是常数;78(2)x(n)j ( 1n)e 8。
解:(1)w 3214T=14 ;7,,这是有理数,因此是周期序列,周期是w3(2)w 1 , 216 ,这是无理数,因此是非周期序列。
8w5. 设系统分别用下面的差分方程描述,x(n) 与 y(n) 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理第三版实验报告 (1)
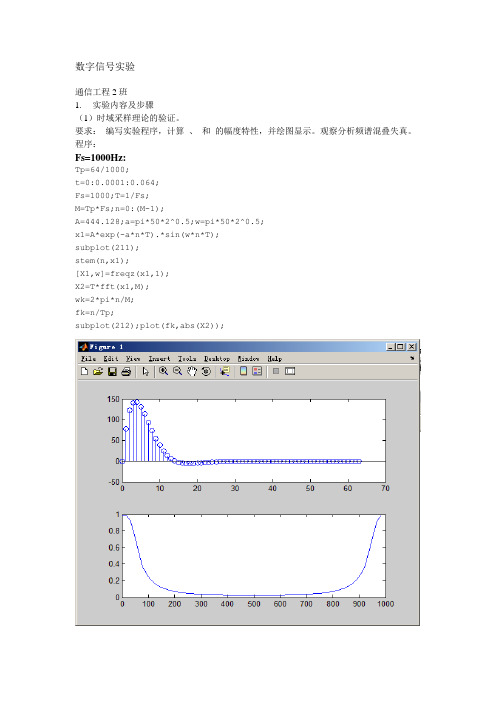
数字信号实验通信工程2班1. 实验内容及步骤(1)时域采样理论的验证。
要求:编写实验程序,计算、和的幅度特性,并绘图显示。
观察分析频谱混叠失真。
程序:Fs=1000Hz:Tp=64/1000;t=0:0.0001:0.064;Fs=1000;T=1/Fs;M=Tp*Fs;n=0:(M-1);A=444.128;a=pi*50*2^0.5;w=pi*50*2^0.5;x1=A*exp(-a*n*T).*sin(w*n*T);subplot(211);stem(n,x1);[X1,w]=freqz(x1,1);X2=T*fft(x1,M);wk=2*pi*n/M;fk=n/Tp;subplot(212);plot(fk,abs(X2));Fs=300Hz:Tp=64/1000;t=0:0.0001:0.064;Fs=300;T=1/Fs;N=Tp*Fs;n=0:N-1;A=444.128;a=pi*50*2^0.5;w=pi*50*2^0.5; x1=A*exp(-a*n*T).*sin(w*n*T);subplot(211);stem(n,x1);[X1,w]=freqz(x1,1);X2=T*fft(x1,N);wk=2*pi*n/N;fk=n/Tp;subplot(212);plot(fk,abs(X2));Fs=200Hz:Tp=64/1000;t=0:0.0001:0.064;Fs=200;T=1/Fs;N=Tp*Fs;n=0:N-1;A=444.128;a=pi*50*2^0.5;w=pi*50*2^0.5;x1=A*exp(-a*n*T).*sin(w*n*T);subplot(211);stem(n,x1);[X1,w]=freqz(x1,1);X2=T*fft(x1,N);wk=2*pi*n/N;fk=n/Tp;subplot(212);plot(fk,abs(X2));(2)频域采样理论的验证。
数字信号处理上机实验答案

第十章上机实验数字信号处理是一门理论和实际密切结合的课程,为深入掌握课程内容,最好在学习理论的同时,做习题和上机实验。
上机实验不仅可以帮助读者深入的理解和消化基本理论,而且能锻炼初学者的独立解决问题的能力。
本章在第二版的基础上编写了六个实验,前五个实验属基础理论实验,第六个属应用综合实验。
实验一系统响应及系统稳定性。
实验二时域采样与频域采样。
实验三用FFT对信号作频谱分析。
实验四IIR数字滤波器设计及软件实现。
实验五FIR数字滤波器设计与软件实现实验六应用实验——数字信号处理在双音多频拨号系统中的应用任课教师根据教学进度,安排学生上机进行实验。
建议自学的读者在学习完第一章后作实验一;在学习完第三、四章后作实验二和实验三;实验四IIR数字滤波器设计及软件实现在。
学习完第六章进行;实验五在学习完第七章后进行。
实验六综合实验在学习完第七章或者再后些进行;实验六为综合实验,在学习完本课程后再进行。
function tstem(xn,yn)%时域序列绘图函数% xn:信号数据序列,yn:绘图信号的纵坐标名称(字符串)n=0:length(xn)-1;stem(n,xn,'.');box onxlabel('n');ylabel(yn);axis([0,n(end),min(xn),1.2*max(xn)])10.1 实验一: 系统响应及系统稳定性1.实验目的(1)掌握求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
2.实验原理与方法在时域中,描写系统特性的方法是差分方程和单位脉冲响应,在频域可以用系统函数描述系统特性。
已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应,本实验仅在时域求解。
在计算机上适合用递推法求差分方程的解,最简单的方法是采用MATLAB 语言的工具箱函数filter 函数。
也可以用MATLAB 语言的工具箱函数conv 函数计算输入信号和系统的单位脉冲响应的线性卷积,求出系统的响应。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
数字信号处理(第三版)_课后习题答案全_(原题+答案+图)
第 1 章
(2) 令输入为
x(n-n0) 输出为
时域离散信号和时域离散系统
y′(n)=2x(n-n0)+3
y(n-n0)=2x(n-n0)+3=y′(n)
故该系统是非时变的。 由于 T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
m
第 1 章
时域离散信号和时域离散系统
题7图
第 1 章
时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章
解法(二)
时域离散信号和时域离散系统
采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
第 1 章
(4) y(n)=x(-n)
令输入为 x(n-n0) 输出为 y′(n)=x(-n+n0)
时域离散信号和时域离散系统
y(n-n0)=x(-n+n0)=y′(n) 因此系统是线性系统。 由于
T[ax1(n)+bx2(n)]=ax1(-n)+bx2(-n)
=aT[x1(n)]+bT[x2(n)] 因此系统是非时变系统。
n n0 k n n0
|x(k)|≤|2n0+1|M, 因
此系统是稳定的; 假设n0>0, 系统是非因果的, 因为输出
还和x(n)的将来值有关。
数字信号处理第三版用MATLAB上机实验

实验二:时域采样与频域采样一、时域采样1.用MATLAB编程如下:%1时域采样序列分析fs=1000A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=1000;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,1);stem(n,xn);xlabel('n,fs=1000Hz');ylabel('xn');title('xn');subplot(3,2,2);plot(n,abs(Xk));xlabel('k,fs=1000Hz'); title('|X(k)|');%1时域采样序列分析fs=200A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=200;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs);Xk=fft(xn);subplot(3,2,3);stem(n,xn);xlabel('n,fs=200Hz'); ylabel('xn');title('xn');subplot(3,2,4);plot(n,abs(Xk));xlabel('k,fs=200Hz'); title('|X(k)|');%1时域采样序列分析fs=500A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=500;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,5);stem(n,xn);xlabel('n,fs=500Hz');ylabel('xn');title('xn');subplot(3,2,6);plot(n,abs(Xk));xlabel('k,fs=500Hz'); title('|X(k)|');2.经调试结果如下图:20406080-200200n,fs=1000Hzxnxn2040608005001000k,fs=1000Hz|X (k)|51015-2000200n,fs=200Hzx nxn510150100200k,fs=200Hz |X(k)|10203040-2000200n,fs=500Hzx nxn102030400500k,fs=500Hz|X (k)|实验结果说明:对时域信号采样频率必须大于等于模拟信号频率的两倍以上,才 能使采样信号的频谱不产生混叠.fs=200Hz 时,采样信号的频谱产生了混叠,fs=500Hz 和fs=1000Hz 时,大于模拟信号频率的两倍以上,采样信号的频谱不产生混叠。
数字信号处理第三版高西全实验

数字信号处理第三版高西全实验数字信号处理第三版高西全实验》是一本旨在介绍数字信号处理的实际应用的教材。
本文档旨在概述该教材的目的和内容。
该教材的目的是通过实验教学的方式,帮助学生更好地理解数字信号处理的原理和技术,并将其应用到实际问题中。
它旨在培养学生的实践能力和解决问题的能力,使他们能够熟练地进行数字信号处理的实际操作。
该教材内容包括许多实验,涵盖了数字信号处理的各个方面。
每个实验都介绍了一个特定的概念或技术,并通过实际的操作和实验数据展示了其应用方式和效果。
学生通过完成实验,可以深入了解数字信号处理的各种算法和方法,研究如何使用相关工具和软件进行信号处理,以及如何分析和评估处理结果。
通过研究《数字信号处理第三版高西全实验》,学生将能够掌握数字信号处理的基本概念和技术,并能够独立地应用这些知识解决实际问题。
这将有助于他们在工程、通信、音视频处理等领域中的职业发展,也为进一步深入研究数字信号处理奠定了坚实的基础。
希望该教材能够对学生们的研究和实践有所帮助,使他们能够更好地理解和运用数字信号处理的方法和技术。
实验目标:本实验旨在介绍数字信号的采样和重构过程,并加深对这两个概念的理解。
实验目标:本实验旨在介绍数字信号的采样和重构过程,并加深对这两个概念的理解。
实验步骤:实验步骤:准备实验所需的信号发生器和示波器设备。
设置信号发生器,产生模拟信号,例如正弦波。
调整示波器参数,将模拟信号接入示波器进行显示。
使用采样器采样模拟信号,并记录采样得到的数字信号。
对采样得到的数字信号进行重构,恢复为原始模拟信号。
使用示波器将重构后的信号进行显示,并比较与原始信号的差异。
实验要点:了解采样和重构的基本概念和原理。
熟悉信号发生器和示波器的操作。
掌握采样器的使用方法。
理解数字信号与模拟信号的差异及其影响。
请参考实验指导书中的详细步骤和注意事项进行实验操作,并记录实验数据和结果。
本文档旨在解释《数字信号处理第三版高西全实验》中的实验二内容。
数字信号处理第三版高西全实验

数字信号处理高西全版课后上机实验1. 实验一:系统响应及系统稳定性clcclearx1=[ones(1,8),zeros(1,20)];subplot(321)stem(x1,'.')title('u8(n)');xlabel('n');ylabel('u(n)');x2=ones(1,30);subplot(322)stem(x2,'.')title('u(n)');xlabel('n');ylabel('u(n)');B=[0.05,0.05];A=[1,-0.9];y1=filter(B,A,x1);subplot(323)stem(y1,'.')title('y(n)');xlabel('n');ylabel('y(n)');y2=filter(B,A,x2);subplot(324)stem(y2,'.')title('y(n)');xlabel('n');ylabel('y(n)');x3=[1,zeros(1,30)];subplot(325)stem(x3,'.')title('单位脉冲');xlabel('n');ylabel('u(n)');y3=filter(B,A,x3);subplot(326)stem(y3,'.')title('单位脉冲响应');xlabel('n');ylabel('y(n)');图1 实验(1)波形clcclearx1=[ones(1,8),zeros(1,20)];subplot(321)stem(x1,'.')title('u8(n)');xlabel('n');ylabel('u(n)');h1=[ones(1,10),zeros(1,20)];subplot(322)stem(h1,'.')title('h1(n)');xlabel('n');ylabel('h(n)');h2=[1,2.5,2.5,1,zeros(1,20)];subplot(323)stem(h2,'.')title('h2(n)');xlabel('n');ylabel('h(n)');y1=conv(x1,h1)subplot(324)stem(y1,'.')axis([0,30,0,10])title('y1(n)');xlabel('n');ylabel('y(n)');y2=conv(x1,h2)subplot(325)stem(y2,'.')axis([0,30,0,10])title('y2(n)');xlabel('n');ylabel('y(n)');图2 实验(2)波形clcclearclfx1=ones(1,50);subplot(221)stem(x1,'.')axis([0,50,0,1])title('u(n)');xlabel('n');ylabel('u(n)');A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49];y1=filter(B,A,x1);subplot(223)stem(y1,'.')axis([0,50,-0.05,0.05])title('y(n)');xlabel('n');ylabel('y(n)');n=0:100;x2=sin(0.014*n)+sin(0.4*n);subplot(222)stem(x2,'.')axis([0,100,-1,2])title('x(n)');xlabel('n');ylabel('x(n)');y2=filter(B,A,x2);subplot(224)stem(y2,'.')axis([0,100,-1,1])title('y(n)');xlabel('n');ylabel('y(n)');图3 实验(3)波形2. 实验二:时域采样与频域采样A=444.128;a=50*sqrt(2)*pi;w=50*sqrt(2)*pi;fs1=1000;N1=0.064*fs1;n=0:N1-1;xn1=A.*exp(-a*n/fs1).*sin(w*n/fs1).*(n>=0);subplot(321)stem(xn1,'.')axis([0,55,-10,150])title('x1(n) fs=1kHz');xlabel('n');ylabel('x1(n)');Xk1=fft(xn1,N1);f1=(0:N1-1)/0.064;subplot(322)plot(f1,abs(Xk1/fs1))title('T*FT[x(nT)], Fs=1000Hz');fs2=300;N2=floor(0.064*fs2);n=0:N2-1;xn2=A.*exp(-a*n/fs2).*sin(w*n/fs2).*(n>=0);subplot(323)stem(xn2,'.')axis([0,20,-10,150])title('x2(n)fs=300Hz');xlabel('n');ylabel('x2(n)');Xk2=fft(xn2,N2);f2=(0:N2-1)/0.064;subplot(324)plot(f2,abs(Xk2/fs2))title('T*FT[x(nT)], Fs=300Hz');fs3=200;N3=floor(0.064*fs3);n=0:N3-1;xn3=A.*exp(-a*n/fs3).*sin(w*n/fs3).*(n>=0);subplot(325)stem(xn3,'.')axis([0,15,-10,150])title('x3(n)fs=200Hz');xlabel('n');ylabel('x3(n)');Xk3=fft(xn3,N3)f3=(0:N3-1)/0.064;subplot(326)plot(f3,abs(Xk3/fs3))title('T*FT[x(nT)], Fs=200Hz');图1 实验(1)时域采样代码:n=0:26;xa=1:14;xb=13:-1:1;xn=[xa,xb]; Xk=fft(xn,512);k=0:2/512:2*(1-1/512); subplot(321)plot(k,abs(Xk))axis([0,1,0,200])title('FT[x(n)]')subplot(322)stem(n,xn,'.')title('三角波序列')X32k=fft(xn,32);x32n=ifft(X32k);X16k=X32k(1:2:32);x16n=ifft(X16k,16);k=0:15;subplot(323)stem(k,abs(X16k),'.')title('16点频域采样')axis([0,10,0,200])subplot(324)stem(k,x16n,'.')title('16点IDFT[X16k]')axis([0,30,0,15])k1=0:31;subplot(325)stem(k1,abs(X32k),'.')title('32点频域采样')axis([0,10,0,200])subplot(326)stem(k1,x32n,'.')title('32点IDFT[X32k]')axis([0,30,0,15])运行结果:图2 实验(2)频域采样3. 实验三:用FFT对信号作频谱分析代码:clcclearn1=0:30;x1=[1,1,1,1,zeros(1,27)];n2=0:27;x2=[1:4,4:-1:1,zeros(1,20)];x3=[4:-1:1,1:4,zeros(1,20)];subplot(331)stem(n1,x1,'.')axis([0,10,0,1])title('x1(n)');xlabel('n');ylabel('x1(n)')subplot(332)stem(n2,x2,'.')axis([0,10,0,4])title('x2(n)');xlabel('n');ylabel('x2(n)')subplot(333)stem(n2,x3,'.')axis([0,10,0,4])title('x3(n)');xlabel('n');ylabel('x3(n)')k1=0:1/4:7/4;k2=0:1/8:15/8;X8k1=fft(x1,8);subplot(334)stem(k1,abs(X8k1),'.')title('8点FFT变换')X16k1=fft(x1,16);subplot(337)stem(k2,abs(X16k1),'.')title('16点FFT变换')X8k2=fft(x2,8);subplot(335)stem(k1,abs(X8k2),'.')title('8点FFT变换')X16k2=fft(x2,16);subplot(338)stem(k2,abs(X16k2),'.')title('16点FFT变换')X8k3=fft(x3,8);subplot(336)stem(k1,abs(X8k3),'.')title('8点FFT变换')X16k3=fft(x3,16);subplot(339)stem(k2,abs(X16k3),'.')title('16点FFT变换')运行结果:图1 实验(1)图形代码:clcclearn=0:30;x4=cos(pi/4*n);x5=cos(pi/4*n)+cos(pi/8*n);subplot(321)stem(n,x4,'.')axis([0,30,-1,1])title('x4(n)=cos(pi/4*n)');xlabel('n');ylabel('x4(n)')subplot(322)stem(n,x5,'.')axis([0,30,-2,2])title('x5(n)=cos(pi/4*n+pi/8*n)');xlabel('n');ylabel('x5(n)')k1=0:1/4:7/4;k2=0:1/8:15/8;X8k1=fft(x4,8);subplot(323)stem(k1,abs(X8k1),'.')axis([0,2,0,5])title('8点FFT变换')X16k1=fft(x4,16);subplot(325)stem(k2,abs(X16k1),'.')axis([0,2,0,8])title('16点FFT变换')X8k2=fft(x5,8);subplot(324)stem(k1,abs(X8k2),'.')axis([0,2,0,10])title('8点FFT变换')X16k2=fft(x5,16);subplot(326)stem(k2,abs(X16k2),'.')axis([0,2,0,10])title('16点FFT变换')图2 实验(2)图形clcclearn=1:100;Fs=64;x6=cos(8*pi*n/Fs)+cos(16*pi*n/Fs)+cos(20*pi*n/Fs); N1=16;F1=Fs/N1;k1=-N1/2:N1/2-1;fk1=F1*k1;X16k=fft(x6,16);X16k1=fftshift(X16k)subplot(311)stem(fk1,abs(X16k1),'.')axis([-30,30,0,10])title('变换区间N=16')N2=32;F2=Fs/N2;k2=-N2/2:N2/2-1;fk2=F2*k2;X32k=fft(x6,32);X32k1=fftshift(X32k)subplot(312)stem(fk2,abs(X32k1),'.')axis([-30,30,0,20])title('变换区间N=32')N3=64;F3=Fs/N3;k3=-N3/2:N3/2-1;fk3=F3*k3;X64k=fft(x6,64);X64k1=fftshift(X64k)subplot(313)stem(fk3,abs(X64k1),'.')axis([-30,30,0,40])title('变换区间N=64')图3 实验(3)图形4. 实验四:IIR数字滤波器设计及软件实现function st=mstgN=800;Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fc1=Fs/10;fm1=fc1/10;fc2=Fs/20;fm2=fc2/10;fc3=Fs/40;fm3=fc3/10;xt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t);xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t);xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t);st=xt1+xt2+xt3;fxt=fft(st,N);subplot(211)plot(t,st);grid;xlabel('t/s');ylabel('s(t)')axis([0,Tp/8,min(st),max(st)]);title('(a) s(t)的波形')subplot(212)stem(f,abs(fxt)/max(abs(fxt)),'.');grid;title('(b) s(t)的频谱');axis([0,2000,0,1]);end图1 信号产生函数图形%低通N=800;Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fp=280;fs=450;wp=2*fp/Fs;ws=2*fs/Fs;rp=0.1;rs=60;[N,wpo]=ellipord(wp,ws,rp,rs)[B,A]=ellip(N,rp,rs,wpo)[H,W]=freqz(B,A,1000)st=mstg;y1=filter(B,A,st)figure(2)subplot(312)plot(t,y1)title('时域波形')axis([0,Tp,min(y1),max(y1)])subplot(311)plot(W/pi,20*log10(abs(H)/max(abs(H))))title('低通滤波器损耗函数')axis([0,1,-80,10])subplot(313)Y1=fft(y1)stem(f,abs(Y1)/max(abs(Y1)),'.')axis([0,Fs/5,0,1.5])title('幅频特性曲线')%带通N=800Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fp1=440;fpu=560;fs1=275;fsu=900wp=[2*fp1/Fs,2*fpu/Fs];ws=[2*fs1/Fs,2*fsu/Fs];rp=0.1;rs=60;[N,wpo]=ellipord(wp,ws,rp,rs)[B,A]=ellip(N,rp,rs,wpo)[H,W]=freqz(B,A,1000)st=mstg;y1=filter(B,A,st)figure(3)subplot(312)plot(t,y1)title('时域波形')axis([0,Tp,min(y1),max(y1)])subplot(311)plot(W/pi,20*log10(abs(H)/max(abs(H)))) title('带通滤波器损耗函数')axis([0,1,-80,10])subplot(313)Y1=fft(y1)stem(f,abs(Y1)/max(abs(Y1)),'.')axis([0,Fs/5,0,1.5])title('幅频特性曲线')%高通N=800;Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fp=890;fs=600;wp=2*fp/Fs;ws=2*fs/Fs;rp=0.1;rs=60;[N,wpo]=ellipord(wp,ws,rp,rs)[B,A]=ellip(N,rp,rs,wpo,'high')[H,W]=freqz(B,A,1000)y1=filter(B,A,st)figure(4)subplot(311)plot(W/pi,20*log10(abs(H)/max(abs(H))))title('高通滤波器损耗函数')axis([0,1,-80,10])subplot(312)plot(t,y1);title('时域波形')axis([0,Tp,min(y1),max(y1)])subplot(313)Y1=fft(y1)stem(f,abs(Y1)/max(abs(Y1)),'.')axis([0,Fs/5,0,1.5]);title('幅频特性曲线')图2 低通图形图3 带通图形图4 高通图形5. 实验五:FIR数字滤波器设计及软件实现function xt=xtgN=1000;Fs=1000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;fc=Fs/10;f0=fc/10;mt=cos(2*pi*f0*t);ct=cos(2*pi*fc*t);xt=mt.*ct;nt=2*rand(1,N)-1;fp=150;fs=200;Rp=0.1;As=70;fb=[fp,fs];m=[0,1];dev=[10^(-As/20),(10^(Rp/20)-1)/(10^(Rp/20)+1)];[n,fo,mo,W]=remezord(fb,m,dev,Fs);hn=remez(n,fo,mo,W);yt=filter(hn,1,10*nt);xt=xt+yt;fst=fft(xt,N);k=0:N-1;f=k/Tp;subplot(211)plot(t,xt);grid;xlabel('t/s');ylabel('x(t)');axis([0,Tp/5,min(xt),max(xt)]);title('(a) 信号加噪声波形') subplot(212)plot(f,abs(fst)/max(abs(fst)));grid;xlabel('f/Hz');ylabel('幅度'); axis([0,Fs/2,0,1.2]);title('(b) 信号加噪声的频谱')end%设计低通滤波器并滤除噪声Fs=1000;N=1000;wp=0.24*pi;ws=0.3*pi;fs=150;fp=120;Wc=(wp+ws)/(2*pi);B=2*pi*(fs-fp)/Fs;Nb=ceil(11*pi/B);hn=fir1(Nb-1,Wc,blackman(Nb));Hw=abs(fft(hn,N))xt=xtg;y=fftfilt(hn,xt,N)f=(0:N-1)*Fs/N;figure(2)subplot(211)plot(f,20*log10(Hw/max(Hw)));title('低通滤波器幅频特性') xlabel('f/Hz');ylabel('幅度');axis([0,Fs/2,-120,10]);subplot(212)plot(f/2000,y);title('滤除噪声后的信号波形')xlabel('t/s');ylabel('yw(t)');图1 信号及其频谱图2 低通滤波器滤除噪声。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理实验(Matlab)实验一: 系统响应及系统稳定性%实验1:系统响应及系统稳定性close all;clear all%======内容1:调用filter解差分方程,由系统对u(n)的响应判断稳定性====== A=[1,-0.9];B=[0.05,0.05]; %系统差分方程系数向量B和Ax1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号x1(n)=R8(n)x2n=ones(1,128); %产生信号x2(n)=u(n)hn=impz(B,A,58); %求系统单位脉冲响应h(n)subplot(2,2,1);y='h(n)';tstem(hn,y); %调用函数tstem绘图title('(a)系统单位脉冲响应h(n)');box ony1n=filter(B,A,x1n); %求系统对x1(n)的响应y1(n)subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b)系统对R8(n)的响应y1(n)');box ony2n=filter(B,A,x2n); %求系统对x2(n)的响应y2(n)subplot(2,2,4);y='y2(n)';tstem(y2n,y);title('(c)系统对u(n)的响应y2(n)');box on%===内容2:调用conv函数计算卷积============================x1n=[1 1 1 1 1 1 1 1 ]; %产生信号x1(n)=R8(n)h1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)];y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y='h1(n)';tstem(h1n,y); %调用函数tstem绘图title('(d)系统单位脉冲响应h1(n)');box onsubplot(2,2,2);y='y21(n)';tstem(y21n,y);title('(e) h1(n)与R8(n)的卷积y21(n)');box onsubplot(2,2,3);y='h2(n)';tstem(h2n,y); %调用函数tstem绘图title('(f)系统单位脉冲响应h2(n)');box onsubplot(2,2,4);y='y22(n)';tstem(y22n,y);title('(g) h2(n)与R8(n)的卷积y22(n)');box on%=========内容3:谐振器分析========================un=ones(1,256); %产生信号u(n)n=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49]; %系统差分方程系数向量B和A y31n=filter(B,A,un); %谐振器对u(n)的响应y31(n)y32n=filter(B,A,xsin); %谐振器对u(n)的响应y31(n)figure(3)subplot(2,1,1);y='y31(n)';tstem(y31n,y);title('(h)谐振器对u(n)的响应y31(n)');box onsubplot(2,1,2);y='y32(n)';tstem(y32n,y);title('(i) 谐振器对正弦信号的响应y32(n)');box on10.1.3 实验程序运行结果及分析讨论程序运行结果如图10.1.1所示。
实验内容(2)系统的单位冲响应、系统对 和 的响应序列分别如图(a)、(b)和(c)所示; 实验内容(3)系统h 1(n)和h 2(n)对的输出响应分别如图(e)和(g)所示;实验内容(4)系统对 和的响应序列分别如图(h)和(i)所示。
由图(h)可见,系统对的响应逐渐衰减到零,所以系统稳定。
由图(i)可见,系统对的稳态响应近似为正弦序列 ,这一结论验证了该系统的谐振频率是0.4 rad。
0.050.1(a) 系统单位脉冲响应h(n)0.51(b) 系统对R8(n)的响应y1(n)00.51(c) 系统对u(n)的响应y2(n)00.51(d) 系统单位脉冲响应h1(n)(e) h1(n)与R8(n)的卷积y21(n)0123(f) 系统单位脉冲响应h2(n)(g) h2(n)与R8(n)的卷积y22(n)(h) 谐振器对u(n)的响应y31(n)(i) 谐振器对正弦信号的响应y32(n)图10.1.110.1.4简答思考题(1) 如果输入信号为无限长序列,系统的单位脉冲响应是有限长序列,可否用线性卷积法求系统的响应。
①对输入信号序列分段;②求单位脉冲响应h(n)与各段的卷积;③将各段卷积结果相加。
具体实现方法有第三章介绍的重叠相加法和重叠保留法。
(2)如果信号经过低通滤波器,把信号的高频分量滤掉,时域信号的剧烈变化将被平滑,由实验内容(1)结果图10.1.1(a)、(b)和(c)可见,经过系统低通滤波使输入信号、和 的阶跃变化变得缓慢上升与下降。
数字信号处理 实验二 时域采样与频域采样1时域采样理论的验证程序清单% 时域采样理论验证程序exp2a.mTp=64/1000; %观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000;T=1/Fs;Fs=1000;T=1/Fs;M=Tp*Fs;n=0:M-1;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M); %M点FFT[xnt)]yn='xa(nT)';subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on;title('(a) Fs=1000Hz');k=0:M-1;fk=k/Tp;subplot(3,2,2);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz'); xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%=================================================% Fs=300Hz和 Fs=200Hz的程序与上面Fs=1000Hz完全相同。
2频域采样理论的验证程序清单%频域采样理论验证程序exp2b.mM=27;N=32;n=0:M;%产生M长三角波序列x(n)xa=0:floor(M/2); xb= ceil(M/2)-1:-1:0; xn=[xa,xb];Xk=fft(xn,1024); %1024点FFT[x(n)], 用于近似序列x(n)的TFX32k=fft(xn,32) ;%32点FFT[x(n)]x32n=ifft(X32k); %32点IFFT[X32(k)]得到x32(n)X16k=X32k(1:2:N); %隔点抽取X32k得到X16(K)x16n=ifft(X16k,N/2); %16点IFFT[X16(k)]得到x16(n)subplot(3,2,2);stem(n,xn,'.');box ontitle('(b) 三角波序列x(n)');xlabel('n');ylabel('x(n)');axis([0,32,0,20]) k=0:1023;wk=2*k/1024; %subplot(3,2,1);plot(wk,abs(Xk));title('(a)FT[x(n)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');axis([0,1,0,200])k=0:N/2-1;subplot(3,2,3);stem(k,abs(X16k),'.');box ontitle('(c) 16点频域采样');xlabel('k');ylabel('|X_1_6(k)|');axis([0,8,0,200]) n1=0:N/2-1;subplot(3,2,4);stem(n1,x16n,'.');box ontitle('(d) 16点IDFT[X_1_6(k)]');xlabel('n');ylabel('x_1_6(n)');axis([0,32,0,20])k=0:N-1;subplot(3,2,5);stem(k,abs(X32k),'.');box ontitle('(e) 32点频域采样');xlabel('k');ylabel('|X_3_2(k)|');axis([0,16,0,200]) n1=0:N-1;subplot(3,2,6);stem(n1,x32n,'.');box ontitle('(f) 32点IDFT[X_3_2(k)]');xlabel('n');ylabel('x_3_2(n)');axis([0,32,0,20])简答思考题先对原序列x(n)以N为周期进行周期延拓后取主值区序列,再计算N点DFT则得到N点频域采样:数字信号处理 实验三:用FFT对信号作频谱分析%第10章实验3程序exp3.m% 用FFT对信号作频谱分析clear all;close all%实验内容(1)===================================================x1n=[ones(1,4)]; %产生序列向量x1(n)=R4(n)M=8;xa=1:(M/2); xb=(M/2):-1:1; x2n=[xa,xb]; %产生长度为8的三角波序列x2(n) x3n=[xb,xa];X1k8=fft(x1n,8); %计算x1n的8点DFTX1k16=fft(x1n,16); %计算x1n的16点DFTX2k8=fft(x2n,8); %计算x1n的8点DFTX2k16=fft(x2n,16); %计算x1n的16点DFTX3k8=fft(x3n,8); %计算x1n的8点DFTX3k16=fft(x3n,16); %计算x1n的16点DFT%以下绘制幅频特性曲线subplot(2,2,1);mstem(X1k8); %绘制8点DFT的幅频特性图title('(1a) 8点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X1k8))])subplot(2,2,3);mstem(X1k16); %绘制16点DFT的幅频特性图title('(1b)16点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X1k16))])figure(2)subplot(2,2,1);mstem(X2k8); %绘制8点DFT的幅频特性图title('(2a) 8点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X2k8))])subplot(2,2,2);mstem(X2k16); %绘制16点DFT的幅频特性图axis([0,2,0,1.2*max(abs(X2k16))])subplot(2,2,3);mstem(X3k8); %绘制8点DFT的幅频特性图title('(3a) 8点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度'); axis([0,2,0,1.2*max(abs(X3k8))])subplot(2,2,4);mstem(X3k16); %绘制16点DFT的幅频特性图title('(3b)16点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度'); axis([0,2,0,1.2*max(abs(X3k16))])%实验内容(2) 周期序列谱分析================================== N=8;n=0:N-1; %FFT的变换区间N=8x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n); %计算x4n的8点DFTX5k8=fft(x5n); %计算x5n的8点DFTN=16;n=0:N-1; %FFT的变换区间N=16x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k16=fft(x4n); %计算x4n的16点DFTX5k16=fft(x5n); %计算x5n的16点DFTfigure(3)subplot(2,2,1);mstem(X4k8); %绘制8点DFT的幅频特性图axis([0,2,0,1.2*max(abs(X4k8))])subplot(2,2,3);mstem(X4k16); %绘制16点DFT的幅频特性图title('(4b)16点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X4k16))])subplot(2,2,2);mstem(X5k8); %绘制8点DFT的幅频特性图title('(5a) 8点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X5k8))])subplot(2,2,4);mstem(X5k16); %绘制16点DFT的幅频特性图title('(5b)16点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X5k16))])%实验内容(3) 模拟周期信号谱分析===============================figure(4)Fs=64;T=1/Fs;N=16;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t)16点采样X6k16=fft(x6nT); %计算x6nT的16点DFTX6k16=fftshift(X6k16); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F; %产生16点DFT对应的采样点频率(以零频率为中心) subplot(3,1,1);stem(fk,abs(X6k16),'.');box on %绘制8点DFT的幅频特性图title('(6a) 16点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k16))])N=32;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t)32点采样X6k32=fft(x6nT); %计算x6nT的32点DFTX6k32=fftshift(X6k32); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F; %产生16点DFT对应的采样点频率(以零频率为中心) subplot(3,1,2);stem(fk,abs(X6k32),'.');box on %绘制8点DFT的幅频特性图title('(6b) 32点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k32))])N=64;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t)64点采样X6k64=fft(x6nT); %计算x6nT的64点DFTX6k64=fftshift(X6k64); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F; %产生16点DFT对应的采样点频率(以零频率为中心) subplot(3,1,3);stem(fk,abs(X6k64),'.'); box on%绘制8点DFT的幅频特性图title('(6a) 64点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k64))])为了便于读取频率值,最好关于π归一化,即以 作为横坐标。
