赫尔默特方差分量估计教学文案
精密工程测量平差软件使用手册范本
精密工程测量平差软件使用手册范本(总28页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--客运专线CPIII一体化测量系统精密工程测量平差软件TSDI_HRSADJ（版）铁道第三勘测集团The Third Railway Survey And Design Institute Group Corporation目录第一章软件安装.......................................... 错误!未定义书签。
软件的运行环境 ................................... 错误!未定义书签。
软件的安装........................................... 错误!未定义书签。
第二章软件操作.......................................... 错误!未定义书签。
数据文件格式定义................ 错误!未定义书签。
工程基本设置................... 错误!未定义书签。
读入数据....................... 错误!未定义书签。
平差计算....................... 错误!未定义书签。
成果输出与查看................. 错误!未定义书签。
网图显示....................... 错误!未定义书签。
工具........................... 错误!未定义书签。
第三章疑难解答.................... 错误!未定义书签。
平面网平差计算步骤............. 错误!未定义书签。
平面网平差迭代计算............. 错误!未定义书签。
如何快速检查数据的错误......... 错误!未定义书签。
第四章附录........................ 错误!未定义书签。
Helmert
0 , P2
T N BT PB B1T P B1 B2 P2 B2 N1 N 2 , 1 T W BT PL B1T P L1 B2 P2 L2 W1 W2 . 1
一般来说，第一次平差时给定的两类观测值 的权 P , P2 是不恰当的，或者说它们的单位 1 权方差不相等，令其分别为 2 , 2
常数项 （-l）
0.18 -0.53 3.15 0.23
5
6 7 8
0.6298
-0.3864 0.7966 -0.8350
0.6368
-0.8400 -0.2572 -0.1523
0.0000
0.0000 -0.2244 0.0384
0.0000
0.0000 -0.3379 0.4095
-2.44
ˆ V1 B1 X L1
B1 N 1W L1 B1 N 1 (W1 W2 ) L1
T ( B1 N 1 B1T P E ) L1 B1 N 1 B2 P2 L2 1
D(V1 ) ( B1 N 1B1T P E ) D( L1 )( B1 N 1B1T P E )T 1 1
表1
点 号
A 坐标 X Y ° 14 123 坐标方位角 ′ 0 10 ″ 35.77 57.97 4001.117 7734.443
边长(m)
4899.846 130.812
B
C
8781.945 1099.443
4548.795 7572.622
表2
编 号 观测角 编 号 观测角 ° 74 77 28 55 72 52 ′ 18 27 13 21 22 16 ″ 16.8 59.1 43.2 9.9 25.8 20.5 编 号 观测边 （m） 2463.94 3414.61 5216.16 6042.94 5085.08 5014.99
方差区间估计推导
方差区间估计推导全文共四篇示例，供读者参考第一篇示例：统计学中的方差是一种衡量数据散布程度的统计量，它用来描述一组数据的离散程度。
方差区间估计是一种统计方法，用于估计总体方差的范围。
在实际应用中，我们往往无法得到总体的所有数据，而只能通过样本来估计总体的参数。
方差区间估计就是借助样本数据来估计总体方差的一种方法。
方差区间估计的推导过程可以分为以下几个步骤：1. 确定总体方差的分布类型：在进行方差区间估计之前，首先需要明确总体方差的分布类型。
常见的总体方差分布有正态分布、均匀分布、指数分布等。
根据总体方差的分布类型，选择相应的统计方法进行推导。
2. 确定抽样分布类型：根据总体方差的分布类型，确定抽样分布的类型。
通常我们会利用中心极限定理来假设样本均值的抽样分布是正态分布。
根据中心极限定理，当样本容量足够大时，样本均值的抽样分布近似服从正态分布。
3. 计算样本方差：从总体中抽取样本数据，通过计算样本方差来估计总体方差。
样本方差是样本数据的离散程度的一种度量，它可以帮助我们估计总体方差的大小。
4. 计算置信区间：根据样本数据和样本方差的抽样分布，计算总体方差的置信区间，即估计总体方差的范围。
一般来说，方差的置信区间是基于样本方差和自由度的t 分布来计算的。
在计算置信区间时，我们需要确定置信水平和置信系数，以确保估计的准确性。
5. 判断总体方差的大小：根据计算得到的置信区间，判断总体方差的大小是否在该区间内。
如果总体方差的估计值在置信区间内，我们就可以认为我们对总体方差的估计是准确的；反之，如果估计值不在置信区间内，我们需要重新调整样本容量或考虑其他统计方法来提高估计的准确性。
方差区间估计是一种通过样本数据来估计总体方差的统计方法，它可以帮助我们了解总体数据的分布情况，并做出相应的推断和决策。
通过合理选择样本数据和统计方法，我们可以获得准确的总体方差估计值，从而为实际问题的解决提供有力支持。
在实际应用中，我们可以根据方差区间估计的结果，对数据进行分析和预测，从而更好地指导决策和实践。
Helmert
它们的权阵分别为 它们的误差方程分别为
n1 n1
P,P 1 2
n2 n2
此时， P 12
0
ˆ V1 B1 X L1 , ˆ V B X L .
2 2 2
且有下列关系式：
L1 V1 B1 P 1 L ,V , B , P L2 V2 B2 0
1
1
2
2 2 2 1
ˆ S
W 0
2 1
1 1 n1 2tr ( N 1 N1 ) tr ( N 1 N1 ) 2 tr ( N N1 N N 2 ) S 1 1 2 （对称） n2 2tr ( N N 2 ) tr ( N N 2 )
ˆ =
2 0 P 2 1(无量纲)，
02 1.52 2 Ps 2 2 0.56 ″ cm 2 , s 2
列误差方程，待定点坐标的近似值取为
X X
0 1 0 2
5656.89m, Y 2475.56 m,
0 1
663.90m, Y 2943.91m.
01 0
2
则有
D( L )
D( L1 )
2
2 P 1， 01 1 2 P 1. 0 2 2
方差分量估计的目的就是利用各次平差后各类 V1T PV1 和V2T P2V2 来估计 2 和 2 。 改正数的平方和 1 0 1 0 2 2, 2 因此，问题就是解决 0 0 是否相等。
0.3255
0.0840 0.9516 0.4030 -0.9772 0.0000 0.0000 -0.0934
-0.0384 -0.4095 8.04
九年级数学上册 23.4 用样本估计总体 EQ综合度量与发展的均值、方差模型素材 (新版)冀教版
EQ综合度量与开展的均值、方差模型摘要本文从EQ(Emotional Intelligence Quotient)的综合度量出发，推导出EQ 度量的均值—方差模型，用来描述EQ的开展与控制，为大学新生培养提高心理素质和描绘自身心理轨迹提供了形象直观的工具。
关键词 EQ、均值—方差模型一、EQ的一般概念与度量EQ，常译为情商，全称为Emotional Intelligence Quotient，可译为情绪智力商数。
它和智商(IQ，Intelligence Quotient)相比较而存在，用作测定人的情绪智力水平的指标。
其实更加标准的术语应为“情绪智力(Emotional Intelligence)〞。
EQ理论一般认为由**的两位心理学家—耶鲁大学的彼得·塞拉维和新罕布什尔大学的约翰·梅耶创立的。
西方学者认为情绪智力应该包括如下5个方面：〔1〕对情绪的自我认知感受能力；〔2〕妥善管理自己的情绪，及时摆脱焦虑、忧郁、烦躁不安的能力；〔3〕自我鼓励，克制冲动，延迟满足，保持热忱的能力；〔4〕认知他人情绪的能力；〔5〕调整人际关系的能力。
其实EQ理论不是一朝一夕形成的。
早在1986年，中国的科学出版社出版了一本?科学创造心理学?。
作者在全书12章里用5章研究智力因素对于科学创造的奉献，而用了7章研究非智力因素对于科学创造的奉献。
该书认为智力因素可以分为5类25种，它们是〔1〕观察力〔观察敏锐性、观察准确性〕；〔2〕记忆力〔记忆速度、记忆准确性、联想能力〕；〔3〕思维能力〔思维深度、思维广度、**思考、思维灵活性、思维分析能力思维综合能力、思维比较能力、思维抽象能力、思维概括能力、判断能力〕；〔4〕想象力〔想象丰富性、想象新颖性〕；〔5〕操作能力〔操作准确性、操作速度、操作协调性〕。
非智力因素也可以分为5种25类，它们是〔1〕情绪〔情绪稳定性、控制情绪水平、激情、热情〕；〔2〕心境〔事业心、责任心、自信心、好奇心、疑心感、进取心〕；〔3〕兴趣〔求知欲、兴趣广度、兴趣深度、兴趣持久性〕；〔4〕意志〔意志顽强性、意志果断性、意志自制力〕；〔5〕性格〔勤奋、谦逊、献身精神〕。
方差分量估计算例
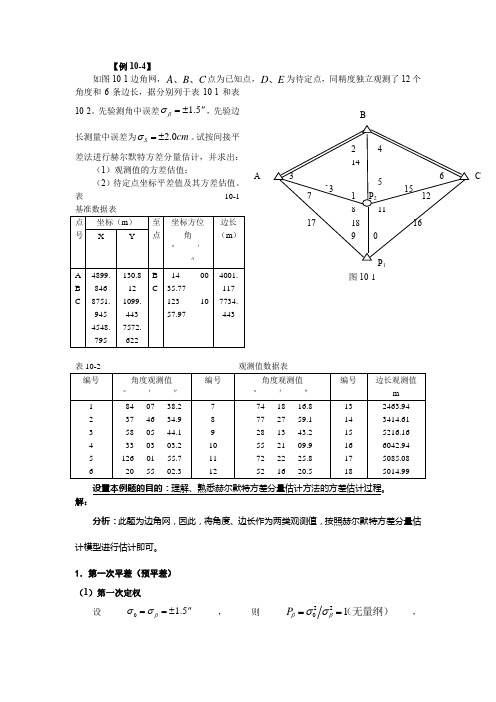
【例10-4】如图10-1边角网，C B A 、、点为已知点，E D 、为待定点，同精度独立观测了12个角度和6条边长，据分别列于表10-1和表10-2。
先验测角中误差"±=5.1βσ，先验边长测量中误差为cm S 0.2±=σ。
试按间接平差法进行赫尔默特方差分量估计，并求出：（1）观测值的方差估值；（2）待定点坐标平差值及其方差估值。
表10-1基准数据表 表10-2 观测值数据表 设置本例题的目的：理解、熟悉赫尔默特方差分量估计方法的方差估计过程。
解：分析：此题为边角网，因此，将角度、边长作为两类观测值，按照赫尔默特方差分量估计模型进行估计即可。
1．第一次平差（预平差） （1）第一次定权设"±==5.10βσσ，则（无量纲）1220==ββσσP ，)(56.00.25.12222220秒===S s P σσ（2）计算近似坐标使用余切公式由A B 、和B C 、分别计算D 近似坐标，然后取平均值作为近似坐标；由D C 、和A D 、分别计算E 近似坐标，然后取平均值作为近似坐标。
计算结果为，，；，m Y m X m Y m X D E D D 055.2944969.663552.2475923.56560000==== （3）计算误差方程的b a 、系数（见表10-3、表10-4） 方位角改正数方程：j kj k j j kj k j i kj k j i kj k j k j yS x S y S x S ˆcos 65.2062ˆsin 65.2062ˆcos 65.2062ˆsin 65.206200000000ααααδα⨯+⨯-⨯-⨯=系数量纲为：厘米秒 边长误差方程：k j k j S j k j j k j j k j j k j S l y x y x V -++--=ˆsin ˆcos ˆsin ˆcos 0000αααα（系数无量纲）（4）误差方程组成（见表10-5）角度误差方程：设编号为i 的角度，测站点点号为j ，第一照准点点号为h ，第二照准点点号为k ，则角度误差方程按下式组成i k k j k k j h h j h h j j h j k j j h j k j i h j k j i l y b x a y b x a y b b xa a l v ---++-+-=--=ˆˆˆˆˆ)(ˆ)(δαδα 其中).(00ih ik i i L l αα--=组成结果列于表7-5 边长误差方程：设编号为i 的观测边长，两端点点号为j 和k ，则角度误差方程按下式组成i i S j k j j k j j k j j k j S l y x y x V -++--=ˆsin ˆcos ˆsin ˆcos 0000αααα（系数无量纲）.0i i i S S l -=表10-5 误差方程组成表根据表10-5，可得到⎪⎭⎪⎬⎫-=-=-=P l xB V P l x B V P l x B V ˆˆˆ22221111 其中12,12114,121,0.22-0.260.080.39-0.41-0.040.330.35-0.190.30-0.410.04--0.070.180.410.040.410.04-0.150.84--0.34-0.22-0.260.8000-0.080.39-000.640.6400-0.560.25-000.260.8-000.560.2500-0.820.55E P B =⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=，6,6224,6256.0,0.09-1.00-0.091.000.55-0.8300-0.77-0.640000-0.980.21000.410.91-000.950.31E P B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛= ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=212,66,12118,182100,P P P B B B（5）法方程组及解利用表10-5中误差方程数据组成法方程 0ˆ=-W x N 其中⎪⎪⎪⎪⎪⎭⎫⎝⎛== 1.0472 0.0647 -0.2019 0.3471- 0.0647 1.4168 0.0184 0.8618- -0.2019 0.0184 3.4667 0.2814- -0.3471-0.8618-0.2814 4.3548PB B N T⎪⎪⎪⎪⎪⎭⎫ ⎝⎛== 2.2917- 16.2824- 0.5436 4.0296Pl B W T ，⎪⎪⎪⎪⎪⎭⎫⎝⎛=-0.99520.00510.06480.08450.00510.80270.00900.15980.06480.00900.29430.02600.08450.15980.02600.26971N ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==- 2.2917-16.2824- 0.5436 4.0296ˆ1W N x bb（6）改正数计算()3.562.332.09-0.660.89-1.130.471.98-0.311.660.61- 1.751=V() 0.161.07-3.91-2.73-0.27- 1.15-2=V（7）进行赫尔默特估计⎪⎪⎪⎪⎪⎭⎫⎝⎛=-0.99520.00510.06480.08450.00510.80270.00900.15980.06480.00900.29430.02600.08450.15980.02600.26971N ⎪⎪⎪⎪⎪⎭⎫⎝⎛==0.99520.00510.06480.08450.00510.80270.00900.15980.06480.00900.29430.02600.08450.15980.02600.26971111B P B N T⎪⎪⎪⎪⎪⎭⎫⎝⎛== 0.5060 0.0301- 0.0045-0.0504 0.0301- 1.1752 0.05040.5600- 0.0045-0.0504 1.14190.2097- 0.05040.5600-0.2097- 1.10222222B P B N T组成估计方程θθW S =⨯⨯1222ˆ 式中⎥⎦⎤⎢⎣⎡+-+-=----------)()(2)()()()(21212122121112111111111N N N N tr N N tr n N N N N tr N N N N tr N N N N tr N N tr n S []T202201ˆˆˆσσθ= []TT T V P V V P V W 222111=θtr(N 1N -1)2.1012 tr(N 2N -1) 1.8988根据以上数据，求得⎪⎪⎭⎫ ⎝⎛=3417.37595.07595.01394.9S ，⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=18096.1442301.35111111V PV V P V W T T θ 估计方程⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛18096.1442301.35ˆˆ3417.37595.07595.01394.9202201σσ解得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-42747.359103.318096.1442301.353417.37595.07595.01394.9ˆˆ12020S σσβ 两者之比：0.9544532第二次平差（1）计算测角和测边的方差估值由第一次平差求得的角度和边长对应的单位权方差估值，计算角度观测值和边长观测值的方差，公式为SSS P P 1ˆˆ1ˆˆ202202σσσσβββ==， 如果为不等精度观测值，则计算式为12020,12020,ˆˆˆˆ2211--====S P Q D P Q D S SS S n n SS n n σσσσβββββββ，从而求得12048.656.0142747.31ˆˆ59103.31ˆ1ˆˆ20220202=⨯===⨯==S SS P P σσσσσββββ，（2）第二次定权令220ˆβσσ=则59.012048.659103.3ˆ1ˆ220220=====S S P P σσσσββ，（3）求第二次平差的法方程、V 1T P 1V 1、V 2TP 2V 2解得V 1TP 1V 1=35.9089，V 2TP 2V 2=13.70754 （7）进行赫尔默特估计根据以上数据，求得⎪⎪⎭⎫ ⎝⎛=2988.37627.07627.01757.9S ，⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=7075.139089.35111111V P V V P V W T T θ 估计方程⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛7075.139089.35ˆˆ2988.37627.07627.01757.9202201σσ 解得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-4729723.35718162.37075.139089.352988.37627.07627.01757.9ˆˆ12020S σσβ 两者之比为：1：0.9723273.第三次平差（1）计算测角和测边的方差估值由第二次平差求得的角度和边长对应的单位权方差估值，计算角度观测值和边长观测值的方差，公式为SSS P P 1ˆˆ1ˆˆ202202σσσσβββ==， 从而求得886393729.559.014729723.31ˆˆ5718162.31ˆ1ˆˆ20220202=⨯===⨯==S SS P P σσσσσββββ，（2）第三次定权 令220ˆβσσ=则61.0886393729.55718162.3ˆ1ˆ220220=====S S P P σσσσββ，（3）求第三次平差的法方程、V 1T P 1V 1、V 2TP 2V 2解得111222（7）进行赫尔默特估计根据以上数据，求得⎪⎪⎭⎫ ⎝⎛=2715.37646.07646.01993.9S ，⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=41716.1321996.36111111V P V V P V W T T θ V 1T P 1V 1 V 2T P 2V 236.21996 13.41716V 1T P 1V 1=36.21996，V 2T P 2V 2=13.41716估计方程⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛41716.1321996.36ˆˆ2715.37646.07646.01993.9202201σσ 解得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-502829.355947.341716.1321996.362715.37646.07646.01993.9ˆˆ12020S σσβ 即502829.3ˆ55947.3ˆ2020==S σσβ，两者之比为：0.9840871ˆˆ2020：：=S σσβ4．第四次平差（1）计算测角和测边的方差估值由第三次平差求得502829.3ˆ55947.3ˆ2020==S σσβ， 742342623.561.01502829.31ˆˆ55947.31ˆ1ˆˆ20220202=⨯===⨯==S SS P P σσσσσββββ，（2）第四次定权 令220ˆβσσ=则62.0742342623.555947.3ˆ1ˆ220220=====S S P P σσσσββ，（3）求第四次平差的法方程、V 1TP 1V 1、V 2TP 2V 2解得V 1TP 1V 1=36.37183，V 2TP 2V 2=13.27887 （7）进行赫尔默特估计根据以上数据，求得⎪⎪⎭⎫ ⎝⎛= 3.25820.76550.76559.2109S ，⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=13.2788736.37183111111V P V V P V W T T θ 估计方程⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛13.2788736.37183ˆˆ3.25820.76550.76559.2109202201σσ 解得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛- 3.5176053.5534413.2788736.371833.25820.76550.76559.2109ˆˆ12020S σσβ 即3.517605ˆ3.55344ˆ2020==S σσβ， 两者之比为：0.9899150.9899151ˆˆ2020：：=S σσβ 5．第五次平差（1）计算测角和测边的方差估值由第四次平差求得673556452.562.013.5176051ˆˆ3.553441ˆ1ˆˆ20220202=⨯===⨯==S SS P P σσσσσββββ，（2）第四次定权 令220ˆβσσ=则63.0673556452.53.55344ˆ1ˆ220220=====S S P P σσσσββ，（3）求第五次平差的法方程、V 1TP 1V 1、V 2TP 2V 2解得111222（7）进行赫尔默特估计S -1 W 0.1106 -0.0261 35.42301 -0.0261 0.3143 14.18096S9.2224 0.7662 0.7662 3.2451根据以上数据，求得⎪⎪⎭⎫ ⎝⎛= 3.24510.76620.76629.2224 S ，⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=14.1809635.42301111111V P V V P V W T T θ 估计方程⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛14.1809635.42301ˆˆ3.24510.76620.76629.2224 202201σσ 解得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛- 3.5322813.54750214.1809635.423013.24510.76620.76629.2224 ˆˆ12020S σσβ 即3.532281ˆ3.547502ˆ2020==S σσβ， 两者之比为：0.9899150.9957091ˆˆ2020：：=S σσβ 6．第六次平差（1）计算测角和测边的方差估值由第五次平差求得606795238.563.013.5322811ˆˆ3.5475021ˆ1ˆˆ20220202=⨯===⨯==S SS P P σσσσσββββ，（2）第wu 次定权令220ˆβσσ=则63.0606795238.53.547502ˆ1ˆ220220=====S S P P σσσσββ，可以看出，经过5次迭代计算，权已稳定，因此，可取第5次平差结果作为最后结果，已没有必要再继续做下去。
山东理工大学硕士学位论文第一章绪...
独创性声明本人声明所呈交的论文是我个人在导师指导下进行的研究工作及取得的研究成果。
尽我所知，除了文中特别加以标注和致谢的地方外，论文中不包含其他人已经发表或撰写过的研究成果，也不包含为获得山东理工大学或其它教育机构的学位或证书而使用过的材料。
与我一同工作的同志对本研究所做的任何贡献均已在论文中作了明确的说明并表示了谢意。
研究生签名：时间：年月日关于论文使用授权的说明本人完全了解山东理工大学有关保留、使用学位论文的规定，即：学校有权保留送交论文的复印件和磁盘，允许论文被查阅和借阅；学校可以用不同方式在不同媒体上发表、传播学位论文的全部或部分内容，可以采用影印、缩印或扫描等复制手段保存、汇编学位论文。
(保密的学位论文在解密后应遵守此协议)研究生签名：时间：年月日导师签名：时间：年月日摘要本文结合某矿区的实际，针对概率积分法参数反演中的病态性以及自适应拟合推估在开采沉陷预计中的应用，以MATLAB为平台，展开研究，主要研究内容和成果如下：1、阐述了概率积分法的基本原理，包括静态预计和动态预计；推导了概率积分法参数反演的基本过程；讨论了非充分开采的参数修正。
2、探讨分析了概率积分法参数估计中法矩阵的病态性问题，并考虑应用岭估计法、截断奇异值法以及新的奇异值修正方案削弱法矩阵病态的可行性；研究分析病态性的处理与参数初值敏感性的关系，由于病态性的改善往往伴随参数初值敏感性的增加，因此引入分辨率的概念，对参数初值的敏感性做定量分析。
3、地表下沉可分为倾向部分和随机部分，对倾向部分可通过概率积分法函数描述，而随机部分则当作先验期望和方差已知的信号处理，用拟合推估方法来处理开采沉陷问题，根据自适应滤波的思想，引入赫尔默特方差分量估计，对信号的先验方差进行调整；引入抗差估计，建立抗差自适应拟合推估模型，处理含有粗差和异值的观测量。
并结合实例，应用抗差自适应拟合推估对开采沉陷的静态预计与动态预计进行研究，算例结果表明：自适应拟合推估调整了信号与观测值之间的权比，使信号向量协方差矩阵与观测向量的协方差矩阵协调一致，提高了估值的精度；在观测值含有粗差的情况下，抗差自适应拟合推估参数估值的精度和稳定性得到明显提高。
多类观测量联合平差中方差分量估计的序贯算法
第25卷第3期2005年8月大地测量与地球动力学JOURNAL OF GEODESY AND GEODYN AM ICSVo l.25,N o.3Aug.,2005文章编号:1671 5942(2005)03 0034 05多类观测量联合平差中方差分量估计的序贯算法*张朝玉1) 陶本藻1) 时 晋2)1)武汉大学测绘学院地球空间环境与大地测量教育部重点实验室,武汉 4300792)洛阳市规划建筑设计研究院,洛阳 471000摘 要 在赫尔默特公式的基础上,推导了多类观测数据联合平差中方差分量估计的序贯算法,它区别于以前文献中使各类观测量所对应的验后单位权方差整体趋于一致的做法,而采用逐类(次)平差法,在每次平差后进行方差分量估计,依次使各类观测量的验后单位权方差趋于相等。
该算法未作任何近似,依然保留原赫尔默特方差分量估计公式所具有的优良统计特性;它克服了原来严密公式计算中占用内存大、计算繁琐的缺点,不需要额外保留逐类(次)平差的历史数据,非常适合计算机程序实现。
关键词 联合平差 赫尔默特公式 方差分量估计 序贯平差 迭代计算中图分类号:P207+.2 文献标识码:ASEQUENTIAL ALGORITHM ON VARIANC E COMPONENT ESTIMATION IN JO INT ADJUSTMENT OF VARIOUS OBSERVATIONSZhang Chao yu1),T ao Benzao1)and Shi Jin2)1)L abor ator y of Geosp ace Environment and Geodesy,Ministr y of Education,China,S chool of Geodesy&G eomatics,Wuhan Univ ersity,Wuhan 4300792)I nstitute of Planning&Desig n of Civil Ser vant Residential Ar ea of L uoy ang,L uoy ang 471000Abstract On the basis of H elmert s form ula fo r variance component estim ation,a sequential alg orithm fo r joint adjustment o f v ario us observations is put fo rw ar d in this paper.This method is different from the av ailable methods w hich let the po st adjustm ent w eight variances corr esponding various observatio ns be i dentical w holely.H ow ever,it is sequential adjustment,doing the v ar iance co mpo nent estimation after the adjustment o f each class of observations,and then in proper order m ake the po st adjustm ent unit w eight variances equal to each other.It conquers the disadvantag es of using a lo ts of memor y and calculating com plicated matrices.There is no t any appro ximate pr ocessing of the o riginal H elm ert s formula w itho ut sav ing ex tra historic data beyond sequential adjustment.T his algor ithm is very suitable for prog ram ming on com puter s.Key words:joint adjustment,H elmert s form ula,variance component estimation,sequential adjustment, iteratio n arithmetic*收稿日期:2005-03-20基金项目:武汉大学地球空间环境与大地测量教育部重点实验室开放研究基金(905276031-04-10)作者简介:张朝玉,男,1970年生,讲师,博士生,主要从事大地测量数据处理方面的教学与科研。
方差分量估计
边角网方差分量估计的一种简捷方法
边角 网（ 包括 导线 网） 存在 方 向和 边长 两 种类 型 的 观测值 ， 严 密平 差 时 ， 首 先需 要 对 这 两 类 观 测值 进 行 分别 定权 ， 以便 在 ［ ｐ ｖ ｖ ］＝ｒ ａ ｉ ｎ的 原 则下 进 行 整体 平差 计 算 。观 测 值 的 权 依 据 其 中 误 差 确 定 。平 差 前， 方 向和边 长 观测 值 的 中误 差 都 是 不 能 准 确 知 道 的， 只能 近似 地 估 计 ， 称 为 验 前 中误 差 ； 平 差 后 可 以 得 到计算 的方 向和 边 长 观 测 中误 差 ， 称 为 验 后 中误 差 。边角 网 的平 差 计 算 只 有 在 验 前 、 验 后 方 差 完 全
分量 ， …… 如此迭 代 计算 ， 致 使 验前 验 后方 差 趋 于 一
致。
边 角 网平差 中方 差分 量估 计 的步骤 为 ： （ １ ） 初 始 定权 。按 照 常规方 法估 算方 向 、 边 长观
致 时才 是 严 密 的 ， 其 平 差 值 才 是 统 计 意 义 上 的最
测值 的中误 差 ， 并根据定权公式 ， 确 定 方 向、 边 长 观 测值 的先 验 权 。通 常 取 方 向 观测 值 的 权 Ｐ。＝１ ， 边
ｒ “ 卢－ ｔ ｒ （ Ｎ 。 ‘
…
）
ｔ ｒ Ｎ～Ｎ１ Ｉ Ｎ ～Ｎ ２ ２
１
。 ’ 【 Ｌ ｔ ｒ Ｎ Ｎ 一 ＿ ｌ 。 １ １— １ Ｎ 一 ， １ Ｎ ， ，
ｎ ｓ － ｔ ｒ （ Ｎ 一 Ｎ ２ ２ ） 卜 一 ｔ ｒ （ Ｎ 一 。 Ｎ １ １ Ｎ 一 Ｎ ２ ２ Ｊ ｌ
ｍ ｏＢ 、 ｍ ０ Ｓ：
２ ２
分 量估 计 的 步 骤 和 方 法 。 这 种 方 法 简 单 快 捷 、 成 本 低、 效 率高 、 易 实现 。
XX方差分量估计
P 0 1 R = 1 0 0
Q 0 U = 1 1 0 0
0 P 12 R = 2 0 P 12
0 0 R = 3 0 P 2
0 0 U3 = 00 12
j=1
3
型方差－ 二、Helemrt型方差－协方差分量估计 型方差
E TRiV ==∑ (GTRiG j )σ2 (V ) tr U j
j=1 3
写成矩阵形式： 写成矩阵形式：
tr(GT RGU ) tr(GT RGU2) tr(GT RGU3)σ1 VT RV ˆ2 1 1 1 1 1 2 T T T T ˆ 2 1 2 2 2 tr(G R GU ) tr(G R GU2) tr(G R GU3)σ2 = V RV tr(GT RGU ) tr(GT RGU2) tr(GT RGU3)σ3 VT RV ˆ 2 3 1 3 3 3
满足： 满足：
ˆ E(X) = X
tr(QX ) = m in ˆ
ˆ X 为最优线性无偏估计量
一、概述（续） 概述（
最小二乘估计的最优性及其条件 函数模型误差不显 著 随机模型误差不显 著 无异常误差
参数最小二乘估值是最 优线性无偏估计量 单位权方差的估值具有 无偏性和渐进最优性。 无偏性和渐进最优性。
解为： 解为：
ˆ σ 2 = S−1W V
三、Helemrt型方差分量估计 型方差分量估计
K类观测情形 类观测情形
k×k k× 1
ˆ 2 =W Sσ V
k× 1
ˆ ˆ σ = [σ
2
T 2 2 2
2 01
ˆ σ
2 02
ˆ L σ
2 T 0k
赫尔默特方差分量估计
1 赫尔默特方差分量估计我们知道，平差前观测值向量的方差阵一般是未知的，因此平差时随机模型都是使用观测值向量的权阵。
而权的确定往往都是采用经验定权，也称为随机模型的验前估计，对于同类观测值可按第一章介绍的常用定权方法定权；对于不同类的观测值，就很难合理地确定各类观测值的权。
为了合理地确定不同类观测值的权，可以根据验前估计权进行预平差，用平差后得到的观测值改正数来估计观测值的方差，根据方差的估计值重新进行定权，以改善第一次平差时权的初始值，再依据重新确定的观测值的权再次进行平差，如此重复，直到不同类观测值的权趋于合理，这种平差方法称为验后方差分量估计。
此概念最早由赫尔默特（F.R.Helmert ）在1924年提出，所以又称为赫尔默特方差分量估计。
一、赫尔默特方差分量估计公式为推导公式简便起见，设观测值由两类不同的观测量组成，不同类观测值之间认为互不相关，按间接平差时的数学模型为222111~~∆-=∆-=X B L X B L （函数模型） （8-4-1）0),(()()()()(2121122022112011=∆∆==∆==∆=--D L L D P D L D P D L D ），σσ （随机模型） （8-4-2）其误差方程为111ˆl xB V -= 权阵1P （8-4-3）222ˆl xB V -= 权阵2P （8-4-4） 作整体平差时，法方程为0ˆ=-W xN （8-4-5）式中2222111121B P B N B PB N N N N TT==+=，， 2222111121l P B W l PB W W W W TT ==+=，，一般情况下，由于第一次给定的权1P 、2P 是不恰当的，或者说它们对应的单位权方差是不相等的，设为201σ和202σ，则有122022112011)()(--==P L D P L D σσ（8-4-6）但只有20202201σσσ==才认为定权合理。
9.2.4总体离散程度的估计教学设计-高一下学期数学人教A版(2019)必修第二册
9.2.4总体离散程度的估计一、内容和内容解析内容：极差、方差和标准差的概念和统计含义，总体方差或标准差的估计.内容解析：本节课选自《普通高中课程标准数学教科书-必修第二册》（人教A版）第九章第2节第4课时的内容．在统计学中，为了了解一组数据的特征，我们可以从这组数据的取值规律、集中趋势和离散程度等进行研究.一组数据的离散程度可以反映这组数据的波动情况或稳定性.刻画一组数据的离散程度的统计量有很多，最常用的是极差、方差和标准差．极差是一种较为简单的刻画方式，它反映了一组数据的取值范围.极差只用了这组数据中最大和最小两个数据的信息，对其他数据的取值情况没有涉及，所以极差包含的信息量极少.方差运用平均距离的思想来刻画一组数据的离散程度，它反映了各个数据聚集于平均数周围的程度.方差越小，表明该组数据在平均数的周围越集中；方差越大，表明该组数据越分散.方差的单位是原始数据的单位的平方，与原始数据不一致.对方差开平方，取其算术平方根得到标准差.标准差的单位与数据的单位相同，其含义与方差相同.假设有两组数据，而且已知每组数据的观测个数、平均数和标准差(或方差)，可以通过它们直接计算两组数据合并后全部数据的方差，这大大提高了计算效率.如果一组数据是总体中全部个体的观测值，那么这组数据的方差，标准差和极差就称为总体的方差、标准差和极差，如果这组数据是样本观测值，那么这组教据的方差、标准差和极差就是样本的方差、标准差和极差. 与用样本均值估计总体均值的思想类似，可以用样本方差，标准差和极差估计总体方差、标准差和极差.二、目标和目标解析目标：（1）通过实例、理解极差、方差、标准差等离散程度参数的统计意义．（2）掌握用样本的离散程度参数估计总体的离散程度的方法，体会样本估计总体的思想，发展数据分析素养．目标解析：（1）知道极差、方差、标准差可以刻画数据离散程度，反映数据的稳定性；能用平均数、中位数、众数和极差、方差、标准差对数据进行比较和评价；能用平均数和标准差描述数据的取值范围；知道多数数据在平均数减去两倍标准差与平均数加两倍标准差的范围内. （2）对于通过试验、简单随机抽样等途径获得的样本数据，会计算样本方差和样本标准差；对于两组数据汇总得到的数据，能通过两组数据各自的样本量、平均数和标准差(或方差)计算两组数据合并后所有数据的平均数和标准差(或方差).能用样本数据的方差和标准差估计总体的方差和标准差，在此过程中体会样本估计总体的思想．基于上述分析，本节课的教学重点定为：方差和标准差的意义与计算；已知两组数据的观测个数、平均数和标准差或方差时，两组数据合并后所有数据的平均数和标准差的计算方法与思想．三、教学问题诊断分析1．教学问题一：在大数据时代，数据众多，有时需将不同来源的数据进行整合.针对数据多、计算量大的实际问题，可以采用分步计算的方法，先分别处理不同来源的数据，再计算所有数据的统计结果.在分层随机抽样中，每层得到的调查数据作为一个组，学生已经学习了已知每组数据的均值和样本量，计算两组数据合并后所有数据总均值的方法——加权平均，但总方差的计算需要知道每组数据的个数、平均数和标准差.在推导总方差的计算公式时，需要用符号对样本进行表示，通过代数变形进行推导，推导过程较复杂.学生在初中仅会计算简单数据的方差，对这类问题未曾接触，同时学生对大量复杂的数学符号存在认知障碍.解决方案：在教学过程中，教师应尽量多用语言(符号代表的统计意义)对公式的含义进行解释，帮助学生逐步适应复杂的数学符号．基于上述情况，本节课的教学难点定为：已知每组数据个数、平均数和方差，获得各组数据合并后全部数据的方差的计算公式，及计算中的递推思想.四、教学策略分析本节课的教学目标与教学问题为我们选择教学策略提供了启示．为了让学生通过观察、归纳得到方差、标准差、极差的公式，应该为学生创造积极探究的平台．因此，在教学过程中使用计算器或计算机软件计算方差．既可以解决复杂计算问题，也可以让学生从被动学习状态转到主动学习状态中来．在教学设计中，采取问题引导方式来组织课堂教学．问题的设置给学生留有充分的思考空间，让学生围绕问题主线，通过自主探究达到突出教学重点，突破教学难点．在教学过程中，重视极差、方差、标准差的推导与证明，让学生体会到数学推导的基本过程，同时，公式的应用其实就是数学模型的建立与应用的典范．因此，本节课的教学是实施数学具体内容的教学与核心素养教学有机结合的尝试．教学环节问题或任务师生活动设计意图创设[问题1]有两位射击运动员在一次射击测教师1：提出问题1．学生1：学生思考.通过具体问题，让学生情境，引入新课试中各射靶10次,每次命中的环数如下:甲:7879549107 4乙:9578768677如果你是教练,你应当如何对这次射击作出评价?[问题2]甲、乙两人本次射击的平均成绩分别为多少环?他们的平均成绩一样吗?[问题3]难道这两个人的水平就没有什么差异了吗?你能作出这两人成绩的频率分布条形图来说明其水平差异在哪里吗?教师2：提出问题2．学生2：经计算得(7+8+7+9+5+4+9+10+7+4)=7,同理可得=7.他们的平均成绩一样.教师3：提出问题3．学生3：从图上可以直观地看出,他们的水平还是有差异的,甲成绩比较分散,乙成绩相对集中.感受反映样本数字离散程度的估计量；极差、方差与标准差学学习解决实际问题中的运用，发展学生数学抽象、逻辑推理的核心素养。
【国家自然科学基金】_helmert方差分量估计_基金支持热词逐年推荐_【万方软件创新助手】_20140729
科研热词 推荐指数 间接平差 1 赫尔默特方差分量估计 1 粗差探测 1 无碴轨道高速铁路 1 方差分量估计 1 探月工程 1 拟稳平差 1 卫星测轨 1 仿真计算 1 minque 1 helmert型方差分量估计 1 bique 1
科研热词 helmert方差分量估计 赫尔默特法 虚拟观测 自适应因子 简化公式 极大似然估计 最小范数二次无偏估计 最小二乘方差分量估计 最优不变二次无偏估计 方差分量估计 拟合推估 定位精度 单点定位 协方差函数 半参数回归模型 gps高程拟合 gps beidou
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 随机信号 自适应因子 精密定位 方差分量估计 拟合推估 形变分析 地球物理模型 地壳变形分析 先验信息 helmert方差分量估计 gps
推荐指数 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 helmert方差分量估计 随机模型 虚拟观测值 相对精度 正交分解 最小范数二次无偏估计 无碴轨道铁路 方差因子 方差-协方差分量估计 方位向偏移量 拟合推估 幅度匹配 单位权方差 全局最优化 二次型 三维形变 insar bam地震
科研热词 联合反演 方差分量估计 赫尔默特方差分量估计 赫尔墨特方差分量估计 相对权比 相对定位 模糊度解算 最小二乘配置 序贯算法 大地测量数据处理 单位权方差 两步法 helmert估计 gps/glonass
测量数据处理理论及方法-0
条件平差
n t r=n-t 0
附有参数的 条件平差
n t r=n-t 0<u<t且独立
间接平差 附有限制条件
的间接平差
n t r=n-t u=t且独立
n
t
r=n-t U>t且包含t个
独立
r n F (Lˆ ) = 0
AΔ +W = 0
r+u
n+u
F (Lˆ Xˆ ) = 0
AΔ+BX~+W =0
r+u=n n+u Lˆ = F ( Xˆ ) Δ = BX~ − l
武汉大学测绘学院 孙
海燕 武汉大学测绘学院 黄海兰
2
2015-10-25
9 教学内容
课程教学大纲
¾ 针对经典测量平差的局限性，系统地研究极大验后估计等若
干估计方法，构造广义测量平差原理；
¾ 讨论并突破经典平差理论及应用上限制，完成最小二乘平差
的统一理论与方法建立；
¾ 讨论测量平差的随机模型验后估计的赫尔默特法及二次无偏
sin sin(Lˆ1
Xˆ sin(Lˆ3 + Lˆ5 ) sin Lˆ1 + Lˆ4 ) sin(Lˆ6 − Xˆ ) sin Lˆ3
−1 =
0
Lˆ7 + Xˆ + α BD − α BC = 0
武汉大学测绘学院 黄海兰
8
2015-10-25
间接平差
1
A
B Xˆ1
4
2
Xˆ 2
C
3
5
D Xˆ 3
⎡1 0 0 1 −1 0 ⎤
⎡2⎤
A = ⎢⎢0 1 0 0 1 −1⎥⎥ , W = ⎢⎢− 3⎥⎥ ,
人教版数学八年级下册20.2.2用样本方差估计总体方差第2课时优秀教学案例
一、案例背景
本节内容是“人教版数学八年级下册20.2.2用样本方差估计总体方差”的第二课时，这是学生在学习了样本方差的基础知识后，进一步探究如何利用样本方差来估计总体方差的过程。通过本节课的学习，学生需要掌握用样本方差估计总体方差的方法，并能够运用这一方法解决实际问题。
（二）问题导向
1.引导学生提出问题，激发他们的思考和探究欲望。
2.通过问题的提出和解决，让学生掌握样本方差估计总体方差的原理和方法。
3.培养学生的问题解决能力，使他们能够独立思考和解决问题。
在教学过程中，我将注重问题导向，引导学生提出问题，激发他们的思考和探究欲望。通过问题的提出和解决，让学生掌握样本方差估计总体方差的原理和方法，使他们能够独立思考和解决问题。在解决问题的过程中，我会引导学生运用已学的知识，将理论知识与实际问题相结合，提高他们的问题解决能力。
在设计本节课的教学案例时，我以“生活中的方差”为主题，通过引入实际生活中的数据和问题，激发学生的学习兴趣，引导学生主动探究和理解用样本方差估计总体方差的原理和方法。在教学过程中，我注重与学生的互动，鼓励他们提出问题、解决问题，培养他们的数学思维和解决问题的能力。
此外，我还设计了丰富的实践活动，让学生通过实际操作和计算，加深对方差概念的理解，提高他们运用数学知识解决实际问题的能力。在教学评价环节，我采用多元化的评价方式，不仅关注学生的知识掌握程度，还注重评价他们的学习过程和能力发展，以促进学生的全面进步。
（四）反思与评价
1.引导学生对学习过程进行反思，帮助他们总结经验，提高学习效果。
2.采用多元化的评价方式，关注学生的知识掌握程度和能力发展，进行全面评价。
总体均值与方差的矩估计量的表达式课件
n
i 1
X
i
X.
这一估计量与矩估计量是相同的.
例2 设总体 ~ N (, 2 ), , 2为未知参数,
x1, x2, , xn 是来自 的一个样本值, 求 和 2
的最大似然估计量.
解 的概率密度为
p( x; , 2 )
1
( x )2
e 2 2 ,
2π
ˆ ,
一般地:
ˆ 2
1 n
n
(i )2.
i 1
用样本均值
1 n
n i 1
i作为总体的均值的矩估计,
用样本二阶中心矩
m2
1 n
n i 1
(i
)2作为总体的
方差的矩估计.
矩法的优点是简单易行, 缺点是，当总体类型已知时，没有 充分利用分布提供的信息 . 一般场合下, 矩估计量不具有唯一性 .
点估计的求法: (两种) 矩估计法和最大似然估计法.
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 .
理论依据: 大数定律
设1 , 2 , ...n是来自总体的一个样本，
设的k阶矩k E k 存在.
(4).用方程组的解ˆ 1,ˆ 2 ,,ˆ k分别作为1,2 ,,k的 估计量,这个估计量称为矩估计量.
矩估计量的观察值称为矩估计值.
例 1 设总体 服从泊松分布 P()， 求参数 的估计量.
解：设 1,2, n 是总体 的一个 样本,由于 E ,可得
n
个样本,求 p的最大似然估计量.
解 设 x1, x2, , xn为相应于样本1,2, ,n 的
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
赫尔默特方差分量估计1 赫尔默特方差分量估计我们知道，平差前观测值向量的方差阵一般是未知的，因此平差时随机模型都是使用观测值向量的权阵。
而权的确定往往都是采用经验定权，也称为随机模型的验前估计，对于同类观测值可按第一章介绍的常用定权方法定权；对于不同类的观测值，就很难合理地确定各类观测值的权。
为了合理地确定不同类观测值的权，可以根据验前估计权进行预平差，用平差后得到的观测值改正数来估计观测值的方差，根据方差的估计值重新进行定权，以改善第一次平差时权的初始值，再依据重新确定的观测值的权再次进行平差，如此重复，直到不同类观测值的权趋于合理，这种平差方法称为验后方差分量估计。
此概念最早由赫尔默特（F.R.Helmert ）在1924年提出，所以又称为赫尔默特方差分量估计。
一、赫尔默特方差分量估计公式为推导公式简便起见，设观测值由两类不同的观测量组成，不同类观测值之间认为互不相关，按间接平差时的数学模型为222111~~∆-=∆-=X B L X B L （函数模型） （8-4-1）0),(()()()()(2121122022112011=∆∆==∆==∆=--D L L D P D L D P D L D ），σσ （随机模型） （8-4-2）其误差方程为111ˆl xB V -= 权阵1P （8-4-3） 222ˆl xB V -= 权阵2P （8-4-4）作整体平差时，法方程为0ˆ=-W x N （8-4-5）式中2222111121B P B N B P B N N N N TT==+=，，2222111121l P B W l PB W W W W TT==+=，， 一般情况下，由于第一次给定的权1P 、2P 是不恰当的，或者说它们对应的单位权方差是不相等的，设为201σ和202σ，则有122022112011)()(--==P L D P L D σσ（8-4-6）但只有20202201σσσ==才认为定权合理。
方差分量估计的目的就是根据事先初定的权1P 、2P 进行预平差，然后利用平差后两类观测值的111V P V T 、222V P V T 来求估计量202201ˆˆσσ、，再根据（8-4-6）式求出)(ˆ)(ˆ21L D L D 、，由这个方差估值再重新定权，再平差，直到202201ˆˆσσ=为止。
为此需要建立111V P V T 、222V P V T与估计量202201ˆˆσσ、之间的关系式。
由数理统计知识可知，若有服从任一分布的q 维随机变量1⨯q Y，已知其数学期望为1⨯q η，方差阵为qq ⨯∑，则1⨯q Y向量的任一二次型的数学期望可以表达为：ηηB B tr BY Y E T T +∑=)()(（8-4-7）式中B 为任意q 阶的对称可逆阵。
现用V 向量代替上式中的Y 向量，则其中η的应换为)(V E ，∑应换为)(V D ，B 阵可以换成权阵P ，于是有)()())(()(V PE V E V PD tr PV V E TT += （8-4-8）前面已经证明0)(=V E ，于是有：))(()(111V PD tr PV V E T= （8-4-9）而1111l W N B V -=-12111)(l W W N B -+=-12221111111l l P B N B l P B N B TT -+=--2221111111)(l P B N B l I P B N B TT --+-=对上式应用协因数传播律得+--=--TT T I P B N B L D I P B N B V D ))(()()(1111111111 T TB N B P L D P B N B 112222211)(--将122022112011)()(--==P L D P L D σσ、代入上式，整理后得TT T B N N N B P B N B B N N N B V D 1121120211111111112011)2()(------++-=σσ 将上式代入（8-4-9）式，得 ))(()(11111V D P tr V P V E T=)()2(1121112021111111111111201T TTB N N N B P tr P P B N B P B N N N B P tr ------++-=σσ顾及矩阵迹的性质，上式可写为)()]()(2[)(12112021111111201111-----++-=N N N N tr N N N N tr N N tr n V P V E Tσσ同理可得)()]()(2[)(12112011212122202222-----++-=N N N N tr N N N N tr N N tr n V P V E Tσσ 去掉上面两式的期望符号，相应的单位权方差202201σσ、也改用估值符号202201ˆˆσσ、表示，整理顺序后得11120212112011111111ˆ)(ˆ)]()(2[V P V N N N N tr N N N N tr N N tr n T =++------σσ（8-4-10）22220212121222011211ˆ)]()(2[ˆ)(V P V N N N N tr N N tr n N N N N tr T =+-+-----σσ（8-4-11）其矩阵形式可写为 θθW S =⨯⨯1222ˆ （8-4-12） θθW S 112ˆ-⨯=（8-4-13）式中⎥⎦⎤⎢⎣⎡+-+-=----------)()(2)()()()(21212122121112111111111N N N N tr N N tr n N N N N tr N N N N tr N N N N tr N N tr n S[]T202201ˆˆˆσσθ=[]TTT V P V V P V W 222111=θ （8-4-12）、（8-4-13）两式即为赫尔默特方差分量估计的严密公式。
由此式可以求得两类观测值的单位权方差估值，从而可以根据（8-4-6）式求得观测值方差的估值，以此方差估值再次定权，再次平差，直至满足要求为止。
现将以上推导扩展至m 组观测值。
误差方程为i i i l xB V -=ˆ )21(m i ，= 令120)(-=i i i P L D σ∑==mii i TiN N B P B N 1，∑==mii i T iW W l P B W 1，则得参数的估值为W N x1ˆ-=按照上述类似的推导，则有)()]()(2[)(1120,111120--≠=---∑++-=N N N N tr N N N N tr N N tr n V P V E j i j mij j i i i i ii i Ti σσ去掉期望符号，相应的单位权方差20i σ也改为用估值符号20ˆi σ，则有θθW S m m m =⨯⨯1ˆ （8-4-14）式中⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-+-=---------------------)()(2)()()()()(2)()()()()(211112111112121212122111211112111111111N N N N tr N N tr n N N N N tr N N N N tr N N N N tr N N N N tr N N tr n N N N N tr N N N N tr N N N N tr N N N N tr N N tr n S m m m m m m m ，，，[]Tm 20202201ˆˆˆˆσσσθ =[]Tm m Tm T T V P V V P V V P V W 222111=θ 二、计算步骤1.将观测值分类，并进行验前权估计，即确定各类观测值的权的初值m P P P 21、；2.进行第一次平差，求得i i Ti V P V ；3.按（8-4-14）式求各类观测值单位权方差估值20ˆi σ； 4.按（8-4-6）式计算各类观测值方差的估值；5.依据定权公式再次定权，再次平差，如此反复，直到各类单位权方差的估值相等或接近相等为止。
2 秩亏自由网平差在前面介绍的经典平差中，都是以已知的起算数据为基础，将控制网固定在已知数据上。
如水准网必须至少已知网中某一点的高程，平面网至少要已知一点的坐标、一条边的边长和一条边的方位角。
当网中没有必要的起算数据时，我们称其为自由网，本节将介绍网中没有起算数据时的平差方法，即自由网平差。
在经典间接平差中，网中具备必要的起算数据，误差方程为 111ˆ⨯⨯⨯⨯-=n t t n n l xB V （8-2-1）式中系数阵B 为列满秩矩阵，其秩为t B R =)(。
在最小二乘准则下得到的法方程为0ˆ11=-⨯⨯⨯t t tt bb W xN （8-2-2）由于其系数阵的秩为t B R PB B R N R T bb ===)()()(，所以bb N 为满秩矩阵，即为非奇异阵，具有凯利逆bbN1-，因此具有唯一解，即W N xbb1ˆ-=（8-2-3）当网中无起算数据时，网中所有点均为待定点，设未知参数的个数为u ，误差方程为111ˆ⨯⨯⨯⨯-=n u u n n l xB V （8-2-4）式中d t u +=d 为必要的起算数据个数。
尽管增加了d 个参数，但B 的秩仍为必要观测个数，即u t B R <=)(其中B 为不满秩矩阵，称为秩亏阵，其秩亏数为d 。
组成法方程 0ˆ11=-⨯⨯⨯u u u u W xN （8-2-5）式中PlB W PB B N T u T uu ==⨯⨯1，，且u t B R PB B R N R T<===)()()(，所以N 也为秩亏阵，秩亏数为：t u d -=（8-2-6）由上式知，不同类型控制网的秩亏数就是经典平差时必要的起算数据的个数。
即有：⎪⎩⎪⎨⎧=测角网网测边网、边角网、导线水准网、测站平差,4,3,1d在控制网秩亏的情况下，法方程有解但不唯一。
也就是说仅满足最小二乘准则，仍无法求得xˆ的唯一解，这就是秩亏网平差与经典平差的根本区别。
为求得唯一解，还必须增加新的约束条件，来达到求唯一解的目的。
秩亏自由网平差就是在满足最小二乘min =PV V T和最小范数min ˆˆ=x xT 的条件下，求参数一组最佳估值的平差方法。
下面将推导自由网平差常用两种解法的有关计算公式。
一、直接解法根据广义逆理论，相容方程组0ˆ11=-⨯⨯⨯u u u u W xN 虽然具有无穷多组解，但它有唯一的最小范数解，即：W N x m r 1ˆ-= （8-2-7）式中--=)(T T m NN N N ，称为矩阵N 的最小范数g 逆。