全等三角形之手拉手模型
完整版)全等三角形之手拉手模型

完整版)全等三角形之手拉手模型
本文将介绍手拉手模型中的全等三角形。
所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型如下:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
可以得出三个结论:结论1:△ABC≌△AB'C'(SAS),BC=B'C';结论2:
∠BOB'=∠BAB';结论3:AO平分∠BOC'。
在共顶点的等腰直角三角形中,也可以应用手拉手模型。
例如,如下图所示,△ABC和△ADE是等腰直角三角形,且
∠BAC=∠DAE=90°。
可以证明:⑴BD=CE⑵BD⊥CE。
另外,在共顶点的等边三角形中,也可以使用手拉手模型。
如下图,点A为线段BD上一点,△ABC和△ADE均是等边
三角形。
可以求出:(1)CD=BE;(2)∠DAE+
∠BFD=180°;(3)∠BFA=∠DFA=60°。
总之,手拉手模型在全等三角形的证明中是一个非常有用的工具,能够帮助我们更好地理解和应用三角形的性质。
人教版数学八年级上册 综合专题2—全等三角形手拉手模型

长线交 CE 于 F 点.
证明重要结论:
C
① △ABD≌△ACE;
FD
② BD = CE;
③ BD 的延长线 BF⊥CE;
EA
B
解:∵△ABC、△ADE 都是等腰直角三角形, ∴ AB = AC,AD = AE. 在△ABD 和△ACE 中,
∴ △ABD≌△ACE(SAS). ∴ BD = CE. ∴ ∠ABD = ∠ACE. ∵ ∠BDC = ∠ABD + ∠BAC
E
① △ABD≌△ACE
② BD = CE
③ ∠BFC = ∠BAC = ∠DAE B
F D G
C
解:∵△ABC、△ADE 都是等腰三角形,
∴ AB = AC,AD = AE.
又∵∠BAC = ∠DAE,
A
∴∠BAC + ∠CAD =∠DAE +∠CAD,
即∠BAD = ∠CAE.
在△ABD 和△ACE 中
BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点
Q,连接 PQ,则有以下五个结论: B ① AD = BE; ② PQ∥AE;
③ AP = BQ; ④ DE = DP;
⑤∠AOB = 60°.
P
OD Q
其中正确的结论有__①__②__③__⑤___.
A
C
E
=∠ACE + ∠BFC, ∴ ∠BFC = ∠BAC = 90°. ∴ BF⊥CE.
C FD
EA
B
练一练
2. 如图,△ABC、△ADE 都是等腰直角三角形,
∠BAC = ∠DAE = 90°,连接 BD、CE 交于点 F.
(1) 求证:BD = CE; (2) 求证:BD⊥CE. C
全等典型模型:“手拉手”模型

《三角形证明》题型解读12 全等典型模型:“手拉手”模型【知识梳理】(一)“手拉手模型”的基本图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点在同一直线上。
解题方法:一定有以下六个结论(三组全等、一个60°、一个等边△、一组平行线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠2=∠3=60°,∴∠ABE=∠CBD=120°,∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②△ABH ≌△CBF证明过程:∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠1=∠2,∴△ABH ≌△CBF (SAS ) ③△BHE ≌△BFD证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,∵BE=BD ,∠2=∠3,∴△BHE ≌△BFD (SAS ) ④∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ⑤△BHF 是等边三角形证明过程:∵△BHE ≌△BFD (SAS ),∴BH=BF ,∵∠2=60°,∴△BHF 是等边三角形(有一个角是60°的等腰三角形是等边三角形) ⑥HF//AD证明过程:∵△BHF 是等边三角形,∴∠8=60°,∵∠3=60°,∴∠8=∠3,∴HF//AD (二)“手拉手模型”的变化图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点不在同一直线上。
图2M N 765431H GFEDCBA765431HG F ED CBA解题方法:一定有以下三个结论(一组全等,一个60°、一个角平分线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠3=60°,∴∠ABE=∠CBD (共角模型),∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ③BG 平分∠HBF证明过程:作BM ⊥AE 于点M ,BN ⊥GD 于点N ,如图2,∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠AMB=∠CNB=90°,∴△ABM ≌△CBN (AAS ),∴BM=BN ,∴BG 平分∠HBF (到角两边的距离相等的点,在这个角的角平分线上) (三)常见“手拉手”变化图形【典型例题】例1.如图,C 为线段AE 上一动点(不与A 、E 重合),在AE 同侧分别作等边△ABC 和等 边△CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,以下五个结论: ①AD =BE ;②PQ ∥AE ;③CP =CQ ;④BO =OE ;⑤∠AOB =60°,恒成立的结论有( )。
全等三角形——手拉手模型(完整资料).doc

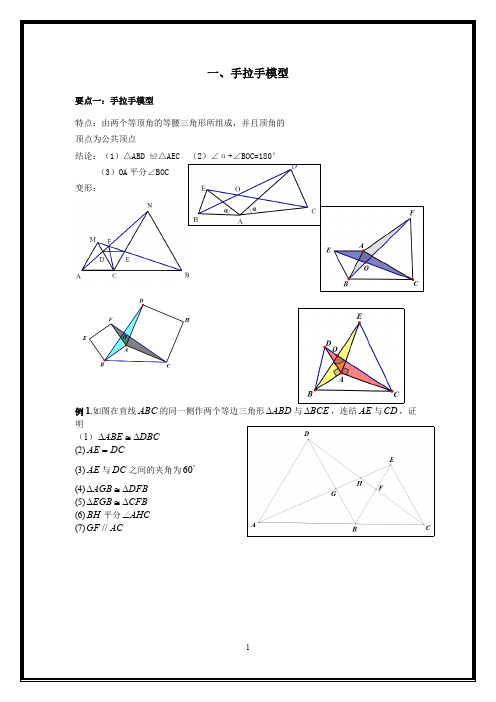
【最新整理,下载后即可编辑】手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA平分∠BOC变形:例1.如图在直线ABC的同一侧作两个等边三角形ABD∆,∆与BCE 连结AE与CD,证明(1)DBC∆ABE∆≅(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFB≅∆AGB∆(5)CFB≅∆EGB∆(6)BH平分AHC∠(7)ACGF//变式精练1:如图两个等边三角形ABD∆与∆,连结AE与CD,BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠变式精练2:如图两个等边三角形ABD∆与∆,连结AE与CD,BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠例2:如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?。
初中数学课件全等三角形-手拉手模型

∠ = 90°.
(1)求证: = ;
(2)求证:和垂直。
确认预判Ⅲ
• 如图,分别以△ 的边,向外作等边三角形和等边三角形,
线段与相交于点,连接.
(1)求证: = ;
(2)求∠的度数;
(3)求证:平分∠.
课程目标
∴ ∠ = ∠
∠ = ∠ = 60°
∵∠ = ∠,
∴ ∠ = ∠
∠ + ∠ + ∠ = 180°
∴ △ ≌ △
∠ + ∠ + ∠ = 180°
(2). ∵△ ≌ △
∴ ∠ = ∠ = 60°,
,
例题讲解
•
如图,已知△ 和△ 都是等腰直角三角形,∠ = ∠ = 90°,
点为边上一点.
(1)求证:△ ≅△ ;
(2)求证:△ 是直角三角形;
例题解析
(1) 证明: ∵△ 和 △ 都是等腰直角三角形,
∴ ∠ = ∠ = 45°, = , = ,
、分别是线段、的中点.
(1)求证:=;
(2)求∠的度数;
应用练习
• 如图,点是线段上一点,且 < .如图,当△ 和△ 都是等
边三角形时,连接,,分别交、于点、.
(1)求证: = ;
(2)判断△ 是何特殊三角形并说明理由;
∴ =
即与的夹角为60°
解题方法
应用练习
如图,点、、在同一条直线上,△ 与△ 都是等边三角形,则下
列结论不一定成立的是(
A. △ ≅△
B. △ ≅△
C. △ ≅△
D. △ ≅△
)
应用练习
• 已知:如图,△ 、 △ 都是等边三角形,、相交于点,点
全等模型-手拉手模型--常见几何模型归纳(学生版)

全等模型-手拉手模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(三角形)【模型解读】将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得△ABD≅△ACE。
【常见模型及证法】(等边)(等腰直角)(等腰)1(2022·北京东城·九年级期末)如图,在等边三角形ABC中,点P为△ABC内一点,连接AP,BP,CP,将线段AP绕点A顺时针旋转60°得到AP ,连接PP ,BP .(1)用等式表示BP 与CP的数量关系,并证明;(2)当∠BPC=120°时, ①直接写出∠P BP的度数为;②若M为BC的中点,连接PM,请用等式表示PM与AP的数量关系,并证明.2(2022·黑龙江·中考真题)△ABC和△ADE都是等边三角形.(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+ PB=PC(或PA+PC=PB)成立;请证明.(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)将△ADE绕点A 旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.3(2023·黑龙江哈尔滨·九年级校考期中)如图,在△ABC中,∠C=90°,AC=BC,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则∠C′BA的度数为()A.15°B.20°C.30°D.45°4(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE是顶角相等的等腰三角形,BC,DE分别是底边.求证:BD= CE;(2)解决问题:如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.图1 图25(2022秋·江苏·八年级期中)点D为△ABC外一点,∠ACB=90°,AC=BC.(1)如图1,∠DCE=90°,CD=CE,求证:∠ADC=∠BEC;(2)如图2,若∠CDB=45°,AE∥BD,CE⊥CD,求证:AE=BD;模型2.手拉手模型(正多边形型)【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
全等三角形——手拉手模型

全等三角形——手拉手模型-CAL-FENGHAI.-(YICAI)-Company One1手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA平分∠BOC变形:例1.如图在直线ABC的同一侧作两个等边三角形ABD∆,连结AE与∆与BCECD,证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFB≅∆AGB∆(5)CFB≅∆EGB∆(6)BH平分AHC∠(7)ACGF//变式精练1:如图两个等边三角形ABD∆,连结AE与CD,∆与BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠变式精练2:如图两个等边三角形ABD∆,∆与BCE连结AE与CD,证明(1)DBCABE∆∆≅(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠例2:如图,两个正方形ABCD与DEFG,连结AG,,二者相交于点HCE问:(1)CDEADG∆∆是否成立≅(2)AG是否与CE相等(3)AG与CE之间的夹角为多少度(4)HD是否平分AHE∠例3:如图两个等腰直角三角形ADC与AG,,二者相交于点HEDG,连结CE问:(1)CDE∆是否成立ADG∆≅(2)AG是否与CE相等(3)AG与CE之间的夹角为多少度(4)HD是否平分AHE∠例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立(2)AE 是否与CD 相等(3)AE 与CD 之间的夹角为多少度(4)HB 是否平分AHC ∠。
(完整)三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结,推荐文档
1
变式精练 1:如图两个等边三角形 ABD 与 BCE ,连结 AE 与 CD , 证明(1) ABE DBC (2) AE DC (3) AE 与 DC 之间的夹角为 60 (4) AE 与 DC 的交点设为 H , BH 平分 AHC
BAP BCP 1800 。
M
A 1 2
B
N P
C DC
3. 如图所示,在 RtABC 中,AB=AC, BAC 900 , ABD CBD ,CE 垂直于
BD 的延长线于 E。求证:BD=2CE。 A
E
D
5 如图所示,在 ABC 中, ABC 900 ,AD 为 BAC 的平分 C
2
A
B
M
C
【练 1】在△ ABC 中, AB 5,AC 9 ,则 BC 边上的中线 AD 的长的取值范围是什么?
【练 2】如图所示,在 ABC 的 AB 边上取两点 E 、 F ,使 AE BF ,连接 CE 、 CF ,求 证: AC BC EC F如图,已知在 ABC 中, AD 是 BC 边上的中线, E 是 AD 上一点,延长 BE 交 AC 于 F , AF EF ,求证: AC BE .
一、手拉手模型
要点一:手拉手模型 特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点 结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°
(3)OA 平分∠BOC 变形:
例 1.如图在直线 ABC 的同一侧作两个等边三角形 ABD 与 BCE ,连结 AE 与 CD ,证
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形之手拉手模型专题
➢手拉手模型:
定义:所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
➢基本模型:
例题:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
➢共顶点的等腰直角三角形中的手拉手
变式精练1、下图,△ABC和△ADE 是等腰直角三角形,∠BAC=∠DAE=90°,求证:⑴BD=CE ⑵BD⊥CE
三个结论
结论1:△ABC≌△AB'C'(SAS)
BC=B'C'
结论2:∠BOB'=∠BAB'
结论3: AO平分∠BOC'
➢共顶点的等边三角形中的手拉手
变式精练2:如图,点A为线段BD上一点,△ABC和△ADE均是等边三角形,求:(1)CD=BE (2)∠DAE+∠BFD=180°(3)∠BFA=∠DFA=60°
模型应用1:如图,分别以△ABC 的边AB、AC 同时向外作等腰直角三角形,其中AB =AE ,AC =AD,∠BAE =∠CAD=90°,点G为BC中点,点F 为BE 中点,点H 为CD中点。
探索GF 与GH 的位置及数量关系并说明理由。
(选讲)模型应用2:如图,在五边形ABCDE中,∠ABC =∠AED =90°,∠BAC =∠EAD=α,F 为CD的中点。
求证:(1)BF=EF
课堂小测:
练习1:如图,两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。
求:(1)AG=CE (2)AG与CE之间的夹角为多少度?(3)HD平分∠AHE。
