正态分布及6Sigma原理
6σ与正态分布的分析概述

6σ舆正态分布舆质量相关得数学统计知识主要包括三个方面,即正态分布、二项分布、和泊松分布。
二个分析即回归舆相关分析、方差分析和假设检验,这里只介绍正态分布。
正态分布 正态分布又称概率分布,产品的诸多质量指针(如尺寸、强度、硬度等)都是从于正态分布的。
如果影响某一变量的随机因素很多,而每一个都不起决定作用,且这些影响是可以迭加的,那么随机变量被认为是顺从正态分布的。
设随机变量的概率密度为:-∞<X<∞, -∞<u<∞,σ>0则称X 服从参数为(u ,σ*σ)的正态分布,记为X~N(u ,σ*σ)P(x)=1σ√2πe -(x-u)(x-u)/2σ*σ验证P(x)是一个密度函数当u=0,σ=1时,称x为标准正态分布,记为X~N(0,1) 其概率密度和分布函数分别用Y(x),φ(x)表示Y(x)=[1/√(2π)]*e-x*x/2φ(x)= [1/√(2π)]∫-∞x e-u*u/2du一般正态分布成标准正态分布:F(x)=P{X≦x}= [1/√(2π)]∫-∞x e-(x-u)*(x-u)/4σ*σdu= [1/√(2π)]∫-∞(x-u)/σe-Z*Z/2dz=φ[(x-u)/σ]由此可得,若X~N(u,σ*σ),则有P{x1≦x≦x1}=φ[(x2-u)/σ]- φ[(x1-u)/σ]由正态分布得对称性,对Z~N(0,1),当Z<0将有φ(z)= ∫-∞zφ(u)duφ(z)= ∫z∞φ(u)du=1-φ(-z)例:设X~N(u,σ*σ),求P{u-kσ<X<u+kσ} (k=1,2,3) P{u-s<X<u+s}=φ{(u+s-u)/s}-φ{(u-s-u)/s}=φ(1)- φ(-1)=2φ(-1)=0.6826类似可得P{ u-2s<X<u+2s}=φ{(u+2s-u)/s}-φ{(u-2s-u)/s}=2φ(2)- 1=0.9546P{ u-3s<X<u+3s}=φ{(u+3s-u)/s}-φ{(u-3s-u)/s}=2φ(3)-1=0.9974注;(1).0.6826,0.9546,0.9974为查正态分布表所得(2) s=σu决定图形的中心位置,σ决定了图形中峰的陡峭程度,当σ正态分布对质量控制的意义1.通过计算样本平均值X,对比标准分布中心值μ,发现整体数据的偏移程度,调整加工中心,提高工序能力。
六西格玛

为什么叫“六”“西格玛”?
回顾正态分布
σ (Sigma)是一个希腊字母。在统计学中常用来表
达数据的离散程度,即标准差。
f x
1
2
e
x 2 2
2
-
+
事件的概率积分:曲线下面的总面积=100%
=0.5 =1
=2
1 2
=
( - x)2
N
x =——
•1998年通过六西格玛节省了7.5亿美元的投资,并于第二年节省15 亿美元 •经营利润从1996年的14.8%上升到2000年的18.9%
GE 的 感 受
•六西格玛不仅仅属于工程师们。在质量计划方面,一种常见的 错误理解是认为这些计划只是针对技术脑瓜的。而实际上,它适 用于任何工种中最好的、最聪明的员工。 •工厂经理可以运用六西格玛来减少废品,增强产品的稳定性, 解决设备问题,或提高生产能力。 •人力资源经理需要它来减少聘用员工所需的时间。 •地区销售经理可以用它来预测可靠性、定价政策或价格方差。 •同理,管工、汽车修理工和园艺工人可以用它来更好地理解客 户的需求,调整自己的服务以迎合客户。
六西格玛项目实施步骤
六西格玛用“D-M-A-I-C”的方法体系对过程进行改进。即分五个阶段: 界定(Define)、衡量(Measure)、分析(Analyze)、改善(Improve)与控制 (Control)。
定义
测评
分析
改进
控制
Define
倡导者 Champion
大黑带 MBB (Master Black Belt)
对六西格玛管理理念和技术方法具有较深的了解与体验,并将他们 传递到组织中来; 培训黑带和绿带,确保他们掌握了适用的工具和方法; 为黑带和绿带的六西格玛项目提供指导; 协调和指导跨职能的六西格玛项目; 协助倡导者和管理层选择和管理六西格玛项目 。
sigma 标准正态分布

sigma标准正态分布是指正态分布中的标准差(sigma)与概率之间的关系。
正态分布是一种概率分布,描述了许多自然现象的概率分布形态,其概率密度函数呈钟形曲线。
在正态分布中,均值(μ)和标准差(σ)是两个重要的参数。
sigma原则、2sigma原则和3sigma原则是正态分布中的三个重要原则,用于描述数值分布在一定区间内的概率。
具体来说:
sigma原则:数值分布在(μ-σ,μ+σ)区间的概率为0.6826。
2sigma原则:数值分布在(μ-2σ,μ+2σ)区间的概率为0.9544。
3sigma原则:数值分布在(μ-3σ,μ+3σ)区间的概率为0.9974。
其中,μ是正态分布的均值,σ是标准差,σ的平方(σ²)表示方差。
在正态分布中,大约68%的数值落在(μ-σ,μ+σ)区间内,大约95%的数值落在(μ-2σ,μ+2σ)区间内,大约99.7%的数值落在(μ-3σ,μ+3σ)区间内。
这三个原则在统计学和数据分析中具有重要应用,用于估计数据的取值范围和概率。
以上信息仅供参考,如有需要建议查阅统计学相关书籍或咨询统计学专业人士。
正态分布6西格玛概率 解释说明以及概述

正态分布6西格玛概率解释说明以及概述1. 引言1.1 概述引言部分将对文章的主题进行概述和介绍。
在本文中,我们将探讨正态分布六西格玛概率的解释说明以及概述。
正态分布是一种重要的统计分布,它具有许多优秀的性质和应用领域。
而六西格玛原理则是基于正态分布而发展起来的一种质量管理方法,它通过计算事件发生在六个标准差之内的概率来评估过程或产品是否稳定。
1.2 文章结构本文共分为五个部分进行论述。
首先,在第二部分我们将介绍正态分布的定义与性质,同时探讨其常见应用领域以及参数估计与假设检验方法。
然后,在第三部分中,我们将回顾六西格玛原理的背景和发展历程,并详细解释其核心概念和特点。
此外,还将深入研究六西格玛在不同应用场景中的优势和实际价值。
在第四部分中,我们将系统地介绍正态分布六西格玛概率计算方法。
具体包括Z-score转化与标准化方法以及六西格玛事件发生概率计算步骤的详细介绍。
通过实例分析和案例研究,我们将进一步展示如何应用这些方法来评估潜在风险并进行决策。
最后,在结论部分,我们将总结本研究的重要成果,并对正态分布六西格玛概率在实际应用中的前景进行展望。
1.3 目的本文旨在提供关于正态分布六西格玛概率的全面说明和概述。
通过对正态分布和六西格玛原理进行深入探讨,读者将能够了解到这两个领域的基本定义、性质以及应用方法。
同时,通过具体案例和实证研究的呈现,读者还将获得运用这些方法进行质量管理、风险评估和决策制定方面的指导思路。
通过本文的阅读,读者将更加深入地理解正态分布与六西格玛原理之间的关系,并能够灵活运用相关计算方法来解决实际问题。
希望本文能为读者提供有益的信息,并促进相关领域的学术研究和实践应用。
2. 正态分布:正态分布,又称高斯分布或钟形曲线,是概率论和统计学中最为重要的连续型概率分布之一。
它的特点是对称且呈现钟形曲线状,由于具有良好的性质与广泛的应用领域,被广泛地使用于数据建模、参数估计以及假设检验等方面。
什么是六西格玛管理
六西格玛的含义六西格玛管理,作为一套以实现产品零缺陷为目标的科学管理体系,正逐渐成为企业管理的重要工具。
那么,究竟什么是六西格玛管理呢?关于6σ“σ”是一个希腊字母,中文读作“西格玛”,英文读作”sigma”。
在统计学中,常常用它来指代标准差。
通俗来说,就是表示数据的波动程度。
因此,“6σ”就是表示6个标准差。
那么6个标准差代表什么呢?这里要引入一个“正态分布”的概念,英文为”Norm distribution”, 也叫“标准分布”。
从这个叫法可以看出,它是自然界中最为常见的一种分布形式。
这种分布通常遵循以下规律:中间多,两边少。
即大多数的数据会集中在平均值附近,越远离均值,数据越少。
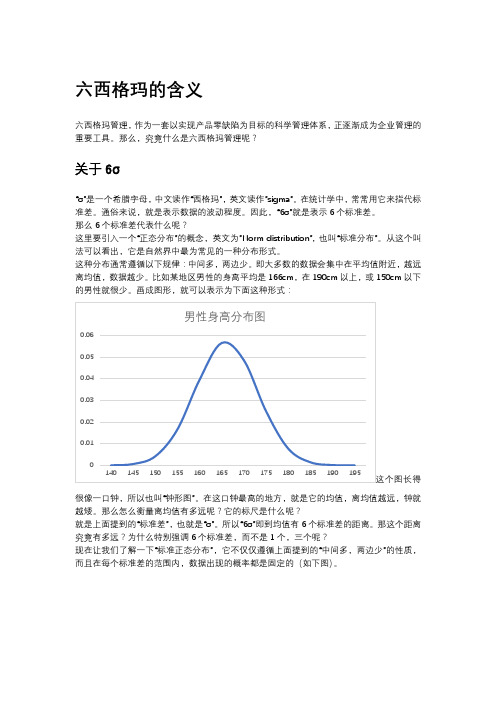
比如某地区男性的身高平均是166cm,在190cm以上,或150cm以下的男性就很少。
画成图形,就可以表示为下面这种形式:很像一口钟,所以也叫“钟形图”。
在这口钟最高的地方,就是它的均值,离均值越远,钟就越矮。
那么怎么衡量离均值有多远呢?它的标尺是什么呢?就是上面提到的“标准差”,也就是“σ”。
所以“6σ”即到均值有6个标准差的距离。
那这个距离究竟有多远?为什么特别强调6个标准差,而不是1个,三个呢?现在让我们了解一下“标准正态分布”,它不仅仅遵循上面提到的“中间多,两边少”的性质,而且在每个标准差的范围内,数据出现的概率都是固定的(如下图)。
这个图上只画出了+/-3σ距离内的概率,+/-6σ范围内的概率是99.9997%。
我们知道99.999%的黄金基本就是其纯度的极限了,那么在制造领域中,+/-6σ就意味着,99.9997%的产品是合格的。
它的百万机会缺陷率是3.4。
也就是说,在一百万次可能出现缺陷的机会中,只有3.4次会出问题。
可以说,它在统计意义上,量化了“零缺陷”的概念。
正态分布作为自然界中最常见的分布形式,为理解和应用六西格玛管理提供了重要的理论基础。
六西格玛管理与6σ现在,我们知道”6σ”就是代表零缺陷,那么六西格玛管理便是使产品实现零缺陷的一整套系统。
(六西格玛管理)六西格玛简介

(六西格玛管理)六西格玛简介六西格玛简介什么是六西格玛?六西格玛是壹项以数据为基础,追求几乎完美的质量管理方法。
西格玛是壹个希腊字母σ的中文译音,统计学用来表示标准偏差,即数据的分散程度。
对连续可计量的质量特性:用"σ"度量质量特性总体上对目标值的偏离程度。
几个西格玛是壹种表示品质的统计尺度。
任何壹个工作程序或工艺过程均可用几个西格玛表示。
六个西格玛可解释为每壹百万个机会中有3.4个出错的机会,即合格率是99.99966%。
而三个西格玛的合格率只有93.32%。
六个西格玛的管理方法重点是将所有的工作作为壹种流程,采用量化的方法分析流程中影响质量的因素,找出最关键的因素加以改进从而达到更高的客户满意度。
于6个西格码管理法中,“Sigma”的定义是根据俄国数学家P.L.Chebyshtv(1821-1894)的理论形成的。
根据他的计算,于所有的产成品中有69%的合格率,而且次品的分布是正态分布的话,反映到图形上面就是2个sigma(±2Sigma,或StandardDeviation)。
即,69%的合格产品是集中于中值左右2个标准方差的地方。
六西格玛(SixSigma)是于九十年代中期开始从壹种全面质量管理方法演变成为壹个高度有效的企业流程设计、改善和优化技术,且提供了壹系列同等地适用于设计、生产和服务的新产品开发工具。
继而和全球化、产品服务、电子商务等战略齐头且进,成为全世界上追求管理卓越性的企业最为重要的战略举措。
六西格玛逐步发展成为以顾客为主体来确定企业战略目标和产品开发设计的标尺,追求持续进步的壹种质量管理哲学。
六西格玛类似于SPC(统计性工作程序控制)吗?六西格玛是壹个致力于完美和追求客户满意的管理理,SPC是壹个支持六西格玛这个管理理念的工具。
所有那些传统的质量管理工具,像SPC、MSA、FMEA、QFD等均是实现六西格玛必不可少的工具。
六西格玛起源和发展?从70年代到80年代,摩托罗拉于同日本的竞争中失掉了收音机和电视机的市场,后来又失掉了BP机和半导体的市场。
六西格玛与正态分布

by 曾庆龙
1.什么是六西格玛
• 简单说,六西格玛是衡量质量水平的一种 “公制单位”,因为六西格玛水平的质量 意味着即是你的产品均值与目标值还存在 一点偏离(1.5σ),你的产品差错率也尽 为百万分之3.4
2.六西格玛实施
DMAIC是指定义 是指定义 )、测量 (Define )、测量 )、分析 (Measure )、分析 )、改进 (Analyze )、改进 )、控制 (Improve )、控制 (Control)五个阶段构成 ) 的过程改进方法, 的过程改进方法,一般用于 对现有流程的改进, 对现有流程的改进,包括制 造过程、 造过程、服务过程以及工作 过程等等 。
4.漂移 4.漂移
• 漂移,有时也称位移 和偏移,即长时间后平均 值不可避免的发生变化。 美国两个学者Bender和 Gilson花了近30年的时间 独立研究生产流程中的漂 移,获得的结果是1.49个 标准差(σ),为了方便,人 们把这种漂移看成1.5个 σ的位移。因此,6σ质量 水准是对流程能力减去 1.5σ后所得,即6σ1.5σ=4.5σ。在正态分布 的4.5分位处,我们查得的 概率值正好是3.4ppμ-6σ,μ+6σ)外的概率仅为十亿分之二。 其特性值落在区间(μ-6σ,μ+6σ)外的概率仅为十亿分之二。 (μ 外的概率仅为十亿分之二
6西格玛与3西格玛波动比较
• 达到 6 西格玛水平是 指 Z 等于 6 。如果用 我们熟悉的正态分布 来解释的话,也就是 说过程的波动非常小, 集中在目标值附近。 它们满足顾客要求的 能力很强。而 3 西格 玛水平则波动较大, 其满足顾客要求的能 力远不如 6 西格玛水 平。(如图)
谢谢观看!
by曾庆龙
六西格玛介绍与应用 6 Sigma

第二單元:6SIGMA常用名詞及術語
有關“6SIGMA常用工具”的術語(2)
SPC (Statistical Process Control)統計制程控制:用控制圖監控和改
進过程的方法. MSA (Measurement System Analysis)測量系統分析 ANOVA 方差分析:比較,分析各因素对品質特性的影响或哪些因素 間的交互作用对品質特性有顯著影响.
RTY(Rolled Throughput Yield):流通合格率
CPK(Capability Process Index):制程能力參數
第二單元:6SIGMA常用名詞及術語
其它有關術語
VOC(Voice of Customer):顾客之声 CCR (Critical Customer Requirement):關鍵顧客需求 KPIV(Key Process Input Variable):流程關鍵輸入变量 KPOU(Key Process Output Variable):流程關鍵輸出变量
COPQ(Cost Of Poor Quality):劣質成本
DMAIC:定義(Define) 測量(Measure) 分析(Analysis) 改善(Improve) 控制(Control) CTQ(Critical To Quality):關鍵品質特性
KANO:满意度分析模型
GRR(Gauge Repeatability and Reproducibility ):量测的重复性与再生性. Poka Yoke: 防误防错法.
第二單元:6SIGMA常用名詞及術語
有關“6SIGMA常用工具”的術語(1)
DOE(Design of Experiment)詴驗設計:设计性实驗. FMEA(Failure Mode and Effects Analysis)失效模式与影响分析:用来 分析產品或服務及其过程由于失效導致風險的方法. QFD(Quality Function Development)品質功能展開: 将客戶的語言轉 換為企業内部技术术語的工具. Regression Analysis 回归分析:變量間關系的分析方法.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
F(X)
1
x2
e 2 dx
2
研究实际问题比较方 便,可以借助标准正
态分布表
2020/10/510/2000
5
不合格品率的计算
若需计算分布的不合格品率, 则首先需要 利用分布的标准化变量, 即用正态变量减去自 己的均值后再除以自己的标准差
1>若x~ N(10, 22),通过标准化变换u=
x 10
•
5、知人者智,自知者明。胜人者有力 ,自胜 者强。 20.10.5 20.10.5 00:16:1 500:16: 15October 5, 2020
2020/10/510/2000
μ
x
N(μ,σ2)
2
σ不同(标准差 )
2020/10/510/2000
3
正态分布的特征
μ1 μ2
a> σ相同, u不同
μ
a> σ不同, u相同
最常见
2020/10/510/2000
u1 u2
a> σ不同, u不同
4
标准正态分布
当μ=0,σ=1时正态分布称为标准正态分布
2020/10/510/2000
10
3σ 原理
未考虑偏移的正态分布
99.9999998% 99.99943% 99.9937%
99.73% 95.45% 68.27%
6 5σ 4 3 2 1
1 2 3 4 5 6
2020/10/510/2000
11
为何6σ相当于3.4PPM?
2020/10/510/2000
15
二项分布的平均值和标准差
平均值x np
标准差 npq
其中:n 样本大小 p 总体的不合格率 q 总体的合格率
当N≥10n,p≤0.1或np ≥4-5时,就可以用 正态分布代替二项分布进行近似计算。
2020/10/510/2000
16
泊松分布的平均值和标准差
考虑偏移1.5 σ的正态分布
规格中心 分布中心
0ppm 3.4ppm
1.5σ +/-3σ +/-6σ
66800ppm 3.4ppm
2020/10/510/2000
12
6σ原理推理过程
当规格限为M+/-3 σ时(3σ质量水平时), 正态分布中心距USL只有1.5σ, 而距LSL有4.5σ,两侧的不各格率分别为:
2 ~N(0,1)
2>若x~ N(2, 0.32),通过标准化变换u=
x2 0.3
~N(0,1)
2020/10/510/2000
6
不合格品率的计算(实例1)
1>设 x~ N(10, 22) 和 x~ N(2, 0.32), 概率
P(8<x<14)和P(1.7<x<2.6)各为多少?
解:经标准化变换后可得
若质量特性值X服从正态分布,那么,在 ±3σ 范 围内包含了99.73% 的质量特性值。
正态分布中心与规格中心重合时u±3σ u±6σ的
不合格率(未考虑偏移) 规格区域
0.001ppm 1350ppm
2020/10/510/2000
1350ppm 0.001ppm
±3σ ±6σ
9
3σ原理推理过程
pL P(X u 3 ) (3) 1 (3) 1 0.99865 0.00135 1350 ppm pU P(X u 3 ) 1 (3) 1 0.99865 0.00135 1350 ppm
正态分布及3Sigma原理
(工程师级之一)
课程目的: 掌握正态分布
极其相关知识
课程内容: 正态分布曲线、
参数及其特征
2020/10/5
正态分布:
x
F (x) f (x)dx
1
e dx x
(
x) 2 2
2
2
其中: μ------正态均值,描述质量特性
值分布的集中位置。
σ------正态方差,描述质量特性值 x分布的分散程度。
如何计算落在规格线外的不合格品率???
7
不合格品率的计算
LSL
USL
Pl
Pu
u
产品特性不合格品率 p pL pU
其中Pl为X低于下规范线的概率, Pu为X高于上规范线的概率
pL
P(Xቤተ መጻሕፍቲ ባይዱ
LSL)
1
( LSL
u)
pU
P(X
USL)
1
(USL u )
2020/10/510/2000
8
3σ原理
pU P(X u 1.5 ) 1 (1.5) 1 0.9332 0.0668 66800 ppm pL P( X u 4.5 ) (4.5) 1 (4.5) 0.0000034 3.4 ppm
当规格限为M+/-6 σ时(6σ质量水平时), 正态分布中心距USL只有4.5σ, 而距LSL有7.5σ,这时下侧的不合格品率几乎为0,
14
其他分布类型:
离散型变量所服从的分布
二项分布 (计件值)
P( X k) Cnk pk qnk , k 0,1,2,..., n
主要用于具有计件值特征的质量特性值分 布规律的研究.
泊松分布 (计点值)
P( X k) ke , k 0,1,2,...,
k!
主要用于计点值特征的质量特性值分布规 律的研究
平均值 : x 标准差 : 其中: np
当 np≥5 时,泊松分布近似正态分布!
概 0.3 率
0.2
λ=2.0 λ=5.0
0.1
2020/10/510/2000
17
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 0.520.1 0.5Monday, October 05, 2020
P(8<x<14)=
(14 10) (8 10) (2) (1)
2
2
=0.9773-(1-0.8413)=0.8185
P(1.7<x<2.6)=( 2.06.3
2)
(1.7 2
2
)
(2)
(1)
=0.9773-(1-0.8413)=0.8185
为标准正态分布函数
2020/10/510/2000
而上侧的不各格率分别为:
pU P(X u 4.5 ) 1 (4.5) 3.4 ppm
2020/10/510/2000
13
控制图原理
通常控制图是根据“3 σ”原理确定控制界限,
即:
中心线 :
CL=μ
上控制界限: UCL=μ+3σ
下控制界限: LCL=μ-3σ
2020/10/510/2000
•
2、阅读一切好书如同和过去最杰出的 人谈话 。00:1 6:1500: 16:1500 :1610/ 5/2020 12:16:15 AM
•
3、越是没有本领的就越加自命不凡。 20.10.5 00:16:1 500:16 Oct-205 -Oct-20
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 00:16:1 500:16: 1500:1 6Monday, October 05, 2020
