惠州市2011届高三第三次调研考试数学(文科)
惠州市2011届高三第二次调研考试数学(文科)答案(打印版)

惠州市2011届高三第二次调研考试数学试题(文科)答案一.选择题(本大题共10小题,每小题5分,共50分)1.【解析】∵{}0,2,A a =,{}21,B a =,{}0,1,2,4,16A B =∴2164a a ⎧=⎨=⎩∴4a =,故选D.2.【解析】由210110x x x ⎧-=⇒=-⎨-≠⎩ 故选A3.【解析】⌝p:1x >,q:110x x<⇔<或1x >,故q 是⌝p 成立的必要不充分条件,故选B. 4.【解析】当0x ≤时,令2230x x +-=解得3x =-;当0x >时,令2ln 0x -+=解得2x e =,所以已知函数有两个零点,选B 。
5.【解析】由已知(1)2g '=,而()()2f x g x x ''=+,所以(1)(1)214f g ''=+⨯=。
6.【解析】()sin 2f x x =, sin(2)sin 2()36y x x ππ=+=+,∴只需将()f x 的图象向左平移6π个单位,答案选D 。
7.【解析】路程s 是时间t 的函数∴随着时间t 的变大,路程s 也逐渐增大,故排除D ;汽车减速行驶之后停车,汽车速度的变化是逐渐变小故选A8.【解析】C ; 3123133S a a a a d =++=+,21212S a a a d =+=+; ∴()32113222S S d d a d a ⎛⎫-=+-+= ⎪⎝⎭,因此2d =.9.【解析】由题设可知m n >,再由椭圆和双曲线的定义有12||||PF PF +=及12||||PF PF -=±12||||PF PF m p =-.10.【解析】因为点B 、M 、F 三点共线,则存在实数t ,使AM (1)t AB t AF =-+.又2AB AE =,13AF AC =,则AM 2(1)3tt AE AC =-+. 因为点C 、M 、E 三点共线,则2(1)13t t -+=,所以35t =.故43,55x y ==,故选A.二.填空题(本大题每小题5分,共20分,把答案填在题后的横线上)11.12800;12. m =-3;13. 5(6)i i ≤<或 14. )4π; 写(1,1)也给分; 15. MN =211.【解析】该组合体的表面积为:222212800S S S cm ++侧视图主视图俯视图=12.【解析】由题意得:2m +3<3且|491|45m -+=,解得m =-313.【解析】: sum=122334455670⨯+⨯+⨯+⨯+⨯=,i 等于5时再运行一次循环体程序就要跳出,故5(6)i i ≤<或14.【解析】(0,0) ,)4π; 写(0,0),(1,1)也给分;15.【解析】∵45BNA ∠=∴90BOA ∠=,∵OM=2,BO=4,∵BM·MN=CM·MA=(,∴MN=2.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.解:(1)(,1),(sin ,cos )a m b x x ==且()f x a b =⋅∴()sin cos f x m x x =+,又()12f π=sincos122m ππ∴+= 1m ∴= ………….2分()sin cos )4f x x x x π∴=+=+ …………….4分∴函数的最小正周期2T π= …………….5分当2()4x k k Z ππ=+∈时, ()f x ,当52()4x k k Z ππ=+∈时,()f x 最小值为 …………….7分(2)因为()12f A π= 即()123f A ππ== ∴sin sin3A π= ……….8分∵A 是锐角ABC ∆的内角, ∴3A π= ……….9分∵2AB =,AC=3由余弦定理得:2222cos 7BC AC AB AB AC A =+-⋅⋅= ……….10分∴BC =……….12分17.解:(1)416015n P m ===∴某同学被抽到的概率为115……….2分 设有x 名男同学,则45604x=,3x ∴=∴男、女同学的人数分别为3,1…….4分(2)把3名男同学和1名女同学记为123,,,a a a b ,则选取两名同学的基本事件有:121312123231323(,),(,),(,),(,),(,),(,),(,),(,),(,),a a a a a b a a a a a b a a a a a b 123(,),(,),(,)b a b a b a 共12种, ……….6分其中有一名女同学的有6种∴选出的两名同学中恰有一名女同学的概率为61122P == ……….8分 (只是列出组合,没考虑顺序的同样给分) (3)16870717274715x ++++==,26970707274715x ++++==2221(6871)(7471)45s -+-==,2222(6971)(7471) 3.25s -+-==∴第二同学B 的实验更稳定 ……….12分(每个结果算对给1分)18.解(1)正视图如下:(没标数据扣1分)…………3分主视图面积214242S cm =⨯⨯=……………….4分 (2)设PB 的中点为F ,连接,EF CF ………………5分//,//,//EF AB DC AB EF AB ∴,且12EF DC AB == ………………6分故四边形CDEF 平行四边形,可得//ED CF , ………………7分 ED ⊂平面PBC ,CF ⊂平面PBC ,//ED 平面PBC ………………9分 (3)PD ⊥底面ABCD ,AB ⊂平面ABCD ,AB PD ∴⊥ ………10分又,,AB AD PD AD D AD ⊥=⊂平面PAD ,PD ⊂平面PADAB ⊥平面PAD ………………11分 ED ⊂平面PAD ,所以ED AB ⊥, ………………12分 又,PD AD E =为PA 的中点,所以ED PA ⊥, ………………13分 ,PA AB A PA =⊂平面PAB ,AB ⊂平面PAB ,所以DE ⊥平面PAB ……14分19.解:(1)由题意得2()32f x ax x b '=++, ……….1分3()()()(31)(2).g x f x f x ax a x b x b '∴=+=+++++又因为()g x 是奇函数所以()()g x g x -=-,即对任意的实数x 有3232()(31)()(2)()((31)(2))a x a x b x b ax a x b x b -++-++-+=-+++++….3分从而有310,0a b +==即1,03a b =-=, ……….5分 因此()f x 的解析式为321()3f x x x =-+ ……….6分(2)由(1)得31()23g x x x =-+,所以 2()2g x x '=-+ ……….7分令()0g x '=解得12x x == ……….8分则当x x ()0,g x '〈即()g x 在区间(),,-∞+∞上是减函数; ….9分当x 时()0,g x '〉即()g x 在区间(上是增函数 ……….10分由前面讨论知,()g x 在区间[]1,2上的最大值与最小值只能在2x =处取得,而54(1),(2)33g g g === ……….12分因此()g x 在区间[]1,2上的最大值为3g = ……….13分 最小值为4(2)3g =……….14分 20.解:(1)证明:将112222=++=by a x x y 代入,消去x ,得0)1(2)(222222=-+-+a b y b y b a ① ……………3分由直线l 与椭圆相交于两个不同的点,得0)1(4)1)((44222222224>-+=-+-=∆b a b a a b a b b所以 122>+b a …………5分 (2)解:设),(),(2211y x B y x A ,由①,得 22222122221)1(2ba ab y y b a b y y +-=+=+, …………7分 因为 2122y y -== …………8分所以, 222222212222212)1(2y b a a b y y y b a b y y -=+-=-=+=+, 消去2y ,得22222222)2(2)1(b a b b a a b +-=+- 化简,得22228)1)((b a b a =-+ …② ……11分 因F 是椭圆的一个焦点,则c=1,b 2=a 2-1 代入②式,解得 272922==b a ,………………13分 所以,椭圆的方程为 1729222=+y x …………14分 21.解: (1)设202x ax bx c+=-的不动点为和 ∴0010421222aa c cbc ca b b c⎧==⎧⎪⎪⎪-=+≠⎨⎨+=+⎪⎪=⎩⎪-⎩即即且 ……………3分 (2)∵c =2 ∴b =2 ∴()()()2121x f x x x =≠-,由已知可得2S n =a n -a n 2……①,且a n ≠1. 当n ≥2时,2 S n -1=a n -1-a n -12 ……②, ①-②得(a n +a n -1)( a n -a n -1+1)=0,∴a n =-a n -1 或 a n =-a n -1 =-1, ……5分 当n =1时,2a 1=a 1-a 12 ⇒a 1=-1,若a n =-a n -1,则a 2=1与a n ≠1矛盾.∴a n -a n -1=-1, ∴a n =-n .……6分∴要证不等式,只要证 ()111111n n n e n -+-⎛⎫⎛⎫+<<+ ⎪⎪⎝⎭⎝⎭,即证 11111n n e n n +⎛⎫⎛⎫+<<+ ⎪ ⎪⎝⎭⎝⎭,只要证 ()11ln 111ln 1n n n n ⎛⎫⎛⎫+<<++ ⎪ ⎪⎝⎭⎝⎭,即证 111ln 11n n n⎛⎫<+< ⎪+⎝⎭.……7分 考虑证不等式()ln 11xx x x <+<+(x >0) ** . ………………8分 令g (x )=x -ln(1+x ), h (x )=ln(x +1)-1xx + (x >0) .∴g '(x )=1x x +, h '(x )=()21x x +, ∵x >0, ∴g '(x )>0, h '(x )>0,∴g (x )、h (x )在(0, +∞)上都是增函数,……9分 ∴g (x )>g (0)=0, h (x )>h (0)=0,∴x >0时,()ln 11xx x x <+<+. 令1x n =则**式成立,∴111n a n a +⎛⎫- ⎪⎝⎭<1e <11na n a ⎛⎫- ⎪⎝⎭, ……………10分 (3)由(2)知b n =1n ,则T n =111123n+++⋅⋅⋅⋅⋅⋅+. 在111ln 11n n n⎛⎫<+< ⎪+⎝⎭中,令n =1,2,3,……,2008,并将各式相加, 得111232009111ln ln ln 1232009122008232008++⋅⋅⋅⋅⋅⋅+<++⋅⋅⋅⋅⋅⋅+<+++⋅⋅⋅⋅⋅⋅+, 即T 2009-1<ln2009<T 2008. …………………14分。
惠州市2011届高三第三次调研考试数学(文科)试题答案

数学试题(文科)答案
一.选择题(本大题共 10 小题,每小题 5 分,共 50 分)
题号
1
2
3
4
5
6
7
8
9 10
答案 D B C B C C D A B A
1.【解析】∵zl·z2=3-i, 故选 D。
2.【解析】由 a b = a b cos 60 cos = 1 ,故 1200 ,选 B。 2
因为抛物线焦点到准线距离等于 4, 所以圆心的轨迹是 x2 8 y ………………6 分
(2)直线AB与x轴不垂直, 设AB : y kx 2. A(x1, y1), B(x2 , y2 ).………………8 分
y kx 2,
由
y
1 8
x2.
可得 x2 8kx 16 0 ,
∵过点 A(1, m) (m 2) 可作曲线 y f (x) 的三条切线
………………6 分
∴方程 2x 3 3x 2 m 3 0 (*)有三个不同实数根. 记 g(x) 2x 3 3x2 m 3 , g(x) = 6x2 6x 6x(x 1) . 令 g(x) 0, x 0 或 1.
log log
3 3
(2a (5a
b) b)
1 2
,解得
a b
2 1
,
…………2 分
f (x) log3 (2x 1) an 3log3 (2n1) 2n 1, n N * …………4 分
(2)由(1)得 bn
2n 1
,
2n
Tn
广东省惠州市届高三第三次调研考试数学文试题含解析

惠州市2017届高三第三次调研考试文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务势必自己的姓名、准考据号、座位号等考生信息填写在答题卡上。
2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需变动,用橡皮擦洁净后,再选涂其余答案标号,写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一.选择题:本大题共12小题,每题 5分。
在每个小题给出的四个选项中,只有一项是切合题目要求的。
(1)若会合B x|x0,且AIB A,则会合A可能是()(A)1,2(B)x|x1(C)1,0,1(D)R(2)已知向量uur(t1,1),r(t2,2),若uurr uur rt() m(mn)(mn),则n(A)0(B)3(C)3(D)1(3)设函数y f(x),x R,y f(x)y f(x)的图像对于原点对称”的“是偶函数”是“()条件(A)充足不用要(B)必需不充足条件(C)充要(D)既不充足也不用要(4)双曲线C:x2y21(a0,b0)的离心率e13,则它的渐近线方程为()a2b22(A)y3x(B)y2x(C)y9x(D)y4x2349 5)齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的低等马,劣于齐王的中等马,田忌的低等马劣于齐王的低等马,现从两方的马匹中随机选一匹进行一场竞赛,则田忌马获胜的概率为()数学试题(文科)第1页,共14页(A )1(B )1(C )1(D )13456(6)以下图,将图(1)中的正方体截去两个三棱锥,获得图(2)中的几何体,则该几何体的侧视图为 ()D E CEFAFABA 1 D 1C 1C 11D1B 1AB 1(A)(B)(C)(D)(1)(2)(7)在ABC 中,角A,B,C 的对边分别是a,b,c ,已知b2,c22 ,且C,4则ABC 的面积为()开始(A )31(B )31(C )4 (D )2 i=1,S=0(8)履行以下列图所示的程序框图,则输出的结果为 ()(A )7(B )9(C )10(D )11S=Slgii=i2i 2x +3y +5≥0S1?否(9)已知实数 x ,y 知足: x +y -1≤0,若z =x +2y 的最小值是x +a ≥0输出i为-4,则实数a =()结束(A )1(B )2(C )4 (D )8(10)已知函数f(x)sinxcosx(R)的图象对于x对称,则把函数f(x)的4图象上每个点的横坐标扩大到本来的2倍,再向右平移,获得函数g(x)的图象,3则函数g(x)的一条对称轴方程为()(A )x(B )x(C )x(D )x116436(11)已知一个平放的各棱长为4的三棱锥内有一个小球O (重量忽视不计),现从该三棱锥顶端向内灌水,小球慢慢上调,若注入的水的体积是该三棱锥体积的7时,小8球与该三棱锥各侧面均相切(与水面也相切),则小球的表面积等于()(A )7(B )4(C )2(D )6331 2(12)已知f(x)xsinx cosxx 2,则不等式f(lnx)f(ln)2f(1)的解集为()x(A)(e,)(B)(0,e)11(C)(0,)U(1,e)(D)(,)e e第Ⅱ卷本卷包含必考题和选考题两部分。
惠州市2011届高三第一次调研考试文科数学试题答案ok

惠州市2011届高三第一次调研考试数学(文科)评分标准一、选择题(本大题共10小题,每小题5分,满分50分)1.【解析】11i i i+=- 故选D. 2.【解析】A={}10x x ->={}1x x <,B={}0y y ≥,故选B3.【解析】242,12p p p =⇒=∴=,∴抛物线24y x =的焦点是()1,0,故选C ; 4.【解析】设(,)b x y =,则cos1802,a b xy =- (1)2x y -=- (1)= (2), 由(1)(2)可解得x=-3,y=6故选A ;5.【解析】结合题意知该几何体是四棱锥,棱锥的的底面是边长为8和6的长方形,棱锥的高是5, ∴由棱锥的体积公式得1865803V =⨯⨯⨯=,故选B 6.【解析】||OP =,由三角函数的定义得sin 5α== B. 7.【解析】作出可行区域可得,当0,1x y ==时,z 取得最小值-1当2,0x y ==时,z 取得最大值2,故选C8.【解析】若p q ∧为假命题,则只需,p q 至少有一个为假命题即可。
故选C9.【解析】由于(1)0,(3)0f f ><,所以0(1,3)x ∈.在(1,3)上1()()5x g x =是减函数,3()log x x φ=是增函数, 所以31()()log 5x f x x =- 在(1,3)上是减函数,所以0()()0f x f x >=,故选C. 10.【解析】8482(84)(82)(82)(8)8882n n n n n n n n --=-+--=-+数列共有251项,∴结果为(8)2512008-⋅=-,故选A. 二、填空题(本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只需选做其中一题,两题全答的,只以第一小题计分.)11、760 12、4 13、9910 14、1:1 15、08011.【解析】由952001600x =,得760x =. 12.【解析】1110.8248++>,因此输出 4.n = 13.【解析】设第一日读的字数为a ,由“每日添增一倍多”得此数列是以a 为首项,公比为2的等比数列,可求得三日共读的字数为3(12)12a --=7a =34685,解得a =4955,则2a =9910,即该君第二日读的字数为9910.14.【解析】∵直线()4R πθρ=∈过圆ρ=4两部分的面积之比是1:115.【解析】连接BC ,AB 是O 的直径90ACB ∴∠=, 又40ACE ∠=,50PCB PBC ∴∠=∠=,∴80P ∠=三、解答题(本大题共6小题,满分80分,解答应写出文字说明,证明过程或演算步骤。
惠州市2011届高三第三次调研考试(文综)
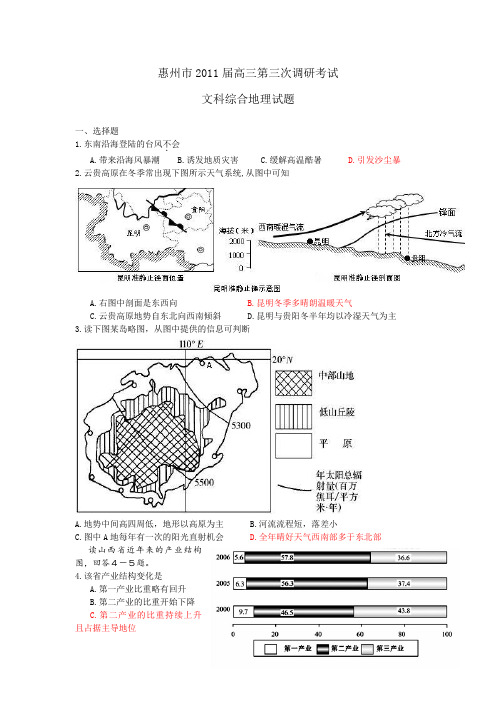
惠州市2011届高三第三次调研考试文科综合地理试题一、选择题1.东南沿海登陆的台风不.会A.带来沿海风暴潮B.诱发地质灾害C.缓解高温酷暑D.引发沙尘暴2.云贵高原在冬季常出现下图所示天气系统,从图中可知A.右图中剖面是东西向B.昆明冬季多晴朗温暖天气C.云贵高原地势自东北向西南倾斜D.昆明与贵阳冬半年均以冷湿天气为主3.读下图某岛略图,从图中提供的信息可判断A.地势中间高四周低,地形以高原为主B.河流流程短,落差小C.图中A地每年有一次的阳光直射机会D.全年晴好天气西南部多于东北部读山西省近年来的产业结构图,回答4-5题。
4.该省产业结构变化是A.第一产业比重略有回升B.第二产业的比重开始下降C.第二产业的比重持续上升且占据主导地位▲D.第三产业的比重下降幅度最大5.该省工业主导产业是A.机械制造B.有色冶金C.能源工业D.轻纺工业右图图①为“某市同一地区不同时期地价曲线图”,图②为“该市城市规模的变化图”,读图完成6-7题。
6.图①中郊区地价变化的原因最有可能是A .中心商务区整体外迁B .城市规模缩小,用地紧张C .郊区基础设施比城区更完善D .郊区交通通达度提高7.图②反映了该城市A .城市化水平比较高,城市人口增长趋缓 B .上世纪60年代以前,城市核心区面积增长速度明显高于城乡过渡带C .城市规模扩大,出现郊区城市化D .城市核心区规模减小,出现逆城市化根据土地利用结构调整的需要,科研人员对某生态脆弱区的农业土地利用拟定了三种方案(下表)。
回答8-9题。
8.对三种方案的评价准确的是A . A 方案环境效益最好B . B 方案3-8年内的收入最高C . C 方案经济效益年年最佳D . C 方案更有利于当地农业的持续发展9.该地最有可能位于A .黄土高原B .江汉平原C .四川盆地D .两广丘陵 读“我国南、北方水资源、人口及耕地分布对照图,回答10-11题。
10.下列说法与图中内容相符的是A .我国人口重心在北方地区B .耕地面积南方多于北方C .南方的人均耕地面积不到北方的一半D .北方水土资源搭配更佳11.造成我国南方和北方地区水资源总量差异大的主要原因是两地A.河流湖泊数量差异大B.年降水总量差异大C.植被覆盖率差异大 D.年蒸发总量差异大40.阅读下面材料,回答问题(26分)材料一: 我国铁矿石主要进口来源示意图材料二:1996-2007年中国铁矿石进口量及均价材料三:加工贸易是我国第一大对外贸易方式,但目前我国的加工贸易主要从事是低层次的加工贸易,附加价值低。
2011惠州市高三第一次调研考试文科数学试题答案ok

惠州市2011届高三第一次调研考试数学(文科)评分标准一、选择题(本大题共10小题,每小题5分,满分50分)题号12345678910答案D B C A B B C C C A1.【解析】 故选D.2.【解析】A==,B=,故选B3.【解析】,抛物线的焦点是,故选C;4.【解析】设,则 (1)又 (2), 由(1)(2)可解得x=-3,y=6故选A;5.【解析】结合题意知该几何体是四棱锥,棱锥的的底面是边长为8和6的长方形,棱锥的高是5, ∴由棱锥的体积公式得,故选B6.【解析】,由三角函数的定义得,∴选B.7.【解析】作出可行区域可得,当时,z取得最小值-1当时,z取得最大值2,故选C8.【解析】若为假命题,则只需至少有一个为假命题即可。
故选C 9.【解析】由于,所以.在上是减函数,是增函数,所以在上是减函数,所以,故选C.10.【解析】数列共有251项,结果为,故选A.二、填空题(本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只需选做其中一题,两题全答的,只以第一小题计分.)11、760 12、4 13、9910 14、 15、11.【解析】由,得.12.【解析】,因此输出13.【解析】设第一日读的字数为,由“每日添增一倍多”得此数列是以为首项,公比为2的等比数列,可求得三日共读的字数为=7=34685,解得=4955,则2=9910,即该君第二日读的字数为9910.14.【解析】∵直线过圆ρ=4的圆心,∴直线把圆分成CBEAPO(第15题图)两部分的面积之比是1:115.【解析】连接,是的直径,又,,三、解答题(本大题共6小题,满分80分,解答应写出文字说明,证明过程或演算步骤。
)16、解:(1)……4分当,即时,取得最大值.因此,取得最大值的自变量x的集合是.……8分(2)由题意得,即.因此,的单调增区间是. …………12分17.(本小题满分12分)(1)共有 种情况 …………4分函数有零点,,有共6种情况满足条件 ………6分所以函数有零点的概率为 ………8分(2)函数的对称轴为在区间上是增函数则有, 共13种情况满足条件……10分所以函数在区间上是增函数的概率为 ………12分18.(本小题满分14分)解:(1)证明:连结,则是的中点,为的中点故在△中, , …………3分且平面PAD,平面PAD,∴∥平面PAD …………6分(2)取的中点M,连结,, …………8分又平面⊥平面, 平面∩平面=,, ……………10分……………14分19解:(1)设切线的斜率为k,则 ………2分又,所以所求切线的方程为: …………5分即 …………6分(2),要使为单调增函数,必须满足即对任意的 …………8分…………11分而,当且仅当时,等号成立,所以所求满足条件的a值为1…………………………………14分20.解析:(1)依题意,圆的半径等于圆心到直线的距离,即. …………………4分∴圆的方程为. …………………6分(2)设,由,得,即. ……………………………………9分……11分∵点在圆内,∴,∴的取值范围为. ……………………………………………14分21.解:(1)由题意 即∴ ………………2分∴ ∵m>0且,∴m2为非零常数,∴数列{a n}是以m4为首项,m2为公比的等比数列 …………4分(2)由题意,当∴ ① …………6分①式乘以2,得 ② …7分②-①并整理,得=………… 10分(3)由题意 ,要使对一切成立,即对一切 成立,①当m>1时, 成立; …………12分②当0<m<1时,∴对一切 成立,只需,解得 , 考虑到0<m<1, ∴0<m<综上,当0<m<或m>1时,数列中每一项恒小于它后面的项 (14)分。
惠州市2011届高三第一次模拟考试数学文科)试题答案
惠州市2011届高三第一次模拟考试数学试题(文科)答案与评分标准一.选择题(本大题共10小题,每小题5分,共50分)1.【解析】{}2,3,5U M =ð,{}1,3,5N =,则()UN M =ð{}1,3,5{}2,3,5={}3,5,故选C2.【解析】1231122i a bi i i +-==++,因此31,22a b ==-.故选A .3.【解析】6148,343m m =≠⇒=-直线6140x my ++=可化为3470x y ++=,两平行线之间的距离是2d ==。
故选D4.【解析】由||10a =可得8x =±。
反之,由8x =得(8,6)a =,所以||10a =;故选B5.【解析】由标准差公式s =. 故选D6.【解析】13456360.p =⨯⨯⨯⨯= 故选B7.【解析】依题意,()y f x =的最小正周期为π,故2ω=,因为5cos(2)sin(2)sin(2)3326y x x x ππππ=+=++=+,所以把sin 2y x =的图像向左平移512π个单位即可得到cos(2)3y x π=+的图像。
∴故选D另解:把sin 2y x =的图像向左平移4π个单位,可得到cos 2y x =的图像,再把cos 2y x =的图像向左平移6π个单位,即可得到cos(2)3y x π=+的图像,共向左平移512π个单位。
8.【解析】,M N 两点位于直线l 的两侧,()()2312310a a ∴++-+<⇒ 11a -<<故选D.9.【解析】设容器的高为xcm ,容器的容积为3()V x cm ,则32()(902)(482)42764320(024)V x x x x x x x x =--=-+<<,(第15题图)∵2()125524320V x x x '=-+,22()1255243200463600V x x x x x '=-+=⇒-+=由,解得110x =,236x =(舍去).∵当010x <<时,()0V x '>,当1024x <<时,()0V x '<,∴当10x =时,()V x 在区间()0,24内有唯一极值,且取极大值.∴容器高10x cm =时,容器容积()V x 最大。
广东省惠州市高三数学第三次调研考试题 文
广东省惠州市2015届高三第三次调研考数学文试题本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁.考试结束后,将答题卡一并交回。
参考公式:锥体的体积公式13V Sh =,其中S 为锥体的底面积,h 为锥体的高. 一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项. 1.若集合{0,1,2,3},{1,2,4},A B ==则集合AB =( )A .{0,1,2,3,4}B .{1,2,3,4}C .{1,2}D .{0} 2.已知0<a <2,复数z a i =+(i 是虚数单位),则||z 的取值范围是( )A .B .(1,5)C .(1,3)D . 3.函数()ln(1)f x x =++的定义域为( ) A .(2,)+∞ B .(1,2)(2,)-+∞ C .(1,2)- D .(]1,2-4.等差数列{}n a 的前n 项和为n S ,且316,4S a ==,则公差d 等于( )A .1B .53C .2-D .3 5.已知a R ∈,则“22a a <”是“2a <”成立的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件6.圆4)2(22=++y x 与圆9)1()2(22=-+-y x 的位置关系为( )A .内切B .相交C .外切D .相离 7.下列命题正确的是( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行8.设变量,x y 满足约束条件20701x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩,则yx的最大值为( ) A .3 B .6 C .95D .19.右图是某个四面体的三视图,该四面体的体积为( A .72 B .36 C .24 D .1210.已知函数(1)f x -是定义在R 上的奇函数,若对于任意两个实数12x x ≠,不等式()1212()0f x f x x x ->-恒成立,则不等式(3)0f x +<的解集为( )A .(,3)-∞-B .(4,)+∞C .(,1)-∞D .(,4)-∞-二、填空题:(本大题共5小题,分为必做题和选做题两部分.每小题5分,满分20分) (一)必做题:第11至13题为必做题,每道试题考生都必须作答. 11.已知向量(1,2),(2,1)a x b =-=,且a b ⊥,则实数x =____________.12.在ABC △中,内角A B C ,,对边的边长分别是a b c ,,,若15a =,10b =,3A π=,则cos =B ____________.13.,,A B C 是平面内不共线的三点,点P 在该平面内且有20PA PB +=uu r uu r r,现将一粒黄豆随机撒在ABC △内,则这粒黄豆落在PBC △内的概率为___________.(二)选做题:第14、15题为选做题,考生只选做其中一题,两题全答的,只计前一题的得分。
惠州市届高三第三次调研考试数学(文科)答案与评分标准.doc
惠州市201X 届高三第三次调研考试文科数学参考答案与评分标准一.选择题(本大题共10小题,每小题5分,共50分)1.【解析】{2,4,5}U A =ð,{1,5}U B =ð;故{}5U UA B ⋂=痧,所以选D.2.【解析】()21i -i 2-=.故选A3.【解析】原不等式等价于(2)(4)040x x x -+≥⎧⎨+≠⎩,解得42x -<≤,故原不等式的解集为(]4,2-.选A.4.【解析】由直线垂直有斜率积为-1得2a =- 选C5.【解析】由下标和性质知239a =,∴23,a =又()()d a d a a 3.2222+-=,得2=d 故选B 6.【解析】3)1()41()3()7(-=-=+-==f f f f 故选A 7.【解析】由线面垂直的定义得B 正确8.【解析】i 是计数变量,共有10个数相加,故选A 9.【解析】()f x =2sin 12cos x x-=22sin 2cos .sin 2+=+x x x ,而142sin =π⋅,故选B10.【解析】因为12c e a ==,所以2c a =,由222a b c =+,得b a =12x x +=2b a-=,12x x =12c a =,点P (1x ,2x )到原点(0,0)的距离为:d 2 二.填空题(本大题每小题5分,共20分,把答案填在题后的横线上) 11. 36; 12.9; 13. 4π; 14.1; 15.3。
11.【解析】36)6080100120(10012022=+++⋅+12.【解析】做出可行域易得y x z +=3的最大值为913.【解析】22()(3)2336722cos ,216108a b a b a a b b a b -+=+-=+<>-=- 2cos ,a b ∴<>=又,[0,]a b π<>∈ ,4a b π∴<>= 14.【解析】在相应直角坐标系中,)2,0(-p ,直线l 方程:0343=--y x ,所以p 到l 的距离:d =|3×0---3|32+42=1.15.【解析】如右图,连接AB ,∵PA 是⊙O 的切线,∴∠PAB =∠C , 又∵∠APB =∠CPA ,∴△PAB ∽△PCA ,∴PA AC =PB AB ,即PA 2R =PB AB ,∴R =PA·AB 2PB =2×22-122×1= 3. 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本题满分12分)解:(1)22111coscos 2(1cos )2cos 12222A A A A ++=++-+ …………3分 =211614422cos cos 22252525A A +=⨯+⨯=……………………6分 (2)133sin ,2,sin ,3,5255S bc A b A c c ===∴⨯=∴= ……………………8分由余弦定理22242cos 425225135a b c bc A =+-=+-⨯⨯⨯= …………11分a ∴=……………………………………………………………12分17.(本题满分12分)解:(1)依题意,80~90间的频率为:1-(0.01+0.015+0.025+0.035+0.005)⨯10=0.1 ……………2分 频数为: 40×0.1=4 …………………………………4分 (2)这次环保知识竞赛成绩的平均数、众数、中位数分别是:68.5、75、70 ………8分 (3)因为80~90有4人,设为a,b,c,d , 90~100有2人,设为A ,B ,从中任选2人,共有如下15个基本事件(a,b ),(a,c),(a,d),(a,A),(a,B),(b,c),(b,d),(b,A),(b,B),(c,d),(c,A), (c,B ),(d,A ),(d,B ),(A,B) ………………………………10分设分在同组记为事件M ,分在同一组的有(a,b ),(a,c),(a,d), (b,c),(b,d), (c,d), (A,B)共7个, …………………………………11分所以 ()M P =157…………………………………12分 18.(本小题满分14分) (1)证明:连结BD ,则BD //11B D ,…………1分 ∵ABCD 是正方形,∴AC BD ⊥. …………2分 ∵CE ⊥面ABCD ,∴CE BD ⊥. …………3分 又C =ACCE ,∴BD ⊥面ACE . …………4分∵AE ⊂面ACE ,∴BD AE ⊥, …………5分 ∴11B D AE ⊥. …………6分 (2)证明:连结AF CF EF 、、. ∵E F 、是1BB 1CC 、的中点,∴CE1B F ,……7分∴四边形1B FCE 是平行四边形, …………8分 ∴ 1CF// B E .面⊄CF 1B DE ⊂E B 1面1B DE∴ CF//面1B DE …………10分∵,E F 是1BB 1CC 、的中点,∴//EF BC , 又//BC AD ,∴//EF AD .∴四边形ADEF 是平行四边形,AF ∴//ED ,…… 12分面⊄AF 1B DE ⊂ED 面1B DE AF//面1B DE …………13分∵AFCF C =,∴平面//ACF 面1B DE . …………14分19. (本小题满分14分)解:(1)∵ 对任意n ∈N*,有2()3n n a S n =+,且11S a =,A11A E C∴11122(1)(1)33a S a =+=+,得1a = 2. …………… 1分 又由2()3n n a S n =+,得 32n n S a n =-.当n ≥2且n ∈N* 时,有1113333()[(1)]12222n n n n n n n a S S a n a n a a ---=-=----=--,…………… 3分 即132n n a a --=, ∴113(1)n n a a -+=+,由此表明{}1n a +是以1a + 1 = 3为首项,3为公比的等比数列。
惠州市2011届高三第二次调研考试数学(文科)答案
惠州市2011届高三第二次调研考试数学试题(文科)答案1.【解析】∵{}0,2,A a =,{}21,B a =,{}0,1,2,4,16A B =∴2164a a ⎧=⎨=⎩∴4a =,故选D.2.【解析】由210110x x x ⎧-=⇒=-⎨-≠⎩故选A3.【解析】⌝p :1x >,q :110x x<⇔<或1x >,故q 是⌝p 成立的必要不充分条件,故选B.4.【解析】当0x ≤时,令2230x x +-=解得3x =-;当0x >时,令2ln 0x -+=解得2x e =,所以已知函数有两个零点,选B 。
5.【解析】由已知(1)2g '=,而()()2f x g x x ''=+,所以(1)(1)214f g ''=+⨯=。
6.【解析】()sin 2f x x =, sin(2)sin 2()36y x x ππ=+=+,∴只需将()f x 的图象向左平移6π个单位,答案选D 。
7.【解析】路程s 是时间t 的函数∴随着时间t 的变大,路程s 也逐渐增大,故排除D ;汽车减速行驶之后停车,汽车速度的变化是逐渐变小故选A 8.【解析】C ; 3123133S a a a a d =++=+,21212S a a a d =+=+; ∴()32113222S S d d a d a ⎛⎫-=+-+= ⎪⎝⎭,因此2d =.9.【解析】由题设可知m n >,再由椭圆和双曲线的定义有12||||PF PF +=及12||||PF PF -=±12||||PF PF m p =-.10.【解析】因为点B 、M 、F 三点共线,则存在实数t ,使AM (1)t AB t AF =-+. 又2AB AE =,13AF AC =,则AM 2(1)3tt AE AC =-+.因为点C 、M 、E 三点共线,则2(1)13t t -+=,所以35t =.故43,55x y ==,故选A.二.填空题(本大题每小题5分,共20分,把答案填在题后的横线上)11.12800;12. m =-3;13. 5(6)i i ≤<或 14. )4π; 写(1,1)也给分; 15. MN =211.【解析】该组合体的表面积为:222212800S S S cm ++侧视图主视图俯视图=12.【解析】由题意得:2m +3<3且|491|45m -+=,解得m =-313.【解析】: sum=122334455670⨯+⨯+⨯+⨯+⨯=,i 等于5时再运行一次循环体程序就要跳出,故5(6)i i ≤<或14.【解析】(0,0) ,)4π; 写(0,0),(1,1)也给分;15.【解析】∵45BNA ∠=∴90BOA ∠=,∵OM=2,BO=,∵BM·MN=CM·MA=(,∴MN=2.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.解:(1)(,1),(sin ,cos )a m b x x ==且()f x a b =⋅∴()sin cos f x m x x =+,又()12f π=sincos122m ππ∴+= 1m ∴= ………….2分()sin cos )4f x x x x π∴=+=+ …………….4分∴函数的最小正周期2T π= …………….5分当2()4x k k Z ππ=+∈时, ()f x ,当52()4x k k Z ππ=+∈时,()f x 最小值为 …………….7分(2)因为()12f A π= 即()123f A ππ== ∴sin sin3A π= ……….8分∵A 是锐角ABC ∆的内角, ∴3A π= ……….9分∵2AB =,AC=3由余弦定理得:2222cos 7BC AC AB AB AC A =+-⋅⋅= ……….10分∴7BC =……….12分17.解:(1)416015n P m ===∴某同学被抽到的概率为115……….2分 设有x 名男同学,则45604x=,3x ∴=∴男、女同学的人数分别为3,1…….4分(2)把3名男同学和1名女同学记为123,,,a a a b ,则选取两名同学的基本事件有:121312123231323(,),(,),(,),(,),(,),(,),(,),(,),(,),a a a a a b a a a a a b a a a a a b 123(,),(,),(,)b a b a b a 共12种, ……….6分其中有一名女同学的有6种∴选出的两名同学中恰有一名女同学的概率为61122P == ……….8分 (只是列出组合,没考虑顺序的同样给分) (3)16870717274715x ++++==,26970707274715x ++++==2221(6871)(7471)45s -+-==,2222(6971)(7471) 3.25s -+-==∴第二同学B 的实验更稳定 ……….12分(每个结果算对给1分)18.解(1)正视图如下:(没标数据扣1分)…………3分主视图面积214242S cm =⨯⨯=……………….4分 (2)设PB 的中点为F ,连接,EF CF ………………5分//,//,//EF AB DC AB EF AB ∴,且12EF DC AB == ………………6分故四边形CDEF 平行四边形,可得//ED CF , ………………7分 ED ⊂平面PBC ,CF ⊂平面PBC ,//ED 平面PBC ………………9分 (3)PD ⊥底面ABCD ,AB ⊂平面ABCD ,AB PD ∴⊥ ………10分又,,AB AD PD AD D AD ⊥=⊂平面PAD ,PD ⊂平面PADAB ⊥平面PAD ………………11分 ED ⊂平面PAD ,所以ED AB ⊥, ………………12分又,PD AD E =为PA 的中点,所以ED PA ⊥, ………………13分 ,PA AB A PA =⊂平面PAB ,AB ⊂平面PAB ,所以DE ⊥平面PAB ……14分19.解:(1)由题意得2()32f x ax x b '=++, ……….1分3()()()(31)(2).g x f x f x ax a x b x b '∴=+=+++++又因为()g x 是奇函数所以()()g x g x -=-,即对任意的实数x 有3232()(31)()(2)()((31)(2))a x a x b x b ax a x b x b -++-++-+=-+++++….3分从而有310,0a b +==即1,03a b =-=, ……….5分 因此()f x 的解析式为321()3f x x x =-+ ……….6分(2)由(1)得31()23g x x x =-+,所以 2()2g x x '=-+ ……….7分令()0g x '=解得12x x == ……….8分则当x x ()0,g x '〈即()g x 在区间(),,-∞+∞上是减函数; ….9分当x 时()0,g x '〉即()g x 在区间(上是增函数 ……….10分由前面讨论知,()g x 在区间[]1,2上的最大值与最小值只能在2x =处取得,而54(1),(2)333g g g === ……….12分因此()g x 在区间[]1,2上的最大值为g = ……….13分 最小值为4(2)3g =……….14分 20.解:(1)证明:将112222=++=by a x x y 代入,消去x ,得0)1(2)(222222=-+-+a b y b y b a ① ……………3分由直线l 与椭圆相交于两个不同的点,得0)1(4)1)((44222222224>-+=-+-=∆b a b a a b a b b所以 122>+b a …………5分 (2)解:设),(),(2211y x B y x A ,由①,得 22222122221)1(2ba ab y y b a b y y +-=+=+, …………7分 因为 2122y y FB AF -==,得 …………8分所以, 222222212222212)1(2y b a a b y y y b a b y y -=+-=-=+=+, 消去2y ,得 22222222)2(2)1(ba b b a a b +-=+- 化简,得22228)1)((b a b a =-+ …② ……11分 因F 是椭圆的一个焦点,则c=1,b 2=a 2-1 代入②式,解得 272922==b a ,………………13分 所以,椭圆的方程为 1729222=+y x …………14分 21.解: (1)设202x ax bx c+=-的不动点为和 ∴0010421222aa c cbc ca b b c⎧==⎧⎪⎪⎪-=+≠⎨⎨+=+⎪⎪=⎩⎪-⎩即即且 ……………3分 (2)∵c =2 ∴b =2 ∴()()()2121x f x x x =≠-,由已知可得2S n =a n -a n 2……①,且a n ≠1. 当n ≥2时,2 S n -1=a n -1-a n -12 ……②, ①-②得(a n +a n -1)( a n -a n -1+1)=0,∴a n =-a n -1 或 a n =-a n -1 =-1, ……5分当n =1时,2a 1=a 1-a 12 ⇒a 1=-1,若a n =-a n -1,则a 2=1与a n ≠1矛盾.∴a n -a n -1=-1, ∴a n =-n .……6分∴要证不等式,只要证 ()111111n nn e n -+-⎛⎫⎛⎫+<<+ ⎪⎪⎝⎭⎝⎭,即证 11111nn e n n +⎛⎫⎛⎫+<<+ ⎪ ⎪⎝⎭⎝⎭,只要证 ()11ln 111ln 1n n n n ⎛⎫⎛⎫+<<++ ⎪ ⎪⎝⎭⎝⎭,即证 111ln 11n n n⎛⎫<+< ⎪+⎝⎭.……7分 考虑证不等式()ln 11xx x x <+<+(x >0) ** . ………………8分 令g (x )=x -ln(1+x ), h (x )=ln(x +1)-1xx + (x >0) .∴g '(x )=1x x +, h '(x )=()21x x +, ∵x >0, ∴g '(x )>0, h '(x )>0,∴g (x )、h (x )在(0, +∞)上都是增函数,……9分 ∴g (x )>g (0)=0, h (x )>h (0)=0,∴x >0时,()ln 11xx x x <+<+. 令1x n =则**式成立,∴111n a n a +⎛⎫- ⎪⎝⎭<1e <11na n a ⎛⎫- ⎪⎝⎭, ……………10分 (3)由(2)知b n =1n ,则T n =111123n+++⋅⋅⋅⋅⋅⋅+. 在111ln 11n n n⎛⎫<+< ⎪+⎝⎭中,令n =1,2,3,……,2008,并将各式相加, 得111232009111ln ln ln 1232009122008232008++⋅⋅⋅⋅⋅⋅+<++⋅⋅⋅⋅⋅⋅+<+++⋅⋅⋅⋅⋅⋅+, 即T 2009-1<ln2009<T 2008. …………………14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
惠州市2011届高三第三次调研考试数学试题(文科)本试卷共6页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
参考公式:锥体的体积公式13V Sh =,其中s 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共10 小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项是符合题目要求. 1.已知复数i z +=21,i z -=12,则z = 21z z ∙在复平面上对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.已知向量12||,10||==,且60-=⋅,则向量与的夹角为( ) A .060 B .0120 C .0135 D .0150 3.在等比数列{}n a 中,5113133,4,a a a a ⋅=+=则155a a =( ) A .3 B .13 C .3或13 D .3-或13- 4. 设α表示平面,b a ,表示直线,给定下列四个命题:①αα⊥⇒⊥b b a a ,//; ②αα⊥⇒⊥b a b a ,//; ③αα//,b b a a ⇒⊥⊥; ④b a b a //,⇒⊥⊥αα. 其中正确命题的个数有( )A.1个B.2个C.3个D.4个 5.2(sin cos )1y x x =+-是( )C. 最小正周期为π的奇函数D. 最小正周期为π的偶函数6. 命题“,11a b a b >->-若则”的否命题是( )A.,11a b a b >-≤-若则B.若b a ≥,则11-<-b aC.,11a b a b ≤-≤-若则D.,11a b a b <-<-若则 7.若方程()20f x -=在(,0)-∞内有解,则()y f x =的图象是( )8.设椭圆22221(00)x y m n m n+=>>,的右焦点与抛物线28y x =的焦点相同,离心率为12,则此椭圆的方程为( )A .2211612x y +=B .2211216x y += C .2214864x y += D .2216448x y += 9.已知定义域为(-1,1)的奇函数()y f x =又是减函数,且2(3)(9)0.f a f a -+-<则a 的取值范围是( )A .(3,10)B .(22,3)C .(22,4)D .(-2,3)10.对任意实数,x y ,定义运算x y ax by cxy *=++,其中,,a b c 是常数,等式右边的运算是通常的加法和乘法运算。
已知123,234*=*=,并且有一个非零常数m ,使得对任意实数x , 都有x m x *=,则m 的值是( )A.4B.4-C.5-D.6二、填空题(本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只需选做其中一题,两题全答的,只以第一小题计分.)11.已知函数2(4)()(1)(4)x x f x f x x ⎧<=⎨-≥⎩, 则(5)f _____________.12.已知点P(x,y)满足条件y x z k k y x x y x 3),(02,,0+=⎪⎩⎪⎨⎧≤++≤≥若为常数的最大值为8, 则k =_____________.13.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体 的体积是_____________.(二)选做题(14—15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知直线:40l x y -+=与圆{12cos 12sin :x y C θθ=+=+,则C 上各点到l 的距离的最小值为_____________.15.(几何证明选讲选做题)如图,已知⊙O 的割线PAB 交⊙O 于A ,B两点,割线PCD 经过圆心,若PA=3,AB=4,PO=5,则⊙O 的半径为_____________.三、解答题:本大题共6小题,共80分.解答应写出文字说明、演算步骤或推证过程. (★请在答题卷的指定区域内作答,否则该题计为零分.) 16.(本小题满分12分)如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A 、B ,观察对岸的点C,测得75CAB ∠=,45CBA ∠=,且100AB =米。
(1)求sin 75; (2)求该河段的宽度。
正视图 俯视图侧视图某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图; (2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试? (3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A 考官进行面试,求第4组至少有一名学生被考官A 面试的概率?18.(本题满分14分)如图,己知BCD ∆中,090BCD ∠=,1,BC CD AB BCD ==⊥平面,060,,AC,AD ADB E F ∠=分别是上的动点,且AE AF==,(0<<1)AC ADλλ (1)求证:不论λ为何值,总有EF ABC;⊥平面 (2)若1=,2λ求三棱锥A-BEF 的体积.已知动圆过定点(0,2)F ,且与定直线:2L y =-相切. (1)求动圆圆心的轨迹C 的方程;(2)若AB 是轨迹C 的动弦,且AB 过(0,2)F , 分别以A 、B 为切点作轨迹C 的切线,设两切线交点为Q ,证明:AQ BQ ⊥. 20.(本题满分14分)已知函数3()3.f x x x =-(1)求曲线()y f x =在点2x =处的切线方程;(2)若过点(1,)(2)A m m ≠-可作曲线()y f x =的三条切线,求实数m 的取值范围.21.(本题满分14分)已知函数3()log ()f x ax b =+的图象经过点)1,2(A 和)2,5(B ,记()*3,.f n n a n N =∈(1)求数列}{n a 的通项公式; (2)设n n n nn b b b T a b +++==21,2,若)(Z m m T n ∈<,求m 的最小值; (3)求使不等式12)11()11)(11(21+≥+++n p a a a n对一切*N n ∈均成立的最大实数p .惠州市2011届高三第三次调研考试数学试题(文科)答案1.【解析】∵z l ·z 2=3-i , 故选D 。
2.【解析】由a ∙b =cos 60a b θ=-⇒cos θ=21-,故0120θ=,选B 。
3.【解析】5113133133133,4,1,3a a a a a a a a ⋅=⋅=+=∴== 或3133,1,a a ==1513533a a a a ∴==或13,故选C 。
4.【解析】考虑α⊂a 的情形,则排除①③,故正确命题有②、④,故选B 。
5.【解析】2(sin cos )1y x x =+-=x 2sin ,故选C 。
6.【解析】由原命题与否命题的关系易得正确答案为C 。
7.【解析】方程()20f x -=在(,0)-∞内有解,即,2)(,000=<∃x f x 使得故选D 。
8.【解析】抛物线28y x =的焦点为(2,0),∴椭圆焦点在x 轴上且半焦距为2,∴2142m m =⇒=,∴2224212n =-=,∴椭圆的方程为2211612x y +=故选A 。
9.【解析】由条件得f (a -3)<f (a 2-9),即⎪⎩⎪⎨⎧->-<-<-<-<-9319113122a a a a ∴a ∈(22,3) 故选B 。
10.【解析】由定义有x cxm bm ax m x =++=*对任意实数x 恒成立,且m ≠0,令⎩⎨⎧-==⎩⎨⎧=⨯⨯+⨯=⨯⨯+⨯+=*∴=∴=∴=1543223211..0,0,0c a c a c a cxy ax y x b bm x 得由 ∴5x-mx=x 对任意实数x 恒成立, ∴m=4. 故选A 。
DBAC11.8; 12. k =-6; 13.π63; 14. 2; 15. 2。
11.【解析】82)3()4()5(3====f f f 。
12.【解析】画图,联立方程组20y x x y k =⎧⎨++=⎩得33k x ky ⎧=-⎪⎪⎨⎪=-⎪⎩,代入3()8,633k k k -+⨯-=∴=-13.【解析】由三视图知几何体的直观图是半个圆锥,21132V π⋅==。
14.【解析】圆方程为22()(1)x y ⋅+-=-14,∴d ==∴距离最小值为2。
15.【解析】设圆的半径为R,由PD PC PB PA ⋅=⋅得3(34)(5)(5)R R ⨯+=-+解得R=2。
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.解:(1)sin 75sin(3045)=+sin 30cos 45cos30sin 45=+122224=⨯+=………………4分 (2)∵75CAB ∠=,45CBA ∠=∴18060ACB CAB CBA ∠=-∠-∠=, 由正弦定理得:sin sin AB BCACB CAB=∠∠∴sin 75sin 60AB BC =………………7分 如图过点B 作BD 垂直于对岸,垂足为D,则BD 的长就是该河段的宽度。
在Rt BDC ∆中,∵45BCD CBA ∠=∠=,sin ,BDBCD BC∠=………………9分∴sin 45BD BC ==100sin 75sin 45sin 602AB ⋅==33350)(+(米) ………………12分17.解:(1)由题可知,第2组的频数为0.3510035⨯=人, ……………… 1分第3组的频率为300.300100=, ……………… 2分 频率分布直方图如下: ……………… 5分(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:第3组:306360⨯=人, ……… 6分 第4组:206260⨯=人, ……… 7分 第5组:106160⨯=人, ……… 8分 所以第3、4、5组分别抽取3人、2人、1人。
