信号与线性系统分析 吴大正 第四版习题答案第六章
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
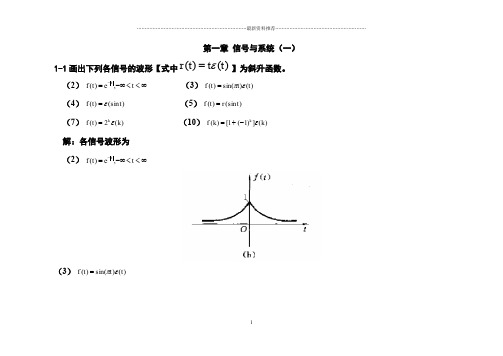
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析吴大正:第四版习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
吴大正《信号与线性系统分析》(第4版)笔记和课后习题考研真题详解

吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解
更多资料请在薇♥号精研学习网查找下载
本书是吴大正主编的《信号与线性系统分析》(第4版)的学习辅导书,主要包括以下内容:
(1)整理教材笔记,浓缩内容精华。
本书每章的复习笔记均对该章的知识点进行了整理,突出重点和考点。
(2)解析课后习题,提供详尽答案。
本书参考相关辅导资料,对教材的课后习题进行了详细的解答。
(3)精选考研真题,巩固重难点知识。
本书精选了多所名校近年的考研真题,并提供了详细的解答。
本书提供电子书及打印版,方便对照复习。
第1章信号与系统
1.1复习笔记
1.2课后习题详解
1.3名校考研真题详解
第2章连续系统的时域分析
2.1复习笔记
2.2课后习题详解
2.3名校考研真题详解
第3章离散系统的时域分析
3.1复习笔记
3.2课后习题详解
3.3名校考研真题详解
第4章傅里叶变换和系统的频域分析4.1复习笔记
4.2课后习题详解
4.3名校考研真题详解
第5章连续系统的s域分析
5.1复习笔记
5.2课后习题详解
5.3名校考研真题详解
第6章离散系统的z域分析
6.1复习笔记
6.2课后习题详解
6.3名校考研真题详解
第7章系统函数
7.1复习笔记
7.2课后习题详解
7.3名校考研真题详解
第8章系统的状态变量分析
8.1复习笔记
8.2课后习题详解8.3名校考研真题详解。
信号与线性系统分析 (吴大正 第四版)第六章习题答案

6.4 根据下列象函数及所标注的收敛域,求其所对应的原序列。
(1)1)(=z F ,全z 平面 (2)∞<=z z z F ,)(3 (3)0,)(1>=-z z z F(4)∞<<-+=-z z z z F 0,12)(2(5)a z azz F >-=-,11)(1(6)a z az z F <-=-,11)(16.5 已知1)(↔k δ,a z z k a k-↔)(ε,2)1()(-↔z z k k ε,试利用z 变换的性质求下列序列的z 变换并注明收敛域。
(1))(])1(1[21k kε-+ (3))()1(k k k ε- (5))1()1(--k k k ε (7))]4()([--k k k εε (9))()2cos()21(k k kεπ6。
8 若因果序列的z 变换)(z F 如下,能否应用终值定理?如果能,求出)(lim k f k ∞→。
(1))31)(21(1)(2+-+=z z z z F (3))2)(1()(2--=z z z z F6.10 求下列象函数的双边逆z 变换。
(1)31,)31)(21(1)(2<--+=z z z z z F (2)21,)31)(21()(2>--=z z z z z F (3)21,)1()21()(23<--=z z z z z F(4)2131,)1()21()(23<<--=z z z z z F6.11 求下列象函数的逆z 变换. (1)1,11)(2>+=z z z F (2)1,)1)(1()(22>+--+=z z z z zz z F (5)1,)1)(1()(2>--=z z z zz F(6)a z a z azz z F >-+=,)()(326.13 如因果序列)()(z F k f ↔,试求下列序列的z 变换.(1))(0i f a k i i∑= (2)∑=ki ki f a 0)(6.15 用z 变换法解下列齐次差分方程。
吴大正《信号与线性系统分析》(第4版)配套题库【章节题库】(下册)-第5~6章【圣才出品】

第5章连续系统的s域分析一、选择题1.信号的拉普拉斯变换为()。
【答案】C【解析】为t与u(t)的卷积,u(t)的拉氏变换为1/s,t的拉氏变换为,时域的卷积对应频域的乘积,所以×=。
2.f(t)=e2t u(t)的拉氏变换及收敛域为()。
【答案】C【解析】u(t)的拉氏变换为1/s,根据频域的平移性质,x(t)jcte-←−→X(s-c)。
题中c=2,右边信号的收敛域大于极点。
3.已知某信号的拉氏变换式为,则该信号的时间函数为()。
A.e-α(t—T)u(t-T)B.e-αt u(t-T)C.e-αt u(t-α)D .e -αu (t -T ) 【答案】B【解析】可采用从时域到频域一一排除的方法,u (t )的拉氏变换为1/s,根据时移性,u (t -T )的拉氏变换为s e sT -,再根据频域的时移性,e -αt u (t -T )的拉氏变换为sesT-的s 左移α,即se sT-中的s 加上α。
可推断出B 项的拉氏变换为。
4.信号f (t )=(t +1)u (t +1)的单边拉普拉斯变换为( )。
【答案】B【解析】f (t )是tu (t )向左移1个单位时间后的结果,由于单边拉氏变换只研究0t ≥的时间函数,故不能利用性质求F (s )。
因此可认为f (t )与(t +1)u (t )的单边拉氏变换相同,于是2111(t )u(t )s s+↔+。
5.信号u (t )-u (t -2)的拉普拉斯变换及收敛域为( )。
【答案】A【解析】阶跃u (t )的拉普拉斯变换为s1,根据拉普拉斯变换的时移性,f (t -0t ))(0s F ets -−→←,则u (t )的拉普拉斯变换为se s2-。
6.象函数的拉普拉斯逆变换为( )。
【答案】B【解析】由常用拉氏变换和拉氏变换的性质知()1(),,s sT s a T ate e u t s s s a--+-↔↔↔+时域平移u(t-T)域平移e u(t-T) 首先将F (s )变形为:e sT T e s αα--+,e st s α+的逆变换为(t T )e u(t T )α---,T e α-为常数,所以所求的逆变换为(t T )eu(t T )α---T e α-=t e u(t T )α--。
信与线性系统分析习题答案吴大正第四版高等教育出版社

第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t)t(t)】为斜升函数。
(2)f(t) et t(3)f(t)sin( t) (t)(4)f (t) (sint)(5)f(t)r(sin t)(7)f(t) 2k (k)(10f(k) [1 ( 1)k] (k))解:各信号波形为(2)f(t) e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。
(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。
如果是,确定其周期。
Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形。
(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解:各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形。
线性系统分析_(吴大正_第四版)习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
信号与系统课后答案第六章作业答案
⋅
2⎤⎥⎦
⋅
u
(n
−
3)
=
2⋅
( −1)n
⎡2 ⎢⎣ k =0
( −1)− k
⎤ ⎥⎦
⋅
u
(n
−
3)
∑ y
f
(3)
=
2
⋅
(
−1)3
⎡ ⎢⎣
k
2 =0
(
−1)−k
⎤ ⎥⎦
=
2
⋅
( −1)
⋅
(1
−1
+
1)
=
−2
∑ y
f
(4)
=
2
⋅
(
−1)4
⎡ ⎢⎣
k
2 =0
(
−1)−k⎤ ⎥⎦=2⋅(1)
⋅
(1
−1
+
1)
-1
对应时刻点相乘后累加得 y(1) = 4 。 由于 f1(n) 和 f2 (n) 为有限序列,故该题可采用数乘法进行计算:
11112 2 2 2 ↑ 1 1 1 1 −1 −1 −1 ↑
−1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2
u
(
n
+
4)
(4)利用卷积的性质( f (n) *δ(n − m) = f (n − m) )可得:
nu(n) * δ(n + 3) = nu(n) n=n+3 = (n + 3) u(n + 3)
6-7 如题图 6-4 所示,如果 y(n) = f1(n) * f2 (n) ,则试求 y(−2)、y(0)、y(1) 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章
6.4 根据下列象函数及所标注的收敛域,求其所对应的原序列。
(1),全z平面1(z)?F(2)3?zz?,zF()?(3)1?0?,(z)?zzF (4)2??z?,0?z)?2z?1z?(F1(5)?)za(F,z?1?az1?1 6)(az?)zF(,?
1?az?1.
zz,,试利用z变换的性质求下列序列的z变换并注明收敛域。
,已知6.5 k????k)k(?ka()1k()?2)1?(za?z
1)(3 )(1 kk??))?1(kk()k]()?[1(?12(7))(5 ???)](k?4k[k)?)?(kk1(k1()??k1(9)k?))(cos(()k22。
变换如下,能否应用终值定理?如果能,求出若因果序列的6.8
z)klim(f)F(z??k221?z z)(3 )(1?(F)z?z)(F
11)(zz?2)(1?)z(z)(??
32.
6.10 求下列象函数的双边逆z变换。
(1)F(z)?,z?113(z?)(z?)2321z(2)F,z?(z)? 2?11z
112(z?)(z?)2331z 3 ()?,(Fz)?z
122)z(??z)(12
(4)??(Fz)z?,1322)z?(z)(?12 3z11
6.11 求下列象函数的逆z变换。
1 1)(1z??,F(z)2?1z2?zz(2)F(z)?,z?1
5)(1?,zzF()?2?1z)(z?1)(2?zaz(6)2?z?11)(z)(z?z
a??,z)(Fz
3)a?z(
6.13 如因果序列变换。
z,试求下列序列的)z(F?)k(f kk??)2 )( 1 (ki)(iafi(fa)00?ii?
6.15 用z变换法解下列齐次差分方程。
(1)1?)(?1)k?1?0,y(0(yk)?.9y(3)3?)(,?0y0)(2)?(?2k(y?)yk1?yk?,()0y1
6.17 描述某LTI离散系统的差分方程为
)(k2)?f(k?1)?2yk?(ky()?y1。
,求该系统的零输入响应及全响应,零状态响应已知?)(ykk(y))(yk)1?1(y?)?,?)(f,)2?y(?k(k zszi4
6.19 图6-2为两个LTI离散系统框图,求各系统的单位序列响应和阶跃响应。
)(kh()gk
6.20 如图6-2的系统,求激励为下列序列时的零状态响应。
1)(3 1 ()k??)?kf()(()k)f(k?)kk(
3.
6.23 如图6-5所示系统。
(1)求该系统的单位序列响应。
)k(h
1,求零状态响应。
(2)若输入序列k?)k(y))(fk?k()(zs2
6.24 图6-6所示系统,
(1)求系统函数;)H(z(2)求单位序列响应;)(hk(3)列
写该系统的输入输出差分方程。
1k?(k)?()(fk)时的零状态响应为6.26 已知某LTI因果系统在输入211kk?)())?2(k]([)(yk?2zs23求该系统的系统函数,并画出它的模拟框图。
)z(H
图6-12
6-29 已知某一阶LTI系统,当初始状态,输入时,其全响应;当初始状态,??)?2?((k)ky(k))f(k1??(?1)?(y?1)1y1111。
求输入输入时的零状态响应。
时,其全响应k???)k?1)(k()(yk?)f()(fk)kk?)(k(?)(k2222
6.31 如图6-10所示的复合系统由3个子系统组成,已知子系统2的单位序列响应,子系统3k?)k)()h(k?(?12z,当输入时复合系统的零状态响应。
求子系统的系统数1的单位序??)?k((fk)))(3k?1k(?k(y)?Hk()13z?1列
响应。
)(hk1
6.33 设某LTI系统的阶跃响应为,已知当输入为因果序列时,其零状态响应)k(f)k(g
k?)?ig(y(k)zk0i?求输入。
)f(k
6.34 因果序列满足方程)(kf k??)(?k(k)if?kf()0i?求序列。
)f(k
6.37 移动平均是一种用以滤除噪声的简单数据处理方法。
当接收到输入数据后,就将本次输入数据与其)kf(个数据)进行平均。
求该数据处理系统的频率响应。
4次的输入数据(共3前
6.46 如图6-所示为因果离散系统,为输入,为输出。
)y(kf(k)(1)列出该系统的输入输出差分方程。
(2)问该系统存在频率响应否?为什么?
?。
)若频响函数存在,求输入(3时系统的稳态响应
)y(k))(fk?30?k20cos(.8
ss2.。
