计量经济学第三版(庞浩)版课后答案全之欧阳学文创作
庞皓计量经济学第三版课后习题及答案 顶配
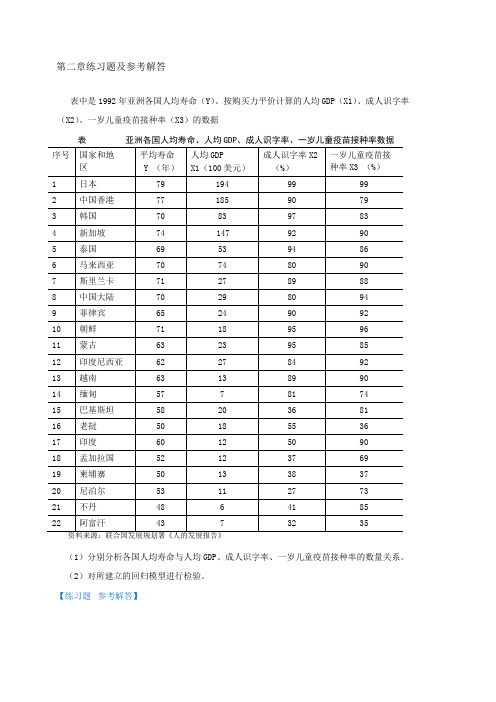
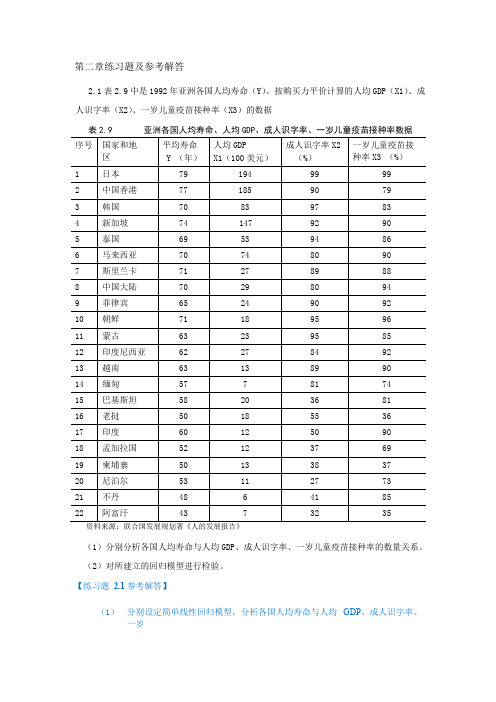
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
计量经济学 庞皓 第三版课后答案
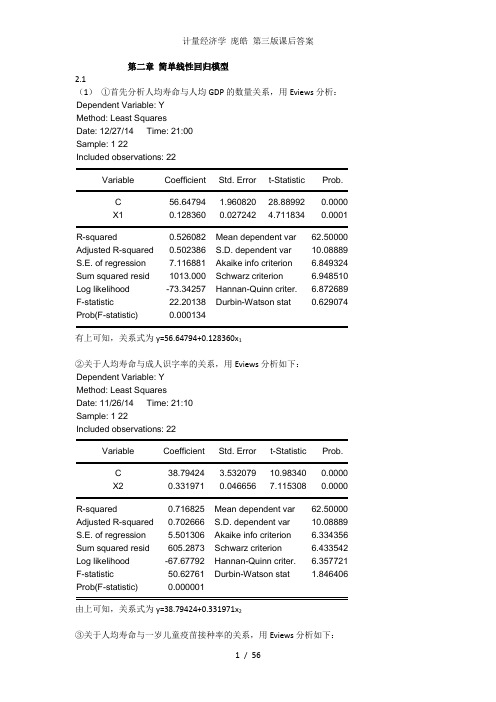
第二章简单线性回归模型2.1(1)①首先分析人均寿命与人均GDP的数量关系,用Eviews分析:Dependent Variable: YMethod: Least SquaresDate: 12/27/14 Time: 21:00Sample: 1 22Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C 56.64794 1.960820 28.88992 0.0000X1 0.128360 0.027242 4.711834 0.0001R-squared 0.526082 Mean dependent var 62.50000 Adjusted R-squared 0.502386 S.D. dependent var 10.08889 S.E. of regression 7.116881 Akaike info criterion 6.849324 Sum squared resid 1013.000 Schwarz criterion 6.948510 Log likelihood -73.34257 Hannan-Quinn criter. 6.872689 F-statistic 22.20138 Durbin-Watson stat 0.629074 Prob(F-statistic) 0.000134有上可知,关系式为y=56.64794+0.128360x1②关于人均寿命与成人识字率的关系,用Eviews分析如下:Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:10Sample: 1 22Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C 38.79424 3.532079 10.98340 0.0000X2 0.331971 0.046656 7.115308 0.0000R-squared 0.716825 Mean dependent var 62.50000 Adjusted R-squared 0.702666 S.D. dependent var 10.08889 S.E. of regression 5.501306 Akaike info criterion 6.334356 Sum squared resid 605.2873 Schwarz criterion 6.433542 Log likelihood -67.67792 Hannan-Quinn criter. 6.357721 F-statistic 50.62761 Durbin-Watson stat 1.846406 Prob(F-statistic) 0.000001由上可知,关系式为y=38.79424+0.331971x2③关于人均寿命与一岁儿童疫苗接种率的关系,用Eviews分析如下:Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:14Sample: 1 22Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C 31.79956 6.536434 4.864971 0.0001X3 0.387276 0.080260 4.825285 0.0001R-squared 0.537929 Mean dependent var 62.50000Adjusted R-squared 0.514825 S.D. dependent var 10.08889S.E. of regression 7.027364 Akaike info criterion 6.824009Sum squared resid 987.6770 Schwarz criterion 6.923194Log likelihood -73.06409 Hannan-Quinn criter. 6.847374F-statistic 23.28338 Durbin-Watson stat 0.952555Prob(F-statistic) 0.000103由上可知,关系式为y=31.79956+0.387276x3(2)①关于人均寿命与人均GDP模型,由上可知,可决系数为0.526082,说明所建模型整体上对样本数据拟合较好。
计量经济学(庞皓)第三版课后答案

第二章简单线性回归模型2.1(1)①首先分析人均寿命与人均GDP 的数量关系,用Eviews 分析:Dependent Variable: YMethod: Least SquaresDate: 12/27/14 Time: 21:00Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 56.64794 1.960820 28.88992 0.0000X1 0.128360 0.027242 4.711834 0.0001 R-squared 0.526082 Mean dependent var 62.50000Adjusted R-squared 0.502386 S.D. dependent var 10.08889S.E. of regression 7.116881 Akaike info criterion 6.849324Sum squared resid 1013.000 Schwarz criterion 6.948510Log likelihood -73.34257 Hannan-Quinn criter. 6.872689F-statistic 22.20138 Durbin-Watson stat 0.629074Prob(F-statistic) 0.000134 有上可知,关系式为y=56.64794+0.128360x1②关于人均寿命与成人识字率的关系,用Eviews 分析如下:Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:10Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 38.79424 3.532079 10.98340 0.0000X2 0.331971 0.046656 7.115308 0.0000 R-squared 0.716825 Mean dependent var 62.50000Adjusted R-squared 0.702666 S.D. dependent var 10.08889S.E. of regression 5.501306 Akaike info criterion 6.334356Sum squared resid 605.2873 Schwarz criterion 6.433542Log likelihood -67.67792 Hannan-Quinn criter. 6.357721F-statistic 50.62761 Durbin-Watson stat 1.846406Prob(F-statistic) 0.000001 由上可知,关系式为y=38.79424+0.331971x2③关于人均寿命与一岁儿童疫苗接种率的关系,用Eviews 分析如下:Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:14Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 31.79956 6.536434 4.864971 0.0001X3 0.387276 0.080260 4.825285 0.0001 R-squared 0.537929 Mean dependent var 62.50000Adjusted R-squared 0.514825 S.D. dependent var 10.08889S.E. of regression 7.027364 Akaike info criterion 6.824009Sum squared resid 987.6770 Schwarz criterion 6.923194Log likelihood -73.06409 Hannan-Quinn criter. 6.847374F-statistic 23.28338 Durbin-Watson stat 0.952555Prob(F-statistic) 0.000103 由上可知,关系式为y=31.79956+0.387276x3(2)①关于人均寿命与人均GDP 模型,由上可知,可决系数为0.526082,说明所建模型整体上对样本数据拟合较好。
计量经济学庞皓第三版课后答案解析
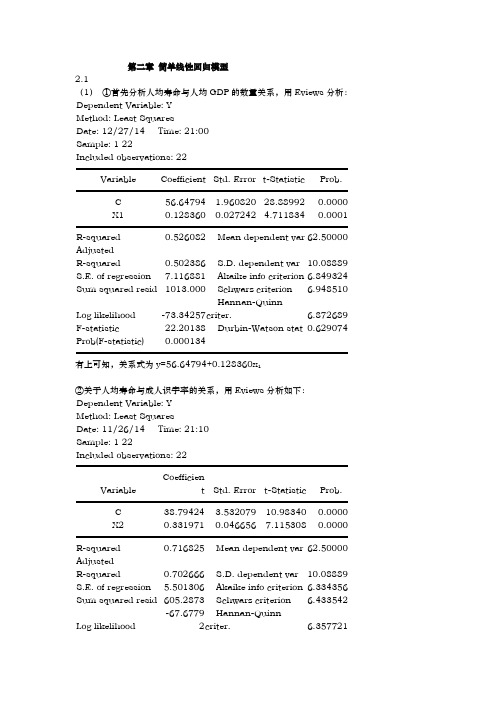
第二章 简单线性回归模型2.1(1) ①首先分析人均寿命与人均GDP 的数量关系,用Eviews 分析:Dependent Variable: YMethod: Least SquaresDate: 12/27/14 Time: 21:00Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 56.64794 1.960820 28.88992 0.0000X1 0.128360 0.027242 4.711834 0.0001 R-squared 0.526082 Mean dependent var 62.50000AdjustedR-squared 0.502386 S.D. dependent var 10.08889S.E. of regression 7.116881 Akaike info criterion 6.849324Sum squared resid 1013.000 Schwarz criterion 6.948510Log likelihood -73.34257 Hannan-Quinncriter. 6.872689F-statistic 22.20138 Durbin-Watson stat 0.629074Prob(F-statistic) 0.000134 有上可知,关系式为y=56.64794+0.128360x 1②关于人均寿命与成人识字率的关系,用Eviews 分析如下:Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:10Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 38.79424 3.532079 10.98340 0.0000X2 0.331971 0.046656 7.115308 0.0000 R-squared 0.716825 Mean dependent var 62.50000AdjustedR-squared 0.702666 S.D. dependent var 10.08889S.E. of regression 5.501306 Akaike info criterion 6.334356Sum squared resid 605.2873 Schwarz criterion 6.433542Log likelihood -67.67792 Hannan-Quinncriter. 6.357721F-statistic 50.62761 Durbin-Watson stat 1.846406Prob(F-statistic) 0.000001 由上可知,关系式为y=38.79424+0.331971x 2③关于人均寿命与一岁儿童疫苗接种率的关系,用Eviews 分析如下:Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:14Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 31.79956 6.536434 4.864971 0.0001X3 0.387276 0.080260 4.825285 0.0001 R-squared 0.537929 Mean dependent var 62.50000AdjustedR-squared 0.514825 S.D. dependent var 10.08889S.E. of regression 7.027364 Akaike info criterion 6.824009Sum squared resid 987.6770 Schwarz criterion 6.923194Log likelihood -73.06409 Hannan-Quinncriter. 6.847374F-statistic 23.28338 Durbin-Watson stat 0.952555Prob(F-statistic) 0.000103 由上可知,关系式为y=31.79956+0.387276x 3(2)①关于人均寿命与人均GDP 模型,由上可知,可决系数为0.526082,说明所建模型整体上对样本数据拟合较好。
庞皓第三版计量经济学练习题及参考解答(完整版)
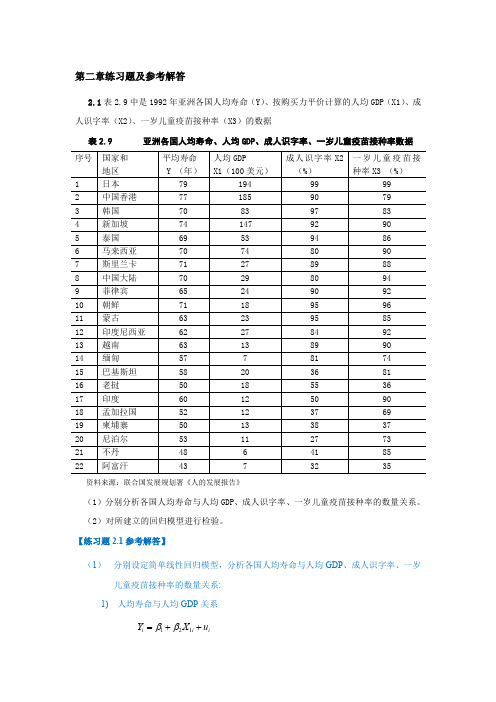
百户拥有 家用汽车量(辆) Y 37.71 20.62 23.32 18.60 19.62 11.15 11.24
北 京 天 津 河 北 山 西 内蒙古 辽 宁 吉 林
黑龙江 上 海 江 苏 浙 江 安 徽 福 建 江 西 山 东 河 南 湖 北 湖 南 广 东 广 西 海 南 重 庆 四 川 贵 州 云 南 西 藏 陕 西 甘 肃 青 海 宁 夏 新 疆
5 6 7 8 9 10 11 12 根据上表资料:
2.56 3.54 3.89 4.37 4.82 5.66 6.11 6.23
1678 1640 1620 1576 1566 1498 1425 1419
(1)建立建筑面积与建造单位成本的回归方程; (2)解释回归系数的经济意义; (3)估计当建筑面积为 4.5 万平方米时,对建造的平均单位成本作区间预测。
650 m 2.23 5.4772 1 5.0833 650 m 30.1250
2.4 假设某地区住宅建筑面积与建造单位成本的有关资料如表 2.11: 表 2.11 建筑地编号 1 2 3 4 某地区住宅建筑面积与建造单位成本数据 建筑面积(万平方米)X 0.6 0.95 1.45 2.1 建造单位成本(元/平方米)Y 1860 1750 1710 1690
(1)消费支出 C 的点预测值;
(2)在 95%的置信概率下消费支出 C 平均值的预测区间。 (3)在 95%的置信概率下消费支出 C 个别值的预测区间。
【练习题 2.3 参考解答】 (1)当 X f 1000 时,消费支出 C 的点预测值;
ˆ 50 0.6 X =50+0.6*1000=650 C i i
e2 ˆ2 i n 1 ˆ
2
庞皓计量经济学第三版课后习题及答案(顶配word版)
第二章练习题及参考解答2.1表2.9中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题2.1 参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于0.05,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显著影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为0.5261 人均寿命与成人识字率回归的可决系数为0.7168 人均寿命与一岁儿童疫苗接种率的可决系数为0.5379相对说来,人均寿命由成人识字率作出解释的比重更大一些2.2为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长9.0%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义【练习题2.2 参考解答】建议学生独立完成2.3 由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
庞皓计量经济学第三版课后习题及答案顶配

庞皓计量经济学第三版课后习题及答案顶配庞皓计量经济学第三版课后习题及答案顶配 Last revised by LE LE in 2021第⼆章练习题及参考解答表中是1992年亚洲各国⼈均寿命(Y)、按购买⼒平价计算的⼈均GDP(X1)、成⼈识字率(X2)、⼀岁⼉童疫苗接种率(X3)的数据(1)分别分析各国⼈均寿命与⼈均GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系。
(2)对所建⽴的回归模型进⾏检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国⼈均寿命与⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系:1)⼈均寿命与⼈均 GDP 关系Y i 1 2 X1i u i估计检验结果:2)⼈均寿命与成⼈识字率关系3)⼈均寿命与⼀岁⼉童疫苗接种率关系(2)对所建⽴的多个回归模型进⾏检验由⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命回归结果的参数 t 检验值均明确⼤于其临界值,⽽且从对应的P 值看,均⼩于 ,所以⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命都有显着影响.(3)分析对⽐各个简单线性回归模型⼈均寿命与⼈均 GDP 回归的可决系数为⼈均寿命与成⼈识字率回归的可决系数为⼈均寿命与⼀岁⼉童疫苗接种率的可决系数为相对说来,⼈均寿命由成⼈识字率作出解释的⽐重更⼤⼀些为了研究浙江省财政预算收⼊与全省⽣产总值的关系,由浙江省统计年鉴得到以下数据:的显着性,⽤规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果 2011 年,全省⽣产总值为 32000 亿元,⽐上年增长 %,利⽤计量经济模型对浙江省 2011 年的财政预算收⼊做出点预测和区间预测(3)建⽴浙江省财政预算收⼊对数与全省⽣产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学⽣独⽴完成由12对观测值估计得消费函数为:(1)消费⽀出C的点预测值;(2)在95%的置信概率下消费⽀出C平均值的预测区间。
计量经济学庞浩第三版第四章习题答案

第四章习题4.1(1)存在因为:23223223232322-))(())((-))((ˆ)(ΣΣΣΣΣΣΣ=βi i i i i i i i i i i x x x x x x x y x x y 23223223222233-))(())((-))((ˆ)(ΣΣΣΣΣΣΣ=βi i i i i i i i i i i x x x x x x x y x x y 且032=x x r ,则032=Σi i x x 原式变形为:))(())((ˆ23222322i i i i i x x x x y ΣΣΣΣ=β=222ii i x x y ΣΣ=2αˆ ))(())((ˆ23222233i i i i i x x x x y ΣΣΣΣ=β=2333ˆi i i x x y ΣΣ=β=3αˆ (2)会等于(3)存在因为)r -1()ˆvar(i3i 22222i x Σσ=β, )r -1()ˆvar(i3i 23232i x Σσ=β 且032=x x r原式变形为2222)ˆvar(ix Σσ=β=)ˆvar(2α, 2323)ˆvar(i x Σσ=β=)ˆvar(3α 4.2因为 )ˆ(-ˆ111βββ=SE t 所以 t(c)=92.8133.8=0.91177 , 2294.60.171.059)ˆt(1==β 6848.00.660.452)ˆt(2==β , 111.01.090.121)ˆt(3==β R 2是0.95,说明模型对样本拟合较好。
F检验,F=107.37> F(3,23)=3.03,回归方程显著。
t检验,t统计量分别为0.91177,6.2294,0.6848,0.111,X2,X3对应的t 统计量绝对值均小于t(23)=2.069,X2,X3的系数不显著,可能存在多重共线性。
4.3(1)LnY=-3.111486+1.338533lnGDP-0.421791lnCPI(2)R2是0.988051,修正的R2为0.987055,说明模型对样本拟合较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章欧阳学文2.2(1)①对于浙江省预算收入与全省生产总值的模型,用Eviews 分析结果如下:Dependent Variable: YMethod: Least SquaresDate: 12/03/14 Time: 17:00Sample (adjusted): 1 33Included observations: 33 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.X0.1761240.00407243.256390.0000C-154.306339.08196-3.9482740.0004R-squared0.983702 Mean dependent var902.5148Adjusted R-squared0.983177 S.D. dependent var1351.009S.E. of regression175.2325 Akaike info criterion13.22880Sum squared resid951899.7 Schwarz criterion13.31949Log likelihood-216.2751 Hannan-Quinn criter.13.25931F-statistic1871.115 Durbin-Watson stat0.100021Prob(F-statistic)0.000000②由上可知,模型的参数:斜率系数0.176124,截距为—154.3063③关于浙江省财政预算收入与全省生产总值的模型,检验模型的显著性:1)可决系数为0.983702,说明所建模型整体上对样本数据拟合较好。
2)对于回归系数的t检验:t(β2)=43.25639>t0.025(31)=2.0395,对斜率系数的显著性检验表明,全省生产总值对财政预算总收入有显著影响。
④用规范形式写出检验结果如下:Y=0.176124X—154.3063(0.004072) (39.08196)t= (43.25639) (-3.948274)R2=0.983702 F=1871.115 n=33⑤经济意义是:全省生产总值每增加1亿元,财政预算总收入增加0.176124亿元。
(2)当x=32000时,①进行点预测,由上可知Y=0.176124X—154.3063,代入可得:Y= Y=0.176124*32000—154.3063=5481.6617②进行区间预测:先由Eviews分析:由上表可知,∑x2=∑(Xi—X)2=δ2x(n—1)= 7608.0212 x (33—1)=1852223.473(Xf—X)2=(32000— 6000.441)2=675977068.2当Xf=32000时,将相关数据代入计算得到:5481.6617—2.0395x175.2325x√1/33+1852223.473/675977068.2≤Yf≤5481.6617+2.0395x175.2325x√1/33+1852223.473/6759770 68.2即Yf的置信区间为(5481.6617—64.9649, 5481.6617+64.9649)(3) 对于浙江省预算收入对数与全省生产总值对数的模型,由Eviews分析结果如下:Dependent Variable: LNYMethod: Least SquaresDate: 12/03/14 Time: 18:00Sample (adjusted): 1 33Included observations: 33 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.LNX0.9802750.03429628.582680.0000C-1.9182890.268213-7.1521210.0000R-squared0.963442 Mean dependent var 5.573120Adjusted R-squared0.962263 S.D. dependent var 1.684189S.E. of regression0.327172 Akaike info criterion0.662028Sum squared resid 3.318281 Schwarz criterion0.752726Log likelihood-8.923468 Hannan-Quinn criter.0.692545F-statistic816.9699 Durbin-Watson stat0.096208Prob(F-statistic)0.000000①模型方程为:lnY=0.980275lnX-1.918289②由上可知,模型的参数:斜率系数为0.980275,截距为-1.918289③关于浙江省财政预算收入与全省生产总值的模型,检验其显著性:1)可决系数为0.963442,说明所建模型整体上对样本数据拟合较好。
2)对于回归系数的t检验:t(β2)=28.58268>t0.025(31)=2.0395,对斜率系数的显著性检验表明,全省生产总值对财政预算总收入有显著影响。
④经济意义:全省生产总值每增长1%,财政预算总收入增长0.980275%2.4(1)对建筑面积与建造单位成本模型,用Eviews分析结果如下:Dependent Variable: YMethod: Least SquaresDate: 12/01/14 Time: 12:40Sample: 1 12Included observations: 12Variable Coefficient Std. Error t-Statistic Prob.X-64.18400 4.809828-13.344340.0000C1845.47519.2644695.796880.0000R-squared0.946829 Mean dependent var1619.333Adjusted R-squared0.941512 S.D. dependent var131.2252S.E. of regression31.73600 Akaike info criterion9.903792Sum squared resid10071.74 Schwarz criterion9.984610Log likelihood-57.42275 Hannan-Quinn criter.9.873871F-statistic178.0715 Durbin-Watson stat 1.172407Prob(F-statistic)0.000000由上可得:建筑面积与建造成本的回归方程为:Y=1845.475--64.18400X(2)经济意义:建筑面积每增加1万平方米,建筑单位成本每平方米减少64.18400元。
(3)①首先进行点预测,由Y=1845.475--64.18400X得,当x=4.5,y=1556.647②再进行区间估计:用Eviews分析:由上表可知,∑x2=∑(Xi—X)2=δ2x(n—1)= 1.9894192 x (12—1)=43.5357 (Xf—X)2=(4.5— 3.523333)2=0.95387843当Xf=4.5时,将相关数据代入计算得到:1556.647—2.228x31.73600x√1/12+43.5357/0.95387843≤Yf≤1556.647+2.228x31.73600x√1/12+43.5357/0.95387843即Yf的置信区间为(1556.647—478.1231, 1556.647+478.1231)第三章3.21)对出口货物总额计量经济模型,用Eviews分析结果如下::Dependent Variable: YMethod: Least SquaresDate: 12/01/14 Time: 20:25Sample: 1994 2011Included observations: 18Variable Coefficient Std. Error t-Statistic Prob.X20.1354740.01279910.584540.0000X318.853489.776181 1.9285120.0729C-18231.588638.216-2.1105730.0520R-squared0.985838 Mean dependent var6619.191Adjusted R-squared0.983950 S.D. dependent var5767.152S.E. of regression730.6306 Akaike info criterion16.17670Sum squared resid8007316. Schwarz criterion16.32510Log likelihood-142.5903 Hannan-Quinn criter.16.19717F-statistic522.0976 Durbin-Watson stat 1.173432Prob(F-statistic)0.000000①由上可知,模型为:Y = 0.135474X2 + 18.85348X3 - 18231.58②对模型进行检验:1)可决系数是0.985838,修正的可决系数为0.983950,说明模型对样本拟合较好2)F检验,F=522.0976>F(2,15)=4.77,回归方程显著3)t检验,t统计量分别为X2的系数对应t值为10.58454,大于t(15)=2.131,系数是显著的,X3的系数对应t值为1.928512,小于t(15)=2.131,说明此系数是不显著的。
(2)对于对数模型,用Eviews分析结果如下:Dependent Variable: LNYMethod: Least SquaresDate: 12/01/14 Time: 20:25Sample: 1994 2011Included observations: 18Variable Coefficient Std. Error t-Statistic Prob.LNX2 1.5642210.08898817.577890.0000LNX3 1.7606950.682115 2.5812290.0209C-20.52048 5.432487-3.7773630.0018R-squared0.986295 Mean dependent var8.400112Adjusted R-squared0.984467 S.D. dependent var0.941530S.E. of regression0.117343 Akaike info criterion-1.296424Sum squared resid0.206540 Schwarz criterion-1.148029Log likelihood14.66782 Hannan-Quinn criter.-1.275962F-statistic539.7364 Durbin-Watson stat0.686656Prob(F-statistic)0.000000①由上可知,模型为:LNY=-20.52048+1.564221 LNX2+1.760695 LNX3②对模型进行检验:1)可决系数是0.986295,修正的可决系数为0.984467,说明模型对样本拟合较好。
