高考数学函数专题训练《含绝对值的函数》含答案解析
【精品高考数学】2020年高三数学(江苏专用)-第05讲(含有绝对值函数的取值范围问题)+答案

第05讲(含有绝对值函数的取值范围问题)【目标导航】在数学高考中,函数问题一直占有较大的分量,而绝对值函数是函数中较为困难的一类函数,绝对值函数在高考中往往以填空小题的形式出现,绝对值函数可以视为分段函数,也可以整体处理,因此恰当的进行分类整合,探究绝对值函数的图象与性质是解决此类问题的核心方法. 【例题导读】例1、已知函数f (x )=x |x -4|,x ∈[0,m ],其中m >0,且函数f (x )的值域为[0,4],则实数m 的取值范围是_________.例2、已知函数f (x )=x |x -a |在[0,2]上的值域为[0,4],则实数a 的值是_________.例3、已知函数f (x )=x ||x -a +2x -3,若f (x )在R 上为增函数,则实数a 的取值范围是_________.例4、 若函数f (x )=x 2|x -a |在区间[0,2]上是增函数,则实数a 的取值范围是_________.例5、 已知函数f (x )=e x |x 2-a |(其中实数a >0),则f (x )的单调减区间是_______________.例6、已知函数f (x )=⎩⎨⎧||x +3,x ≤0,x 3-12x +3,x >0,设g (x )=kx +1,且函数y =f (x )-g (x )的图象经过四个象限,则实数k 的取值范围是________.例7、 已知f (x )=||x 2-4+x 2+kx ,若f (x )在(0,4)上有两个不同的零点x 1,x 2,则k 的取值范围是________.例8、 已知函数f (x )是定义在[1,+∞)上的函数,且f (x )=⎩⎪⎨⎪⎧1-|2x -3|,1≤x <2,12f ⎝ ⎛⎭⎪⎫12x , x ≥2,则函数y =2xf (x )-3在区间(1,2 015)上的零点个数为________.【反馈练习】1、函数y =|x -1|+|x +a |是偶函数,则实数a 的值是__________.2、函数y =2||x -m 在(2,+∞)上是增函数,则实数m 的取值范围是________.3、设f (x )=|lg(x -1)|,若0<a <b ,且f (a )=f (b ),则ab 的取值范围是________.4、已知f (x )是定义在R 上的偶函数,且对于任意的x ∈[0,+∞),满足f (x +2)=f (x ),若当x ∈[0,2)时,f (x )=|x 2-x -1|,则函数y =f (x )-1在区间[-2,4]上的零点个数为________.5、若不等式|x -2a |≥12x +a -1对x ∈R 恒成立,则a 的取值范围是________.6、若函数g (x )=x 2-a |x |+3只有两个单调区间,则a 的取值范围为_________.7、已知函数f (x )=|sin x |-kx (x ≥0,k ∈R )有且只有三个零点,设此三个零点中的最大值为x 0,则x 0(1+x 20)sin2x 0=________.8、已知t 为常数,函数f (x )=||x 3-3x -t +1在区间[-2,1]上的最大值为2,则实数t =_________.9、设函数f (x )=x |x +2|,则不等式f (f (x ))≤3的解集为________.10、已知函数f (x )=⎩⎨⎧a -|x +1|,x ≤1,x -a 2,x >1,函数g (x )=2-f (x ),若函数y =f (x )-g (x )恰有4个零点,则实数a 的取值范围是________.11、已知函数f (x )=x |x -a |+2x ,若存在a ∈[0,4],使得关于x 的方程f (x )=tf (a )有三个不相等的实根,则实数t 的取值范围为________.12、设a 为实数,函数f (x )=e 2x +|e x -a |(x ∈R ),则当0<a <12时,函数f (x )的值域为_________(用a 表示).13、已知函数f (x )=⎩⎨⎧ax -1,x ≤0,x 3-ax +|x -2|,x >0的图象恰好经过三个象限,则实数a 的取值范围是________.14、已知函数f(x)=a +3+4x -|x +a|有且仅有三个零点,并且这三个零点构成等差数列,则实数a 的值为________.第05讲(含有绝对值函数的取值范围问题)【目标导航】在数学高考中,函数问题一直占有较大的分量,而绝对值函数是函数中较为困难的一类函数,绝对值函数在高考中往往以填空小题的形式出现,绝对值函数可以视为分段函数,也可以整体处理,因此恰当的进行分类整合,探究绝对值函数的图象与性质是解决此类问题的核心方法. 【例题导读】例1、已知函数f (x )=x |x -4|,x ∈[0,m ],其中m >0,且函数f (x )的值域为[0,4],则实数m 的取值范围是_________. 【答案】[2,2+22]【解析】 由函数f (x )=x |x -4|图象可知(如图4-1所示),当x >4时,令x |x -4|=4,即x 2-4x -4=0,解得x =2+22,若函数f (x )的值域为[0,4],所以实数m 的取值范围是[2,2+22].例2、已知函数f (x )=x |x -a |在[0,2]上的值域为[0,4],则实数a 的值是_________. 【答案】 0或4【解析】(1)当a <0时,f (x )=x (x -a ),f (2)=2(2-a )>4,显然不满足条件;(2)当a =0时,f (x )=x 2,在[0,2]上的值域为[0,4],满足条件; (3)当a >0时,①当0<a ≤2时,f (x )=|x 2-ax |,f (0)=0,f (2)=|4-2a |=4-2a <4,f⎝⎛⎭⎫a 2=a 22-a 24=a 24≤1,不满足条件;②当2<a <4时,f (x )=-x 2+ax =-⎝⎛⎭⎫x -a 22+a 24≤a24<4,不满足条件; ③当a =4时,f (x )=-x 2+4x =-(x -2)2+4≤4,满足条件; ④当a >4时,f (x )=-x 2+ax ,f (2)=-4+2a >4,不满足条件.综上所述,a =0或a =4.例3、已知函数f (x )=x ||x -a +2x -3,若f (x )在R 上为增函数,则实数a 的取值范围是_________. 【答案】 [-2,2]【解析】 f (x )=⎩⎪⎨⎪⎧x 2+2-a x -3,x ≥a ,-x 2+2+a x -3,x <a =⎩⎨⎧⎝⎛⎭⎫x -a -222-a -224-3, x ≥a ,-⎝⎛⎭⎫x -a +222+a +224-3,x <a .f (x )在R 上恒为增函数的充要条件是⎩⎨⎧a -22≤a ,a +22≥a .解得-2≤a ≤2.例4、 若函数f (x )=x 2|x -a |在区间[0,2]上是增函数,则实数a 的取值范围是_________.【答案】 (-∞,0]∪[3,+∞)【解析】 (1)当a ≤0时,f (x )=x 3-ax 2,显然在区间[0,2]上是增函数;(2)当a >0时,记g (x )=x 3-ax 2,令g ′(x )=3x 2-2ax =0,解得x =0,x =2a3,g (x )在(-∞,0)上单调递增,在⎝⎛⎭⎫0,2a 3上单调递减,在⎝⎛⎭⎫2a3,+∞上单调递增,又g (0)=g (a )=0,所以f (x )=|g (x )|在(-∞,0)上单调递减,在⎝⎛⎭⎫0,2a 3上单调递增,在⎝⎛⎭⎫2a3,a 上单调递减,在(a ,+∞)上单调递增.要使f (x )在区间[0,2]上是增函数,只要2a3≥2,即a ≥3.综上所述,实数a 的取值范围为(-∞,0]∪[3,+∞).例5、 已知函数f (x )=e x |x 2-a |(其中实数a >0),则f (x )的单调减区间是_______________. 【答案】 ()-a +1-1,-a 和()a +1-1,a【解析】 因为f (x )=⎩⎨⎧e x x 2-a ,x |>a ,e x a -x 2,x |≤a .当|x |>a 时,f ′(x )=e x (x 2+2x -a ),由f ′(x )<0,解得-1-a +1<x <-1+a +1.因为-1-a +1<-a ,-1+a +1<a ,所以f (x )的单调减区间为(-1-a +1,-a ),同理当|x |≤a ,f ′(x )=-e x (x 2+2x -a ),所以 f (x ) 的单调减区间为(a +1-1,a ). 所以f (x )的单调减区间为()-a +1-1,-a 和()a +1-1,a .例6、已知函数f (x )=⎩⎨⎧||x +3,x ≤0,x 3-12x +3,x >0,设g (x )=kx +1,且函数y =f (x )-g (x )的图象经过四个象限,则实数k 的取值范围是________. 【答案】 ⎝⎛⎭⎫-9,13 【解析】 令h (x )=f (x )-g (x ).(1)当x ≤0时,h (x )=||x +3-(kx +1),因为h (0)=2,所以h (x )必过第二象限,即只须使h (x )过第三象限, 当k ≥1时,h (x )只在第二象限,故不合题意; 当k ≤-1时,h (x )必过第三象限,故符合题意; 当-1<k <1时,需h (-3)<0,所以-1<k <13,故k <13;(2)当x >0时,h (x )=x 3-(12+k )x +2,因为h ′(x )=3x 2-(12+k ),所以须使h (x )过第四象限, 必须⎩⎪⎨⎪⎧ 12+k >0,f ⎝ ⎛⎭⎪⎫12+k 3-g ⎝ ⎛⎭⎪⎫12+k 3<0,所以⎩⎪⎨⎪⎧12+k >0,12+k 3·12+k3>1,所以k >-9 综上,-9<k <13.例7、 已知f (x )=||x 2-4+x 2+kx ,若f (x )在(0,4)上有两个不同的零点x 1,x 2,则k 的取值范围是________. 【答案】 (-7,-2)【解析】一 (大函数法)因为f (x )=⎩⎪⎨⎪⎧kx +4,0<x ≤2,2x 2+kx -4,2<x <4,(1)当k ≥0时,因为f (x )在(0,2]上没有零点,且f (x )在(2,4)递增即至多一个零点,所以不合题意; (2)当k <0时,当f (2)>0即-2<k <0时,因为f (x )在(0,2]上没有零点,且f (x )在(2,4)递增即至多一个零点,所以不合题意;当f (2)=0即k =-2时,不合题意;当f (2)<0即k <-2时,因为f (x )在(0,2]上有一个零点,所以须f (x )在(2,4)有一个零点.因为f (2)<0, 由二次函数图象得只须f (4)>0,解得k >-7. 综上,-7<k <-2.【解析】二(小函数法)因为f (x )=||x 2-4+x 2+kx 在(0,4)上有两个不同的零点,所以方程||x 2-4+x 2+kx =0在(0,4)上有两个不同的解, 即||x 2-4=-(x 2+kx )在(0,4)上有两个不同的解,所以函数y =||x 2-4与y =-(x 2+kx )图象在(0,4)上有两个不同的交点. 由两函数图象发现只须满足:错误!解得-7<k <-2.【解析】三(分离参数法)因为f (x )=||x 2-4+x 2+kx 在(0,4)上有两个不同的零点,所以方程-k =||x 2-4+x 2x在(0,4)上有两个不同的解,所以函数y =-k 与y =⎩⎨⎧4x,0<x ≤2,2x -4x ,2<x <4图象在(0,4)上有两个不同的交点.由函数y =⎩⎨⎧4x ,0<x ≤2,2x -4x ,2<x <4的图象可知,只须2<-k <7,即-7<k <-2.例8、 已知函数f (x )是定义在[1,+∞)上的函数,且f (x )=⎩⎪⎨⎪⎧1-|2x -3|,1≤x <2,12f ⎝⎛⎭⎫12x , x ≥2,则函数y =2xf (x )-3在区间(1,2 015)上的零点个数为________. 【答案】11 【解析】解法1 由题意得当1≤x <2时,f (x )=⎩⎨⎧2x -2,1≤x ≤32,4-2x , 32<x <2. 设x ∈[2n-1,2n )(n ∈N *),则x 2n -1∈[1,2),又f (x )=12n -1f ⎝⎛⎭⎫12n -1x ,①当x 2n -1∈⎣⎡⎦⎤1,32时,则x ∈[2n -1,3·2n -2],所以f (x )=12n -1f ⎝⎛⎭⎫12n -1x =12n -1⎝⎛⎭⎫2·12n -1x -2,所以2xf (x )-3=2x ·12n -1⎝⎛⎭⎫2·12n -1x -2-3=0,整理得x 2-2·2n -2x -3·22n -4=0.解得x =3·2n -2或x =-2n -2.由于x ∈[2n -1,3·2n -2],所以x =3·2n -2;②当x2n -1∈⎝⎛⎭⎫32,2时,则x ∈(3·2n -2,2n ),所以f (x )=12n -1f ⎝⎛⎭⎫12n -1x =12n -1⎝⎛⎭⎫4-2·12n -1x ,所以2xf (x )-3=2x ·12n -1⎝⎛⎭⎫4-2x 2n -1-3=0,整理得x 2-4·2n -2x +3·22n -4=0.解得x =3·2n -2或x =2n -2.由于x ∈(3·2n -2,2n ),所以无解.综上所述,x =3·2n -2.由x =3·2n -2∈(1,2 015),得n ≤11,所以函数y =2xf (x )-3在区间(1,2 015)上零点的个数是11.解法2 由题意得当x ∈[2n-1,2n )时,因为f (x )=12n -1·f ⎝⎛⎭⎫12n -1x ,所以f (x )max =f ⎝⎛⎭⎫32·2n -1=12n -1.令g (x )=32x .当x =32·2n -1时,g (x )=g ⎝⎛⎭⎫32·2n -1=12n -1,所以当x ∈[2n -1,2n)时,x =32·2n -1为y =2xf (x )-3的一个零点. 下面证明:当x ∈[2n -1,2n )时,y =2xf (x )-3只有一个零点.当x ∈[2n-1,3·2n -2]时,y =f (x )单调递增,y =g (x )单调递减,f (3·2n -2)=g (3·2n -2),所以x ∈[2n-1,3·2n -2]时,有一零点x =3·2n -2;当x ∈(3·2n -2,2n)时,y =f (x )=12n -1-12n -1⎝⎛⎭⎫x 2n -2-3,k 1=f ′(x )=-122n -3,g (x )=32x ,k 2=g ′(x )=-32x 2∈⎝⎛⎭⎫-13·22n -3,-322n +1,所以k 1<k 2.又因为f (3·2n -2)=g (3·2n -2),所以当x ∈[2n -1,2n)时,y =2xf(x)-3只有一个零点.由x=3·2n-2∈(1,2 015),得n≤11,所以函数y=2xf(x)-3在区间(1,2 015)上零点的个数是11.解法3 分别作出函数y=f(x)与y=32x的图像,如图,交点在x1=32,x2=3,x3=6,…,x n=3·2n-2处取得.由x=3·2n-2∈(1,2 015),得n≤11,所以函数y=2xf(x)-3在区间(1,2 015)上零点的个数是11.【反馈练习】1、函数y=|x-1|+|x+a|是偶函数,则实数a的值是__________.【答案】 1【解析】由函数y=|x-1|+|x+a|的图象所示)知:“断”点位置为x=1和x=-a,所以-a=-1,即a=1.2、函数y=2||x-m在(2,+∞)上是增函数,则实数m的取值范围是________.【答案】(-∞,2]x-m的图象所示)知:m≤2.【解析】由函数y=2||3、设f(x)=|lg(x-1)|,若0<a<b,且f(a)=f(b),则ab的取值范围是________.【答案】(4,+∞)【解析】由于函数f(x)=|lg(x-1)|的图象如图所示.由f(a)=f(b)可得-lg(a-1)=lg(b-1),解得ab=a+b>2ab(由于a<b),所以ab的取值范围是(4,+∞).图444、已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2-x-1|,则函数y=f(x)-1在区间[-2,4]上的零点个数为________.【答案】7【解析】由题意作出y =f (x )在区间[-2,4]上的图象所示,与直线y =1的交点共有7个,故函数y =f (x )-1在区间[-2,4]上的零点个数为7.5、若不等式|x -2a |≥12x +a -1对x ∈R 恒成立,则a 的取值范围是________.【答案】 ⎝⎛⎦⎤-∞,12 【解析】作出y =|x -2a |和y =12x +a -1的简图如图所示,依题意知应有2a ≤2-2a ,故a 的取值范围是⎝⎛⎦⎤-∞,12.6、若函数g (x )=x 2-a |x |+3只有两个单调区间,则a 的取值范围为_________. 【答案】 ( -∞,0]【解析】 若函数g (x )=x 2-a |x |+3只有两个单调区间,则a2≤0,所以a 的取值范围是(-∞,0].7、已知函数f (x )=|sin x |-kx (x ≥0,k ∈R )有且只有三个零点,设此三个零点中的最大值为x 0,则x 0(1+x 20)sin2x 0=________.【答案】 12【解析】由y =|sin x |(x ≥0)和y =kx 的图像可知,当曲线与直线恰有三个公共点时,直线y =kx 与曲线y =-sin x (x ∈[π,2π])相切,设切点横坐标为x 0,斜率为-cos x 0.由⎩⎪⎨⎪⎧-sin x 0=kx 0,-cos x 0=k ,得tan x 0=x 0. 因为sin2x 0=2sin x 0cos x 0cos 2x 0+sin 2x 0=2tan x 01+tan 2x 0=2x 01+x 20,所以x 0(1+x 20)sin2x 0=12.8、已知t 为常数,函数f (x )=||x 3-3x -t +1在区间[-2,1]上的最大值为2,则实数t =_________. 【答案】 1【解析】所示,先作出函数y =x 3-3x 的图象,发现其经过点(-2,-2),(-1,2),(1,-2),所以函数y =||x 3-3x 的图象经过点(-2,2),(-1,2),(1,2).因为函数f (x )=||x 3-3x -t +1在区间[-2,1]上的最大值为2,当1-t >0,t <1,不符合题意.当1-t =0,t =1,符合题意.当1-t <0,t >1,f (-2)=f (1)=|t +1|>2,不符合题意.所以t =1.9、设函数f (x )=x |x +2|,则不等式f (f (x ))≤3的解集为________. 【答案】 (-∞,2-1]【解析】设f (x )=t ,则f (t )≤3,由函数f (x )=x |x +2|图象可得t ≤1,即f (x )≤1,所以,x ≤2-1,不等式f (f (x ))≤3的解集为(-∞,2-1].10、已知函数f (x )=⎩⎪⎨⎪⎧a -|x +1|,x ≤1,x -a 2,x >1,函数g (x )=2-f (x ),若函数y =f (x )-g (x )恰有4个零点,则实数a 的取值范围是________. 【答案】 (2,3]【解析】由题意,当y =f (x )-g (x )=2[f (x )-1]=0时,即方程f (x )=1有4个解.又由函数y =a -|x +1|与函数y =(x -a )2的大致形状可知,直线y =1与函数f (x )=⎩⎪⎨⎪⎧a -|x +1|,x ≤1,x -a 2,x >1的左右两支曲线都有两个交点,如图所示.那么,有错误!即错误! 所以实数a 的取值范围是(2,3].11、已知函数f (x )=x |x -a |+2x ,若存在a ∈[0,4],使得关于x 的方程f (x )=tf (a )有三个不相等的实根,则实数t 的取值范围为________. 【答案】 ⎝⎛⎭⎫1,98 【解析】f (x )=x |x -a |+2x =⎩⎪⎨⎪⎧x 2-a -2x ,x ≥a ,-x 2+a +2x ,x <a ,f (x )=⎩⎨⎧⎝⎛⎭⎫x -a -222-a -224,x ≥a ,-⎝⎛⎭⎫x -a +222+a +224,x <a ,因为0≤a ≤4,所以a -22<a ,(1)当a +22≥a ,即0≤a ≤2时,f (x )在R 上递增, 不合题意; (2)当a +22<a ,即2<a ≤4时,f (x )在⎝⎛⎭⎫-∞,a +22上递增,在⎝⎛⎭⎫a +22,a 上递减,在(a ,+∞)上递增,若关于x 的方程f (x )=tf (a )有三个不相等的实根,则f (a )<tf (a )<f ⎝⎛⎭⎫a +22,2a <2at <⎝⎛⎭⎫a +222,所以1<t <18⎝⎛⎭⎫a +4a +4,所以实数t 的取值范围是⎝⎛⎭⎫1,98. 12、设a 为实数,函数f (x )=e 2x +|e x -a |(x ∈R ),则当0<a <12时,函数f (x )的值域为_________(用a 表示).【答案】 [a 2,+∞)【解析】令e x =t >0,则f (x )=g (t )=t 2+|t -a |,因为0<a <12,所以g (t )=t 2+||t -a =⎩⎪⎨⎪⎧t 2+t -a ,t ≥a ,t 2-t +a , 0<t <a ,所以 g (t )在(0,a ]递减,在[a ,+∞)递增,所以g (t )值域为[a 2,+∞),即所以f (x )值域为[a 2,+∞).13、已知函数f (x )=⎩⎪⎨⎪⎧ax -1,x ≤0,x 3-ax +|x -2|,x >0的图象恰好经过三个象限,则实数a 的取值范围是________.【答案】 (-∞,0)∪(2,+∞)【解析】因为f (0)=-1,x →+∞时,f (x )→+∞,所以函数f (x )过第一、三象限,①若a <0,显然成立;②若a ≥0,只需x >0时,f (x )min <0即可,即存在x >0,使得f (x )<0分离参数,得⎝⎛⎭⎫x 2+|x -2|x min <a ,易求得⎝⎛⎭⎫x 2+|x -2|x min =2,所以,此时a >2,综上所述,实数a 的取值范围是(-∞,0)∪(2,+∞).14、已知函数f(x)=a +3+4x -|x +a|有且仅有三个零点,并且这三个零点构成等差数列,则实数a 的值为________. 【答案】116或-1-332【解析】 思路分析1 函数f(x)有且仅有三个零点,通常转化为方程f(x)=0有三相异实根,再转化为两个新函数的图像有三个不同的交点,这两个新函数如何构建是关键,通常的原则是:一是两个新函数图像是常见初等函数图像,二是一个函数图像是定的,另一个函数图像是动的,三是参数放在直线型中,即定曲线动直线,这样便于解决问题,基于这三点,所以构造的是函数y =4x +3与y =|x +a|-a =⎩⎪⎨⎪⎧x ,x≥-a ,-x -2a ,x<-a 的图像有且仅有三个不同的交点,再通过分类讨论的思想方法和三个零点构成等差数列建立关于a 的方程,从而求得a 的值.思路分析2 注意所研究的函数为分段函数f(x)=⎩⎨⎧x +4x +3+2a ,x<-a ,-x +4x+3,x≥-a ,因此,分别来研究每一段中的零点的个数,由于函数分为两段,因此,只有两种可能,一段为两个零点,另一段为一个零点.另外,注意到当x≥-a 时,函数为f(x)=-x +4x+3不含参数,可以直接求解,因此需对这两个零点是否在解法1 由f(x)=a +3+4x -|x +a|=0,得4x +3=|x +a|-a ,原函数有三个零点,即可转化为函数y =4x+3与y =|x +a|-a =⎩⎪⎨⎪⎧x ,x≥-a ,-x -2a ,x<-a图像有且仅有三个不同的交点,设三个交点的横坐标为x 1,x 2,x 3,且x 1<x 2<x 3,易知a≠0.下面分两种情况讨论:(1)a>0.如图1所示.,图1)由⎩⎪⎨⎪⎧y =4x +3,y =x ,解得x 2=-1,x 3=4. 又三个零点构成等差数列,则x 2=x 1+x 32,得x 1=-6,则有4-6+3=-(-6)-2a ,解得a =116符合题意.(2)a<0.如图2所示.,图2)由⎩⎪⎨⎪⎧y =4x +3,y =x ,解得x 3=4,由x 2=x 1+x 32,得x 1-2x 2=-4;再由⎩⎪⎨⎪⎧y =4x +3,y =-x -2a ,消去y ,得x 2+(2a +3)x +4=0 (*).由根据与系数的关系得⎩⎪⎨⎪⎧x 1+x 2=-(2a +3),x 1x 2=4,且x 1-2x 2=-4,解得⎩⎨⎧x 1=-4a -103,x 2=1-2a3,即(-4a -10)(1-2a )9=4,化简得4a 2+8a -23=0,综上(1)(2)可得a 的值为116或-1-323. 解得a =-2±332,检验方程(*)Δ(2a +3)2-16=4a 2+12a -7>0,但a<0,则a =-2-332满足题意.解法2 因为f(x)=⎩⎨⎧x +4x +3+2a ,x<-a ,-x +4x+3,x≥-a ,所以由f(x)=-x +4x+3=0得x =-1或4.(1)若-1≥-a ,即a≥1时,由于函数有三个零点,且成等差数列,所以,另一个零点x 0<-1,故-2=4+x 0,从而x 0=-6,故-6+4-6+3+2a =0,解得a =116,满足条件;(2)若-1<-a ,即a<1时,设函数f(x)=x +4x +3+2a(x<-a)的两个零点为x 1,x 2(x 1<x 2),即x 1,x 2是方程x 2+(2a +3)x +4=0 (*)的两个实数根,从而x 1+x 2=-2a -3,x 1x 2=4,又由于三个零点成等差数列,所以2x 2=x 1+4,消去x 1,x 2得4a 2+8a -23=0,解得a =-2±332,检验方程(*)Δ>0,而a<1,则a=-2-332满足题意. 综上,实数a 的值为116或-2-332.。
[数学]-专题41 含绝对值的一次函数(原版)
![[数学]-专题41 含绝对值的一次函数(原版)](https://img.taocdn.com/s3/m/d577f0c7a1116c175f0e7cd184254b35eefd1aa6.png)
专题41 含绝对值的一次函数1.请你用学习“一次函数”时积累的经验和方法研究函数y x =的图象和性质,并解决问题: (1)完成下列步骤,画出函数y x =的图象; ①列表、填空:②描点; ③连线.(2)观察函数图象,写出该函数图象的一条性质.2.请你用学习“一次函数”时积累的经验和方法研究函数|1|y x =+的图象和性质,并解决问题.(1)按照下列步骤,画出函数|1|y x =+的图象; ①列表;②描点; ③连线.(2)观察图象,填空;①当x ___________时,y 随x 的增大而减小;x ___________时,y 随x 的增大而增大; ②此函数有最 ___________值(填“大”或“小” ),其值是 ___________; (3)根据图象,不等式11|1|22x x +>+的解集为 ___________.3.请你用学习“一次函数和二次根式”时积累的经验和方法解决下列问题:(1)在平面直角坐标系中,画出函数|1|y x =-的图象; ①列表填空:②描点、连线,画出|1|y x =-的图象;(2)结合所画函数图象,写出|1|y x =-两条不同类型的性质;(3)1102x -=的近似解. 4.某班“数学兴趣小组”对函数11y x =---的图象和性质进行了探究,探究过程如下: (1)自变量x 的取值范围是全体实数,x 与y 的几组对应值如下:其中,m = ___________,n = ___________.(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.(3)观察这个函数图象,写出它的两条性质:①___________;②___________.(4)请根据函数图象,直接写出当方程111x m ---=-有解时,m 的取值范围___________. 5.某学习小组在综合与实践活动中,研究一元一次不等式、一元一次方程和一次函数的关系课题时,对函数13y x =+-的图像和性质做了探究. 下面是该学习小组的探究过程,请补充完整; (1)下表是y 与x 的几组对应值,请将表格补充完整:表格中m 的值为__________,n 的值为___________.(2)如图,在平面直角坐标系中描点并画出此函数的图像:(提示:先用铅笔画图确定后用签字笔画图)(3)请观察函数的图像,直接写出如下结论;①当自变量x ________时,函数y 随x 的增大而增大; ②方程132x +-=的解是x =____________; ③不等式14x +<的解集为________.6.在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程.结合学习函数的经验,探究函数1y x a =-+的图象与性质,探究过程如下.请补充完整.(1)列表:请根据表格中的信息,可得=a __________,b = __________.(2)①根据(1)中结果,请在给出的平面直角坐标系中,画出这个函数的图象.②若点()11,A x y ,()22,B x y 在函数图象上,且121x x <<,观察图像写出1y 、2y 的大小关系. 并说明理由.(3)结合画出的函数图象,解决问题:若关于x 的方程112x a x m -+=+有且只有一个正数解和一个负数解,则满足条件的m 取值范围是___________.7.在一次函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质的过程.小红对函数1(3)2(3)x x y x -<⎧=⎨≥⎩的图象和性质进行了如下探究,请同学们认真阅读探究过程并解答:(1)请同学们把小红所列表格补充完整,并在平面直角坐标系中画出该函数的图象:(2)根据函数图象,以下判断该函数 性质的说法,正确的有 . ①函数图象关于y 轴对称; ②此函数无最小值;③当x <3时,y 随x 的增大而增大;当x ≥3时,y 的值不变.(3)若直线y =12x +b 与函数y =1(3)2(3)x x x -<⎧⎨≥⎩的图象只有一个交点,则b = .8.某“数学兴趣小组”根据学习函数的经验,对函数312y x =+-的图象和性质进行了探究,探究过程如下,请补充完整.(1)如图,在平面直角坐标系xoy 中,请同学们自己列表并画出函数图象;(2)根据函数图象,写出该函数的两条性质: ①____________②_____________(3)若关于x 的方程312x b +-=有两个互不相等的实数根,则实数b 的取值范围是______. 9.请你用学习“一次函数和二次根式”时积累的经验和方法解决下列问题: (1)在平面直角坐标系中,画出函数|1|y x =-的图象: ①列表填空:②描点、连线,画出|1|y x =-的图象:(2)结合所画函数图象,写出|1|y x =-两条不同类型的性质; (3)结合所画函数图象,当x =________时,|1|1x -=. 10.已知函数32x ky -+=,且当1x =时2y =;请对该函数及其图像进行如下探究: (1)根据给定的条件,可以确定出该函数的解析式为___________; (2)根据解折式,求出如表的m ,n 的值;m =___________,n =___________.(3)根据表中数据.在如图所示的平面直角坐标系中描点并画出函数图像; (4)写出函数图像一条性质___________; (5)请根据函数图像写出当312x kx -+>+时,x 的取值范围.11.请你用学习一次函数时积累的经验和方法研究函数1y x =-的图象和性质,并解决问题. (1)根据函数数表达式,填写下表:m =______,n =______.(2)利用(1)中表格画出函数1y x =-的图象.(3)观察图象,当x ______时,y 随x 的增大而减小. (4)利用图象,直接写出不等式1112x x -<+的解集. 12.小颖根据学习函数的经验,对函数11y x =--的图象与性质进行了探究,下面是小颖的探究过程,请你补充完整. (1)列表:①k =______;②若()7,5A -,(),5B m -为该函数图象上不同的两点,则m =______. (2)描点并画出该函数的图象.(3)根据函数图象可得: ①该函数的最大值为______;②观察函数11y x =--的图象,写出该图象的两条性质:______,______; ③已知直线1112y x =-与函数11y x =--的图象相交,则当1y y ≤时x 的取值范围是______. 13.在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.学习了一次函数之后,现在来解决下面的问题: 在y a x b =+中,下表是y 与x 的几组对应值.(1)求a 、b 的值;(2)m =______,n =______;(3)在给出的平面直角坐标系xOy 中,描出以上表格中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.根据函数图象可得: ①该函数的最小值为______;②写出该函数的另一条性质____________;(4)已知直线14y x =+与函数y a x b =+的图象交于两点,则当1y y >时,x 的取值范围为______. 14.小时在学习了一次函数知识后,结合探究一次函数图像与性质的方法,对新函数21y x =--及其图像进行如下探究.(1)自变量x 的取值范围是全体实数,x 与y 的几组对应值如表:其中m = ,n = .(2)请在给出的平面直角坐标系中画出该函数的图像,并结合图像写出该函数的一条性质: .(3)当112133x x --≤+时,x 的取值范围为___________.15.小颖根据学习函数的经验,对函数1|1|y x =--的图象与性质进行了探究,下面是小颍的探究过程,请你补充完整.(1)列表:①k =__________;②若(8,6),(,6)A B m --为该函数图象上不同的两点,则m =___________; (2)描点并画出该函数的图象.(3)根据函数图象可得:该的数的最大值为_____________;观察函数1|1|y x =--的图象,写出该图象的一条性质:_____________________; (4)已知直线1112y x =-与函数1|1|y x =--的图象相交,则当1y y <时x 的取值范围是__________.16.九年级某数学兴趣小组在学习了一次函数的图象与性质后,进一步研究了函数1y x =+的图象与性质.其探究过程如下:(1)绘制函数图象,列表:下表是x 与y 的几组对应值,其中m = .描点:根据表中各组对应值(),x y ,在平面直角坐标系中描出各点,请你描出剩下的点; 连线:顺次连接各点,已经画出了部分图象,请你把图象补充完整;(2)通过观察图象,下列关于该函数的性质表述正确的是: ;(填写代号) ①函数值y 随x 的增大而减小; ②1y x =+关于y 轴对称; ③1y x =+有最小值1. (3)在上图中,若直线1522y x =+交函数1y x =+的图象于A ,B 两点(A 在B 左侧),记()0,1为C 点.则ABC S ∆= .17.某校数学兴趣小组根据学习函数的经验,对函数13y x =+-的图象和性质进行了探究,探究过程如下:自变量x 的取值范围是全体实数,x 与y 的几组对应值如下表:(1)①表中a 的值为 ,b 的值为 ;②以每组对应值作为一个点的坐标,在平面直角坐标系中描出表中的所有点,并按照自变量从小到大的顺序连线,画出该函数的图象,并观察图象,发现函数的最小值为 ; (2)在函数13y x =+-的图象所在坐标系中,作13y x =的图象,交13y x =+-的图象于点A ,B (A 在B 的左侧),并观察图象,直接写出下列结果: ①方程组1313y x y x ⎧=+-⎪⎨=⎪⎩的解为 ; ②不等式1133x x +-<的解集为 .18.有这样一个问题:探究函数21y x =-+的图像与性质.小明根据学习函数的经验,对函数21y x =-+的图像与性质进行了探究.(1)①函数21y x =-+的自变量x 的取值范围是_____________;②若点A (-7,a ),B (9,b )是该函数图像上的两点,则a ___________b (填“>”“<”或“=”);(2)请补全下表,并在平面直角坐标系xOy 中,画出该函数的图像:(3)函数12y x =-和函数2211y x =-++的图像如图所示,观察函数图像可发现:①12y x =-的图像向___________平移________个单位长度得到21y x =-+,2211y x =-++的图像向___________平移________个单位长度得到21y x =-+; ②当21211x x -+=-++时,x =_____________;③观察函数2211y x =-++的图像,写出该图像的一条性质.19.学习函数时,我们经历了“确定函数解析式、画出函数图象、利用函数图象研究函数性质、利用函数性质解决问题”的学习过程.以下是我们研究函数2y x =-+的图象和性质的部分过程,请按要求完成下列问题.(1)列表:y 与x 的部分对应值如下表,则m =______,n =______;(2)描点、连线:根据上表中的数据,在平面直角坐标系中画出函数2y x =-+的图象;(3)结合图象,写一条函数2y x =-+的性质:________________; (4)根据函数图象填空:①方程22x -+=有______个解;②若关于x 的方程2x a -+=无解,则a 的取值范围是______.20.小慧根据学习函数的经验,对函数y =|x ﹣1|+1的图象与性质进行了探究,下面是小慧的探究过程,请补充完整.(1)函数y =|x ﹣1|+1的自变量x 可以取 ; (2)列表,找出y 与x 的几组对应值.若A (8,8),B (m ,8)为该函数图象上不同的两点,则m = ;(3)在平面直角坐标系xOy 中,描出以上表中各对对应值为坐标的点,并根据描出的点画出该函数的图象,根据函数图象可得: ①该函数的最小值为 ;x+3与函数y=|x﹣1|+1的图象交于C,D两点,当y1≥y时x的取值范围②已知直线y1=12是.。
含绝对值的三角函数题型归纳
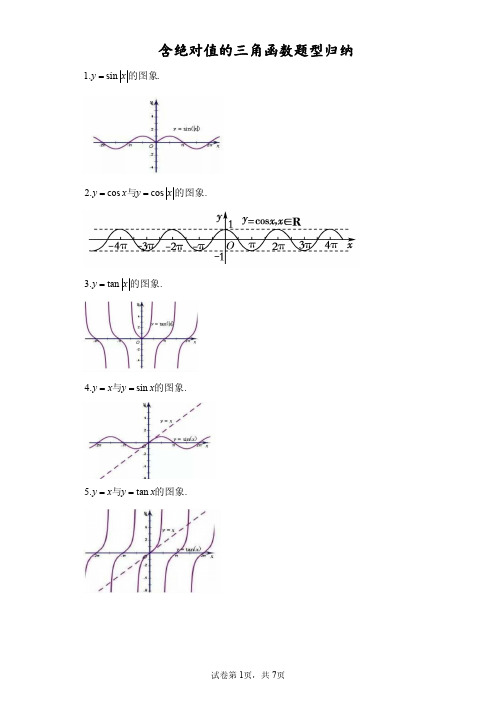
含绝对值的三角函数题型归纳1.sin .y x =的图象2.cos cos y x y x ==与的图象.3.tan y x =的图象.4.sin y x y x ==与的图象.5.tan y x y x ==与的图象.题型一:含绝对值的三角函数判断与应用1.关于三角函数的图像,有下列说法:①sin ||y x =与sin y x =的图像相同;②cos()y x =-与cos ||y x =的图像相同;③|sin |y x =与sin()y x =-图像关于x 轴对称;④cos y x =与cos()y x =-图像关于y 轴对称.其中正确的是__________.(写出所有正确说法的序号)【答案】②④【解析】对于②,()cos cos ,cos ||cos y x x y x x =-===,故其图像相同;对于④,()coscos y x x =-=,故其图像关于y 轴对称;由函数图像可知①③均不正确.故正确的说法是②④.故填②④2.图中的曲线对应的函数解析式是()A.|sin |y x =B.sin ||y x =C.sin ||y x =-D.|sin |y x =-【答案】C【解析】当x>0,所以y=-sinx,又因为此函数为偶函数,所以y=-sin|x|.3(多选).给出下列四个命题,其中正确的命题有()A.函数tan y x =的图象关于点(),02k k Z π⎛⎫∈⎪⎝⎭对称B.函数sin y x =是最小正周期为π的周期函数C.θ为第二象限的角,且cos tan θθ>,则sin cos θθ>.D.函数2cos sin y x x =+的最小值为1-答案AD 解:对于A:函数tan y x =的图象关于点(),02k k Z π⎛⎫∈⎪⎝⎭对称,故A 正确;对于B:函数sin y x ==sin ,0sin ,0x x x x ≥⎧⎨-<⎩,图象关于y 轴对称,不是周期函数,故B 错误;对于C:由为第二象限的角,得tan sin θθ>,由cos tan θθ>,得sin cos θθ<,故C 错误;对于D:函数22215cos sin sin sin 1sin ,24y x x x x x ⎛⎫=+=-++=--+ ⎪⎝⎭当sin 1x =-时,函数的最小值为-1,故D 正确.故选:AD.3.函数sin sin y x x =-的值域是()A.0B.[]1,1- C.[]0,1D.[]2,0-【答案】D【解析】:00y sinx sinx 20sinx sinx sinx >⎧=-=⎨<⎩,,,由此值域为[]y 2,0∈-4.在()0,2π内使sin cos x x >成立的x 的取值范围是()A.3,44ππ⎛⎫⎪⎝⎭B.53,,4242ππππ⎛⎫⎛⎫⋃⎪ ⎪⎝⎭⎝⎭C.,42ππ⎛⎫⎪⎝⎭D.57,44ππ⎛⎫⎪⎝⎭【答案】A,【解析】∵sin cos x x >,∴sin 0x >,∴()0,x π∈.在同一坐标系中画出sin y x =,()0,x π∈与cos y x =,()0,x π∈的图像,如图.观察图像易得使sin cos x x >成立的3,44x ππ⎛⎫∈ ⎪⎝⎭.故选A.5.已知函数()sin cos f x x x =,则(D )A.()f x 的值域为[]1,1- B.()f x 在0,2π⎡⎤⎢⎣⎦上单调C.π为()f x 的周期D.,02π⎛⎫⎪⎝⎭为()f x 图象的对称中心6.(多选).已知函数()[]sin cos f x x x =([]x 表示不超过实数x 的最大正数部分),则(AB)A.()f x 的最小正周期为2πB.()f x 是偶函数C.()f x 在0,2π⎛⎫⎪⎝⎭上单调递减 D.()f x 的值域为[]sin1,sin1-.题型二:方程零点与函数交点问题1.(2022·全国课时练)方程cos x x =在(),-∞+∞内()A.没有根B.有且仅有一个根C.有且仅有两个根D.有无穷多个根【答案】C【解析】在同一坐标系中作出函数y x =及函数cos y x =的图象,如图所示.发现有2个交点,所以方程cos x x =有2个根.2.方程3sin ([2,2])xx x ππ=∈-的实数解有_______________个.【答案】2.【解析】在区间[]2π,2π-上,分别画出3x y =和sin y x =的图像如下图所示,由图可知,两个函数图像在区间[]2π,2π-上有两个交点,也即3sin ([2,2])x x x ππ=∈-的实数解有2个.故填:2.3.函数()lg cos f x x x =-在(),-∞+∞内的零点个数为__________.【答案】6.【解析】在同一平面直角坐标系中作出函数lg y x =和cos y x =的图像如图,结合图像的对称性可以看出两函数lg y x =和cos y x =的图像应有六个交点,即函数()lg cos f x x x =-在(),-∞+∞内有六个零点,应填答案6。
高考数学二次函数绝对值的问题典型试题及答案详解(6页)

高考数学二次函数绝对值的问题典型试题及答案详解 二次函数是最简单的非线性函数之一,而且有着丰富的内容,它对近代数仍至现代数学影响深远,这部分内容为历年来高考数学考试的一项重点考查内容,经久不衰,以它为核心内容的高考试题,形式上也年年有变化,此类试题常常有绝对值,充分运用绝对值不等式及二次函数、二次方程、二次不等式的联系,往往采用直接法,利用绝对值不等式的性质进行适当放缩,常用数形结合,分类讨论等数学思想,以下举例说明例1 设为实数,函数, (1)讨论的奇偶性;(2)求的最小值解;(1)时,为偶函数时,为非奇非偶函数(2)当当当例2 已知函数,. (1)若关于的方程只有一个实数解,求实数的取值范围;(2)若当时,不等式恒函数成立,求实数的取值范围;(3)求函数在区间[-2,2]上的最大值(直接写出结果,不需给出演a 2()||1f x x x a =+-+x R ∈()f x ()f x 0a =()f x 0a ≠()f x 22222131,24()||1131,24x x a x a x a f x x x a x x a x a x a ⎧⎛⎫+-+=++-≥⎪ ⎪⎪⎝⎭=+-+=⎨⎪⎛⎫-++=-++< ⎪⎪⎝⎭⎩()min 13,24a f x a ≤-=-()2min 11,122a f x a -<<=+()min 13,24a f x a ≥=+1)(2-=x x f |1|)(-=x a x g x )(|)(|x g x f =a R x ∈)()(x g x f ≥a )(|)(|)(x g x f x h +=算步骤).解:(1)方程,即,变形得,显然,已是该方程的根,从而欲原方程只有一解,即要求方程,有且仅有一个等于1的解或无解 ,结合图形得.(2)不等式对恒成立,即(*)对恒成立, ①当时,(*)显然成立,此时;②当时,(*)可变形为,令因为当时,,当时,,所以,故此时.综合①②,得所求实数的取值范围是.(3)因为=|()|()f x g x =2|1||1|x a x -=-|1|(|1|)0x x a -+-=1x =|1|x a +=0a<()()f x g x ≥x ∈R 2(1)|1|x a x --≥x ∈R 1x =a ∈R 1x ≠21|1|x a x -≤-21,(1),1()(1),(1).|1|x x x x x x x ϕ+>⎧-==⎨-+<-⎩1x >()2x ϕ>1x <()2x ϕ>-()2x ϕ>-2a -≤a 2a -≤2()|()|()|1||1|h x f x g x x a x =+=-+-2221,(1),1,(11),1,(1).x ax a x x ax a x x ax a x ⎧+--⎪--++-<⎨⎪-+-<-⎩≤≥当时,结合图形可知在上递减,在上递增, 且,经比较,此时在上的最大值为.当时,结合图形可知在,上递减, 在,上递增,且,, 经比较,知此时在上的最大值为.当时,结合图形可知在,上递减, 在,上递增,且,, 经比较,知此时 在上的最大值为.当时,结合图形可知在,上递减, 在,上递增,且, ,经比较,知此时 在上的最大值为.当时,结合图形可知在上递增,在上递减, 故此时 在上的最大值为.综上所述,当时,在上的最大值为;当时, 在上的最大值为;当时, 在上的最大值为0.1,22a a >>即()h x [2,1]-[1,2](2)33,(2)3h a h a -=+=+()h x [2,2]-33a +01,22a a 即0≤≤≤≤()h x [2,1]--[,1]2a -[1,]2a --[1,2](2)33,(2)3h a h a -=+=+2()124a a h a -=++()h x [2,2]-33a +10,02a a -<<即-2≤≤()h x [2,1]--[,1]2a -[1,]2a --[1,2](2)33,(2)3h a h a -=+=+2()124a a h a -=++()h x [2,2]-3a +31,222a a -<-<-即-3≤≤()h x [2,]2a -[1,]2a -[,1]2a [,2]2a -(2)330h a -=+<(2)30h a =+≥()h x [2,2]-3a +3,322a a <-<-即()h x [2,1]-[1,2]()h x [2,2]-(1)0h =0a ≥()h x [2,2]-33a +30a -<≤()h x [2,2]-3a +3a <-()h x [2,2]-练习:1. 已知函数.(1)讨论函数的奇偶性;(2)求函数的最小值2. 已知函数(1)若,,求的值(2)若时,恒成立,求的取值范围3. 已知函数,其中a 是实数.(1)判断的奇偶性,并说明理由;(2)当时,的最小值为,求a 的值答案:1.(1)函数为偶函数非奇非偶函数(2)2||)(2+-+=a x x x f )(x f )(x f ()221()f x x mx m R =-+∈2m =[]0,3x ∈()()max min D f x f x =-[]0,2x ∈()8f x ≤m |21|21)(2a x x x f -++=)(x f ]1,1[-∈x )(x f 221a 0a =0a ≠()22117,2(),24x a f x x x a x a ≥=++-=++-()22217,224x a f x x x a x a ⎛⎫<=-++=-++ ⎪⎝⎭2.(1)4(2)分类讨论二次函数对称轴与区间的关系,寻找最大值的位置 当在上递增 ,当在上递减,上递增当在上递减 综上所述: 3.(1)①当时,,有,所以为偶函数; ②当时,,所以不是奇函数;又因为,而, 即,所以不是偶函数; 综上,当时,既不是奇函数也不是偶函数.(2)①若,即,当时,,2min 71,4211()2,2271,42a a f x a a a a ⎧-≤-⎪⎪⎪=+-<<⎨⎪⎪+≥⎪⎩0,m <()f x []0,2()32804f m ≤∴-≤<02,m ≤≤()f x []0,m [],2m ()()833428f m m f ⎧≥-⎪∴-≤≤⎨≤⎪⎩2,m >()f x []0,2()132824f m ≥-∴<≤31344m -≤≤21=a ||21)(2x x x f +=)()(-x f x f =)(x f 21≠a 0|21|)0(≠-=a f )(x f 2)12(21)1-2(-=a a f |21|2)12(21)2-(12a a a f -+-=)12()2-(1-≠a f a f )(x f 21≠a )(x f 2213(1)2,2122()11(1)2,2122x a x a f x x a x a ⎧--+<-⎪⎪=⎨⎪++-≥-⎪⎩112-≤-a 0≤a ]1,1[-∈x a x a x x x f 221)1(212121)(22-++=-++=故在上递增,所以,得.②若,即, 当时,, 故在上递减,所以,得或.③若,即, 故在上递减,在上递增; 所以,得.综上,或或或.)(x f ]1,1[-=-=-=a f x f 221)1()(min 221a 52--=a 112≥-a 1≥a ]1,1[-∈x a x a x x x f 223)1(212121)(22+--=+--=)(x f ]1,1[-=+-==a f x f 223)1()(min 221a 1=a 3=a 1121<-<-a 10<<a ⎪⎪⎩⎪⎪⎨⎧≤≤--++-<≤-+--=)112(221)1(21)121(223)1(21)(22x a ax a x ax x f )(x f ]12,1[--a ]1,1[2-a 22min 212122)12()(a a a a f x f =+-=-=31=a 52--=a 31=a 1=a 3=a。
2024年高考数学专题复习冲A专题(1)含绝对值的函数

-2-
冲A专题(1) 含绝对值的函数
知识提要
知识提要
专题考点
二、已知y=|f(x)-(kx+b)|在区间x∈[s,t]上的最大值为M,则M的最小
值是
.
这里仅通过类比或数形结合进行理解.
1.多点控制:|f(x)|在x∈[s,t]上的最大值的最小值问题(端点或切比雪
式为|x-t|≤1-tx2,即 tx2-1≤x-t≤1-tx2,
+1
1
且
t≥,
2 +1
+1
2+1
t∈[-1,
].
2
பைடு நூலகம்
化简得 t≤
解得
-7-
冲A专题(1) 含绝对值的函数
知识提要
专题考点
专题考点
3.(2019年6月浙江学考)已知f(x)是定义在R上的偶函数,且在[0,+∞)
上单调递增.若对任意x∈R,不等式f(a+|x-b|)≥f(|x|-2|x-1|)(a,b∈R)
冲A专题(1)
含绝对值的函数
-1-
冲A专题(1) 含绝对值的函数
知识提要
知识提要
专题考点
一、绝对值的意义
1.绝对值函数的代数表达:f(x)=|x-a|=
-, ≥ ,
-, < .
一般解决绝对值问题,常规方法是采用分类讨论去绝对值,比较适
合大题的解答;对选择填空,可采用几何意义或两边夹逼近的思想.
则f(x)≤4恒成立⇔M≤4.
(i)当a≤0时,由(2)可知,
对于任意的x∈[-1,1],f(x)≤a2-a+2恒成立,
所以M=a2-a+2.
专题32:绝对值函数答案

专题21:含有绝对值的问题一.V 形函数相关问题1.已知函数f (x )=|2x -3|,若0<2a <b +1,且f (2a )=f (b +3),则T =3a 2+b 的取值范围为__⎝ ⎛⎭⎪⎫-516,0______. 2.已知关于x 的方程1+=ax x 有一个负根,但没有正根,则实数a 的取值范围是 a ≥1 ;3.若关于x 的不等式22x x t <--至少有一个负数解,则实数t 的取值范围 是9,24⎛⎫- ⎪⎝⎭_. 二.平底函数相关问题1.不等式21x x a -++≤,对[1,5]x ∀∈恒成立的实数a 的取值范围 是 9a ≥ ;2.已知|3||1|)(-++=x x x f ,若对一切R x ∈都有a x f >)(成立,则实数a 的取值范围是 。
3.若函数|||1|)(a x x x f -+-=的对称同轴方程为2=x ,则实数a 的取值范围 是 3=a ;4.函数||||)(a x x x f ++=在),0[+∞上为增函数,则a 的取值范围为____(答:0≥a )5.若函数|||2|)(a x x x f -+-=的对称方程为3=x ,则实数=a 。
三.“Z ”型函数1.已知|3||1|)(--+=x x x f ,若对一切R x ∈都有a x f >)(成立,则实数a 的取值范围是 。
2.直线y kx =与曲线|ln ||2|x y e x =--有3个公共点时,实数k 的取值范围 是 (0,1) .3.设直线x=t 与函数2()f x x =, ()ln g x x = 的图像分别交于点M,N,则当MN 达到最小时t 的值为 22 : 4.设,m n Z ∈,函数()()2log 4f x x =-+的定义域是[],m n ,值域是[]0,2,若关于x 的方程012||=++m x 有唯一的实数解,则m n += 1 .5.设函数2()sin (,)3sin f x x m x R m R x=++∈∈+最大值为()g m ,则()g m 的最小值 为 34 . 6.函数2121(0)()2(0)x x x x f x ax -⎧+-≤⎪=⎨+>⎪⎩有两个不同的零点,则实数a 的取值范围 为 12a <- . 7.已知t 为常数,函数3()31f x x x t =--+在区间[]2,1-上的最大值为2,则实数t = 1 .8.已知函数|11|)(xx f -=,若b a <<0,且)()(b f a f =,则b a +2的最小 值为 32+9.设函数f(x)=|x 2-1|,若a <b <0,且f(a)=f(b),则a 2-1b 2的取值范围为___(-∞,0)__.10.若关于x 的方程2||1x kx x =-有四个不同的实数根,则实数k 的取值范围 是 4-<k .11.若函数f (x)满足(1)-()f x f x +=,且 (1,1]时,(),x f x x ∈-=则函数y=f(x)的图象与函数3log y x =的图象的交点的个数为 4 。
高考数学难点突破:含绝对值三角函数问题含详解

高考数学难点突破:含绝对值三角函数问题一、单选题1.已知函数()cos sin f x x x =-,则下列结论中,正确的有()A .π是f (x )的最小正周期B .f (x )在(4π,2π)上单调递增C .f (x )的图像的对称轴为直线()4x k k ππ=+∈Z D .f (x )的值域为[02.已知函数()sin 2062f x x ππϕϕ⎛⎫⎛⎫=++<< ⎪ ⎪⎝⎭⎝⎭在,32ππ⎛⎫ ⎪⎝⎭上单调递增,则ϕ的取值范围为()A .0,4π⎛⎤⎥⎝⎦B .,63ππ⎡⎤⎢⎥⎣⎦C .,62ππ⎡⎫⎪⎢⎣⎭D .,43ππ⎡⎤⎢⎥⎣⎦3.关于函数()11cos sin f x x x =+有下述四个结论:①()f x 是偶函数;②()f x 在区0,2π⎛⎫⎪⎝⎭内单调递增;③()f x 是周期函数,且最小正周期为π;④()f x a ≥恒成立的充要条件是a ≤则其中所有正确结论的编号是()A .①②④B .①③C .②③D .①④4.已知函数sin 24()e xx xf x +=的图像大致为()A .B .C .D .5.已知函数1()sin 22f x x =+.给出下列结论:①()f x 最小正周期为π;②()f x 最小值为12;③把函数()y f x =的图象上所有点向左或向右平移4π个单位所得()y g x =都是偶函数;④()f x 在0,2π⎛⎫⎪⎝⎭上单调递增.其中所有正确结论的序号是()A .①④B .③C .②③D .①②③6.若关于x 的不等式sin |sin |2x x k -≤对任意5,66x ππ⎡⎤∈⎢⎥⎣⎦恒成立,则实数k 的取值范围为()A .[1,3]-B .75,22⎡⎤-⎢⎥⎣⎦C .[1,-D .[1,7.关于函数()|2sin |cos =+f x x x 有下述四个结论:①()f x 是偶函数;②()f x 在区间0,2π⎛⎫⎪⎝⎭上单调;③函数()f x 的最大值为M ,最小值为m ,则-=M m ;④若12a <<,则函数()y f x a =-在[,]-ππ上有4个零点.其中所有正确结论的编号是()A .①④B .①③C .②④D .①②③8.已知()sin 2cos 2f x a x b x =+,其中,,0a b ab ∈≠R .若()π6f x f ⎛⎫≤ ⎪⎝⎭对一切的x ∈R 恒成立,且π02f ⎛⎫> ⎪⎝⎭,则()f x 的单调递增区间是()A .πππ,π()36k k k ⎡⎤-+∈⎢⎥⎣⎦Z B .π2ππ,π()63k k k ⎡⎤++∈⎢⎥⎣⎦Z C .ππ,π()2k k k ⎡⎤+∈⎢⎥⎣⎦Z D .ππ,π()2k k k ⎡⎤-∈⎢⎥⎣⎦Z 9.已知函数()sin 02{e 0x x x f x x π=<,, ,若存在实数()12345i x i =,,,,.当()11234i i x x i -<=,,,时,满足()()()()()12345f x f x f x f x f x ====.则()51i i i x f x =∑的取值范围为()A .61e ∞⎛⎤-- ⎥⎝⎦,B .510e ⎡⎫-⎪⎢⎣⎭,C .()4∞-,D .514e ⎡⎫-⎪⎢⎣⎭,10.函数()()3sin x x f ωϕ=+(0>ω,2πϕ<),已知||33f π⎛⎫= ⎪⎝⎭,且对于任意的R x ∈都有066f x f x ππ⎛⎫⎛⎫-++-= ⎪ ⎪⎝⎭⎝⎭,若()f x 在52,369ππ⎛⎫⎪⎝⎭上单调,则ω的最大值为()A .11B .9C .7D .511.定义在R 上的偶函数f (x )满足()(2)f x f x =-,当x ∈[0,1]时2()f x x =,则函数()()sin 2()g x x f x π=-在区间1522⎡⎤-⎢⎥⎣⎦,上的所有零点的和为()A .10B .9C .8D .612.已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭,现有下列四个结论:①()f x 的最小正周期为π;②()510log 42f <<;③()f x 的图象关于直线3x π=-对称;④()451log log 23f f ⎛⎫< ⎪⎝⎭.其中所有正确结论的序号为()A .①③④B .①②④C .①③D .②④二、多选题13.已知函数()f x =()A .()f x 的图象关于2x π=对称B .()f x 的最小正周期为2πC .()f x 的最小值为1D .()f x 的最大值为34214.已知函数()sin cos sin 2f x x x x =++,则()A .π是函数()f x 的一个周期B .4x π=-是函数()f x 的一条对称轴C .函数()f x1,最小值为1-D .函数()f x 在35[,]43ππ上单调递增15.已知函数f (x )=sin(|cos x |)+cos(|sin x |),则以下结论正确的是()A .f (x )的图象关于直线2x π=对称B .f (x )是最小正周期为2π的偶函数C .f (x )在区间(0,)2π上单调递减D .方程1()2f x x =恰有三个不相等的实数根16.高斯是德国著名的数学家,人们称他为“数学王子”,他和阿基米德、牛顿并列为世界三大数学家.用其名字命名的“高斯函数”为:设R x ∈,用[]x 表示不超过x 的最大整数(例如:[3.8]4-=-,[1.5]1=),则[]y x =称为高斯函数.已知函数()sin sin f x x x =+,()[()]ϕ=x f x ,下列结论中不正确是()A .函数()ϕx 是周期函数B .函数()ϕx 的图象关于直线2x π=对称C .函数()ϕx 的值域是{}012,,D .函数()()2g x x x πϕ=-只有一个零点17.关于函数()sin ,024,2x x f x x x π⎧≤≤=⎨->⎩,下列说法正确的是()A .()1(32f f >B .17(()34f f >C .不等式()1f x >的解集为()2,3D .若存在实数(),,,,a b c d e a b c d e <<<<满足()()()()()f a f b f c f d f e ====,则()()()()()af a bf b cf c df d ef e ++++的取值范围为()0,718.已知函数()(sin cos )|sin cos |f x x x x x =+⋅-,下列说法正确的是()A .()f x 的最小正周期为πB .若()()122f x f x +=.则12(Z)2k x x k π+=∈C .()f x 在区间,22ππ⎡⎤-⎢⎥⎣⎦上是增函数D .()y f x =的对称轴是(Z)4x k k ππ=+∈第II 卷(非选择题)请点击修改第II 卷的文字说明三、填空题19.已知函数()sin f x x x =-,下列关于函数()f x 的说法正确的序号有________.①函数()f x 在73,62ππ⎡⎤⎢⎥⎣⎦上单调递增;②2π是函数()f x 的周期;③函数()f x 的值域为[2,1]-;④函数()f x 在[2,2]ππ-内有4个零点.20.设函数()cos f x x x =-,给出下列四个结论:①()f x 的最小正周期为π;②()f x 的值域为⎡-⎣;③()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增;④()f x 在[],ππ-上有4个零点.其中所有正确结论的序号是__________.21.若关于x 的不等式2sin sin 1(0)a x b x c a ++≤>的解集为[]2,2,k k k Z πππ+∈,则a 的取值范围是_______.22.已知函数()|2cos 2|f x x x =+的图象关于直线(02)x m m π=<<对称,则m 的最大值为________.23.函数()sin cos 2f x x x =+的值域是________.24.不等式sin 02x x π⎛⎫-⋅< ⎪⎝⎭,[],2x ππ∈-的解集为________.四、双空题25.已知函数()[][]sin cos 32x x f x =+,[]0,2x π∈,其中[]x 表示不超过x 的最大整数.例如:[]11=,[]0.50=,[]0.51-=-.①56f ⎛⎫=⎪⎝⎭π______;②若()f x x m >+对任意[]0,2x π∈都成立,则实数m 的取值范围是______.26.已知函数()3log ,03sin ,3156x x f x x x π⎧<<⎪=⎨≤≤⎪⎩,方程()f x m =有四个不相等的实数根()12341234,,,x x x x x x x x <<<.(1)实数m 的取值范围为_____________;(2)1234x x x x 的取值范围为______________.27.已知函数()f x =()f x 的最小正周期为___________;当,3x ππ⎡⎤∈⎢⎥⎣⎦时,()f x 的值域为___________.28.函数()3sin cos 2f x x x =-[]()0,2x π∈的最大值为_________,所有零点之和为_________.参考答案:1.B 【解析】【分析】根据()()2f x f x π+=可知()f x 的一个周期为2π,由此可判断A ;化简()f x 在(4π,)2π上解析式,即可得出()f x 的单调性,由此可判断B ;根据()f x 的奇偶性判断C ;根据()2f x 的范围即可求f (x )值域,由此可判断D .【详解】①cos sin 222f x x x πππ⎛⎫⎛⎫⎛⎫+=+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()sin cos cos sin x x x x f x =--=-=,∴2π是()f x 的一个周期,故A 错误;②当(4x π∈,)2π时,()cos sin sin cos 4f x x x x x x π=-=--,(4x π∈ ,)2π,(0,)44x ππ∴-∈,()f x ∴在(4π,)2π上单调递增,故B 正确;③显然()f x 是偶函数,故0x =是()f x 的一条对称轴,故C 错误;④[]2cos sin 12sin cos 1sin 20,1x x x x x -=-=-∈,∴()[]0,1f x ∈,故D 错误.故选:B.2.B 【解析】【分析】由,32x ππ⎛⎫∈ ⎪⎝⎭可求得26x πϕ++的取值范围,根据函数sin y x =的单调性可得出关于ϕ的不等式组,由此可解得ϕ的取值范围.【详解】因为,32x ππ⎛⎫∈ ⎪⎝⎭,所以572,666x πππϕϕϕ⎛⎫++∈++⎪⎝⎭.因为02πϕ<<,所以554663πππϕ<+<,则775663πππϕ<+<,因为函数sin y x =在,2ππ⎛⎫ ⎪⎝⎭和3,22ππ⎛⎫⎪⎝⎭上单调递减,在3,2ππ⎛⎫ ⎪⎝⎭上单调递增,所以567362πϕπππϕ⎧+≥⎪⎪⎨⎪+≤⎪⎩,解得63ππϕ≤≤.故选:B.3.D 【解析】【分析】根据奇偶性定义判断出①正确;当0,2x π⎛⎫∈ ⎪⎝⎭时()2144f x x x ππ=⎛⎫+- ⎪⎛⎫⎝⎭+ ⎪⎝⎭,结合正弦型函数单调性、复合函数单调性的判断方法可知②错误;由()2f x f x π⎛⎫+= ⎪⎝⎭知③错误;利用②③的结论可知()min f x =.【详解】对于①,由cos 0sin 0x x ≠⎧⎨≠⎩得:x k π≠且()2x k k Z ¹+Îpp ,()f x ∴定义域关于原点对称;又()()()()1111cos sin cos sin f x f x x xx x -=+=+=--,()f x ∴为定义域上的偶函数,①正确;对于②,当0,2x π⎛⎫∈ ⎪⎝⎭时,()11sin cos cos sin sin cos x x f x x x x x +=+=,()2211sin cos sin cos 44f x x x x x xx ππ∴==⎛⎫+-+-⎪+⎛⎫⎝⎭+ ⎪⎝⎭当0,2x π⎛⎫∈ ⎪⎝⎭时,3,444x πππ⎛⎫+∈ ⎪⎝⎭;则当,442x πππ⎛⎫+∈ ⎪⎝⎭时,144y x x ππ⎛⎫=+- ⎪⎛⎫⎝⎭+ ⎪⎝⎭单调递增,()f x ∴单调递减;当3,424x πππ⎛⎫+∈ ⎪⎝⎭时,144y x x ππ⎛⎫=+- ⎪⎛⎫⎝⎭+ ⎪⎝⎭单调递减,()f x ∴单调递增;②错误;对于③,()11112sin cos cos sin 22f x f x x x x x πππ⎛⎫+=+=+= ⎪⎛⎫⎛⎫⎝⎭++ ⎪⎪⎝⎭⎝⎭ ,2π∴是()f x 的周期,即()f x 的最小正周期不是π,③错误;对于④,由②推导过程可知:()f x 在0,2π⎛⎫⎪⎝⎭上的最小值为4f π⎛⎫= ⎪⎝⎭由③知:2π是()f x 的周期;()f x ∴在定义域上的最小值为∴对于实数a ,()f x a ≥恒成立的充要条件是a ≤.故选:D.4.A 【解析】【分析】利用排除法求解,先判断函数的奇偶性,再取特殊值根据函数图象的变化趋势判断【详解】定义域为R ,因为sin(2)(4)sin 24()()e ex xx x x xf x f x --+-+-==-=-,所以()f x 为奇函数,所以其图象关于原点对称,所以排除CD ,当1x =,sin 24(1)(1,2)ef +=∈,当x →+∞时,e x 的增加幅度远大于sin 24x x +的变化幅度,则x →+∞时,()0f x →,所以排除B ,故选:A 5.C 【解析】【分析】①根据绝对值的意义,结合图像即可判断;②根据正弦函数值域即可求解;③求出平移后函数解析式判断即可;④去掉绝对值符号判断即可.【详解】y =sin2x 的最小正周期为π,sin 2y x =的图像是:y =sin2x 图像在x 轴上方部分保持不变,将在x 轴下方部分翻折到x 轴上方,根据对称性可知,sin 2y x =的最小正周期缩短为y =sin2x 周期的一半,为2π;sin 2y x =+12是将sin 2y x =图像向上平移12个单位,周期保持不变,∴f (x )的最小正周期为2π,故①错误;111()sin 20222f x x =++=≥,∴()f x 最小值为12,故②正确;π1π11()sin 2sin 2cos 242222g x x x x ⎛⎫⎛⎫=±+=±+=+ ⎪ ⎪⎝⎭⎝⎭,∴()y g x =是偶函数,故③正确;0,2x π⎛⎫∈ ⎪⎝⎭,则()20,πx ∈,sin2x >0,∴()1sin 22f x x =+,∴f (x )在π0,2⎛⎫ ⎪⎝⎭上不单调,故④错误.故选:C .6.A 【解析】【分析】令1sin ,[,1]2t x t =∈,则||2t t k -≤.对k 进行讨论,即可求出答案.【详解】令1sin ,[,1]2t x t =∈,则||2t t k -≤.(1)当12k <时,则2()220t t k t kt -≤⇒--≤,令2()2g t t kt =--,max ()(1)101g t g k k ==--≤⇒≥-.故112k -≤<.(2)当1k >时,则2()220t k t t kt -≤⇒-+≥,令2()2g t t kt =-+①当12k<时,212k k <⇒<<,则22min ()()201242k k k g t g k ==-+≥⇒<≤②当12k≥时,2k ≥,则min ()(1)120323g x g k k k ==-+≥⇒≤⇒≤≤故13k <<(3)当112k ≤≤时,则||2t t k -≤在1[,1]2t ∈上恒成立,故112k ≤≤.综上所述:[1,3]k ∈-故选:A.7.A 【解析】【分析】①利用函数奇偶性的定义判断;②③④由()2sin cos f x x x =+=)x ϕ+,结合函数的对称性和周期性,作出()f x 的大致图象判断;【详解】由 ()|2sin()|cos()|2sin |cos ()f x x x x x f x -=-+-=+=,可知()f x 为偶函数,①对.由2sin(2π)cos()|2sin |cos (()2π)||2πx f x x x x f x -+==+-=-,得()f x 关于πx =对称;由(2π)()f x f x +=,得()f x 的周期为2π;当[0π]x ∈,时,()2sin cos f x x x =+=)x ϕ+,其中1tan 2ϕ=且π06ϕ⎛⎫∈ ⎪⎝⎭,;作出()f x 在[0π],上的图象,并根据()f x 的对称性及周期性作出()f x 的大致图象.由图可知,()f x 在π02ϕ⎛⎫- ⎪⎝⎭,上单调递增,在ππ2ϕ⎛⎫- ⎪⎝⎭,上单调递减,所以()f x 在π02⎛⎫ ⎪⎝⎭,上不单调,②错;()f x的最大值M ,最小值1m =-,故1M m -=+,③错;若12a <<,则()y f x a =-在[ππ]-,上有4个零点,④对,故选:A.8.B 【解析】【分析】利用辅助角公式,化简得())f x x θ=+.根据()6f x f π⎛⎫⎪⎝⎭对一切x ∈R 恒成立,可得当6x π=时函数有最大值或最小值,从而得出6k πθπ=+,k ∈Z .再由()02f π>知1k =-,56πθ=-,进而得到5())6f x x π=-,最后根据正弦函数单调增区间即可求得()f x 的单调递增区间.【详解】根据题意,可得()sin 2cos2)f x a x b x x θ=+=+,其中tan b aθ=.()()6f x f π对一切x ∈R 恒成立,∴当6x π=.因此,262k ππθπ⨯+=+,解得6k πθπ=+,k ∈Z ,())02f ππθθ+=> ,sin 0θ∴<,从而取1k =-得到566ππθπ=-=-.由此可得5()6f x x π-,令5222262k x k πππππ-+-,得263k x k ππππ++ ,()f x ∴的单调递增区间是[6k ππ+,23k ππ+,k ∈Z .故选:B .9.D 【解析】【分析】由正弦函数的性质可知,231x x +=,453x x +=,10x <,所以()()()()15111144x iii x f x xf x x e ==+=+∑,令()()4e (0)xg x x x =+<,利用导数得到函数()g x 的单调性和极值,求出()g x 在0x <时的值域,从而得到()51i i i x f x =∑的取值范围.【详解】由正弦函数的性质可知,231x x +=,453x x +=,10x <,()()()()()()15123451111144e x i i i x f x x x x x x f x x f x x =∴=++++=+=+∑,令()()4e (0)xg x x x =+<,则()()5e x g x x +'=,当()5x ∞∈--,时,()0g x ¢<,()g x 单调递减;当()50x ∈-,时,()0g x ¢>,()g x 单调递增,又 当4x <-时,()0g x <,且()04g =,()min 51()5g x g e ∴=-=-,()514e g x ∴-≤<,()51i i i x f x =∴∑的取值范围为514e ⎡⎫-⎪⎢⎣⎭,,故选:D .10.D 【解析】【分析】结合正弦函数的最值,对称性求ϕ的值,再结合单调性确定ω的最大值.【详解】∵||33f π⎛⎫= ⎪⎝⎭,()()3sin x x f ωϕ=+,∴32k ππωϕπ+=+,k Z ∈,又对于任意的R x ∈都有066f x f x ππ⎛⎫⎛⎫-++--= ⎪ ⎪⎝⎭⎝⎭,∴6m πωϕπ-+=,m Z ∈,∴3(2)2k m πϕπ=++,又2πϕ<,∴6π=ϕ或6πϕ=-,当6π=ϕ时,31w k =+,k Z ∈且61w m =-+,当7w =时,()3sin 76f x x π⎛⎫ ⎪⎝=⎭+,若52,369x p p 骣琪Î琪桫,则4131736618x πππ≤+≤,∴()f x 在52,369ππ⎛⎫⎪⎝⎭上不单调,C 错误,当6πϕ=-时,32w k =+,k Z ∈且61w m =--,当11w =时,()3sin 116f x x π⎛⎫ ⎪⎝-⎭=,若52,369x p p 骣琪Î琪桫,则49411136618x πππ≤-≤,∴()f x 在52,369ππ⎛⎫⎪⎝⎭上不单调,A 错误,当5w =时,()3sin 56f x x π⎛⎫ ⎪⎝=⎭-,若52,369x p p 骣琪Î琪桫,则1917536618x πππ≤-≤,∴()f x 在52,369ππ⎛⎫⎪⎝⎭上单调,D 正确,故选:D.【点睛】已知f (x )=Asin (ωx +φ)(A >0,ω>0)的性质求函数解析式的关键在于转化为正弦函数的问题.11.A 【解析】【分析】根据条件()(2)f x f x =-可得函数f (x )的图象关于直线x =1对称;根据函数的解析式及奇偶性,对称性可得出函数f (x )在512⎛⎤⎝⎦,的图象;令()()sin 2h x x π=,画出其图象,进而得出函数()sin 2y x π=的图象.根据函数图象及其对称性,中点坐标公式即可得出结论.【详解】因为定义在R 上的偶函数f (x )满足()(2)f x f x =-,所以函数f (x )的图象关于直线x =1对称,当x ∈[0,1]时,2()f x x =,可以得出函数f (x )在112⎡⎤-⎢⎥⎣⎦,上的图象,进而得出函数f (x )在1522⎡⎤-⎢⎥⎣⎦,的图象.画出函数2()f x x =,1522x ⎡⎤∈-⎢⎥⎣⎦,的图象;令()()sin 2h x x π=,可得周期T 22ππ==1,画出其图象,进而得出函数()sin 2y x π=的图象.由图象可得:函数()()sin 2()g x x f x π=-在区间1522⎡⎤-⎢⎥⎣⎦,上共有10个零点,即5对零点,每对零点的中点都为1,所以所有零点的和为5210⨯=.故选:A .12.A 【解析】【分析】根据绝对值对函数图像的影响,作出函数图像,有图像即可判断①③;根据02x π<<时f (x )的值域可判断()5log 4f 范围,根据f (x )在,36ππ⎛⎫- ⎪⎝⎭的单调性,可比较()451log log 23f f ⎛⎫ ⎪⎝⎭、的大小.【详解】作出()sin 3f x x π⎛⎫=+ ⎪⎝⎭的部分图象,如图所示,由图可知,()f x 的最小正周期是π,且()f x 的图象关于直线3x π=-对称,故①③正确;当02x π<<时,1()2f x >,而50log 412π<<<,∴()51log 412f <<,故②错误;∵()f x 在,36ππ⎛⎫- ⎪⎝⎭上单调递增,且44511log 3log log 123263ππ<-=<<<<--,∴()451log log 23f f ⎛⎫< ⎪⎝⎭,故④正确.故选:A.【解析】【分析】A :验证()f x π-与()f x 是否相等即可;B :验证()f x π+与()f x 相等,从而可知π为f (x )的一个周期,再验证f (x )在(0,π)的单调性即可判断π为最小正周期;C 、D :由B 选项即求f (x )最大值和最小值.【详解】()()f x f x π-=,故选项A 正确;∵()()f x f x π+=,故π为()f x 的一个周期.当(0,)x π∈时,()f x =此时3322cossin 22()cos sin 22x x x x f x '⎡⎤⎛⎫⎛⎫⎥=- ⎪ ⎪⎥⎝⎭⎝⎭⎦,令()0f x '=,得cossin 22x x =,故,242x x ππ==.∵当0,2x π⎛⎫∈ ⎪⎝⎭时,()0f x '>;当,2x ππ⎛⎫∈ ⎪⎝⎭时,()0f x '<,故()f x 在0,2π⎛⎫ ⎪⎝⎭上单调递增,在,2ππ⎛⎫⎪⎝⎭上单调递减,故()f x 的最小正周期为π,选项B 错误;由上可知()f x 在[0,]x π∈上的最小值为()(0)1f f π==,最大值为3422f π⎛⎫= ⎪⎝⎭,由()f x 的周期性可知,选项CD 均正确.故选:ACD.14.ABC 【解析】【分析】根据给定条件利用周期定义、对称性性质判断选项A ,B ;换元借助二次函数最值判断选项C ;利用复合函数单调性判断选项D 作答.因()()()()()sin cos sin 2sin cos sin 2f x x x x x x x f xππππ+=+++++=++=,A 正确;因()|sin()cos()|sin 2()|cos sin |2222f x x x x x x ππππ--=--+--+--=--+sin(2)x π--sin cos sin 2()x x x f x =++=,B 正确;令sin cos x x t +=,有2sin 21x t =-,则2sin cos sin 21y x x x t t =++=+-,0,4t x π⎛⎫⎡=+∈ ⎪⎣⎝⎭,因为21y t t =+-在⎡⎣上单调递增,即函数()f x 1,最小值为1-,C正确;函数()f x 由21y t t =+-和sin cos x x t +=复合而成,函数21y t t =+-在⎡⎣上单调递增,4t x π⎛⎫=+ ⎪⎝⎭在35[,)44ππ上递增,在55(,]43ππ上递减,则函数()f x 在35[]43ππ,上不单调,D 不正确.故选:ABC 【点睛】结论点睛:函数()y f x =的定义域为D ,x D ∀∈,存在常数a 使得()(2)()()f x f a x f a x f a x =-⇔+=-,则函数()y f x =图象关于直线x a =对称.15.ACD 【解析】【分析】根据对称性,周期性,复合函数单调性可判断选项ABC ,结合单调性和周期性对函数1()2g x x =和()f x 的图象交点情况讨论可判断D.【详解】()sin(cos())cos(sin())sin(sin )cos(cos )222f x x x x x πππ-=-+-=+ ,()sin(cos())cos(sin())sin(sin )cos(cos )222f x x x x x πππ+=+++=+,()()22f x f x ππ∴-=+,故A 正确;()sin(cos())cos(sin())sin(cos )cos(sin )()f x x x x x f x πππ+=+++=+= ,故B 不正确;当(0,2x π∈时,cos t x =单调递减,sin ,(0,1)y t t =∈单调递增,所以,sin(cos )sin(cos )y x x ==单调递减,同理,cos(sin )cos(sin )y x x ==单调递减,故函数()f x 在区间(0,2π上单调递减,所以C 正确;易知()f x 为偶函数,综上可知:()f x 的周期为π,且在区间(0,2π上单调递减,在区间(,)2ππ上单调递增,在区间3(,)2ππ上单调递减.令1()2g x x =,因为(0)sin11(0)0f g =+>=,()cos1cos ()24224f g ππππ=<==,故函数()f x 与()g x 的图象在区间(0,)2π内有且只有一个交点;又2()sin11sin 1()422f g ππππ=+>+==,故函数()f x 与()g x 的图象在区间(,)2ππ内有且只有一个交点;又333(cos1()224f g πππ=<=,故函数()f x 与()g x 的图象在区间3(,2ππ内有且只有一个交点.因为(2)sin11(2)f g πππ=+<=,由()f x 周期性和()g x 单调性可知,当2x π>或0x ≤时,两函数图象无交点.综上所述,方程1()2f x x =恰有三个不相等的实数根故选:ACD 16.AB 【解析】【分析】由题可知函数()sin sin f x x x =+为偶函数,结合条件可得2,225()[()]0,22,222,Z 6651,22,2662x k x f x k x k k x k k k x k x k ππππϕπππππππππππ⎧=+⎪⎪⎪==<<++<≤+∈⎨⎪⎪+≤≤+≠+⎪⎩,然后逐项判断即得.【详解】∵()sin sin ,R f x x x x =+∈,∴()()sin sin sin sin ()f x x x x x f x -=-+-=+=,∴函数()sin sin f x x x =+为偶函数,sin y x =不是周期函数,sin y x =是周期函数,对于0x >,当22,Z k x k k πππ<≤+∈时,()2sin f x x =,当222,Z k x k k ππππ+≤≤+∈时,()0f x =,∴2,225()[()]0,22,222,Z 6651,22,2662x k x f x k x k k x k k k x k x k ππππϕπππππππππππ⎧=+⎪⎪⎪==<<++<≤+∈⎨⎪⎪+≤≤+≠+⎪⎩,由函数()sin sin f x x x =+为偶函数,函数()ϕx 是偶函数,0x >时函数()f x 成周期性,但起点为0x =,所以函数()ϕx 不是周期函数,故选项A 不正确;由函数()ϕx 是偶函数,函数()ϕx 的图象关于0x =对称,由()22πϕ-=,3()02πϕ=,故函数()ϕx 的图象不关于2x π=对称,故B 不正确;由上可知函数()ϕx 的值域是{}012,,,故C 正确;由()()02g x x x πϕ=-=可得,2()x x ϕπ=,当20x π=时,0x =,(0)0ϕ=,当21x π=时,2x π=,()22ϕπ=,当22x π=时,x π=,()0ϕπ=,故直线2y x π=与()y x ϕ=的图象只有一个交点,即函数()()2g x x x πϕ=-只有一个零点,故D 正确.故选:AB.【点睛】关键点点睛:本题的关键是利用正弦函数的性质分析函数()f x 的图象和性质,进而利用高斯函数的定义可得函数()ϕx 的性质即得.17.BCD 【解析】【分析】根据给定条件计算判断选项A ,B ;解不等式()1f x >判断选项C ;作出函数()y f x =的图象与直线y t =,数形结合计算判断D 作答.【详解】因函数()sin ,024,2x x f x x x π⎧≤≤=⎨->⎩,则1()|sin |122f π==,(3)431f =-=,A 不正确;1(|sin |33f π==77()|sin |44f π==,B 正确;当02x ≤≤时,()01f x ≤≤,则不等式()1f x >化为241x x >⎧⎨->⎩,解得23x <<,()1f x >的解集为()2,3,C 正确;因存在实数(),,,,a b c d e a b c d e <<<<满足()()()()()f a f b f c f d f e ====,令()f a t =,则方程()f x t =有4个互异实根,,,,a b c d e ,即函数()y f x =的图象与直线y t =有4个公共点,作出函数()y f x =的图象与直线y t =,如图,因当02x ≤≤时,()01f x ≤≤,则01t <<,又()|sin |f x x π=在[0,1]上的图象关于直线12x =对称,在[1,2]上的图象关于直线32x =对称,因此有:1,3,4a b c d e t +=+==-,则()()()()()(8)af a bf b cf c df d ef e t t ++++=-,而函数28t t -+在(0,1)上递增,则有0(8)7t t <-<,所以()()()()()af a bf b cf c df d ef e ++++的取值范围为()0,7,D 正确.故选:BCD【点睛】关键点睛:涉及用分段函数零点特性求参数范围问题,可以先独立分析各段上的零点,再综合考查所有零点是解决问题的关键.18.BD 【解析】【分析】把函数()f x 化成分段函数,作出函数图象,再逐一分析各个选项即可判断作答.【详解】依题意,3cos 2,2244()(Z)5cos 2,2244x k x k f x k x k x k ππππππππ⎧-+<<+⎪⎪=∈⎨⎪-+≤≤+⎪⎩,函数()f x部分图象如图,函数()f x 是周期函数,周期为2π,而()[sin()cos()]|sin()cos()|()f x x x x x f x πππππ+=+++⋅+-+=-,即π不是()f x 的周期,A 不正确;因()11f x ≤且()21f x ≤,则当()()122f x f x +=时,1|cos 2|1x =且2|cos 2|1x =,则112k x π=且222k x π=,12,Z k k ∈,因此,1212()22k k k x x ππ++==,12Z k k k +=∈,B 正确;观察图象知,()f x 在区间,22ππ⎡⎤-⎢⎥⎣⎦上不单调,事实上,(0)10()4f f π=>=,()f x 在区间,22ππ⎡⎤-⎢⎥⎣⎦上不是增函数,C 不正确;观察图象知,4x π=,34x π=-是函数()y f x =图象的相邻两条对称轴,且相距半个周期长,事实上()[sin()cos()]|sin()cos()|()22222f x x x x x f x πππππ-=-+-⋅---=,即()y f x =图象关于4x π=对称,同理有()y f x =图象关于34x π=-对称,而函数()f x 的周期是2π,所以函数()y f x =图象对称轴,Z 4x k k ππ=+∈,D 正确.故选:BD 【点睛】结论点睛:存在常数a 使得()(2)()()f x f a x f a x f a x =-⇔+=-,则函数()y f x =图象关于直线x a =对称.19.①③④【解析】【分析】①化简解析式,求出3x π+范围,根据正弦函数的单调性即可判断;②根据奇偶性举特例验证f (x +2π)与f (x )关系即可;③分类讨论求出f (x )解析式,研究在x ≥0时的周期性,再求出值域即可;④根据值域和单调性讨论即可.【详解】∵函数()sin f x x x =-,定义域为R ,()()()sin sin f x x x x x f x -=--=-=,∴()f x 为偶函数.当73,62x ππ⎡⎤∈⎢⎥⎣⎦时,cos 0x <,()sin 2sin 3f x x x x π⎛⎫=+=+ ⎪⎝⎭,311326x πππ⎡⎤+∈⎢⎥⎣⎦,,此时正弦函数为增函数,故①正确;∵sin 0333f πππ⎛⎫=-= ⎪⎝⎭,∴033f f ππ⎛⎫⎛⎫-== ⎪ ⎝⎭⎝⎭,而52333f f f ππππ⎛⎫⎛⎫⎛⎫-+==-- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,∴2π不是函数()f x 的周期,故②错误;当022x k ππ⎡⎫∈+⎪⎢⎣⎭,或32222k k ππππ⎡⎫++⎪⎢⎣⎭,,k ∈Z 时,cos cos x x =,此时()sin 2sin 3f x x x x π⎛⎫==-⎪⎝⎭,当32222x k k ππππ⎡⎫∈++⎪⎢⎣⎭,,k ∈Z 时,cos cos x x =-,此时()sin 2sin 3f x x x x π⎛⎫=+=+ ⎪⎝⎭,故0x 时,2π是函数的一个周期,故考虑[]0,2x π∈时,函数的值域,当02,π⎡⎤∈⎢⎥⎣⎦x 时,()2sin 3f x x π⎛⎫=- ⎪⎝⎭,,336x πππ⎡⎤-∈-⎢⎥⎣⎦,此时()f x 单调递增,();f x ⎡⎤∈⎣⎦当3,22x ππ⎛⎫∈ ⎪⎝⎭时,()2sin 3f x x π⎛⎫=+ ⎪⎝⎭,53,362x πππ⎛⎫+∈ ⎪⎝⎭,此时()f x 单调递减,()()2,1f x ∈-;当322x ππ⎡⎤∈⎢⎥⎣⎦,时,()2sin 3f x x π⎛⎫=- ⎪⎝⎭,75,363x πππ⎡⎤-∈⎢⎥⎣⎦,此时()2,f x ⎡∈-⎣,综上可知,()[]2,1f x ∈-,故③正确;由③知,02,π⎡⎤∈⎢⎣⎦x 时,()002f f π⎛⎫⋅< ⎪⎝⎭,且函数单调递增,故存在一个零点,当726x ππ⎡⎤∈⎢⎥⎣⎦,时,7026f f ππ⎛⎫⎛⎫⋅< ⎪ ⎪⎝⎭⎝⎭,且函数单调递减,故存在一个零点,其他区域无零点,故当[]0,2x π∈时,函数有2个零点,∵函数为偶函数,∴函数()f x 在[]2,2ππ-内有4个零点.故④正确;故答案为:①③④.20.①②④【解析】【分析】讨论x 的范围去掉绝对值可得到()f x ,结合图象逐项分析可得答案.【详解】当()2,2,2πππ⎡⎫∈+∈⎪⎢⎣⎭x k k k Z 时,()cos sin cos 2sin 6π⎛⎫=--=- ⎪⎝⎭f x x x x x x ,当()22,2,ππππ⎡⎫∈++∈⎪⎢⎣⎭x k k k Z 时,()cos sin cos 2sin 6π⎛⎫=-+=+ ⎪⎝⎭f x x x x x x ,当()322,2,ππππ⎡⎫∈++∈⎪⎢⎣⎭x k k k Z 时,()cos cos 2sin 6π⎛⎫=-=+=-- ⎪⎝⎭f x x x x x x ,当()3222,2ππππ⎡⎫∈++∈⎪⎢⎣⎭x k k k Z 时,()cos cos 2sin 6π⎛⎫=-=-=-+ ⎪⎝⎭f x x x x x x ,所以()2sin 2,2622sin 2262()32sin 226232sin 22262,,,,,,,πππππππππππππππππππ⎧⎛⎫⎡⎫-∈+ ⎪⎪⎪⎢⎝⎭⎣⎭⎪⎪⎛⎫⎡⎫+∈++⎪ ⎪⎪⎢⎪⎝⎭⎣⎭=∈⎨⎛⎫⎡⎫⎪--∈++ ⎪⎪⎢⎪⎝⎭⎣⎭⎪⎛⎫⎡⎫⎪-+∈++ ⎪⎪⎢⎪⎝⎭⎣⎭⎩x x k k x x k k f x k Z x x k k x x k k ,()f x的图象如下所以()f x 的最小正周期为π,①正确;()f x的值域为⎡-⎣,②正确;()f x 在,22ππ⎛⎫-⎪⎝⎭上有增有减,③错误;()f x 在[],ππ-上有4个零点,④正确.故答案为:①②④.21.(]0,8【解析】【分析】令sin t x =,将原问题转化为关于t 的不等式211(0)at bt c a -≤++≤>的解集为[]0,1,结合二次函数的性质,即可求出结果.【详解】令sin t x =,若关于x 的不等式2sin sin 1(0)a x b x c a ++≤>的解集为[]2,2,k k k Z πππ+∈,等价于若关于t 的不等式21(0)at bt c a ++≤>的解集为[]0,1,即关于t 的不等式211(0)at bt c a -≤++≤>的解集为[]0,1,若0a >,可知函数2y at bt c =++的对称轴为10122t +==,开口向上,所以函数2y at bt c =++图象如图所示:当0=t 时,1c =,当1t =时,1a b c ++=,即=-b a 最小值为12t =时,11142a b c ++≥-,所以111142a a -+≥-,解得08a <≤,即(]0,8a ∈.故答案为:(]0,822.2312π##2312π【解析】【分析】先利用三角恒等变换化简,再根据sin y x =的对称轴,即可求解.【详解】解:()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,又sin y x =的对称轴为()2k x k Z π=∈,令2()62k x k ππ+=∈Z ,得()124k x k ππ=-+∈Z ,因为02m π<<,所以当8k =时,m 的最大值为2312π.故答案为:2312π23.90,8⎡⎤⎢⎥⎣⎦【解析】【分析】由题知函数()f x 为偶函数,且当0x ≥时,函数()f x 为周期函数,最小正周期为π,进而将问题转化为求[]0,x π∈时函数的值域,再结合二倍角公式和二次函数性质求解即可.【详解】解:因为()()()sin cos 2sin cos 2sin cos 2f x x x x x x x f x -=-+-=-+=+=,所以函数()f x 为偶函数,所以当0x ≥时,()sin cos 2f x x x =+,()()()()sin cos 2sin cos 2f x x x x x f x πππ+=+++=+=⎡⎤⎣⎦,所以当0x ≥时,()f x 为周期函数,周期为π,所以当[]0,x π∈时,()2219sin cos 22sin sin 12sin 48f x x x x x x ⎛⎫=+=-++=--+ ⎪⎝⎭,因为[]sin 0,1∈x ,所以当1sin 4x =时,()f x 取得最大值98;当sin 1x =时,()f x 取得最小值0,所以当0x ≥时,()90,8f x ⎡⎤∈⎢⎥⎣⎦,所以根据偶函数性质,函数()f x 的值域为90,8⎡⎤⎢⎥⎣⎦.故答案为:90,8⎡⎤⎢⎥⎣⎦24.(),0,,222πππππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ 【解析】【分析】分别在[],2x ππ∈-时解不等式组02sin 0x x π⎧-<⎪⎨⎪>⎩、02sin 0x x π⎧->⎪⎨⎪<⎩,综合可得出原不等式的解集.【详解】因为[],2x ππ∈-,若02x π-<,可得22x ππ-<<,由sin 0x >可得0πx <<,则不等式组02sin 0x x π⎧-<⎪⎨⎪>⎩在[],2x ππ∈-时的解为02x π<<;若02x π->,可得2x ππ-≤<-或22x ππ<<,由sin 0x <可得0x π-<<或2x ππ<<,则不等式组02sin 0x x π⎧->⎪⎨⎪<⎩在[],2x ππ∈-时的解为2x ππ-<<-或2x ππ<<.综上所述,不等式sin 02x x π⎛⎫-⋅< ⎪⎝⎭在[],2x ππ∈-时的解集为(),0,,222πππππ⎛⎫⎛⎫-- ⎪ ⎝⎭⎝⎭ .故答案为:(),0,,222πππππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ .25.324,23π⎛⎤-∞- ⎥⎝⎦【解析】【分析】①代入,由函数的定义计算可得答案;②分别计算0x =时,0,2x π⎛⎫∈ ⎪⎝⎭时,2x π=时,,2x π⎛⎤∈π ⎥⎝⎦时,3,2x ππ⎛⎫∈ ⎪⎝⎭时,3,22x ππ⎡⎫∈⎪⎢⎣⎭时,2x π=时,()f x x -的值,建立不等式,求解即可.【详解】解:①∵()[][]sin cos 32x x f x =+,∴551sin cos 016625332323262f πππ⎡⎡⎤⎡⎤⎡⎤⎢⎢⎥⎢⎥⎢-⎢⎣⎦⎣⎦⎣⎦⎣⎦⎛⎫=+=+=+=⎪⎝⎭.②当0x =时,()013203f x x -=+-=;当0,2x π⎛⎫∈ ⎪⎝⎭时,()003222,22f x x x x π⎛⎫-=+-=-∈- ⎪⎝⎭;当2x π=时,()1032422f x x ππ-=+-=-;当,2x π⎛⎤∈π ⎥⎝⎦时,()0133332,2222f x x x x ππ-⎡⎫-=+-=-∈--⎪⎢⎣⎭;当3,2x ππ⎛⎫∈ ⎪⎝⎭时,()11553532,6626f x x x x ππ--⎛⎫-=+-=-∈-- ⎪⎝⎭;当3,22x ππ⎡⎫∈⎪⎢⎣⎭时,()104443322,3332f x x x x ππ-⎛⎤-=+-=-∈-- ⎥⎝⎦;当2x π=时,()0132232f x x ππ-=+-=-.又()f x x m >+对任意[]0,2x π∈都成立,即()m f x x <-恒成立,∴()423f x x π->-,∴423m π≤-,∴实数m 的取值范围是4,23π⎛⎤-∞- ⎥⎝⎦.故答案为:32;4,23π⎛⎤-∞- ⎥⎝⎦.【点睛】关键点睛:本题考查函数的新定义,关键在于理解函数的定义,分段求值,建立不等式求解.26.(0,1)(45,72)【解析】【分析】利用数形结合可得实数m 的取值范围,然后利用对数函数的性质可得121=x x ,再利用正弦函数的对称性及二次函数的性质即求.【详解】作出函数()y f x =与函数y m =的图象,则可知实数m 的取值范围为(0,1),由题可知,12340136,1215x x x x <<<<<<<<,∵3132log log x x =,∴3133211log log log x x x -==,即121=x x ,又3436,1215x x <<<<,3492x x +=,∴()2123433331818x x x x x x x x =-=-,又函数23318y x x =-在()3,6上单调递增,∴()2331845,72x x -∈,即()123445,72x x x x ∈.故答案为:(0,1);()45,72.【点睛】关键点点睛;本题的关键是数形结合,结合对数函数的性质及正弦函数的性质可得()12343318x x x x x x =-,再利用二次函数的性质即解.27.π542⎤⎥⎦【解析】【分析】先根据函数周期性的定义说明π是函数()f x =说明函数的单调性,从而证明π是最小正周期;根据函数()f x =的单调性可求得最大值,再比较,3x ππ⎡⎤∈⎢⎥⎣⎦时端点处的函数值大小,即可求得答案.【详解】因为(+)()f x f x π==,故x π=为()f x 的一个周期,而当()0,x π∈时,()f x ,由题意可知3322cos sin 22()cos sin 22x x x x f x ⎛⎫⎡⎤⎪⎛⎫⎛⎫⎥'==- ⎪ ⎪⎥⎝⎭⎝⎭⎦,令()0f x '=,得cossin 22x x =,故24x π=,2x π=,因为当0,2x π⎛⎫∈ ⎪⎝⎭时,()0f x '>,当,2x ππ⎛⎫∈ ⎪⎝⎭时,()0f x '<,故()f x 在0,2π⎛⎫ ⎪⎝⎭上单调递增,在,2ππ⎛⎫⎪⎝⎭上单调递减,故()f x 的最小正周期为π,且()f x 在,3ππ⎡⎤⎢⎥⎣⎦上的最大值为5422f π⎛⎫= ⎪⎝⎭,而()f π=,14313f π⎛⎫=+ ⎪⎝⎭,故2()3f f ππ⎛⎫>> ⎪⎝⎭,故当,3x ππ⎛⎫∈ ⎪⎝⎭时,函数()f x的值域为542⎤⎥⎦,故答案为:π;542⎤⎥⎦28.2-143π【解析】(1)化简函数得()26f x x π⎛⎫=-- ⎪⎝⎭,可得()max 2f x =-;(2)令6t x π=-,将函数()f x 的零点问题转化为sin y t =与33y =的交点求解,作出两个函数的图象,根据图象可求解.【详解】(1)()3sin 2f x x x =-- ,()26f x x π⎛⎫∴=-- ⎪⎝⎭,又[]0,2x π∈,11,666x πππ⎡⎤∴-∈-⎢⎣⎦,()max 2f x ∴=;(2)令6t x π=-,则()0f x =即可转化为311sin ,366t t ππ⎡⎤=∈-⎢⎣⎦,作出sin y t =与3y ,由图知:交点关于直线322,x x ππ==对称,设函数()f x 的零点为1x ,2x ,3x ,4x 则有1266x x πππ-+-=,34366x x πππ-+-=1234143x x x x π∴+++=.故答案为:(1).2(2).143π【点睛】本题主要考查了三角函数的图象与性质,函数零点问题的求解,考查了数形结合的数学思想,转化与化归的思想.。
含绝对值的函数专题.docx

已知函数f (x) =X2 - 2ax+5 (a>l),若f (x)在区间(-8, 2]上是减函数,R对任意的X:, x,e [1,a+1],总有|f (x,) - f (xj |W4,求a的取值范围.【试题來源】辽宁省大连二十四中、四十八中2015-2016学年高一上学期期中联考数学试题【答案解析】【考点】二次函数的性质.【专题】综合题;函数思想;综合法;函数的性质及应用.【分析】由条件利用二次函数的性质可得a^2.故只要f(l)・f(a) W4即可,即(a -1) W4,求得a的范围.【解答】解:由于函数f (x)二X」2ax+5的图象的对称轴为x=a,函数f (x)二x」2ax+5 在区间(・8, 2]上单调递减,・・・aN2.故在区间G上,1离对称轴x=a最远,故要使对任意的X;, X G ,都有If(X,) - f(X,) |W4,只要f (1)・f (a) W4即可,即(a・l) W4,求得・1再结合a^2,可得2WaW3,故a的取值范围为:.【点评】本题主要二次函数的性质,绝对值不等式的解法,体现了转化的数学思想,属于基础题._1 _1已知函数f (x) =|x+x| - |x - x|.I丄(1)指出f (x)二|x+x| - |x- x|的基本性质(两条即可,结论不要求证明),并作出函数f(X)的图象;(2)关于x的方程P (x) +m|f (x) |+n二0 (m, n^R)恰有6个不同的实数解,求m 的取值范围.▲ X421 1 1 1 1 1 1V 1 1 1 ■-50-2-4---------------------------- k. 5【试题来源】辽宁省大连二卜四中、四卜八中2015-2016^年离一上学期期中联考数学试题【答案解析】【考点】分段函数的应用.【专题】计算题;作图题;数形结合;函数的性质及应用.-2x, -l<x<02x,【分析】(1)化简f⑴4?x>1,判断函数的性质,再作其图象即可;(2)结合右图可知方程xH-mx+n=O有两个不同的根x;, x.,且x二2, x e (0, 2);从而可得故xFnx+n二(x - 2) (x - x,),从而解得.U X<-1X-2x, - l<x<02x,2, Ql【解答】解:(1)化简可得f (x)二I"故f (x)是偶函数,且最大值为2;作其图象如右图,(2) I关于x的方程f,(x) +m|f (x) |+n=0 (m, n^R)恰有6个不同的实数解, ・••结合右图可知,方程x;+mx+n二0有两个不同的根x:, x“且x尸2, x£ (0, 2);故x;+mx+n= (x - 2) (x - xj=x1 - (2+x?) x+2x..,故nF- (2+xJ ,故・4VmV・2.【点评】本题考查了分段函数的应用及绝对值函数的应用,同时考查了数形结合的思想应用设偶函数f(X)满足f (x)觇・4 (x$0),若f (x-2) >0,则X的取值范围是( ) A.(-8,0) B. (0,4) C. (4,+g) D.(- 8, 0) U (4, +8)[试题来源]辽宁省大连二十四中、四十八中2015 2016学年商一上学期期中联考数学试题【答案解析】D【考点】指数型复合函数的性质及应用.【专题】整体思想;数形结合法;函数的性质及应用.【分析】先利用偶函数的图象关于y轴对称得出f (x) >0的解集,再运用整体思想求f (x・2) >0的解集.【解答】解:根据题意,当x$0时.f (x)二2-4,令f (x)二2、・4>0,解得x>2,又Tf(X)是定义在R上的偶函数f (x),其图象关于y轴对称,・••不等式f (x) >0在xeR的解集为(・8,・2) U (2, +8),因此,不等式f (x-2) >0等价为:x・2E (・8,・2) U (2, +8), 解得xW ( - °°, 0) U (4, +°°),故选D.【点评】本题主要考查了指数世复合函数的图象和性质,涉及函数的奇偶性和不等式的解法,属于屮档题.设f (x)是定义在R上的偶函数,且f (2+x) =f (2-x),当xw时,f (x) = (V2)* - 1,若关于x的方程f (x) - log, (x+2) =0 (a>0且aHl)在区间(-2, 6)内恰有4个不等的实数根,则实数a的取值范围是( )_1A. (4, 1)B. (1, 4)C. (1, 8) 1). (8, + oo )[试题來源]山西省太原市2016届高三上学期期中数学试题【答案解析】D【考点】根的存在性及根的个数判断;抽象函数及其应用.【专题】转化思想;数形结合法;函数的性质及应用.【分析】由题意,讨论0Va< 1时,当0Va< 1时,-2<xV0时,y二f (x)和y=log, (x+2)只有一个交点;故a>l.关于x的方程f (x) - log. (x+2) =0 (a>l),在区间(・2, 6)内恰有四个不同实根可化为函数f (x)与函数y二log”(x+2)有四个不同的交点,作出函数f (x)与函数y=log. (x+2)的图象,由图象解出答案.【解答】解:由f(x)是定义在R上的偶函数,且f (2+x) =f (2 - x),即为f (x+4)二f (・ x) =f (x),则f (x)为周期为4的函数.当xW 时,f (x) = (V2) * - 1,可得xG 时,f (x) =f ( -x)=(迈)一1,又Tf (x)二log”(x+2) (a>0 且a#l),当OVaVl 时,-2<xVO 时,y二f (x)和y=log. (x+2)只有一个交点; 在0<x<6 时,f (x) >0, log, (x+2) <0,则没有交点,故a>l,作出它们在区间(・2, 6)内图象如右图:当x二6 时,f (6)二f (2) =1, log. (6+2)二1,解得沪8, 由于・2<x<6,即有a>8,y=f (x)和y=log. (x+2)有四个交点.【点评】本题考查了方程的根与函数的冬点Z间的关系,同时考查了数形结合的数学思想应用,属于屮档题.偶函数y=f (x)的图象关于直线x=2对称,f (3) =3,贝'J f ( - 1) = ____________ .[试题來源]陕两省西安音乐7浣阳屮岛M高7 L;;:期期屮数7试观【答案解析】3【考点】函数奇偶性的性质.【专题】函数的性质及应用.【分析】根据函数奇偶性和对称性的性质,得到f (x+4) =f (x),即可得到结论.【解答】解:法1:因为偶函数尸f (x)的图象关于直线x=2対称,所以f (2+x) =f (2 - x) =f (x-2),即f (x+4) =f (x),贝lj f (・ 1) =f (・ 1+4) =f (3) =3,法2:因为函数y二f (x)的图象关于直线x=2对称,所以f (1) =f (3) =3,因为f (x)是偶函数,所以f ( - 1)二f (1)二3,故答案为:3.【点评】本题主要考查函数值的计算,利用函数奇偶性和对称性的性质得到周期性f(x+4) =f (x)是解决本题的关键,比较基础函数f (x)二lgx的单调递减区间是 ______________ .[试题来源]陕西省西安音乐学院附中商三2016届高三上学期期中数学试题【答案解析】(-0)【考点】复合函数的单调性.【专题】函数的性质及应用.【分析】先将f(X)化简,注意到XH0,即f(X)=21g|x|,再讨论其单调性,从而确定其减区间;也可以函数看成山I尸复介而成,再分别讨论内层函数和外层函数的单调性,根据“同増异减”再來判断.【解答】解:方法一:y二lgx=21g|x|,・••当x>0时,f (x) =21gx在(0, +8)上是增函数;当x<0时,f (x) =21g ( - x)在(-8, 0)上是减函数.・•・函数f (x)二lgx啲单调递减区间是(-8, 0). 故答案为:(・8, 0)・方法二:原函数是由I尸复合而成,Tt二疋在(・8, 0)上是减函数,在(0, +8)为增函数;乂y=lgt在其定义域上为增函数,.*.f (x) =lgx?在(・g, 0)上是减函数,在(0, +°°)为增函数,・•・函数f (x) =lgx啲单调递减区间是(・8, 0)•故答案为:(■ 8, 0).【点评】本题是易错题,学生在方法一中,化简时容易将y=lgx-21g|x|屮的绝对值丢掉,方法二对复合函数的结构分析也是最常用的方法,此外,木题还可以利用数形结合的方式,即画出y=21g|x|的图象,得到函数的递减区间.1 V2已知幕函数尸f(X)的图象过点(2 叵),则logf (2)的值为()_1 _1A.刁B. - 刁C. 2D. - 2[试题來源]陕西省西安音乐学院附中高三2016届高三上学期期中数学试题【答案解析】A【考点】幕函数图象及其与指数的关系;对数的运算性质;函数的零点.【专题】函数的性质及应用.【分析】先利用待定系数法将点的朋标代入解析式求出函数解析式,再将x用2代替求出函数值.1 V2【解答】解:由设f(X)二x”,图象过点(2 T),丄返丄:.(2) -= 2_,解得a=2,1 1Alog;f (2) =log;2 二4.故选A.【点评】本题考查利用待定系数法求函数解析式、知函数解析式求函数值.已知f (x)是定义在R上的奇函数,且当时,购C,则的值为()1 1A. -3B. 3C.彳1). 3【试题來源】河北定州中学2016届高三上学期月考一数学(文理)试题【答案解析】B:因为h"时,购",所以工“时,只-©=-/厲=1*,即/»=-尸,所 /0"«4勿=/^勿"T 1*1=-£以3,故选B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学函数专题训练 含绝对值的函数一、选择题 1.函数xxx x x x y tan tan cos cos sin sin ++=的值域为( ) A .{}3,1 B.{}3,1- C.{}3,1-- D.{}3,1- 【答案】B【解析】当sin 0,cos 0x x >>时3y =,sin 0,cos 0x x ><时1y =-,sin 0,cos 0x x <>时1y =-,sin 0,cos 0x x <<时3y =,∴值域为{}3,1-2.函数()ln 11x f x x-=-的图象大致为 ( )A .B .C .D .【答案】D【解析】由于()ln 3022f =>,排除C 选项,()ln 1220f =->,排除B 选项,11221ln20f ⎛⎫=< ⎪⎝⎭,不选A,故选D.3.设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,设)1()1()(-+-=x g x f x h ,则下列结论中正确的是( )A .)(x h 关于)0,1(对称B .)(x h 关于)0,1-(对称C .)(x h 关于1=x 对称D .)(x h 关于1-=x 对称 【答案】C【解析】因为函数()f x 是奇函数,所以()f x 是偶函数,即()f x 与()g x 均为偶函数,其图象均关于y 对称,所以(1)f x -与(1)g x -的图象都关于直线1x =对称,即()(1)(1)h x f x g x =-+-的图象关于直线1x =对称,故选C .4.已知()()211f x ax x a x =+--≤≤且1a ≤,则()f x 的最大值为( )A .54B .34C .3D .1【答案】A【解析】由题意得:()()222111f x a x x a x x x x =-+≤-+≤-+11x -≤≤ 22221511124x x x x x x x ⎛⎫∴-+=-+=-++=--+ ⎪⎝⎭∴当12x =,即12x =±时,()2max514x x -+=即:()54f x ≤,即()f x 的最大值为54,故选A .5.若函数()111101x x f x x x ⎧+-≠⎪=-⎨⎪=⎩,,,关于x 的方程2() ()0f x b f x c ++=有3个不同的实数根,则( ) A .b <﹣2且c >0 B .b >﹣2且c <0 C .b =﹣2且c =0 D .b >﹣2且c =0【答案】C【解析】令t =f (x ),则t 2+bt +c =0,设关于t 的方程有两根为t =t 1,t =t 2,关于x 的方程2() ()0f x b f x c ++=有3个不同的实数根等价于函数t =f (x )的图象与直线t =t 1,t =t 2的交点个数为3个,作出()f x 的简图如下:由函数t =f (x )的图象与直线t =t 1,t =t 2的位置关系可得: t 1=2,t 2=0,由韦达定理可得:1212022020b t t c t t -=+=+=⎧⎨=⋅=⨯=⎩,即b =﹣2,c =0,故选C . 6.已知函数()ln(1)f x x =-,满足()(4)f a f a >-,则实数a 的取值范围是( ) A .(1,2) B .(2,3)C .(1,3)D .(2,4)【答案】A【解析】函数()ln(1)f x x =-的定义域为()1,+∞,由()(4)f a f a >-可得:ln(1)ln(41)ln(3)a a a ->--=-,两边平方:[][][][]22ln(1)ln(3)ln(1)ln(3)ln(1)ln(3)0a a a a a a ->-⇔----+->则ln(1)ln(3)0ln(1)ln(3)01030a a a a a a --->⎧⎪-+->⎪⎨->⎪⎪->⎩(1)或ln(1)ln(3)0ln(1)ln(3)01030a a a a a a ---<⎧⎪-+-<⎪⎨->⎪⎪->⎩(2)解(1)得:a 无解 ,解(2)得:12a <<,所以实数a 的取值范围是(1,2),故选A.7.已知函数)0(|4|||)(>---=a a x a x x f ,若对R ∈∀x ,都有)(1)2(x f x f ≤-,则实数a 的最大值为( ) A .81 B .41 C .21D .1【答案】B【解析】(2)1()f x f x -≤,即为(2)()1f x f x -≤,即22441x a x a x a x a -----+-≤,设()2244g x x a x a x a x a=-----+-,则0,242,2 ()22,282,240,4axax a x ag x x a a x aa x a x ax a⎧≤⎪⎪⎪-<≤⎪⎪=-<≤⎨⎪⎪-<≤⎪⎪>⎪⎩,由题意,当2ax a<≤时,1()42212g x x a a a=-≤≤⇒≤,当2a x a<≤时,1()22212g x x a a a=-≤≤⇒≤,当24a x a<≤时,1()22414g x x a a a=-<≤⇒≤,所以14a≤,即a的最大值为14,选B.8.若函数()221f x x x ax=-+--没有零点,则实数a的取值范围是A.332a-≤<B.31a-≤<C.332a a≥<-或D.13a a≥<-或【答案】A【解析】因为函数()221f x x x ax=-+--没有零点,所以方程221x x ax-+-=无实根,即函数()221g x x x=-+-与()h x ax=的图像无交点,如图所示,则()h x的斜率a应满足332a-≤<,故选A.9.定义一种运算⎩⎨⎧>≤=⊗babbaaba,,,令()()t xxxxf-⊗-+=224(t为常数),且[]3,3-∈x,则使函数()x f最大值为4的t值是()A.2-或6B.4或6C.2-或4D.4-或4【答案】C.【解析】y=4+2x﹣x2在x∈[﹣3,3]上的最大值为4,所以由4+2x﹣x2=4,解得x=2或x=0.所以要使函数f(x)最大值为4,则根据定义可知,当t<1时,即x=2时,|2﹣t|=4,此时解得t=﹣2.当t>1时,即x=0时,|0﹣t|=4,此时解得t=4.故t=﹣2或4.10.已知函数()||––10||f x mx x m =>(), f (x )=|mx |–|x –1|(m >0),若关于x 的不等式()0f x <的解集中的整数恰有3个,则实数m 的取值范围为( ).A.0<m ≤1 B .34m ≤<23C.1<m <23D.23≤m <2【答案】B【解析】不等式()0f x <的解集中的整数恰有3个,即|||–|1mx x <的解集中的整数恰有3个. |||–|1mx x <可化为22()10,()mx x --<即([m (1)1]10][1,)m x x +-⋅-+<由于不等式解集中整数恰有三个,所以10,1,m m ->>不等式的解为11111x m m -<<<-+,从而解集中的三个整数为2,1,0--,132,1m --≤<--即1231m <≤-,2233m n m -<≤-,所以34m ≤<23.11.已知函数21,0()log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<,则3122341()x x x x x ++的取值范围是( ) A .(1,)-+∞ B .(]1,1- C .(,1)-∞ D .[)1,1- 【答案】B【解析】先画出函数21,0()log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩的图象,方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<,由0x ≤时,()1f x x =+,则横坐标为1x 与2x 两点的中点横坐标为1x =-,即:122x x +=-,当0x >时,由于2log y x =在(0,1)上是减函数,在(1,)+∞上是增函数,又因为34x x <,4232log log x x =,则4310x x <<<,有1log log 434232=⇒=-x x x x ,又因为方程ax f =)(有四个不同的解,所以1log 32≤-x ,则213≥x ,则3122341()x x x x x ++=3312x x +-,)121(3<≤x ,设t t t g 12)(+-=,(121<≤t ),由于012)(2<--='tt g ,则)(t g 在)1,21[上是减函数,则1)(1≤<-t g .12.已知函数()121f x x =--,[0,1]x ∈.定义:1()()f x f x =,21()(())f x f f x =,……,1()(())n n f x f f x -=,2,3,4,n =满足()n f x x =的点[0,1]x ∈称为()f x 的n 阶不动点.则()f x 的n 阶不动点的个数是( )A.2n 个B.22n 个 C.2(21)n-个 D.2n 个【答案】D.【解析】函数12, 02()121122,12x x f x x x x ⎧≤≤⎪⎪=--=⎨⎪-<≤⎪⎩,当1[0,]2x ∈时,1()20f x x x x ==⇒=,当1(,1]2x ∈时,12()223f x x x x =-=⇒=,∴1()f x 的1阶不动点的个数为2,当1[0,]4x ∈,1()2f x x =,2()40f x x x x ==⇒=,当11(,]42x ∈,1()2f x x =,22()245f x x x x =-=⇒=,当13(,]24x ∈,1()22f x x =-,22()423f x x x x =-=⇒=,当3(,1]4x ∈,1()22f x x =-,24()445f x x x x =-=⇒=,∴2()f x 的2阶不动点的个数为22,以此类推,()f x 的n 阶不动点的个数是2n个.二、填空题 13.方程18|cos()||log |2x x π+=的解的个数为__________.(用数值作答)【答案】12【解析】由题意得求方程18sin log x x = 的解的个数,因为sin y x = 周期为π,而5π186π<<,又(0,1)x ∈时sin y x =与18log y x =-有一个交点,(1,π)x ∈时sin y x =与18log y x =有一个交点, (π,π+π),(1,2,3,4,5)x k k k ∈=时sin y x =与18log y x =有两个交点,因此共有2612⨯=个.14. 已知,函数在区间上的最大值是2,则__________.【答案】3或 【解析】当时,= 函数,对称轴为,观察函数的图像可知函数的最大值是.令,经检验,a=3满足题意.令,经检验a=5或a=1都不满足题意. 令,经检验不满足题意.当时,, 函数,对称轴为,观察函数的图像得函数的最大值是.当时,, 函数,对称轴为,观察函数的图像可知函数的最大值是.令, 令,所以.综上所述,故填3或.15.a 为实数,函数2()||f x x ax =-在区间[01],上的最大值记为()g a . 当a = 时,()g a 的值最小. 【答案】322-【解析】()()2f x x ax x x a =-=-.①当0a <时,函数()f x 的图像如图所示.函数()f x 在区间[]0,1上单调递增,()()()max 11f x g a f a ===-.aO yx②当0a =时,2()f x x =,()f x 在区间[]0,1上的最大值为()()11f g a a ==-.③当0a >时,函数()f x 的图像如图所示.xyO a(i )若12aa <<,即12a <<,()()2max 4a f a g a ==;(ii )若12a,即2a,()max 1f a a =-;(iii )若01a <<,()()()22max,22114max ,141,0221a a a f a a a a ⎧-<⎧⎫⎪=-=⎨⎬⎨⎩⎭⎪-<<-⎩. 综上所述,()()()212212212412a a ag a a a a ⎧-<-⎪⎪=-<⎨⎪⎪-⎩,,,,因此()()min 221322g a g ⎡⎤=-=-⎣⎦.16. 已知函数有六个不同零点,且所有零点之和为3,则的取值范围为__________. 【答案】【解析】根据题意,有,于是函数关于对称,结合所有的零点的平均数为,可得,此时问题转化为函数,在上与直线有个公共点,此时,当时,函数的导函数,于是函数单调递增,且取值范围是,当时,函数的导函数,考虑到是上的单调递增函数,且,于是在上有唯一零点,记为,进而函数在上单调递减,在上单调递增,在处取得极小值,如图:接下来问题的关键是判断与的大小关系,注意到,,函数,在上与直线有个公共点,的取值范围是,故答案为.。
