金属电子论思考题
第5~9章 思考题答案

第五章思考题1. 在电极界面附近的液层中,是否总是存在着三种传质方式?为什么?每一种传质方式的传质速度如何表示?答:电极界面附近的液层通常是指扩散层,可以同时存在着三种传质方式(电迁移、对流和扩散),但当溶液中含有大量局外电解质时,反应离子的迁移数很小,电迁移传质作用可以忽略不计,而且根据流体力学,电极界面附近液层的对流速度非常小,因此电极界面附近液层主要传质方式是扩散。
三种传质方式的传质速度可用各自的电流密度J来表示。
2. 在什么条件下才能实现稳态扩散过程?实际稳态扩散过程的规律与理想稳态扩散过程有什么区别?答:当电极反应所消耗的反应粒子数和扩散补充来的反应粒子数相等,就可以达到一种动态平衡状态,即扩散速度与电极反应速度相平衡。
这时反应粒子在扩散层中各点的浓度分布不再随时间变化而变化,而仅仅是距离的函数;扩散层的厚度不再变化;离子的浓度梯度是一个常数,这就是稳态扩散过程。
理想条件下,人为地把扩散区和对流区分开了,因此理想稳态扩散过程中,扩散层有确定的厚度;而实际情况下,扩散区与对流区是相互重叠、没有明显界限的,只能根据一定的理论来近似求得扩散层的厚度。
二者在扩散层内都是以扩散作用为主。
因此二者具有相似的扩散动力学规律,但推导实际情况下的稳态扩散动力学公式需要借用理想稳态扩散的动力学公式。
3. 旋转圆盘电极和旋转圆环圆盘电极有什么优点?它们在电化学测量中有什么重要用途?答:旋转圆盘电极和旋转圆环圆盘电极上各点的扩散层厚度是均匀的,因此电极表面各处的电流密度分布均匀。
这克服了平面电极表面受对流作用影响不均匀的缺点。
它们可以测量并分析极化曲线,研究反应中间产物的组成及其电极过程动力学规律。
4. 试比较扩散层、分散层和边界层的区别。
扩散层中有没有剩余电荷?答:根据扩散传质理论,紧靠电极表面附近,有一薄层,此层内存在反应粒子的浓度梯度,这层叫做扩散层;电极表面的荷电粒子由于热运动而倾向于均匀分布,从而使剩余电荷不可能完全紧贴着电极表面分布,而具有一定的分散性,形成所谓分散层;靠近电极表面附近的液流层叫做边界层,越接近电极表面,其液流流速越小。
(完整版)第四章金属自由电子理论

第四章 金属自由电子理论1.金属自由电子论作了哪些假设?得到了哪些结果?解:金属自由论假设金属中的价电子在一个平均势场中彼此独立,如同理想气体中的粒子一样是“自由”的,每个电子的运动由薛定谔方程来描述;电子满足泡利不相容原理,因此,电子不服从经典统计而服从量子的费米-狄拉克统计。
根据这个理论,不仅导出了魏德曼-佛兰兹定律,而且而得出电子气对晶体比热容的贡献是很小的。
2.金属自由电子论在k 空间的等能面和费米面是何形状?费米能量与哪些因素有关?解:金属自由电子论在k 空间的等能面和费米面都是球形。
费米能量与电子密度和温度有关。
3.在低温度下电子比热容比经典理论给出的结果小得多,为什么?解:因为在低温时,大多数电子的能量远低于费米能,由于受泡利原理的限制基本上不能参与热激发,而只有在费米面附近的电子才能被激发从而对比热容有贡献。
4.驰豫时间的物理意义是什么?它与哪些因素有关?解:驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间,它的引入是用来描写晶格对电子漂移运动的阻碍能力的。
驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。
5.当2块金属接触时,为什么会产生接触电势差?解:由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同,所以这2块金属接触时,会产生接触电势差。
6.已知一维金属晶体共含有N 个电子,晶体的长度为L ,设0=T K 。
试求: (1)电子的状态密度; (2)电子的费米能级; (3)晶体电子的平均能量。
解:(1)该一维金属晶体的电子状态密度为:dEdkdk dZ dE dZ E ⋅==)(ρ …………………………(1) 考虑在k 空间中,在半径为k 和dk k +的两线段之间所含的状态数为:dk Ldk dZ π=∆=k 2 …………………………(2) 又由于 mk E 222η=所以 mkdk dE 2η= …………………………(3) 将(2)和(3)式代入(1)式,并考虑到每个状态可容纳2个自旋相反的电子,得该一维金属晶体中自由电子的状态密度为:EmL E 22)(ηπρ= (4)(2)由于电子是费米子,服从费米—狄拉克统计,即在平衡时,能量为E 的能级被电子占据的几率为:11)(+=-TK E E B F eE f (5)于是,系统中的电子总数可表示为:⎰∞=)()(dE E E f N ρ (6)由于0=T K ,所以当0F E E >,有0)(=E f ,而当0F E E ≤,有1)(=E f ,故(6)式可简化为:⎰=)(FE dE E N ρ=⎰0022FE dE E m L ηπ=240FmE L ηπ由此可得: 222208mL N E Fηπ= (7)(3)在0=T K 时,晶体电子的平均能量为: ⎰∞=0)()(1dEE E Ef N E ρ=dE EmL E N FE 2210⎰⋅ηπ=230)(232F E m N L ηπ=022223124F E mL N =ηπ 7.限制在边长为L 的正方形中的N 个自由电子,电子的能量为)(2),(222y x y x k k mk k E +=η。
材料物理导论-思考题4

第三章 材料的电学1.说明量子自由导电理论与经典导电理论的异同。
经典导电理论:金属是由原子点阵组成的,价电子是完全自由的,可以在整个金属中自由运动自由电子的运动遵守经典力学的运动规律,遵守气体分子运动论。
这些电子在一般情况下可沿所有方向运动。
在电场作用下自由电子将沿电场的反方向运动,从而在金属中产生电流。
电子与原子的碰撞妨碍电子的继续加速,形成电阻。
量子自由导电理论:金属离子所形成的势场各处都是均匀的,价电子是共有化的,它们不束缚于某个原子上,可以在整个金属内自由地运动,电子之间没有相互作用。
电子运动服从量子力学原理 。
2. 一块n 型硅半导体,其施主浓度N D =1015/cm 3,本征费米能级Ei 在禁带正中,费米能级E F 在Ei 之上0.29eV 处,设施主电离能∆E D =0.05eV ,试计算在T =300K 时,施主能级上的电子浓度对于硅半导,其禁带E=E C -E V =1.12ev又由题可知:E F -Ei=0.29ev ,∆E D = E C -E D = 0.05eV所以 E D -E F =0.5E-∆E D -(E F -Ei )=0.22ev将 N D =1015/cm 3,E D -E F = 0.22ev ,T=300K ,k=1.38 x 10-23带入下式因此施主能级上的电子浓度n D =4.06 x 1011/cm 33.为什么金属的电阻随温度的上升而增加,半导体却降低?半导体是靠载流子(空穴或电子)导电的,温度升高,载流子增多,导电性增强;金属晶体里边,温度升高原子核振动加剧,碰撞电子使之减速的概率增加,电阻率上升4.在实际工程中往往需要金属既有良好的导电性又有高的强度,假如足够高的强度既可以通过冷加工获得,也可以由固溶强化得到,从导电率的要求看,你建议采用哪种强化方法?为什么?采用冷加工的方法,固溶强化会使金属的电导率大大降低,主要原因是溶质原子的溶入引起溶剂点阵的畸变,量子力学可以证明,当电子波在绝对零度下通过一个完整的晶体点阵()11exp()2DD D D D F N n N fE E E kT==-+时,将不受到散射而无阻碍地传播,这时电阻率为0,而电导率应为无穷大。
材料物理导论-思考题4

材料物理导论-思考题4第三章材料的电学1.说明量子自由导电理论与经典导电理论的异同。
经典导电理论:金属是由原子点阵组成的,价电子是完全自由的,可以在整个金属中自由运动自由电子的运动遵守经典力学的运动规律,遵守气体分子运动论。
这些电子在一般情况下可沿所有方向运动。
在电场作用下自由电子将沿电场的反方向运动,从而在金属中产生电流。
电子与原子的碰撞妨碍电子的继续加速,形成电阻。
量子自由导电理论:金属离子所形成的势场各处都是均匀的,价电子是共有化的,它们不束缚于某个原子上,可以在整个金属内自由地运动,电子之间没有相互作用。
电子运动服从量子力学原理。
2. 一块n 型硅半导体,其施主浓度N D =1015/cm 3,本征费米能级Ei 在禁带正中,费米能级E F 在Ei 之上0.29eV 处,设施主电离能?E D =0.05eV ,试计算在T =300K 时,施主能级上的电子浓度对于硅半导,其禁带E=E C -E V =1.12ev又由题可知:E F -Ei=0.29ev ,?E D = E C -E D = 0.05eV所以 E D -E F =0.5E-?E D -(E F -Ei )=0.22ev将 N D =1015/cm 3,E D -E F = 0.22ev ,T=300K ,k=1.38 x 10-23带入下式因此施主能级上的电子浓度n D =4.06 x 1011/cm 33.为什么金属的电阻随温度的上升而增加,半导体却降低?半导体是靠载流子(空穴或电子)导电的,温度升高,载流子增多,导电性增强;金属晶体里边,温度升高原子核振动加剧,碰撞电子使之减速的概率增加,电阻率上升4.在实际工程中往往需要金属既有良好的导电性又有高的强度,假如足够高的强度既可以通过冷加工获得,也可以由固溶强化得到,从导电率的要求看,你建议采用哪种强化方法?为什么?采用冷加工的方法,固溶强化会使金属的电导率大大降低,主要原因是溶质原子的溶入引起溶剂点阵的畸变,量子力学可以证明,当电子波在绝对零度下通过一个完整的晶体点阵()11exp()2DD D D D F N n N fE E E kT==-+时,将不受到散射而无阻碍地传播,这时电阻率为0,而电导率应为无穷大。
电子行业金属电子论

电子行业金属电子论引言电子行业是现代工业的重要组成部分,而金属电子则是电子行业中的一个关键领域。
金属电子主要研究和应用于电子器件中的金属材料和技术。
随着科技的进步,金属电子在电子行业中的地位变得越来越重要。
本文将介绍金属电子在电子行业中的应用和发展,并探讨其未来的发展趋势。
金属电子的应用1. 电子元件金属电子在电子元件中起着重要的作用。
例如,金属电子常被用于制造电路板上的导线和焊接点。
金属电子的导电性能优异,可以提供稳定的电流传输。
此外,金属电子也常用于制造电子器件的连接件,如插座和插头。
2. 电子器件封装金属电子还用于电子器件的封装。
电子器件通常需要在外部环境中工作,而金属电子能提供对电子器件的保护和支撑。
金属电子封装提供了对电子器件的物理保护,并且可以帮助散热,保持器件的稳定性和可靠性。
3. 金属电子导体金属电子也常被用作电子设备中的导体。
金属电子的导电性能好,能够快速传输电流和信号。
在电子行业中,金属导体被广泛用于电路板、导线、电缆等电子设备中,保证了电子设备的正常运作。
4. 电子屏幕金属电子在电子屏幕中也发挥着重要的作用。
例如,液晶屏的背光源一般采用金属电子灯条,能够提供均匀明亮的背光效果。
此外,金属电子也用于制造电子设备的外壳和框架,提供结构支撑和保护。
金属电子的发展随着电子行业的不断发展,金属电子也面临着新的挑战和机遇。
以下是金属电子的一些发展趋势:1. 轻薄化和小型化随着消费者对便携式电子设备的需求增加,金属电子需要更加轻薄和小型化。
为了满足这些需求,金属电子材料需要更高的强度和更好的加工性能。
同时,金属电子制造技术也需要不断创新和改进,以实现更高的精度和效率。
2. 材料和工艺创新为了适应新的电子行业需求,金属电子材料和工艺也在不断创新。
例如,一些新型金属材料具有更好的导电性能和耐腐蚀性能,可以提高电子器件的性能和可靠性。
同时,新的金属电子制造工艺也在不断提高,以满足更高的工艺要求。
金属自由电子理论

金属自由电子理论文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]第四章金属自由电子理论1.金属自由电子论作了哪些假设得到了哪些结果解:金属自由论假设金属中的价电子在一个平均势场中彼此独立,如同理想气体中的粒子一样是“自由”的,每个电子的运动由薛定谔方程来描述;电子满足泡利不相容原理,因此,电子不服从经典统计而服从量子的费米-狄拉克统计。
根据这个理论,不仅导出了魏德曼-佛兰兹定律,而且而得出电子气对晶体比热容的贡献是很小的。
2.金属自由电子论在k空间的等能面和费米面是何形状费米能量与哪些因素有关解:金属自由电子论在k空间的等能面和费米面都是球形。
费米能量与电子密度和温度有关。
3.在低温度下电子比热容比经典理论给出的结果小得多,为什么解:因为在低温时,大多数电子的能量远低于费米能,由于受泡利原理的限制基本上不能参与热激发,而只有在费米面附近的电子才能被激发从而对比热容有贡献。
4.驰豫时间的物理意义是什么它与哪些因素有关解:驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间,它的引入是用来描写晶格对电子漂移运动的阻碍能力的。
驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。
5.当2块金属接触时,为什么会产生接触电势差解:由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同,所以这2块金属接触时,会产生接触电势差。
6.已知一维金属晶体共含有N 个电子,晶体的长度为L ,设0=T K 。
试求:(1)电子的状态密度; (2)电子的费米能级; (3)晶体电子的平均能量。
解:(1)该一维金属晶体的电子状态密度为:dEdkdk dZ dE dZ E ⋅==)(ρ (1)考虑在k 空间中,在半径为k 和dk k +的两线段之间所含的状态数为:dk Ldk dZ π=∆=k 2 (2)又由于 mk E 222 =所以mkdk dE 2 = …………………………(3) 将(2)和(3)式代入(1)式,并考虑到每个状态可容纳2个自旋相反的电子,得该一维金属晶体中自由电子的状态密度为:EmLE 22)(πρ= (4)(2)由于电子是费米子,服从费米—狄拉克统计,即在平衡时,能量为E 的能级被电子占据的几率为:11)(+=-TK E E B F eE f (5)于是,系统中的电子总数可表示为:⎰∞=0)()(dE E E f N ρ (6)由于0=T K ,所以当0F E E >,有0)(=E f ,而当0F E E ≤,有1)(=E f ,故(6)式可简化为:⎰=)(FE dE E N ρ=⎰0022FE dE E m L π=240FmE L π由此可得:222208mLN E Fπ= …………………………(7) (3)在0=T K 时,晶体电子的平均能量为: ⎰∞=0)()(1dEE E Ef N E ρ=dE EmL E N FE 2210⎰⋅π=230)(232F E m N L π=022223124F E mLN = π 7.限制在边长为L 的正方形中的N 个自由电子,电子的能量为)(2),(222y x y x k k mk k E += 。
固体物理(第11课)金属电子论和索末菲模型解读

V
2 3
k被限制在第一布里渊区
k
2
nx
I
2
V
ny
J
2
nz
K
L
L
L
2 a
2
Na
2 a
kz
2
Γ
a
kx
2
a
ky
2
Na
k
2
nx
I
2
ny
J
2
nz
K
L
L
L
L Na1 L Na2 L Na3
k空间 波矢空间 倒易点阵
b3 N3
b2 N2
b1 电子具有的波长 N1 k L L L 2 nx ny nz
独立电子:电子之间无相互作用 自由电子:近似于自由电子,即单电子近似。 忽略离子作用,不考虑碰撞,忽略晶格周期场。 引入了泡利不相容原理 服从费米-狄喇克统计分布 根据量子力学的波动现象,电子的波函数满足自由 电子的薛定谔方程。
平均势能为能量零点,电子处于无限深度的势阱内, 需作功才能逸出,电子的运动满足薛定谔方程。
波与晶面垂直。
➢可见金属晶体边长L是电子波长的l倍,这里采用了波恩
-卡门周期性边界条件。 ➢驻波一定要求格波在边界处为0,相比之下,波恩-卡门 周期性边界条件是一种行波,比驻波的要求更加宽松。
5.2 索末菲自由电子论
前提:1925年1月,物理学家泡利提出了不相容原理:一 切由自度等于半整数的粒子——费米子组成的系统中, 不能有两个或两个以上的粒子处于完全相同的状态。
晶格常数为a 的简立方
a
晶格常数b为2π/a
的倒易格点。
b对应面间距。
最大的 k,对应波
b V
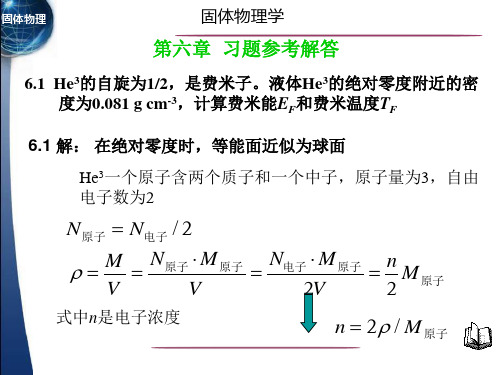
第六章金属电子论习题
电导率
q2 m*
n (EF0 )
弛豫时间
( E F0
)
m*
nq 2
平均自由程
v (EF0 )
m*v
nq 2
kF
nq2
0 K到室温之间的费密半径变化很小
9
固体物理
固体物理学
或近自由电子近似情况下
EF
EF0
1
2
12
kBT EF0
2
kF m
1.055
10 34 1.20 9.1110 31
0
10
1.39 106 m / s
固体物理
固体物理学
(4) 费密球面的横截面积
S (kF sin )2 4.52 sin 2m2
是 与 轴之间的夹角
kF
(3n
2
)
1 3
8
固体物理
固体物理学
(5) 在室温以及低温时电子的平均自由程
3
固体物理
固体物理学
N
N(
( E F0
E
)
)
4V
(
2m h2
3N / 2EF0
)3/2 E1/2
N(E)
(
EF EF0
)1/
2
N
(
EF0
)
TF
EF0 kB
3N 2kB N (EF0 )
3 6.0221023 21.3811023 3.321042
19624K
N
固体物理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 金属电子论
思 考 题
1.如何理解电子分布函数)(E f 的物理意义是: 能量为E 的一个量子态被电子所占据的平均几率?
[解答]
金属中的价电子遵从费密-狄拉克统计分布, 温度为T 时, 分布在能级E 上的电子数目
1/)(+=-T k E E B F e g n ,
g 为简并度, 即能级E 包含的量子态数目. 显然, 电子分布函数
11)(/)(+=-T k E E B F e E f
是温度T 时, 能级E 的一个量子态上平均分布的电子数. 因为一个量子态最多由一个电子所占据, 所以)(E f 的物理意义又可表述为: 能量为E 的一个量子态被电子所占据的平均几率.
2.绝对零度时, 价电子与晶格是否交换能量?
[解答]
晶格的振动形成格波,价电子与晶格交换能量,实际是价电子与格波交换能量. 格波的能量子称为声子, 价电子与格波交换能量可视为价电子与声子交换能量. 频率为i ω的格波的声子数
11/-=T k i B i e n ω .
从上式可以看出, 绝对零度时, 任何频率的格波的声子全都消失. 因此, 绝对零度时, 价电子与晶格不再交换能量.
3.你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?
[解答]
自由电子论只考虑电子的动能. 在绝对零度时, 金属中的自由(价)电子, 分布在费密能级及其以下的能级上, 即分布在一个费密球内. 在常温下, 费密球内部离费密面远的状态全被电子占据, 这些电子从格波获取的能量不足以使其跃迁到费密面附近或以外的空状态上, 能够发生能态跃迁的仅是费密面附近的少数电子, 而绝大多数电子的能态不会改变. 也就是说, 常温下电子的平均动能与绝对零度时的平均动能一定十分相近.
4.晶体膨胀时, 费密能级如何变化?
[解答]
费密能级
3
/222
0)3(2πn m E F
=,
其中n 是单位体积内的价电子数目. 晶体膨胀时, 体积变大, 电子数目不变, n 变小, 费密能级降低.
5.为什么温度升高, 费密能反而降低?
[解答]
当0≠T 时, 有一半量子态被电子所占据的能级即是费密能级. 温度升高, 费密面附近的电子从格波获取的能量就越大, 跃迁到费密面以外的电子就越多, 原来有一半量子态被电子所占据的能级上的电子就少于一半, 有一半量子态被电子所占据的能级必定降低. 也就是说, 温度升高, 费密能反而降低.
6.为什么价电子的浓度越大, 价电子的平均动能就越大?
[解答]
由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子浓度的关系.
价电子的浓度越大价电子的平均动能就越大, 这是金属中的价电子遵从费密-狄拉克统计分布的必然结果. 在绝对零度时, 电子不可能都处于最低能级上, 而是在费密球中均匀分布. 由式
3/1
2
0)
3(πn
k
F
=
可知, 价电子的浓度越大费密球的半径就越大,高能量的电子就越多, 价电子的平均动能就越大. 电子的平
均动能E正比与费密能
F
E, 而费密能又正比与电子浓度3/2n:
()3/22
2
03
2
πn
m
E
F
=
,
()3/22
2
03
10
3
5
3
πn
m
E
E
F
=
=
.
所以价电子的浓度越大, 价电子的平均动能就越大.
7.为什么价电子的浓度越高, 电导率越高?
[解答]
电导σ是金属通流能力的量度. 通流能力取决于单位时间内通过截面积的电子数. 但并不是所有价电子对导电都有贡献, 对导电有贡献的是费密面附近的电子. 费密球越大, 对导电有贡献的电子数目就越多. 费密球的大小取决于费密半径
3/1
2)
3(πn
k
F
=.
可见电子浓度n越高, 费密球越大, 对导电有贡献的电子数目就越多, 该金属的电导率就越高.。
