高中数学《线性回归方程》教案
高中数学 2.4.2线性回归方程学案2 苏教版必修3-苏教版高二必修3数学学案
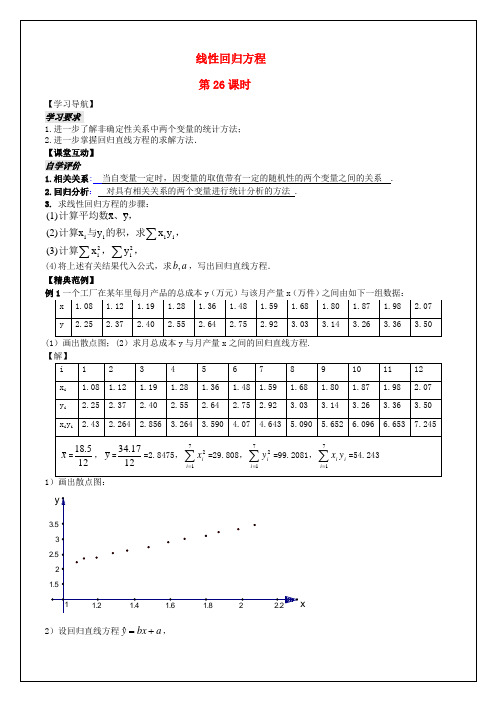
例2已知10只狗的血球体积及红血球数的测量值如下:
45
42
46
48
42
35
58
40
39
50
6.53
6.30
9.52
7.50
6.99
5.90
9.49
6.20
6.59
8.72
(血球体积 ), (红血球数,百万)
(1)画出上表的散点图;(2)求出回归直线度且画出图形.
【解】(1)图略
(2)
=
设回归直线方程为 ,则 , =
所以所求回归直线的方程为
追踪训练
1、以下是收集到的新房屋销售价格 与房屋的大小 的数据:
房屋大小 ( )
80
105
110
115
135
销售价格 (万元)
18.4
22
21.6
24.8
29.2
(1)画出数据的散点图;(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线.y2.923.033.14
3.26
3.36
3.50
(1)画出散点图;
(2)求出月总成本 与月产量x之间的线性回归方程。
解:散点图:
(2)所求的回归直线方程是:
=1.216x+0.9728.
2.92
3.03
3.14
3.26
3.36
3.50
(1)画出散点图;(2)求月总成本y与月产量x之间的回归直线方程.
【解】
i
1
2
3
4
5
6
7
8
9
10
11
12
xi
1.08
高中数学 2.4线性回归方程第2课时教案 苏教版必修3
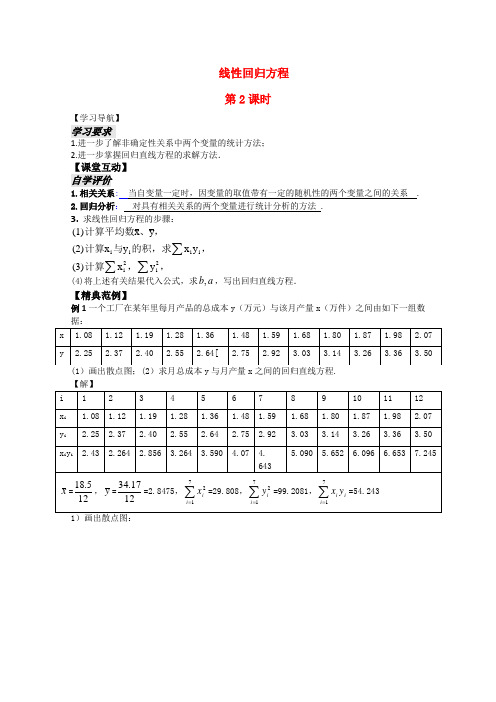
线性回归方程第2课时【学习导航】学习要求1.进一步了解非确定性关系中两个变量的统计方法;2.进一步掌握回归直线方程的求解方法.【课堂互动】自学评价1.相关关系: 当自变量一定时,因变量的取值带有一定的随机性的两个变量之间的关系 .2.回归分析: 对具有相关关系的两个变量进行统计分析的方法 .3. 求线性回归方程的步骤:(1)x y (2)x y x y (3)i i i i 计算平均数、,计算与的积,求,计算,,∑∑∑x y i i 22(4)将上述有关结果代入公式,求,b a ,写出回归直线方程.【精典范例】例1一个工厂在某年里每月产品的总成本y (万元)与该月产量x (万件)之间由如下一组数据:(1)画出散点图;(2)求月总成本y 与月产量x 之间的回归直线方程.1)画出散点图:x2)设回归直线方程a bx y+=ˆ, 利用⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=∑∑==xb y a x x y x y x b i i i i i 121221211212,计算a ,b ,得b ≈1.215, a=x b y -≈0.974,∴回归直线方程为:974.0215.1ˆ+=x y例2 已知10只狗的血球体积及红血球数的测量值如下:x ((1)画出上表的散点图;(2)求出回归直线度且画出图形. 【解】(1)图略 (2)1(45424648423558403950)44.5010x =+++++++++= 1(6.53 6.309.527.50 6.99 5.909.49 6.20 6.558.72)10y =+++++++++=7.37 设回归直线方程为 y bx a =+,则10110221100.17510i ii ii x y x yb xx==-==-∑∑,a y bx =-=0.418-所以所求回归直线的方程为 0.1750.148y x =-追踪训练(1)画出数据的散点图;(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线. 【解】(1)散点图(略)网](2)55115,545,109,116,23.2,ii i i n xx y y =======∑∑5521160952,12952ii i i i xx y ====∑∑25129525451160.1962,23.20.1962109 1.8166560952545b a ⨯-⨯=≈=-⨯≈⨯-所以,线性回归方程为0.1962 1.8166y x =+.2、一个工厂在某年里每月产品的总成本y(单位:万元)与月产量x( 单位:万件)之间有如下一(2) 求出月总成本yˆ与月产量x 之间的线性回归方程。
高中数学2.4《线性回归方程》第1课时教案(苏教版必修3)

线性回归方程第1课时【学习导航】学习要求1.理解线性回归的基本思想和方法,体会变量之间的相关关系。
线性回归方程的求法。
2.会画出一组数据的散点图,并会通过散点图判断出这组数据是否具有线性关系。
【课堂互动】自学评价在实际问题中,变量之间的常见关系有两类:一类是确定性函数关系,变量之间的关系可以用函数表示,另一类是相关关系,变量之间有一定的联系,但不能完全用函数来表达2.建立平面直角坐标系,将数据构成的数对所表示的点在坐标系内标出,这样的图称为散点图(scatter diagram)3.在散点图中如果点散布在一条直线的附近,可用线性函数近似地表示x 和y 之间的关系。
选择怎样的直线我们有下列思考方案: (1)选择能反映直线变化的两个点(2)取一条直线,使得位于该直线一侧和另一侧点的个数基本相同(3)多取几组点,确定几条直线方程,再分别 算出各条直线斜率、截距的平均值,作为所求直线的斜率、截距4.用方程为a bx y+=ˆ的直线拟合散点图中的点,应使得该直线与散点图中的点最接近。
用最小二乘法来求a 、b 的原理和方法 见教科书P725.能用直线方程a bx y+=ˆ近似表示的相关关系叫做线性相关关系(linear correlation) 6.设有(x,y)的n 对观察数据如下:当a,b 使+--=211)(a bx y Q2222)()(a bx y a bx y n n --+⋯+--取得最小值时,就称a bx y+=ˆ为拟合这n 对数据的线性回归方程(linear regression equation),将该方程所表示的直线称为回归直线。
6.用书上的方法3,可求得线性回归方程a bx y+=ˆ中的系数: 2112111)())((∑∑∑∑∑=====--=ni i n i i ni i n i i n i i i x x n y x y x n ba =xb y - (*)7.用回归直线进行拟合的一般步骤为:(1)作出散点图,判断散点是否在一条直线附近(2)如果散点在一条直线附近,用上面的公式求出a,b,并写出线性回归方程【精典范例】例1 下表为某地近几年机动车辆数与交通事故数的统计资料,请判断机动车辆数与交通事故数之间是否具有线性相关关系,如果具有线性相关关系,求出线性回归方程;如果不具有线性相关关系,说明理由。
《2.4线性回归方程(2)》教案

《线性回归方程(2)》教案教学目标:1.了解非确定性关系中两个变量的统计方法;2.掌握散点图的画法及在统计中的作用;3.掌握回归直线方程的求解方法.教学重难点:重点:掌握散点图的画法及在统计中的作用;难点:掌握回归直线方程的求解方法.教学过程:一、复习练习1.已知回归方程ˆ0.50.81y x=-,则x=25时,y的估计值为2.三点()3,10,(7,20),(11,24)的线性回归方程是( D ) A.ˆ 5.75 1.75=+y xy x=-B.ˆ 1.75 5.75C.ˆ 1.75 5.75y x=+y x=- D.ˆ 5.75 1.753.我们考虑两个表示变量x与y之间的关系的模型,δ为误差项,模型如下:模型1:64y x e=++.=+;模型2:64y x(1)如果3,1==,分别求两个模型中y的值;x e(2)分别说明以上两个模型是确定性模型还是随机模型.解:(1)模型1:6464318=+=+⨯=;y x模型2:64643119y x e=++=+⨯+=(2)模型1中相同的x值一定得到相同的y值,所以是确定性模型;模型2中相同的x值,因δ的不同,所得y值不一定相同,且δ为误差项是随机的,所以模型2是随机性模型.二、数学运用1.例题讲解.例1 一个车间为了规定工时定额,需要确定加工零件所花费的时间.为此进行了10次试验,测得数据如下:y y回归方程.解:在直角坐标系中画出数据的散点图,直观判断散点在一条直线附近,故具有 线性相关关系.由测得的数据表可知:1010102211155,91.7,38500,87777,55950i ii i i i i x y x y x y ========∑∑∑∴1011022211055950105591.70.66838500105510i ii ii x y x yb xx==--⨯⨯==≈-⨯-∑∑91.70.6685554.96a y bx =-=-⨯≈,因此,所求线性回归方程为$0.66854.96y bx a x =+=+.例2 已知10只狗的血球体积及红血球数的测量值如下:x45 42 46 48 42 35 58 40 39 50 y6.536.309.527.506.995.909.496.206.598.72,ml y (1)画出上表的散点图;(2)求出回归直线方程且画出图形. 解:(1)(2)1(45424648423558403950)44.5010x =+++++++++=,1(6.53 6.309.527.50 6.99 5.909.49 6.20 6.558.72)10y =+++++++++=7.37,设回归直线方程为$y bx a=+,则10110221100.17510i ii ii x y x yb xx==-==-∑∑,a y bx =-0.418-,所以所求回归直线的方程为$0.1750.148y x =-图形:说明:对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数,a b 的计算公式,算出,a b .由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误,求线性回归方程的步骤:计算平均数,x y ;计算i x 与i y 的积,求i i x y ∑;计算2i x ∑;将结果代入公式求b ;用a y bx =-求a ;写出回归直线方程.2.巩固深化,反馈矫正.(1)下面是南京市与哈尔滨2001年12个月的月平均气温(单位:︒C)试分析这两个城市的月平均气温是否具有相关关系,若有,求出线性回归方程;若没有,说明理由.月份 1 2 3 4 5 6 南京月平均气温 2 3.8 8.4 14.8 19.9 24.5 哈尔滨月平均气温-19.4 -15.4 -4.8 6 14.3 20 月份 7 8 9 10 11 12 南京月平均气温 28 27.8 22.7 16.9 10.54.4哈尔滨月平均气温22.821.114.45.6-5. 7 -15.6y 使用年限x 2 3456维修费用y2.23.8 5.5 6.5 7.0设y 对x 程线性相关关系.试求:①线性回归方程ˆy bx a =+的回归系数,a b ; ②估计使用年限为10年时,维修费用多少? 三、归纳整理,整体认识 求线性回归方程的步骤: 1. 计算平均数x y , ;2. 计算x i 与y i 的积,求i i x y ∑;3. 计算∑x i 2,y i 2 ;4.将上述有关结果代入公式,求b ,a ,写出回归直线方程.。
线性回归方程教案

线性回归方程1.下列关系中,是相关关系的为(填序号).①学生的学习态度与学习成绩之间的关系;②教师的执教水平与学生的学习成绩之间的关系;③学生的身高与学生的学习成绩之间的关系;④家庭的经济条件与学生的学习成绩之间的关系.2.为了考察两个变量x、y之间的线性相关关系,甲、乙两同学各自独立地做10次和15次试验,并利用最小二乘法求得回归直线分别为l1和l2.已知在两人的试验中发现变量x的观测数据的平均值恰好相等,都为s,变量y的观测数据的平均值也恰好相等,都为t,那么下列说法中正确的是(填序号).①直线l1,l2有交点(s,t) ②直线l1,l2相交,但是交点未必是(s,t)③直线l1,l2由于斜率相等,所以必定平行④直线l1,l2必定重合3.下列命题:①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归直线yˆ=bˆx+aˆ及回归系数bˆ,可以估计和预测变量的取值和变化趋势.④任一组数据都有回归直线方程其中正确命题的序号是 .4.已知回归方程为yˆ=0.50x-0.81,则x=25时,yˆ的估计值为 .5.观察下列散点图,则①正相关;②负相关;③不相关.它们的排列顺序与图形对应顺序是 .6.回归方程yˆ=1.5x-15,则下列说法正确是 .①y=1.5x-15 ②15是回归系数a③1.5是回归系数a ④x=10时,y=07.某地区调查了2~9岁儿童的身高,由此建立的身高y(cm)与年龄x(岁)的回归模型为yˆ=8.25x+60.13,下列叙述正确的是 .①该地区一个10岁儿童的身高为142.63 cm②该地区2~9岁的儿童每年身高约增加8.25 cm③该地区9岁儿童的平均身高是134.38 cm④利用这个模型可以准确地预算该地区每个2~9岁儿童的身高8.三点(3,10),(7,20),(11,24)的回归方程是 .9.某人对一地区人均工资x(千元)与该地区人均消费y(千元)进行统计调查,y与x有相关关系,得到回归直线方程yˆ=0.66x+1.562.若该地区的人均消费水平为7.675千元,估计该地区的人均消费额占人均工资收入的百分比约为 .10.某化工厂为预测产品的回收率y ,需要研究它和原料有效成分含量x 之间的相关关系,现取8对观测值,计算,得∑=81i ix=52,∑=81i iy=228,∑=812i i x =478,∑=81i ii yx =1 849,则其线性回归方程为 .11.有下列关系:①人的年龄与他(她)拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一种树木,其断面直径与高度之间的关系.其中,具有相关关系的是 .12.已知关于某设备的使用年限x 与所支出的维修费用y (万元),有如下统计资料:若y 对x 呈线性相关关系,则回归直线方程yˆ=b ˆx +a ˆ表示的直线一定过定点.13 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨)标准煤的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程yˆ=b ˆx +a ˆ; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)3.某企业上半年产品产量与单位成本资料如下:(1)求出线性回归方程;(2)指出产量每增加1 000件时,单位成本平均变动多少?(3)假定产量为6 000件时,单位成本为多少元?一、填空题二、解答题9.期中考试结束后,记录了5名同学的数学和物理成绩,如下表:(1)数学成绩和物理成绩具有相关关系吗?(2)请你画出两科成绩的散点图,结合散点图,认识(1)的结论的特点.10.(1)画出数据对应的散点图;(2)求线性回归方程,并在散点图中加上回归直线.11.某公司利润y与销售总额x(单位:千万元)之间有如下对应数据:(1)画出散点图;(2)求回归直线方程;(3)估计销售总额为24千万元时的利润.,12.某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:(1)画出散点图;(2)求回归直线方程;(3)试预测广告费支出为10百万元时,销售额多大?。
高中数学线性回归概念教案

高中数学线性回归概念教案1. 理解线性回归的基本概念和原理2. 掌握线性回归的计算方法和应用技巧3. 能够通过实例理解线性回归在实际问题中的应用教学重点:1. 线性回归的定义和特点2. 最小二乘法求解线性回归方程3. 线性回归在实际问题中的应用教学难点:1. 线性回归的计算方法和应用技巧2. 如何通过实例理解线性回归在实际问题中的应用教学准备:1. 教学课件2. 实例数据3. 计算工具、软件教学内容:一、线性回归的定义和特点1. 线性回归是一种用于分析变量之间线性关系的统计方法2. 线性回归模型可以表示为y = β0 + β1x1 + β2x2 + ... + βnxn + ε3. 线性回归的基本假设包括线性关系、正态分布、独立性等二、最小二乘法求解线性回归方程1. 最小二乘法是一种常见的求解线性回归方程的方法2. 最小二乘法的核心思想是使残差平方和最小化来求解回归系数3. 求解线性回归方程的步骤包括建立模型、计算回归系数、评估模型等三、线性回归在实际问题中的应用1. 线性回归可以用于预测和控制变量之间的关系2. 实际问题中的线性回归应用包括销售预测、市场分析等3. 通过实例数据进行线性回归分析,可以更好地理解线性回归的应用技巧和方法教学步骤:1. 引入线性回归的基本概念和原理,并进行概念讲解2. 通过实例数据演示最小二乘法求解线性回归方程的方法3. 分组讨论,学生分析实际问题中的线性回归应用4. 带领学生进行实例数据分析和线性回归计算5. 总结课程内容,答疑解惑教学评估:1. 学生课堂表现2. 课后作业完成情况3. 学生对线性回归应用的理解和运用能力教学反思:1. 教学内容是否贴近实际应用2. 学生对线性回归的理解程度和应用能力3. 教学方法和手段是否合理有效。
高中数学线性回归教案

高中数学线性回归教案教学目标:
1. 了解线性回归的基本概念和原理;
2. 学会使用最小二乘法进行线性回归分析;
3. 掌握线性回归模型的建立和应用。
教学重点:
1. 理解线性回归的意义;
2. 学会求解线性回归模型中的系数;
3. 掌握线性回归模型的应用。
教学难点:
1. 学会使用最小二乘法求解线性回归系数;
2. 理解线性回归模型的推导过程。
教学准备:
1. 教师准备PPT讲解线性回归的基本概念和原理;
2. 课堂上需要使用电脑进行实例演示;
3. 学生需要准备笔记本记录重要知识点。
教学过程:
1. 引入:通过实例引入线性回归的概念;
2. 讲解线性回归模型的建立和求解过程;
3. 使用最小二乘法进行线性回归模型的求解;
4. 通过实例演示线性回归模型的应用;
5. 总结线性回归的主要知识点。
教学延伸:
1. 学生可以通过实际数据进行线性回归分析;
2. 学生可以进一步了解多元线性回归和非线性回归。
课堂反馈:
1. 学生通过实例演示线性回归的能力;
2. 学生通过习题练习线性回归的应用。
教学资源:
1. 电脑和投影仪;
2. 练习题目和实例数据。
教学评价:
1. 通过课堂表现评价学生对线性回归的掌握情况;
2. 通过作业评价学生对线性回归的应用能力。
2020年高中数学教案必修三:2.4 线性回归方程(1)

教学目标:1.通过收集现实问题中两个有关联变量的数据作出散点图,并利用散点图直观认识变量间的相关关系;2.在两个变量具有线性相关关系时,会在散点图中作出线性直线,会用线性回归方程进行预测;3.知道最小二乘法的含义,知道最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程,了解(线性)相关系数的定义.教学重点:散点图的画法,回归直线方程的求解方法.教学难点:回归直线方程的求解方法.教学方法:引导发现、合作探究.教学过程:一、创设情景,揭示课题客观事物是相互联系的.过去研究的大多数是因果关系,但实际上更多存在的是一种非因果关系.比如说:某某同学的数学成绩与物理成绩,彼此是互相联系的,但不能认为数学是“因”,物理是“果”,或者反过来说事实上数学和物理成绩都是“果”,而真正的“因”是学生的理科学习能力和努力程度.所以说,函数关系存在着一种确定性关系,但还存在着另一种非确定性关系——相关关系.二、学生活动提出问题:两个变量之间的常见关系有几种?(1)确定性的函数关系,变量之间的关系可以用函数表示;(2)相关关系,变量之间有一定的联系,但不能完全用函数来表示.说明:不要认为两个变量间除了函数关系,就是相关关系,事实是,两个变量间可能毫无关系.比如地球运行的速度与某个人的行走速度就可认为没有关系.某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:-气温/0C 26 18 13 10 4 1杯数20 24 34 38 50 64 如果某天的气温是5-0C,你能根据这些数据预测这天小卖部卖出热茶的杯数吗?从下图可以看出,这些点散布在一条直线的附近,故可用一个线性函数近似地表示热茶销量与气温之间的关系.选择怎样的直线近似地表示热茶销量与气温之间的关系?我们有多种思考方案:(1)选择能反映直线变化的两个点,例如取(4,50),(18,24)这两点的直线;(2)取一条直线,使得位于该直线一侧和另一侧的点的个数基本相同;(3)多取几组点,确定几条直线方程,再分别算出各条直线斜率、截距的平均值,作为所求直线的斜率、截距;……怎样的直线最好呢?三、建构数学1.最小平方法:用方程为ˆy bx a=+的直线拟合散点图中的点,应使得该直线与散点图中的点最接近.那么,怎样衡量直线ˆy bx a=+与图中六个点的接近程度呢?我们将表中给出的自变量x 的六个值带入直线方程,得到相应的六个ˆy 的值: 26,18,13,10,4,b a b a b a b a b a b a +++++-+.这六个值与表中相应的实际值应该越接近越好.所以,我们用类似于估计平均数时的思想,考虑离差的平方和222222(,)(2620)(1824)(1334)(1038)(450)(64)Q a b b a b a b a b a b a b a =+-++-++-++-++-+-+- 21286b =26140382046010172a ab b a ++--+说明: (,)Q a b 是直线ˆy bx a =+与各散点在垂直方向(纵轴方向)上的距离的平 方和,可以用来衡量直线ˆybx a =+与图中六个点的接近程度,所以,设法取,a b 的 值,使(,)Q a b 达到最小值.这种方法叫做最小平方法(又称最小二乘法)(method of least square ).先把a 看作常数,那么Q 是关于b 的二次函数.易知,当140382021286a b -=-⨯时, Q取得最小值.同理, 把b 看作常数,那么Q 是关于a 的二次函数.当14046012b a -=-时, Q 取得最小值.因此,当14038202128614046012a b b a -⎧=-⎪⎪⨯⎨-⎪=-⎪⎩时,Q 取的最小值,由此解得 1.6477,57.5568b a ≈-≈.所求直线方程为ˆ 1.647757.5568yx =-+.当5x =- 时,ˆ66y≈,故当气温为5-0C 时,热茶销量约为66杯. 2.线性相关关系:像这样能用直线方程ˆybx a =+近似表示的相关关系叫做线性相关关系(liner correlation).3.线性回归方程:一般地,设有n 个观察数据如下:当,a b 使2221122()()...()n n Q y bx a y bx a y bx a =--+--++--取得最小值时,就称ˆybx a =+为拟合这n 对数据的线性回归方程(linear regression equation ), 该方程所表示的直线称为回归直线.上述式子展开后,是一个关于,a b 的二次多项式,应用配方法,可求出使Q 为最小值时的,a b 的值.即结论:1112211()()()n n ni i i i i i i n ni i i i n x y x y b n x x a y bx=====⎧-⎪⎪=⎨-⎪⎪=-⎪⎩∑∑∑∑∑,(*) ∑==n i i x n x 11, ∑==ni i y n y 11 说明:公式(*)的推导比较复杂,这里不作要求. 四、数学运用例题 下表为某地近几年机动车辆数与交通事故数的统计资料,请判断机动 车辆数与交通事故数之间是否有线性相关关系,如果具有线性相关关系,求出线 性回归方程;如果不具有线性相关关系,说明理由.机动车辆数x /千台95 110 112 120 129 135 150 180交通事故数y /千件 6.2 7.5 7.7 8.5 8.7 9.8 10.2 131.下面是我国居民生活污水排放量的一组数据(单位:103 t )试分别估计1996年和2004年我国居民生活污水排放量. 年份19951996 1997 1998 1999 2000 2001 2002 排放量 151189.1194.8203.8220.9227.7232.32.一个工厂在某年里每月产品的总成本y(单位:万元)与月产量(单位:万件)之间有如下一组数据:(1)画出散点图; (2)求线性回归方程. 五、归纳整理,整体认识1.对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数,a b 的计算公式,算出,a b .由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误.2.求线性回归方程的步骤:①计算平均数y x ,;②计算i i y x 与的积,求∑i i y x ;③计算∑2i x ;④将结果代入公式求a ;⑤用 x a y b -=求b ;⑥写出回归方程.....................................使用本文档删除后面的即可致力于打造全网一站式文档服务需求,为大家节约时间文档来源网络仅供参考欢迎您下载可以编辑的word文档谢谢你的下载本文档目的为企业和个人提供下载方便节省工作时间,提高工作效率,打造全网一站式精品需求!欢迎您的下载,资料仅供参考!(本文档收集于网络改编,由于文档太多,审核难免疏忽,如有侵权或雷同,告知本店马上删除)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性回归方程
教学目标:
(1)了解非确定性关系中两个变量的统计方法; (2)掌握散点图的画法及在统计中的作用; (3)掌握回归直线方程的实际应用。
教学重点: 线性回归方程的求解。
教学难点: 回归直线方程在现实生活与生产中的应用。
教学过程: 一、复习练习
1.下例说法不正确的是( B )
A.在线性回归分析中,x 和y 都是变量;
B.变量之间的关系若是非确定关系,那么x 不能由y 唯一确定;
C.由两个变量所对应的散点图,可判断变量之间有无相关关系;
D.相关关系是一种非确定性关系.
2.已知回归方程81.05.0ˆ-=x y
,则x =25时, y 的估计值为__11.69____. 3.三点)24,11(),20,7(),10,3(的线性回归方程是 ( D ) A x y 75.175.1ˆ-= B x y 75.575.1ˆ
+=
C x y 75.575.1ˆ-=
D x y 75.175.1ˆ+=
4.我们考虑两个表示变量x 与y 之间的关系的模型,δ为误差项,模型如下: 模型1:x y 46+=:;模型2:e x y ++=46. (1)如果1,3==e x ,分别求两个模型中y 的值; (2)分别说明以上两个模型是确定性模型还是随机模型. 解 (1)模型1:y=6+4x=6+4×3=18; 模型2:y=6+4x+e=6+4×3+1=19.
(2)模型1中相同的x 值一定得到相同的y 值.所以是确定性模型;模型2中相同的x 值,因 δ不同,且δ为误差项是随机的,所以模型2是随机性模型。
二、典例分析
例1、一个车间为了规定工时定额,需要确定加工零件所花费的时间.为此进行了10次试验,测得数据如下:
零件个数x (个) 10 20 30 40 50 60
70
80 90 100
加工时间y (分)
62 68 75 81 89 95 102 108 115 122
请判断y 与x 是否具有线性相关关系,如果y 与x 具有线性相关关系,求线性回归方程.
解:在直角坐标系中画出数据的散点图,直观判断散点在一条直线附近,故具有线性相关关系.由测得的数据表可知:
101010
2
2
1
1
1
55,91.7,38500,87777,55950
i i i i i i i x y x y x y ========∑∑∑
10
110
2
2
21
1055950105591.7
0.668385001055
10i i
i i i x y x y
b x x
==--⨯⨯∴=
=
≈-⨯-∑∑
91.70.6685554.96a y bx =-=-⨯≈
因此,所求线性回归方程为0.66854.96y bx a x =+=+ 例2、已知10只狗的血球体积及红血球数的测量值如下:
x
45 42 46 48 42 35 58 40 39 50
y
6.53 6.30 9.52
7.50 6.99 5.90 9.49 6.20 6.59
8.72
x (血球体积,ml ),y (红血球数,百万)
(1)画出上表的散点图;(2)求出回归直线方程并画出图形.
解:
1
(45424648423558403950)44.5010x =
+++++++++=
1
(6.53 6.309.527.50 6.99 5.909.49 6.20 6.558.72)10y =
+++++++++=7.37
设回归直线方程为y bx a =+
则
10
1
10
2
2
1
100.175
10i i
i i
i x y x y
b x
x
==-=
=-∑∑ a y bx =-= -0.418
所以所求回归直线的方程为0.1750.148y x =-
例3、以下是收集到的新房屋销售价格y 与房屋的大小x 的数据:
房屋大小x (2
m ) 80 105 110 115] 135 销售价格y (万元)
18.4
22
21.6
24.8
29.2
(1)画出数据的散点图;(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线;(3)计算此时(,)Q a b 和(2,0.2)Q 的值,并作比较. 解:(1)
(2)
55
1
1
5,545,109,116,23.2,
i i i i n x x y y =======∑∑
5
5
2
1
1
60952,12952
i
i i i i x
x y ====∑∑
2
512952545116
0.1962,23.20.1962109 1.8166560952545b a ⨯-⨯=
≈=-⨯≈⨯-
所以,线性回归方程为0.1962 1.8166y x =+ (3) (1.8166,0.1962) 5.171,(2,0.2)7.0Q Q ≈≈
由此可知,求得的 1.8166,0.9162a b ==是函数Q(a,b)取最小值的a ,b 值.
三、课堂练习
1.为了考察两个变量x 和y 之间的线性相关性,甲乙两位同学各自独立做了10次和15次实验,并且利用线性回归直线分别为1l ,2l ,已知两人获得的实验数据中,变量x 和y 的数据平均值都相等,且分别为s,t 那么下例说话正确的是( )
A .直线1l 和2l 一定有公共点(s,t)
B .直线1l 和2l 相交,但交点不一定是(s,t)
销售价格y(万元)
0510
1520
2530350
50
100
150
销售价格y(万
元)
C .必有1l // 2l
D .1l 和2l 与必定重合
2.已知关于某设备的使用年限x 与所支出的维修费用y (万元),有如下统计资料: 使用年限x 2 3 4 5 6 维修费用y
2.2
3.8
5.5
6.5
7.0
设y 对x 程线性相关关系.试求:
(1)线性回归方程ˆ
y bx a =+的回归系数a,b ; (2)估计使用年限为10年时,维修费用多少?
四、回顾小结:求线性回归方程的步骤:
(1)x y (2)x y x y (3)i i i i 计算平均数、,
计算与的积,求,
计算,,∑∑∑x y i
i 22
(4)将上述有关结果代入公式,求b ,a 写出回归直线方程. 五、课外作业: 课本第82页第9题.。
