统计学案例作业
统计案例练习题(附答案)

统计案例练习题(附答案)一、选择题 1.对具有线性相关关系的两个变量建立的线性回归方程y=a+bx中,回归系数b( ) A.可以小于0 B.只能大于0 C.可能等于0 D.只能小于0 【解析】b可能大于0,也可能小于0,但当b=0时,x,y不具有线性相关关系.【答案】 A 2.下列两个变量间的关系不是函数关系的是( ) A.正方体的棱长与体积 B.角的弧度数与它的正弦值 C.单产为常数时,土地面积与粮食总产量 D.日照时间与水稻亩产量【解析】∵A、B、C都可以得出一个函数关系式,而D不能写出确定的函数关系式,它只是一个不确定关系.【答案】 D 3.某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元) 4 2 3 5 销售额y(万元) 49 26 39 54 根据上表可得回归方程y=bx+a中的b为9.4,据此模型预报广告费用为6万元时销售额为( ) A.63.36万元 B.65.5万元C.67.7万元 D.72.0万元【解析】x=4+2+3+54=3.5, y=49+26+39+544=42,∴a=y-bx=42-9.4×3.5=9.1,∴回归方程为y=9.4x+9.1,∴当x=6时,y=9.4×6+9.1=65.5,故选B. 【答案】 B 4.由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到回归直线方程y=bx+a,那么下列说法中不正确的是( ) A.直线y=bx+a必经过点(x,y) B.直线y=bx+a至少经过点(x1,y1)(x2,y2),…,(xn,bn)中的一个点 C.直线y=bx+a的斜率为∑ni=1xiyi-nx•y∑ni=1x2i-nx2 D.直线y=bx+a的纵截距为y-bx 【解析】回归直线可以不经过任何一个点.其中A:由a=y-bx代入回归直线方程y=bx+y-ax,即y=b(x-x)+y过点(x,y).∴B错误.【答案】 B 5.已知两个变量x和y 之间具有线性相关性,甲、乙两个同学各自独立地做了10次和15次试验,并且利用线性回归的方法求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y 的观测数据的平均数都是t,则下列说法正确的是( ) A.l1与l2一定有公共点(s,t) B.l1与l2相交,但交点一定不是(s,t) C.l1与l2必定平行 D.l1与l2必定重合【解析】由于回归直线y=bx+a恒过(x,y)点,又两人对变量x的观测数据的平均值为s,对变量y的观测数据的平均值为t,所以l1和l2恒过点(s,t).【答案】 A 二、填空题 6.从某大学随机选取8名女大学生,其身高x(cm)和体重y(kg)的线性回归方程为y=0.849x-85.712,则身高172 cm的女大学生,由线性回归方程可以预测其体重约为________.【解析】将x=172代入线性回归方程y=0.849x-85.712,有y=0.849×172-85.712=60.316(kg).【答案】60.316 kg 7.面对竞争日益激烈的消费市场,众多商家不断扩大自己的销售市场,以降低生产成本.某白酒酿造企业市场部对该企业9月份的产品销量(单位:千箱)与单位成本的资料进行线性回归分析,结果如下:x=72,y=71,∑6i=1x2i=79,∑6i=1xiyi=1 481. b=1 481-6×72×7179--1.818 2, a=71-(-1.8182)×72≈77.36,则销量每增加1 000箱,单位成本下降________元.【解析】由上表可得,y=-1.818 2x+77.36,销量每增加1千箱,则单位成本下降1.818 2元.【答案】 1.818 2 8.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:y=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.【解析】由题意知[0.254(x+1)+0.321]-(0.254x+0.321)=0.254. 【答案】0.254 三、解答题 9.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:推销员编号 1 2 3 4 5 工作年限x/年 3 5 6 7 9 推销金额y/万元 2 3 3 4 5 (1)求年推销金额y关于工作年限x的线性回归方程; (2)若第6名推销员的工作年限为11年,试估计他的年推销金额.【解】(1)设所求的线性回归方程为y=bx+a,则b=i=--=-=1020=0.5, a=y-bx=0.4. 所以年推销金额y关于工作年限x的线性回归方程为y=0.5x+0.4. (2)当x=11时,y=0.5x+0.4=0.5×11+0.4 =5.9(万元).所以可以估计第6名推销员的年推销金额为5.9万元. 10.一种机器可以按各种不同速度运转,其生产物件中有一些含有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺点物件个数.现观测得到(x,y)的4组值为(8,5),(12,8),(14,9),(16,11). (1)假设y与x之间存在线性相关关系,求y与x之间的线性回归方程. (2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒?(精确到1) 【解】(1)设回归方程为y=a+bx,则x=8+12+14+164=12.5, y=5+8+9+114=8.25,∑4i=1x2i=660,∑4i =1xiyi=438, b=∑4i=1xiyi-4xy∑4i=1x2i-4x2=438-4×12.5×8.25660-4×12.52≈0.73, a=y-bx=8.25-0.73×12.5=-0.875,所以所求回归方程为y=-0.875+0.73x. (2)由y≤10,即-0.875+0.73x≤10,得x≤10.8750.73≈15,即机器速度不得超过15转/秒. 11.高二(3)班学生每周用于数学学习的时间x(单位:小时)与数学成绩y(单位:分)之间有如下数据:x 24 15 23 19 16 11 20 16 17 13 y 92 79 97 89 64 47 83 68 71 59 若某同学每周用于数学学习的时间为18小时,试预测该同学的数学成绩.【解】显然学习时间与学习成绩间具有相关关系,可以列出下表,并用科学计算器进行计算.i 1 2 3 4 5 6 7 8 9 10 xi 24 15 23 19 16 11 20 16 17 13 yi 9279 97 89 64 47 83 68 71 59 xiyi 2 208 1 185 2 231 1 691 1 024 517 1 660 1 088 1 207 767 ∑10i=1x2i=3 182,∑10i=1xiyi=13 578于是可得b=∑10i=1xiyi-10xy∑10i=1x2i-10x2=545.4154.4≈3.53, a=y-bx=74.9-3.53×17.4≈13.5. 因此可求得回归直线方程为y=3.53x+13.5. 当x=18时,y=3.53×18+13.5≈77. 故该同学预计可得77分左右.。
统计学作业

统计学作业
将抗生素注入人体会产生抗生素与血浆蛋白质结合现象,以致减少了药性,下表列出5种常用的抗生素注入牛的体内时,抗生素与血浆蛋白质结合的百分比
抗生素青霉素四环素链霉素红霉素氯霉素
1 29.6 27.3 5.8 21.6 29.2
2 24.
3 32.6 6.2 17.
4 32.8
3 28.5 30.8 11.0 18.3 25.0
4 32.0 34.8 8.3 19.0 24.2
试在显著性水平a=0.05下检验这些百分比的均值有无显著性差异。
解:以u1,u2,u3,u4,u5依次表示青霉素,四环素,链霉素,红霉素,氯霉素与血浆蛋白质结合的百分比均值,本题需假设检验
Ho:u1=u2=u3=u4=u5,
H1:u1,u2,u3,u4,u5不全相等。
折线散点图:
SUMMARY
组观测数求和平均方差
青霉素 4 114.4 28.6 10.35333
四环素 4 125.5 31.375 10.05583
链霉素 4 31.3 7.825 5.6825
红霉素 4 76.3 19.075 3.2625
氯霉素 4 111.2 27.8 15.92
方差分析
差异源SS df MS F P-value F crit 组间1480.823 4 370.2058 40.88488 6.73978E-08 3.055568 组内135.8225 15 9.054833
总计1616.646 19
Fa(4,15)=3.06 <F=40.88488 所以接受H0,认为这些均值无显著性差异。
统计学误用案例

统计学误用案例案例一:平均数的陷阱。
咱就说有个小公司,老板想显示员工工资待遇还不错。
公司有10个员工,1个经理月薪10万,然后9个普通员工月薪3000。
老板一算,平均工资=(100000 + 9×3000)÷10 = 12700元。
然后对外宣称公司平均月薪12700元,好多人一听,哇,这工资挺高啊。
但实际上呢,除了那个经理,大部分普通员工的工资少得可怜,这个平均数就完全误导了大家对这个公司工资水平的真实印象。
这就像是拿姚明的身高和一群小学生的身高求平均,然后说这个平均身高就代表大家的身高水平,那可太扯了。
案例二:样本偏差。
有个保健品公司想做个产品调查,证明他们的保健品特别有效。
他们就在自己的专卖店门口找那些来买保健品的人做调查,问“您觉得我们的保健品效果好不好呀?”结果大部分人都说好。
为啥呢?因为来专卖店买的人本来就是相信这个产品才来买的呀,这就是一个有偏差的样本。
就好比你想知道大家喜不喜欢吃榴莲,你专门跑到榴莲专卖店门口去问,那肯定大部分人都说喜欢,这根本就不能代表全体人群的真实想法。
这保健品公司就拿着这个不靠谱的调查结果到处宣传,这就是对统计学的误用。
案例三:相关性误为因果性。
你看,有人发现,在某个城市,冰淇淋的销量和溺水死亡人数在夏天都上升了。
然后就有个“天才”说,冰淇淋会导致溺水。
这可就太荒谬了。
其实呢,这两者只是有相关性,因为夏天到了,天气热,吃冰淇淋的人多了,同时去游泳的人也多了,所以溺水死亡人数也增加了。
这就像每次公鸡打鸣之后太阳就升起来了,但我们不能说公鸡打鸣是太阳升起的原因一样,这种把相关性硬说成因果性的事儿,在统计学里可是个大错特错的事儿。
统计学实验作业

1、一家大型商业银行在多种地区设有分行,其业务重要是进行基础设施建设、国家重点项目建设、固定资产投资等项目旳贷款。
近年来,该银行旳贷款额平稳增长,但不良贷款额也有较大比例旳增长,这给银行业务旳发展带来较大压力。
为弄清晰不良贷款形成旳因素,管理者但愿运用银行业务旳有关数据做些定量分析,以便找出控制不良贷款旳措施。
该银行所属旳25家分行旳有关业务数据是“例11.6.x ls”。
(1)试绘制散点图,并分析不良贷款与贷款余额、合计应收贷款、贷款项目个数、固定资产投资额之间旳关系;2计算不良贷款、贷款余额、合计应收贷款、贷款项目个数、固定资产投资额之间旳有关系数(2)求不良贷款对贷款余额旳估计方程;从表系数可以看出常量、应收贷款、项目个数、固定资产投资额,都接受原假设,只有贷款余额回绝原假设,因此只有贷款余额对不良贷款起作用。
系数a模型 非原则化系数原则系数 t S ig. B 原则 误差试用版1(常量) -1.022.782-1.306 .206 各项贷款余额 (亿元).040.010.8913.837.001本年合计应收贷款 (亿元) .148.079.2601.879.075贷款项目个数 (个).015.083.034.175.863本年固定资产投资额 (亿元)-.029.015-.325-1.937.067a. 因变量: 不良贷款 (亿元)从共线性可以看出,第五个特性值对贷款余额解释87%,相应收账款解释度为12%、对贷款个数解释度为63%、对固定资产投资解释度为5%。
因此不是太共线。
、线性方程为Y=0.01X Y为不良贷款,X为贷款余额。
4 检查不良贷款与贷款余额之间线性关系旳明显性(α=0.05);回归系数旳明显性(α=0.05);通过对上表分析得出:贷款余额线性关系通过明显性检查,回归系数2.练习《记录学》教材P330练习题11.1、11.6、11.7、11.8、11.15,相应旳数据文献为“习题11.1.xls”、“习题11.6.xls”、“习题11.7.xls”、“习题11.8.xls”、“习题11.15.xls”。
统计学案例
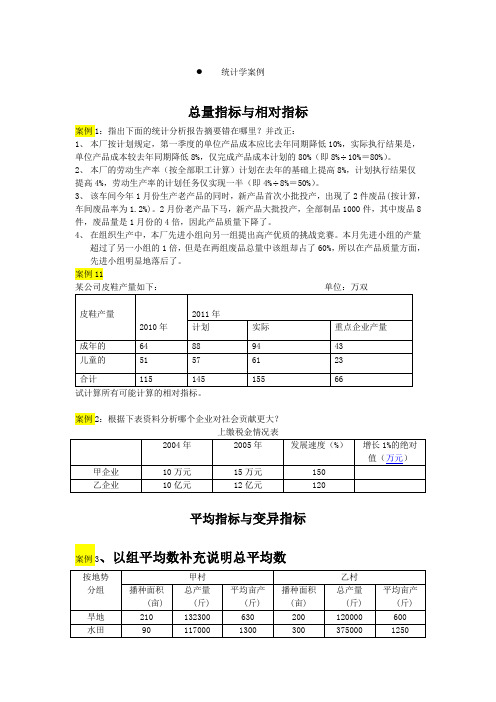
统计学案例总量指标与相对指标案例1:指出下面的统计分析报告摘要错在哪里?并改正:1、本厂按计划规定,第一季度的单位产品成本应比去年同期降低10%,实际执行结果是,单位产品成本较去年同期降低8%,仅完成产品成本计划的80%(即8%÷10%=80%)。
2、本厂的劳动生产率(按全部职工计算)计划在去年的基础上提高8%,计划执行结果仅提高4%,劳动生产率的计划任务仅实现一半(即4%÷8%=50%)。
3、该车间今年1月份生产老产品的同时,新产品首次小批投产,出现了2件废品(按计算,车间废品率为1.2%)。
2月份老产品下马,新产品大批投产,全部制品1000件,其中废品8件,废品量是1月份的4倍,因此产品质量下降了。
4、在组织生产中,本厂先进小组向另一组提出高产优质的挑战竞赛。
本月先进小组的产量超过了另一小组的1倍,但是在两组废品总量中该组却占了60%,所以在产品质量方面,先进小组明显地落后了。
案例11试计算所有可能计算的相对指标。
案例2:根据下表资料分析哪个企业对社会贡献更大?平均指标与变异指标案例3、以组平均数补充说明总平均数案例4:某单位有10个人,其中1人月工资为10万元,9人每人月工资为1000元。
该单位职工月平均工资为10900元。
即:)(109001091000100000元=⨯+你认为这个平均数有代表性吗?如果缺乏代表性应如何改正?案例5:以下是各单位统计分析报告的摘录1、 本局所属30个工厂,本月完成生产计划的情况是不一致的。
完成计划90%的有3个,完成96%的有5个,完成102%的有10个,完成110%的有8个,完成120%的有4个。
平均全局生产计划完成程度为104.33%。
即:304%1208%11010%1025%963%90⨯+⨯+⨯+⨯+⨯=104.33%2、 本厂开展增产节约运动以后,产品成本月月下降,取得显著的成绩,根据财务部门的报告,1 月份开支总成本15000元,平均单位产品成本为15元,2月份开支总成本25000元,平均单位产品成本下降为10元,3月份开支总成本45000元,平均单位产品成本仅8元。
《统计学》案例——时间序列趋势分析

《统计学》案例——时间序列趋势分析囤积粮食可以创高价吗1、问题的提出某贸易公司是经营粮油副食品的批发公司,基于前4年当地的消费物价指数的变化,该公司认为今后两年内消费物价指数将有大幅度上涨,为此该公司计划囤积粮食至下一年(第6年)以创高价。
这个计划是否可行?2、方法的选择根据下表的数据,可采用时间序列的趋势分析方法和季节变动分析方法,进行相应的分析预测,以了解消费物价指数的发展趋势。
表23 122.434 139.373、消费物价指数的预测根据题意需预测出第6年各季的物价指数,若指数升幅较大,那么粮食价格将会提高,否则囤积货物只会增加保管成本而不可能得到高价。
在物价指数预测中,循环变动和不规则变动难以准确预测,故仅考虑长期趋势与季节变动的影响。
本案例分析应用EXCEL软件。
(1)计算移动平均数。
输出结果见下表和图:表3.(2)分离长期趋势T。
对于T×C,按照表8.14中时间顺序,用最小平方法建立长期趋势模型yc=111.498+1.173t ,据以计算各期趋势值T(见上表)。
(3)分离季节变动S。
首先剔除长期趋势的影响y/T×C,即T×C×S×I/T×C=S×I;然后根据S×I序列计算各期季节比率S。
计算结果为:1季度季节比率=0.9773,2季度季节比率=0.9874,3季度季节比率=1.0076,4季度季节比率=1.0277。
(4)预测第6年各季消费物价指数。
首先需要根据时间序列模型计算第6年各季的趋势值,即将t=19、20、21、22分别代入yc=111.498+1.173t计算得第6年各季度趋势值:1季的趋势值为133.792季趋势值为134.963季趋势值为136.144季趋势值为137.31然后分别乘以各自季节比率得到各季预测值,1季物价指数=133.79×0.9773=130.75%2季物价指数=134.96×0.9874=133.26%3季物价指数=136.14×1.0076=137.17%4季物价指数=137.31×1.0277=141.11%。
有趣的统计学案例

有趣的统计学案例
第一个案例是有关“猜猜看”的游戏。
在这个游戏中,一个人会想一个数字,然后其他人可以猜这个数字是多少。
我们可以用统计学的方法来分析这个游戏。
比如,我们可以计算所有猜测的平均值,然后和真实的数字进行比较,看看平均值是否接近真实值。
通过这个案例,我们可以了解到平均值在统计学中的重要性,以及如何利用平均值来估计未知的数值。
第二个案例是有关“点菜”的餐厅统计。
假设我们去一家餐厅吃饭,我们可以观察到不同菜品被点的频率。
通过统计每道菜被点的次数,我们可以得出哪些菜是最受欢迎的,哪些菜是不受欢迎的。
这个案例可以帮助我们了解如何利用统计学来分析消费者的偏好,以及如何根据统计结果来调整菜单和经营策略。
第三个案例是有关“天气预报”的统计分析。
天气预报是我们日常生活中经常关注的事情,而天气预报的准确性也是大家关心的问题。
我们可以通过统计方法来分析天气预报的准确性,比如计算实际天气和预报天气的差异,然后得出准确率和误差范围。
通过这个案例,我们可以了解到如何利用统计学的方法来评估和改进天气预报的准确性。
通过以上几个案例,我们可以看到统计学在日常生活中的应用和意义。
无论是游戏、餐厅还是天气预报,统计学都可以帮助我们理解和解释现象,从而更好地应对各种问题。
希望这些有趣的统计学案例能够激发你对统计学的兴趣,让你在日常生活中也能够运用统计学的知识来思考和解决问题。
统计学案例分析单选题100道及答案解析

统计学案例分析单选题100道及答案解析1. 为了了解某工厂生产的一批灯泡的使用寿命,从中抽取了100 只进行检测,在这个问题中,样本是()A. 工厂生产的一批灯泡B. 抽取的100 只灯泡C. 100D. 每只灯泡的使用寿命答案:B解析:样本是从总体中抽取的一部分个体,这里抽取的100 只灯泡就是样本。
2. 一组数据的最大值与最小值之差称为()A. 极差B. 方差C. 标准差D. 平均差答案:A解析:极差是一组数据中的最大值减去最小值。
3. 下列指标中,属于位置平均数的是()A. 算术平均数B. 调和平均数C. 几何平均数D. 中位数答案:D解析:中位数是将数据排序后,位于中间位置的数值,属于位置平均数。
4. 若一组数据的偏态系数为0,则该组数据的分布为()A. 对称分布B. 右偏分布C. 左偏分布D. 无法确定答案:A解析:偏态系数为0 时,数据分布为对称分布。
5. 抽样调查中,样本容量的确定取决于()A. 总体标准差B. 允许误差C. 抽样方法D. 以上都是答案:D解析:样本容量的确定需要考虑总体标准差、允许误差和抽样方法等因素。
6. 在假设检验中,原假设和备择假设()A. 只有一个成立B. 都有可能成立C. 都有可能不成立D. 原假设一定成立,备择假设不一定成立答案:A解析:原假设和备择假设相互对立,只有一个成立。
7. 对于两个变量之间的线性相关程度,常用()来衡量。
A. 相关系数B. 决定系数C. 回归系数D. 残差平方和答案:A解析:相关系数用于衡量两个变量之间的线性相关程度。
8. 下列哪种抽样方法不是概率抽样()A. 简单随机抽样B. 系统抽样C. 方便抽样D. 分层抽样答案:C解析:方便抽样是非概率抽样方法。
9. 一组数据的标准差越大,说明()A. 数据的离散程度越大B. 数据的离散程度越小C. 平均数越大D. 平均数越小答案:A解析:标准差越大,数据的离散程度越大。
10. 若一组数据服从正态分布,则其均值和中位数的关系是()A. 均值大于中位数B. 均值小于中位数C. 均值等于中位数D. 无法确定答案:C解析:正态分布的数据,均值等于中位数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例:联合食品公司
联合食品公司在新墨西哥州、亚利桑那州和加利福尼亚州经营连锁超市。
近来的一项促销活动已通知连锁店提供一项新的信用卡政策,使联合食品的顾客除了通常的支付现金或个人支票选择外,还有用信用卡如VISA和MasterCard卡进行购买支付的选择权。
新的政策正基于试验基础而执行,希望信用卡选择权将鼓励顾客加大采购量。
在第一月经营之后,在一个周期内选择了有100名顾客的随机样本。
100名顾客中的每一个的支付方式和消费多少的数据被收集上来。
样本数据列示在下表中。
在新的信用卡政策出现之前,大约50%的联合食品顾客用现金支付,约50%用个人支票支付。
管理报告1
使用描述性统计的表格法和图形法来汇总下表中的样本数据。
你的报告应该包括诸如下列的摘要:
支付方式的频数分布和相对频数分布。
支付方式的条形图或饼形图
每一支付方式下花费金额的频数和相对频数分布
每一支付方式下花费金额的直方图和茎叶图
你对联合食品的消费金额和支付方式有了什么样的初步了解?
管理报告2
对于客户购买以金支付金额,以支票支付金额和以信用卡支付金额的数据分别加以概括,报告应包含的概括和讨论:
对于各个平均数和中位数的比较和理解
对于各个显示变异程度的度量,如全距何标准差进行比较和理解
分别对于3种支付方式用多种多种指标进行比较和理解
在你报告的总结部分,讨论一下从中可以得出关于联合食品公司的客户支付方式和支付金额的什么结论。
现金个人支票信用卡现金个人支票信用卡
7.40 27.60 50.30 5.08 52.87 69.77
5.15 30.60 33.76 20.48 78.16 48.11
4.75 41.58 2
5.57 1
6.28 25.96
15.10 36.09 43.24 15.57 31.07
8.81 2.67 46.13 6.93 35.38
1.85 34.67 14.44 7.17 58.11
7.41 58.61 43.79 11.54 49.21
11.77 57.59 19.78 13.09 31.74
12.07 43.14 52.35 16.69 50.58
9.00 21.11 52.63 7.02 59.78
案例:预测食品和饮料的销售量
Vintage饭店位于靠近佛罗里达的Fort Myers的Captiva岛上,是一个公众常去的场所。
它由Karen Payne拥有和经营,到目前经营已超过30年。
在这期间,Karen一直在寻求店建立以新鲜海味设置的高质量正餐的饭店信誉。
Karen及其员工的努力被证实是成功的,她的饭店成为岛上最好的和营业额增长最快的饭店之一。
Karen为确定饭店未来的增长计划,需要建立一个系统,这个系统使她可提前一年预测今后每个月食品和饮料的销售量。
Karen拥有如下资料,这些资料是在三年的经营中有关食品和饮料的销售总量。
管理报告:
分析Vintage饭店的销售资料,为Karen准备一份包括你的发现、预测和建议的报告。
其内容包括:
时间数列的图形
对数据的季节性分析。
指出每个月的季节指数,并讨论个月销售量的高低。
季节指数有直观上的意义吗?对此应加以讨论。
预测第四年1~12月的销售量。
当用来说明新的销售资料时,提出对你所建立的系统的建议。
在你的报告附录中,给出分析评论的结果。
假设第四年1月份的销售额为295000美元,你的预测误差为多少?如果这个误差太大,Karen 可能会对你的预测值和实际销售额的差异产生疑虑,你将如何消除她对预测方法的疑虑?
案例:预测损失的销售额
1992年8月31日,当飓风侵袭时,Carlson百货商店遭受严重的损坏,商店被迫关闭了四个月(1992年9~12月)。
Carlson现在正与其保险公司就关闭商店期间损失的销售额进行讨价还价。
必须解决的两个关键性问题是:(1)如果没有遭到飓风的侵袭,Carlson可能得到的销售总额;(2)在飓风过后,由于增加的商业活动,额外的销售额是否是Carlson得到的补偿。
县里得到了超过80亿美元的联邦灾难救济基金和保险金,这导致了百货商店销售额的增加和其他大多数的商业活动。
如下表1给出了Carlson在飓风前48个月的销售资料,表2是美国商务部报告的在飓风前48个月和Carlson百货商店关闭4个月中,该县所有百货商店的销售总额资料。
Carlson的管理人员请你分析这些资料,以便得到Carlson百货商店1992年9~12月所示的销售额的估计。
他们也请你确定,事否可得到一个与飓风相关的同期额外销售额的案例。
如果可得到这样的案例,除正常销售额之外得到的额外销售额,将是Carlson得到的补偿。
表1 Carlson百货商店1998年9月到2002年8月的销售额(单位:十亿美元)
月份1998 1999 2000 2001 2002
1 1.45 2.31 2.31 2.56
2 1.80 1.89 1.99 2.28
3 2.03 2.02 2.42 2.69
4 1.99 2.23 2.4
5 2.48
5 2.32 2.39 2.57 2.73
6 2.20 2.14 2.42 2.37
7 2.13 2.27 2.40 2.31
8 2.43 2.21 2.50 2.23
9 1.71 1.90 1.89 2.09
10 1.90 21.3 2.29 2.54
11 2.74 2.56 2.83 2.97
12 4.20 4.16 4.04 4.35
月份1998 1999 2000 2001 2002
1 46.8 46.8 43.8 48
2 48. 48.6 45.6 51.6
3 60 59.
4 57.6 57.6
4 57.6 58.2 53.4 58.2
5 61.8 60.
6 56.4 60
6 58.2 55.2 52.8 57
7 56.4 51 54 57.6
8 63 58.8 60.6 61.8
9 55.8 57.6 49.8 47.4 69
10 56.4 53.4 54.6 54.6 75
11 71.4 71.4 65.4 67.8 85.2
12 117.6 114 102 100.2 121.8
为Carlson百货商店的管理人员准备一份包括你的发现、预测和建议的报告。
其内容包括:若没有飓风Carlson百货商店销售额的估计
若没有飓风全县百货商店销售额的估计
Carlson百货商店2002年9-12损失的销售额的估计。
