八年级上册数学第一章勾股定理知识点与练习知识讲解
八年级上册数学 第一章 勾股定理基本题型总结(经典全面)

CA BDBAC DB专题复习:勾股定理1、勾股定理考点一、勾股定理定义:直角三角形两直角边的平方和等于斜边的平方。
解释:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2(古时候把直角三角形中较短边叫做“勾”,较长的直角边为“股”,斜边称为“弦”)典型例题例题1、(1)在直角三角形ABC中,AC=5,BC=12,求AB的长。
(2)在直角三角形ABC中,AB=25,AC=20,求BC的长。
常见的勾股数:3,4,5;5,12,13;6,8,10等技巧总结:利用勾股定理,在直角三角形中,已知两边可求第三边;一般情况下,用a,b 表示直角边,c表示斜边,则有a2+b2=c2,还可以有其他形式的变式。
例题2、一个零件的的形状如图所示,已知AC=3,AB=4,BD=12,求CD的长.例题3、如图所示,已知三角形ABC中,AB=10,BC=21,AC=17,求BC边上的高。
技巧总结:有时某些线段不可以直接写出来,可以用数学转化的思想,构造直角三角形,再求出答案,也可以用勾股定理建立方程去求。
例题4、如图,台风过后某小学的旗杆在B处断裂,旗杆顶部A落在离旗杆底部点C8米处,已知旗杆长16米,则旗杆是在距底部多少米处断裂?技巧总结:要用勾股定理的变形公式。
例题5、已知:在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证:a 2+b 2=c 2。
技巧总结:分析:左右两边的正方形边长相等,则两个正方形的面积相等。
左边S=4×21ab +c 2,右边S=(a+b )2,左边和右边面积相等,即4×21ab +c 2=(a+b )2 对应的课堂练习:1. 下列说法正确的是( )A .若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2B .若 a 、b 、c 是Rt △ABC 的三边,则a 2+b 2=c 2C .若 a 、b 、c 是Rt △ABC 的三边, 90=∠A ,则a 2+b 2=c 2D .若 a 、b 、c 是Rt △ABC 的三边, 90=∠C ,则a 2+b 2=c 22. △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( ) A .c b a =+ B.c b a >+ C.c b a <+ D.222c b a =+ 3.一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( ) A .斜边长为25 B .三角形周长为25C .斜边长为5D .三角形面积为20 4.在R t A B C ∆中, 90=∠C , (1)如果a =3,b =4,则c = ; (2)如果a =6,b =8,则c = ; (3)如果a =5,b =12,则c = ;(4) 如果a =15,b =20,则c = .5.如图,三个正方形中的两个的面积S 1=25,S 2=144,则另一个的面积S 3为_______1.如图,直角△ABC 的主要性质是:∠C=90°,(用几何语言表示)⑴两锐角之间的关系: ;⑵若D 为斜边中点,则斜边中线 ;⑶若∠B=30°,则∠B 的对边和斜边: ;⑷三边之间的关系: 。
北师版八年级数学上册第一章 勾股定理1 探索勾股定理

式中,涉及三个量,可“知二求一”.如果在直角
三角形中,已知两边的比值和另一边时,通常引入
一个辅助量,建立方程来求未知的边 .
2.运用勾股定理时,若分不清哪条边是斜边,则要分
类讨论,写出所有可能情况,以免漏解或错解 .
知1-练
例1 [母题 教材P4习题T1]在Rt△ABC中, ∠A,∠B,∠C 的对边分别为a,b,c,∠C=90° . (1)已知a=3,b=4,求c; (2)已知c=13,a=5,求b.
a2=c2-b2; b2=c2-a2
知1-讲
图示
感悟新知
知1-讲
勾股定理把“形”与 “数”有机地结合
基本思想
起来,即把直角三角形这个“形”与三 边关系这一“数”结合起来,它是数形
结合思想的典范
感悟新知
特别提醒
知1-讲
1. 在 Rt △ ABC 中,∠ C=90°,∠ A,∠ B,∠C的
对边分别为a,b,c,则有关系式a2+b2=c2. 在此关系
特别提醒
知2-讲
通过拼图验证定理的思路:
1. 图形经过割补拼接后,只要没有重叠、没有空隙,面积就不
会改变;
2. 根据同一种图形的面积的不同表示方法列出等式;
3. 利用等式性质变换验证结论成立.
即拼出图形→写出图形面积的表达式→找出等量关系→恒等变
形→推导结论.
续表 方法
伽菲尔德 总统拼图
图形
知2-讲
知1-练
感悟新知
1-1.在 Rt △ ABC 中,∠ C=90 °,∠ A,∠ B,∠ C知1-练 的对边分别为 a,b, c. 若 a ∶ b=3 ∶ 4,c=75, 求 a, b. 解:设a=3x(x>0),则b=4x. 由勾股定理得a2+b2=c2, 则(3x)2+(4x)2=752,解得x=15(负值已舍去). 所以a=3×15=45,b=4×15=60.
八年级上册数学第一章勾股定理知识点与练习

八年级上册数学第一章勾股定理知识点与练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN勾股定理知识点一:勾股定理勾股定理: . 勾股数: .常见勾股数:3、4、5; 6、8、10; 5、12、13; 8、15、17; 7、24、25。
要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用: (1)已知直角三角形的两边求第三边(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边 (3)利用勾股定理可以证明线段平方关系的问题 例1、若Rt ABC 中,90C ︒∠=且a=5,b=12,则c= ,例2、Rt △ABC 中,若c=10,a ∶b=3∶4,则a= ,b= .例3、如图,由Rt△ABC 的三边向外作正方形,若最大正方形的边长为8cm ,则正方形M 与正方形N 的面积之和为2_____cm4、下列各组数:①0.3,0.4,0.5;②9,12,16;③4,5,6;④a 8,a 15,a 17(0≠a ); ⑤9,40,41。
其中是勾股数的有( )组 A 、1 B 、2 C 、3 D 、4练习1、在△ABC 中,∠C=90°,c=37,a=12,则b=( )A 、50B 、35C 、34D 、262、在Rt △ABC 中,∠C=90°,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是( )A.5、4、3B.13、12、5C.10、8、6D.26、24、103、若一个直角三角形的三边分别为a 、b 、c, 22144,25a b ==,则2c =( ) A 、169 B 、119 C 、169或119 D 、13或25知识点二:勾股定理的逆定理勾股定理的逆定理:例1、三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形是 ( ).S 3S 2S 1CBAA 、钝角三角形B 、锐角三角形C 、直角三角形D 、等边三角形例2、在△ABC 中,若AB=2,AC=2,BC=2,则∠B= 。
数学八年级上册知识点第一章

数学八年级上册知识点第一章数学八年级上册知识点第一章1.勾股定理的内容:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方。
注:勾最短的边、股较长的直角边、弦斜边。
勾股定理又叫毕达哥拉斯定理2.勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
3.勾股数:满足a2 +b2=c2的三个正整数,称为勾股数.勾股数扩大相同倍数后,仍为勾股数.常用勾股数:3、4、5; 5、12、13;7、24、25;8、15、17。
4.勾股定理常常用来算线段长度,对于初中阶段的线段的计算起到很大的作用例题精讲:练习:例1:若一个直角三角形三边的.长分别是三个连续的自然数,则这个三角形的周长为解析:可知三边长度为3,4,5,因此周长为12(变式)一个直角三角形的三边为三个连续偶数,则它的三边长分别为解析:可知三边长度为6,8,10,则周长为24例2:已知直角三角形的两边长分别为3、4,求第三边长.解析:第一种情况:当直角边为3和4时,则斜边为5第二种情况:当斜边长度为4时,一条直角边为3,则另一边为根号7例3:一个直角三角形中,两直角边长分别为3和4,以下说法正确的是( )A.斜边长为25B.三角形周长为25C.斜边长为5D.三角形面积为20解析:根据勾股定理,可知斜边长度为5,选择C数学学习方法诀窍1细心地发掘概念和公式很多同学对概念和公式不够重视,这类问题反映在三个方面:一是,对概念的理解只是停留在文字表面,对概念的特殊情况重视不够。
例如,在代数式的概念(用字母或数字表示的式子是代数式)中,很多同学忽略了“单个字母或数字也是代数式〞。
二是,对概念和公式一味的死记硬背,缺乏与实际题目的联系。
这样就不能很好的将学到的知识点与解题联系起来。
三是,一部分同学不重视对数学公式的记忆。
记忆是理解的基础。
如果你不能将公式烂熟于心,又怎能够在题目中熟练应用呢?我们的建议是:更细心一点(观察特例),更深入一点(了解它在题目中的常见考点),更熟练一点(无论它以什么面目出现,我们都能够应用自如)。
北师大版八年级上册数学第一章勾股定理全章知识点及习题(经典)
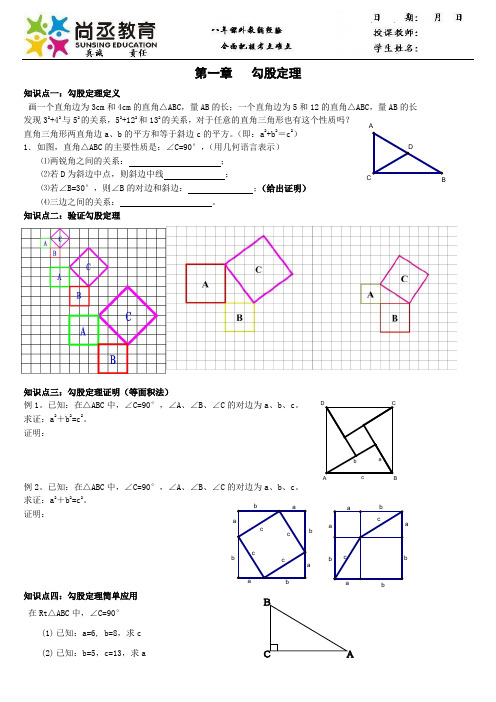
cbaD CAB第一章 勾股定理知识点一:勾股定理定义画一个直角边为3cm 和4cm 的直角△ABC ,量AB 的长;一个直角边为5和12的直角△ABC ,量AB 的长 发现32+42与52的关系,52+122和132的关系,对于任意的直角三角形也有这个性质吗? 直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 1.如图,直角△ABC 的主要性质是:∠C=90°,(用几何语言表示)⑴两锐角之间的关系: ; ⑵若D 为斜边中点,则斜边中线 ;⑶若∠B=30°,则∠B 的对边和斜边: ;(给出证明) ⑷三边之间的关系: 。
知识点二:验证勾股定理知识点三:勾股定理证明(等面积法)例1。
已知:在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证:a 2+b 2=c 2。
证明:例2。
已知:在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证:a 2+b 2=c 2。
证明:知识点四:勾股定理简单应用 在Rt △ABC 中,∠C=90°(1) 已知:a=6, b=8,求c bbbbccccaaaabbb ba accaaACBDAB如果三角形的三边长为c b a ,,,满足222c b a =+,那么,这个三角形是直角三角形. 利用勾股定理的逆定理判别直角三角形的一般步骤: ①先找出最大边(如c )②计算2c 与22a b +,并验证是否相等。
若2c =22a b +,则△ABC 是直角三角形。
若2c ≠22a b +,则△ABC 不是直角三角形。
1.下列各组数中,以a ,b ,c 为边的三角形不是Rt △的是( ) A.a=7,b=24,c=25 B.a=7,b=24,c=24C.a=6,b=8,c=10D.a=3,b=4,c=52.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A. 等边三角形B. 钝角三角形C. 直角三角形D. 锐角三角形3.已知0)10(862=-+-+-z y x ,则由此z y x ,,为三边的三角形是 三角形. 知识点六:勾股数(1)满足222c b a =+的三个正整数,称为勾股数.(2)勾股数中各数的相同的整数倍,仍是勾股数,如3、4、5是勾股数,6、8、10也是勾股数. (3)常见的勾股数有:①3、4、5②5、12、13;③8、15、17;④7、24、25; ⑤11、60、61;⑥9、40、41.1.设a 、b 、c 是直角三角形的三边,则a 、b 、c 不可能的是( ).A.3,5,4B. 5,12,13C.2,3,4D.8,17,15 1. 若线段a ,b ,c 组成Rt △,则它们的比可以是( )A.2∶3∶4B.3∶4∶6C.5∶12∶13D.4∶6∶7知识点七:确定最短路线1.一只长方体木箱如图所示,长、宽、高分别为5cm 、4cm 、3cm, 有一只甲虫从A 出发,沿表面爬到C ',最近距离是多少?2.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程(π 取3)是 .知识点八:逆定理判断垂直1.在△ABC 中,已知AB 2-BC 2=CA 2,则△ABC 的形状是( )A .锐角三角形;B .直角三角形;C .钝角三角形;D .无法确定. 2.如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是( )ABCD A 'B 'C 'D 'BC5米3米1.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?2.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要________米.3.一根直立的桅杆原长25m,折断后,桅杆的顶部落在离底部的5m处,则桅杆断后两部分各是多长?4.某中学八年级学生想知道学校操场上旗杆的高度,他们发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?综合练习一一、选择题1、下面几组数:①7,8,9;②12,9,15;③m 2+ n 2, m 2– n 2, 2mn(m,n 均为正整数,m >n);④2a ,12+a ,22+a .其中能组成直角三角形的三边长的是( )A.①②;B.①③;C.②③;D.③④2已知一个Rt △的两边长分别为3和4,则第三边长的平方是( )A.25B.14C.7D.7或253.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A. 等边三角形;B. 钝角三角形;C. 直角三角形;D. 锐角三角形. 4.△ABC 的三边为a 、b 、c 且(a+b)(a-b)=c 2,则( )A.a 边的对角是直角B.b 边的对角是直角C.c 边的对角是直角D.是斜三角形5.以下列各组中的三个数为边长的三角形是直角三角形的个数有( )①6、7、8,②8、15、17,③7、24、25,④12、35、37,⑤9、40、41 A 、1个 B 、2个 C 、3个 D 、4个6.将直角三角形的三边扩大相同的倍数后,得到的三角形是 ( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形7.若△ABC 的三边a 、b 、c 满足(a-b)(a 2+b 2-c 2)=0,则△ABC 是 ( ) A.等腰三角形 B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形8.如图,∠C =∠B =90°,AB =5,BC =8,CD =11,则AD 的长为 ( )A 、10B 、11C 、12D 、139.如图、山坡AB 的高BC =5m ,水平距离AC =12m ,若在山坡上每隔0.65m 栽一棵茶树,则从上到下共 ( )A 、19棵B 、20棵C 、21棵D 、22棵10.Rt △ABC 中,∠C =90°,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,若c =2,则2a +2b +2c 的值是 ( )A 、6B 、8C 、10D 、4 11.下列各组数据中,不能构成直角三角形的一组数是( )A、9,12,15 B 、45,1,43C 、0.2,0.3,0.4D 、40,41,9 12.已知,一轮船以16海里/时的速度从港口A 出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后,则两船相距( )A.25海里B.30海里C.35海里D.40海里二、填空题1.在Rt △ABC 中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a ∶b=3∶4,c=10则S Rt △ABC =________2.现有长度分别为2cm 、3cm 、4cm 、5cm 的木棒,从中任取三根,能组成直角三角形,则其周长为 cm .3.勾股定理的作用是在直角三角形中,已知两边求 ;勾股定理的逆定理的作用是用来证明 .4.如图中字母所代表的正方形的面积:A = B = . A815.在△ABC 中,∠C =90°,若 a =5,b =12,则 c = .6.△ABC 中,AB=AC=17cm ,BC=16cm ,则高AD= ,S △ABC = 。
八年级上第一章勾股定理知识点与常见题型总结及练习

一.知识归纳
1.勾股定理 内容:直角三角形两直角边的平方和等于斜边的平方; 表示方法:如果直角三角形的两直角边分别为 a , b ,斜边为 c ,那么 a2 b2 c2
2.勾股定理的证明 勾股定理的证明方法很多,常见的是拼图的方法
m2 n2 , 2mn,m2 n2 ( m n, m , n 为正整数)
A、40
B、80
C、40 或 360 D、80 或 360
7、如图,在 Rt△ABC 中,∠C=90°,D 为 AC 上一点,且 DA=DB=5,又△DAB 的面积为 10,那么 DC 的 长是( )
A、4
B、3
C、5
D、4.5
A B
D C
C D
A E
A′ B′
第 9 题图
D′ C′
A
第 7 题图
B
分析:此题将勾股定理与全等三角形的知识结合起来 例 4.如图 RtABC , C 90 AC 3, BC 4 ,分别以各边为直径作半圆,求阴影部分面积
n2 1, 2n,n2 1 ( n 2, n 为正整数); 2n 1, 2n2 2n, 2n2 2n 1 ( n 为正整数)
7.勾股定理的应用 8..勾股定理逆定理的应用 9.勾股定理及其逆定理的应用
二、常见考题分析
3.勾股定理的适用范围 勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形 的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用 ①已知直角三角形的任意两边长,求第三边
在 ABC 中, C 90 ,则 c a2 b2 , b c2 a2 , a c2 b2
八年级数学上册 知识点总结

八年级数学上册知识点总结数学》(八年级上册)知识点总结第一章勾股定理1、勾股定理:直角三角形两直角边a,b的平方和等于斜边c的平方,即a²+b²=c²。
2、勾股定理的逆定理:如果三角形的三边长a,b,c有关系a²+b²=c²,那么这个三角形是直角三角形。
3、勾股数:满足a²+b²=c²的三个正整数,称为勾股数。
第二章实数一、实数的概念及分类1、实数的分类:正有理数、有理数零有限小数和无限循环小数、实数负有理数、正无理数、无理数无限不循环小数、负无理数。
2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一特点,归纳起来有四类:1)开方开不尽的数,如7、32等;2)有特定意义的数,如圆周率π,或化简后含有π的数,如222π+8等;3)有特定结构的数,如0.xxxxxxxx01…等;4)某些三角函数值,如sin60等。
二、实数的倒数、相反数和绝对值1、相反数:实数与它的相反数是一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a与b互为相反数,则有a+b=0,a=−b,反之亦成立。
2、绝对值:在数轴上,一个数所对应的点与原点的距离,叫做该数的绝对值(|a|≥)。
零的绝对值是它本身,也可看成它的相反数,若|a|=a,则a≥;若|a|=−a,则a≤。
3、倒数:如果a与b互为倒数,则有ab=1,反之亦成立。
倒数等于本身的数是1和−1.零没有倒数。
4、数轴:规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
5、估算。
三、平方根、算数平方根和立方根1、算术平方根:一般地,如果一个正数x的平方等于a,即x²=a,那么这个正数x就叫做a的算术平方根。
北师大版八年级上册第一章知识点

北师大版八年级上册第一章知识点一、勾股定理。
1. 定理内容。
- 直角三角形两直角边的平方和等于斜边的平方。
如果直角三角形的两条直角边长度分别为a和b,斜边长度为c,那么a^2+b^2=c^2。
- 例如,一个直角三角形的两条直角边分别为3和4,那么斜边的平方c^2=3^2+4^2=9 + 16=25,所以斜边c = 5。
2. 勾股定理的证明。
- 常见的证明方法有赵爽弦图证明法等。
- 赵爽弦图:以直角三角形的斜边c为边长的正方形的面积等于以直角边a、b 为边长的四个直角三角形与一个小正方形面积之和。
即c^2=4×(1)/(2)ab+(b - a)^2,化简后可得c^2=a^2+b^2。
3. 勾股定理的应用。
- 已知直角三角形的两边求第三边。
- 当已知两条直角边a、b时,斜边c=√(a^2)+b^{2}。
- 当已知一条直角边a和斜边c时,另一条直角边b=√(c^2)-a^{2}。
- 解决实际问题中的直角三角形问题。
- 例如,在一个长方形中求对角线长度(长方形的相邻两边与对角线构成直角三角形);在一个梯形中,通过作高构造直角三角形来求相关线段长度等。
二、勾股定理的逆定理。
1. 定理内容。
- 如果三角形的三边长a、b、c满足a^2+b^2=c^2,那么这个三角形是直角三角形。
2. 判断直角三角形的方法。
- 首先计算三边的平方,看是否满足两短边的平方和等于长边的平方。
- 例如,三角形三边分别为3、4、5,因为3^2+4^2=9 + 16 = 25=5^2,所以这个三角形是直角三角形,其中边长为5的边所对的角为直角。
3. 勾股数。
- 满足a^2+b^2=c^2的三个正整数,称为勾股数。
常见的勾股数有(3,4,5)、(5,12,13)、(8,15,17)等。
- 如果(a,b,c)是一组勾股数,那么ka、kb、kc(k为正整数)也是一组勾股数。
例如,(3,4,5)是勾股数,那么(6,8,10)(k = 2时)也是勾股数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册数学第一章勾股定理知识点与
练习
勾股定理
知识点一:勾股定理
勾股定理: . 勾股数: .
常见勾股数:3、4、5; 6、8、10; 5、12、13; 8、15、17; 7、24、25。
要点诠释:
勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用: (1)已知直角三角形的两边求第三边
(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边 (3)利用勾股定理可以证明线段平方关系的问题 例1、若Rt ABC 中,90C ︒∠=且a=5,b=12,则c= ,
例2、Rt △ABC 中,若c=10,a ∶b=3∶4,则a= ,b= .
例3、如图,由Rt△ABC 的三边向外作正方形,若最大正方形的边长为8cm ,
则正方形M 与正方形N 的面积之和为2_____cm
4、下列各组数:①0.3,0.4,0.5;②9,12,16;③4,5,6;④a 8,a 15,a 17(0≠a ); ⑤9,40,41。
其中是勾股数的有( )组 A 、1 B 、2 C 、3 D 、4
练习
1、在△ABC 中,∠C=90°,c=37,a=12,则b=( )
A 、50
B 、35
C 、34
D 、26
2、在Rt △ABC 中,∠C=90°,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是( )
A.5、4、3
B.13、12、5
C.10、8、6
D.26、24、10
3、若一个直角三角形的三边分别为a 、b 、c, 22144,25a b ==,则2c =( ) A 、169 B 、119 C 、169或119 D 、13或25
知识点二:勾股定理的逆定理
勾股定理的逆定理:
例1、三角形的三边长a,b,c满足2ab=(a+b)2
-c2
,则此三角形是 ( ).
S 3
S 2
S 1
C
B
A
A 、钝角三角形
B 、锐角三角形
C 、直角三角形
D 、等边三角形
例2、在△ABC 中,若AB=2,AC=2,BC=2,则∠B= 。
练习
1、 已知a 、b 、c
是三角形的三边长,如果满足2(6)100a c --=,则三角形的形状是( )
A :底与边不相等的等腰三角形
B :等边三角形
C :钝角三角形
D :直角三角形
2、△ABC 中,若a ∶b ∶c=1∶3∶2,则∠A ∶∠B ∶∠C= .
知识点三:运用勾股定理和勾股定理的逆定理解生活中的实际问题
①勾股定理揭示了直角三角形三边的关系,其作用:已知两边求第三边;证明三角形中某些线段的平方关系;作长为m 的线段。
②勾股定理的逆定理常用来判断一个三角形是否为直角三角形。
例1、有一个小孩站在距他1米且比他高50厘米的向日葵旁边,当风吹倒向日葵时, 向日葵的顶处正好可以碰到他的头顶,那么你能计算出向日葵和小孩的高度吗? 练习
1、一艘轮船以16km/h 速度离开港口向东北方向航行,另一艘轮船同时离开港口以12km/h 的速度向东南方向航行,它们离开一个半小时后相距 。
综合练习
1、在Rt △ABC 中,∠C =90°,a =12,b =16,则c 的长为( )
A .26
B .18
C .20
D .21 2、在下列数组中,能构成一个直角三角形的有( ) ①10,20,25;②10,24,25;③9,80,81;④8;15;17 A 、4组 B 、3组 C 、2组 D 、1组
3、将Rt △ABC 的三边都扩大为原来的2倍,得△A ’B ’C ’,则△A ’B ’C ’为( ) A 、 直角三角形 B 、锐角三角形 C 、钝角三角形 D 、无法确定
4、如图所示,以Rt ABC 的三边向 外作正方形,其面积分别
为123,,S S S ,且1234,8,S S S ===则 ;
5、如图,为修通铁路凿通隧道AC ,量出∠A=40°∠B =50°, AB =5公里,BC =4公里,若每天凿隧道0.3公里, 问几天才能把隧道AB 凿通?
6、有两棵树,一棵高6米,另一棵高2米,两树相距5米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米.
勾股定理作业
1、在Rt △ABC 中,斜边AB=2,则=++222CA BC AB .
2、.如图一轮船以16海里/时的速度从港口A 出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后,则两船相距 ( ) A 、25海里
B 、30海里
C 、35海里
D 、40海里
3、一直角三角形的斜边长比直角边长大2,另一直角边长为6,则斜边长为( ) A.4 B.8 C.10 D.12
4、已知等腰三角形的腰长为10,一腰上的高为6,则以底边为边长的正方形的面积为( )
A 、40
B 、80
C 、40或360
D 、80或360
5、要登上12米高的建筑物,为了安全起见,要使梯子的底端离建筑物5米,则至少需要 米长的梯子。
6、在四边形ABCD 中,∠C=90°,AB=13,BC=4,CD=3,AD=12.
C
A
B
D
①AD ⊥BD 吗?为什么?②求四边形ABCD 的面积。
7、如图,已知在△ABC 中,CD ⊥AB 于D ,AC =20,BC =15,DB =9。
(1)求DC 的长。
(2)求AB 的长。
C
A
D。
