常应变三角形单元
三角形常应变单元程序的编制与使用11页

三角形常应变单元程序的编制与使用有限元法是求解微分方程边值问题的一种通用数值方法,该方法是一种基于变分法(或变分里兹法)而发展起来的求解微分方程的数值计算方法,以计算机为手段,采用分片近似,进而逼近整体的研究思想求解物理问题。
有限元分析的基本步骤可归纳为三大步:结构离散、单元分析和整体分析。
对于平面问题,结构离散常用的网格形状有三角形、矩形、任意四边形,以三个顶点为节点的三角形单元是最简单的平面单元,它较矩形或四边形对曲边边界有更好的适应性,而矩形或四边形单元较三节点三角形有更高的计算精度。
Matlab语言是进行矩阵运算的强大工具,因此,用Matlab语言编写有限元中平面问题的程序有优越性。
本章将详细介绍如何利用Matlab语言编制三角形常应变单元的计算程序,程序流程图见图1。
有限元法中三节点三角形分析结构的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,离散结构并进行单元编码、结点编码、结点位移编码、选取坐标系。
2)单元分析,建立单元刚度矩阵。
3)整体分析,建立总刚矩阵。
4)建立整体结构的等效节点荷载和总荷载矩阵5)边界条件处理。
6)解方程,求出节点位移。
7)求出各单元的单元应力。
8)计算结果整理。
计算结果整理包括位移和应力两个方面;位移计算结果一般不需要特别的处理,利用计算出的节点位移分量,就可画出结构任意方向的位移云图;而应力解的误差表现在单元内部不满足平衡方程,单元与单元边界处应力一般不连续,在边界上应力解一般与力的边界条件不相符合。
图1 程序流程图1.1 程序说明% 三角形常应变单元求解结构主程序●功能:运用有限元法中三角形常应变单元解平面问题的计算主程序。
●基本思想:单元结点按右手法则顺序编号。
●荷载类型:可计算结点荷载。
●说明:主程序的作用是通过赋值语句、读取和写入文件、函数调用等完成算法的全过程,即实现程序流程图的程序表达。
1 程序准备format short e %设定输出类型clear all %清除所有已定义变量clc %清屏●说明:format short e -设定计算过程中显示在屏幕上的数字类型为短格式、科学计数法;clear all -清除所有已定义变量,目的是在本程序的运行过程中,不会发生变量名相同等可能使计算出错的情况;clc -清屏,使屏幕在本程序运行开始时2 全局变量定义global NNODE NPION NELEM NVFIX NFORCE COORD LNODS YOUNG POISS THICKglobal FORCE FIXEDglobal BMATX DMATX SMATX AREAglobal ASTIF ASLOD ASDISPglobal FP1●说明:NNODE—单元结点数,NPION—总结点数,NELEM—单元数,NVFIX—受约束边界点数,NFORCE—结点力数,COORD—结构结点坐标数组,LNODS —单元定义数组,YOUNG—弹性模量,POISS—泊松比,THICK—厚度FORCE —节点力数组(n,3) n:受力节点数目,(n,1):作用点,(n,2):x方向,(n,3):y 方向;FIXED—约束信息数组(n,3) n:受约束节点数目, (n,1):约束点(n,2)与(n,3)分别为约束点x方向和y方向的约束情况,受约束为1否则为0BMATX—单元应变矩阵(3*6),DMATX—单元弹性矩阵(3*3),SMATX—单元应力矩阵(3*6),AREA—单元面积ASTIF—总体刚度矩阵,ASLOD—总体荷载向量,ASDISP—结点位移向量FP1—数据文件指针3 打开文件FP1=fopen('input.txt','rt'); %打开输入数据文件存放初始数据●说明:FP1=fopen('input.txt','rt'); -打开已存在的输入数据文件input.txt,且设置其为只读格式,使程序在执行过程中不能改变输入文件中的数值,并用文件句柄FP1来执行FP2=fopen('output.txt','wt'); -打开输出数据文件,该文件不存在时,通过此命令创建新文件,该文件存在时则将原有内容全部删除。
有限元基础知识归纳

有限元知识点归纳1.、有限元解的特点、原因?答:有限元解一般偏小,即位移解下限性原因:单元原是连续体的一局部,具有无限多个自由度。
在假定了单元的位移函数后,自由度限制为只有以节点位移表示的有限自由度,即位移函数对单元的变形进行了约束和限制,使单元的刚度较实际连续体加强了,因此,连续体的整体刚度随之增加,离散后的刚度较实际的刚度K为大,因此求得的位移近似解总体上将小于精确解。
2、形函数收敛准那么〔写出某种单元的形函数,并讨论收敛性〕P49(1)在节点i处N i=1,其它节点N i=0;(2)在单元之间,必须使由其定义的未知量连续;(3)应包含完全一次多项式;(4)应满足∑Ni=1以上条件是使单元满足收敛条件所必须得。
可以推证,由满足以上条件的形函数所建单元是完备协调的单元,所以一定是收敛的。
4、等参元的概念、特点、用时注意什么?〔王勖成P131〕答:等参元—为了将局部坐标中几何形状规那么的单元转换成总体〔笛卡尔〕坐标中的几何形状扭曲的单元,以满足对一般形状求解域进行离散化的需要,必须建立一个坐标变换。
即:为建立上述的变换,最方便的方法是将上式表示成插值函数的形式,即:其中m是用以进行坐标变换的单元节点数,xi,yi,zi是这些结点在总体〔笛卡尔〕坐标内的坐标值,Ni’称为形状函数,实际上它也是局部坐标表示的插值函数。
称前者为母单元,后者为子单元。
还可以看到坐标变换关系式和函数插值表示式:在形式上是相同的。
如果坐标变换和函数插值采用相同的结点,并且采用相同的插值函数,即m=n,Ni’=Ni,那么称这种变换为等参变换。
5、单元离散?P42答:离散化既是将连续体用假想的线或面分割成有限个局部,各局部之间用有限个点相连。
每个局部称为一个单元,连接点称为结点。
对于平面问题,最简单、最常用的离散方式是将其分解成有限个三角形单元,单元之间在三角形顶点上相连。
这种单元称为常应变三角形单元。
常用的单元离散有三节点三角形单元、六节点三角形单元、四节点四边形单元、八节点四边形单元以及等参元。
计算力学(有限单元法)第三章重点整理

第三章一、三角形单元(常应变单元)1)三角形单元位移函数:123456u a a x a yv a a x a y =++⎧⎨=++⎩2)位移函数用形函数来表示:i i j j m mi i j j m mu N u N u N u v N v N v N v =++⎧⎨=++⎩其中1()(,,)2i i i i N a bx c y i j m A =++,,(,,)i j m m ji j m ij m a x y x y b y y i j m c x x ⎧=-⎪=-⎨⎪=-+⎩,11121i i j j mmx y A x y x y = 形函数用单元节点位移分量来描述位移函数的插值函数,反映了单元的位移形态,数学是反映了节点位移对单元内任一点位移的插值。
矩阵形式:0000i i ijm j ijm jm m u v N N N u u N NN v v u v ⎧⎫⎪⎪⎪⎪⎪⎪⎡⎤⎧⎫⎪⎪=⎨⎬⎨⎬⎢⎥⎩⎭⎣⎦⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭或{}[]{}[][]{}i j m f N N N N δδ⎡⎤⎡⎤==⎣⎦⎣⎦4)单元应变:{}[]{}B εδ=(其中[]B 为常量)由x y xy u x v y u v y x εεγ⎧⎫∂⎪⎪∂⎪⎪⎧⎫⎪⎪∂⎪⎪=⎨⎬⎨⎬∂⎪⎪⎪⎪⎩⎭⎪⎪∂∂+⎪⎪∂∂⎩⎭得到[]001002ii i i i i i i i Nx b N B c y Ac b N N yx ⎡⎤∂⎢⎥∂⎢⎥⎡⎤⎢⎥∂⎢⎥==⎢⎥⎢⎥∂⎢⎥⎢⎥⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦应变和节点位移关系式:00010002i i x i j m j y i j m j xy iijjmm m m u v b b b u c c c v A c b c b c b u v εεγ⎧⎫⎪⎪⎪⎪⎧⎫⎡⎤⎪⎪⎪⎪⎢⎥⎪⎪=⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭⎣⎦⎪⎪⎪⎪⎪⎪⎩⎭5)单元应力:{}[][]{}{}[]D B S σδδ==其中36[][[][][]]i j k S S S S ⨯=平面应力问题2[],(,,)2(1)1122i i i i ii i b c ES b c i j m Ac b μμμμμ⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥--⎢⎥⎣⎦平面应变问题将上式中的21E E μ=-6)单元平衡方程:{}{}[]d k F δ=,{}{}{}{}d V S c F F F p =++7)单元刚度矩阵:[][][][]TVk B D B dv=⎰(表示单元力和单元位移关系间的系数,代表单元的刚度特性)性质:(1)三角形单元刚度矩阵与坐标系无关,即单元刚度矩阵[]k 不随单元或坐标轴的平行移动或作n π角度的转动而改变(平面问题的单元刚度矩阵可以认为是结构坐标系中的单元刚度矩阵,没有坐标变换问题) (2)单元刚度矩阵中每个元素ij k 的物理意义表示单元第j 个自由度产生单位位移,其它自由度固定时,第i 个自由度产生的节点力。
4平面问题有限元分析

引 言 常应变三角形单元 矩形双线性单元 三角形类单元形函数 矩形类单元形函数 平面等参数单元 Wilson 非协调元及程序
引
言
杆系问题以结点作为分割单元的“结点”是很自然的, 杆系问题以结点作为分割单元的“结点”是很自然的, 但对于平面问题,待分析物体是连续的, 但对于平面问题,待分析物体是连续的,并不存在实际 结点。要将物体“ 成单元, 结点。要将物体“拆”成单元,必须用一些假想的线或 将物体进行分割时, 将物体进行分割时,必须保证相 面作人为地分割。 面作人为地分割。 邻单元具有公共边界。假定相邻单元仅在一些点(顶点 邻单元具有公共边界。假定相邻单元仅在一些点( 或顶点加边中点)相连接。这些点即为“结点” 或顶点加边中点)相连接。这些点即为“结点”。实际 计算时,可将连续体分成多种形状单元,为讨论简单, 计算时,可将连续体分成多种形状单元,为讨论简单, 现暂时规定只用一种单元来分割。 现暂时规定只用一种单元来分割。 以位移为未知量的有限元法, 以位移为未知量的有限元法,最关键的工作是建立单 元位移场,因此本章主要介绍各种单元位移场的建立。 元位移场,因此本章主要介绍各种单元位移场的建立。 平面问题有限元法可用的单元很多, 平面问题有限元法可用的单元很多,先介绍两种最简 单的单元:三角形和矩形。然后再介绍其它的单元。 单的单元:三角形和矩形。然后再介绍其它的单元。
常应变三角形单元
由于面积坐标有形函数性质, 3 位移模式 由于面积坐标有形函数性质,因 3 此根据试凑法可得 形函数= 形函数 Ni=Li = 面积坐标 y P 位移为u 如果结点 i 位移为 i、vi,则 2 单元位移模式(位移场) 单元位移模式(位移场)为 1 x u=Σ Niui ; v=Σ Nivi Σ Σ 1) 面积坐标和直角坐标关系
结构力学练习题及答案
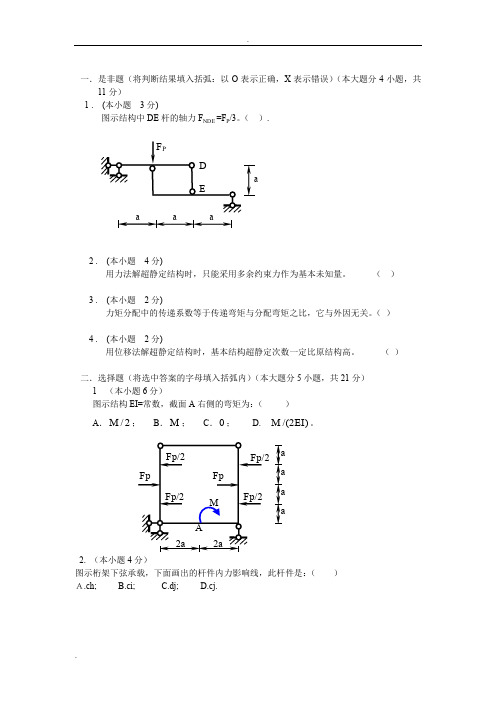
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
9第2章弹性力学平面问题及空间问题有限元

假定的位移函数是多项式,它是连续函数,可以肯定,在单元内部位移函数是单值连续的。由于单 元的位移函数 u 、 v 都是坐标 x 、 y 的线性函数,在单元边界上位移也是线性变化的,两个相邻单元在 公共节点上具有相同的节点位移,因而相邻单元在公共边界上位移连续,即协调条件得到满足。 由上面分析可以看出,三角形常应变单元的位移模式可以保证计算结果的收敛。
px
py
px
py ]
T
(2-1-7b)
(2 )若在 jm 边上受线性分布的水平方向的面力,它在 j 点的集度为 q ,在 m 点的集度为零 (如图 2-5) 。可预计由该面力求得的等效节点载荷只有 R xj 、
R xm ,其余节点载荷分量必为零。
将 jm 边上的分布面力写成 s 的函数,为
s { p} [ (1 ) q 0]T l 在 jm 边上的形函数也需用变量 s 表示,根据形函数的含义,
Ve
[k ii ] [k ij ] [ k im ] [k ji ] [k ij ] [k jm ] [k mi ] [ k mj ] [k mm ]
式中, t 为单元的厚度,当单元划分得足够小时,可以认为每个单元的厚度 t 为常值。子阵为
(2-1-5)
[k rs ] [ Br ]T [ D][B s ]tA
101
二、 单元刚度矩阵 1、单元几何矩阵 [ B ] 有了单元的位移模式,利用平面问题的几何方程求得应变分量
0 x x u e e 0 { } [ L][ N ]{} [B ]{} y y v xy y x
三角形常应变单元

第五章P77,求解三角形常应变单元刚度矩阵****************************************************************************** function y=linear_triangle_element_stiffness(E,NU,t,xi,yi,xj,yj,xm,ym,p)%A=(xi*(yj-ym)+xj*(ym-yi)+xm*(yi-yj))/2;betai=yj-ym;betaj=ym-yi;betam=yi-yj;gammai=xm-xj;gammaj=xi-xm;gammam=xj-xi;B=[betai 0 betaj 0 betam 0;0 gammai 0 gammaj 0 gammam;gammai betai gammaj betaj gammam betam]/(2*A);if p==1D=(E/(1-NU*NU))*[1 NU 0;NU 1 0;0 0 (1-NU)/2];else if p==2D=(E/(1+NU)/(1-2*NU))*[1-NU NU 0;NU 1-NU 0;0 0 (1-2*NU)/2];endendBDDB=D*By=t*A*B'*D*B;******************************************************************************* function y=linear_triangle_assemble(K,k,i,j,m)%K(2*i-1,2*i-1)=K(2*i-1,2*i-1)+k(1,1);K(2*i-1,2*i)=K(2*i-1,2*i)+k(1,2);K(2*i-1,2*j-1)=K(2*i-1,2*j-1)+k(1,3);K(2*i-1,2*j)=K(2*i-1,2*j)+k(1,4);K(2*i-1,2*m-1)=K(2*i-1,2*m-1)+k(1,5);K(2*i-1,2*m)=K(2*i-1,2*m)+k(1,6);K(2*i,2*i-1)=K(2*i,2*i-1)+k(2,1);K(2*i,2*i)=K(2*i,2*i)+k(2,2);K(2*i,2*j-1)=K(2*i,2*j-1)+k(2,3);K(2*i,2*j)=K(2*i,2*j)+k(2,4);K(2*i,2*m-1)=K(2*i,2*m-1)+k(2,5);K(2*i,2*m)=K(2*i,2*m)+k(2,6);K(2*j-1,2*i-1)=K(2*j-1,2*i-1)+k(3,1);K(2*j-1,2*i)=K(2*j-1,2*i)+k(3,2);K(2*j-1,2*j-1)=K(2*j-1,2*j-1)+k(3,3);K(2*j-1,2*j)=K(2*j-1,2*j)+k(3,4);K(2*j-1,2*m-1)=K(2*j-1,2*m-1)+k(3,5);K(2*j-1,2*m)=K(2*j-1,2*m)+k(3,6);K(2*j,2*i-1)=K(2*j,2*i-1)+k(4,1);K(2*j,2*i)=K(2*j,2*i)+k(4,2);K(2*j,2*j-1)=K(2*j,2*j-1)+k(4,3);K(2*j,2*j)=K(2*j,2*j)+k(4,4);K(2*j,2*m-1)=K(2*j,2*m-1)+k(4,5);K(2*j,2*m)=K(2*j,2*m)+k(4,6);K(2*m-1,2*i-1)=K(2*m-1,2*i-1)+k(5,1);K(2*m-1,2*i)=K(2*m-1,2*i)+k(5,2);K(2*m-1,2*j-1)=K(2*m-1,2*j-1)+k(5,3);K(2*m-1,2*j)=K(2*m-1,2*j)+k(5,4);K(2*m-1,2*m-1)=K(2*m-1,2*m-1)+k(5,5);K(2*m-1,2*m)=K(2*m-1,2*m)+k(5,6);K(2*m,2*i-1)=K(2*m,2*i-1)+k(6,1);K(2*m,2*i)=K(2*m,2*i)+k(6,2);K(2*m,2*j-1)=K(2*m,2*j-1)+k(6,3);K(2*m,2*j)=K(2*m,2*j)+k(6,4);K(2*m,2*m-1)=K(2*m,2*m-1)+k(6,5);K(2*m,2*m)=K(2*m,2*m)+k(6,6);y=K;******************************************************************************* function y=linear_tiangle_element_stress(E,NU,xi,yi,xj,yj,xm,ym,p,u)%A=(xi*(yj-ym)+xj*(ym-yi)+xm*(yi-yj))/2;betai=yj-ym;betaj=ym-yi;betam=yi-yj;gammai=xm-xj;gammaj=xi-xm;gammam=xj-xi;B=[betai 0 betaj 0 betam 0;0 gammai 0 gammaj 0 gammam;gammai betai gammaj betaj gammam betam]/(2*A);if p==1D=(E/(1-NU*NU))*[1 NU 0;NU 1 0;0 0 (1-NU)/2];else if p==2D=(E/(1+NU)/(1-2*NU))*[1-NU NU 0;NU 1-NU 0;0 0 (1-2*NU)/2];endendy=D*B*u;******************************************************************************* ******************************************************************************* *************************************************************************clc;E= ;v= ;t= ;k1=linear_triangle_element_stiffness(E,v,t, , , , , , ,1) %(E,v,t,x1,y1,x2,y2, x3,y3,1)k2=linear_triangle_element_stiffness(E,v,t, , , , , , ,1) %(E,v,t,x1,y1,x2,y2, x3,y3,1)k3=linear_triangle_element_stiffness(E,v,t, , , , , , ,1) %(E,v,t,x1,y1,x2,y2, x3,y3,1)k4=linear_triangle_element_stiffness(E,v,t, , , , , , ,1) %(E,v,t,x1,y1,x2,y2, x3,y3,1)K=zeros();%节点坐标个数,节点个数乘以2K=linear_triangle_assemble(K,k1, , , );%节点编号K=linear_triangle_assemble(K,k2, , , );%节点编号K=linear_triangle_assemble(K,k3, , , );%节点编号K=linear_triangle_assemble(K,k4, , , );%节点编号KB=K([ , , , , , , , ,],:) ; %取特定的行5 6 7 8 9 10 11 12k=B(:,[ , , , , , , , ]) %取特定的列5 6 7 8 9 10 11 12f=[ ]’u=k\f %求解位移列向量U=[u(1);0;u(2);u(3);0;0;0;0]%总的位移列向量u1=[U( );U( );U( );U( );U( );U( )];%三角形单元一的位移列向量u2=[U( );U( );U( );U( );U( );U( )]; %三角形单元二的位移列向量u3=[U( );U( );U( );U( );U( );U( )];%三角形单元三的位移列向量u4=[U( );U( );U( );U( );U( );U( )]; %三角形单元四的位移列向量sigma1=linear_tiangle_element_stress(E,v, , , , , , ,1,u1)%单元一的应力大小,(E,v,x1,y1,x2,y2,x3,y3,1,u)sigma1=linear_tiangle_element_stress(E,v, , , , , , ,1,u2) %单元二的应力大小(E,v,x1,y1,x2,y2,x3,y3,1,u)sigma1=linear_tiangle_element_stress(E,v, , , , , , ,1,u3)%单元三的应力大小,(E,v,x1,y1,x2,y2,x3,y3,1,u)sigma1=linear_tiangle_element_stress(E,v, , , , , , ,1,u4) %单元四的应力大小(E,v,x1,y1,x2,y2,x3,y3,1,u)。
三角形常应变单元程序的编制与使用共18页文档

三角形常应变单元程序的编制与使用有限元法是求解微分方程边值问题的一种通用数值方法,该方法是一种基于变分法(或变分里兹法)而发展起来的求解微分方程的数值计算方法,以计算机为手段,采用分片近似,进而逼近整体的研究思想求解物理问题。
有限元分析的基本步骤可归纳为三大步:结构离散、单元分析和整体分析。
对于平面问题,结构离散常用的网格形状有三角形、矩形、任意四边形,以三个顶点为节点的三角形单元是最简单的平面单元,它较矩形或四边形对曲边边界有更好Array的适应性,而矩形或四边形单元较三节点三角形有更高的计算精度。
Matlab语言是进行矩阵运算的强大工具,因此,用Matlab语言编写有限元中平面问题的程序有优越性。
本章将详细介绍如何利用Matlab语言编制三角形常应变单元的计算程序,程序流程图见图1。
有限元法中三节点三角形分析结构的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,离散结构并进行单元编码、结点编码、结点位移编码、选取坐标系。
2)单元分析,建立单元刚度矩阵。
3)整体分析,建立总刚矩阵。
4)建立整体结构的等效节点荷载和总荷载矩阵5)边界条件处理。
6)解方程,求出节点位移。
7)求出各单元的单元应力。
8)计算结果整理。
计算结果整理包括位移和应力两个方面;位移计算结果一般不需要特别的处理,利用计算出的节点位移分量,就可画出结构任意方向的位移云图;而应力解的误差表现在单元内部不满足平衡方程,图1 程序流程图单元与单元边界处应力一般不连续,在边界上应力解一般与力的边界条件不相符合。
1.1 程序说明% 三角形常应变单元求解结构主程序●功能:运用有限元法中三角形常应变单元解平面问题的计算主程序。
●基本思想:单元结点按右手法则顺序编号。
●荷载类型:可计算结点荷载。
●说明:主程序的作用是通过赋值语句、读取和写入文件、函数调用等完成算法的全过程,即实现程序流程图的程序表达。
1 程序准备format short e %设定输出类型clear all %清除所有已定义变量clc %清屏●说明:format short e -设定计算过程中显示在屏幕上的数字类型为短格式、科学计数法;clear all -清除所有已定义变量,目的是在本程序的运行过程中,不会发生变量名相同等可能使计算出错的情况;clc -清屏,使屏幕在本程序运行开始时2 全局变量定义global NNODE NPION NELEM NVFIX NFORCE COORD LNODS YOUNG POISS THICKglobal FORCE FIXEDglobal BMATX DMATX SMATX AREAglobal ASTIF ASLOD ASDISPglobal FP1说明:NNODE—单元结点数,NPION—总结点数, NELEM—单元数,NVFIX—受约束边界点数,NFORCE—结点力数,COORD—结构结点坐标数组,LNODS —单元定义数组,YOUNG—弹性模量,POISS—泊松比,THICK—厚度FORCE —节点力数组(n,3) n:受力节点数目,(n,1):作用点,(n,2):x方向,(n,3):y方向; FIXED—约束信息数组(n,3) n:受约束节点数目, (n,1):约束点 (n,2)与(n,3)分别为约束点x方向和y方向的约束情况,受约束为1否则为0BMATX—单元应变矩阵(3*6), DMATX—单元弹性矩阵(3*3),SMATX—单元应力矩阵(3*6),AREA—单元面积ASTIF—总体刚度矩阵,ASLOD—总体荷载向量,ASDISP—结点位移向量FP1—数据文件指针3 打开文件FP1=fopen('input.txt','rt'); %打开输入数据文件存放初始数据●说明:FP1=fopen('input.txt','rt'); -打开已存在的输入数据文件input.txt,且设置其为只读格式,使程序在执行过程中不能改变输入文件中的数值,并用文件句柄FP1来执行FP2=fopen('output.txt','wt'); -打开输出数据文件,该文件不存在时,通过此命令创建新文件,该文件存在时则将原有内容全部删除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四.应力结果的整理
位移的计算结果一般比应力、内力结果精度高。位移达到满意结果, 由几何方程求应变,再由物理方程求应力,结果的精度较差。上述三角形 单元为常应力,矩形单元应力线性变化,而工程问题的应力是比较复杂的。 为更好地反应实际应力情况,需要对计算结果进行整理。常用处理方法有 两种:绕结点平均法和两单元平均法。
四.应力结果的整理
位移的计算结果一般比应力、内力结果精度高。位移达到满意结果, 由几何方程求应变,再由物理方程求应力,结果的精度较差。上述三角形 单元为常应力,矩形单元应力线性变化,而工程问题的应力是比较复杂的。 为更好地反应实际应力情况,需要对计算结果进行整理。常用处理方法有 两种:绕结点平均法和两单元平均法。
宜
不宜
5.相邻单元的尺寸尽可能接近。 6.结点所连接的单元个数尽可能一致。 宜 二.结点编码 尽可能使相关结点的结点编码差值最小. 1 2 3 4 5 6 7 1 3 5 7 9 11 13 不宜
8
9
10
11 12
13
14
2
4
6
8
10
12
14
总刚半带宽=(相关结点最大差值+1)*结点位移数 总刚半带宽=(7+1)*2=16 总刚半带宽=(2+1)*2=6 总刚需占用的存贮空间为: 6 *14*2=168
宜
不宜
5.相邻单元的尺寸尽可能接近。 6.结点所连接的单元个数尽可能一致。 宜 不宜
§3.3 有限元分析应注意的问题和结果整理
一.结点的选择和单元划分 1.集中力作用点、分布力突变点、支承点应选作结点。 2.不同厚度、不同材料的部分不应划在同一个单元。 3.应力变化大处单元应密集一些。结点的多少与疏密要考虑计算 机的容量和计算精度。 4.单元边界的边长之比应尽可能靠近1。
§3 平面问题的有限元分析
§3.1 常应变三角形单元 §3.2 矩形双线性单元 §3.3 有限元分析应注意的问题和结果整理
一.结点的选择和单元划分 1.集中力作用点、分布力突变点、支承点应选作结点。 2.不同厚度、不同材料的部分不应划在同一个单元。 3.应力变化大处单元应密集一些。结点的多少与疏密要考虑计算 机的容量和计算精度。 4.单元边界的边长之比应尽可能靠近1。
1.绕结点平均法 以交于同一结点各单元此结点处某应力分量的代数平均值,作为此结 点该实际应力的近似值。 对于边界处的结点,由内结点结果的外得到。 B 1 D C 2 3
4
A
1 1 ( 1A 1B 1C 1D 1E 1F ) 6
结点4的应力由结点1、2、3的应力 外插得到
F
E
2.两单元平均法 三角形单元时,以两相邻单元应力平均值作为边中点的应力近似值。 矩形单元时,以两相邻单元公共边两端结点四个应力的平均值作为边中点 的应力近似值。对于边界处的结点,同样由内结点结果的外插得到。
