双样本t检验
两个独立总体样本均值的t检验
1、单击Analyze Compare Means Independent-sample T Test，打开 Independent-sample T Test 主对话框如图。 2、选择要检验的变量“综合得分”进入检验框中, 选择分组变量“性别”进入分组框中 。
3、然后单击Define Group按纽，打开分组对话 框如图所示，确定分组值后返回主对话框，如果 没有分组，可以选择Cut point单选项，并在激 活的框内输入一个值作为分组界限值。
人中抽取30人，将他们培训前后的数据每加工
500个零件的不合格品数进行对比，得到数据表， 见表3。试根据表中数据检验培训前后工人的平 均操作技术水平是否有显著提高，也就是检验培 训效果是否显著。
工人培训前后不合格品数据表3
序号 培训前 培训后 序号 培训前 培训后
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Test Value = 10000 95% Confidence Interval of the Difference Mean Difference 置信区间 Lower Upper 均值差 3559.90323 1795.5916 5324.2148
t值 国有单位 4.121
Sig. df (2-tailed) 自由度 P值 30 .000
单个总体均值的 t 检验（One-Sample T Test）； 两个独立总体样本均值的 t 检验 （Independent-Sample T Test）；
两个有联系总体均值均值的 t 检验（PairedSample T Test）；
单因素方差分析（One-Way ANOVA）；
双因素方差分析（General Linear ModelUnivariate）。
实验七 两个独立样本t检验
2、确定检验统计 n1 n2
(n1 1) s1 (n2 1) s2 2 se n1 n2 2
2
2
2
两个 独立样本t 检验操作步骤： 1、选择菜单【Anaiyze】 【Independent-Samples T Test 】 弹出如下所示“Independent-Samples T Test ”对话框,将待检验 的变量送入“Test Variable(s)”框中;选择分组变量进入 “Grouping Variable”
2、在该对话框中单击“Define Groups”按纽得到下面对话框 “ Define Groups”
3
3、单击【 Continue】
4
4、单击【 Continue】
【 Ok】系统输出统计量值及p值
Group Statistics 班 级 一 班 二 班 N 20 20 Mean 26.95 31.65 Std. Deviation 8.236 6.434 Std. Error Mean 1.842 1.439
Std. Error Difference 2.337 2.337
结论:两个班成绩存在显著差异。
5
6
成 绩
Independent Samples Test Levene's Test for Equality of Variances t-test for Equality of Means 95% Confidence Interval of the Difference Lower Upper -9.431 -9.440 .031 .040
两个独立样本t检验
1
一、两个独立样本t检验的基本概念
是利用来自两个正态总体的两个独立样本的数据,来推断两个总体 的均值是否存在显著差异的一种统计推断方法。
Excel中双样本t检验之等方差异方差假设
Excel 中双样本t 检验之等方差异方差假设成组资料（非配对资料）的t 检验，是生物统计中必须掌握的基本技能贮备之一。
在Excel 完全安装情况下，加载“分析工具库”，之后会在菜单上出现“数据分析”选项，我们会发现“分析工具”中有两个选项，分别是：“t 检验：双样本等方差假设”、“t 检验：双样本异方差假设”。
那么，对于成组资料t 检验，什么时候用等方差，什么时候用异方差呢？最好的办法就是进行“F 检验 双样本方差”齐性检验。
如果通过检验，两个样本方差差异不显著，则选用“t 检验：双样本等方差假设”，如果两样本方差差异显著，则选用“t 检验：双样本异方差假设”。
例：有人曾对公雏鸡作了性激素效应试验。
将22只公雏鸡完全随机地分为两组，每组11只。
一组接受性激素A （睾丸激素）处理；另一组接受激素C （雄甾烯醇酮）处理。
在第15天取它们的鸡冠个别称重，所得数据如下表。
题解：在excel 中录入数据，在菜单“数据分析”中，选择“F 检验 双样本方差”，选择A1:A12”所在区域为“变量1的区域”，选择“B1:B12”区域为“变量2 的区域”。
勾选标志“a （A ）”，默认为0.05，在输出区域中随便找一个单元格（如单元格D1）， “确定”（见图1）。
图1 双样本方差的F-检验图2 t-检验：双样本等方差假设检验 从上图可以看出，p=0.4452221﹥0.05，表示激素A 与激素C 的对应的鸡冠，方差差异不显著。
换言之，就是样本A 与样本B 为等方差，在t 检验时，就选择“t 检验：双样本等方差假设”，得到图2结果。
从图2输出结果可以看出，t检验的结果是p=0.003000143﹤0.01，表明差异极显著。
也就是说，激素A 处理的鸡冠重（97mg ）极显著地高于激素C 处理的鸡冠重（56mg ）。
目前不管是本科教材，还是高职高专教材，生物统计仍是以公式手动计算为主，所采用的基本都是按照“t 检验：双样本等方差假设”，而且很多资料也表示，如果双样本都来源于同一总体，可以采用“t 检验：双样本等方差假设”。
sas统计分析_利用SAS解决两个独立样本的t检验
利用SAS解决两个独立样本的t检验班级：学号：指导教师：姓名：目录1. SAS简介 (2)1.1 SAS的设计思想 (2)1.2 SAS的功能 (2)1.3 SAS的特点 (3)2. 方法及原理——两个独立样本的t检验 (4)2.1假设检验的思想和步骤 (4)2.2 t检验的原理与方法 (4)2.3 检验统计量t的公式 (5)2.4两个独立样本的t检验的步骤 (5)3.SAS常用命令 (6)4.题目与解答 (6)4.1题目 (6)4.2解答与分析 (6)1. SAS简介SAS是美国使用最为广泛的三大著名统计分析软件（SAS，SPSS和SYSTAT）之一，是目前国际上最为流行的一种大型统计分析系统，被誉为统计分析的标准软件。
SAS为“Statistical Analysis System”的缩写，意为统计分析系统。
它于1966年开始研制，1976年由美国SAS软件研究所实现商品化。
1985年推出SAS PC 微机版本，1987年推出DOS下的SAS6.03版，之后又推出6.04版。
以后的版本均可在WINDOWS下运行，目前最高版本为SAS6.12版。
SAS集数据存取，管理，分析和展现于一体，为不同的应用领域提供了卓越的数据处理功能。
它独特的“多硬件厂商结构”（MV A）支持多种硬件平台，在大，中，小与微型计算机和多种操作系统（如UNIX，MVS WINDOWS 和DOS等）下皆可运行。
SAS 采用模块式设计，用户可根据需要选择不同的模块组合。
它适用于具有不同水平于经验的用户，处学者可以较快掌握其基本操作，熟练者可用于完成各种复杂的数据处理。
目前SAS已在全球100多个国家和地区拥有29000多个客户群，直接用户超过300万人。
在我国，国家信息中心，国家统计局，卫生部，中国科学院等都是SAS系统的大用户。
SAS以被广泛应用于政府行政管理，科研，教育，生产和金融等不同领域，并且发挥着愈来愈重要的作用。
SPSS生物统计分析示例2-两样本t检验
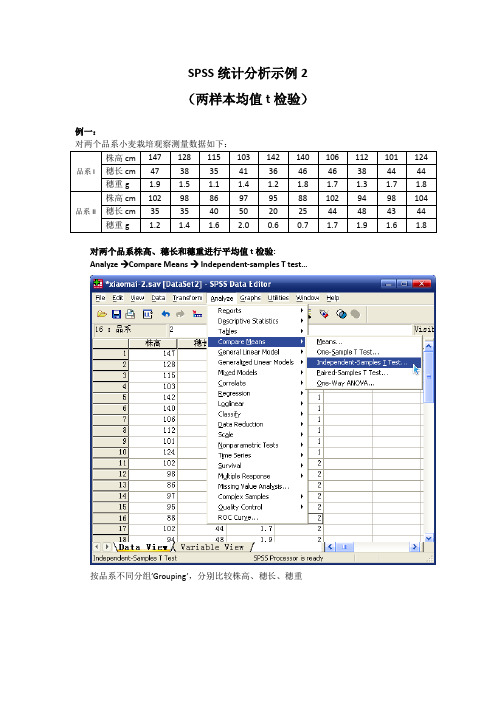
SPSS统计分析示例2（两样本均值t检验）例一：对两个品系株高、穗长和穗重进行平均值t检验:Analyze →Compare Means → Independent-samples T test…按品系不同分组’Grouping’，分别比较株高、穗长、穗重SPSS输出：汇总表：品系I 品系II t 株高cm(M±SD) 121.80±16.98 96.40±5.89 4.468**穗长cm(M±SD) 41.50±4.48 38.40±9.74 0.914穗重g (M±SD) 1.54±0.28 1.45±0.48 0.511**:P<0.01从t检验的结果看：（1）株高数据不满足方差齐性，用近似t检验，t=4.468 (df=11.136), 双侧检验P=0.001<<0.01，两品系的株高具有极显著差异，品系I株高显著大于品系II（2）穗长数据不满足方差齐性，用近似t检验，t=0.914 (df=12.640), 双侧检验P=0.378>0.05，两品系的穗长无显著差异（3）穗重数据满足方差齐性，用t检验，t=0.511 (df=18), 双侧检验P=0.615>0.05，两品系的穗重无显著差异例二：将20名某病患者随机分为两组，分别用甲乙两药治疗，测得治疗前后的血沉（mm/小时）如下表：试分甲乙两药是否有疗效？两药疗效是否有差异？并用图或表对数据和结果进行描述。
1．对两种药物治疗效果比较的统计分析（以下结果均使用SPSS统计软件获得）（1）对甲药疗效做配对t检验：治疗前后血沉值的差值的配对检验SPSS结果显示：t=5.237(df=9)，单侧检验P=0.001/ 2 = 0.0005<0.01，结论甲药疗效极显著。
（2）对乙药疗效做配对t检验：治疗前后血沉值的差值的配对检验SPSS结果显示：t=5.303(df=9)，单侧检验P<<0.01，结论乙药疗效极显著。
excel双样本 t检验法的计算方法
excel双样本t检验法的计算方法摘要：1.Excel双样本T检验的概念与原理2.准备工作：数据准备与输入3.执行双样本T检验：步骤与操作4.解读结果：假设检验与结论5.实际应用案例与注意事项正文：在数据分析和统计研究中，Excel双样本T检验法被广泛应用于比较两组数据的均值是否存在显著差异。
本文将详细介绍Excel双样本T检验的计算方法，包括操作步骤、结果解读以及实际应用案例。
1.Excel双样本T检验的概念与原理双样本T检验是一种统计分析方法，用于检验两个独立样本的均值是否存在显著差异。
它基于t分布理论，通过计算t统计量及其对应的p值来判断假设检验的结果。
2.准备工作：数据准备与输入在进行双样本T检验之前，需要首先准备好两组要分析的数据。
这两组数据可以来自不同来源、不同时间或不同条件下收集。
确保数据具有可比性，例如单位、尺度等要保持一致。
将数据输入Excel，建议将两组数据分别放在两个工作表中，以便于进行数据分析。
通常，第一列表示样本编号或组别，后续列表示各样本的观测值。
3.执行双样本T检验：步骤与操作在Excel中进行双样本T检验，可以遵循以下步骤：步骤1：打开Excel，点击“数据”菜单，选择“数据分析”。
步骤2：在“数据分析”对话框中，选择“t-检验：双样本假设检验”模块。
步骤3：分别选取两组数据所在的工作表和输出区域。
步骤4：点击“确定”，等待Excel计算结果。
4.解读结果：假设检验与结论Excel会输出双样本T检验的结果，包括t统计量、p值以及结论。
根据p 值与预设的显著性水平（通常为0.05）进行比较，可以得出以下结论：- 如果p值小于显著性水平，说明两组数据的均值存在显著差异；- 如果p值大于显著性水平，不能拒绝原假设，即两组数据的均值之间没有显著差异。
5.实际应用案例与注意事项实际应用中，双样本T检验可用于比较不同实验组之间的效果、评估干预措施的有效性等。
在进行双样本T检验时，请注意以下几点：- 确保数据具有可比性，如单位、尺度一致；- 检查数据是否存在异常值，如有需要，进行数据清洗；- 选择合适的显著性水平，根据实际情况调整；- 注意样本容量，确保样本足够大以获得可靠结果。
两样本t检验计算公式
两样本t检验计算公式1.对于两个独立样本的t检验：t=(x1-x2)/√(s1^2/n1+s2^2/n2)其中t表示t值；x1和x2分别表示两个样本的均值；s1和s2分别表示两个样本的标准差；n1和n2分别表示两个样本的样本容量。
2.对于两个相关样本的t检验：t = (x1 - x2) / (sdiff / √n)其中t表示t值；x1和x2分别表示两个样本的均值差；sdiff表示两个样本的均值差的标准差；n表示样本容量。
接下来，我们将具体介绍两个不同情况下的两样本t检验计算过程。
一、独立样本t检验计算过程：1.收集两个样本的数据并计算样本均值和样本标准差；2.计算两个样本的样本容量；3.计算两个样本的方差；4.根据计算得到的数据，带入公式计算t值；5.查表或使用统计软件计算得到的t值对应的P值；6.对比P值与设定的显著性水平（通常为0.05），如果P值小于显著性水平，则可以拒绝原假设，即认为样本均值存在显著差异；反之，接受原假设，即认为样本均值不存在显著差异。
二、相关样本t检验计算过程：1.收集两个样本的相关数据并计算样本均值差；2.计算样本均值差的标准差；3.计算样本容量；4.根据计算得到的数据，带入公式计算t值；5.查表或使用统计软件计算得到的t值对应的P值；6.对比P值与设定的显著性水平（通常为0.05），如果P值小于显著性水平，则可以拒绝原假设，即认为样本均值存在显著差异；反之，接受原假设，即认为样本均值不存在显著差异。
需要注意的是，在进行两样本t检验前，需要满足以下前提条件：1.数据来自正态分布的总体；2.数据具有相同的方差；3.对于独立样本t检验，两个样本之间应相互独立；4.对于相关样本t检验，两个样本之间应具有相关性。
总结起来，两样本t检验是一种比较两个样本均值是否有显著差异的统计方法，通过计算t值和P值来进行假设检验。
根据计算得到的P值是否小于设定的显著性水平，判断两个样本的均值是否存在显著差异。
双样本t检验
双样本t检验
双样本t检验是一种用于比较两个独立样本均值差异的统计方法。
它的假设是两个样本来自于正态分布总体，并且两个样本方差相等。
双样本t检验的步骤如下：
1. 建立假设：
- 零假设（H0）：两个样本的均值相等。
- 备择假设（H1）：两个样本的均值不相等。
2. 计算样本均值：
- 计算第一个样本的均值（X1）和标准差（s1）。
- 计算第二个样本的均值（X2）和标准差（s2）。
3. 计算t统计量：
- 计算t统计量（t）= (X1 - X2) / sqrt(sp^2/n1 + sp^2/n2)，其中sp^2 = ((n1-1)s1^2 + (n2-1)s2^2) / (n1 + n2 - 2)，n1和n2分别为第一个和第二个样本的样本容量。
4. 计算p值：
- 根据计算得到的t统计量和自由度(n1 + n2 - 2)，查找t分布表，找到相应的临界值。
- 根据临界值和双侧检验或单侧检验的要求，计算p值。
5. 做出决策：
- 如果p值小于设定的显著性水平（通常为0.05），则拒绝零假设，认为两个样本均值存在显著差异。
- 如果p值大于设定的显著性水平，则接受零假设，认为两个样本均值无显著差异。
需要注意的是，以上步骤基于一些前提条件，如正态分布的假设和方差相等的假设。
如果数据不满足这些假设，可以考虑使用非参数方法进行比较，如Wilcoxon秩和检验或Mann-Whitney U检验。
统计学 两样本均数比较的t检验
统计学两样本均数比较的t检验统计学中，两样本均数比较是一种常见的数据分析方法。
这种方法又称为t检验，主要用于比较两组数据的均值是否有显著差异。
t检验分为独立样本t检验和配对样本t检验两种。
独立样本t检验用于比较两组独立样本的均值；配对样本t检验则用于比较同一组样本在不同时间或者不同条件下均值的变化。
本文将重点介绍独立样本t检验的原理、假设检验及其应用。
独立样本t检验的原理独立样本t检验的原理基于中心极限定理，即当样本大小足够大时，样本均数的分布近似正态分布。
在均值比较问题中，我们对两个总体做出如下假设：- 零假设：两个总体的均值相等。
- 备择假设：两个总体的均值不相等。
考虑两个独立的样本，样本容量分别为n1和n2。
我们可以计算出两个样本的样本均数和样本标准差，分别记作x1、s1和x2、s2。
接下来，我们根据两个样本均数和方差的差异，计算t值。
t值可以用以下公式表示：t= (x1 - x2) / (√(s1²/n1 + s2²/n2))如果t值比较大，则说明两个样本的均值差异比较显著，从而我们可以拒绝零假设。
在独立样本t检验中，我们需要进行假设检验，以确定两个总体均值是否相等。
在进行假设检验时，我们通常会采用0.05的显著性水平，即拒绝零假设的概率为5%。
具体做法如下：1. 建立假设在进行独立样本t检验时，我们需要建立零假设和备择假设。
零假设指两个总体的均值相等，备择假设指两个总体的均值不相等。
通常，我们会先假设两个总体的均值相等，即零假设为H0: μ1 = μ2，备择假设为H1: μ1 ≠μ2。
2. 计算t值计算t值时，我们需要用到样本数据的均数、标准差和样本量。
根据公式计算出t 值。
3. 确定自由度自由度是指在样本数据中自由变动的部分，通常计算方法为自由度=（样本量1-1）+（样本量2-1）。
4. 查找t分布表在t分布表中查找对应的临界值，以确定t值是否显著。
查找时需要指定显著性水平和自由度。
双样本t检验的原假设
双样本t检验的原假设
双样本t检验是一种常用的假设检验方法，用于比较两个样本的均值是否存在显著差异。
在进行双样本t检验时，我们需要先制定原假设和备择假设。
本文将讨论双样本t检验的原假设，包括其定义、意义和应用场景。
定义
原假设是指在假设检验中所提出的关于总体参数的某种假设，通常用H0表示。
在双样本t检验中，原假设通常是指两个样本的均值相等，即μ1 = μ2。
这意味着两个样本来自同一总体，其均值没有显著差异。
意义
原假设的设定是为了进行假设检验，以验证某种假设是否成立。
在双样本t检验中，如果我们无法拒绝原假设，就意味着两个样本的均值没有显著差异。
这可能有多种原因，例如两个样本来自同一总体，或者两个样本在总体均值上存在一定的差异，但是这种差异并不显著。
应用场景
双样本t检验通常应用于以下两种情况：
1.比较两个独立样本的均值是否有显著差异。
例如，我们想要比较男性和女性在身高方面是否存在显著差异。
我们可以分别抽取一组男性和女性的样本，然后进行双样本t检验，检验两组样本的身高均值是否有显著差异。
2.比较两个相关样本的均值是否有显著差异。
例如，我们想要比较一组学生在两次考试中的成绩是否存在显著差异。
我们可以抽取一组学生的两次考试成绩，然后进行双样本t检验，检验两次考试成绩的均值是否有显著差异。
双样本t检验的原假设通常是指两个样本的均值相等，如果我们无法拒绝原假设，就意味着两个样本的均值没有显著差异。
双样本t 检验通常应用于比较两个独立或相关样本的均值是否存在显著差异。
双样本t检验
两正态总体， 两正态总体， 或非正态总体、 或非正态总体、 (X − X ) ± Z ⋅ 1 2 α 大样本， 大样本，总体 2 方差已知 两正态总体， 两正态总体， 或非正态总体、 或非正态总体、(X −X )±t ⋅ 1 2 α µ1-µ2 大样本，总体 大样本， 2 方差未知但无 显著差异 两正态总体， 两正态总体， 总体方差未知 但有显著差异
两个样本均值之差的抽样分布 σ12和σ22未知
• 若两个总体均为正态分布总体，但是两 若两个总体均为正态分布总体， 总体方差未知，且知道σ 则有： 总体方差未知，且知道 12≠σ22 ，则有：
t' =
( X 1 − X 2 ) − ( µ1 − µ 2 )
2 S12 S 2 + n1 n2
~ t df '
σ
n1
2 1
+Hale Waihona Puke σ2 2n2
2 2
(n −1S +(n2 −1S 1 1 ) 1 ) ( + ) n +n2 −2 n n2 1 1
2 1 2 2
(X1 − X2 ) ±t'α ⋅
2
S S + n n df ' = 12 2 2 2 2 2 S12 S2 S1 S2 n n + 1 + 2 n1 n2 n1 n2
临界值的另一种求法
• 计算 后，不计算df’，而计算： 计算t’后 不计算 ，而计算：
S S tα + tα n1 2 ( n1 −1) n2 2 ( n2 −1) t 'α = 2 2 S1 S 2 2 + n1 n2
2 1
两组独立样本T检验
两独立样本T检验-SPSS步骤详解
1）首先确认是否为相互独立，没有任何关系的两组数据（如何确认）。
2）确定样本量：
（1）样本量N≥30，默认为大样本（有的要求为N≥50）进行方差齐性分析，方差齐采用两独立样本T检验，方差不齐采用秩和检验。
（2）如样本量N<30，为小样本，首先应进行各组资料正态性分布分析，如为正态分布，进行方差分析，方差齐，进行独立样本T检验，方差不齐，采用秩和检验；
如为非正态分布，采用秩和检验。
3）如确定应采用两独立样本T检验，则按照以下步骤进行分析，以两组患者收缩压水平为例，首先在SPSS“变量视图”（variable view）中对变量进行命名，可修改变量类型，定义变量宽度（即数字长度）等
随后调整到“数据视图（data view）”，录入数据
随后在上方菜单栏“分析（Analyze）”找到“比较均值（Compare Means）”，找到“独立
样本T检验（Independent Sample T Test）”，得到以下对话框：
将变量收缩压选入“检验变量”，分组情况选入“分组变量”，点击“定义组”，得到以下对话框：
定义组1为“1”，定义组2为“2”，点击继续，并点击“独立样本T检验”对话框（即上一对话框）中的“确定”，得到以下数据：
1组均值±标准差为126.25±12.45，2组均值±标准差为168.75±16.25
一般不确定数据方向，应检测双尾P值（Sig-two tail）=0.000，P<0.05,组间差异有统计学意义。
当确定2组数据一定大于1组时（即数据方向一定），可选用单尾P值，否则选用双尾P值。
使用SPSS进行两组独立样本的t检验、F检验、显著性差异、计算p值
使用SPSS 进行两组独立样本的t检验、F检验、显著性差异、计算p值SPSS版本为SPSS 20.如有以下两组独立的数据，名称分别为“111”，“222”。
111组：4、5、6、6、4222组：1、2、3、7、7首先打开SPSS，输入数据，命名分组，体重和组名要对应，111组的就不要输入到222组了。
数据视图如下：变量视图如下，名称可以改成“分组嗷嗷嗷”“体重喵喵喵”等点击“分析”-“比较均值”-“独立样本T检验”来到这里，分组变量为“分组嗷嗷嗷”，检验变量为“体重喵喵喵”。
【关键的一步】点击分组嗷嗷嗷，进行“定义组”【关键的一步】输入对应的两组数据的组名：“ 111”和“222”点击确定，可见数据与组名对应上了。
点击“确定”，生成T检验的报告，即将大功告成！第一个表都知道什么回事就不缩了，excel都能实现的。
第二个表才是重点，不然用SPSS干嘛。
F检验：在两样本t检验中要用到F检验，F检验又叫方差齐性检验，用于判断两总体方差是否相等，即方差齐性。
如图：F旁边的 Sig的值为.007 即0.007， <0.01, 即两组数据的方差显著性差异！看到“假设方差相等”和“假设方差不相等”了么？此时由于F检验得出Sig <0.01，即认为假设方差不相等！因此只关注红框中的数据即可。
如图，红框内，Sig（双侧），为.490即0.490，也就是你们要求的P值啦，Sig ( 也就是P值 ) >0.05，所以两组数据无显著性差异。
PS：同理，如果F检验的Sig >.05（即>0.05），则认为两个样本的假设方差相等。
所以相应的t检验的结果就看上面那行。
by 20150120 深大医学院 FG。
两独立样本t检验与两配对样本t检验的异同
一、两独立样本t检验
• 1.什么是两独立样本t检验？ ——根据样本数据对两个样本来自的两个 独立总体的均值是否有显著差异进行判断。
• 2.前提： ①两样本应该是相互独立的； ②样本设总体 X1 服从正态分布 N 1,12 ，总体 X2 服从正
态分布
N
2
,
2 2
，分别从这两个总体中抽取样本
x11, x12,x1n1 和 x21, x22 , x2n2 ，且两样本相互独立。
要求检验 1 和 2是否有显著差异。
建立假设：H
0
:
2 1
2 2
，H1
:
2 1
2 2
两个正态方差
2 1
和
2 2
常用各自的样本无偏方差
s x2和去
s
2 y
• 3.基本实现思路 设两总体 X ,Y分别服从正态分布，为实现我们的目的， 最好的方法是去考察成对数据的差di xi yi ,i 1,2,, n 。 由于两测量值之差可认为服从正态分布，故di ~ N (, 2) ， 检验两样本差异转化为检验如下假设：H0 : 0, H1 : 0
这是单个正态总体均值是否为0的检验问题。 由于未知，因此对此问题用t检验，检验统计连变 成t d ，
解：数据之差为：-3.1 -9.8 -6.1 1.4 5.2 -7.8 -4.9
均值与标准差分别为 检验统计量
d 3.586, sd 5.271
t d 3.586 1.80
sd
5.271
n
7
• 拒绝域为
t t0.9756 2.4469
样本未落入拒绝域中，所以在 0.05水平上
总体 X（甲） Y（乙）
t检验双样本异方差假设
双侧检验
2 未知小样本均值的检验
(例题分析)
•H 0 : = 5 •H 1 : 5 = 0.05 •n = 10 •临界值(s):
拒绝 H0
.025
检验统计量:
x 0 5.3 5 t 3.16 s n 0.3 10
决策：
拒绝 H0
.025
在 = 0.05的水平上拒绝H0
双侧检验
2 已知均值的检验
(例题分析)
•H0: = 0.081 •H1: 0.081 = 0.05 •n = 200 •临界值(s):
拒绝 H0
.025
检验统计量:
z
x 0
n
0.076 = 0.05的水平上拒绝H0
2 未知小样本均值的检验
(例题分析)
• 【例】 一个汽车轮胎制造商声 称，某一等级的轮胎的平均寿命 在一定的汽车重量和正常行驶条 件下大于40000公里，对一个由20 个轮胎组成的随机样本作了试验 ，测得平均值为41000公里，标准 差为 5000 公里。已知轮胎寿命的 公里数服从正态分布，我们能否 根据这些数据作出结论，该制造 商的产品同他所说的标准相符？ ( = 0.05)
大
z 检验
z 检验
t 检验
Z
X 0
n
Z
X 0 S n
t
X 0 S n
总体均值的检验
(2 已知或2未知大样本)
• 1.假定条件
– 总体服从正态分布 – 若不服从正态分布, 可用正态分布来近似(n30)
2. 使用Z-统计量
2 已知： 2 未知：
Z Z
X 0
拒绝 H0
两独立样本和配对样本T检验
两独立样本T检验目的：利用来自两个总体的独立样本，推断两个总体的均值是否存在显著差异。
检验前提：样本来自的总体应服从或近似服从正态分布；两样本相互独立，样本数可以不等。
两独立样本T检验的基本步骤：提出假设原假设H_0：μ_1-μ_2=0备择假设H_1：μ_1-μ_2≠0建立检验统计量如果两样本来自的总体分别服从N(μ_1,σ_1^2 )和N(μ_2,σ_2^2 )，则两样本均值差(x_1 ) ?-x ?_2应服从均值为μ_1-μ_2、方差为σ_12^2的正态分布。
第一种情况：当两总体方差未知且相等时，采用合并的方差作为两个总体方差的估计，为：s^2=((n_1-1) s_1^2+(n_2-1) s_2^2)/(n_1+n_2-2)则两样本均值差的估计方差为：σ_12^2=s^2 (1/n_1 +1/n_2 )构建的两独立样本T检验的统计量为：t= ((x_1 ) ?-x ?_2)/√(s^2 (1/n_1 +1/n_2 ) )此时，T统计量服从自由度为n_1+n_2-2个自由度的t分布。
第二种情况：当两总体方差未知且不相等时，两样本均值差的估计方差为：σ_12^2=(s_1^2)/n_1 +(s_2^2)/n_2构建的两独立样本T检验的统计量为：t= ((x_1 ) ?-x ?_2)/√((s_1^2)/n_1 +(s_2^2)/n_2 )此时，T统计量服从修正自由度的t分布，自由度为：f= ((s_1^2)/n_1 +(s_2^2)/n_2 )^2/(((s_1^2)/n_1 )^2/n_1 +((s_2^2)/n_2 )^2/n_2 )可见，两总体方差是否相等是决定t统计量的关键。
所以在进行T检验之前，要先检验两总体方差是否相等。
SPSS中使用方差齐性检验（Levene F检验）判断两样本方差是否相等近而间接推断两总体方差是否有显著差异。
三、计算检验统计量的观测值和p值将样本数据代入，计算出t统计量的观测值和对应的概率p值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
两总体均值之差的假设检验（一）
已知条件 假设
H0:μ1＝μ2 H1:μ1≠μ2
检验统计量
H0的拒绝 域 |Z|≥Zα/2
两正态总 体，或非 正态总体、 大样本， 总体方差 已知
Z
H0:μ1≥μ2 H1:μ1＜μ2
X1 X 2
2 1
n1
2 2
n2
Z≤－Zα
H0:μ1≤μ2 H1:μ1＞μ2
两个样本均值之差的抽样分布 2和σ22未知 σ1
• 若两个总体均为正态分布总体，但是两 总体方差未知，且知道σ12≠σ22 ，则有：
t'
( X 1 X 2 ) ( 1 2 )
2 S12 S 2 n1 n2
~ t df '
两个样本均值之差的抽样分布 ２和σ2２未知 σ1
• 其中
关于总体平均数之差的推断统计
两个样本均值之差的抽样分布
• 需考虑的问题：
– 两总体方差σ12和σ22是否已知；如果未知,则 是否σ12 = σ22 ； – 两总体是否正态分布； – 两样本为大样本还是小样本。
两个样本均值之差的抽样分布 σ12和σ22已知
• 若 X 1 是独立地抽自总体X1~N(μ1，σ12)的一个容 量为n1的样本的均值， X 2 是独立地抽自总体 X2~N(μ2，σ22)的一个容量为n2的样本的均值， 则有：
X 1 X 2 ~ N 1 2 , n1 n2
2 1 2 2
Z
( X 1 X 2 ) ( 1 2 )2 1 Nhomakorabean1
2 2
~ N (0,1 )
2
n2
两个样本均值之差的抽样分布 2和σ22未知 σ1
• 如果σ12＝σ22 ，则有：
例题
随机地从A厂生产的导线中抽取4根，从B 厂生产的导线中抽取5根，测得以欧姆表 示的电阻为 A厂：0.143, 0.142, 0.143, 0.137 B厂：0.140, 0.142, 0.136, 0.138, 0.140 若已知两工厂导线的电阻均服从正态分布， 且方差齐性，试求（μ1-μ2 ）的95%置信 水平下的置信区间。
t≥tα
两总体均值之差的假设检验（三）
已知条 件 假设
H0:μ1＝μ2 H1:μ1≠μ2
检验统计量
H0的拒绝 域 |t|≥tα/2
2
t'
X1 X 2
2 S12 S 2 n1 n2
2 1 2 2
两正态 总体， 总体方 差未知 但有显 著差异
H0:μ1≥μ2 H1:μ1＜μ2
H0:μ1≤μ2 H1:μ1＞μ2
n1 n2
2 1
(n1 1)S (n2 1)S 1 1 ( ) n1 n2 2 n1 n2
2 2
2 1 2 2
S S ( X 1 X 2 ) t ' n1 n2 2
S S n n2 df ' 12 2 2 S12 S 2 n n 1 2 n1 n2
例题
• 甲乙两公司生产同种产品。从甲公司 产品中抽取20件进行检验，得出这20 件产品的平均抗压能力为45.2公斤， S12 =30；从乙公司产品中抽取12件产 品的平均抗压能力为34.6公斤，S22 =43。 若两公司产品的抗压能力均服从正态 分布，而且没有理由认为它们的方差 一样，试估计两公司产品平均抗压能 力之差（α=0.05） 。
t
( X 1 X 2 ) ( 1 2 ) (n1 1) S (n2 1) S 1 1 ( ) n1 n2 2 n1 n2
2 1 2 2
~ t n1 n2 2
• 以上结论均可推广到两个非正态总体且两个样 本均为大样本的情况。但是对于两个非正态总 体且小样本的情况则不适用。
H0:μ1＝μ2 H1:μ1≠μ2
检验统计量
H0的拒绝 域 |t|≥tα/2
t
X1 X 2
2 (n1 1) S12 (n2 1) S 2 1 1 ( ) n1 n2 2 n1 n2
H0:μ1≥μ2 H1:μ1＜μ2
t≤－tα
自由度df=n1+n2-2
H0:μ1≤μ2 H1:μ1＞μ2
例题
• 某校进行教改实验，甲班45人，乙班36人， 分别采用不同的教学方法。学期结束时进行 测验，得到以下结果： 甲班平均分69.5，总体标准差估计值8.35； 乙班平均分78.0，总体标准差估计值16.5。 试问两种教学方法其效果有无显著差异？ （α=.01）
临界值的另一种求法
• 计算t’后，不计算df’，而计算：
S S t t n1 2 ( n1 1) n2 2 ( n2 1) t ' 2 2 S1 S 2 2 n1 n2
2 1
2 2
结果
• 2.816
• df’时，2.682
• 非df’时，2.719
相关样本平均数差异的 显著性检验
• 两个样本内个体之间存在着一一对应的关系， 这 两 个 样 本 称 为 相 关 样 本 （ correlatedgroups----independent groups）。两种情况：
– 用同一测验对同一组被试在试验前后进行两次测 验 ， 所 获 得 的 两 组 测 验 结 果 ； ----repeated measures design – 根据某些条件基本相同的原则，把被试一一匹配 成对，然后将每对被试随机地分入实验组和对照 组，对两组被试施行不同的实验处理之后，用同 一测验所获得的测验结果。----matched-group design
2 1 2 2
2
例题
• 从某市近郊区和远郊区中各自独立地 抽取25户家庭，调查平均每户年末手 存现金和存款余额。得出两个样本均 值分别为近郊区65000元，远郊区 48000元。已知两个总体均服从正态分 布，且σ1=12000，σ2=10600，试估计 该市近郊区与远郊区平均每户 年末手 存现金和存款余额之差（α=0.05）。
S S n 1 n2 df ' 2 2 2 2 S1 S 2 n n 1 2 n1 n2
2 1 2 2
2
示意图
两个总体均值之差的区间估计
待估 参数 已知条件 置信区间 备注
2 1 2 2
两正态总体， 或非正态总体、 ( X X ) Z 1 2 大样本，总体 2 方差已知 两正态总体， 或非正态总体、( X X ) t 1 2 μ1-μ2 大样本，总体 2 方差未知但无 显著差异 两正态总体， 总体方差未知 但有显著差异
相关样本平均数差异的 显著性检验
• 如果两个样本是相关样本，即两个样本 内个体之间存在着一一对应的关系，则 有 ( X1 X 2 )
t
D Di / n i 1 i 1 n(n 1)
n n 2 i
2
其中D＝X1－X2
例题
• 为了调查两种不同识字教学法的效果， 随机抽取了10名小学生，记录下他们使 用两种教学法的成绩如下。问两种教学 法有无显著差异？
S S n n2 df ' 12 2 2 2 S1 S 2 n n 1 2 n1 n2
t≤－tα
t≥tα
例题
• 甲乙两公司生产同种产品。从甲公司 产品中抽取20件进行检验，得出这20 件产品的平均抗压能力为45.2公斤， S12 =30；从乙公司产品中抽取12件产 品的平均抗压能力为34.6公斤，S22 =43。 若两公司产品的抗压能力均服从正态 分布，而且没有理由认为它们的方差 一样，试估计两公司产品抗压能力有 无显著差异（α=0.05） 。
学生号 1 2 3 4 5 6 7 8 9 10 A法成绩 11.3 15.0 15.0 13.5 12.8 10.0 11.0 12.0 13.0 12.3 B法成绩 14.0 13.8 14.0 13.5 13.5 12.0 14.7 11.4 13.8 12.0
Z≥Zα
例题
• 某部门欲采购一批灯泡。从两个灯泡厂 的产品中各自抽取50个进行检验，测得 两个灯泡厂的灯泡的样本均值为1282小 时和1208小时。若已知两厂灯泡的使用 寿命均服从正态分布，且方差分别为802 和942，问：两厂灯泡的平均使用寿命有 无显著差异？
两总体均值之差的假设检验（二）
已知条 件 两正态 总体， 或非正 态总体、 大样本， 总体方 差未知 但无显 著差异 假设