试验一异方差的检验与修正-时间序列分析
时序预测中的异方差性检验方法探讨

时序预测中的异方差性检验方法探讨时序预测是指使用历史数据和模型来预测未来的趋势和变化。
在进行时序预测时,我们经常会遇到异方差性的问题。
异方差性是指随着时间的推移,数据的方差发生变化,这种变化可能会对预测结果产生影响。
因此,对时序数据中的异方差性进行检验是非常重要的。
一、异方差性的影响在时序预测中,如果数据呈现异方差性,那么传统的预测方法可能会得出不准确的结果。
因为异方差性会导致模型的参数估计出现偏差,从而影响预测的准确性。
因此,我们需要对时序数据中的异方差性进行检验,并采取相应的措施来纠正。
二、异方差性的检验方法针对时序数据中的异方差性,目前有多种检验方法可供选择。
常见的方法包括波特-阿格检验、怀特检验、拉格朗日乘积检验等。
这些方法都可以通过对模型残差的分析,来判断时序数据是否存在异方差性。
但是,不同的方法在实际应用中可能会有不同的适用性和效果。
三、波特-阿格检验波特-阿格检验是一种常用的异方差性检验方法。
它通过对模型残差的平方和进行分析,来检验时序数据中是否存在异方差性。
在进行波特-阿格检验时,我们需要先拟合一个时间序列模型,然后计算残差的平方和,并进行统计检验。
如果检验结果显著,就表明时序数据存在异方差性。
四、怀特检验怀特检验是另一种常用的异方差性检验方法。
它通过对模型残差的平方和进行滞后相关性分析,来检验时序数据中是否存在异方差性。
在进行怀特检验时,我们需要计算残差的平方和,并对其进行滞后相关性检验。
如果检验结果显著,就表明时序数据存在异方差性。
五、拉格朗日乘积检验除了波特-阿格检验和怀特检验外,拉格朗日乘积检验也是一种常用的异方差性检验方法。
它通过对模型残差的平方和进行拉格朗日乘积分析,来检验时序数据中是否存在异方差性。
在进行拉格朗日乘积检验时,我们需要计算残差的平方和,并进行拉格朗日乘积分析。
如果检验结果显著,就表明时序数据存在异方差性。
六、选择合适的异方差性检验方法在实际应用中,选择合适的异方差性检验方法非常重要。
计量经济学实验报告(三)

2012 — 2013 第 1 学期计量经济学实验报告实验(三):计量经济检验与修正实验学号:0101702 姓名:宋蕾专业: 财务管理选课班级:A(2实验日期: 2 0 11.112实验地点:南区综合楼经济管理与创业模拟实验中心实验室实验名称:计量经济检验与修正实验【实验目标、要求】使学生掌握用Eviews做1.异方差性检验和修正方法;2.自相关性检验和修正方法;3.【实验内容】实验内容以课后练习:以114页第6题、130页应用题第2题为例进行操作【实验步骤】一、第114页第6题(一)创建工作文件在主菜单上依次单击File T New^Workfile ,选择数据类型和起止日期。
时间序列提供起止日期(年、季度、月度、周、日),非时间序列提供最大观察个数。
本题中在workfile structure type 中选Unstructured/Undated, 在Data range Observation 中填 2 8。
单击OK后屏幕出现Workfile工作框,如图所示。
(二)输入和编辑数据在命令窗口直接输入:Data Y X . 屏幕出现数据编辑框,如下图所示。
点击上图中对话框的"Edit +/-",将数据进行输入,如下图所示。
数据输入完毕,单击工作文件窗口工具条的存入磁盘。
(三)0 LS估计参数利用2008年中国部分省市城镇居民家庭平均全年可支配收入(的相关数据表,作散点图。
Eviews命令:scat X Y ; 如图所示X)与消费性支出(Y)Save或单击菜单兰的File宀Save将数据可看出2 0 0 8年中国部分省市城镇居民家庭平均全年可支配收入 (X)与消费性支出(Y)的关系近似直线关系可建立线性回归模型。
在主菜单命令行键入:“LS Y C X ”,然后回车。
即可直接出现如下图所示的计算结果Depe ndent Variable: Y Method: Least Squares Date: 12/12/12 Time: 20:15 Sample: 1 28In cluded observati ons: 28VariableCoefficie ntStd. Errort-StatisticProb.C 735.1080 477.1123 1.540744 0.1355 X0.6662220.03055821.802130.0000R-squared0.948138Mean depe ndent var 10780.65 Adjusted R-squared 0.946144 S.D. dependent var 2823.752 S.E. of regressi on 655.3079 Akaike info criteri on 15.87684 Sum squared resid 11165139 Schwarz criteri on 15.97199 Log likelihood -220.2757 F-statistic 475.3327 Durb in -Watson stat1.778976Prob(F-statistic)0.000000(477. 1123) (0 . 030558) 点击 store to DB,将估计式以“ eq01 ”为名保存。
时间序列异方差检验

时间序列异方差检验时间序列数据是指按时间顺序排列的一组观测数据,它们可以是连续的,也可以是离散的。
在许多实际问题中,时间序列数据的方差可能随着时间的变化而发生改变,这种现象被称为异方差性。
异方差性可能会对数据的分析和模型建立产生影响,因此需要进行异方差检验。
一种常用的异方差检验方法是利用残差的变化来判断异方差性。
具体来说,我们可以通过拟合一个回归模型,然后检验残差是否存在异方差性。
我们需要选择一个合适的回归模型来拟合时间序列数据。
常见的回归模型包括线性回归模型、多项式回归模型和指数回归模型等。
选择合适的回归模型需要考虑数据的特点和目标,可以借助统计方法和经验进行选择。
在选择了合适的回归模型后,我们可以通过拟合这个模型来得到残差。
残差是观测值与预测值之间的差异,可以表示模型无法解释的随机波动。
如果残差存在异方差性,那么其方差应该会随着预测值的变化而发生改变。
为了检验残差的异方差性,我们可以使用一些统计检验方法,如Breusch-Pagan检验和White检验等。
这些检验方法的基本思想是通过构造一个统计量,然后与相应的分布进行比较,以判断残差是否存在异方差性。
Breusch-Pagan检验是一种常用的异方差检验方法,它假设残差的方差与自变量之间存在线性关系。
具体来说,我们可以通过拟合一个辅助回归模型来估计残差的方差与自变量之间的关系,然后利用残差的平方和进行统计检验。
White检验是另一种常用的异方差检验方法,它不依赖于对残差方差与自变量关系的假设。
White检验将残差的平方和作为统计量,然后与自变量之间的交叉项进行比较,以判断残差是否存在异方差性。
除了上述方法外,还有一些其他的异方差检验方法,如Goldfeld-Quandt检验和ARCH检验等。
这些方法的具体原理和应用范围可以根据实际情况进行选择。
时间序列数据的异方差性可能会对数据的分析和模型建立产生影响,因此需要进行异方差检验。
我们可以通过拟合回归模型,然后检验残差的变化来判断异方差性。
异方差实验报告步骤(3篇)

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。
2. 学会运用统计软件进行异方差的检验和修正。
3. 提高对计量经济学模型中异方差性处理能力的实践应用。
二、实验原理1. 异方差性:在回归分析中,若回归模型的误差项(残差)的方差随着自变量或因变量的取值而变化,则称模型存在异方差性。
2. 异方差性的检验方法:图形检验、统计检验(如F检验、Breusch-Pagan检验、White检验等)。
3. 异方差性的修正方法:加权最小二乘法(WLS)、广义最小二乘法(GLS)等。
三、实验步骤1. 数据准备1. 收集实验所需数据,确保数据质量和完整性。
2. 对数据进行初步处理,如剔除异常值、缺失值等。
2. 模型设定1. 根据研究问题,选择合适的回归模型。
2. 利用统计软件(如Eviews、Stata等)进行初步的回归分析。
3. 异方差性检验1. 图形检验:绘制散点图,观察残差与自变量或因变量的关系,初步判断是否存在异方差性。
2. 统计检验:- F检验:检验回归系数的显著性。
- Breusch-Pagan检验:检验残差平方和与自变量或因变量的关系。
- White检验:检验残差平方和与自变量或因变量的多项式关系。
4. 异方差性修正1. 若检验结果表明存在异方差性,则需对模型进行修正。
2. 选择合适的修正方法:- 加权最小二乘法(WLS):根据残差平方与自变量或因变量的关系,计算权重,加权最小二乘法进行回归分析。
- 广义最小二乘法(GLS):根据残差平方与自变量或因变量的关系,选择合适的方差结构,广义最小二乘法进行回归分析。
5. 结果分析1. 对修正后的模型进行回归分析,观察回归系数的显著性、拟合优度等指标。
2. 对实验结果进行分析,解释实验现象,验证研究假设。
6. 实验报告撰写1. 撰写实验报告,包括以下内容:- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。
EViews计量经济学实验报告-异方差的诊断及修正模板(word文档良心出品)
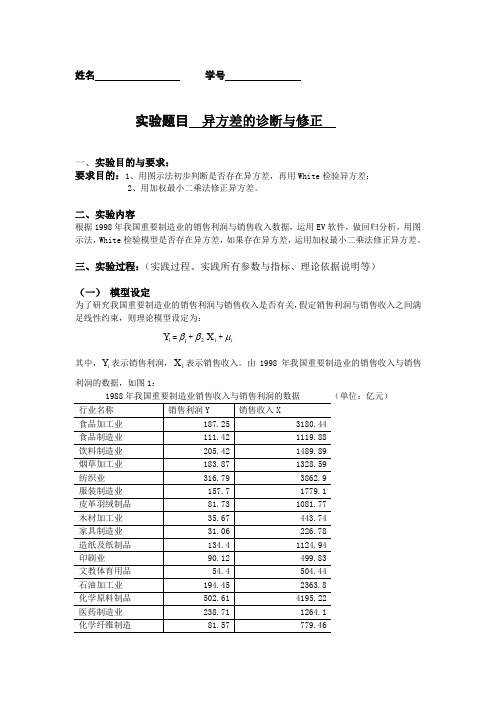
姓名 学号实验题目 异方差的诊断与修正一、实验目的与要求:要求目的:1、用图示法初步判断是否存在异方差,再用White 检验异方差;2、用加权最小二乘法修正异方差。
二、实验内容根据1998年我国重要制造业的销售利润与销售收入数据,运用EV 软件,做回归分析,用图示法,White 检验模型是否存在异方差,如果存在异方差,运用加权最小二乘法修正异方差。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等)(一) 模型设定为了研究我国重要制造业的销售利润与销售收入是否有关,假定销售利润与销售收入之间满足线性约束,则理论模型设定为:i Y =1β+2βi X +i μ其中,i Y 表示销售利润,i X 表示销售收入。
由1998年我国重要制造业的销售收入与销售利润的数据,如图1:1988年我国重要制造业销售收入与销售利润的数据 (单位:亿元)(二) 参数估计Dependent Variable: Y Method: Least Squares Date: 10/19/05 Time: 15:27 Sample: 1 28Included observations: 28Variable Coefficient Std. Error t-Statistic Prob. C 12.03564 19.51779 0.616650 0.5428 X0.1043930.008441 12.366700.0000R-squared 0.854696 Mean dependent var 213.4650 Adjusted R-squared 0.849107 S.D. dependent var 146.4895 S.E. of regression 56.90368 Akaike info criterion 10.98935 Sum squared resid 84188.74 Schwarz criterion 11.08450 Log likelihood -151.8508 F-statistic 152.9353 Durbin-Watson stat1.212795 Prob(F-statistic)0.000000估计结果为: iY ˆ = 12.03564 + 0.104393i X (19.51779) (0.008441) t=(0.616650) (12.36670)2R =0.854696 2R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下,销售收入每增长1元,销售利润平均增长0.104393元。
异方差的检验与修正

西安财经学院本科实验报告学院(部)统计学院实验室 313 课程名称计量经济学学生姓名学号 1204100213 专业统计学教务处制2014年12 月 15 日《异方差》实验报告开课实验室:313 2014年12月22第六部分异方差与自相关4. 在本例中,参数估计的结果为:2709030.01402097.01402.728X X Y ++=Λ(2.218) (2.438) (16.999)922173.02=R D.W.=1.4289 F=165.8853 SE=395.2538三.检查模型是否存在异方差 1.图形分析检验 (1)散点相关图分析分别做出X1和Y 、X2和Y 的散点相关图,观察相关图可以看出,随着X1、X2的增加,Y 也增加,但离散程度逐步扩大,尤其表现在X1和Y.这说明变量之间可能存在递增的异方差性。
在Graph/scatter 输入log(x2) e^2,结果如下:(2)残差相关图分析建立残差关于X1、X2的散点图,可以发现随着X 的增加,残差呈现明显的扩大趋势,表明模型很可能存在递增的异方差性。
但是否确实存在异方差还应通过更进一步的检验。
2.GQ 检验首先在主窗口Procs菜单里选Sort current page命令,输入排序变量x2,以递增型排序对解释变量X2进行排序,然后构造子样本区间,分别为1-12和20-31,再分别建立回归模型。
(1)在Sample菜单里,将区间定义为1—12,然后用OLS方法求得如下结果(2)在Sample菜单里,将区间定义为20—31,然后用OLS方法求得如下结果则F的统计量值为:6699.834542929948192122===∑∑iieeF在05.0=α下,式中分子、分母的自由度均为9,查F分布表得临界值为:18.3)9,9(05.0=F,因为F=8.6699>18.3)9,9(05.0=F,所以拒绝原假设,表明模型确实存在异方差。
回归模型的OLS估计及异方差的检验与修正

实验1 回归模型的OLS估计及异方差的检验与修正实验内容及要求:表1列出了2000年中国部分省市城镇居民每个家庭平均全年可支配收入x与消费性支出y的统计数据。
(1)利用OLS法建立人均消费支出与可支配收入的线性模型。
(2)检验模型是否存在异方差。
(3)如果存在异方差,试采用适当的方法加以消除。
表1 2000年中国部分省市城镇居民人均可支配收入与消费性支出(单位:元)实验如下:1、通过Y-X的散点图判断,并不存在异方差。
回归结果分析:图1人均消费支出与可支配收入的线性模型:Y =272.3635 + 0.755125Xt =(1.705713) (32.38690)R2=0.983129 D.W.=1.301563 F=1048.912残差分析:图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
2,Goldfeld-Quandt检验⑴将样本安解释变量排序(SORT X)并分成两部分(分别有 1 到8共8个样本合13 到20 共8个样本)⑵利用样本1 建立回归模型1(回归结果如图3),其残差平方和为126528.3Smpl 1 8LS Y C X图3⑶利用样本2 建立回归模型2(回归结果如图4),其残差平方和为615472.0。
图4⑷计算F 统计量:RSS2/RSS1=615472.0/126528.3=4.864,RSS2、RSS1分别是模型1 和模型2 的残差平方和。
取α=0.05时,查F分布表得F0.05(8-1-1,8-1-1)=4.28,而实际上F=4.864>F0.05=4.28 ,所以存在异方差。
3,White检验⑴建立回归模型:LS Y C X,回归结果如图5图5⑵在方程窗口上点击White Heteroskedastcity,检验结果如图6。
图6由图6中的数据,得到e2=-180998.9+49.42846X-0.002115X2t=(-1.751858) (1.708006) (-1.144742)R2=0.632606White统计量2200.63260612.65212nR=⨯=,该值大于5%显著性水平下自由度为2的2χ分布的相应临界值20.05(2) 5.99χ=,(在估计模型中含有两个解释变量,所以自由度为2)因此拒绝同方差性的原假设。
时序预测中的异方差性检验方法探讨(十)

时序预测是统计学和经济学中一个重要的课题,通常用来预测未来某一时间点的数值。
然而,在进行时序预测时,我们经常会遇到异方差性的问题。
异方差性指的是时间序列数据的方差不是恒定的,而是随时间变化的情况。
在异方差性存在的情况下,传统的预测方法可能会出现问题,因此需要采用一些特殊的方法来进行检验和处理。
本文将探讨时序预测中的异方差性检验方法,为读者提供一些参考和借鉴。
一、异方差性的检验方法在进行时序预测之前,我们首先需要检验数据是否存在异方差性。
常用的异方差性检验方法包括LM检验、BP检验和White检验。
LM检验是利用残差平方和的序列进行检验,其原假设是数据不存在异方差性。
BP检验是对LM检验的一种改进,可以检验更多的异方差性形式。
White检验是一种广义的异方差性检验方法,适用于多元回归模型。
通过对数据进行这三种检验,我们可以初步判断数据是否存在异方差性,并选择合适的处理方法。
二、异方差性的处理方法一旦确定数据存在异方差性,我们需要对数据进行处理,以确保预测模型的准确性。
常用的异方差性处理方法包括加权最小二乘法、异方差稳健标准误差和变换方法。
加权最小二乘法是一种根据异方差性的严重程度对数据进行加权的方法,可以有效减少异方差性对预测结果的影响。
异方差稳健标准误差是一种对参数估计的标准误差进行修正的方法,可以提高参数估计的准确性。
变换方法是通过对原始数据进行变换,使其满足异方差性的假设,从而得到更准确的预测结果。
通过选择合适的处理方法,我们可以有效处理数据的异方差性,提高预测模型的准确性。
三、异方差性对时序预测的影响异方差性对时序预测模型的影响是不可忽视的。
在存在异方差性的情况下,传统的预测方法可能会出现参数估计偏误、标准误差过低等问题,导致预测结果的不准确性。
因此,及时发现和处理数据的异方差性是非常重要的。
通过合适的异方差性检验和处理方法,我们可以有效降低异方差性对时序预测的影响,得到更准确的预测结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例三 ARIMA 模型的建立
一、实验目的
了解ARIMA 模型的特点和建模过程,了解AR ,MA 和ARIMA 模型三者之间的区别与联系,掌握如何利用自相关系数和偏自相关系数对ARIMA 模型进行识别,利用最小二乘法等方法对ARIMA 模型进行估计,利用信息准则对估计的ARIMA 模型进行诊断,以及如何利用ARIMA 模型进行预测。
掌握在实证研究如何运用Eviews 软件进行ARIMA 模型的识别、诊断、估计和预测。
二、基本概念
所谓ARIMA 模型,是指将非平稳时间序列转化为平稳时间序列,然后将平稳的时间序列建立ARMA 模型。
ARIMA 模型根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA )、自回归过程(AR )、自回归移动平均过程(ARMA )以及ARIMA 过程。
在ARIMA 模型的识别过程中,我们主要用到两个工具:自相关函数ACF ,偏自相关函数PACF 以及它们各自的相关图。
对于一个序列{}t X 而言,它的第j 阶自相关系数j ρ为它的j 阶自协方差除以方差,即j ρ=j 0γγ ,它是关于滞后期j 的函数,因此我们也称之为自相关函数,通常记ACF(j )。
偏自相关函数PACF(j )度量了消除中间滞后项影响后两滞后变量之间的相关关系。
三、实验内容及要求 1、实验内容:
(1)根据时序图的形状,采用相应的方法把非平稳序列平稳化;
(2)对经过平稳化后的1950年到2007年中国进出口贸易总额数据运用经典B-J 方法论建立合适的ARIMA (,,p d q )模型,并能够利用此模型进行进出口贸易总额的预测。
2、实验要求:
(1)深刻理解非平稳时间序列的概念和ARIMA 模型的建模思想;
(2)如何通过观察自相关,偏自相关系数及其图形,利用最小二乘法,以及信息准则建立合适的ARIMA 模型;如何利用ARIMA 模型进行预测; (3)熟练掌握相关Eviews 操作,读懂模型参数估计结果。
四、实验指导 1、模型识别 (1)数据录入
打开Eviews 软件,选择“File”菜单中的“New --Workfile”选项,在“Workfile structure type ”栏选择“Dated –regular frequency ”,在“Date specification ”栏中分别选择“Annual ”(年数据) ,分别在起始年输入1950,终止年输入2007,点击ok ,见图3-1,这样就建立了一个工作文件。
点击File/Import ,找到相应的Excel 数据集,导入即可。
图3-1 建立工作文件窗口
(2)时序图判断平稳性
(3
因为数据有指数上升趋势,为了减小波动,对其对数化,在Eviews命令框中输入相应的命令“series y=log(ex)”就得到对数序列,其时序图见图3-3,对数化后的序列远没有原始序列波动剧烈:
图3-3 对数进出口总额时序图
从图上仍然直观看出序列不平稳,进一步考察其自相关图和偏自相关图3-4:
图3-4 对数序列y自相关图
从自相关系数可以看出,衰减到零的速度非常缓慢,所以断定y 序列非平稳。
为了证实这个结论,进一步对其做ADF检验,结果见图3-5,可以看出在显著性水平0.05下,接受存在一个单位根的原假设,进一步验证了原序列不平稳。
为了找出其非平稳的阶数,需要对其一阶差分序列和二阶差分序列等进行ADF检验。
图3-5 序列y的ADF检验结果
(4)差分次数d的确定
y序列显著非平稳,现对其一阶差分序列进行ADF检验,在图3-6中的对话框中选择“1st difference”,检验结果见图3-7,可以看出在显著性水平0.05下显著拒绝存在单位根的原假设,说明一阶差分序列是平稳的,因此d=1。
图3-6
图3-7 一阶差分序列平稳性检验
(5)建立一阶差分序列
在Eviews对话框中输入“series x=y-y(-1)”,并点击“回车”,如图3-8,便得到了经过一阶差分处理后的新序列x,其时序图见图3-9,从直观上来看,序列x也是平稳的,这就可以对x序列进行ARMA模型分析了。
图3-8
(6)模型的识别
做平稳序列x 的自相关图3-10:
图3-10 x 的自相关-偏自相关图
从x 的自相关函数图和偏自相关函数图中我们可以看到,偏自相关系数是明显截尾的,而自相关系数在滞后6阶和7阶的时候落在2倍标准差的边缘,有待于进行模型选择。
2、模型的参数估计
点击“Quick ”-“Estimate Equation ”,会弹出如图3-11所示的窗口,在“Equation Specification”空白栏中键入“ x C MA(1) MA(2) MA(3) MA(4) MA(5) AR(1) AR (2)”等,在“Estimation Settings”中选择“LS -Least Squares(NLS and ARMA)”,然后“OK”。
或者在命令窗口直接输入ls x C MA(1) MA(2) MA(3) MA(4) MA(5) AR(1) AR(2) 等。
针对序列x 我们尝试几种不同的模型拟合,比如ARMA (1,1),ARMA (1,2),ARMA (1,3)等。
各种模型的参数估计结果和相关的检验统计量见表3-1
经过不断的尝试,我们最终选择了ARMA (1,7)模型,并且该模型中移动平均部分的部分系数不显著,最终得到的模型见图3-12:
图3-11 方程设定窗口
图3-12 ARMA(1,7)估计结果
可以看到,模型所有解释变量的参数估计值在0.01的显著性水平下都是显著的。
3、模型的诊断检验
DW统计量在2附近,残差不存在一阶自相关,但需要对残差做进一步分析:点击“V iew”—“R esidual test”—“Correlogram-Q-statistics”,在弹出的窗口中选择滞后阶数为默认24,点击“Ok”,见图3-13,从图上钢可以看出,残差不再存在自相关,说明模型拟合很好,模型拟合图见图3-14。
4、模型的预测 点击“Forecast ”,会弹出如图3-15所示的窗口。
在Eviews 中有两种预测方式:“Dynamic ”和“Static ”,前者是根据所选择的一定的估计区间,进行多步向前预测;后者是只滚动的进行向前一步预测,即每预测一次,用真实值代替预测值,加入到估计区间,再进行向前一步预测。
点击Dynamic forecast ,“Forecast sample ”中输入1950 2007,结果见图3-16:
图3-15
图中实线代表的是x 的预测值,两条虚线则提供了2倍标准差的置信区间。
可以看到,随着预测时间的增长,预测值很快趋向于序列的均值(接近0)。
图的右边列出的是评价预测的一些标准,如平均预测误差平方和的平方根(RMSE ),Theil 不相等系数及其分解。
可以看到,Theil 不相等系数为0.4295,表明模型的预测能力不太好,而对它的分解表明偏误比例很小,方差比例较大,说明实际序列的波动较大,而模拟序列的波动较小,这可能是由于预测时间过长。
下面我们再利用“Static ”方法来预测,得到如图3-17所示的结果。
从图中可以看到,“Static ”方法得到的预测值波动性要大;同时,方差比例的下降也表明较好的模拟了实际序列的波动 ,Theil 不相等系数为0.306,其中协方差比例为0.79,表明模型的预测结果较
综合上述分析过程,实际上我们是针对原序列(EX ):1950年—2007年我国进出口贸易总额数据序列,建立了一个ARIMA (1,1,7)模型进行拟合,模型形式如下: 11267(1)(ln )0.16430.4889(ln ) 1.18640.41440.41940.5729t t t t t t t B EX EX εεεεε------=-+++++。
