2019-2020学年江苏省淮安市开明中学八上期中模拟数学试卷(无答案)

合集下载

江苏省淮安市八年级上学期数学期中考试试卷

江苏省淮安市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共10分)1. （1分）(2020·阿城模拟) 下列图形中，是轴对称图形，但不是中心对称图形的是（）A .B .C .D .2. （1分） (2020八上·大冶期末) 活动课上，老师给出长度分别是3cm，4cm，7cm，10cm的四根木棒，要求从中任选三根围成一个三角形，下面是四位同学分别选择的结果，你认为能围成三角形的是（）A . 3cm，4cm，7cmB . 3cm，4cm，10cmC . 3cm，7cm，10cmD . 4cm，7cm，10cm3. （1分） (2020九下·重庆月考) 已知A（﹣3，2）关于x轴对称点为A'，则点A'的坐标为（）A . （3，2）B . （2，﹣3）C . （3，﹣2）D . （﹣3，﹣2）4. （1分）(2020·无锡模拟) 如果一个多边形的内角和等于900°，这个多边形是（）A . 四边形B . 五边形C . 六边形D . 七边形5. （1分）在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），则与△ABC有一条公共边且全等的所有格点三角形的个数是（）A . 1B . 2C . 3D . 46. （1分） (2017七下·宝安期中) 在△ABC中, 若∠A :∠B :∠C = 1 : 2 : 3 , 则△ABC 是（）A . 锐角三角形.B . 直角三角形C . 钝角三角形D . 等腰三角形7. （1分） (2016八上·绍兴期中) 若x，y满足|x﹣3|+ =0，则以x，y的值为两边长的等腰三角形的周长为（）A . 12B . 14C . 15D . 12或158. （1分） (2020八下·郑州月考) 如图，等边的边长为12，是边上的中线，是上的动点，是边上一点，若的最小值为（）A .B .C .D .9. （1分）如图，在△ABC中，，，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E，则弧BD的度数为（）A .B .C .D .10. （1分）边长为2的等边三角形的面积是（）A . 2B .C . 3D . 6二、填空题 (共6题；共6分)11. （1分）如图，在Rt△ABC中，∠C=90°，AC=18，BC=7，AB=PQ，P，Q两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP=________时，△ABC和△PQA全等．12. （1分） (2019八上·盐津月考) 在中，若，则是________三角形.13. （1分） (2017八上·独山期中) 如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分成三个三角形，则S△ABO：S△BCO：S△C AO等于________．14. （1分） (2019八上·合肥期中) 若点在x轴上，则a=________．15. （1分） (2019八下·江苏月考) 如图，在菱形ABCD中，∠ADC=120°,AD=4,P是AB边上的一点，E,F分别是DP ,BP的中点，则线段EF的长为________16. （1分） (2016八上·江宁期中) 如图，在等腰△ABC中，AB=AC，AD为△ABC的中线，∠B=72°，则∠DAC=________°．三、解答题 (共8题；共13分)17. （1分）一个三角形的两边b＝4，c＝7，试确定第三边a的范围．当各边均为整数时，有几个三角形？有等腰三角形吗？等腰三角形的边长各是多少？18. （1分） (2020八下·北京期中) 如图，为中边上一点，，，，求的度数．19. （2分） (2019七下·永寿期末) 如图，已知网格上小正方形的边长为1个单位长度，点A、B、C在格点上.（1）画出△ABC关于直线l对称的△A'B'C'；（2）求出△ABC的面积.20. （2分） (2019八上·武安期中) “8字”的性质及应用：（1）如图①，AD、BC相交于点O ，得到一个“8字”ABCD ，求证：∠A+∠B＝∠C+∠D ．（2）图②中共有多少个“8字”？（3）如图②，∠ABC和∠ADC的平分线相交于点E ，利用（1）中的结论证明∠E＝（∠A+∠C）．21. （1分）如图,在△ABC中,∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC 于点D,AD交PE于点F.求证:DF=DC.22. （1分）(2020·中模拟) 如图，点A，F，C，D在同一直线上，点B与点E分别在直线AD的两侧，且AB ＝DE，∠A＝∠D，AF＝DC，求证：BC＝EF．23. （3分）(2014·贵港) 如图，AB是大半圆O的直径，AO是小半圆M的直径，点P是大半圆O上一点，PA 与小半圆M交于点C，过点C作CD⊥OP于点D．（1）求证：CD是小半圆M的切线；（2）若AB=8，点P在大半圆O上运动（点P不与A，B两点重合），设PD=x，CD2=y．①求y与x之间的函数关系式，并写出自变量x的取值范围；②当y=3时，求P，M两点之间的距离．24. （2分） (2019八上·北碚期末) 如图1，在中，于E，，D是AE上的一点，且，连接BD，CD．（1）试判断BD与AC的位置关系和数量关系，并说明理由；（2）如图2，若将绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；（3）如图3，若将中的等腰直角三角形都换成等边三角形，其他条件不变．试猜想BD与AC的数量关系，请直接写出结论；你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．参考答案一、单选题 (共10题；共10分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共6分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共8题；共13分)17-1、18-1、19-1、19-2、20-1、20-2、20-3、21-1、22-1、23-1、24-1、24-2、24-3、。

江苏省淮安市2019-2020学年中考数学一模考试卷含解析

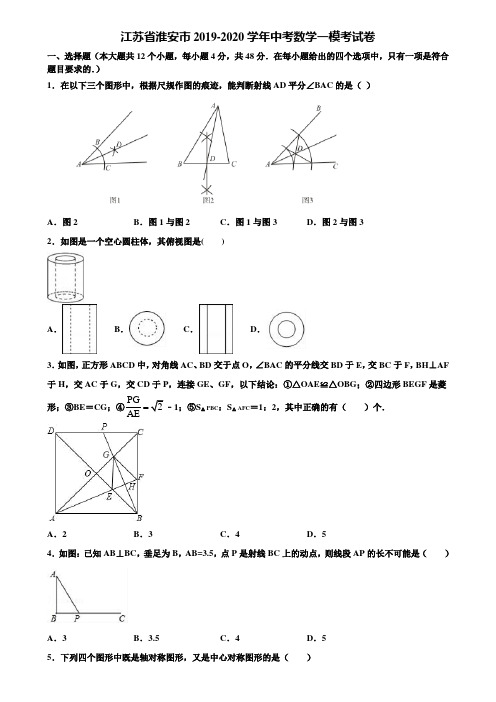
江苏省淮安市2019-2020学年中考数学一模考试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．在以下三个图形中，根据尺规作图的痕迹，能判断射线AD平分∠BAC的是（）A．图2 B．图1与图2 C．图1与图3 D．图2与图32．如图是一个空心圆柱体，其俯视图是( )A．B．C．D．3．如图，正方形ABCD中，对角线AC、BD交于点O，∠BAC的平分线交BD于E，交BC于F，BH⊥AF 于H，交AC于G，交CD于P，连接GE、GF，以下结论：①△OAE≌△OBG；②四边形BEGF是菱形；③BE＝CG；④PG2AE﹣1；⑤S△PBC：S△AFC＝1：2，其中正确的有（）个．A．2 B．3 C．4 D．54．如图：已知AB⊥BC，垂足为B，AB=3.5，点P是射线BC上的动点，则线段AP的长不可能是（）A．3 B．3.5 C．4 D．55．下列四个图形中既是轴对称图形，又是中心对称图形的是（）A．B．C．D．6．如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC=()A．3B．2 C．3 D．3+27．若()292m-=1，则符合条件的m有（）m-A．1个B．2个C．3个D．4个8．定义运算：a⋆b=2ab．若a，b是方程x2+x-m=0(m＞0)的两个根，则(a+1)⋆a -(b+1)⋆b的值为（）A．0 B．2 C．4m D．-4m9．如图，在平行四边形ABCD中，都不一定成立的是（）①AO=CO；②AC⊥BD；③AD∥BC；④∠CAB=∠CAD．A．①和④B．②和③C．③和④D．②和④10．已知关于x的方程x2﹣4x+c+1=0有两个相等的实数根，则常数c的值为（）A．﹣1 B．0 C．1 D．311．甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.1．其中说法正确的有（）A．4个B．3个C．2个D．1个12．△ABC在正方形网格中的位置如图所示，则cosB的值为( )A ．55B ．255C ．12D ．2二、填空题：（本大题共6个小题，每小题4分，共24分．） 13．已知：如图，△ABC 内接于⊙O ，且半径OC ⊥AB ，点D 在半径OB 的延长线上，且∠A=∠BCD=30°，AC=2，则由»BC，线段CD 和线段BD 所围成图形的阴影部分的面积为__．14．若一个扇形的圆心角为60°，面积为6π，则这个扇形的半径为__________．15．如图，在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上．（Ⅰ）AC 的长等于_____；（Ⅱ）在线段AC 上有一点D ，满足AB 2=AD•AC ，请在如图所示的网格中，用无刻度的直尺，画出点D ，并简要说明点D 的位置是如何找到的（不要求证明）_____．16．一元二次方程2x 2﹣3x ﹣4＝0根的判别式的值等于_____．17．如图，菱形ABCD 的边AD ⊥y 轴，垂足为点E ，顶点A 在第二象限，顶点B 在y 轴的正半轴上，反比例函数y ＝k x(k≠0，x ＞0)的图象经过顶点C 、D ，若点C 的横坐标为5，BE ＝3DE ，则k 的值为______．18．若一组数据1，2，3，x 的平均数是2，则x 的值为______．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）如图1，在等边三角形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A 的对应点E 落在射线BC 上，连接BQ ，设DAQ α∠=（060α<<o o 且30α≠o ）．（1）当030α<<o o 时，①在图1中依题意画出图形，并求BQE ∠（用含α的式子表示）；②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当3060α<<o o 时，直接写出线段CE ，AC ，CQ 之间的数量关系．20．（6分）某手机店销售10部A 型和20部B 型手机的利润为4000元，销售20部A 型和10部B 型手机的利润为3500元.(1)求每部A 型手机和B 型手机的销售利润；(2)该手机店计划一次购进A ，B 两种型号的手机共100部，其中B 型手机的进货量不超过A 型手机的2倍，设购进A 型手机x 部，这100部手机的销售总利润为y 元.①求y 关于x 的函数关系式；②该手机店购进A 型、B 型手机各多少部，才能使销售总利润最大？(3)在(2)的条件下，该手机店实际进货时，厂家对A 型手机出厂价下调()0100m m <<元，且限定手机店最多购进A 型手机70部，若手机店保持同种手机的售价不变，设计出使这100部手机销售总利润最大的进货方案.21．（6分）某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，并建立如下模型：设第t 个月该原料药的月销售量为P （单位：吨），P 与t 之间存在如图所示的函数关系，其图象是函数P=1204t +（0＜t≤8）的图象与线段AB 的组合；设第t 个月销售该原料药每吨的毛利润为Q （单位：万元），Q 与t 之间满足如下关系：Q=28,01244,1224t t t t +<≤⎧⎨-+<≤⎩（1）当8＜t≤24时，求P 关于t 的函数解析式；（2）设第t 个月销售该原料药的月毛利润为w （单位：万元）①求w 关于t 的函数解析式；②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P 的最小值和最大值．22．（8分）如图，在Rt△ABC中，∠C=90°，O、D分别为AB、AC上的点，经过A、D两点的⊙O分别交于AB、AC于点E、F，且BC与⊙O相切于点D．（1）求证：；（2）当AC=2，CD=1时，求⊙O的面积．23．（8分）“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量y （件）与销售单价x（元）之间存在一次函数关系，如图所示.（1）求y与x之间的函数关系式；（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.24．（10分）已知：如图，四边形ABCD的对角线AC和BD相交于点E，AD=DC，DC2=DE•DB，求证：（1）△BCE∽△ADE；（2）AB•BC=BD•BE．25．（10分）如图1，△ABC中，AB=AC=6，BC=4，点D、E分别在边AB、AC上，且AD=AE=1，连接DE、CD，点M、N、P分别是线段DE、BC、CD的中点，连接MP、PN、MN．（1）求证：△PMN是等腰三角形；（2）将△ADE绕点A逆时针旋转，①如图2，当点D、E分别在边AC两侧时，求证：△PMN是等腰三角形；②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时，请直接写出此时BD的长．26．（12分）某中学为了解八年级学习体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A、B、C、D四个等级．请根据两幅统计图中的信息回答下列问题：（1）本次抽样调查共抽取了多少名学生？（2）求测试结果为C等级的学生数，并补全条形图；（3）若该中学八年级共有700名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名．27．（12分）如图，在▱ABCD中，以点4为圆心，AB长为半径画弧交AD于点F；再分别以点B、F为圆心，大于BF的长为半径画弧，两弧交于点P；连接AP并廷长交BC于点E，连接EF（1）根据以上尺规作图的过程，求证：四边形ABEF是菱形；（2）若AB＝2，AE＝2，求∠BAD的大小．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．C【解析】【分析】根据角平分线的作图方法可判断图1，根据图2的作图痕迹可知D为BC中点，不是角平分线，图3中根据作图痕迹可通过判断三角形全等推导得出AD是角平分线.【详解】图1中，根据作图痕迹可知AD是角平分线；图2中，根据作图痕迹可知作的是BC的垂直平分线，则D为BC边的中点，因此AD不是角平分线；图3：由作图方法可知AM=AE，AN=AF，∠BAC为公共角，∴△AMN≌△AEF，∴∠3=∠4，∵AM=AE，AN=AF，∴MF=EN，又∵∠MDF=∠EDN，∴△FDM≌△NDE，∴DM=DE，又∵AD是公共边，∴△ADM≌△ADE，∴∠1=∠2，即AD平分∠BAC，故选C.【点睛】本题考查了尺规作图，三角形全等的判定与性质等，熟知角平分的尺规作图方法、全等三角形的判定与性质是解题的关键.2．D【解析】【分析】根据从上边看得到的图形是俯视图，可得答案．【详解】该空心圆柱体的俯视图是圆环，如图所示：故选D ．【点睛】本题考查了三视图，明确俯视图是从物体上方看得到的图形是解题的关键.3．C【解析】【分析】根据AF 是∠BAC 的平分线，BH ⊥AF ，可证AF 为BG 的垂直平分线，然后再根据正方形内角及角平分线进行角度转换证明EG ＝EB ，FG ＝FB ，即可判定②选项；设OA ＝OB ＝OC ＝a ，菱形BEGF 的边长为b ，由四边形BEGF 是菱形转换得到CF 2GF ＝2BF ，由四边形ABCD 是正方形和角度转换证明△OAE ≌△OBG ，即可判定①；则△GOE 是等腰直角三角形，得到GE 2OG ，整理得出a ，b 的关系式，再由△PGC ∽△BGA ，得到BG PG＝2，从而判断得出④；得出∠EAB ＝∠GBC 从而证明△EAB ≌△GBC ，即可判定③；证明△FAB ≌△PBC 得到BF ＝CP ，即可求出PBC AFCS S V V ，从而判断⑤. 【详解】解：∵AF 是∠BAC 的平分线，∴∠GAH ＝∠BAH ，∵BH ⊥AF ，∴∠AHG ＝∠AHB ＝90°，在△AHG 和△AHB 中GAH BAH AH AHAHG AHB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AHG ≌△AHB （ASA ），∴GH ＝BH ，∴AF 是线段BG 的垂直平分线，∴EG ＝EB ，FG ＝FB ，∵四边形ABCD 是正方形，∴∠BAF ＝∠CAF ＝12×45°＝22.5°，∠ABE ＝45°，∠ABF ＝90°， ∴∠BEF ＝∠BAF+∠ABE ＝67.5°，∠BFE ＝90°﹣∠BAF ＝67.5°，∴∠BEF ＝∠BFE ，∴EB ＝FB ，∴EG ＝EB ＝FB ＝FG ，∴四边形BEGF 是菱形；②正确；设OA ＝OB ＝OC ＝a ，菱形BEGF 的边长为b ，∵四边形BEGF 是菱形，∴GF ∥OB ，∴∠CGF ＝∠COB ＝90°，∴∠GFC ＝∠GCF ＝45°，∴CG ＝GF ＝b ，∠CGF ＝90°，∴CFGFBF ，∵四边形ABCD 是正方形，∴OA ＝OB ，∠AOE ＝∠BOG ＝90°，∵BH ⊥AF ，∴∠GAH+∠AGH ＝90°＝∠OBG+∠AGH ，∴∠OAE ＝∠OBG ，在△OAE 和△OBG 中OAE OBG OA OBAOE BOG ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△OAE ≌△OBG （ASA ），①正确；∴OG ＝OE ＝a ﹣b ，∴△GOE 是等腰直角三角形，∴GEOG ，∴b（a ﹣b ），整理得a，∴AC ＝2a ＝（）b ，AG ＝AC ﹣CG ＝（）b ，∵四边形ABCD 是正方形，∴PC ∥AB ， ∴BG PG ＝AG C G＝(1b b+＝， ∵△OAE ≌△OBG ，∴AE ＝BG ， ∴AE PG＝， ∴PG AE＝1，④正确； ∵∠OAE ＝∠OBG ，∠CAB ＝∠DBC ＝45°，∴∠EAB ＝∠GBC ，在△EAB 和△GBC 中EAB GBC AB BCABE BCG 45︒∠=∠⎧⎪=⎨⎪∠=∠=⎩， ∴△EAB ≌△GBC （ASA ），∴BE ＝CG ，③正确；在△FAB 和△PBC 中FAB PBC AB BCABF BCP 90︒∠=∠⎧⎪=⎨⎪∠=∠=⎩， ∴△FAB ≌△PBC （ASA ），∴BF ＝CP ， ∴PBC AFC S S V V ＝1212BC CP AB CF ⋅⋅＝CP CF＝2，⑤错误；综上所述，正确的有4个，故选：C ．【点睛】本题综合考查了全等三角形的判定与性质，相似三角形，菱形的判定与性质等四边形的综合题．该题难度较大，需要学生对有关于四边形的性质的知识有一系统的掌握．4．A【解析】。

2020年江苏省淮安市淮阴区开明中学中考数学模拟试卷(一)

2020年江苏省淮安市淮阴区开明中学中考数学模拟试卷（一）一、选择题：（每题3分，共24分，请将答案涂在答题卡上）1．（3分）若使等式（﹣4）□（﹣6）＝2成立，则□中应填入的运算符号是（）A．+B．﹣C．×D．÷2．（3分）下列各数中，属于无理数的是（）A．0.010010001B．C．3.14D．﹣3．（3分）下列图形中，不是中心对称图形的是（）A．B．C．D．4．（3分）已知点M的坐标为（﹣2，1），则点M在直角坐标系中的位置位于（）A．第一象限B．第二象限C．第三象限D．第四象限5．（3分）如图，小明从图1中几何体的某个方向观察看到如图2所示的结果，则小明是从该几何体的（）A．正面B．上面C．左面D．右面6．（3分）某果园2012年水果产量为100吨，2014年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x（）A．144（1﹣x）2＝100B．100（1﹣x）2＝144C．144（1+x）2＝100D．100（1+x）2＝1447．（3分）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A（﹣3，0），（0，4），则该菱形的周长是（）A．5B．10C．16D．208．（3分）我市为迎接2014青奥会的召开，现对某景观道路进行拓宽改造．工程队在工作了一段时间后，因雨被迫停工几天，按时完成了拓宽改造任务．下面能反映该工程尚未改造的道路y（米）与时间x（天）（）A．B．C．D．二、填空题：（每题3分，共24分，请将答案填在答题卡上）9．（3分）﹣2的绝对值是．10．（3分）在某次体育考试中，某班参加仰卧起坐测试的一组女生（每组5人）测试成绩如下：44，48，47．11．（3分）如图，已知∠1＝∠2，若添加一个条件使得△ABC与△ADE相似．（只填写一个你认为正确的答案）12．（3分）若x＝2是关于x的方程x2﹣2x+a﹣1＝0的一个根，则实数a的值＝．13．（3分）已知反比例函数y＝的图象过点A（﹣2，3），B（a，1），则a＝．14．（3分）如图，AB∥CD，∠1＝75°，则∠CAD＝°．15．（3分）如图，⊙O的半径为5，AB切⊙O于点B，AC＝OC，则图中阴影部分的面积＝．16．（3分）如图，正方形ABCD的边长为4，点F为BC的中点，H是AB，AD边上一点，将△AEH沿EH折叠后点A的对应点A′刚好落在DC′上，则sin∠ADA′＝．三、解答题：（共11小题，共102分，请将答案填在答题卡上）17．（8分）（1）计算：|2﹣|+2sin45°﹣（）0；（2）解方程组：．18．（6分）先化简：（﹣a+1）÷，并从0，﹣119．（8分）已知，如图，点A、D、C、F在同一条直线上，AB＝DE，BC＝EF．求证：BC ∥EF．20．（10分）某公司销售部统计了每个销售员在某月的销售额，绘制了不完整的折线统计图和扇形统计图．设销售员的月销售额为x（单位：万元）．销售部规定：当x＜16时为“不称职”，当16≤x＜20时为“基本称职”，当x≥25时为“优秀”．根据以上信息，解答下列问题：（1）填空：该销售部共有销售员人，d＝；（2）所有销售员月销售额的中位数为；众数为；（3）为了调动销售员的积极性，销售部决定根据本月的销售情况制定一个月销售额奖励标准，凡月销售额达到或超过这个标准的销售员将获得奖励．如果要使得本月所有“称职”和“优秀”的销售员中不少于一半人员能获奖万元（结果取整数）．21．（8分）我市为创评“全国文明城市”称号，周末团市委组织志愿者进行宣传活动．班主任梁老师决定从4名班干部（小悦、小惠、小明和小斌，其中小悦、小惠为女生，其他为男生）中通过抽签方式确定2人去参加，把四张卡片背面朝上，洗匀后放在桌面上，记下姓名，再从剩余的3张卡片中随机抽取第二张（1）第一次抽取卡片“抽中女生”的概率为；（2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“抽中一男一女”的概率．22．（8分）在边长为1的正方形网格中，建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上（4，4），请解答下列问题：（1）画出△ABC关于y轴对称的△A1B1C1，并写出点C1的坐标；（2）将△ABC绕点C逆时针旋转90°，画出旋转后的△A2B2C2，写出旋转过程中点A 经过的路径长．23．（8分）如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，然后向西走60m到达C点，测得点B在点C的北偏东60°方向（1）求∠CBA的度数．（2）求出这段河的宽（结果精确到1m，备用数据≈1.41，≈1.73）．24．（10分）如图，AB为⊙O直径，C，D为⊙O上不同于A、B的两点，垂足为E，直线AB与CE相交于F点．（1）试说明：CF为⊙O的切线；（2）若CE＝2，BE＝1，求AB的长．25．（10分）甲，乙两人同时各接受了300个零件的加工任务，甲比乙每小时加工的数量多，其中一人因机器故障停止加工若干小时后又继续按原速加工，直到他们都完成任务（个）与加工时间x（小时）之间的函数关系（1）其中一人因故障，停止加工小时，甲每小时加工的零件数量为个；（2）求线段BC对应的函数关系式和D点坐标；（3）乙在开始加工多少小时后，比甲少加工75个零件？26．（12分）【问题呈现】小华遇到这样一个问题，如图1，△ABC中，BC＝6，AC＝5，连接P A、PB、PC，求P A+PB+PC的最小值．【问题解决】小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，这样依据“两点之间，线段最短”，发现通过旋转可以解决这个问题．他的做法是，如图2，得到△EDC，连接PD、BE（1）请你写出图2中，P A+PB+PC的最小值为；（2）【类比应用】如图3，直角坐标系中有菱形ABCD，点B与原点重合（4，0），∠ABC＝60°，若在菱形ABCD内部有一动点P，并求出此时点P的坐标是多少；（3）【生活实际】如图4，一个矩形菜地的A，B，C三个顶点处建有三个菜窖，经研究发现，运输点P到A，B千米，若AB＝2，则此矩形菜地的面积至少为平方千米．27．（14分）如图，已知一个顶点在原点的抛物线经过点（2，1），点Q是第一象限内的一个定点（3，5），点F是y轴上一定点，F点坐标为（0，1）（1）求出此抛物线对应的函数的解析式，并写出该函数的两条性质；（2）是否存在这样的P点，使得点F恰好位于线段PQ的垂直平分线上？如果存在，请求出P点坐标，请说明理由；（3）当点P在抛物线上运动时，QP+PF的最小值＝，此时P点坐标为．2020年江苏省淮安市淮阴区开明中学中考数学模拟试卷（一）参考答案与试题解析一、选择题：（每题3分，共24分，请将答案涂在答题卡上）1．（3分）若使等式（﹣4）□（﹣6）＝2成立，则□中应填入的运算符号是（）A．+B．﹣C．×D．÷【解答】解：根据题意得：（﹣4）﹣（﹣6）＝﹣7+6＝2，故选：B．2．（3分）下列各数中，属于无理数的是（）A．0.010010001B．C．3.14D．﹣【解答】解：无理数是，故选：B．3．（3分）下列图形中，不是中心对称图形的是（）A．B．C．D．【解答】解：A、是中心对称图形；B、是中心对称图形；C、是中心对称图形；D、不是中心对称图形．故选：D．4．（3分）已知点M的坐标为（﹣2，1），则点M在直角坐标系中的位置位于（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：∵﹣2＜0，4＞0，∴点M（﹣2，6）在直角坐标系中的位置位于第二象限．故选：B．5．（3分）如图，小明从图1中几何体的某个方向观察看到如图2所示的结果，则小明是从该几何体的（）A．正面B．上面C．左面D．右面【解答】解：观察几何体发现，该几何体的左视图为，故选：C．6．（3分）某果园2012年水果产量为100吨，2014年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x（）A．144（1﹣x）2＝100B．100（1﹣x）2＝144C．144（1+x）2＝100D．100（1+x）2＝144【解答】解：设该果园水果产量的年平均增长率为x，则2013年的产量为100（1+x）吨2吨，根据题意，得100（3+x）2＝144，故选：D．7．（3分）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A（﹣3，0），（0，4），则该菱形的周长是（）A．5B．10C．16D．20【解答】解：∵菱形ABCD的顶点A，D的坐标分别为（﹣3，（0，∴OA＝5，OD＝3，由勾股定理得：AD＝，∴该菱形的周长＝3×5＝20，故选：D．8．（3分）我市为迎接2014青奥会的召开，现对某景观道路进行拓宽改造．工程队在工作了一段时间后，因雨被迫停工几天，按时完成了拓宽改造任务．下面能反映该工程尚未改造的道路y（米）与时间x（天）（）A．B．C．D．【解答】解：∵y随x的增大而减小，∴选项A错误；∵施工队在工作了一段时间后，因雨被迫停工几天，∴选项B错误；∵施工队随后加快了施工进度，∴y随x的增大减小得比开始的快，∴选项C错误；选项D正确；故选：D．二、填空题：（每题3分，共24分，请将答案填在答题卡上）9．（3分）﹣2的绝对值是2．【解答】解：﹣2的绝对值是：2．故答案为：6．10．（3分）在某次体育考试中，某班参加仰卧起坐测试的一组女生（每组5人）测试成绩如下：44，48，476．【解答】解：这组数据的极差为48﹣42＝6，故答案为：6．11．（3分）如图，已知∠1＝∠2，若添加一个条件使得△ABC与△ADE相似∠D＝∠B （或∠AED＝∠C）．（只填写一个你认为正确的答案）【解答】解：∵∠1＝∠2，∴∠2+∠BAE＝∠2+∠BAE，即∠BAC＝∠DAE，∴要使△ABC∽△ADE，可添加的条件为：∠D＝∠B或∠AED＝∠C．故答案为：∠D＝∠B（或∠AED＝∠C）．12．（3分）若x＝2是关于x的方程x2﹣2x+a﹣1＝0的一个根，则实数a的值＝1．【解答】解：∵x＝2是关于x的方程x2﹣4x+a﹣1＝0的一个根，∴7﹣4+a﹣1＝5，解得a＝1．故答案为1．13．（3分）已知反比例函数y＝的图象过点A（﹣2，3），B（a，1），则a＝﹣6．【解答】解：∵反比例函数y＝的图象过点A（﹣2，∴k＝﹣2×8＝﹣6；∵反比例函数经过点B，∴1＝﹣，∴a＝﹣6故答案为﹣6．14．（3分）如图，AB∥CD，∠1＝75°，则∠CAD＝70°．【解答】解：∵AB∥CD，∠1＝75°，∴∠ACD＝∠1＝75°，∵∠4＝35°，∴∠CAD＝180°﹣∠ACD﹣∠2＝70°．故答案为：70．15．（3分）如图，⊙O的半径为5，AB切⊙O于点B，AC＝OC，则图中阴影部分的面积＝﹣．【解答】解：∵AB切⊙O于点B，∴OB⊥AB，∴AB＝＝＝5，在Rt△ABO中，sin A＝＝，∴∠A＝30°，∴∠AOB＝60°，∴阴影部分的面积＝×5＝﹣，故答案为：﹣．16．（3分）如图，正方形ABCD的边长为4，点F为BC的中点，H是AB，AD边上一点，将△AEH沿EH折叠后点A的对应点A′刚好落在DC′上，则sin∠ADA′＝．【解答】解：如图，延长DC'交AB于K，分别过H，垂足分别为M，N，∵四边形ABCD为正方形，∴∠A＝∠B＝∠C＝90°，AB＝BC＝6，∵E，F分别为AB，∴AE＝BE＝BF＝FC＝×6＝3，由翻折知，△DCF≌△DC'F，∴∠FC'D＝∠C＝90°，∠A＝∠HA'E＝90°，C'F＝CF＝BF＝4，∴∠B＝∠FC'K＝90°，又∵KF＝KF，∴Rt△FBK≌Rt△FC'K（HL），∴KB＝KC'，设KB＝KC'＝x，在Rt△ADK中，AD＝6，DK＝6+x，∵DK3＝AD2+AK2，∴（3+x）2＝64+（6﹣x）2，解得，x＝，∴BK＝C'K＝，∴DK＝DC'+KC'＝6+＝，EK＝BE﹣BK＝，在Rt△KNE与Rt△KAD中，sin∠EKN＝＝，即＝，解得，EN＝，∵∠DA'H+∠EA'N＝90°，∠EA'N+∠NEA'＝90°，∴∠HA'D＝∠NEA'，在Rt△EA'N中，cos∠A'EN＝＝＝，即cos∠DA'H＝，故答案为：．三、解答题：（共11小题，共102分，请将答案填在答题卡上）17．（8分）（1）计算：|2﹣|+2sin45°﹣（）0；（2）解方程组：．【解答】解：（1）原式＝2﹣+3×＝2﹣+﹣2＝1；（2），①+②，得4x＝4，解得：x＝5，把x＝1代入①，得1+2y＝﹣1，解得：y＝﹣1，所以方程组的解是．18．（6分）先化简：（﹣a+1）÷，并从0，﹣1【解答】解：（﹣a+3）÷＝＝＝，当a＝0时，原式＝．19．（8分）已知，如图，点A、D、C、F在同一条直线上，AB＝DE，BC＝EF．求证：BC∥EF．【解答】证明：∵AD＝CF，∴AD+DC＝CF+DC，即AC＝DF，在△ABC和△ADC中，，∴△ABC≌△DEF（SSS），∴∠ACB＝∠F，∴BC∥EF．20．（10分）某公司销售部统计了每个销售员在某月的销售额，绘制了不完整的折线统计图和扇形统计图．设销售员的月销售额为x（单位：万元）．销售部规定：当x＜16时为“不称职”，当16≤x＜20时为“基本称职”，当x≥25时为“优秀”．根据以上信息，解答下列问题：（1）填空：该销售部共有销售员40人，d＝6；（2）所有销售员月销售额的中位数为22.5；众数为21；（3）为了调动销售员的积极性，销售部决定根据本月的销售情况制定一个月销售额奖励标准，凡月销售额达到或超过这个标准的销售员将获得奖励．如果要使得本月所有“称职”和“优秀”的销售员中不少于一半人员能获奖23万元（结果取整数）．【解答】解：（1）∵被调查的总人数为（4+5+2+3+4）÷50%＝40人，∴不称职的百分比为（8+2）÷40×100%＝10%，基本称职的百分比为（2+8+3+2）÷40×100%＝25%，优秀的百分比为7﹣（10%+25%+50%）＝15%，则优秀的人数为15%×40＝6，∴得26分的人数为6﹣（3+1+1）＝2，故答案为：40，6；（2）由折线图知称职与优秀的销售员职工人数分布如下：20万4人、21万7人、23万3人、25万2人、27万7人，则称职与优秀的销售员月销售额的中位数为（22+23）÷2＝22.5、众数为21；故答案为：22.4，21；（3）月销售额奖励标准应定为23万元．∵称职和优秀的销售员月销售额的中位数为22.5万元，∴要使得所有“称职”和“优秀”的销售员的一半人员能获奖，月销售额奖励标准应定为23万元．故答案为：23．21．（8分）我市为创评“全国文明城市”称号，周末团市委组织志愿者进行宣传活动．班主任梁老师决定从4名班干部（小悦、小惠、小明和小斌，其中小悦、小惠为女生，其他为男生）中通过抽签方式确定2人去参加，把四张卡片背面朝上，洗匀后放在桌面上，记下姓名，再从剩余的3张卡片中随机抽取第二张（1）第一次抽取卡片“抽中女生”的概率为；（2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“抽中一男一女”的概率．【解答】解：（1）∵小悦、小惠为女生，∴第一次抽取卡片“抽中女生”的概率为＝；故答案为：；（2）记小悦、小惠用A，小明和小斌用C，列表如下：A B C DA﹣﹣﹣（B，A）（C，A）（D，A）B（A，B）﹣﹣﹣（C，B）（D，B）C（A，C）（B，C）﹣﹣﹣（D，C）D（A，D）（B，D）（C，D）﹣﹣﹣由表可知，共有12种等可能结果，所以“抽中一男一女”的概率是＝．22．（8分）在边长为1的正方形网格中，建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上（4，4），请解答下列问题：（1）画出△ABC关于y轴对称的△A1B1C1，并写出点C1的坐标（﹣3，1）；（2）将△ABC绕点C逆时针旋转90°，画出旋转后的△A2B2C2，写出旋转过程中点A 经过的路径长π．【解答】解：（1）如图，△A1B1C3为所作，点C1的坐标为（﹣3，4）；故答案为（﹣3，1）；（2）如图，△A6B2C2为所作，CA＝＝，所以旋转过程中点A经过的路径长为＝π．故答案为π．23．（8分）如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，然后向西走60m到达C点，测得点B在点C的北偏东60°方向（1）求∠CBA的度数．（2）求出这段河的宽（结果精确到1m，备用数据≈1.41，≈1.73）．【解答】解：（1）由题意得，∠BAD＝45°，∴∠CBA＝∠BAD﹣∠BCA＝15°；（2）作BD⊥CA交CA的延长线于D，设BD＝xm，∵∠BCA＝30°，∴CD＝＝x，∵∠BAD＝45°，∴AD＝BD＝x，则x﹣x＝60，解得x＝≈82，答：这段河的宽约为82m．24．（10分）如图，AB为⊙O直径，C，D为⊙O上不同于A、B的两点，垂足为E，直线AB与CE相交于F点．（1）试说明：CF为⊙O的切线；（2）若CE＝2，BE＝1，求AB的长．【解答】证明：（1）如图①，连接OC，∵CE⊥DB，∴∠DEF＝90°，∵OC＝OA，∴∠A＝∠ACO，∴∠COF＝∠A+∠ACO＝2∠BAC，∵∠ABD＝2∠BAC，∴∠ABD＝∠COF，∴CO∥ED，∴∠OCF＝∠DEF＝90°，∴OC⊥CF，∴CF为⊙O的切线.（2）如图②，过点O作OG⊥DE，∴∠OGE＝90°，∵CE⊥DB，∴∠DEC＝90°，∵∠OCE＝90°，∴四边形COEG是矩形，∴OG＝CE＝2，OC＝EG＝1+BG，设OC＝x，则BG＝x﹣1，在Rt△OGB中，OB7＝OG2+BG2，∴x4＝4+（x﹣1）7，解得，x＝，∴AB＝7．25．（10分）甲，乙两人同时各接受了300个零件的加工任务，甲比乙每小时加工的数量多，其中一人因机器故障停止加工若干小时后又继续按原速加工，直到他们都完成任务（个）与加工时间x（小时）之间的函数关系（1）其中一人因故障，停止加工1小时，甲每小时加工的零件数量为60个；（2）求线段BC对应的函数关系式和D点坐标；（3）乙在开始加工多少小时后，比甲少加工75个零件？【解答】解：（1）由图象可得，其中一人因故障，停止加工2﹣1＝3（小时），甲每小时加工的零件数量为：300÷[1+（6﹣6）]＝60（个），故答案为：1，60；（2）乙的加工速度为：300÷[6+（6﹣2）]＝30（个/小时），则点C的纵坐标为：300﹣30×6＝120，∴点C的坐标为（2，120），设线段BC对应的函数关系式为y＝kx+b，∵点B（2，0），120）在线段BC上，∴，解得，即线段BC对应的函数解析式为y＝30x﹣60（3≤x≤6），点D的横坐标为6+（6﹣2）＝6+2＝10，∴点D的坐标为（10，0）；（3）在BC段，令y＝75，解得x＝4.5，在CD段，则比甲少加工75个零件时，答：乙在开始加工4.5小时或2.5小时后，比甲少加工75个零件．26．（12分）【问题呈现】小华遇到这样一个问题，如图1，△ABC中，BC＝6，AC＝5，连接P A、PB、PC，求P A+PB+PC的最小值．【问题解决】小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，这样依据“两点之间，线段最短”，发现通过旋转可以解决这个问题．他的做法是，如图2，得到△EDC，连接PD、BE（1）请你写出图2中，P A+PB+PC的最小值为；（2）【类比应用】如图3，直角坐标系中有菱形ABCD，点B与原点重合（4，0），∠ABC＝60°，若在菱形ABCD内部有一动点P，并求出此时点P的坐标是多少；（3）【生活实际】如图4，一个矩形菜地的A，B，C三个顶点处建有三个菜窖，经研究发现，运输点P到A，B千米，若AB＝2，则此矩形菜地的面积至少为8平方千米．【解答】解：（1）如图2中，∵将△APC绕点C顺时针旋转60°，得到△EDC，∴△APC≌△EDC，∴∠ACP＝∠ECD，AC＝EC＝5，∴∠ACP+∠PCB＝∠ECD+∠PCB，∴∠ECD+∠PCB＝∠ACB＝30°，∴∠BCE＝∠ECD+∠PCB+∠PCD＝30°+60°＝90°．菁优网在Rt△BCE中，∵∠BCE＝90°，CE＝4，∴BE＝＝＝，即P A+PB+PC的最小值为．故答案为：．（2）如图3中，连接AC，得到△DEC，DE，当B、P、E，P A+PB+PC值最小，设BD 交AC于点O．∵将△APC绕点C顺时针旋转60°，得到△DEC，∴△APC≌△DEC，∴CP＝CE，∠PCE＝60°，∴△PCE是等边三角形，∴PE＝CE＝CP，∠EPC＝∠CEP＝60°．∵菱形ABCD中，∠ABP＝∠CBP＝，∴∠PCB＝∠EPC﹣∠CBP＝60°﹣∠30°＝30°，∴∠PCB＝∠CBP＝30°，∴BP＝CP，同理，DE＝CE，∴BP＝PE＝ED．连接AC，交BD于点O．在Rt△BOC中，∵∠BOC＝90°，BC＝4，∴BO＝BC•cos∠OBC＝4×＝2，∴BD＝2BO＝4，∴BP＝BD＝，∴P（4，）．∴P A+PB+PC的最小值为4，此时P（7，）．（3）如图4中，将△ABP绕点B逆时针旋转60°得到△TBG，CT．当T，G，P，P A+PB+PC 的值最小．设BC＝m千米，则AB＝2，∵BA＝BT＝2m千米，∠ABT＝60°，∴∠CBT＝150°，∴TH＝BT＝，BH＝BT•cos30°＝6m（千米），∴CH＝4m，由题意CT≥2千米，∴≥2，∵m＞0，∴m≥7，∴BC的最小值为2千米，AB的最小值为4，∴此矩形菜地的面积的最小值为8平方千米，故答案为：3．27．（14分）如图，已知一个顶点在原点的抛物线经过点（2，1），点Q是第一象限内的一个定点（3，5），点F是y轴上一定点，F点坐标为（0，1）（1）求出此抛物线对应的函数的解析式，并写出该函数的两条性质；（2）是否存在这样的P点，使得点F恰好位于线段PQ的垂直平分线上？如果存在，请求出P点坐标，请说明理由；（3）当点P在抛物线上运动时，QP+PF的最小值＝6，此时P点坐标为（3，）．【解答】解：（1）设抛物线的解析式为y＝ax2，将点（2，8）代入解析式得4a＝1，∴a＝，故抛物线的解析式为：y＝x2，性质：①开口向上，②当x＞0时；（2）若存在点P，使得点F恰好位于线段PQ的垂直平分线上，则FQ＝FP，设P（x，y），则FQ＝，FP＝＝，∴5＝y+1，∴y＝4，将y＝4代入y＝x2得，x＝±4，∴点P（6，4）或（﹣4，∴存在这样的P点，使得点F恰好位于线段PQ的垂直平分线上，5）或（﹣4．（3）由（2）知FP＝y+1，即PF为点P到直线y＝﹣3的距离，∴PF＝PB，∴QP+PF的最小值转化为QP+PB最小值，即过点Q作QA垂直于直线y＝﹣1，QP+PF 的最小值为QA的长度，∴QP+PF的最小值为5﹣（﹣4）＝6，此时点P的坐标为（3，），故答案为：6，（4，）．。

江苏省淮安市淮安区2019-2020学年八年级上学期期中考试数学试题含解析

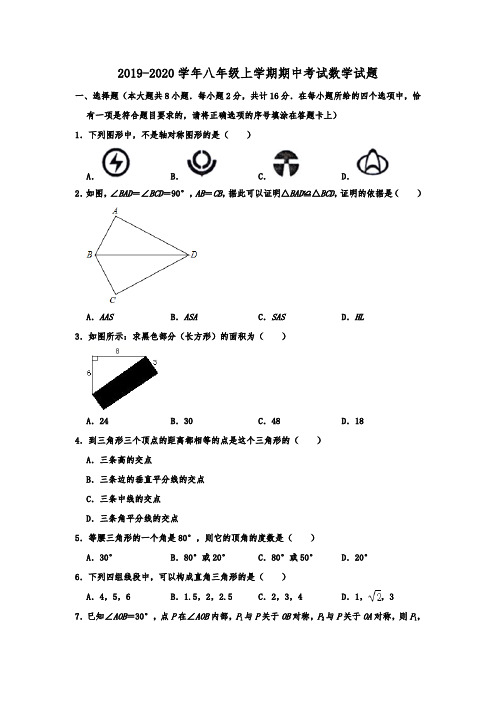
2019-2020学年八年级上学期期中考试数学试题一、选择题（本大题共8小题．每小题2分，共计16分．在每小题所给的四个选项中，恰有一项是符合题目要求的，请将正确选项的序号填涂在答题卡上）1．下列图形中，不是轴对称图形的是（）A．B．C．D．2．如图，∠BAD＝∠BCD＝90°，AB＝CB，据此可以证明△BAD≌△BCD，证明的依据是（）A．AAS B．ASA C．SAS D．HL3．如图所示：求黑色部分（长方形）的面积为（）A．24 B．30 C．48 D．184．到三角形三个顶点的距离都相等的点是这个三角形的（）A．三条高的交点B．三条边的垂直平分线的交点C．三条中线的交点D．三条角平分线的交点5．等腰三角形的一个角是80°，则它的顶角的度数是（）A．30°B．80°或20°C．80°或50°D．20°6．下列四组线段中，可以构成直角三角形的是（）A．4，5，6 B．1.5，2，2.5 C．2，3，4 D．1，，37．已知∠AOB＝30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是（）A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形8．如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE＝5，BC＝8，则△DEF的周长是（）A．21 B．18 C．13 D．15二、填空题（本大题共10小题．每小题3分，共计30分．不需写出解答过程，请把正确答案直接填在答题卡相应的位置上）9．一个等边三角形的对称轴有条．10．一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是；11．直角三角形的斜边长是5，一直角边长是3，则此直角三角形另一直角边是．12．如图，△ABC≌△ADE，若∠C＝35°，∠D＝75°，∠DAC＝25°，则∠BAD＝°．13．如图，Rt△ABC中，∠C＝90°，∠ABC的平分线交AC于点P，PD⊥AB，垂足为D，若PD＝3，则PC＝．14．若△ABC三边之比为5：12：13，则△ABC是三角形．15．如图，∠1＝∠2，∠B＝∠C，则△ABD与△ACD（填“全等”、“不一定全等”）．16．如图，已知△ABC中，∠ABC＝45°，F是高AD和BE的交点，CD＝4，则线段DF的长度为．17．如图，在△ABC中，DE是AC的垂直平分线，AE＝4cm，△ABD的周长为13cm，则△ABC 的周长为cm．18．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）2＝21，大正方形的面积为13，则小正方形的面积为．三、解答题（本大题共8小题，共计74分．请在答题卡指定区域内作答，解答时应写出必要的演算步骤、证明过程或文字说明）19．已知：如图，点E、F在线段BD上，BE＝DF，AB∥CD，∠A＝∠C．求证：△ABF≌△CDE．20．如图，已知点B，E，C，F在一条直线上，AB＝DF，AC＝DE，∠A＝∠D．（1）求证：AC∥DE；（2）若BF＝13，EC＝5，求BC的长．21．如图，BD是△ABC的角平分线，DE⊥AB，DF⊥BC，垂足分别为E，F （1）求证：BE＝BF；（2）若△ABC的面积为70，AB＝16，DE＝5，求BC的长．22．如图，一架长为5米的梯子AB斜靠在地面OM垂直的墙ON上，梯子底端距离强ON有3米．（1）求梯子顶端与地面的距离OA的长．（2）若梯子顶点A下滑1米到C点，求梯子的底端向右滑到D的距离．23．如图，四边形ABCD中，AB＝20，BC＝15，CD＝7，AD＝24，∠B＝90°．（1）判断∠D是否是直角，并说明理由．（2）求四边形ABCD的面积．24．如图，折叠长方形纸片ABCD，使点D落在边BC上的点F处，折痕为AE．已知该纸片宽AB＝3cm，长BC＝5cm．求EC的长．25．如图，网格中的△ABC与△DEF为轴对称图形．（1）利用网格线作出△ABC与△DEF的对称轴l；（2）结合所画图形，在直线l上画出点P，使PA+PC最小；（3）如果每一个小正方形的边长为1，请直接写出△ABC的面积＝．26．在△ABC中，∠BAC＝90°，AB＝AC．点D从点B出发沿射线BC移动，以AD为边在AB 的右侧作△ADE，且∠DAE＝90°，AD＝AE．连接CE．（1）如图1，若点D在BC边上，则∠BCE＝°；（2）如图2，若点D在BC的延长线上运动．①∠BCE的度数是否发生变化？请说明理由；②若BC＝3，CD＝6，则△ADE的面积为．参考答案与试题解析一．选择题（共8小题）1．下列图形中，不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行解答．【解答】解：A、不是轴对称图形，故此选项正确；B、是轴对称图形，故此选项错误；C、是轴对称图形，故此选项错误；D、是轴对称图形，故此选项错误；故选：A．2．如图，∠BAD＝∠BCD＝90°，AB＝CB，据此可以证明△BAD≌△BCD，证明的依据是（）A．AAS B．ASA C．SAS D．HL【分析】依据图形可得到BD＝BD，然后依据全等三角形的判定定理进行判断即可．【解答】解：∵∠BAD＝∠BCD＝90°，∴△BAD和△BCD均为直角三角形．∵，∴△BAD≌BCD（HL）．3．如图所示：求黑色部分（长方形）的面积为（）A．24 B．30 C．48 D．18【分析】首先根据勾股定理求得直角三角形的斜边，即为矩形的长，进一步求其面积．【解答】解：根据勾股定理，得直角三角形的斜边是＝10，则矩形的面积是10×3＝30．故选：B．4．到三角形三个顶点的距离都相等的点是这个三角形的（）A．三条高的交点B．三条边的垂直平分线的交点C．三条中线的交点D．三条角平分线的交点【分析】根据线段垂直平分线的性质可求得答案．【解答】解：∵到两个顶点的距离相等的点在该边的垂直平分线上，∴到三角形三个顶点的距离都相等的点是三条边的垂直平分线的交点，故选：B．5．等腰三角形的一个角是80°，则它的顶角的度数是（）A．30°B．80°或20°C．80°或50°D．20°【分析】分80°角是顶角与底角两种情况讨论求解．【解答】解：①80°角是顶角时，三角形的顶角为80°，②80°角是底角时，顶角为180°﹣80°×2＝20°，综上所述，该等腰三角形顶角的度数为80°或20°．故选：B．6．下列四组线段中，可以构成直角三角形的是（）A．4，5，6 B．1.5，2，2.5 C．2，3，4 D．1，，3 【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．【解答】解：A、42+52＝41≠62，不可以构成直角三角形，故A选项错误；B、1.52+22＝6.25＝2.52，可以构成直角三角形，故B选项正确；C、22+32＝13≠42，不可以构成直角三角形，故C选项错误；D、12+（）2＝3≠32，不可以构成直角三角形，故D选项错误．故选：B．7．已知∠AOB＝30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是（）A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形【分析】根据轴对称的性质可知：OP1＝OP2＝OP，∠P1OP2＝60°，即可判断△P1OP2是等边三角形．【解答】解：根据轴对称的性质可知，OP1＝OP2＝OP，∠P1OP2＝60°，∴△P1OP2是等边三角形．故选：D．8．如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE＝5，BC＝8，则△DEF的周长是（）A．21 B．18 C．13 D．15【分析】根据直角三角形斜边上的中线等于斜边的一半求出DF、EF，再根据三角形的周长的定义解答．【解答】解：∵CD⊥AB，F为BC的中点，∴DF＝BC＝×8＝4，∵BE⊥AC，F为BC的中点，∴EF＝BC＝×8＝4，∴△DEF的周长＝DE+EF+DF＝5+4+4＝13．故选：C．二．填空题（共10小题）9．一个等边三角形的对称轴有 3 条．【分析】根据对称轴：如果沿某条直线对折，对折的两部分是完全重合的，那么就称这样的图形为轴对称图形，这条直线叫做这个图形的对称轴．对称轴绝对是一条点化线，可得答案．【解答】解：如图：一个等边三角形的对称轴有 3条，故答案为：3．10．一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是13cm 或14cm；【分析】分4cm为等腰三角形的腰和5cm为等腰三角形的腰，先判断符合不符合三边关系，再求出周长．【解答】解：当4cm为等腰三角形的腰时，三角形的三边分别是4cm，4cm，5cm符合三角形的三边关系，∴周长为13cm；当5cm为等腰三角形的腰时，三边分别是，5cm，5cm，4cm，符合三角形的三边关系，∴周长为14cm，故答案为：13cm或14cm．11．直角三角形的斜边长是5，一直角边长是3，则此直角三角形另一直角边是 4 ．【分析】根据勾股定理计算即可．【解答】解：由勾股定理得，直角三角形另一直角边＝＝4，故答案为：4．12．如图，△ABC≌△ADE，若∠C＝35°，∠D＝75°，∠DAC＝25°，则∠BAD＝45 °．【分析】依据全等三角形的对应角相等以及三角形内角和定理，即可得到∠BAD的度数．【解答】解：∵△ABC≌△ADE，∠D＝75°，∴∠D＝∠B＝75°，又∵∠C＝35°，∴∠BAC＝70°，又∵∠DAC＝25°，∴∠BAD＝45°，故答案为：45．13．如图，Rt△ABC中，∠C＝90°，∠ABC的平分线交AC于点P，PD⊥AB，垂足为D，若PD＝3，则PC＝ 3 ．【分析】依据角平分线的性质，即可得到PD＝PC，进而得出PC的长．【解答】解：∵∠C＝90°，∠ABC的平分线交AC于点P，PD⊥AB，∴PD＝PC，又∵PD＝3，∴PC＝3，故答案为：3．14．若△ABC三边之比为5：12：13，则△ABC是直角三角形．【分析】由两小边的平方和等于最长边的平方可得△ABC是直角三角形．【解答】解：设△ABC三边之比为5x，12x，13x，∵（5x）2+（12x）2＝（13x）2，∴△ABC是直角三角形．故答案为：直角15．如图，∠1＝∠2，∠B＝∠C，则△ABD与△ACD全等（填“全等”、“不一定全等”）．【分析】根据三角形的外角性质求出∠CAD＝∠BAD，再根据AAS推出全等即可．【解答】解：△ABD与△ACD全等，理由是：∵∠1＝∠C+∠CAD，∠2＝∠B+∠BAD，又∵∠1＝∠2，∠B＝∠C，∴∠CAD＝∠BAD，在△ABD和△ACD中∴△ABD≌△ACD（AAS），故答案为：全等．16．如图，已知△ABC中，∠ABC＝45°，F是高AD和BE的交点，CD＝4，则线段DF的长度为 4 ．【分析】易证BD＝AD，即可证明△BDF≌△ADC，即可求得DF＝CD．【解答】解：∵∠ABC＝45°，AD⊥BC，∴BD＝AD，∵∠CAD+∠AFE＝90°，∠CAD+∠C＝90°，∠AFE＝∠BFD，∴∠AFE＝∠C，∵∠AFE＝∠BFD∴∠C＝∠BFD在△BDF和△ADC中，，∴△BDF≌△ADC（AAS），∴DF＝CD＝4，故答案为4．17．如图，在△ABC中，DE是AC的垂直平分线，AE＝4cm，△ABD的周长为13cm，则△ABC 的周长为21 cm．【分析】根据线段的垂直平分线的性质得到DA＝DC和AC＝2AE＝8cm，根据三角形的周长公式计算即可．【解答】解：∵DE是AC的垂直平分线，∴DA＝DC，AC＝2AE＝8cm，∵△ABD的周长＝AB+BD+DA＝AB+BD+DC＝AB+BC＝13cm，∴△ABC的周长＝AB+BC+AC＝21cm，故答案为：21．18．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）2＝21，大正方形的面积为13，则小正方形的面积为 5 ．【分析】观察图形可知，小正方形的面积＝大正方形的面积﹣4个直角三角形的面积，利用已知（a+b）2＝21，大正方形的面积为13，可以得出直角三角形的面积，进而求出答案．【解答】解：如图所示：∵（a+b）2＝21，∴a2+2ab+b2＝21，∵大正方形的面积为13，2ab＝21﹣13＝8，∴小正方形的面积为13﹣8＝5，故答案为：5三．解答题（共8小题）19．已知：如图，点E、F在线段BD上，BE＝DF，AB∥CD，∠A＝∠C．求证：△ABF≌△CDE．【分析】两角及其中一个角的对边对应相等的两个三角形全等，据此利用AAS进行判定即可．【解答】证明：∵BE＝DF，∴BE+EF＝DF+EF，即BF＝DE，∵AB∥CD，∴∠B＝∠D，在△ABF和△CDE中，，∴△ABF≌△CDE（AAS）．20．如图，已知点B，E，C，F在一条直线上，AB＝DF，AC＝DE，∠A＝∠D．（1）求证：AC∥DE；（2）若BF＝13，EC＝5，求BC的长．【分析】（1）首先证明△ABC≌△DFE可得∠ACE＝∠DEF，进而可得AC∥DE；（2）根据△ABC≌△DFE可得BC＝EF，利用等式的性质可得EB＝CF，再由BF＝13，EC ＝5进而可得EB的长，然后可得答案．【解答】（1）证明：在△ABC和△DFE中，∴△ABC≌△DFE（SAS），∴∠ACE＝∠DEF，∴AC∥DE；（2）解：∵△ABC≌△DFE，∴BC＝EF，∴CB﹣EC＝EF﹣EC，∴EB＝CF，∵BF＝13，EC＝5，∴EB＝＝4，∴CB＝4+5＝9．21．如图，BD是△ABC的角平分线，DE⊥AB，DF⊥BC，垂足分别为E，F （1）求证：BE＝BF；（2）若△ABC的面积为70，AB＝16，DE＝5，求BC的长．【分析】（1）由角平分线的对称性直接证明△DBE≌△DBF即可；（2）先算出三角形ABD的面积，再得出三角形BCD的面积，高DF＝DE＝5，从而直接算出BC．【解答】解：（1）∵DE⊥AB，DF⊥BC，∴∠BED＝∠BFD＝90°，∵BD是△ABC的角平分线，∴∠EBD＝∠FBD，在△BDE和△BDF中，∵，∴△DBE≌△DBF（AAS），∴BE＝BF；（2）∵BD是△ABC的角平分线，DE⊥AB，DF⊥BC，∴DF＝DE＝5，∴S△ABD＝AB•DE＝40，∴S△BCD＝BC•DF＝70﹣40＝30，∴BC＝12．22．如图，一架长为5米的梯子AB斜靠在地面OM垂直的墙ON上，梯子底端距离强ON有3米．（1）求梯子顶端与地面的距离OA的长．（2）若梯子顶点A下滑1米到C点，求梯子的底端向右滑到D的距离．【分析】（1）已知直角三角形的斜边和一条直角边，可以运用勾股定理计算另一条直角边；（2）在直角三角形OCD中，已知斜边仍然是5，OC＝4﹣1＝3，再根据勾股定理求得OD 的长即可．【解答】解：（1）AO＝＝＝4（米）．答：梯子顶端与地面的距离OA的长为4米；（2）OD＝＝＝4（米），BD＝OD﹣OB＝4﹣3＝1（米）．答：若梯子顶点A下滑1米到C点，求梯子的底端向右滑到D的距离是1米．23．如图，四边形ABCD中，AB＝20，BC＝15，CD＝7，AD＝24，∠B＝90°．（1）判断∠D是否是直角，并说明理由．（2）求四边形ABCD的面积．【分析】（1）连接AC，根据勾股定理可知AC2＝BA2+BC2，再根据AC2＝DA2+DC2即可得出结论；（2）根据S四边形ABCD＝S△ABC+S△ADC即可得出结论．【解答】解：（1）连接AC，∵∠B＝90°，∴AC2＝BA2+BC2＝400+225＝625，∵DA2+CD2＝242+72＝625，∴AC2＝DA2+DC2，∴△ADC是直角三角形，即∠D是直角；（2）∵S四边形ABCD＝S△ABC+S△ADC，∴S四边形ABCD＝AB•BC+AD•CD＝×20×15+×24×7＝234．24．如图，折叠长方形纸片ABCD，使点D落在边BC上的点F处，折痕为AE．已知该纸片宽AB＝3cm，长BC＝5cm．求EC的长．【分析】由题意可得AF＝AD＝5cm，根据勾股定理可求BF＝4cm，即可得FC＝1cm，再根据勾股定理可求EC的长．【解答】解：由折叠可知AD＝AF＝5cm，DE＝EF∵∠B＝90°∴AB2+BF2＝AF2，∵AB＝3cm，AF＝5cm∴BF＝4cm，∵BC＝5cm，∴FC＝1cm∵∠C＝90°，∴EC2+FC2＝EF2设EC＝x，则DE＝EF＝3﹣x∴（3﹣x）2＝12+x2∴x＝25．如图，网格中的△ABC与△DEF为轴对称图形．（1）利用网格线作出△ABC与△DEF的对称轴l；（2）结合所画图形，在直线l上画出点P，使PA+PC最小；（3）如果每一个小正方形的边长为1，请直接写出△ABC的面积＝ 3 ．【分析】（1）利用网格特点，作AD的垂直平分线即可；（2）连接CD，与直线l的交点即为所求；（3）利用割补法求解可得．【解答】解：（1）如图所示，直线l即为所求．（2）如图所示，点P即为所求；（3）△ABC的面积＝2×4﹣×1×2﹣×1×4﹣×2×2＝3，故答案为：3．26．在△ABC中，∠BAC＝90°，AB＝AC．点D从点B出发沿射线BC移动，以AD为边在AB 的右侧作△ADE，且∠DAE＝90°，AD＝AE．连接CE．（1）如图1，若点D在BC边上，则∠BCE＝90 °；（2）如图2，若点D在BC的延长线上运动．①∠BCE的度数是否发生变化？请说明理由；②若BC＝3，CD＝6，则△ADE的面积为．【分析】（1）由△ABC和△ADE都是等腰Rt△可得，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，则有∠BAD＝∠CAE，从而可证到△ACE≌△ABD；由△ACE≌△ABD可得∠ACE＝∠ABD＝45°，从而得到∠BCE＝∠BCA+∠ACE＝90°；（2）①由△ABC和△ADE都是等腰Rt△可得，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，则有∠BAD＝∠CAE，从而可证到△ACE≌△ABD；由△ACE≌△ABD可得∠ACE＝∠ABD＝45°，从而得到∠BCE＝∠BCA+∠ACE＝90°；②得出BD，由△ACE≌△ABD可得CE＝BD，运用三角形面积公式解答．【解答】解：（1）∵△ABC和△ADE都是等腰Rt△，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE．在△ACE和△ABD中，，∴△ACE≌△ABD（SAS）；∴∠ACE＝∠ABD＝45°，∴∠BCE＝∠BCA+∠ACE＝45°+45°＝90°；故答案为：90；（2）①不发生变化．∵AB＝AC，∠BAC＝90°∴∠ABC＝∠ACB＝45°，∵∠BAC＝∠DAE＝90°∴∠BAC+∠DAC＝∠DAE+∠DAC∴∠BAD＝∠CAE，在△ACE和△ABD中∴△ACE≌△ABD（SAS）∴∠ACE＝∠ABD＝45°∴∠BCE＝∠BCA+∠ACE＝45°+45°＝90°∴∠BCE的度数不变，为90°；②∵BC＝3，CD＝6，∴BD＝9，∵△ACE≌△ABD，∴CE＝BD＝9，∴AE＝AD＝，∴△ADE的面积＝；故答案为：。

2019-2020学年江苏省淮安市开明中学八年级(上)期中数学试卷(附答案详解)

2019-2020学年江苏省淮安市开明中学八年级（上）期中数学试卷1.下列大学的校徽图案是轴对称图形的是()A. 清华大学B. 北京大学C. 中国人民大学D. 浙江大学2.平面直角坐标系中，点A(−1,−3)在第()象限．A. 一B. 二C. 三D. 四3.下列说法正确的是()A. −√5是5的平方根B. −2的平方根是±23=±4 D. √9=±3C. √644.下列各数组中，不能作为直角三角形的三边长的是()A. 5，12，13B. 3，4，5C. 8，15，17D. 4，5，65.已知点A(−3,a)和点B(b,−2)关于原点对称，则a与b的值分别是()A. a=2，b=3B. a=−2，b=3C. a=−2，b=−3D. a=2，b=−36.一个等腰三角形的两边长分别为3和5，则它的周长为()A. 11B. 12C. 13D. 11或137.如图，在△ABC中，∠C=90°，BD平分∠ABC，AB：BC=2：1，则△ABD与△BCD面积比为()A. 2：1B. 2：3C. 3：2D. 3：18.象棋是流行广泛的益智游戏．如图是一副象棋残局，若表示棋子“炮”和“車”的点坐标分别为(1,3)，(−2,1)，则表示棋子“马”的点坐标为()A. (1,3)B. (3,2)C. (4,3)D. (2,3)9.4是______的算术平方根．10.用四舍五入法将37.26精确到0.1的近似数为______．11.在平面直角坐标系中，点(4,2)到y轴的距离为______．12.比较大小：√33______6.(填“>”、“<”或“=”)13.Rt△ABC中，两条直角边长分别为5和12，则斜边上的中线长等于______．14.若某个正数a的两个平方根分别为m+3与2m−9，则a的值为______．15.如图，AD是等边△ABC的边BC上的中线，且AE=AD，则∠BED的度数为______．16.如图，直角坐标系中有一个电子跳蚤，以每秒1个单位的速度，在第一象限及x轴、y轴上运动．在第1秒钟，它从原点运动到(0,1)，接着按图中箭头所示方向运动．那么第28秒时该跳蚤所在位置的坐标为______．17.(1)计算：√9−(π−3)0+|2−√3|；(2)解方程：(x+1)3=−8．18.已知：如图，(1)画出将△ABC向左平移4个单位得到的图形△A1B1C1；(2)画出△A1B1C1关于x轴对称的图形△A2B2C2．19.(1)如图，用直尺和圆规在△ABC的边AC上确定一点P，使PC=PB.(保留作图痕迹)(2)若△ABP的周长为17，BC=8，则△ABC的周长为______．20.如图，在△ABC中，点D，E分别在AB、AC上，AD=AE，∠ACD=∠ABE，CD与BE相交于点F，求证：BF=CF．21.同学们都玩过荡秋千吧？如图，已知秋千顶端O离地面的距离为2.4m，秋千静止时座位离地面的距离是0.4m.当秋千荡到最高处，此时座位离地面的距离恰为0.8m.你能求出秋千荡出的水平距离BC是多少吗？22.张老师在一次“探究性学习”课中，设计了如下数表：n2345…a22−132−142−152−1…b46810…c22+132+142+152+1…(1)请你分别观察a，b，c与n之间的关系，并用含自然数n(n>1)的代数式表示：a=______ ，b=______ ，c=______ ；(2)猜想：以a，b，c为边的三角形是否为直角三角形并证明你的猜想．23.如图，在直角坐标系中，A、B、C三点的坐标分别为(0,1)，(2,0)，(2,1.5)．(1)△ABC的面积为______．(2)如果在第二象限内有一点P(a,1.8)，试用含a的式子表示四边形ABOP的面积．(3)在(2)的条件下，是否存在点P，使得四边形ABOP的面积是△ABC面积的2倍？若存在，请求出点P的坐标，若不存在，请说明理由．24.阅读理解：如图1，在△ABC的边AB上取一点P，连接CP，可以把△ABC分成两个三角形，如果这两个三角形都是等腰三角形，我们称点P是△ABC的边AB上的完美点．解决问题：(1)如图2，△ABC中，∠ACB=90°，试找出边AB上的完美点P，并说明理由．(2)如图3，已知∠A=36°，△ABC的顶点B在射线l上，点P是边AB上的完美点，请认真分析所有符合要求的点B，直接写出相应的∠B的度数．25.我们知道，长方形的对边相等，对边平行，四个角都是直角，即长方形ABCD中，∠A=∠ABC=∠C=∠ADC=90°，AB=CD，AD=BC，AD//BC，AB//CD．学完轴对称的性质，周老师设计如下三个问题，带领大家研究长方形纸片的折叠问题．请你运用所学知识，解决下面的问题．问题(1)：如图(1)，有一张长方形纸片ABCD，AB=12，AD=16，将纸片折叠，使AB落在对角线AC上，折痕为AE(点E在边BC上)，点B落在点B′处，求线段CE的长度；问题(2)：如图(2)，点G在一张长方形纸片ABCD的边AD上，将纸片折叠，使AB 落在CG所在直线上，设折痕为EF(点E，F分别在边BC、AD上)，利用直尺和圆规画出折痕EF(不写作法，保留作图痕迹)；问题(3)：如图(3)，有一张长方形纸片ABCD，AB=12，AD=27，F为AD边上一点，AF=7，E为BC上一点．将纸片折叠，使点B恰好落在线段ED上的B′处，折痕为EF，点A落在点A′处．求线段B′D的长度．答案和解析1.【答案】B【解析】解：A、不是轴对称图形，本选项错误；B、是轴对称图形，本选项正确；C、不是轴对称图形，本选项错误；D、不是轴对称图形，本选项错误．故选：B．结合轴对称图形的概念进行求解即可．本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2.【答案】C【解析】解：点A(−1,−3)在第三象限．故选C．根据各象限内点的坐标特征解答．本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．3.【答案】A【解析】解：A，∵5的平方根是±√5，∴正确，B∵负数没有平方根，∴B错误，3=4，∴C错误，C∵√64D∵√9=3∴D错误．故选：A．A：由5的平方根是±√5判断；B：负数没有平方根进行判断；C：开立方求出结果，然后判断；D：求出算数平方根，然后判断．本题主要考查了平方根，算术平方根、立方根的概念的运用，掌握这几个定义的区别及实际应用是解题关键．4.【答案】D【解析】解：A、52+122=132，故是直角三角形，不符合题意；B、32+42=52，故是直角三角形，不符合题意；C、82+152=172，故是直角三角形，不符合题意；D、42+52≠62，故不能组成直角三角形，符合题意．故选：D．由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．5.【答案】A【解析】解：∵点A(−3,a)和点B(b,−2)关于原点对称，∴a=2，b=3，故选：A．根据平面直角坐标系中任意一点P(x,y)，关于原点的对称点是(−x,−y)，即关于原点的对称点，横纵坐标都变成相反数，求得a、b的值．本题主要考查了关于原点对称的点的坐标特点，平面直角坐标系中任意一点P(x,y)，关于原点的对称点是(−x,−y)，即关于原点的对称点，横纵坐标都变成相反数．6.【答案】D【解析】【分析】此题考查了等腰三角形的性质与三角形三边关系．此题难度不大，解题的关键是注意分类讨论思想的应用，小心别漏解．由等腰三角形两边长为3、5，分别从等腰三角形的腰长为3或5去分析即可求得答案，注意分析能否组成三角形．【解答】解：①若等腰三角形的腰长为3，底边长为5，∵3+3=6>5，∴能组成三角形，∴它的周长是：3+3+5=11；②若等腰三角形的腰长为5，底边长为3，∵5+3=8>5，∴能组成三角形，∴它的周长是：5+5+3=13，综上所述，它的周长是：11或13．故选D．7.【答案】A【解析】解：作DE⊥AB于E，∵BD平分∠ABC，∠C=90°，DE⊥AB，∴DE=DC，∵AB：BC=2：1，∴设AB=2x，BC=x，∴△ABD与△BDC的面积之比：(12×AB×DE)：(12×BC×CD)=AB：BC=2：1．故选：A．作DE⊥AB于E，根据角平分线的性质得到DE=DC，根据三角形的面积公式计算即可．本题考查的是角平分线的性质，熟练掌握角平分线上的点到角的两边的距离相等是解题的关键．8.【答案】C【解析】解：∵棋子“炮”和“車”的点坐标分别为(1,3)，(−2,1)，∴帅的位置为原点，如图所示，∴棋子“马”的点坐标为(4,3)，故选：C．根据棋子“炮”和“車”的点坐标分别为(1,3)，(−2,1)，得出原点的位置，进而得出答案．本题考查了坐标确定位置，正确得出原点的位置是解决问题的关键．9.【答案】16【解析】解：∵42=16，∴4是16的算术平方根．故答案为：16．如果一个非负数x的平方等于a，那么x是a的算术平方根，由此即可求出结果．此题主要考查了算术平方根的概念，牢记概念是关键．10.【答案】37.3【解析】解：用四舍五入法将37.26精确到0.1的近似数为37.3，故答案为：37.3．对百分位数字四舍五入即可．本题主要考查近似数，一般地说，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位．11.【答案】4【解析】解：∵点到y轴的距离等于横坐标的绝对值，点(4,2)的横坐标为4，∴点(4,2)到y轴的距离为4．故答案为：4．根据点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值解答即可．本题考查了点的坐标，利用点到x轴的距离是纵坐标的绝对值，点到y轴的距离是横坐标的绝对值是解题的关键．12.【答案】<【解析】解：∵33<36，∴√33<6，故答案为：<．通过比较这两个正数的平方来比较大小．本题考查了实数的比较大小，通过比较这两个正数的平方来比较大小是解题的关键．13.【答案】6.5【解析】解：∵直角三角形两直角边长为5和12，∴斜边=√52+122=13，=6.5．∴此直角三角形斜边上的中线的长=132故答案为：6.5．根据勾股定理可求得直角三角形斜边的长，再根据直角三角形斜边上的中线等于斜边的一半即可求解．此题主要考查勾股定理及直角三角形斜边上的中线的性质；熟练掌握勾股定理，熟记直角三角形斜边上的中线的性质是解决问题的关键．14.【答案】25【解析】解：∵一个正数的平方根互为相反数，∴m+3+2m−9=0，解得m=2，∴a的平方根是±5，∴a=25．故答案为：25．由一个正数的平方根互为相反数，列一元一次方程，求出m，最后求出a．此题主要考查了平方根的性质，掌握性质的应用，由一个正数的平方根互为相反数，列一元一次方程，是解题关键．15.【答案】105°【解析】解：∵△ABC为等边三角形，BD=DC，∠BAC=30°，∴∠BAD=12∵AE=AD，×(180°−30°)=75°，∴∠AED=12∴∠BED=180°−∠AED=105°，故答案为：105°．∠BAC=30°，根据等腰三角形的性质计算即根据等腰三角形的三线合一求出∠BAD=12可．本题考查的是等边三角形的性质、三角形内角和定理、等腰三角形的性质，掌握等边三角形的每个内角都是60°是解题的关键．16.【答案】(3,5)【解析】解：电子跳蚤每秒1个单位，按照图中运动的规律，到达(0,1)用1秒，到达(2,0)用4秒，到达(0,3)用9秒，到达(4,0)用16秒，到达(0,5)用25秒，∴到达(3,5)用28秒，故答案为：(3,5)．根据电子跳蚤运动的特点，从中找出规律，即可得出答案．本题考查了坐标确定位置，读懂题意，正确确定跳蚤运动的规律是解决问题的关键．17.【答案】解：(1)原式=3−1+2−√3=4−√3；(2)方程(x+1)3=−8，开立方得：x+1=−2，解得：x=−3．【解析】(1)原式利用算术平方根定义，零指数幂法则，以及绝对值的代数意义计算即可求出值；(2)方程利用立方根定义开立方即可求出解．此题考查了实数的运算，立方根，以及零指数幂，熟练掌握立方根定义，零指数幂法则，以及绝对值的代数意义是解本题的关键．18.【答案】解：(1)如图，△A1B1C1即为所求．(2)如图，△A2B2C2即为所求．【解析】(1)利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可．(2)利用轴对称的性质分别作出A1，B1，C1的对应点A2，B2，C2即可．本题考查作图−轴对称变换，平移变换等知识，解题的关键是掌握平移变换，轴对称变换的性质，属于中考常考题型．19.【答案】25【解析】解：(1)如图，点P为所作；(2)∵PC=PB，∴△ABP的周长=AB+AP+PB=AB+AP+PC=AB+AC=17，∴△ABC的周长=AB+AC+BC=17+8=25．故答案为25．(1)作BC的垂直平分线即可；(2)利用等线段代换得到△ABP的周长=AB+AC=17，然后计算△ABC的周长．本题考查了作图−复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质．20.【答案】证明：在△ABE与△ACD中，{∠A=∠A∠ACD=∠ABE AD=AE，∴△ABE≌△ACD(ASA)，∴AB=AC，∠ADC=∠AEB，∴AB−AD=AC−AE，即DB=EC，∴∠BDF=∠CEF，在△DBF与△ECF中，{∠BDF=∠CEF ∠DFB=∠EFC DB=EC，∴△DBF≌△ECF(AAS)，∴BF=CF．【解析】根据AAS证明△ABE与△ACD全等，利用全等三角形的性质得出AB=AC，进而利用AAS证明△DBF与△ECF全等，利用全等三角形的性质解答即可．考查了全等三角形的判定和性质，根据AAS 证明△ABE 与△ACD 全等是本题的关键．21.【答案】解：能求出秋千荡出的水平距离BC 的长，理由如下：由题意得：秋千最低点为A ，最高点为B ，OD =2.4m ，AD =0.4m ，则OA =OB =OD −AD =2(m)，过B 点作BC ⊥OA 于C ，BE ⊥地面于E ，则CD =BE =0.8m ，∴AC =CD −AD =0.8−0.4=0.4(m)，∴OC =OA −AC =2−0.4=1.6=85(m)，在Rt △OBC 中，由勾股定理得：BC =√OB 2−OC 2=√22−(85)2=65(m)=1.2m ，即秋千荡出的水平距离BC 是1.2m ．【解析】过B 点作BC ⊥OA 于C ，BE ⊥地面于E ，则CD =BE =0.8m ，求出AC =CD −AD =0.4(m)，OC =OA −AC =1.6(m)，再根据勾股定理求出BC 的长即可．本题考查了勾股定理的应用，熟练掌握勾股定理，求出OC 的长是解题的关键．22.【答案】(1)n 2−1；2n ；n 2+1(2)猜想为：以a ，b ，c 为边的三角形是直角三角形．证明：∵a =n 2−1，b =2n ；c =n 2+1∴a 2+b 2=(n 2−1)2+(2n)2=n 4−2n 2+1+4n 2=n 4+2n 2+1=(n 2+1)2 而c 2=(n 2+1)2【解析】解：(1)由题意有：n 2−1，2n ，n 2+1；(2)猜想为：以a ，b ，c 为边的三角形是直角三角形．证明：∵a =n 2−1，b =2n ；c =n 2+1∴a 2+b 2=(n 2−1)2+(2n)2=n 4−2n 2+1+4n 2=n 4+2n 2+1=(n 2+1)2 而c 2=(n 2+1)2∴根据勾股定理的逆定理可知以a ，b ，c 为边的三角形是直角三角形．(1)结合表中的数据，观察a ，b ，c 与n 之间的关系，可直接写出答案；(2)分别求出a 2+b 2，c 2，比较即可．本题需仔细观察表中的数据，找出规律，利用勾股定理的逆定理即可解决问题．23.【答案】1.5【解析】解：(1)∵A、B、C三点的坐标分别为(0,1)，(2,0)，(2,1.5)，∴OA=1，OB=2，BC=1.5，BC//OA，∴△ABC的面积=12×1.5×2=1.5；故答案为：1.5；(2)如图所示，作PE⊥y轴于E，∵在第二象限内有一点P(a,1.8)，∴a<0，则S四边形ABOP =S△AOB+S△AOP=12OA⋅OB+12OA⋅PE=12×1×2+12×1×(−a)=1−12a；(3)存在点P，使得四边形ABOP的面积是△ABC面积的2倍，根据题意得：1−12a=2×1.5，解得：a=−4，∴P(−4,1.8)．(1)根据A、B、C三点的坐标即可得出△ABC的面积；(2)作PE⊥y轴于E，四边形ABOP的面积=△AOB的面积+△AOP的面积，即可得出结果；(3)根据四边形ABOP的面积是△ABC面积的2倍列方程，求出a=−4，即可得出点P 的坐标．本题考查了四边形综合题，综合掌握坐标与图形性质、三角形面积的计算；熟练掌握坐标与图形性质是解决问题的关键．24.【答案】解：(1)取AB的中点P，连接PC即可如图①∵∠ACB=90°，P是AB的中点，∴CP=12AB，AP=BP=12AB，∴AP=PB=CP．∴△APC，△PBC是等腰三角形．∴点P是边AB上的完美点．(2)满足条件的点B如图所示：②③④⑤⑥【解析】(1)取AB的中点P，连接PC即可，利用直角三角形斜边上的中线等于斜边一半证明；(2)根据点P是边AB上的完美点，结合等腰三角形的性质画出图即可．本题考查等腰三角形的性质、直角三角形的性质，掌握性质的熟练应用，理解题意是解题的关键．25.【答案】解：问题(1)∵四边形ABCD是矩形，∴∠ABC=90°，BC=AD=16，∵AB=12，由勾股定理得：AC=√AB2+BC2=√122+162=20，由折叠得：∠AB′E=∠B=90°，AB′=AB=12，BE=B′E，∴∠CB′E=90°，设CE=x，则B′E=BE=16−x，由勾股定理得：CE2=B′E2+B′C2，即x2=(16−x)2+(20−12)2，解得：x=10，∴CE=10；问题(2)如图(2)所示：EF即为所求；问题(3)∵AF=7，AD=27，∴FD=20，∵将纸片折叠，使点B恰好落在线段ED上的B′处，∴∠BEF=∠B′EF，BE=B′E，∵AD//BC，∴∠DFE=∠BEF，∴DE=DF=20，∴CE=√DE2−DC2=√202−122=16，∴BE=BC−CE=11，∴B′E=11，∴B′D=DE−B′E=20−11=9．【解析】问题(1)：设CE=x，根据折叠的性质表示B′E=BE=16−x，由勾股定理计算AC=20，则CB′=8，最后根据勾股定理列方程可得答案；问题(2)：如图(2)中，延长BA交直线CG交于点H，作∠BHC的角平分线交AD于F，交BC于E，直线EF即为所求；问题(3)：首先求出FD=20，由矩形的性质得出AD//BC，BC=AD=27，由平行线的性质得出∠DFE=∠BEF，由翻折不变性可知，∠BEF=∠DEF，证出∠DFE=∠DEF，由等腰三角形的判定定理证出DF=DE=20，再由勾股定理求出CE，可得BE，再利用翻折不变性，可知EB′=EB，由此即可解决问题．本题是四边形综合题，考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用翻折不变性解决问题．。

2019-2020江苏省淮安市开明中学新城校区八上12月份月考试卷(无答案)

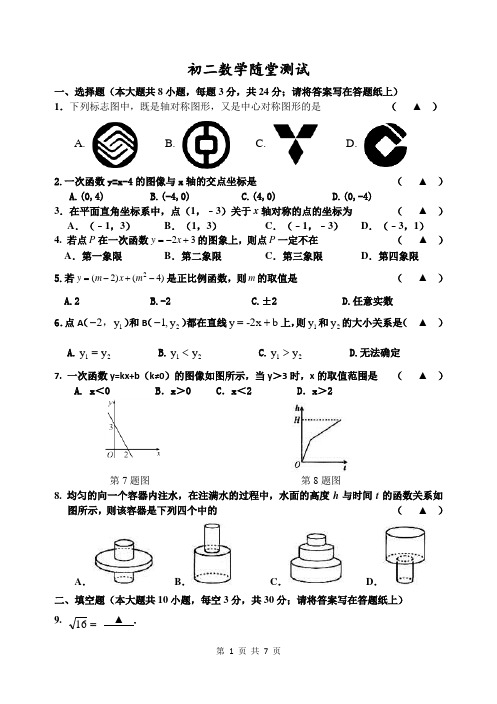
初二数学随堂测试一、选择题（本大题共8小题，每题3分，共24分；请将答案写在答题纸上）1．下列标志图中，既是轴对称图形，又是中心对称图形的是（ ▲ ）A. B. C. D.2.一次函数y=x-4的图像与x 轴的交点坐标是（ ▲ ） A.(0,4) B.(-4,0) C.(4,0) D.(0,-4)3．在平面直角坐标系中，点（1，﹣3）关于x 轴对称的点的坐标为（ ▲ ） A ．（﹣1，3） B ．（1，3） C ．（﹣1，﹣3） D ．（﹣3，1） 4. 若点P 在一次函数23y x =-+的图象上，则点P 一定不在（ ▲ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限5.若)4()2(2-+-=m x m y 是正比例函数，则m 的取值是（ ▲ ） A.2 B.-2 C.±2 D.任意实数6．点A （12y -，）和B （21,y -）都在直线y -2x b =+上，则1y 和2y 的大小关系是（ ▲ ） A.12y y = B.12y y < C.12y y > D.无法确定7. 一次函数y=kx+b （k≠0）的图像如图所示，当y ＞3时，x 的取值范围是（ ▲ ）A. x ＜0 B ．x ＞0 C ．x ＜2 D ．x ＞2第7题图第8题图8. 均匀的向一个容器内注水，在注满水的过程中，水面的高度h 与时间t 的函数关系如图所示，则该容器是下列四个中的（ ▲ ）A ．B ．C ．D ．二、填空题（本大题共10小题，每空3分，共30分；请将答案写在答题纸上） 9.=16 ▲ .10. 一次函数y=(2-m)x+1, 若y随x的增大而增大，则m的取值范围是▲ .11．等腰三角形的一个外角是80°，则其底角是▲度．12．若点（m，n）在函数y＝3x+2的图象上，则3m﹣n＝▲．13、如图，等腰三角形ABC中，AB=AC=13，BC=10，则BC边上的高AD= ▲ .14. 一次函数y=kx+b与y=2x+1平行,且经过点(-3,4),该一次函数表达式为▲ .第13题第15题第16题15.如图，已知函数y ax b=+和y kx=的图像交于一点，则根据图像可得，关于,x y的二元一次方程组的解是▲ .16．如图，已知OA=OB，那么数轴上点A所表示的数是▲ .17.如图，直线y＝﹣x+8与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处,则点M的坐标是▲ .第17题第18题18．如图，点A1（2，2）在直线y＝x上，过点A1作A1B1∥y轴交直线y＝21x于点B1，以点A1为直角顶点，A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1，再过点C1作A2B2∥y轴，分别交直线y＝x和y＝21x于A2，B2两点，以点A2为直角顶点，A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…，按此规律进行下去，则等腰直角△A n B n∁n的面积为▲ .（用含正整数n的代数式表示）⎩⎨⎧=+=kxybaxy初二数学随堂测试题号 12345678答案9. 10. 11. 12. 13. . 14. 15. 16. 17. 18. . 三、解答题（本大题共66分,请将解答过程写在答题纸上） 19.（本题10分）（1）计算：（2）解方程：20. （8分）在正方形网格中建立如图所示的平面直角坐标系，△ABC 的三个顶点都在格点上，点 A 的坐标是（4，4），请解答下列问题：（1）在图中画出△ABC 关于y 轴对称的△A 1B 1C 1，并写出点A 的对应点A 1的坐标___________；（2）将△ABC 绕原点O 顺时针旋转90°得到 △A 2B 2C 2，在图中画出△A 2B 2C 2，并写出点C 的对应点C 2的坐标_____________。

2019-2020学年八年级数学上学期期中试题苏科版

2019-2020学年八年级数学上学期期中试题苏科版（满分：100分时间：100分钟）选择题（每题2分，共20分）1、在，，，π-27010101.0,72⋅⋅⋅ 332-这五个数中，无理数有（） A ．0个 B ．1个 C ．2个 D ．3个2、如图，△ACB ≌△A 'CB '，∠BCB '=35°，则∠ACA '的度数为（）A ．20°B ．30°C ．40°D ．35°3、下列说法正确的是（）A.()24-没有平方根； B ．4±； C.2-的平方是2 ； D ．立方根等于本身的数是0和 1 地球七大洲的总面积约是149 48万km 2，对这一数据精确到10000000可表示为（）A ．28104.1km ⨯B ．281050.1km ⨯C ．281049.1km⨯ D ．28105.1km ⨯ 5、三角形中到三边距离相等的点是（）A ．三条边的垂直平分线的交点B ．三条角平分线的交点C ．三条中线的交点D ．三条高的交点下列三角形中，不是直角三角形的是（）A.△ABC 中，∠C-∠B=∠AB.△ABC 中,a:b:c=3:2:1C.△ABC 中，2))((b a c a c =+-D.△ABC 中,∠A:∠B:∠C=1：3：4A ．1组B ．2组C ．3组D ．4组7、如图，△ABC 中边AB 的垂直平分线分别交BC 、AB 于点D 、E ，AE=4cm ，△ADC•的周长为12cm ，则△ABC 的周长是（）A ．18cmB ．20cmC ．15cmD ．17cm第2题图第7题图第8题图第10题图8、如图，在△ABC 中，∠ACB ＝90°，∠ABC ＝60°，BD 平分∠ABC ，P 点是BD 的中点，若AD ＝7，则CP 的长为（）A ．3B ．3.5C ．4D ．4.59、如图，在数轴上表示实数15的点可能是 ( )A ．点PB ．点QC ．点MD ．点N10、如图，在△ABC 中，AB=AC=10，BC=12，有一点D 在AC 上移动，则AD+BD+CD 的最小值是（）A ．18B ．18.6C ．20D ．19.6二、填空题（每题2分，共18分）平方根是2±的数是______,81的算术平方根是______。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020学学学学学学学学学学学学学学学学学学学学学学
一、选择题
1.下列运算正确的是( )
A. √4=±2
B. √(−5)2=−5
C. (−√7)2=7
D. (√−3)2=−3
2.下列各数：1
,−π,−√3,0．3⋅,−0.1010010001…(两个1之间依次多一个0),−√49中无
7
理数的个数为( )
A. 2个
B. 3个
C. 4个
D. 5个
3.下列说法中,不正确的是( )
①全等形的面积相等；
②形状相同的两个三角形是全等三角形；
③全等三角形的对应边,对应角相等；
④若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的．
A. ①与②
B. ③与④
C. ①与③
D. ②与④
4.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=
EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
A. 2
B. 4
C. 4.5
D. 3
5.如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,
过点E作DF∥BC交AB于D,交AC于F,若AB=4,AC=
3,则△ADF周长为( )
A. 6
B. 7
C. 8
D. 10
6.如图,在△ABC中,AB=AC,,BD平分∠ABC,图
中的等腰三角形有( )。

A. 1个
B. 2个
C. 3个
D. 4个
7.下列各组数,属于勾股数的是( )
A. 4,5,6
B. 5,10,13
C. 3,4,5
D. 8,39,40
8.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走
6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏.问登陆点A与
宝藏埋藏点B之间的距离是( )km．
A. 10
B. 11
C. 12
D. 13
9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水
杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值
范围是( )
A. ℎ≤17cm
B. ℎ≥8cm
C. 15cm≤ℎ≤16cm
D. 7cm≤
ℎ≤16cm
二、填空题
10.16的平方根是______．
11.写出一个比3大且比4小的无理数：______．
12.已知：m、n为两个连续的整数,且m<√11<n,则m+n=______．
13.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=______
度.
14.如图,AD=AE,BE=CD,,,则
∠CAE的度数是________．
15.如图,在△ABC中,,,AD⊥BC
于D,若BC=16,则CD=_____．
16.如图,长为24cm的弹性皮筋绷直放置在直线l上,固
定两端A和B,然后把中点C向上拉升5cm到D点,
则弹性皮筋被拉长了______．
17.游泳员小明横渡一条
河,由于水流的影响,实
际上岸地点C偏离欲
达到点B60米,结果他
在水中实际游了100米,
这条河宽为______米.
18.如图,长方体的底面边长均为3cm,高为5cm,如果用一根细线从点A开始经过4个侧
面缠绕一圈达到点B,那么所用细线最短需要____cm．
三、计算题
3．
19.计算：(−1)2−√25+√27
20. 计算：√16−√273+3−18+√9
4．
21. 解方程
(1)(2x −1)2=169
(2)3(x +2)3=−81
四、解答题
22. 已知x 的两个不同的平方根分别是a +3和2a −15,且 √x +y −23=4,求x ,y 的值．
23. 已知实数a ,b ,c 满足√a −7+|b −5√2|+(c −1)2=0．
(1)求a ,b ,c 的值；
(2)判断以a ,b ,c 为边能否构成三角形？若能构成三角形,判别此三角形的形状,并求出三角形的面积；若不能,请说明理由．
24. 如图,点E ,F 在AB 上,AD =BC ,∠A =∠B ,AE =BF.
求证：△ADF≌△BCE ．
25.如图,已知：E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,
且交OE于点F．
(1)求证：OE是CD的垂直平分线．
(2)若,请你探究OE,EF之间有什么数量关系？并证明你的结论．
26.在等腰△ABC中,AB=AC,,CD是△ABC的高,P是线段AC(不包括端点
A,C)上一动点,以DP为一腰,D为直角顶点(D、P、E三点逆时针)作等腰直角△DPE,连接AE．
(1)如图1,点P在运动过程中,∠EAD=______,写出PC和AE的数量关系；
(2)如图2,连接BE.如果AB=4,CP=√2,求出此时BE的长．。