初三数学计算专练
数学计算题练习题初三

数学计算题练习题初三1. 填空题(1) 27 ÷ 9 × 3 = _______(2) 13 + 25 × 2 = _______(3) 98 - 57 ÷ 3 = _______(4) 35 × 3 ÷ 5 = _______(5) 45 ÷ 15 + 8 = _______2. 选择题(1) 一辆自行车每小时行驶30公里,行驶6小时可以走多远?A. 90公里B. 120公里C. 180公里D. 210公里(2) 计算:9.2 + 6.9 - 4.7 = _______A. 11.4B. 12.2C. 12.4D. 13.6(3) 一个数的三分之一加上9等于这个数,这个数是多少?A. 3B. 6C. 9D. 12(4) 一个矩形的长是25厘米,宽是12厘米,它的面积是多少平方厘米?A. 250B. 300C. 375D. 450(5) 一个数字是7的倍数,它能被9整除吗?A. 能B. 不能3. 解答题(1) 计算:12.5 × 8 - 4.2 ÷ 2 = _______解答:12.5 × 8 = 1004.2 ÷ 2 = 2.1100 - 2.1 = 97.9所以,12.5 × 8 - 4.2 ÷ 2 = 97.9(2) 一条长方形的长是15米,宽是8米,它的周长是多少米?解答:周长 = 2 × (长 + 宽)周长 = 2 × (15 + 8)周长 = 2 × 23周长 = 46所以,该长方形的周长是46米。
(3) 解方程:2x + 5 = 17解答:2x + 5 = 172x = 17 - 52x = 12x = 12 ÷ 2x = 6所以,方程的解为x = 6。
以上是数学计算题的练习题,希望能帮助你巩固数学知识,提高计算能力。
初三数学计算题练习试题集

初三数学计算题练习试题答案及解析1.计算:【答案】.【解析】根据绝对值、有理数的乘方、立方根、特殊角三角函数值的意义分别进行计算即可求出答案.原式.【考点】实数的混合运算.2.计算:(1),(2)【答案】(1);(2).【解析】(1)分别求出值,再化简;(2)化成最简二次根式,再进行计算.试题解析:(1);(2).【考点】1.负指数次幂2.特殊角的三角函数3.绝对值4.零次幂5.二次根式混合运算.3.计算:.【答案】3.【解析】根据特殊角三角函数值、绝对值、零次幂、负整数指数幂、二次根式的意义进行计算即可得出答案.试题解析:=3.考点: 实数的混合运算.4.化简:.【答案】8.【解析】先根据单项式乘以多项式展开,再求出即可.试题解析:考点:5.计算:.【答案】.【解析】任何非零数的零次方都为1,负数的绝对值等于它的相反数,再对二次根式进行化简即可.试题解析:.【考点】二次根式的化简.6.计算:(-)÷+.【答案】.【解析】先去括号,再计算除法,最后计算加减法.试题解析:原式=.【考点】二次根式的混合运算.7.计算题:①、;②、【答案】①、;②、【解析】根据二次根式的混合运算的法则结合二次根式的性质依次计算即可.试题解析:①、;②、.【考点】实数的运算8.计算:.【答案】解:原式=。
【解析】针对特殊角的三角函数值,绝对值,零指数幂,有理数的乘方,负整数指数幂5个考点分别进行计算,然后根据实数的运算法则求得计算结果。
9.(1)解方程:;(2)解方程组:.【答案】(1)x=—6 (2)【解析】(1)方程两边同乘以,得∴检验:当时,≠0,即是原分式方程的解(2)解得x=2把x=2代入x-y=1中,解得y=1∴【考点】分式方程和二元一次方程组点评:该题是常考题,主要考查学生对分式方程和二元一次方程组的解题过程的掌握,记得分式方程要检验。
10.计算:【答案】【解析】根据二次根式的性质、负整数指数幂、特殊角的锐角三角函数值、立方根的定义计算即可.原式==.【考点】实数的运算点评:计算题是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.11.【答案】9【解析】原式= 6分= 9【考点】实数的运算点评:解答本题的关键是熟练掌握任何非0数的0次幂为1;两个式子的积为0,则这两个式子至少有一个为0.,12.一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据:)【答案】77【解析】解:过点C作CM⊥DF于点M,交AE于点N易证CN⊥AE,∴四边形ADMN是矩形,MN=AD=8cm 3分在中,∠CAN=60°∴sin60°=(50+30)×= 6分∴cm 9分答:拉杆把手处C到地面的距离约77cm.【考点】勾股定理,三角函数的值点评:本题属于勾股定理的基本运算和求解方法,在解题中需要合理的作图13.(本题满分12分)如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D。
专题04二次根式-备战2023年中考数学必刷真题考点分类专练(全国通用)【解析版】

备战2023年中考数学必刷真题考点分类专练(全国通用)专题04二次根式一.选择题(共15小题)1.(2022•苏州)下列运算正确的是()A.√(−7)2=−7B.6÷23=9C.2a+2b=2ab D.2a•3b=5ab【分析】直接利用二次根式的性质以及有理数的除法运算法则、合并同类项、单项式乘单项式,分别计算判断即可.【解析】A.√(−7)2=7,故此选项不合题意;B.6÷23=9,故此选项,符合题意;C.2a+2b,无法合并,故此选项不合题意;D.2a•3b=6ab,故此选项不合题意;故选:B.【点评】此题主要考查了二次根式的性质以及有理数的除法运算、合并同类项、单项式乘单项式,正确掌握相关运算法则是解题关键.2.(2022•云南)下列运算正确的是()A.√2+√3=√5B.30=0C.(﹣2a)3=﹣8a3D.a6÷a3=a2【分析】根据二次根式的加减法判断A选项;根据零指数幂判断B选项;根据积的乘方判断C选项;根据同底数幂的除法判断D选项.【解析】A选项,√2和√3不是同类二次根式,不能合并,故该选项不符合题意;B选项,原式=1,故该选项不符合题意;C选项,原式=﹣8a3,故该选项符合题意;D选项,原式=a3,故该选项不符合题意;故选:C.【点评】本题考查了二次根式的加减法,零指数幂,幂的乘方与积的乘方,同底数幂的除法,掌握a0=1(a ≠0)是解题的关键.3.(2022•台州)无理数√6的大小在()A.1和2之间B.2和3之间C.3和4之间D.4和5之间【分析】根据无理数的估算分析解题.【解析】∵4<6<9,∴2<√6<3.故选:B .【点评】本题考查无理数的估算,理解算术平方根的概念是解题关键.4.(2022•眉山)实数﹣2,0,√3,2中,为负数的是( )A .﹣2B .0C .√3D .2【分析】根据负数的定义,找出这四个数中的负数即可.【解析】∵﹣2<0∴负数是:﹣2,故选A .【点评】本题主要考查实的分类,区分正负,解题的关键是熟知实数的性质:负数小于零.5.(2022•株洲)在0、13、﹣1、√2这四个数中,最小的数是( ) A .0 B .13 C .﹣1 D .√2【分析】根据负数小于0,正数大于0比较实数的大小即可得出答案.【解析】∵﹣1<0<13<√2,∴最小的数是﹣1,故选:C .【点评】本题考查了实数大小比较,掌握负数小于0,正数大于0是解题的关键.6.(2022•江西)下列各数中,负数是( )A .﹣1B .0C .2D .√2 【分析】根据负数的定义即可得出答案.【解析】﹣1是负数,2,√2是正数,0既不是正数也不是负数,故选:A .【点评】本题考查了实数,掌握在正数前面添加“﹣”得到负数是解题的关键.7.(2022•金华)在﹣2,12,√3,2中,是无理数的是( ) A .﹣2 B .12 C .√3 D .2【分析】利用有理数,无理数的概念对每个选项进行判断即可得出结论.【解析】﹣2,12,2是有理数,√3是无理数, 故选:C .【点评】本题主要考查了有理数,无理数的意义,掌握上述概念并熟练应用是解题的关键.8.(2022•舟山)估计√6的值在( )A .4和5之间B .3和4之间C .2和3之间D .1和2之间【分析】根据无理数的估算分析解题.【解析】∵4<6<9,∴√4<√6<√9,∴2<√6<3,故选:C .【点评】本题考查无理数的估算,理解算术平方根的概念是解题关键.9.(2022•安徽)下列为负数的是( )A .|﹣2|B .√3C .0D .﹣5【分析】根据实数的定义判断即可.【解析】A .|﹣2|=2,是正数,故本选项不合题意;B .√3是正数,故本选项不合题意;C .0既不是正数,也不是负数,故本选项不合题意;D .﹣5是负数,故本选项符合题意.故选:D .【点评】本题考查了有理数,绝对值以及算术平方根,掌握负数的定义是解答本题的关键.10.(2022•凉山州)化简:√(−2)2=( )A .±2B .﹣2C .4D .2【分析】根据算术平方根的意义,即可解答.【解析】√(−2)2=√4=2,故选:D .【点评】本题考查了算术平方根,熟练掌握算术平方根的意义是解题的关键.11.(2022•泸州)−√4=()A.﹣2B.−12C.12D.2【分析】根据算术平方根的定义判断即可.【解析】−√4=−√22=−2.故选:A.【点评】本题考查了算术平方根,掌握算术平方根的定义是解答本题的关键.12.(2022•泸州)与2+√15最接近的整数是()A.4B.5C.6D.7【分析】估算无理数√15的大小,再确定√15更接近的整数,进而得出答案.【解析】∵3<√15<4,而15﹣9>16﹣15,∴√15更接近4,∴2+√15更接近6,故选:C.【点评】本题考查估算无理数的大小,理解算术平方根的定义以及数的大小关系是正确解答的前提.13.(2022•重庆)估计√3×(2√3+√5)的值应在()A.10和11之间B.9和10之间C.8和9之间D.7和8之间【分析】先计算出原式得6+√15,再根据无理数的估算可得答案.【解析】原式=√3×2√3+√3×√5=6+√15,∵9<15<16,∴3<√15<4,∴9<6+√15<10.故选:B.【点评】本题考查了估算无理数的大小:利用完全平方数和算术平方根对无理数的大小进行估算.也考查了算术平方根.14.(2022•重庆)估计√54−4的值在()A.6到7之间B.5到6之间C.4到5之间D.3到4之间【分析】用夹逼法估算无理数的大小即可得出答案.【解析】∵49<54<64,∴7<√54<8,∴3<√54−4<4,故选:D.【点评】本题考查了估算无理数的大小,无理数的估算常用夹逼法,用有理数夹逼无理数是解题的关键.15.(2022•天津)估计√29的值在()A.3和4之间B.4和5之间C.5和6之间D.6和7之间【分析】估算确定出所求数的范围即可.【解析】∵25<29<36,∴5<√29<6,即5和6之间,故选:C.【点评】此题考查了估算无理数的大小,以及算术平方根,熟练掌握估算的方法是解本题的关键.二.填空题(共20小题)16.(2022•武汉)计算√(−2)2的结果是2.【分析】利用二次根式的性质计算即可.【解析】法一、√(−2)2=|﹣2|=2;法二、√(−2)2=√4=2.故答案为:2.【点评】本题考查了二次根式的性质,掌握“√a2=|a|”是解决本题的关键.17.(2022•常德)要使代数式有意义,则x的取值范围为x>4.√x−4【分析】根据二次根式的被开方数是非负数、分母不为0列出不等式,解不等式得到答案.【解析】由题意得:x﹣4>0,解得:x>4,故答案为:x>4.【点评】本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数、分母不为0是解题的关键.18.(2022•天津)计算(√19+1)(√19−1)的结果等于18.【分析】根据平方差公式即可求出答案.【解析】原式=(√19)2﹣12=19﹣1=18,故答案为:18.【点评】本题考查平方差公式与二次根式的混合运算,解题的关键是熟练运用平方差公式,本题属于基础题型.19.(2022•新疆)若√x−3在实数范围内有意义,则实数x的取值范围为x≥3.【分析】根据二次根式的被开方数是非负数即可得出答案.【解析】∵x﹣3≥0,∴x≥3.故答案为:x≥3.【点评】本题考查了二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.20.(2022•杭州)计算:√4=2;(﹣2)2=4.【分析】根据二次根式的性质、有理数的乘方法则计算即可.【解析】√4=2,(﹣2)2=4,故答案为:2,4.【点评】本题考查的是二次根式的化简、有理数的乘方,掌握二次根式的性质是解题的关键.21.(2022•泰安)计算:√8•√6−3√43=2√3.【分析】化简二次根式,然后先算乘法,再算减法.【解析】原式=√8×6−3×2√3 3=4√3−2√3=2√3,故答案为:2√3.【点评】本题考查二次根式的混合运算,理解二次根式的性质,准确化简二次根式是解题关键.22.(2022•云南)若√x+1有意义,则实数x的取值范围为x≥﹣1.【分析】根据二次根式的被开方数是非负数即可得出答案.【解析】∵x+1≥0,∴x≥﹣1.故答案为:x≥﹣1.【点评】本题考查了二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.23.(2022•遂宁)实数a、b在数轴上的位置如图所示,化简|a+1|−√(b−1)2+√(a−b)2=2.【分析】根据数轴可得:﹣1<a<0,1<b<2,然后即可得到a+1>0,b﹣1>0,a﹣b<0,从而可以将所求式子化简.【解析】由数轴可得,﹣1<a<0,1<b<2,∴a+1>0,b﹣1>0,a﹣b<0,∴|a+1|−√(b−1)2+√(a−b)2=a+1﹣(b﹣1)+(b﹣a)=a+1﹣b+1+b﹣a=2,故答案为:2.【点评】本题考查二次根式的性质与化简、实数与数轴,解答本题的关键是明确题意,利用数形结合的思想解答.24.(2022•滨州)若二次根式√x−5在实数范围内有意义,则x的取值范围为x≥5.【分析】根据二次根式有意义的条件得出x﹣5≥0,求出即可.【解析】要使二次根式√x−5在实数范围内有意义,必须x﹣5≥0,解得:x≥5,故答案为:x≥5.【点评】本题考查了二次根式有意义的条件和解一元一次不等式,能得出关于x的不等式是解此题的关键.25.(2022•扬州)若√x−1在实数范围内有意义,则x的取值范围是x≥1.【分析】直接利用二次根式有意义的条件进而得出答案.【解析】若√x−1在实数范围内有意义,则x﹣1≥0,解得:x≥1.故答案为:x≥1.【点评】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.26.(2022•邵阳)若√x−2有意义,则x 的取值范围是 x >2 .【分析】先根据二次根式及分式有意义的条件列出x 的不等式组,求出x 的取值范围即可. 【解析】∵√x−2有意义,∴{x −2≥0x −2≠0,解得x >0. 故答案为:x >2.【点评】本题考查的是二次根式有意义的条件,熟知二次根式中的被开方数是非负数是解答此题的关键.27.(2022•山西)计算:√18×√12的结果为 3 .【分析】按照二次根式的乘法法则计算即可.【解析】原式=√9=3.故答案为:3.【点评】本题主要考查了二次根式的乘法运算.二次根式的运算法则:乘法法则√a ⋅√b =√ab .28.(2022•衡阳)计算:√2×√8= 4 .【分析】原式利用二次根式的乘法法则计算,将结果化为最简二次根式即可.【解析】原式=√2×8=√16=4.故答案为:4【点评】此题考查了二次根式的乘除法,熟练掌握运算法则是解本题的关键.29.(2022•随州)已知m 为正整数,若√189m 是整数,则根据√189m =√3×3×3×7m =3√3×7m 可知m 有最小值3×7=21.设n 为正整数,若√300n是大于1的整数,则n 的最小值为 3 ,最大值为 75 . 【分析】先将√300n 化简为10√3n ,可得n 最小为3,由√300n 是大于1的整数可得√300n 越小,300n 越小,则n 越大,当√300n =2时,即可求解. 【解析】∵√300n =√3×100n =10√3n ,且为整数, ∴n 最小为3, ∵√300n 是大于1的整数, ∴√300n 越小,300n 越小,则n 越大,当√300n =2时, 300n =4,∴n =75,故答案为:3;75.【点评】本题考查二次根式的乘除法,二次根式的性质与化简,解题的关键是读懂题意,根据关键词“大于”,“整数”进行求解.30.(2022•宿迁)满足√11≥k 的最大整数k 是 3 .【分析】根据无理数的估算分析解题.【解析】∵3<√11<4,且k ≤√11,∴最大整数k 是3.故答案为:3.【点评】本题考查无理数的估算,理解算术平方根的概念是解题关键.31.(2022•湘潭)四个数﹣1,0,12,√3中,为无理数的是 √3 . 【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可解答.【解析】四个数﹣1,0,12,√3中,为无理数的是√3. 故答案为:√3.【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽得到的数;以及像0.1010010001…等有这样规律的数.32.(2022•陕西)计算:3−√25= ﹣2 .【分析】首先利用算术平方根的定义化简,然后加减即可求解.【解析】原式=3﹣5=﹣2.故答案为:﹣2.【点评】本题主要考查了实数的运算,主要利用算术平方根的定义.33.(2022•重庆)|﹣2|+(3−√5)0= 3 .【分析】根据绝对值的性质和零指数幂的性质计算可得答案.【解析】原式=2+1=3.故答案为:3.【点评】本题考查实数的运算,熟练掌握实数的运算性质是解题关键.34.(2022•南充)若√8−x为整数,x为正整数,则x的值是4或7或8.【分析】利用二次根式的性质求得x的取值范围,利用算术平方根的意义解答即可.【解析】∵8﹣x≥0,x为正整数,∴1≤x≤8且x为正整数,∵√8−x为整数,∴√8−x=0或1或2,当√8−x=0时,x=8,当√8−x=1时,x=7,当√8−x=2时,x=4,综上,x的值是4或7或8,故答案为:4或7或8.【点评】本题主要考查了算术平方根的意义,二次根式的性质,利用二次根式的性质求得x的取值范围是解题的关键.35.(2022•连云港)写出一个在1到3之间的无理数:√2(符合条件即可).【分析】由于12=1,32=9,所以只需写出被开方数在1和9之间的,且不是完全平方数的数即可求解.【解析】1到3之间的无理数如√2,√3,√5.答案不唯一.【点评】本题主要考查常见无理数的定义和性质,解题关键是估算无理数的整数部分和小数部分.三.解答题(共9小题)36.(2022•武威)计算:√2×√3−√24.【分析】根据二次根式的乘法法则和二次根式的化简计算,再合并同类二次根式即可.【解析】原式=√6−2√6=−√6.【点评】本题考查了二次根式的混合运算,掌握√a•√b=√ab(a≥0,b≥0)是解题的关键.37.(2022•广元)计算:2sin60°﹣|√3−2|+(π−√10)0−√12+(−12)﹣2.【分析】根据特殊角的三角函数值,绝对值,零指数幂,二次根式的化简,负整数指数幂计算即可.【解析】原式=2×√32+√3−2+1﹣2√3+1(−12)2=√3+√3−2+1﹣2√3+4=3.【点评】本题考查了实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值,掌握a ﹣p =1a p (a ≠0)是解题的关键.38.(2022•宿迁)计算:(12)﹣1+√12−4sin60°. 【分析】先计算(12)﹣1、√12,再代入sin60°算乘法,最后加减. 【解析】原式=2+2√3−4×√32=2+2√3−2√3=2.【点评】本题考查了实数的运算,掌握负整数指数幂的意义、二次根式的化简及特殊角的函数值是解决本题的关键.39.(2022•娄底)计算:(2022﹣π)0+(12)﹣1+|1−√3|﹣2sin60°. 【分析】先计算零次幂、负整数指数幂,再化简绝对值、代入特殊角的三角函数值算乘法,最后算加减.【解析】原式=1+2+√3−1﹣2×√32=1+2+√3−1−√3=2.【点评】本题考查了实数的运算,掌握零指数幂、负整数指数幂、绝对值的意义及特殊角的函数值是解决本题的关键.40.(2022•台州)计算:√9+|﹣5|﹣22.【分析】先化简各式,然后再进行计算即可解答.【解析】√9+|﹣5|﹣22=3+5﹣4=8﹣4=4.【点评】本题考查了实数的运算,准确熟练地化简各式是解题的关键.41.(2022•新疆)计算:(﹣2)2+|−√3|−√25+(3−√3)0.【分析】直接利用零指数幂的性质以及绝对值的性质、二次根式的性质分别化简,进而得出答案.【解析】原式=4+√3−5+1=√3.【点评】此题主要考查了实数的运算,正确化简各数是解题关键.42.(2022•株洲)计算:(﹣1)2022+√9−2sin30°.【分析】根据有理数的乘方,算术平方根,特殊角的三角函数值计算即可.【解析】原式=1+3﹣2×1 2=1+3﹣1=3.【点评】本题考查了实数的运算,特殊角的三角函数值,掌握(﹣1)的偶次幂等于1,(﹣1)的奇次幂等于﹣1是解题的关键.43.(2022•怀化)计算:(3.14﹣π)0+|√2−1|+(12)﹣1−√8.【分析】根据零指数幂,绝对值,负整数指数幂,二次根式的化简计算即可.【解析】原式=1+√2−1+2﹣2√2=2−√2.【点评】本题考查了实数的运算,零指数幂,绝对值,负整数指数幂,考查学生的运算能力,掌握a0=1(a≠0),a﹣p=1a p(a≠0)是解题的关键.44.(2022•遂宁)计算:tan30°+|1−√33|+(π−√33)0﹣(13)﹣1+√16.【分析】根据特殊角的三角函数值、去绝对值的方法、零指数幂、负整数指数幂和算术平方根可以解答本题.【解析】tan30°+|1−√33|+(π−√33)0﹣(13)﹣1+√16=√33+1−√33+1﹣3+4=3.【点评】本题考查实数的运算、特殊角的三角函数值、去绝对值的方法、零指数幂、负整数指数幂和算术平方根,熟练掌握运算法则是解答本题的关键.。
数与式的计算100题(真题专练)备战2023年中考数学考点微专题

考向1.9 数与式的计算100题(真题专练)1.(2019·四川遂宁·中考真题)计算:201920(1)(2)(3.14)4cos30|212|π-︒-+-+--+- 2.(2019·四川乐山·中考真题)如图,点A 、B 在数轴上,它们对应的数分别为2-,1xx +,且点A 、B 到原点的距离相等.求x 的值.3.(2021·湖南张家界·中考真题)计算:2021(1)222cos608-+-︒4.(2021·广东深圳·中考真题)先化简再求值:2169123x x x x ++⎛⎫+÷ ⎪++⎝⎭,其中1x =-. 5.(2021·湖南湘潭·中考真题)计算:011|2|(2)()4tan 453π----+-︒6.(2021·内蒙古呼伦贝尔·中考真题)计算:2122sin 60133---︒+7.(2021·广西柳州·中考真题)计算:391-8.(2021·黑龙江大庆·()2222sin 451+︒-- 9.(2021·上海·中考真题)计算: 1129|1228-+- 10.(2021·青海西宁·中考真题)计算: 121(2)|3|2-⎛⎫-+-- ⎪⎝⎭.11.(2020·新疆·中考真题)计算:()()2012π34-++-12.(2020·青海·中考真题)计算:10311345( 3.14)273π-⎛⎫+︒+- ⎪⎝⎭13.(2020·甘肃天水·中考真题)(1)计算:114sin 6032|2020124-︒⎛⎫-+ ⎪⎝⎭.(2)先化简,再求值:21111211a a a a a a ---÷-+++,其中3a = 14.(2020·北京·中考真题)计算:11()18|2|6sin 453---︒15.(2020·山东菏泽·中考真题)计算:20201202012|63|2345(2)2-⎛⎫++︒--⋅ ⎪⎝⎭.16.(2020·四川乐山·中考真题)计算:022cos60(2020)π--︒+-.17.(2020·浙江·﹣1|.18.(2020·浙江嘉兴·中考真题)(1)计算:(2020)0﹣3|; (2)化简:(a +2)(a ﹣2)﹣a (a +1).19.(2020·浙江台州·中考真题)计算:3-20.(2019·山东东营·中考真题)(1)计算:()101 3.142019π-⎛⎫+- ⎪⎝⎭2sin 4512+-;(2)化简求值:22222a b a ab b a b a ab a ⎛⎫++-÷⎪--⎝⎭,当1a =-时,请你选择一个适当的数作为b 的值,代入求值.21.(2021·甘肃兰州·中考真题)先化简,再求值:22611931m m m m m --÷--+-,其中4m =.22.(2021·河南·中考真题)(1)计算:013(3--; (2)化简:21221x x x -⎫⎛-÷⎪⎝⎭. 23.(2021·湖北鄂州·中考真题)先化简,再求值:2293411x x x x x x -+÷+--,其中2x =.24.(2021·广西玉林·()()01416sin30π--+--°.25.(2021·广西玉林·中考真题)先化简再求值:()2112a a a a -⎛⎫-+÷ ⎪⎝⎭,其中a 使反比例函数ay x=的图象分别位于第二、四象限. 26.(2021·北京·中考真题)已知22210a b +-=,求代数式()()22-++a b b a b 的值.27.(2021·北京·中考真题)计算:02sin60(5π--.28.(2021·江苏宿迁·中考真题)计算:()0π1-4sin45°29.(2021·湖北荆州·中考真题)先化简,再求值:2221211a a a a a ++⎛⎫÷+ ⎪--⎝⎭,其中a =30.(2021·浙江衢州·中考真题)先化简,再求值:2933x x x +--,其中1x =.31.(2021·浙江衢州·01()|3|2cos602--+︒.32.(2021·湖北随州·中考真题)先化简,再求值:2141122x x x -⎛⎫+÷⎪++⎝⎭,其中1x =. 33.(2021·山东菏泽·中考真题)先化简,再求值:22221244m n n m m n m mn n--+÷--+,其中m ,n满足32m n =-. 34.(2021·湖北十堰·中考真题)化简:22214244a a a a a a a a +--⎛⎫-÷⎪--+⎝⎭.35.(2021·湖北十堰·1133-⎛⎫︒+-- ⎪⎝⎭.36.(2021·湖南常德·中考真题)化简:2593111aa a a a a ++⎛⎫+÷⎪---⎝⎭37.(2021·湖南常德·中考真题)计算:012021345-+︒.38.(2021·湖南郴州·中考真题)先化简,再求值:2213111a a a a a a --⎛⎫-÷⎪+--⎝⎭,其中a =39.(2021·湖南郴州·中考真题)计算:11(2021)|2tan 602π-⎛⎫--+⋅︒ ⎪⎝⎭.40.(2021·湖南怀化·中考真题)计算:021(3)()4sin 60(1)3π--+︒--41.(2021·湖北黄冈·中考真题)计算:0|12sin 60(1)π-︒+-.42.(2021·新疆·中考真题)先化简,再求值:22414421x x x x x x ⎛⎫-+⋅⎪+++-⎝⎭,其中3x =.43.(2021·湖南长沙·中考真题)计算:(02sin 451-+°44.(2021·四川广安·中考真题)先化简:2221211a a a a a a -+⎛⎫÷- ⎪-+⎝⎭,再从-1,0,1,2中选择一个适合的数代入求值.45.(2021·四川广安·中考真题)计算:()03.1414sin 60π-︒.46.(2021·湖南邵阳·中考真题)先化简,再从1-,0,1,21中选择一个合适的x 的值代入求值.2211121x x x x x -⎛⎫-÷ ⎪+++⎝⎭.47.(2021·四川眉山·中考真题)计算:(1143tan 602-⎛⎫-︒-- ⎪⎝⎭48.(2021·江苏苏州·中考真题)先化简再求值:21111x x x-⎛⎫+⋅⎪-⎝⎭,其中1x =.49.(2021·江苏苏州·223--.50.(2021·江苏扬州·中考真题)计算或化简:(1)013|tan603⎛⎫-++︒ ⎪⎝⎭; (2)()11a b a b ⎛⎫+÷+ ⎪⎝⎭.51.(2021·湖南邵阳·中考真题)计算:()020212tan 60π--︒.52.(2021·甘肃武威·中考真题)先化简,再求值:2224(2)244x x x x x --÷--+,其中4x =. 53.(2021·甘肃武威·中考真题)计算:011(2021)()2cos 452π--+-︒.54.(2021·云南·中考真题)计算:201tan 452(3)1)2(6)23-︒-++-+⨯-. 55.(2021·浙江金华·中考真题)已知16x =,求()()()2311313x x x -++-的值.56.(2021·浙江金华·中考真题)计算:()202114sin 45+2-︒-.57.(2021·浙江温州·中考真题)(1)计算:()0438⨯-+-.(2)化简:()()215282a a a -++.58.(2021·四川南充·中考真题)先化简,再求值:2(21)(21)(23)x x x +---,其中1x =-. 59.(2021·四川凉山·中考真题)已知112,1x y x y-=-=,求22x y xy -的值.60.(2021·四川泸州·中考真题)计算:120211423cos304.61.(2021·重庆·中考真题)计算:(1)2(23)()a a b a b ++-;(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭.62.(2021·四川自贡·0|7|(2-+.63.(2021·浙江丽水·中考真题)计算:0|2021|(3)-+-64.(2020·广西贺州·中考真题)计算:()24π345+-︒--+︒.65.(2020·福建·中考真题)先化简,再求值:211(1)22x x x --÷++,其中1x =.66.(2020·四川广安·中考真题)计算:202011(1)12cos 45()2--+-.67.(2020·四川广安·中考真题)先化简,再求值:221(1)11x x x -÷+-,其中x=2020.68.(2020·广西柳州·中考真题)计算:11682⨯-+.69.(2020·广西·中考真题)计算:(0+(﹣2)2+|﹣12|﹣sin30°.70.(2020·贵州黔南·中考真题)(1)计算()1013tan602cos6020202-⎛⎫--︒+-︒- ⎪⎝⎭;(2)解不等式组:312324xx -⎧⎪⎨⎪+⎩.71.(2020·辽宁鞍山·中考真题)先化简,再求值:2344111x x x x x ++⎛⎫--÷⎪++⎝⎭,其中2x =. 72.(2020·内蒙古呼伦贝尔·中考真题)计算:1012cos60-(-1)2π-⎛⎫- ⎪⎝⎭.73.(2020·内蒙古呼伦贝尔·中考真题)先化简,再求值:222442342x x x x x x -+-÷+-+,其中4x =-. 74.(2020·江苏宿迁·中考真题)先化简,再求值:2x x -÷(x ﹣4x),其中x﹣2. 75.(2020·四川眉山·中考真题)先化简,再求值:229222a a a -⎛⎫-÷⎪--⎝⎭,其中3=a . 76.(2020·四川眉山·中考真题)计算:(2122sin 452-⎛⎫+-+︒ ⎪⎝⎭77.(2020·云南昆明·中考真题)计算:12021(π﹣3.14)0﹣(﹣15)-1.78.(2020·江苏南通·中考真题)计算: (1)(2m +3n )2﹣(2m +n )(2m ﹣n );(2)22⎛⎫--÷+ ⎪⎝⎭x y y xy x x x 79.(2021·福建·1133-⎛⎫- ⎪⎝⎭.80.(2021·四川达州·中考真题)计算:()02120212sin 601π-+-+︒-.81.(2020·江苏徐州·中考真题)计算:(1)120201(1)2|2-⎛⎫-+- ⎪⎝⎭;(2)2121122a a a a -+⎛⎫-÷⎪-⎝⎭82.(2020·湖南邵阳·中考真题)已知:|1|0m -=, (1)求m ,n 的值;(2)先化简,再求值:22(3)(2)4m m n m n n -++-.83.(2020·湖南怀化·222cos 45|2-︒-+ 84.(2020·湖南张家界·中考真题)阅读下面的材料:对于实数,a b ,我们定义符号min{,}a b 的意义为:当a b <时,min{,}a b a =;当a b 时,min{,}a b b =,如:min{4,2}2,min{5,5}5-=-=.根据上面的材料回答下列问题: (1)min{1,3}-=______;(2)当2322min ,233x x x -++⎧⎫=⎨⎬⎩⎭时,求x 的取值范围. 85.(2020·四川自贡·中考真题)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式2x -的几何意义是数轴上x 所对应的点与2所对应的点之间的距离;因为()+=--x 1x 1,所以1x +的几何意义就是数轴上x 所对应的点与1-所对应的点之间的距离. ⑴. 发现问题:代数式12x x ++-的最小值是多少?⑵. 探究问题:如图,点,,A B P 分别表示的是-1,2,x ,3AB =.∵12x x ++-的几何意义是线段PA 与PB 的长度之和∴当点P 在线段AB 上时,+=PA PB 3;当点点P 在点A 的左侧或点B 的右侧时 +>PA PB 3 ∴12x x ++-的最小值是3. ⑶.解决问题:①.-++x 4x 2的最小值是 ;②.利用上述思想方法解不等式:314x x ++->③.当a 为何值时,代数式++-x a x 3的最小值是2.86.(2021·四川内江·中考真题)计算:0216sin 45|128(2021)()2π-︒----. 87.(2021·青海西宁·中考真题)计算:2(53)(53)(31)-.88.(2021·辽宁盘锦·中考真题)先化简,再求值:2233816164x x xx x x x --÷--+--,其中24x =89.(2021·青海·中考真题)先化简,再求值:2121a a a a a -+⎛⎫-÷ ⎪⎝⎭,其中21a =.90.(2021·江苏南京·中考真题)计算222ab a b b ab a b a ab ab-⎛⎫-+÷⎪+++⎝⎭. 91.(2021·四川成都·中考真题)先化简,再求值:2269111a a a a ++⎛⎫+÷⎪++⎝⎭,其中33=a .92.(2021·四川资阳·中考真题)先化简,再求值:222211111x x x x x x ⎛⎫++-÷ ⎪---⎝⎭,其中30x -=. 93.(2021·重庆·中考真题)计算(1)()()22x y x x y -++; (2)2241244a a a a a -⎛⎫-÷ ⎪+++⎝⎭. 94.(2021·浙江嘉兴·中考真题)(1)计算:12sin 30-︒; (2)化简并求值:11a a -+,其中12a =-. 95.(2021·四川遂宁·中考真题)先化简,再求值:322293443m m m m m m -⎛⎫÷++ ⎪-+-⎝⎭,其中m 是已知两边分别为2和3的三角形的第三边长,且m 是整数. 96.(2021·四川泸州·中考真题)化简:141()22a a a a a --+÷++.97.(2021·山东枣庄·中考真题)先化简,再求值:21(1)11x x x ÷+--,其中1x =.98.(2020·广西贵港·中考真题)(1()0236cos30π+-︒; (2)先化简再求值:221239m m m ÷--,其中5m =-.99.(2020·内蒙古赤峰·中考真题)先化简,再求值:221121m m m m m m ---÷++,其中m 满足:210m m --=.100.(2021·重庆·中考真题)如果一个自然数M 的个位数字不为0,且能分解成A B ⨯,其中A 与B 都是两位数,A 与B 的十位数字相同,个位数字之和为10,则称数M 为“合和数”,并把数M 分解成M A B =⨯的过程,称为“合分解”.例如6092129=⨯,21和29的十位数字相同,个位数字之和为10, 609∴是“合和数”.又如2341813=⨯,18和13的十位数相同,但个位数字之和不等于10, 234∴不是“合和数”.(1)判断168,621是否是“合和数”?并说明理由;(2)把一个四位“合和数”M 进行“合分解”,即M A B =⨯.A 的各个数位数字之和与B 的各个数位数字之和的和记为()P M ;A 的各个数位数字之和与B 的各个数位数字之和的差的绝对值记为()Q M .令()()()P M G M Q M =,当()G M 能被4整除时,求出所有满足条件的M .1.74-【分析】先根据整数指数幂、负指数幂、零指数幂、三角函数和绝对值进行化简,再进行加减运算.解:原式131142324=-++-+ 111232324=-++- 74=-.【点拨】本题考查指数幂、三角函数和绝对值,解题的关键是掌握指数幂、三角函数和绝对值.2.2x =-【分析】根据点A 、B 到原点的距离相等可知点A 、B 表示的数值互为相反数,即21xx =+,解分式方程即可.解:∵点A 、B 到原点的距离相等 ∴A 、B 表示的数值互为相反数 即21xx =+,去分母,得2(1)x x =+, 去括号,得22x x =+, 解得2x =-经检验,2x =-是原方程的解.【点拨】本题考查了相反数,绝对值的定义,解分式方程,解本题的关键是读懂题意,根据题中点A 、B 到原点的距离相等可知点A 、B 表示的数值互为相反数3【分析】先运用乘方、绝对值、特殊角的三角函数值以及平方根的性质化简,然后计算即可.解:2021(1)22cos60-+︒+11222=-+⨯+=【点拨】本题主要考查了乘方、绝对值、特殊角的三角函数值、平方根的性质等知识点,灵活运用相关知识成为解答本题的关键.4.12x +;1 【分析】先把分式化简后,再把x 的值代入求出分式的值即可. 解:原式212331122(3)232x x x x x x x x x +++⎛⎫=+⋅=⋅= ⎪++++++⎝⎭ 当1x =-时,原式1112==-+. 【点拨】本题考查了分式的化简求值,熟练分解因式是解题的关键. 5.0【分析】根据绝对值的性质、零指数幂、负整指数幂的性质及45°角的正切值计算解题即可.解:011|2|(2)()4tan 453π----+-︒21341=-+-⨯0=.【点拨】本题考查实数的混合运算,涉及绝对值、零指数幂、负整指数幂、正切等知识,是基础考点,难度较易,掌握相关知识是解题关键.6. 【分析】分别进行负整数指数幂运算、特殊角的三角函数值运算、绝对值运算、二次根式运算即可解答解:222sin 601---︒+=1214--=54-=. 【点拨】本题考查负整数指数幂、特殊角的三角函数值、绝对值、二次根式,熟记特殊角的三角函数值,掌握运算法则是解答的关键.7.1【分析】根据绝对值的定义及算术平方根的定义即可解决. 解:原式331=-+1=【点拨】本题考查了绝对值的定义、算术平方根的定义及实数的运算,关键是掌握绝对值和算术平方根的定义.8.1【分析】直接利用去绝对值符号、特殊角度的三角函数值、负整数的平方运算计算出结果即可.()222sin 451+︒--221= 1=故答案是:1.【点拨】本题考查了去绝对值符号、特殊角度的三角函数值、负整数的平方运算法则,解题的关键是:掌握相关的运算法则.9.2【分析】根据分指数运算法则,绝对值化简,负整指数运算法则,化最简二次根式,合并同类二次根式以及同类项即可.解:1129|12-+-,(112-⨯=31 =2.【点拨】本题考查实数混合运算,分指数运算法则,绝对值符号化简,负整指数运算法则,化最简二次根式,合并同类二次根式与同类项,掌握实数混合运算法则与运算顺序,分指数运算法则,绝对值符号化简,负整指数运算法则,化最简二次根式,合并同类二次根式与同类项是解题关键.10.3【分析】由乘方、负整数指数幂、绝对值的意义进行化简,即可得到答案.解:原式423=+-3=.【点拨】本题考查了乘方、负整数指数幂、绝对值的意义,解题的关键是掌握运算法则,正确的进行化简.11【分析】按照绝对值的性质、乘方、零指数幂、二次根式的运算法则计算.解:原式112=-=【点拨】本题考查绝对值的性质、乘方、零指数幂、二次根式的运算法则,比较基础.12【分析】根据负整数指数幂,绝对值的性质,零指数幂,立方根,特殊角的三角函数值进行计算即可解:101145( 3.14)3π-⎛⎫+︒+- ⎪⎝⎭3|11|13=++-3113=+-=【点拨】本题考查了负整数指数幂,绝对值的性质,零指数幂,立方根,特殊角的三角函数值,熟知以上计算是解题的关键.13.(13;(2)221a -,1. 【分析】(1)先代入三角函数值、去绝对值符号、计算零指数幂、化简二次根式、计算负整数指数幂,再计算乘法、去括号,最后计算加减可得;(2)先根据分式的混合运算顺序和运算法则化简原式,再将a 的值代入计算可得.解:(1)原式4(214=-+-,214=-,3;(2)原式21111(1)1a a a a a -+=-⨯-+-, 1111a a =--+, 11(1)(1)a a a a +-+=-+, 221a =-,当a ==()222213121===--. 【点拨】本题主要考查实数的混合运算与分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.14.5【分析】分别计算负整数指数幂,算术平方根,绝对值,锐角三角函数,再合并即可得到答案.解:原式=3262+-⨯32=+-5.= 【点拨】本题考查的是负整数指数幂,算术平方根,绝对值,锐角三角函数,以及合并同类二次根式,掌握以上的知识是解题的关键.15.52【分析】根据负整数指数幂,绝对值,特殊角的三角函数值,积的乘方公式的逆向应用进行计算即可.解:202012020123|45(2)2-⎛⎫++︒--⋅ ⎪⎝⎭202011(3(2)22=++-⨯ 1312=+ 52=. 【点拨】本题考查了负整数指数幂,绝对值,特殊角的三角函数值,积的乘方公式的逆向应用,熟知以上运算是解题的关键.16.2【分析】根据绝对值,特殊三角函数值,零指数幂对原式进行化简计算即可.解:原式=12212-⨯+ =2.【点拨】本题考查了绝对值,特殊三角函数值,零指数幂,掌握运算法则是解题关键.17. 1【分析】根据算术平方根定义和绝对值的性质计算,再合并同类二次根式即可.解:原式1.【点拨】本题考查了算术平方根和绝对值以及同类二次根式的合并,解题的关键是正确理解定义.18.(1)2;(2)﹣4﹣a【分析】(1)直接利用零指数幂的性质和二次根式的性质、绝对值的性质分别化简得出答案;(2)直接利用平方差公式以及单项式乘以多项式计算得出答案.解:(1)(2020)0﹣3|=1﹣2+3=2;(2)(a +2)(a ﹣2)﹣a (a +1)=a 2﹣4﹣a 2﹣a=﹣4﹣a .【点拨】本题主要考查了实数的运算,准确运用零指数幂、二次根式的性质和绝对值的性质是解题的关键.19.3【分析】按照绝对值的概念、平方根的概念逐个求解,然后再用二次根式加减运算即可.解:原式=3=故答案为:3.【点拨】本题考查了绝对值的概念、平方根的概念、二次根式的加减运算等,熟练掌握运算公式及法则是解决此类题的关键.20.(1)2020;(2)1【分析】(1)根据负指数幂、零指数幂、绝对值和三角函数、二次根式,即可得到答案;(2)根据分式的性质进行化简,再代入1a =-,即可得到答案.解:1()原式201912++=2020+=2020=;2()原式()()222a b a a a b a b -=-+ ()()()()2a b a b aa ab a b -+=-+ 1a b =+, 当1a =-时,取2b =,原式1112==-+. 【点拨】本题负指数幂、零指数幂、绝对值、三角函数、二次根式和分式的化简,解题的关键是掌握负指数幂、零指数幂、绝对值、三角函数、二次根式和分式的化简.21.11m -,13【分析】先将除法转化为乘法,因式分解,约分,分式的减法运算,再将字母的值代入求解即可. 解:22611931m m m m m --÷--+- 2(3)31(3)(3)11m m m m m m -+=⋅-+--- 2111m m =--- 11m =-. 当4m =时, 原式11413==-. 【点拨】本题考查了分式的化简求值,掌握因式分解是解题的关键.22.(1)1;(2)2x . 【分析】(1)实数的计算,根据实数的运算法则求解即可;(2)分式的化简,根据分式的运算法则计算求解.解:(1)013(3-- 11133=-+ 1=.(2)21221x x x -⎫⎛-÷ ⎪⎝⎭212(1)x x x x -=⨯- 2x =. 【点拨】本题考查了实数的混合运算,负指数幂,二次根式的化简,零次幂的计算,分式的化简等知识,牢记公式与定义,熟练分解因式是解题的关键.23.1x x +,32【分析】先通过约分、通分进行化简,再把给定的值代入计算即可.解:原式()()()313341x x x x x x x -=⨯++--+ 1x x+=, 当2x =时,原式32=. 【点拨】本题主要考查分式的化简求值,解题的关键是熟练掌握因式分解,正确进行约分、通分.24.1【分析】先算算术平方根,零指数幂,负整数指数幂以及特殊角三角函数值,再算加减法,即可求解.解:原式=141162+--⨯ =1【点拨】本题主要考查实数的混合运算,掌握算术平方根,零指数幂,负整数指数幂以及特殊角三角函数值,是解题的关键.25.1-【分析】由题意易得0a <,然后对分式进化简,然后再求解即可.解:∵a 使反比例函数a y x=的图象分别位于第二、四象限, ∴0a <, ∴()2112a a a a -⎛⎫-+÷ ⎪⎝⎭ =()22211a a a a a -+-⨯- =1-.【点拨】本题主要考查反比例函数的图象与性质及分式的化简求值,熟练掌握反比例函数的图象与性质及分式的运算是解题的关键.26.1【分析】先对代数式进行化简,然后再利用整体思想进行求解即可.解:()()22-++a b b a b=22222a ab b ab b -+++=222a b +,∵22210a b +-=,∴2221a b +=,代入原式得:原式=1.【点拨】本题主要考查整式的乘法运算及完全平方公式,熟练掌握利用整体思想进行整式的化简求值是解题的关键.27.4【分析】根据特殊三角函数值、零次幂及二次根式的运算可直接进行求解.解:原式=2514-=. 【点拨】本题主要考查特殊三角函数值、零次幂及二次根式的运算,熟练掌握特殊三角函数值、零次幂及二次根式的运算是解题的关键.28.1【分析】结合实数的运算法则即可求解.解:原式=1411+=+. 【点拨】本题考察非0底数的0次幂等于1、二次根式的化简、特殊三角函数值等知识点,属于基础题型,难度不大.解题的关键是掌握实数的运算法则.29.1a a +【分析】先计算括号内的加法,然后化除法为乘法进行化简,继而把a =即可.解:原式=()()21111a a a a a ++⎛⎫÷ ⎪--⎝⎭()()211=1+1a a a a a +-⎛⎫ ⎪-⎝⎭1=a a +当a =【点拨】本题主要考查分式的化简求值,解题的关键是掌握分式混合运算顺序和运算法则.30.3x +;4【分析】先将这两个分式转化为同分母的分式,再将分母不变,分子相加减,最后化简即可. 解:原式29(3)(3)333x x x x x x +-=-=--- 3x =+当1x =时,原式4=.【点拨】本题考查了分式的化简求值问题,涉及到了分式的通分和约分,解决本题的关键是牢记相关概念与法则,并灵活运用,最后的结果记得化简即可.31.2.【分析】由特殊的三角函数值得到1cos602︒=,由零指数幂公式算出01()=12,,最后算出结果即可. 解:原式13+1322 2=【点拨】本题考查了实数的混合运算,关键注意零指数幂的运算和特殊的三角函数值.32.22x -,-2 【分析】(1)先把括号里通分合并,括号外的式子进行因式分解,再约分,将x=1代入计算即可.解:原式()()()21221222x x x x x x ++=⋅=++-- 当1x =时,原式2212==-- 【点拨】本题考查了分式的化简求值,用到的知识是约分、分式的加减,熟练掌握法则是解题的关键.33.3n m n+;-6. 【分析】先变除法为乘法,后因式分解,化简计算,后变形32n m =-代入求值即可 解:∵22221244m n n m m n m mn n --+÷--+=2(2)12()()m n m n m n n m n m --+⨯--+ =21m n n m --+ =3n m n+, ∵32m n =-, ∴32n m =-, ∴原式=332nn n -+= -6. 【点拨】本题考查了分式的化简求值,熟练掌握分式混合运算的基本顺序,基本计算方法是解题的关键.34.21(2)a - 【分析】先算分式的减法,再把除法化为乘法运算,进行约分,即可求解.解:原式=221(2)(2)4a a a a a a a ⎛⎫+--⋅ ⎪---⎝⎭=()()()22221(2)(2)4a a a a a a a a a a +--⎛⎫-⋅ ⎪---⎝⎭=2224(2)4a a a a a a a --+⋅-- =24(2)4a a a a a -⋅-- =21(2)a - 【点拨】本题主要考查分式的化简,掌握分式的通分和约分,是解题的关键. 35.1【分析】利用特殊角的三角函数值、负整数指数幂、绝对值的性质逐项计算,即可求解.解:原式33=- 1=.【点拨】本题考查实数的运算,掌握特殊角的三角函数值、负整数指数幂、绝对值的性质是解题的关键.36.31a a ++【分析】直接将括号里面的分式,通分运算进而结合分式的混合运算法则,计算得出答案. 解:2593111a a a a a a ++⎛⎫+÷ ⎪---⎝⎭ 222591=113a a a a a a a ++-⨯--+(+) 2691=(1)(1)3a a a a a a ++-⨯+-+ 2(3)1=(1)(1)3a a a a a +-⨯+-+ 31a a +=+ 故答案为:31a a ++. 【点拨】本题考查了分式的化简,分式的通分,因式分解,平方差公式,完全平方公式,分式的混合运算,熟练运用公式和分式的计算法则是解题关键.37.1.【分析】直接利用零次幂的运算法则,负次幂的运算法则、二次根式及特殊角的三角函数值进行计算即可.解:012021345-+︒3132=+ 111=+-1=故答案是:1.【点拨】本题考查了零次幂的运算法则,负次幂的运算法则、二次根式及特殊角的三角函数值,解题的关键是:熟练掌握相关运算法则.38 【分析】先算分式的减法运算,再把除法化为乘法,进行约分化简,最后代入求值,即可.解:原式=2213111a a a a a a --⎛⎫-÷ ⎪+--⎝⎭=131(1)(1)(1)1a a a a a a a ⎛⎫----⋅ ⎪++-⎝⎭=()()2131(1)(1)(1)(1)1a a a aa a a a a a⎛⎫----⋅⎪⎪+-+-⎝⎭=()()2131(1)(1)1a a a aa a a----⋅+-=222131(1)(1)1a a a a aa a a-+-+-⋅+-=11(1)(1)1a aa a a+-⋅+-=1a,原式.【点拨】本题主要考查分式的化简求值,熟练掌握分式的通分和约分,是解题的关键.39.3【分析】先算零指数幂,绝对值,负整数指数幂以及锐角三角函数,再算加减法,即可求解.解:原式=12+-=3.【点拨】本题主要考查实数的混合运算,熟练掌握零指数幂,绝对值,负整数指数幂以及锐角三角函数,是解题的关键.40.11【分析】根据非零实数0二次根式、负整数次幂、特殊角三角函数值根据实数加减混合运算法则计算即可.解:原式=191=11-+.【点拨】本题主要考查非零实数0次幂、二次根式、负整数次幂、特殊角三角函数值根据实数加减混合运算法则,正确掌握每个知识点是解决本题的关键.41.0.【分析】先化简绝对值、计算特殊角的正弦值、零指数幂,再计算实数的混合运算即可得.解:原式121-=,==.【点拨】本题考查了化简绝对值、特殊角的正弦值、零指数幂等知识点,熟练掌握各运算法则是解题关键.42.22x ;25【分析】根据分式混合运算的法则进行化简计算,然后代入条件求值即可.解:原式()()()2221212x x x x x x ⎡⎤+-=+⎢⎥+-+⎢⎥⎣⎦ 21221x x x x x -⎛⎫=+ ⎪++-⎝⎭ 22121x x x -=+- ()21121x x x -=+- 22x =+ 将3x =代入得:原式22325==+. 【点拨】本题考查分式的化简求值问题,掌握分式混合运算法则是解题关键. 43.5.【分析】先化简绝对值、特殊角的正弦值、零指数幂、二次根式的乘法,再计算实数的混合运算即可得.解:原式21=++14=+, 5=. 【点拨】本题考查了化简绝对值、特殊角的正弦值、零指数幂、二次根式的乘法等知识点,熟练掌握各运算法则是解题关键.44.1a ,12【分析】先根据分式的混合运算法则化简,再取使得分式有意义的a 的值代入计算即可.解:2221211a a a a a a -+⎛⎫÷- ⎪-+⎝⎭ =()()()()21112111a a a a a a a a -+⎡⎤÷-+-⎢+⎣+⎥⎦ =()()()()211111a a a a a a +-+⨯-- =1a由原式可知,a 不能取1,0,-1,∴a =2时,原式=12.【点拨】此题考查了分式的化简求值,解题的关键是记住分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.45.0【分析】分别化简各数,再作加减法.解:()03.1414sin 60π-+︒=114-+=11-+=0【点拨】本题考查了实数的混合运算,特殊角的三角函数值,解题的关键是掌握运算法则.46.1;11x --(答案不唯一) 【分析】小括号先通分合并,再将除法变乘法并因式分解即可约分化简,再结合分式有意义的条件和除数不为0,即可代值计算. 解:原式()()()()()()2211111=1111111x x x x x x x x x x x +++-⨯=⨯=++-++-- 代数式有意义,分母和除数不为0∴()()110x x +-≠即1x ≠±∴当0x =时,原式=111101x ==---(答案不唯一). 【点拨】本题考察分式的化简求值、分式有意义的条件、因式分解和分母有理化,属于基础题,难度不大.解题的关键是掌握分式的运算法则和分式有意义的条件.47.3【分析】依次计算“0次方”、tan 60︒等,再进行合并同类项即可.解:原式=()132123--+=-+=【点拨】本题综合考查了非零数的零次幂、特殊角的三角函数、负整数指数幂以及二次根式的化简等内容,解决本题的关键是牢记相关计算公式等,本题易错点为对112-⎛⎫-- ⎪⎝⎭的化简,该项出现的“ -”较多,因此符号易出错,因此要注意.48.1x +【分析】先算分式的加法,再算乘法运算,最后代入求值,即可求解. 解:原式()()111111x x x x x x+--+=⋅=+-.当1x =时,原式【点拨】本题主要考查分式的化简求值,熟练掌握分式的通分和约分,是解题的关键.49.-5【分析】分别化简算术平方根、绝对值和有理数的乘方,然后再进行加减运算即可得到答案.223--229=+-5=-.【点拨】此题主要考查了实数的混合运算,熟练掌握运算法则是解答此题的关键. 50.(1)4;(2)ab【分析】(1)分别化简各数,再作加减法;(2)先通分,计算加法,再将除法转化为乘法,最后约分计算.解:(1)013|tan603⎛⎫-++︒ ⎪⎝⎭=13+=4;(2)()11a b a b ⎛⎫+÷+ ⎪⎝⎭ =()a b a b ab ++÷=()ab a b a b+⨯+ =ab 【点拨】本题考查了实数的混合运算,特殊角的三角函数值,零指数幂,分式的混合运算,解题的关键是熟练掌握运算法则.51.﹣1.【分析】根据零指数幂运算法则、绝对值符号化简、特殊角的三角函数值代入计算,然后根据同类二次根式合并求解即可.解:()020212tan 60π--︒=(12-=12-+=﹣1.【点拨】本题主要考查了实数的综合运算能力,是中考题中常见的计算题型.熟练掌握零指数幂、特殊角的三角函数值、绝对值化简方法,同类二次根式是解题关键.52.42,23x --+ 【分析】小括号内先通分计算,将除法变成乘法并因式分解,根据乘法法则即可化简,再代值计算即可. 解:原式2242(2)()22(2)(2)x x x x x x x --=-⨯--+- 4222x x x --=⨯-+ 42x =-+ 当4x =时,原式42423=-=-+. 【点拨】本题考察分式的化简求值,难度不大,属于基础题型.解题的关键在于熟悉运算法则和因式分解.53.3【分析】先进行零指数幂和负整数指数幂,余弦函数值计算,再计算二次根式的乘法,合并同类项即可. 解:011(2021)()2cos 452π--+-︒,122=+-3=【点拨】本题主要考查零指数幂和负整数指数幂,特殊角三角函数值,掌握零指数幂和负整数指数幂的运算法则,特殊角锐角三角函数值是解题的关键.54.6【分析】原式分别利用乘方,特殊角的三角函数值,零指数幂,负整数指数幂,乘法法则分别计算,再作加减法.解:201tan 452(3)1)2(6)23-︒-++-+⨯- =1191422++-- =6【点拨】此题考查了实数的混合运算,熟练掌握运算法则是解本题的关键.55.1【分析】直接利用完全平方差公式展开及平方差公式展开后,合并同类项化简,再将16x =代入进去计算. 解:原式229611962x x x x =-++-=-+ 当16x =时,原式16216=-⨯+=. 故答案是:1.【点拨】本题考查了代数式的化简求值,解题的关键是:先利用完全平方差公式,平方差公式,合并同类项运算法则化简,然后代值计算.56.1【分析】利用乘方的意义,二次根式的化简,特殊角的函数值,绝对值的化简,化简后合并计算即可解:原式142=-+12=-+ 1=.【点拨】本题考查了二次根式的化简,特殊角的三角函数值,绝对值的化简等知识,熟练运用各自的运算法则化简是解题的关键.57.(1)-6;(2)22625a a -+.【分析】(1)直接利用有理数乘法法则以及绝对值的性质、二次根式的性质、零指数幂的性质分别化简得出答案;(2解:(1)()0438⨯-+- 12831=-+-+6=-;(2)()()215282a a a -++ 2210254a a a a =-+++22625a a =-+.【点拨】此题主要考查了实数运算、整式的混合运算,正确掌握相关运算法则是解题关键.58.1210x -,-22【分析】利用平方差公式和完全平方公式,进行化简,再代入求值,即可求解. 解:原式=2241(4129)x x x ---+=22414129x x x --+-=1210x -,当x =-1时,原式=()12110⨯--=-22.【点拨】本题主要考查整式的化简求值,熟练掌握完全平方公式和平方差公式,是解题的关键.59.-4【分析】根据已知求出xy =-2,再将所求式子变形为()xy x y -,代入计算即可. 解:∵2x y -=, ∴1121y x x y xy xy---===, ∴2xy =-,∴()()22224xy x x y xy y ==---⨯=-.【点拨】本题考查了代数式求值,解题的关键是掌握分式的运算法则和因式分解的应用.60.12.【分析】根据零指数幂,负整指数幂,去括号法则,特殊角的三角函数值化简,然后再计算即可.解:0120211423cos3043144232144312=.【点拨】本题考查了零指数幂,负整指数幂,去括号法则,特殊角的三角函数值等知识点,熟悉相关知识点是解题的关键61.(1)223++a ab b ;(2)-31x x + 【分析】(1)根据单项式乘以多项式以及完全平方公式计算即可;(2)利用分式的混合运算法则进行计算即可.解:(1)2(23)()a a b a b ++-2222+3+2+=a ab a ab b -22=3++a ab b(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭()()()222+3-3+3=11+x x x x x x x ⎛⎫-÷ ⎪++⎝⎭()()()2+3-31=31x x x x x +++ -3=1x x + 【点拨】本题考查了整式的混合运算和分式的混合运算,熟练掌握运算法则是解题的关键.62.1-【分析】利用算术平方根、绝对值的性质、零指数幂分别计算各项即可求解. 解:原式5711=-+=-.【点拨】本题考查实数的混合运算,掌握算术平方根、绝对值的性质、零指数幂是解题的关键.63.2020【分析】先计算绝对值、零指数幂和算术平方根,最后计算加减即可;解:0|2021|(3)-+-202112=+-,2020=.【点拨】本题主要考查实数的混合运算,解题的关键是掌握实数的混合运算顺序及相关运算法则.64.2.【分析】直接利用零指幂的性质、绝对值的性质、特殊角的三角函数值分别化简得出答案.解:()24π345+-︒--︒313=+-+ 3131=+-+2=.【点拨】此题主要考查了实数运算,正确化简各数是解题关键.65.11x - 【分析】先将括号内的项进行通分化简,再分式的除法法则,结合平方差公式因式分解,化简,最后代入数值解题即可.解:原式=2122(1)(1)x x x x x +-+⋅++- 1(1)(1)x x x +=+-。
初三数学计算题练习2附答案

方程不等式专题测试学校:___________姓名:___________班级:___________考号:___________一、解答题1.先化简,再求值:211111x x x x ⎛⎫+÷ ⎪+--⎝⎭,其中x 是6的平方根. 【答案】21x +,7【分析】根据分式的混合运算法则把原式化简,代入计算即可.【详解】 解:原式(1)(1)(1)(1)(1)(1)x x x x x x x ⎡⎤-++=⋅+-⎢⎥+-⎣⎦ 21(1)(1)(1)(1)x x x x x x x -++=⋅+-+- 21x =+.∵x 是6的平方根,∴26x =,∴原式617=+=.【点睛】本题考查的是分式的化简求值,掌握分式的混合运算法则是解题的关键. 2.材料1:因为无理数是无限不循环小数,所以无理数的小数部分我们不可能全部写出来.比如:π等,而常用的“…”或者“≈”的表示方法都不够百分百准确. 材料2:2.5的整数部分是2,小数部分是0.5,小数部分可以看成是2.5−2得来的.材料3:任何一个无理数,都夹在两个相邻的整数之间,如23<<,是因为根据上述材料,回答下列问题:(1的整数部分是 ,小数部分是 .(2)5+5a b <+,求a b +的值.(3)已知3x y +,其中x 是整数,且0<y <1,求x +4y 的倒数.【答案】(1)44;(2)13;(3【分析】(1(2(3x的值,从而表示出y,求出x+4y的结果,再求x+4y的倒数即可.【详解】解:(1)<∴45<,4,故答案为:44;(2),∴12<<,∴67<,∵5<,a b∴a=6,b=7,∴a+b=13;(3)∵12,∴1+3<2+3,∴4<5,∴x=4,y1,x+4y)∴x+4y【点睛】此题主要考查了不等式的性质,以及估算无理数的大小,a≥0)的无理数的整数部分时,常用的方法是“夹逼法”,其依据是平方和开平方互为逆运算.在应用“夹逼法”估算无理数时,关键是找出位于无理数两边的平方数,则无理数的整数部分即为较小的平方数的算术平方根.3.计算:20-211(3).93⎛⎫--+--- ⎪⎝⎭ 【答案】8.9【分析】先计算0次幂和负指数幂及绝对值和有理数的乘方运算,然后运用有理数的加减法法则计算即可.【详解】解:()20211393-⎛⎫--+--- ⎪⎝⎭ 1111999=-+- 8=9. 【点睛】题目主要考查负指数幂、0指数幂、有理数的乘方,去绝对值,有理数的加减混合运算,熟练掌握各运算法则是解题关键.4.先化简再选择一个你喜欢的数代入求值:(22x x x x --+)÷42x x -. 【答案】12x +,x =1,原式=13 【分析】先根据分式混合运算的法则把原式进行化简,再代入合适的x 的值代入进行计算即可.【详解】 解:原式=(2)(2)(2)(2)x x x x x x +--+-÷42x x - =4(2)(2)x x x +-×24x x - =12x +, 当x =1时,原式=112+=13. 【点睛】本题考查了分式的化简求值及使分式有意义的条件,熟练掌握分式的运算法则和分式有意义的条件是解答本题的关键,注意所取x 的值要使原分式有意义.5.已知10x -+.(1)求x 与y 的值;(2)求x +y 的算术平方根.【答案】(1)1x =,3y =;(2)2【分析】(1)根据绝对值和平方根的非负性求出x 与y 的值;(2)先计算x y +的值,即可得出x y +的算术平方根.【详解】(1)由题可得:10250x x y -=⎧⎨-+=⎩, 解得:13x y =⎧⎨=⎩, ∴1x =,3y =;(2)134x y +=+=,∵4的算术平方根为2,∴x y +的算术平方根为2.【点睛】本题考查绝对值与平方根的性质,以及算术平方根,掌握绝对值和平方根的非负性是解题的关键.6.(1)化简:()()11y y +--(2(3)解分式方程:13211x x -=--【答案】(1)-y 2-2y -1;(2)(3)x =3 【分析】 (1)变形后根据完全平方公式计算;(2)先逐项化简,再合并同类二次根式;(3)两边都乘以x -1,化为整式方程求解,再检验.【详解】解:(1)()()11y y +--=-()()1+1y y +=-()21y +=-y 2-2y -1;(2==(3)13211x x-=--两边都乘以x-1,得1-2(x-1)=-3,1-2x+2=-3,解得x=3,检验:当x=3时,x-1≠0,∴x=3是分式方程的解.【点睛】本题考查了全平方公式,二次根式的加减混合运算,以及解分式方程,熟练掌握各知识点是解答本题的关键.7.计算:(11(2)【答案】(1)4;(2)-【分析】(1)先计算二次根式的加法与除法,再计算有理数的减法即可得;(2)先计算二次根式的乘法、分母有理化,再计算二次根式的减法即可得.【详解】解:(1)原式1=151=-4=;(2)原式6==【点睛】本题考查了二次根式的四则混合运算,熟练掌握运算法则是解题关键.8.计算:23122x x x x -----. 【答案】1【分析】直接利用分式的加减运算法则计算即可.【详解】 解:23122x x x x -----, 2312x x x --+=-, 22x x -=-, 1=.【点睛】本题主要考查了分式的加减运算,解题的关键是正确掌握运算法则.9.(101π+.(2)计算:(2--. (3)先化简,再求值:22131693x x x x x x x -+-÷+-+-,其中x = (4)解方程:3111x x x -=-+.【答案】(1)2;(2)22;(3)1x (4)2. 【分析】(1)先根据立方根、算术平方根、绝对值、零次幂的知识化简,然后再计算即可; (2)先运用二次根式的乘方法则和平方差公式计算,然后再运用二次根式的加减运算法则计算即可;(3)先运用分式的四则混合运算法则化简,然后代入计算即可;(4)按照解分式方程的步骤解答即可.【详解】解:(101π+=211-++(2)(2-- =2453-+=22;(3)22131693x x x x x x x -+-÷+-+- =()()2133113x x x x x x ---⨯++- =()1111x x x +++ =()11x x x ++ =1x当x 1x == (4)3111x x x -=-+ x (x +1)-(x +1)(x -1)=3(x -1)x 2+x -x 2+1=3x -3-2x =-4x =2.经检验x =2是分式方程的解.【点睛】本题主要考查了实数的运算、分式的化简求值、解分式方程等知识点,灵活运用相关运算法则成为解答本题的关键.10.有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负来表示,记录如下:(1)20筐白菜中,最重的一筐比最轻的一筐重 千克;(2)与标准重量比较,20筐白菜总计超过或不足多少千克?(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?【答案】(1)5;(2)超过4千克;(3)1310.4元.【分析】(1)根据最重的一筐与最轻的一筐相减即可;(2)将20筐白菜的重量相加计算即可;(3)将总质量乘以价格解答即可.【详解】解:(1)2-(-3)=2+3=5(千克),故答案为:5;(2)-3×1+(-2)×4+(-1.5)×2+0×3+1×2+2×8 =-3-8-3+0+2+16=4(千克),答:与标准重量比较,20筐白菜总计超过4千克;(3)这20筐白菜的总质量为25×20+4=504(千克),则504×2.6=1310.4(元),答:出售这20筐白菜可卖1310.4元.【点睛】本题考查有理数乘法和加法运算的应用,正负数的意义.解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.11.计算:()()012020sin 60tan 30--+︒-︒【答案】3【分析】先根据零指数幂、负整数指数幂、绝对值的性质,特殊角锐角三角函数值化简,再合并,即可求解.【详解】解:()()012020sin 60tan 30--+︒-︒112-=++⎝⎭12= 3= .【点睛】本题主要考查了零指数幂、负整数指数幂、绝对值的性质,特殊角锐角三角函数值等知识,熟练掌握零指数幂、负整数指数幂、绝对值的性质,特殊角锐角三角函数值是解题的关键.12.计算:(1)3622x x x +++; (2)224b ab a -⎛⎫÷ ⎪⎝⎭. 【答案】(1)3;(2)34a【分析】(1)根据同分母分式加法法则计算即可;(2)根据分式的乘方和除法法则计算即可.【详解】解:(1)原式362x x +=+, ()3+2+2x x =,3=.(2)原式2224b ab a =÷, 2224a ab b =⋅, 34a =.【点睛】本题考查了分式的运算,解题关键是熟练掌握分式运算法则,准确计算.13.如图,直线AB 上顺次有A 、B 、M 三点,线段AB =8,AM =50.直角三角形CDE 的一条直角边CD 在线段BM 上,点C 恰好为线段BD 的中点,且CD =6.若三角形CDE 以每秒1个单位长度的速度向右运动,当点D 到达点M 时三角形停止运动;同时线段AB 以每秒3个单位长度的速度向右运动,当点B 到达点M 时线段停止运动.设三角形CDE 的运动时间为t 秒.(1)当点B 与点D 第一次重合时,求t 的值;(2)当点D 为线段CB 中点时,直接写出t 的值;(3)连接AE 和BE ,当ADE 的面积是BDE 面积的3倍时,直接写出t 的值.【答案】(1)6;(2)9或24:(3)4或7【分析】以A 为原点,在数轴上各点表示各点并表示距离,根据题意列方程求解.(1)点B 与点D 第一次重合时,列方程为8320t t +=+;解方程即可.(2)D 为BC 中点时,6BD CD ==时,有两种情况;①点B 停止运动前,列方程为83(20)6t t +-+=,解得1t ;②点B 停止运动,列方程为50(20)6t -+=,解得2t . (3)设点E 到AM 的距离为h ,则12ADE S AD h =⋅,12BDE S BD h =⋅,3ADE BDE S S =有3AD BD =,列方程20332083t t t t +-=+--解得t 即可.【详解】(1)解:t 的值为6.以A 为原点,AM 为正方向,画数轴 由题意知83B t =+,20D t =+当点B 与点D 第一次重合时,有8320+t t += 解得6t =∴ 当点B 与点D 第一次重合时,t 的值为6. (2)解:t 的值为9或24.以A 为原点,AM 为正方向,画数轴 由题意知83B t =+,20D t =+①点B 停止运动前,有83(20)6t t +-+= 解得19t =②点B 停止运动,有50(20)6t -+=解得224t =∴当D 点为BC 中点时, t 的值为9或24. (3)解:t 的值为4或7.以A 为原点,AM 为正方向,画数轴 由题意知3A t =, 83B t =+,20D t =+ 203AD t t ∴=+-, 2083BD t t =+-- 设点E 到AM 的距离为h 则12ADE SAD h =⋅,12BDE S BD h =⋅ 3ADE BDE S S =3AD BD ∴=20332083t t t t ∴+-=+--解得14t =,27t =∴当△ADE 的面积是△BDE 面积的3倍时,t 的值为4或7.【点睛】本题考查了数轴上数与距离的表示,一次方程,去绝对值等知识点.解题的关键与难点在于建数轴,通过数轴表示距离.去绝对值是易错点.14.设M =2269324a a a a a -+-÷+-. (1)化简代数式M ;(2)请在以下四个数中:2,﹣2,3,﹣3,选择一个合适的数代入,求M 的值.【答案】(1)a 2﹣5a +6(2)30【分析】(1)根据分式的除法法则计算即可;(2)根据分式有意义的条件确定a 的值,代入计算即可.(1)解: M =2(3)2a a -+×(2)(2)3a a a +-- =(a ﹣3)(a ﹣2)=a 2﹣5a +6;(2)解:由题意得,a ≠±2,a ≠±3,当a =﹣3时,M =(﹣3)2﹣5×(﹣3)+6=30.【点睛】本题考查的是分式的化简求值,掌握分式的混合运算法则、分式有意义的条件是解题的关键.15.(1)请你把32,(-2)3,0,12-,110-这五个数在数轴上表示出来. (2)将上列各数用“<”号连接起来:____________________________.【答案】(1)见解析;(2)()-<-<<-<3211203102【分析】(1)先计算有理数的乘方和绝对值,然后在数轴上表示出这些数即可;(2)根据数轴上的点表示的数,左边的数小于右边的数进行求解即可.【详解】(1)239=,()328-=-,1122-=, 数轴表示如下所示:(2)由数轴可知:()3211203102-<-<<-<. 【点睛】本题主要考查了有理数的乘方,绝对值,用数轴表示有理数,利用数轴比较有理数的大小,解题的关键在于能够熟练掌握有理数与数轴的关系.16.如图所示,数轴上两点A ,B ,动点P 从点O 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t 秒.(1)写出线段AB 的长_______;(2)当1t =时,线段PA 的长是______;此时线段PA 与线段PB 的数量关系是_____;(3)当2PA PB =时,求t 的值.【答案】(1)8;(2)4,P A =PB ;(3)t 的值为53或7. 【分析】(1)根据两点间的距离公式即可求解;(2)先求出当t =1时,P 点对应的有理数为2×1=2,再根据两点间的距离公式即可求出P A 、PB 的长,继而得解;(3)先求出P 点对应的数为2t ,再根据P A =2PB 列出方程,即可求解.【详解】解:(1)∵A 点对应的数为-2,B 点对应的数为6,∴线段AB 的长为6-(-2)=8,故答案为:8;(2)当t =1时,P 点对应的有理数为2×1=2, ∴线段P A 的长是2-(-2)=4;线段PB 的长是6-2=4;∴P A =PB ;故答案为:4,P A =PB ;(3)∵点P 从点O 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t 秒,∴P 点对应的数为2t ,则P A =2t -(-2)=2t +2,PB =|6-2t|;∵P A =2PB , ∴22262t t +=-,即2t +2=2(6-2t )或2t +2=-2(6-2t ) ,解得:t =53或t =7. ∴t 的值为53或7. 【点睛】本题考查了一元一次方程的应用和数轴,解题的关键是掌握点的移动与点所表示的数之间的关系.17.根据材料完成问题:在含有两个字母的式子中,任意交换两个字母的位置,式子的值始终保持不变,像这样的式子我们称之为对称式,如:11a b +,22a b +,请解决下列问题: ①22a b - ;②22a b ③22a b这3个式子中只有1个属于对称式: (请填序号); (2)已知2()()--=++x a x b x mx n①若1m =,2n =-,求对称式22a b +的值;②若3m =-,1n =,当22a k b k a b--+>0时,求k 的取值范围. 【答案】(1)②;(2)①5;②k 1<.【分析】(1)根据对称式的定义进行判断;(2)①根据已知m =a +b ,n =ab ,整体代入即可求解;②将对称式化简后整理后,解不等式即可求解;【详解】解:(1)①a 2-b 2≠b 2-a 2;②a 2b 2=b 2a 2;③当a ≠0时,由定义知属于对称式的是②,故答案为:②;(2)∵(x -a )(x -b )=x 2-(a +b )x +ab =x 2+mx +n ,∴m =-(a +b ),n =ab ,∴a 2+b 2=(a +b )2-2ab =m 2-2n ,①当m =1,n =-2时,a 2+b 2=12-2⨯(-2)=5; ②∵2222()()0a k b k a b kb ab ka ab a b k a b a b ab ab---+-+-++==>, 当m =-3,n =1时,a +b =3,ab =1, ∴31301k ⨯->, 解得:k 1<.【点睛】本题考查了分式的化简求值,完全平方公式,解一元一次不等式,新定义等知识,解决本题的关键是理解阅读材料,掌握分式计算法则及完全平方公式.18.计算:1201(2)(3.14)|1|3π-⎛⎫-+---+ ⎪⎝⎭. 【答案】7【分析】根据实数的性质化简即可求解.【详解】解:原式4113=+-+ 7=【点睛】此题主要考查实数的混合运算,解题的关键是熟知负指数幂的运算法则.19.先化简,再求值:(x +21x x +)÷(x +1),其中x .【答案】1x x +【分析】根据分式的加法和除法可以化简题目中的式子,然后将x 的值代入化简后的式子即可解答本题.【详解】(x +21x x +)÷(x +1) =22111x x x x ++⋅+ =2(1)11x x x +⋅+=1x x +, 当x =2时,原式=212+=222+. 【点睛】 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.20.先化简:,然后,m 在1,2,3中选择一个合适的数代入求值.【答案】26--m ,-8【分析】先按照分式的混合计算法则进行化简,然后根据分式有意义的条件求出m 的值,最后代值计算即可.【详解】解:532224m m m m ⎛⎫ ⎪⎝-÷⎭++-- ()24532222m m m m m ⎛⎫--=-÷ ⎪---⎝⎭ ()222923m m m m--=⋅-- ()()()332223m m m m m+--=⋅-- ()23m =-+26m =--,∵分式要有意义且除数不为0,∴, ∴,∴当1m =时,原式2168=-⨯-=-.【点睛】本题主要考查了分式的化简求值,分式有意义的条件,解题的关键在于能够熟练掌握分式的相关计算法则.。
2022-2023学年中考数学专项练习(基础+提优+答案解析)6 分式及其运算

分式及其运算一、基础过关练1.(2022·湖南怀化·中考真题)代数式25x ,1π,224x +,x 2﹣23,1x ,12x x ++中,属于分式的有( )A .2个B .3个C .4个D .5个2.(2022·四川绵阳·中考二模)下列分式属于最简分式的是( ) A .265xyxB .x y y x--C .22x y x y++D .2293x y x y-+3.(2022·广东·中考三模)若分式55m m --的值为零,则m =( ) A .5-B .5C .5±D .04.(2022·山西·中考真题)化简21639a a ---的结果是( ) A .13a + B .3a - C .3a + D .13a -5.(2022·辽宁丹东·中考真题)在函数y x 的取值范围是( ) A .x ≥3B .x ≥﹣3C .x ≥3且x ≠0D .x ≥﹣3且x ≠06.(2022·山东威海·中考真题)试卷上一个正确的式子(11a b a b++-)÷★=2a b +被小颖同学不小心滴上墨汁.被墨汁遮住部分的代数式为( ) A .aa b- B .a ba- C .a a b+ D .224aa b -7.(2022·湖北襄阳·中考真题)化简分式:ma mba b a b+++=_____. 8.(2022·贵州黔西·中考二模)已知23x y =,则x y y+=______. 9.(2022·江苏南通·中考真题)分式22x -有意义,则x 应满足的条件是___________.10.(2022·湖南娄底·中考模拟)函数y =x 的取值范围是______. 11.(2022·内蒙古·包头市中考三模)2241244a a a a a -⎛⎫-÷= ⎪+++⎝⎭______________. 12.(2022·贵州遵义·模拟预测)已知a 为24a ≤≤范围的整数,则22421244a a a a a a a a -+-⎛⎫÷- ⎪--+⎝⎭的值是______.13.(2022·陕西·西安市中考三模)分式化简:221441111a a a a a a --+⎛⎫-+÷+⎪++⎝⎭.14.(2022·辽宁抚顺·中考模拟)先化简,再求值:222364(1)244a a a a a a -+--÷+++,其中112cos 45()2a -=+.15.(2022·湖南娄底·中考真题)先化简,再求值:3242244x x x x x ⎛⎫++÷ ⎪--+⎝⎭,其中x 是满足条件2x ≤的合适的非负整数.16.(2022·贵州·仁怀市中考二模)先化简分式2222112111a a a a a a a ⎛⎫+++-÷ ⎪---⎝⎭,再从-2,-1,14个数中选择一个合适的数作为a 的值代入求值.17.(2022·湖北恩施·中考二模)已知2021x =,2022y =,求222225454x xy y x y x yx xy x y x+++-÷+--的值.18.(2022·甘肃嘉峪关·中考三模)先化简,再求值:2222222a b a b a ab b b a a ab ⎛⎫-+÷ ⎪-+--⎝⎭,其中a ,b 满足0b =.19.(2022·黑龙江哈尔滨·中考真题)先化简,再求代数式21321211x x x x x -⎛⎫-÷⎪--+-⎝⎭的值,其中2cos451x =︒+.20.(2022·湖南·中考真题)先化简2121(1)1221a a a a a ---÷+--+,再从1,2,3中选一个适当的数代入求值.二、能力提升练21.(2022·黑龙江绥化·2x -在实数范围内有意义,则x 的取值范围是( ) A .1x >-B .1x -C .1x -且0x ≠D .1x -且0x ≠22.(2022·四川南充·中考真题)已知0a b >>,且223a b ab +=,则2221111a b a b ⎛⎫⎛⎫+÷- ⎪ ⎪⎝⎭⎝⎭的值是( )A B .C D .23.(2022·重庆·中考二模)阅读材料:在处理分数和分式的问题时,有时由于分子大于分母,或分子的次数高于分母的次数,在实际运算时难度较大,这时,我们可将分数(分式)拆分成一个整数(整式)与一个真分数(真分式)的和(差)的形式,通过对它的简单分析来解决问题,我们称这种方法为分离常数法,此法在处理分式或整除问题时颇为有效.将分式分离常数可类比假分数变形带分数的方法进行.如:()()21231223111a a a a a a a a a a a -+-+--+-+==+=---a ﹣121a +-,这样,分式就拆分成一个分式2a 1-与一个整式a ﹣1的和的形式,下列说法正确的有( )个.①若x 为整数,42x x ++为负整数,则x =﹣3;②6226182x x +≤+<9;③若分式25932x x x +-+拆分成一个整式与一个真分式(分子为整数)的和(差)的形式为:5m ﹣1116n +-(整式部分对应等于5m ﹣11,真分式部分对应等于16n -),则m 2+n 2+mn 的最小值为27. A .0B .1C .2D .324.(2022·浙江中考三模)若要使得分式211x -有意义,则x 的取值范围为_______.25.(2022·北京市中考一模)在函数0(4)y x =+-中,自变量x 的取值范围是___________. 26.(2022·四川成中考模拟)已知非零实数x ,y 满足1xy x =+,则3x y xy xy -+的值等于_________.27.(2022·四川达州·0.618≈这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设a =b =11111S a b =+++,2222211S a b =+++,…,10010010010010011S a b =+++,则12100S S S +++=_______.28.(2022·湖北·广水市中考二模)对于实数0x >,规定()1=+xf x x ,例如()222213f ==+,111212312f ⎛⎫== ⎪⎝⎭+,那么计算1111(1)(2)(3)(2020)2020201920182f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋯+++++⋯+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的结果是______.29.(2022·北京朝阳·中考模拟)(1)计算:23(3)3x xx x--- (2)计算:22111121x x x x x x x ++⎛⎫+÷ ⎪---+⎝⎭ (3)先化简,再求值:已知ab =3,求222443a ab b b a b a b a b ⎛⎫++÷-- ⎪--⎝⎭的值.答案与解析一、基础过关练1.(2022·湖南怀化·中考真题)代数式25x ,1π,224x +,x 2﹣23,1x ,12x x ++中,属于分式的有( )A .2个B .3个C .4个D .5个2.(2022·四川绵阳·中考二模)下列分式属于最简分式的是( ) A .265xyxB .x y y x--C .22x y x y ++D .2293x y x y-+A .5-B .5C .5±D .0【答案】A【分析】根据分式的值为零的条件列式计算即可.【详解】解:由题意得:|m |−5=0且m −5≠0, 解得:m =−5, 故选:A .【点睛】本题考查的是分式的值为零的条件,掌握分式值为零的条件是分子等于零且分母不等于零是解题的关键.4.(2022·山西·中考真题)化简21639a a ---的结果是( ) A .13a + B .3a - C .3a + D .13a -A .x ≥3B .x ≥﹣3C .x ≥3且x ≠0D .x ≥﹣3且x ≠0【答案】D【分析】根据二次根式的被开方数是非负数、分母不为0列出不等式组,解不等式组即可得到答案. 【详解】解:由题意得:x +3≥0且x ≠0, 解得:x ≥﹣3且x ≠0, 故选:D .【点睛】本题考查的是函数自变量的取值范围的确定,掌握二次根式的被开方数是非负数、分母不为0是解题的关键.6.(2022·山东威海·中考真题)试卷上一个正确的式子(11a b a b++-)÷★=2a b +被小颖同学不小心滴上墨汁.被墨汁遮住部分的代数式为( ) A .aa b- B .a ba- C .a a b+ D .224aa b -7.(2022·湖北襄阳·中考真题)化简分式:ma mba ba b+++=_____. 8.(2022·贵州黔西·中考二模)已知3y =,则y=______. 【详解】解:9.(2022·江苏南通·中考真题)分式22x -有意义,则x 应满足的条件是___________.【答案】0x ≥且3x ≠##x ≠3且x ≥0【分析】根据二次根式中的被开方数是非负数与分母不能为0进行求解. 【详解】由题意知,0x ≥且30x -≠, 解得,0x ≥且3x ≠, 故答案为:0x ≥且3x ≠.【点睛】本题考查函数自变量的取值范围,自变量的取值范围必须使含有自变量的表达式都有意义,①当函数表达式是分式时,考虑分式的分母不能为0;②当函数表达式是二次根式时,被开方数非负. 11.(2022·内蒙古·包头市中考三模)2241244a a a a a -⎛⎫-÷= ⎪+++⎝⎭______________.12.(2022·贵州遵义·中考模拟)已知a 为24a ≤≤范围的整数,则22421244a a a a a a a a -+-⎛⎫÷- ⎪--+⎝⎭的值是______. 【答案】-113.(2022·陕西·西安市中考三模)分式化简:2214411 11a a aaa a--+⎛⎫-+÷+⎪++⎝⎭.14.(2022·辽宁抚顺·中考模拟)先化简,再求值:222364(1)244a a aa a a-+--÷+++,其中112cos45()2a-=+.分式化简求值的方法.15.(2022·湖南娄底·中考真题)先化简,再求值:3242244x x x x x ⎛⎫++÷ ⎪--+⎝⎭,其中x 是满足条件2x ≤的合适的非负整数. x16.(2022·贵州·仁怀市中考二模)先化简分式2222112111a a a aa a a ⎛⎫+++-÷ ⎪---⎝⎭,再从-2,-1,14个数中选择一个合适的数作为a 的值代入求值.17.(2022·湖北恩施·中考二模)已知2021x =,2022y =,求225454x xy y x y x yx xy x y x+++-÷+--的值.18.(2022·甘肃嘉峪关·中考三模)先化简,再求值:2222222a b a b a ab b b a a ab ⎛⎫-+÷ ⎪-+--⎝⎭,其中a ,b 满足0b =.19.(2022·黑龙江哈尔滨·中考真题)先化简,再求代数式21211x x x x ⎛⎫-÷⎪--+-⎝⎭的值,其中2cos451x =︒+.20.(2022·湖南·中考真题)先化简2121(1)1221a a a a a ---÷+--+,再从1,2,3中选一个适当的数代入求值.二、能力提升练21.(2022·黑龙江绥化·2x -在实数范围内有意义,则x 的取值范围是( ) A .1x >- B .1x -C .1x -且0x ≠D .1x -且0x ≠【答案】C【分析】根据二次根式被开方数不能为负数,负整数指数幂的底数不等于0,计算求值即可; 【详解】解:由题意得:x +1≥0且x ≠0, ∴x ≥-1且x ≠0, 故选: C .【点睛】本题考查了二次根式的定义,负整数指数幂的定义,掌握其定义是解题关键.22.(2022·四川南充·中考真题)已知0a b >>,且223a b ab +=,则2221111a b a b ⎛⎫⎛⎫+÷- ⎪ ⎪⎝⎭⎝⎭的值是( )A B .C D .23.(2022·重庆·中考二模)阅读材料:在处理分数和分式的问题时,有时由于分子大于分母,或分子的次数高于分母的次数,在实际运算时难度较大,这时,我们可将分数(分式)拆分成一个整数(整式)与一个真分数(真分式)的和(差)的形式,通过对它的简单分析来解决问题,我们称这种方法为分离常数法,此法在处理分式或整除问题时颇为有效.将分式分离常数可类比假分数变形带分数的方法进行.如:()()21231223111a a a a a a a a a a a -+-+--+-+==+=---a ﹣121a +-,这样,分式就拆分成一个分式2a 1-与一个整式a﹣1的和的形式,下列说法正确的有()个.①若x为整数,42xx++为负整数,则x=﹣3;②6226182xx+≤+<9;③若分式25932x xx+-+拆分成一个整式与一个真分式(分子为整数)的和(差)的形式为:5m﹣1116n+-(整式部分对应等于5m﹣11,真分式部分对应等于16n-),则m2+n2+mn的最小值为27.A.0B.1C.2D.3212x为负整数,3,x∴=-故①的结论正确;∵( 226182xx++=(x −1)2+27, ∵(x −1)2≥0,∴m 2+n 2+mn 有最小值为27, ∴③的结论正确, 故选:D .【点睛】本题主要考查了分式的加减法,整式的加减法,本题是阅读型题目,理解并熟练应用题干中的方法是解题的关键.24.(2022·浙江·中考三模)若要使得分式211x -有意义,则x 的取值范围为_______.【答案】x ≠±1【分析】根据分式有意义的条件即可求出答案. 【详解】解:由题意可知:|x 2-1|≠0, ∴x 2-1≠0, ∴x ≠±1, 故答案为:x ≠±1.【点睛】本题考查分式的有意义条件,解题的关键是熟练运用分式有意义的条件. 25.(2022·北京市中考一模)在函数0(4)y x =+-中,自变量x 的取值范围是___________. 【答案】3x >-且4x ≠【分析】根据二次根式有意义的条件、分母不为0、零指数幂的概念列出不等式,解不等式,得到答案. 【详解】解:由题意得,3040x x +>-≠,, 解得,3x >-且4x ≠, 故答案为:3x >-且4x ≠.【点睛】本题考查的是函数自变量的取值范围的确定,掌握二次根式有意义的条件、零指数幂的概念是解题的关键.26.(2022·四川成都·中考模拟预测)已知非零实数x ,y 满足1xy x =+,则3x y xy xy-+的值等于_________.27.(2022·四川达州·0.618≈这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设a =b =11111S a b =+++,2222211S a b =+++,…,10010010010010011S a b =+++,则12100S S S +++=_______.【详解】解:a 111a S =+2221S a =+…,1001001S a =+100S ++=1故答案为:5050【点睛】本题考查了分式的加减法,二次根式的混合运算,求得28.(2022·湖北·广水市中考二模)对于实数0x >,规定()1=+xf x x ,例如()222213f ==+,111212312f ⎛⎫== ⎪⎝⎭+,那么计算1111(1)(2)(3)(2020)2020201920182f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋯+++++⋯+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的结果是______.29.(2022·北京朝阳·中考模拟预测)(1)计算:23(3)3x xx x--- (2)计算:22111121x x x x x x x ++⎛⎫+÷ ⎪---+⎝⎭ (3)先化简,再求值:已知ab =3,求222443a ab b b a b a b a b ⎛⎫++÷-- ⎪--⎝⎭的值.。
河南中考数学18题几何证明与计算专练(含手写版答案)几何证明与推理——四边形存在性
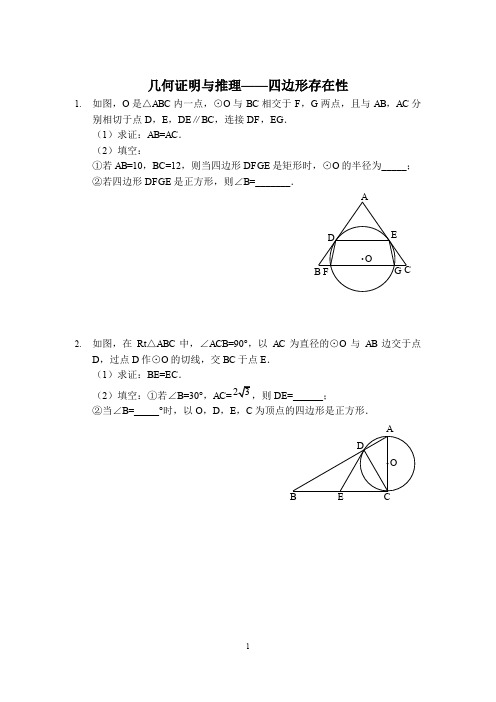
几何证明与推理——四边形存在性1.如图,O是△ABC内一点,⊙O与BC相交于F,G两点,且与AB,AC分别相切于点D,E,DE∥BC,连接DF,EG.(1)求证:AB=AC.(2)填空:①若AB=10,BC=12,则当四边形DFGE是矩形时,⊙O的半径为_____;②若四边形DFGE是正方形,则∠B=_______.2.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.(1)求证:BE=EC.(2)填空:①若∠B=30°,AC=DE=______;②当∠B=_____°时,以O,D,E,C为顶点的四边形是正方形.3.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD (AE<BD)的长是一元二次方程x2-5x+6=0的两个实数根.(1)求证:P A·BD=PB·AE.(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.4.如图,在Rt△ABC中,∠C=90°,点D在线段AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,∠B=∠BAE=30°.(1)求证:BC是⊙O的切线;(2)若AC=3,则⊙O的半径r为____________;(3)判断以A,O,E,F为顶点的四边形为哪种特殊四边形,并说明理由.5.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.(1)求证:MD=ME.(2)填空:①若AB=6,当AD=2DM时,DE=___________;②连接OD,OE,当∠A的度数为__________时,四边形ODME是菱形.6.如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.(1)求证:GC是⊙F的切线.(2)填空:①若∠BAD=45°,AB=CDG的面积为_______;②当∠GCD的度数为_______时,四边形EFCD是菱形.7.如图所示,半圆O的直径AB=4,=,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.(1)求证:△CDF≌△BDE.(2)填空:①当AD=_______时,四边形AODC是菱形;②当AD=_______时,四边形AEDF是正方形.8.如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC,交⊙O于另一点D,连接P A,PB.(1)求证:AP平分∠CAB;(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则:①当弦AP的长是________时,以A,O,P,C为顶点的四边形是正方形;②当的长度是___________时,以A,D,O,P为顶点的四边形是菱形.CB9.如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC.(1)求证:AC是⊙O的切线;(2)连接EF,当∠D=______°时,四边形FOBE是菱形.CF EADO B10.如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D,连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.(1)求证:CD∥AB;(2)填空:①若DF=AP,当∠DAE=__________时,四边形ADFP是菱形;②若BF⊥DF,当∠DAE=__________时,四边形BFDP是正方形.A11.如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.(1)求证:CE=EF;(2)连接AF并延长,交⊙O于点G.填空:①当∠D的度数为_________时,四边形ECFG为菱形;②当∠D的度数为_________时,四边形ECOG为正方形.B AB。
初三数学计算题练习试题集

初三数学计算题练习试题答案及解析1.解不等式组:.【答案】x>5.【解析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).试题解析:解:解①得:x≥3;解②得:x>5,∴不等式组的解集为x>5.【考点】解一元一次不等式组.2.-(-4)-1+-2cos30°【答案】.【解析】先计算绝对值、负整数指数幂、零次幂、特殊角的三角函数值,再进行加减运算即可.原式=.【考点】1.绝对值;2.零次幂;3.负整数指数幂;4.特殊角的三角函数值.3.计算:.【答案】.【解析】针对立方根化简,绝对值,特殊角的三角函数值,负整数指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.原式.【考点】1.立方根化简;2.绝对值;3.特殊角的三角函数值;4.负整数指数幂.4.计算:【答案】9.【解析】分别求出,,,,再进行计算即可.试题解析:.【考点】1.二次根式的化简2.特殊角的三角函数3.零次幂.5.计算:【答案】8.【解析】根据二次根式、零次幂、绝对值、负整数指数幂的意义进行计算即可求出答案.试题解析:原式=2+1-5+1+9=8.考点: 1.二次根式;2.零次幂;3.绝对值;4.负整数指数幂.6.已知:实数,在数轴上的位置如图所示,化简:.【答案】【解析】解:由数轴可知,所以,.所以.7.计算:【答案】.【解析】先化成最简二次根式,再进行计算.试题解析:.【考点】二次根式化简.8.计算(1);(2)【答案】(1);(2).【解析】(1)根据二次根式的运算顺序进行计算即可;(2)针对零指数幂,二次根式化简,特殊角的三角函数值,负整数指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:(1)原式=;(2)原式=.【考点】1.实数的运;2.零指数幂;3.二次根式化简;4.特殊角的三角函数值;5.负整数指数幂.9.计算:2-1-(π-2014)0+cos245°+tan30°•sin60°.【答案】.【解析】根据实数的运算法则和顺序,首先分别计算出-1次幂,0次幂,以及三角函数值,然后再根据实数的加减计算步骤,可以最终求得实数的运算结果,记得检验是否正确.试题解析:解:原式=-1+()2+•,=-1++.=.【考点】实数运算.10.解方程:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 32 4 (5) 7 (2)3
(2) (4 6 6 2) 2 2 ;
(2) 3 [32 ( 2)2 3 8]
2
3
(3)
14
6
27
2;
3.计算下列各题:(每小题 5 分,共 10 分) (1) 20 125 ( 2 1)0
第7页 共6页
◎
第8页 共6页
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
参考答案
1.(1)、-13;(2)、-3 2 ;(3)、-14;(4)、23
3
4
【解析】 试题分析:(1)、根据有理数加减法的计算法则 进行计算;(2)、首先根据根式和绝对值的计算 法则求出各式的值,然后进行求和;(3)、利用 乘法分配律进行简便计算;(4)、首先根据平方 的计算法则得出各式的值,然后进行求和得出答 案. 试题解析:(1)、原式=(-16)+3= -13
2b)2,其中 a= 1 ,b=-( 2011 2011)0 ( 1 )1 2010
( 2 )( 4 分 ) 先 化 简 , 再 求 值 :
,其中 . a2 4 a 2
a2 6a 9 2a 6
a 5
21.计算: 2 (2)0 2sin30.
(2) ( 6 1 ) 2 2 23
◎
第4页 共6页
(3)先化简,在求值。
a
1 a
4b
a b 2
1 b
,其中
a=2,
b=3
8.(5’)(1)计算:(1 3)0 2 2cos45 (1)1 4
5. 12 2 1 12
3 35
2
3
32 2
41
2
11.(本小题满分 12 分)
2
9
2
考点:实数的计算
3.(1)6;(2) 4 3 4 .
【解析】
试题分析:根据二次根式的运算顺序依次运算即
可.
试 题 解 析 : 解 :( 1 )
. 20 125 ( 2 1)0 2 5 5 5 1 7 5 1 7 1 6
5
5
5
(2) + ( 3 1)(3 3) (1 3)2 48
= 3 3 3 3 3 (1 2 3 3) 4 3
=3 3 33 3 1 2 3 3 4 3
=4 34
考点:二次根式的运算.
4.(1)30;(2)-4;(3)-34;(4)-1 1 25
【解析】 试题分析:根据有理数的混合运算的法则,添去 括号法则,可逐步解答即可.
答案第 2 页,总 15 页
3 2
16.(本小题满分 5 分)
第5页 共6页
◎
第6页 共6页
先化简,再求值:(1- 1 )÷ a ,
a 1
a2 2a 1
其中a =sin60°.
17 . ( 2011• 湛 江 ) 计 算 :
.
18.(2011•衢州)(1)计算:|﹣2|﹣(3 ﹣π)0+2cos45°;
(2)化简:
.
19
.
(2)、原式=(-2)+ 4 -3=-3 2
3
3
(3)、原式=(-24)× 1 -(-24)× 1 +(-24)× 5 =
2
3
12
-12+8-10=-14
(4)、原式=-9× 1 +(-8)÷(-1)=- 9 +8= 23
4
4
4
考点:实数的计算
2.(1)、7;(2)、9
【解析】
试题分析:(1)、首先根据幂的计算法则得出各
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
试题解析:(1) 4 (28) (2) =4+28-2 =30
(2) 1 1 (24) 3 6
= 1 24 1 24
3
6
=-8+4
=-4
(3) 23 (13) ( 1) 2
=-8-26 =-34
(4) 12 1 0.5 5 1 25
(6)
(5’)(2)解不等式组
.
9 . 计 算 或 化 简 :( 1 ) 计 算 . 21 3 tan 60 ( 2011)0 1
2
(1) 1 2
24 4 3
18
2
81 3
54 .
(2) 1 2000
1 2
3
sin
58
2
0
|
3 4con60 |
12.计算: 3 - 8 ( - 3)0 (1- 2)2
式的值,然后进行求和得出答案;(2)、首先根
答案第 1 页,总 15 页
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
据幂的计算法则和立方根的计算法则求出各式 的值,然后进行计算. 试题解析:(1)、原式=-9×4+35+8=7
(2)、原式= 3 ×(-9× 4 -2)= 3 ×(-6)=9.
初三数学计算专练
1.计算:
(1)11 5 3
(2) 3 8 16 3 9
(3)( 24)(1 1 5 ) 2 3 12
(4) 32 ( 1)2 ( 2)3 (2 3) 2
2.计算题二:
(2) 1 1 (24) 3 6
(3) 23 (13) ( 1) 2
(4) 12 1 0.5 5 1 25
5
(4) (
0.5 2
1)( 3
1 8
75 ) .
6.化简下列各式:
(1) ; 2(a 1)2 (a 1)(1 2a)
(2) + ( 3 1)(3 3) (1 3)2 48 4.计算 (1) 4 (28) (2)
第3页 共6页
(2) .
2x 1 x 1
x
1
x2
x
2 2x 1
7. 计算(1) 18 3 2 8
13 . ( 2011• 舟 山 ) 计 算 :
10..计算:
(1)
m 2
n 3
m 2
n 3
12 1 3 15
(
3
)
(4) 3(3 3 75 )
. (2) 14.(9 分)先化简,再求值: , (x 3)2 x(x 8)
其中 x 2 4.
12 6 8
15 .( 本 题 满 分 10 分 ) 计 算 : (3)0 27 |1 2 | 1 .
=1 1 2 1 255
=1 1 25
=1 1 25
考点:有理数的混合运算
5.(1)- 2 ;(2)2 3-3;(3)3 14 ;(4) 2 + 13 3 .
22.(1)计算:
(2)化简:
23.先化简,再求值(x+1)2-(x+2) (x-2),其中 5<x< 10 ,且 x 为整数.
24.计算:
(1)
30
1 2
1
2 3
2008
1.5 2009
(2)2(a4)3+(-2a3)2·(-a2)3+a2a10
(3)先化简,再求值:2a(a-2b)-(a-
