电子测量技术 第二章 测量误差分析与数据处理
测量误差分析与数据处理(1)

2.1.2 测量误差的表示方法(续)
• 二、相对误差
• 1 、实际相对误差——绝对误差与实际值之比。
A
x A
100%
x
A 100% A
– 只具有大小、正负,但无量纲
– 接上例可得:
A1
1 100
100%
1%;
A2
1 5
100%
20%
– 相对误差可以表征测量的准确程度。
x x A0
• 重点:
– 误差的表示和分类 – 三种误差的特征及其处理方法 – 数据的处理 – 误差的合成
• 难点:
– 三种误差的特征及其处理方法
2.1 测量误差的基本原理
• 2.1.1 误差的定义 • 2.1.2 测量误差的表示方法 • 2.1.3 电子测量仪器误差的表示方法 • 2.1.4 一次直接测量时最大误差的估计
例1:
• 一个被测电压,真值U0=100V,用一只电压 表测量,指示值U为101V,则绝对误差:
U U U0 101100 1V
• 表明: 测得值比真值大1V,为正误差。
2.1.2 测量误差的表示方法(续)
• 2 、修正值(校正值)
C x A x
– 给出:通过校准由上一级标准以表格或曲线的形 式给出受检仪器的修正值。
– 等级度越低,仪器越准确。0.1、0.2是精密仪器 。
2.1.3 电子测量仪器的表示方法(续)
• (2)附加误差
– 是指仪器在超过规定的正常条件下所增加的误差, 与影响误差相似。例如:环境温度、电源电压等
– 例:MF-20型晶体管万用表。
• 基本误差: – 直流电压、电流为±2.5%
• 附加误差:
– 根据误差的性质,测量误差可分为系统误差、 随机误差、疏失(粗大)误差三类。
第2章 电子测量技术思维导图

精密度 准确度 精确度
测量结果的评价
有效数字 多余数字的舍入规则
有效数字的处理
有效数字的运算规则
等精度测量结果的处理
权的概念 加权平均值
非等精度测量结果的处理
加权平均值的标准差
误差的传递公式 常用函数的合成误差
误差的合成
系统误差的合成
等准确度分配 等作用分配
误差的分配
最佳测量方案的选择
绝对误差 相对误差 装置误差 方法误差 环境误差 人员误差 使用误差 随机误差
系统误差
粗大ห้องสมุดไป่ตู้差
实际相对误差 示值相对误差 分贝误差
引用误差
单峰性 对称性 抵偿性 有界性 确定性 重现性 不具抵偿性 可修正性 偶然性和不可预见性 无抵偿性 奇异性
随机误 差分析
随机误差的统计处理
数学期望 剩余误差
方差与标准差
理论分析法 校准和比对法 改变测量条件法 剩余误差观察法
公式判断法
恒值系差检查方法 变值系差检查方法
系统误差的特征 系统误差的判断
替代法 零式法 交换法 补偿法 微差法
削弱系统误差的方法
测量数据 的处理
误差的合 成与分配
系统误 差分析
测量误差与 数据处理
基础 知识
误差的表示方法 测量误差的来源 测量误差的分类
随机误差的分布
正态分布
均匀分布
非正态分布
三角形分布
反正弦分布
有限次测量的计算方法
贝塞尔公式 算术平均值的标准差
极差法求标准差
置信概率与置信区间
测量结果的置信度
正态分布下的置信度 t分布下的置信度
非正态分布的置信因子
电子测量技术课后习题答案林占江版-17页文档资料
4.14 P144
4.15 0.05%, 20%
4.16 0.056% 4.17 100kHz, 40μs, 10
4.18 9.4ns 4.19 用外触发方式 4.20 滞后电源电压 45°
超前 45°
第5章 时域测量
5.1,5.2 参阅本间相关内容 5.3 李沙育图形,是圆形。 5.4 李沙育图形(1)椭圆形(2)“8”字形 5.5 被测信号频率与扫描信号频率不成整数倍,图形向左“跑动”。 5.6 被测信号频率与扫描信号频率不成整数倍,波形紊乱。 5.7 前沿有上冲,前沿弯曲。 5.8 最小周期T=0.2μs×10×10=20μs, 频率50k 5.9 最高工作频率是20MHz 5.10 最低工作频率是0.4Hz
2.14 正态分布,1215.01±6.11,
2.15 86.4, 3.18, 0.00312, 5.84E4
2.16 3.3, 38 2.17 mγA+n γB, ±9.5% 2.18 ±4% 2.19 160±0.16%, 9.4±1.0%, 2.20 ±5%, ±5% 2.21 2级
第3章模拟测量方法
第6章 频域测量
7.1 P236 7.2 P237 7.3 P238 7.4 P241 7.5 P243 7.6 P246 7.7 P249 7.8 P265
第7章 逻辑分析仪
8.1 P270 8.2 P272 8.3 P272 8.4 P274 8.5 P275 8.6 P276 8.7 P277
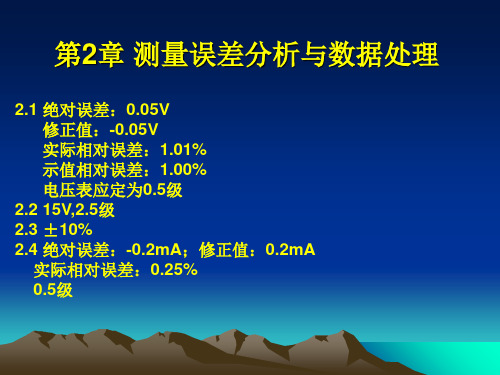
第2章 测量误差分析与数据处理
2.1 绝对误差:0.05V 修正值:-0.05V 实际相对误差:1.01% 示值相对误差:1.00% 电压表应定为0.5级
2.2 15V,2.5级 2.3 ±10% 2.4 绝对误差:-0.2mA;修正值:0.2mA
电子测量技术复习资料

电⼦测量技术复习资料第⼀章绪论1.测量:测量就是利⽤试验⼿段,借助各种测量仪器量具,获得未知量量值的过程。
2.电⼦测量:电⼦测量泛指以电⼦技术为基本⼿段的⼀种测量技术。
3.智能仪器:⼈们习惯把内含微型计算机和GPIB接⼝的仪器称为智能仪器。
4.虚拟仪器:通常是指以计算机为核⼼的,由强⼤的测试应⽤软件⽀持的具有虚拟仪器⾯板,⾜够的仪器硬件及通信功能的测量信息处理系统。
5.电⼦测量的特点:1测量频率范围宽,低⾄10-6Hz以下,⾼⾄1012Hz以上。
2仪器量程范围宽。
3测量准确度⾼低相差悬殊。
4测量速度快。
5可以进⾏遥测。
6显⽰⽅式清晰直观。
7宜于实现测试智能化和测试⾃动化。
8易于实现仪器⼩型化。
9影响因素众多,误差处理复杂。
6.电⼦测量的⽅法:按测量⼿段分类:1直接测量:直接从测量仪表的读书获取被测量量值的⽅法。
2间接测量:它是利⽤直接测量量与被测量量之间的函数关系,间接得到被测量量值得⽅法。
3组合测量:当某测量参数需⽤多个未知参数表⽰时,可通过改变测量条件进⾏多次测量,根据测量量与未知参数之间的函数关系列出⽅程组并求解,进⽽得到未知量,这种测量⽅法叫组合测量。
按测量⽅式分类:1偏差式测量法:⽤仪器仪表指针的位移表⽰被测量量⼤⼩的测量⽅法。
2零⽰式测量法:⼜称平衡式测量法,测量时⽤被测量与标准量相⽐较,⽤指零仪表指⽰被测量与标准量相等,从⽽测得被测量。
3微差式测量法:偏差式测量法与零⽰式测量法相结合。
按被测量性质分类:1时域测量:主要测量被测量随时间的变化规律。
2频域测量:主要⽬的是获取待测量与频率之间的关系。
3数据域测量:主要是⽤逻辑分析仪等设备对数字量,或逻辑电路的逻辑状态进⾏测量7.智能仪器的特点:1是操作⾃动化2具有对外接⼝功能8.智能仪器的组成:主要与⼀般计算机的区别:多⼀个专⽤的外围设备-----测试电路。
9.计量与测量的区别:计量是利⽤技术和法制⼿段实现单位统⼀和量值准确可靠地测量。
检测技术 第二章:误差分析与数据处理

可以得到精确的测量结果,否则还可能损坏仪器、设备、元器件等。
2.理论误差 理论误差是由于测量理论本身不够完善而采用近似公式或近似值计算测量 结果时所引起的误差。例如,传感器输入输出特性为非线性但简化为线性 特性,传感器内阻大而转换电路输入阻抗不够高,或是处理时采用略去高 次项的近似经验公式,以及简化的电路模 型等都会产生理论误差。
误差,周期性系统误差和按复杂规律变化的系统误差。如图2.1所示,其中1为定值系差,2 为
线性系统误差,3为周期系统误差,4为按复杂规律变化的系统误差。 系统误差的来源包括仪表制造、安装或使用方法不正确,
测量设备的基本误差、读数方法不正确以及环境误差等。
系统误差是一种有规律的误差,故可以通过理论分析采 用修正值或补偿校正等方法来减小或消除。
•理论真值又称为绝对真值,是指在严格的条件下,根据一定的理论,按定义确定的数值。 例如三角形的内角和恒为180°一般情况下,理论真值是未知的。 •约定真值是指用约定的办法确定的最高基准值,就给定的目的而言它被认为充分接近于 真值,因而可以代替真值来使用。如:基准米定义为“光在真空中1/299792458s的时间 间隔内行程的长度”。测量中,修正过的算术平均值也可作为约定真值。
表等级为0.2级。
r=
0.12 100% 100% 0.12 A 100
在选仪表时,为什么应根据被测值的大小,在满足被测量数值范围的前提下,尽可能 选择量程小的仪表,并使测量值大于所选仪表满刻度的三分之二。在满足使用 要求时,满量程要有余量,一般余量三分之一,为了装拆被测工件方便。 (同一精度,量程越大,误差越大,故量程要小,但留余量)
第二章 误差分析与数据处理
三.测量误差的来源
1.方法误差 方法误差是指由于测量方法不合理所引起的误差。如用电压表测量电压时,
第2章-测量误差分析及处理-习题-答案

电子测量技术第二章(一)填空题1、相对误差定义为测量值与真值的比值,通常用百分数表示。
2、绝对误差是指由测量所得到的真值与测量值之差。
3、测量误差就是测量结果与被测量____真值____的差别,通常可以分为__ 绝对误差_____和____相对误差___两种。
4、根据测量的性质和特点,可将测量误差分为随机误差、系统误差、粗大误差。
5、精密度用以表示随机误差的大小,准确度用以表示系统误差的大小,精确度用以表示系统误差与随机误差综合影响的大小。
6、可以用____系统误差_____来作为衡量测量是否正确的尺度,称为测量的准确度。
7、随机误差的大小,可以用测量值的___精密度___来衡量,其值越小,测量值越集中,测量的___密集度___越高。
8、误差的基本表示方法有_绝对误差_、_相对误差_和最大引用误差(满度误差)9、消弱系统误差的典型测量技术有零示法、替代法、补偿法、对照法、微差法和交叉读数法。
10、多次测量中随机误差具有___有界_____性、____对称____性和___抵偿_____性。
11、满度(引用)误差表示为绝对误差与满量程之比,是用量程满度值代替测量真值的相对误差。
12、测量仪器准确度等级一般分为7级,其中准确度最高的为_0.1_级,准确度最低的为_5.0_级。
13、1.5级100mA的电流表,引用相对误差为±1.5% ,在50mA点允许的最大绝对误差为___±1.5mA 。
14、为保证在测量80V电压时,误差≤±1%,应选用等于或优于0.5 级的100V量程的电压表。
15、___马利科夫_____判据是常用的判别累进性系差的方法。
16、____阿贝一赫梅特____判据是常用的判别周期性系差的方法。
三种,在工程上凡是要求计算测量结果的误差时,一般都要用__相对误差__。
17、对以下数据进行四舍五入处理,要求小数点后只保留2位。
4.850=__4.85__;200.4850000010=_____200.48___。
第2章 测量误差和测量结果处理

稳定误差是仪器的标称值在其他影响量和影响特性
保持恒定的情况下,于规定时间内产生的误差极限。
第2章 测量误差和测量结果处理
[例5] 用4 1/2位数字电压表2V档和200V档测量1V
电压,该电压表各档容许误差均为 0.03% 1个字, 试分析用上述两档分别测量时的相对误差。
解:
①用2V档测量,仿照式(2.1-20),绝对误差为
效显示数字是四位到五位。相对误差为
x
1
x1
x1
100% 0.04%
第2章 测量误差和测量结果处理
②用200V档测量,绝对误差为
200 x2 0.03% 1 1 19999 3 10 100 10 103 104 (V )
4 4
第2章 测量误差和测量结果处理
第2章 测量误差和测量结果处理
前已叙述,绝对误差是不随测量值改变的。 而测得值分别为100 A、80 A、20 A时的示值相 对误差各不相同,分别为
1 x1 100% 100% 100% 1% x1 x1 100
x
xm
x2
1 100% 100% 100% 1.25% x2 x2 80
第2章 测量误差和测量结果处理
由上述分析我们得出,在实际测量工作中,当基
本消除系统误差又剔除粗大误差后,虽然仍有随机误 差存在,但多次测得值的算术平均值很接近被测量真 值,因此就将它作为最后测量结果,并称之为被测量 的最佳估值或最可信赖值。
第2章 测量误差和测量结果处理
2.剩余误差
当进行有限次测量时,各次测得值与算术平均值 之差,定义为剩余误差或残差:
第2章 测量误差和测量结果处理
《电子测量技术》课程标准(电子信息技术专业)

《电子测量技术》课程标准课程名称:电子测量技术 Electronic Measurement Technology课程性质:专业选修学分:2.5总学时:45,理论学时:36,实验(上机)学时:9适用专业:电子信息技术先修课程:模拟电子技术、数字电子技术、信号与系统、微机原理一、教学目的与要求《电子测量技术》是电子信息、自动控制、测量仪器等专业的通用技术基础课程。
包括电子测量的基本原理、测量误差分析和实际应用,主要电子仪器的工作原理,性能指标,电参数的测试方法,该领域的最新发展等。
电子测量技术综合应用了电子、计算机、通信、控制等技术。
通过本课程的学习,培养学生具有电子测量技术和仪器方面的基础知识和应用能力;通过本课程的学习,可开拓学生思路,培养综合应用知识能力和实践能力;培养学生严肃认真,求实求真的科学作风,为后续课程的学习和从事研发工作打下基础。
二、教学内容与学时分配三、各章节主要知识点与教学要求第1章序论第一节测量的基本概念一、测量的定义二、测量的意义三、测量技术第二节计量的基本概念一、计量二、单位和单位制三、计量标准四、测量标准的传递第三节电子测量技术的内容,特点和方法一、电子测量二、电子测量的内容和特点三、电子测量的一般方法第四节电子测量的基本技术一、电子测量的变换技术二、电子测量的放大技术三、电子测量的比较技术四、电子测量的处理技术五、电子测量的显示技术第五节本课程的任务重点:测量的基本概念、基本要素;单位和单位制,基准和标准,量值的传递准则。
难点:量值的传递准则教学要求:理解测量的基本概念、基本要素,测量误差的基本概念和计算方法。
理解计量的基本概念,单位和单位制,基准和标准,量值的传递准则。
理解测量的基本原理,信息获取原理和量值比较原理。
理解电子测量的实现原理:变换、比较、处理、显示技术。
第2章测量误差理论与数据处理第一节测量误差的基本概念一、有关误差的基本概念二、测量误差的基本表示方法第二节测量误差的来源与分类一、测量误差的来源二、测量误差的分类第三节测量误差的分析与处理一、随机误差的分析与处理二、系统误差的判断及消除方法三、粗大误差的分析与处理第四节测量误差的合成与分配一、测量误差的合成二、测量测量不确定度及其合成三、误差分配及最佳测量方案第五节测量数据处理一、有效数字处理二、测量结果的处理三、最小二乘法与回归分析重点:测量误差的分类估计和处理,系统误差和粗大误差的判断及处理,不确定度的评定方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•
2.2.2按照误差的性质分类
• •
单次测量的随差没有规律, 单次测量的随差没有规律,但多次测量的总体却服从统计规 律。 随机误差的定量定义:测量结果与在重复性条件下, 随机误差的定量定义:测量结果与在重复性条件下,对同一 被测量进行无限多次测量所得结果的平均值之差。 被测量进行无限多次测量所得结果的平均值之差。
2.1.4一次直接测量时最大误差估计 2.1.4一次直接测量时最大误差估计
•
•
例子: 例子:
某待测电流约为100mA,现有0.5级量程为0 400mA和 某待测电流约为100mA,现有0.5级量程为0-400mA和 100mA 0.5级量程为 1.5级量程为 100mA的两个电流表 级量程为0 的两个电流表, 1.5级量程为0-100mA的两个电流表,问用哪一个电流表 测量较好? 测量较好? 0.5级量程为 400mA电流表测100mA时 级量程为0 电流表测100mA 解:用0.5级量程为0-400mA电流表测100mA时,最大相对 误差为
第二章 测量误差分析与数据处理
田宝凤 仪器科学与电气工程学院
主要内容
• • • • • • •
2.1 2.2 2.3 2.4 2.5 2.6 2.7
测量误差的基本原理 测量误差的分类 随机误差的统计特性及估算方法 系统误差的特征及判断方法 疏失误差及其判断准则 测量数据的处理 误差的合成与分配
2.1 测量误差的基本原理
•
•
•
与绝对误差的绝对值大 小相等, 小相等 , 但符号相反的 量值,称为修正值。 量值,称为修正值。 测量仪器的修正值可以 通过上一级标准的检定 给出, 给出 , 修正值可以是数 表格、 值 、 表格 、 曲线或函数 表达式等形式。 表达式等形式。 被测量的实际值: 被测量的实际值: A =
C = −∆x = A − x
在温度 -10~+40 C ,相对湿度80%以下,大气压力86 106kPa的 相对湿度80%以下,大气压力86~106kPa的 80%以下 86 106kPa 环境内,连续工作7小时。 环境内,连续工作7小时。
o
2.1.4一次直接测量时最大误差估计 2.1.4一次直接测量时最大误差估计
• •
仪器仪表的最大绝对误差为 仪器仪表的最大绝对误差为 最大的示值相对误差
2.1.3电子测量仪器误差的表示方法 2.1.3电子测量仪器误差的表示方法
•
工作误差 是在额定工作条件下测定的仪器误差极限。 是在额定工作条件下测定的仪器误差极限。可以利 用工作误差直接估计测量结果误差的最大范围。 用工作误差直接估计测量结果误差的最大范围。
50Hz-1MHz,10mV-1V量程为: ± 1.5%读数 ± 满量程的 0.5% 50Hz-1MHz,10mV-1V量程为: 量程为
xm 400 s% = × 0.5% = 2% γ x1 = x 100
用1.5级量程为0-100mA电流表测量100mA时,最大相对 1.5级量程为 100mA电流表测量100mA时 级量程为0 电流表测量100mA 误差为
xm 100 γ x2 = S% = ×1.5% = 1.5% 100 x
• •
•
•
测量的目的:获得被测量的真值。 测量的目的:获得被测量的真值。 真值: 在一定的时间和空间环境条件下, 真值: 在一定的时间和空间环境条件下,被测量 本身所具有的真实数值。 本身所具有的真实数值。 任何测量仪器的测得值都不可能完全准确的等于 被测量的真值 。 测量误差:在实际测量过程中, 测量误差:在实际测量过程中,人们对于客观认 识的局限性,测量工具不准确,测量手段不完善, 识的局限性,测量工具不准确,测量手段不完善, 受环境影响或测量工作中的疏忽等原因 ,都会使 测量结果与被测量的真值在数量上存在差异。 测量结果与被测量的真值在数量上存在差异。
∆x m = ±S% ⋅ x m
γ xm ∆x m xm = × 100% = ±S% ⋅ x x
在使用这类仪表测量时, 在使用这类仪表测量时 , 应 选择适当的量程, 选择适当的量程 , 使示值尽 可能接近于满度值, 可能接近于满度值 , 指针最 好能偏转在不小于满度值 以上的区域。 2/3以上的区域。
ε = E x − A0
2.2.2按照误差的性质分类
•
•
2.随机误差 2.随机误差
定义: 定义: 在同一测量条件下多次重复测量同一量值时 (等精度测量),每次测量误差的绝对值和符号都以 等精度测量),每次测量误差的绝对值和符号都以 ),每次 不可预知的方式变化的误差, 不可预知的方式变化的误差,称为随机误差或偶然误 差,简称随差。 简称随差。 产生的原因: 产生的原因: 测量仪器中零部件配合的不稳定或有摩擦, (1)测量仪器中零部件配合的不稳定或有摩擦,仪器 内部器件产生噪声等; 内部器件产生噪声等; 温度及电源电压的频繁波动,电磁场干扰, (2)温度及电源电压的频繁波动,电磁场干扰,地基 振动等; 振动等; 测量人员感觉器官的无规则变化, (3)测量人员感觉器官的无规则变化,读数不稳定等 原因所引起的误差。 原因所引起的误差。
•
影响误差 只有当某一影响量在工作误差中起重要作用时才给出, 只有当某一影响量在工作误差中起重要作用时才给出, 它是一种误差极限。 它是一种误差极限。
温度影响误差:1kHz,1V时温度系数为: 10 −4 / o C 时温度系数为: 温度影响误差: , 时温度系数为
•
稳定误差 是仪器的标称值在其它影响量及影响特性保持恒定的 情况下,于规定时间内所产生的误差极限。 情况下,于规定时间内所产生的误差极限。
测量方法不合理所造成, 测量方法不合理所造成,采用近似公式计算
•
4.人身误差 4.人身误差
测量者本身分辨能力、视觉疲劳、 测量者本身分辨能力、视觉疲劳、固有习惯等
2.2.2按照误差的性质分类
•
1.系统误差 1.系统误差
定义:在同一测量条件下,多次重复测量同一量时, 定义:在同一测量条件下,多次重复测量同一量时, 测量误差的绝对值和符号都保持不变,或在测量条件 测量误差的绝对值和符号都保持不变, 的误差, 改变时按一定规律变化的误差 称为系统误差。 改变时按一定规律变化的误差,称为系统误差。 产生的原因: 产生的原因: 测量仪器设计原理及制作上的缺陷。 (1)测量仪器设计原理及制作上的缺陷。 测量时的实际温度、 (2)测量时的实际温度、湿度及电源电压等环境条件 与仪器要求条件不一致等。 与仪器要求条件不一致等。 采用近似的测量方法或近似的计算公式等。 (3)采用近似的测量方法或近似的计算公式等。 测量人员估计读数时, (4)测量人员估计读数时,习惯偏于某一方向或有滞 后倾向等原因所引起的误差。 后倾向等原因所引起的误差。
Gx = 20 lg Au [dB ]
γ A = ∆A A
分贝误差
γ x = ∆A Au
γ dB ≈ 20 lg(1 + γ A ) ≈ 20 lg(1 + γ x )
2.1.2测量误差的表示方法 2.1.2测量误差的表示方法
•
例子: 例子:
2.1.2测量误差的表示方法 2.1.2测量误差的表示方法
定义:绝对误差与被测量的真值之比。 (1)定义:绝对误差与被测量的真值之比。
∆x × 100% γ= A0
相对误差是两个有相 相对误差是两个有相 同量纲的量的比值, 同量纲的量的比值, 只有大小和符号, 只有大小和符号,没 有单位。 有单位。
2.1.2测量误差的表示方法 2.1.2测量误差的表示方法
分贝误差——相对误差的对数表示 (2)分贝误差 相对误差的对数表示
分贝误差是用对数形式(分贝数)表示的一种相对误差, 分贝误差是用对数形式(分贝数)表示的一种相对误差,单 位为分贝(dB)。 位为分贝(dB)。 U Au = o 电压增益的测得值为 误差为 ∆A = Au − A Ui 用对数表示为增益测得值的分贝值
2.2.2按照误差的性质分类
•
•
系统误差表明了一个测量结果偏离真值或实际值 的程度。系差越小,测量就越准确。 的程度。系差越小,测量就越准确。 系统误差的定量定义:在重复性条件下, 系统误差的定量定义:在重复性条件下,对同一 被测量进行无限多次测量所得结果的平均值与被 测量的真值之差。 测量的真值之差。
x+C
2.1.2测量误差的表示方法 2.1.2测量误差的表示方法
2.相对误差 2.相对误差
一个量的准确程度,不仅与它的绝对误差的大小有关, 一个量的准确程度,不仅与它的绝对误差的大小有关,而 且与这个量本身的大小有关。 且与这个量本身的大小有关。 测量足球场的长度和长春市到吉林市的距离, 例:测量足球场的长度和长春市到吉林市的距离,若绝对 误差都为1 测量的准确程度是否相同? 误差都为1米,测量的准确程度是否相同?
2.1.2测量误差的表示方法 2.1.2测量误差的表示方法
测量误差有绝对误差和相对误差两种表示方法。 测量误差有绝对误差和相对误差两种表示方法。 1.绝对误差 1.绝对误差 定义:由测量所得到的被测量值与其真值之差, ( 1)定义: 由测量所得到的被测量值与其真值之差,称为
绝对误差。 绝对误差。
∆x = x − A0
Байду номын сангаас
2.1.1 研究误差的目的
研究误差的目的: 研究误差的目的: (1)正确认识误差的性质和来源,以减小测量误差。 (1)正确认识误差的性质和来源,以减小测量误差。 正确认识误差的性质和来源 (2)正确处理测量数据 以得到接近真值的结果。 正确处理测量数据, (2)正确处理测量数据,以得到接近真值的结果。 (3)合理地制定测量方案,组织科学实验, (3)合理地制定测量方案,组织科学实验,正确选择 测量方法和测量仪器, 测量方法和测量仪器,以便在条件允许的情况下 得到理想的测量结果。 得到理想的测量结果。 (4)设 (4)设计中需要用误差理论进行分析并适当控制这些 误差因素,使仪器的测量准确程度达到设计要求。 误差因素,使仪器的测量准确程度达到设计要求。
