高中数学对勾函数
对勾函数

对勾函数是一种类似于反比例函数的一般双曲函数,是形如f(x)=ax+b/x(a>0)的函数。
中文名对勾函数别称耐克函数、双勾函数、对号函数、双飞燕函数表达式f(x)=ax+b/x (a>0)1定义定义所谓的对勾函数(双曲函数),是形如(a>0)的函数。
名称由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。
也被形象称为“耐克函数”或“耐克曲线”。
2性质图像对勾函数是数学中一种常见而又特殊的函数,见图示,在作图时最好画出渐近线最值当x>0时,有最小值(这里为了研究方便,规定a>0,b>0),也就是当时,f(x)取最小值。
奇偶性、单调性奇偶性双勾函数是奇函数。
单调性令k=,那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k}变化趋势:在y轴左边先增后减,在y轴右边先减后增,是两个勾。
渐近线对勾函数的图像是分别以y轴和y=ax为渐近线的两支曲线,且图像上任意一对勾函数点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3对勾函数最小值与均值不等式对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道展开,得,即两边同时加上2ab,整理得,两边开平方,就得到了均值定理的公式:将中看做a,看做b代入上式,得这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
4导数求解其实用导数也可以研究对勾函数的性质。
对勾函数的图象及性质

对勾函数一、定义对勾函数是由两个幂函数相加得到的,对勾函数是一种类似于反比例函数的一般双曲函数,其标准形式为f(x)=ax+(其中ab>0)。
由于函数图像形似两个中心对称的对勾,因此得名“对勾函数”,又被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。
在许多情况下,为了简化分析,常取a=b=1,即函数形式为f(x)=x+。
研究初等函数的一般路径,背景—概念—图象—性质—应用二、图象及性质图像特征:1、对勾函数的图像是分别以y 轴和直线y=ax 为渐近线的两支曲线。
2、图像上任意一点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3、函数图像整体呈两个“对勾”的形状,且关于原点呈中心对称。
定义域:,即除了x=0外,所有实数都是其定义域内的元素。
值域:。
单调性:函数在(−∞,−1)∪(1,+∞)上单调递增,在(1,0)∪(0,1)上单调递减。
奇偶性:对勾函数是奇函数,即满足f(−x)=−f(x)。
x 122严禁复制三、题型1、基础计算题给定对勾函数表达式,求函数在特定点的值或特定区间的最值。
2.、图像结合题根据对勾函数的图像,判断函数在哪些区间内满足特定条件(如大于某值、小于某值)。
利用图像分析函数与直线、其他曲线的交点情况。
3.、综合应用题求最值问题:利用对勾函数的性质,可以快速求解形如ax+(ab>0)的函数的最值问题。
不等式证明:在不等式证明中,对勾函数的性质也常被用来进行放缩或构造反例。
实际问题建模:在某些经济学问题中,如成本分析、收益最大化等,也可能涉及到对勾函数的应用。
4、参数变化分析:探讨参数a 和b 变化时,对勾函数图像和性质的变化规律。
5、复杂函数组合将对勾函数与其他函数(如二次函数、指数函数等)组合,分析新函数的性质和应用。
四、解题步骤1、对勾函数求最值问题的解题步骤(1)理解函数形式确认函数f(x)=ax+的形式,注意a 和b 都是正数且不相等。
对勾函数(目前最全面的版本了吧)
对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
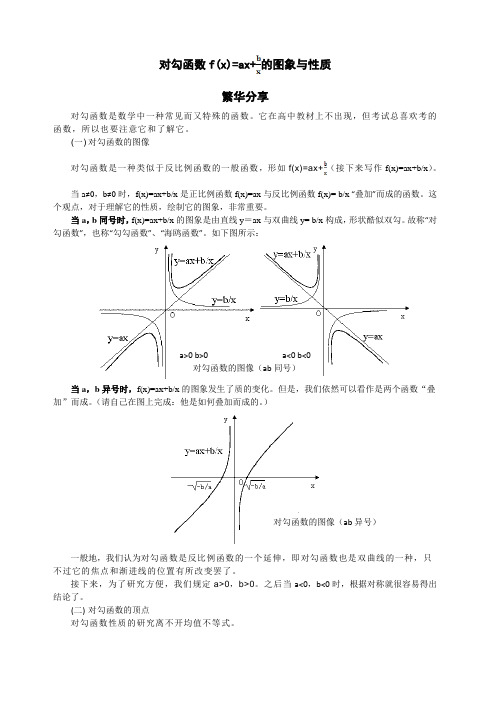
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,X。
对勾函数专题讲解

对勾函数专题讲解专题:对勾函数及其应用1.对勾函数定义对勾函数是指形如 y = ax + (a>0.b>0) 的一类函数,因其图像形态极像对勾,因此被称为“对勾函数”。
2.对勾函数 y = ax + (a>0,b>0) 的性质1) 定义域:(-∞。
0) ∪ (0.+∞)。
2) 值域:(-∞。
-2ab] ∪ [2ab。
+∞)。
3) 奇偶性:在定义域内为奇函数。
4) 单调性:(-∞。
-a/b),(a/b。
+∞) 上是增函数;(-a/b。
0),(0.a/b) 上是减函数。
3.对勾函数 y = ax + (a>0,b>0) 的单调区间的分界点:±a/b。
求分界点方法:令 ax = 0,即可得到 x = ±a/b。
特殊的,当 a>0 时,y = x + 的单调区间的分界点为 ±a。
4.对勾函数应用时主要是利用其单调性求其最值,解题时要先找出对应的单调区间,然后求解。
5.利用对勾函数求最值,常常用到如下的重要不等式:若 a>0,b>0,则 x>0 时,ax + b ≥ 2ab。
当且仅当 ax = b,x = a/b 时取等号。
例1:已知 f(x) = x + (x>0),求 f(x) 在下列区间的最小值:(1) [1,2]。
(2) [3,4]。
(3) [-3,-1]。
变式训练:已知函数 f(x) = x^2 - 2x - 1,求其值域。
例2:求函数 f(x) = (x+2)/((1+x^2)(x^2+5)) 的最小值,并求此时 x 的值。
变式训练:求函数 f(x) = (x-1)/(x-1) 的值域。
强化训练:1.下列函数中最小值是 4 的是 ()。
A。
y = x^4 + x^2B。
y = x^4 + xC。
y = x^4 - xD。
y = x^2 + 42.函数 y = x/(x^2+1)。
x∈(1,3] 的值域为 ()。
对勾函数图象性质
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ bx 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+bx (接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
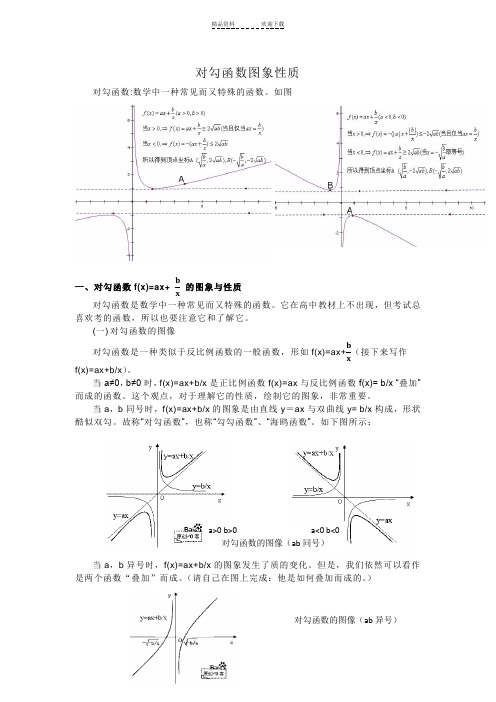
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,f (x )=ax +bx ≥2√ab (当且尽当ax =bx 时取等号),此时x =√ba 。
当x<0时,f (x )=ax +bx ≤−2√ab (当且尽当ax =bx 时取等号),此时x =−√ba 。
(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性对勾函数的图像(ab异号)(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明: 1、求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+=根据对号函数t t y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数_中学教育-中考

对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,X。
对勾函数的性质及应用(史上上最完整版)

对勾函数的性质及应用一、概念:【题型1】函数()(0,0)af x x a k =+>≠【例1】函数1()f x x =+的值域为【例2】函数3()x f x x +=+的值域为【题型2】函数()(0)ax bx cf x ac ++=>。
【例3】函数1()x x f x ++=的值域为【题型3】函数2()(0,0)axf x a b =≠>。
【例4】函数2()1xf x x =+的在区间[)2,+∞上的值域为 【解析】2x ≥,∴,函数15222≥+=【例5】如2214xa x +=-+,(1,2)x ∈,则实数a 的取值范围是(1,2)x ∈4y x x =+1144x x <+,7352a <-<【题型4】函数2()(0)ax bx cf x a ++=≠.【例6】已知1x >-,求函数710()1x x f x x ++=+的最小值。
,1x >-,7101x ++的最小值【例7】已知1x <,求函数299()x x f x +-=的最大值。
,1x <,2991x x +--的最大【题型5】函数2()(0)x mf x a +=≠ 【例8】求函数21()2x f x x x -=++在区间(1,)+∞上的最大值。
【例9】求函数2223()x x f x ++=在区间[0,)+∞上的最大值。
【例10】求函数()f x =的最小值。
类型九:函数2()0)f x a>。
【例12】求函数2()f x=的最小值。
【解析】由题可知,函数22()f x===2t=,则1()()f xg t tt==+,显然在[)2,+∞上单调递增,故min15()(2)222g t g==+=,此时0x=,故函数2()f x=的最小值为52。
【例13】求函数()f x=的值域.。
