清华大学贾仲孝老师高等数值分析考试资料
清华大学高等数值分析(李津)所有作业答案合集

20130917题目求证:在矩阵的LU 分解中,111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明:在高斯消去过程中,假设0jj a ≠ ,若a=0,可以通过列变换使得前面的条件成立,这里不考虑这种情况。
对矩阵A 进行LU 分解,()()()()()1111111L M n M M M n ---=-=∙∙-………… ,其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ,i e 、j e 为n 维线性空间的自然基。
()M j 是通过对单位阵进行初等变换得到,通过逆向的变换则可以得到单位阵,由此很容易得到()M j 的逆矩阵为1n Tn ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。
故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换,从右向左乘,则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。
由于最初的矩阵为单位阵,变换从右向左展开,因而每一次变换不改变已经更新的数据,既该变换是从右向左一列一列更新数据,故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。
数学证明:1nTi j i ji j ee α=+⎛⎫ ⎪⎝⎭∑具有,000n j jA -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式,且有+1,-11,10000=000n j j n j n j AB --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭ 而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式,因此:1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问:能否用逐次householder 相似变换变实矩阵A 为上三角矩阵,为什么?解:不能用逐次householder 相似变换变A 为上三角矩阵,原因如下:A 记作:()12=,,n A a a a ……, ,存在householder 阵1H s.t. 1111H a e α= ,则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数,故无法通过householder 变换实现上三角化。
清华大学贾仲孝老师(贾哥)高等数值分析证明题汇总

又因为A可对角化, A= -1 则p(A)=p( ) -1 则 rk
n
pPk ,p (0)1
min
p( ) -1r0
取r0 i xi Xy, 其中y =(1, 2 , 3 k-1, k ,0,0 0,0)T
i 1
则 rk
pPk ,p (0)1
i 2
n
i 2 i 2 k 1 (vk , Avk ) i 1 1 1 n 1 2 2k (vk , vk ) i i
i 1
n
1212 k 1 2 2 2 2 k 1 i 2 i 2 k 1
2 2k 1 1
又因为A可对角化, A= -1 则p(A)=p( ) -1 则 rk
pPk , p (0)1
min
p( ) -1r0 ( ) r0
pPk ,p (0) 1 1 i n
pPk , p (0)1
min
p( )
即 rk ( ) r0 可取pk (t )
n
2 2 i 2 i 2 k
2 2k i 3
i 3 n
1
2 2 k ) 2 …… 1 1 12 2 2 ( 2 ) 2 k …… 1 2 2 ( 2 ) 2 k 2 2 2 ( 2 ) 2 k 1 1 1 =o ( 2 ) 2 k 2 1 1 121 2 2 (
证毕 15. 叙述幂法 解,见讲义 P80。
5 / 6
结语: 最后三道题为四个月后补录,准确性已经无法保证,仅供参考,祝君顺利。
6 / 6
12 1 C2T X 2T A X 2C 2 1 (12 1)1 C2T ( X 2T A X 2 )C 2 C2 1 X 2 C2 =o(e 2 k ) ( o C2 )
数值分析复习提纲(修改完)

第一章 绪论【考点1】绝对误差概念。
近似数的绝对误差(误差):()a =x a E -,如果()δa E ≤则称δ为a 的绝对误差限(误差限)。
【考点2】相对误差限的概念。
近似数a 的相对误差:()()/x a x =a E r -,实际运算()()/a a x a E r -=,a r /δδ=。
【考点3】有效数字定义。
设*x 的近似值a 可表示为n m a a .a a= 21010⨯±,m 为整数,其中1a 是1到9中的一个整数,n a a 2为0到9中的任意整数,若使()n m a||=|x a |E -*⨯≤-1021成立,则a 称近似*x 有位有效数字。
例:设256010002560,00256702.×=.a .=x -*=,则4-10×21=0.00005a -x ≤*。
因为,2-m=所以2n=,a 有2位有效数字。
若257.01000257.02⨯==-a ,则5102100000500000030-≤×=..=x-a ,因为2-=m ,所以3=n ,a 有3位有效数字。
例:设000018.x=,则00008.a=具有五位有效数字。
41021000010-≤×.=x-a ,因为1=m ,所以5=n ,即a 具有五位有效数字。
例:若3587.64=x *是x 的具有六位有效数字的近似值,求x 的绝对误差限。
410×0.358764=x *,即4=m ,6=n ,0.005=1021x -x 6-4⨯≤*【考点4】四舍五入后得到的近似数,从第一位非零数开始直到末位,有几位就称该近似数有几位有效数字。
【考点5】有效数字与相对误差的关系。
设x 的近似数为n m a a .a ×a= 21010±,)(a 01≠如果a 具有n 位有效数字,则的相对误差限为()111021--≤n r ×a δ,反之,若a 的相对误差限为()()1110121--+≤n r ×a δ,则a 至少具有n 位有效数字。
数值分析试题_A卷与答案

三.求一个次数不高于3的多项式 ,满足下列插值条件:
1
2
3
2
4
12
3
并估计误差。(10分)
四.试用 的牛顿-科特斯求积公式计算定积分 。(10分)
五.用Newton法求 的近似解。(10分)
六.试用Doolittle分解法求解方程组:
2) 的值域是定义域的子集;(2分)
3) 在其定义域内满足李普希兹条件。(2分)
3.解:参照幂法求解主特征值的流程(8分)
步1:输入矩阵A,初始向量v0,误差限,最大迭代次数N;
步2:置k:=1,μ:=0,u0=v0/||v0||∞;
步3:计算vk=Auk-1;
步4:计算
并置mk:=[vk]r, uk:=vk/mk;
(1分)
应用科特斯公式得:
(2分)
(2分)
五.解:由零点定理, 在 内有根。(2分)
由牛顿迭代格式 (4分)
取 得,
(3分)
故取 (1分)
六.解:对系数矩阵做三角分解:
分)
七.解:(1)对于方程组,雅可比方法的迭代矩阵为
(2分)
其特征多项式为 ,且特征值为
青岛科技大学试题
__2014__年~__2015___年第一学期
课程名称:数值分析专业年级:2014级(研究生)
考生学号:考生姓名:
试卷类型:A卷√B卷□考试方式:开卷√闭卷□
………………………………………………………………………………………………………
一.填空题(本大题共4小题,每小题4分,共16分)
则 (1分)
2.证:牛顿迭代格式为 (3分)
计算方法第7章/《数值分析》/清华大学/上海交通大学/西安交通大学

Euler-Maclaurin 公式
å ò Tn - I =
k
c2 j [ f (2 j-1) (b) - f (2 j-1) (a)]h2 j +
b a
P2k ( x) f (2k ) (x)dx
j =1
8
å c2 j
=
(-1)
j +1
1
(2p )2
j
¥ k =1
1 k2j
,|
P2k (x) |£ c2k h2k
同上
ò RS =
b f (4) (x ) (x - a)(x - c)2 (x - b)dx a 4!
=- b - a (b - a )4 f (4) (h) 180 2
5
复化公式及误差分析
由上述误差表达式可知,区间越小,绝对误差越小,复化梯形公式:
将积分区间
n
等分,节点是
xi
=
a
+ ih, h
=
值公式
pn (xk ) = f (xk ) = yk
利用 Lagrange 插
1
å Õ pn (x) =
nn
(
k=0 j=0 j¹k
x xk
- xj - xj
)yk
¬ 做代换 x = a + th,t
=
x-a
å Õ n n t - j
=
(
k =0
j=0
k
-
j )yk
h
j¹k
以 pn (x) 代 f (x) 得
k -1
<e
停止
输出 Tk(k )
»
I
。否则 h
Ü
h 2
数值分析整理版试题及答案

例1、 已知函数表求()f x 的Lagrange 二次插值多项式和Newton 二次插值多项式。
解:(1)插值基函数分别为()()()()()()()()()()1200102121()1211126x x x x x x l x x x x x x x ----===--------()()()()()()()()()()021*******()1211122x x x x x x l x x x x x x x --+-===-+---+-()()()()()()()()()()0122021111()1121213x x x x x x l x x x x x x x --+-===-+--+-故所求二次拉格朗日插值多项式为()()()()()()()()()()()2202()11131201241162314121123537623k k k L x y l x x x x x x x x x x x x x ==⎡⎤=-⨯--+⨯-+-+⨯+-⎢⎥⎣⎦=---++-=+-∑(2)一阶均差、二阶均差分别为[]()()[]()()[][][]010*********011201202303,11204,41234,,52,,126f x f x f x x x x f x f x f x x x x f x x f x x f x x x x x ---===-----===----===---故所求Newton 二次插值多项式为()()[]()[]()()()()()20010012012,,,35311126537623P x f x f x x x x f x x x x x x x x x x x x =+-+--=-++++-=+-例2、 设2()32f x xx =++,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的最佳平方逼近多项式。
清华大学高等数值分析_第三次作业答案

得如下算法: (1) 选初始 x0 ∈ Rn , 计算初始残差 r0 = b − Ax0 , ε > 0 为停机准则; (2) 对 k = 1, 2, . . .直到 rk < ε
T 求解 (D1 D1 + E T E )y1 = (AT rk−1 )(1 : m) ; T 求解 (D2 D2 + F T F )y2 = (AT rk−1 )(m + 1 : n) ;
1 0 0 0 √ √ 3 2 − 2 / 6 0 H= √ √ 0 2/ 6 1/2 − 3/6 √ 0 0 3/6 −1/2
1 1 7. 取 上 题 中 的 矩 阵 A 以 及 b = , m = 2, x0 = 0, 完 成 求 解 Ax = 1 1 G b 的 Arnoldi 和 GMRES 算法, 得出 xA 2 和 x2 . 8. 分别取 A1 = (aij ) = ( 2 1 ), i+j−1 1
?1102??????????nna3?????????????????????????2?112?1
高等数值分析第三章作业参考答案
1. 考虑线性方程组 Ax = b, 其中 A 是对称正定矩阵. 用 Galerkin 原理求解方 程 K = L = Span(v ), 这里 v 是一个固定的向量. e0 = x∗ − x0 , e1 = x∗ − x1 证明 (e1 , Ae1 ) = (e0 , Ae0 ) − (r, v )2 /(Av, v ), 其中 r = b − Ax0 . v 应当取哪个向量在某种意义上是最佳的? (∗)
证明. 令 x1 = x0 + αv , 那么 r1 = r − αAv, e1 = e0 − αv . 由 Galerkin 原
清华大学高等数值分析实验设计及答案
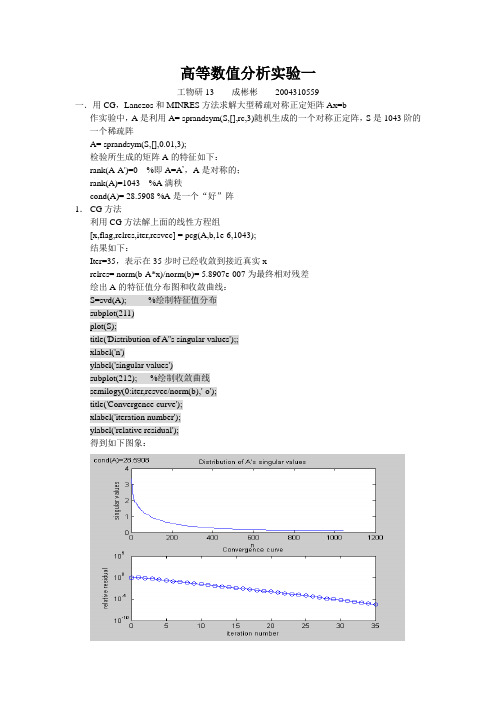
高等数值分析实验一工物研13 成彬彬2004310559一.用CG,Lanczos和MINRES方法求解大型稀疏对称正定矩阵Ax=b作实验中,A是利用A= sprandsym(S,[],rc,3)随机生成的一个对称正定阵,S是1043阶的一个稀疏阵A= sprandsym(S,[],0.01,3);检验所生成的矩阵A的特征如下:rank(A-A')=0 %即A=A’,A是对称的;rank(A)=1043 %A满秩cond(A)= 28.5908 %A是一个“好”阵1.CG方法利用CG方法解上面的线性方程组[x,flag,relres,iter,resvec] = pcg(A,b,1e-6,1043);结果如下:Iter=35,表示在35步时已经收敛到接近真实xrelres= norm(b-A*x)/norm(b)= 5.8907e-007为最终相对残差绘出A的特征值分布图和收敛曲线:S=svd(A); %绘制特征值分布subplot(211)plot(S);title('Distribution of A''s singular values');;xlabel('n')ylabel('singular values')subplot(212); %绘制收敛曲线semilogy(0:iter,resvec/norm(b),'-o');title('Convergence curve');xlabel('iteration number');ylabel('relative residual');得到如下图象:为了观察CG方法的收敛速度和A的特征值分布的关系,需要改变A的特征值:(1).研究A的最大最小特征值的变化对收敛速度的影响在A的构造过程中,通过改变A= sprandsym(S,[],rc,3)中的参数rc(1/rc为A的条件数),可以达到改变A的特征值分布的目的:通过改变rc=0.1,0.0001得到如下两幅图以上三种情况下,由收敛定理2.2.2计算得到的至多叠代次数分别为:48,14和486,由于上实验结果可以看出实际叠代次数都比上限值要小较多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∗
������
=
6 ������
5
+
2 3
7. (2011.1)用 Givens 变换 QR 分解一个 3*2 矩阵,并求解最小二乘。
2 0 2
1
1
1
1 1 1
A=
B=
(2010.4)采用 Givens 算法对 A 进行 QR 分解,并利用得到的分解,进行最小二乘运算 min||Ax-b||
v(2) Au(1) (0.5, 2, 2.5)T , 2.5,
v(8) Au(7) (2.7650948, 2.9981848, 2.9990924)
2.9990924
u(8) (0.9219772, 0.9996973,1) v(9) Au(8) (2.8436517, 2.9993946, 2.9996973)
此例中比值为
2 2 .
1
3
(2008.6)
������������
=
������ √������
(������,
������,
������)������,P0=v0HAv0
|Av0-p0v0|较大
v1=Av0=√������������ (−������, ������, −������)������
A=
2
2 0
1 1 1 1 B= 1 1 1
(2006) 用 Givens 变换 QR 分解一个 3*2 矩阵,并求解最小二乘。
2 0 1
A=
1
1 B= 1
1
1
1
(2006)
1) A a1 a2
2
1
Givens 见第 7 题。 2. (2012.2) (1).证 Rayleigh 商收敛于主特征值,参考讲义。 (2).幂法算主特征值对应的主特征向量,按步骤做,一般的初值都是一步收敛。 (2011.5)A=uv’,u、v 均为向量,A 的秩为 1. (1) 证明 u’v 为 A 的特征值 (2)A 还有哪些其他的特征值。答案:0 (3)用幂法求 A 的主特征值,几步可以收敛?为什么?答案:1 步 (2009.5)(1)叙述求特征值的幂法。证明:当特征值向量方向的误差 sin(准确特征向量和近似特征向量)=ek 的时候, 相应特征值的误差为 0(ek2)
可以验证 QQT=I,且 R 是上三角阵 ∴QR 分解完成 1)用 HouseHolder 求解的另解
A=[a1 a2]
2
2
a1
1
1
x1
0
0
1
a1 y 1 a1 y
(2 2,1,1)T 2 2 2
2
2
H1
0 1 2 (2008.6) 最大的特征值和相应的特征向量。
取v(0) (0, 0,1)T , 103.
解: u(0) v(0) (0, 0,1)T ,
v(1) Au(0) (0, 1, 2)T , 2,
u (1) v(1) (0, 0.5,1)T ,
111 111 111
λ*I-A = [λ- 1, -1, -1] [ -1, λ- 1, -1] [ -1, -1, λ- 1]
det(ans) =λ3 - 3*λ2 特征多项式λ3 - 3*λ2=0 特征值λ1=0λ2=0λ3=3 特征向量
2 1 0 例:用幂法求矩阵A 0 2 1的按模
2)解:因为 A 的秩为 1,所以������ = ������′������和 n-1 个 0
3)解:因为幂法收敛速度������������ = ������ = ������ 所以一步收敛
������������ ������������
完全一样的另一种写法: 1) (2009.5)(1)
(2) A =
φ1)=∫−11
3
������2������������
=
2
������
5 2
1
|
5 −1
=
4 5
4
4
∴
������0∗
=
((φ������0,φ,φ00))=
3
2
=23,������1∗
=
((φ������1,φ,φ11))=
5 2 3
=65
∴一阶最佳平方估计的插值函数为������0∗
+
������1∗
0
1
2 1
2 1
G2G1A 0 1 A (G2G1)1 0 1
0 0
0 0
∵G2、G1 是正交矩阵
1
Q
G
T 1
G
T 2
1
2 1
1
1
1
2
2 1
2
1
2 1
2
2 2
(2)描述经典/精化的 Arnoldi 方法过程 (2008.4)描述计算计算部分特征值和特征向量的 Arnoldi 方法和精化 Arnoldi 方法。 讲义 P93 95
6.(2012.6)(2008.1)(1)使用插值点 x0=2,x1=2.5,x2=4,求 f(x)=1/x 的二次 Lagrange 插值多项式。f(3)近似值是 多少?实际误差是多少?Ans: 1/60 (2).f(x)= √������,权函数 1,问一阶最佳平方估计的插值函数是多少。Ans: 4/5x+2/15?这题其实用 chebyshev 和 拉格朗日都一样,一阶情况下一样的。 (2009.1)(1)f(x)=√������,x0=0,x1=0.6,x2=0.9,求二项差值。 即用插值计算 f(0.44)并求误差
(2011.5)(1)������=v’u (2) ������������=v’u ������������ = ������������ = ������ (3)一步收敛
1)证明:Au=uv’u=u(v’u)=(v’u)u (即 A uvT
)故 (v’u,u)为特征对
Au uvT u u(vT u)
������������
=
������������ ‖������������‖
=
������ √������
(−������
������
−������)������ ������������ = ������������������������������������ = −������
������
2 1
H 2H 1A
0
1
0 0
1 1
2
2
Q
H 1H 2
1 2
1 2
1 2
1 2
0
2 1
1
2 1
R
0
0
1 0
2
8. (2011.2)证明:对于 Minres 和 Gmres (1)A 有 k 个特征值时,至多 k 步收敛 (2)A 有 n 个不同的特征值,r0 由 k 个属于不同特征值的特征向量构成时,k 步收敛
−������ ������ ������ (2008.6)令 A=( ������ −������ ������ )
������ ������ −������
取初始向量������������
=
������ √������
(������,
������,
������)������,用幂法准确计算
A
的主特征值������和主特征向量。
a1
1
G1
C1
S
1
C1
1 2
S1
1 2
1
S1 C 1
G1A G1a1
2
G1a2
2
0
0
2
C2 S2
2
a (1) 1
2
G2
S 2
C2
C2
2 2
S2
2 2
0
111 (2)用幂法求矩阵[1 1 1]的主特征值和主特征向量。这道题是 05 年秩为 1 的问题的变形,其秩也为 1,看出他
111
1 只有 0 和 u’v=3 两个特征值。3 是主特征值,对应的特征向量是√13*[11]。所以可以一开始就把其初始向量选为和[1
1 1]相同方向的向量,一步就发现收敛。
������ ������ ������ (2008.3)令 A=(������ ������ ������)
������ ������ ������ 分别用 Givens 变换和 Householder 变换计算 A 的 QR 分解。
0 3 1 A 0 4 2,
2 1 1 Householder
������
|������������������
−
������������������������|
=
|[−������������] ������
������ √������
−
������ √������
[−������������]| ������������
