清华大学贾仲孝老师高等数值分析报告第二次实验
清华大学贾仲孝老师(贾哥)高等数值分析证明题汇总

又因为A可对角化, A= -1 则p(A)=p( ) -1 则 rk
n
pPk ,p (0)1
min
p( ) -1r0
取r0 i xi Xy, 其中y =(1, 2 , 3 k-1, k ,0,0 0,0)T
i 1
则 rk
pPk ,p (0)1
i 2
n
i 2 i 2 k 1 (vk , Avk ) i 1 1 1 n 1 2 2k (vk , vk ) i i
i 1
n
1212 k 1 2 2 2 2 k 1 i 2 i 2 k 1
2 2k 1 1
又因为A可对角化, A= -1 则p(A)=p( ) -1 则 rk
pPk , p (0)1
min
p( ) -1r0 ( ) r0
pPk ,p (0) 1 1 i n
pPk , p (0)1
min
p( )
即 rk ( ) r0 可取pk (t )
n
2 2 i 2 i 2 k
2 2k i 3
i 3 n
1
2 2 k ) 2 …… 1 1 12 2 2 ( 2 ) 2 k …… 1 2 2 ( 2 ) 2 k 2 2 2 ( 2 ) 2 k 1 1 1 =o ( 2 ) 2 k 2 1 1 121 2 2 (
证毕 15. 叙述幂法 解,见讲义 P80。
5 / 6
结语: 最后三道题为四个月后补录,准确性已经无法保证,仅供参考,祝君顺利。
6 / 6
12 1 C2T X 2T A X 2C 2 1 (12 1)1 C2T ( X 2T A X 2 )C 2 C2 1 X 2 C2 =o(e 2 k ) ( o C2 )
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
清华大学 李津老师 数值分析第二次实验作业

就不再赘述了。 二、实际计算 生成十个不同的(最好属不同类型或有不同性质的)的 m n 矩阵,这里 m, n 100 , 用你选择的算法对其做 SVD,比较不同方法的效果(比如计算小气一直和对应左右奇异向量的 误差,效率等),计算时间和所需存储量等,根据结果提出对算法的认识。 1.误差 在实验中,我们取 m=200,n=100,利用 orth()函数生成了正交矩阵������、������,再生成 了不同奇异值分布的奇异值矩阵������,再通过������ = ������������������,计算出不同的待分解矩阵。 各矩阵奇异值分不如下表所示 序号 1 2 3 4 5 6 7 8 9 10 奇异值个数 10 20 30 40 50 60 70 80 90 100 奇异值分布 10 → 1 20 → 1 30 → 1 40 → 1 50 → 1 60 → 1 70 → 1 80 → 1 90 → 1 100 → 1
−1 −1 −1 −1 −1 −1 −1 −1 −1 −1
经过 matlab 计算,我们得到了两种算法对奇异值的估计误差表,如下所示
序号 svd 1 2 3 4 5 1.2135e-29 1.0336e-28 3.9976e-28 7.9768e-28 1.5711e-27
i 1
100
i
i
2.5232e-27 4.6720e-27 5.8535e-27 8.7958e-27 9.8885e-27
r
i 1
ui uis r
2 2
i 1
vi vis r
2 2
lansvd
svd
lansvd
2 1.6 2.1333 2 2.16 1.8 2.3429 2.15 2 2
谷根代数值分析--上机实习报告

《数值分析》实验报告实验题目非线性方程求解()/21;else a x endx a b n n end==+=+由于本题中()f x 恒大于0,不满足二分法()()0f a f b <的条件,故本例无法通过二分法求出方程的根。
(2)牛顿迭代法牛顿迭代法迭代法迭代公式为:1'()()k k k k f x x x f x +=-a).对单根条件下,牛顿迭代法平方收敛,牛顿迭代法程序框图如下所示:b). 对重根条件下,此时迭代公式修改为1'(),()k k k k f x x x m m f x +=-⨯为根的重数 此时,牛顿迭代法至少平方收敛。
(3)割线法割线法的迭代公式为:111()(),1,2()()k k k k k k k f x x x x x k f x f x +--=--=-…]割线法是超线性收敛,其程序流程图为(4)斯蒂芬森迭代法斯蒂芬森迭代法的计算格式为21()()()2n n n n n n n n n n ny x z y y x x x z y x ϕϕ+==-=--+《数值分析》实验报告实验题目插值与拟合(1)求以上数据形如2012()y x c c x c x =++的拟合曲线及其平方误差;(2)求以上数据形如()b xy x ae-=的拟合曲线及其平方误差;(3)通过观察(1)、(2)的结果,写出你对数据拟合的认识。
算法分析2.1.1 插值(1)牛顿插值法Lagrange 插值公式结构紧凑,便于理论分析。
利用插值基函数也容易到插值多项式的,Lagrange 插值公式的缺点是,当插值节点增加,或其位置变化时,全部插值基函数均要随之变化,从而整个插值公式的结构也发生变化,这在实际计算中是非常不利的。
下面引入的Newton 插值公式可以克服这个缺点。
Newton 插值多项式可以灵活地增加插值节点进行递推计算。
该公式形式对称,结构紧凑,因而容易编写计算程序。
贾忠孝高等数值分析第一次上机作业

【运行结果】 当 m=300 时,下图表示实验结果,其中 k 为停机循环次数
当 m=995 时,停机循环次果表明当 m 越小时,收敛速度越快,在有限精度下,停机循环次数越小。这 与 Lanczos 方法最多 m 步找到准确解这一结论相吻合。
4. 取初始近似解为零向量, 右端项 b 仅由 A 的 m 个不同个特征向量的线性组 合表示时, Lanczos 方法的收敛性如何? 数值计算中方法的收敛性和m 的大小关 系如何? 【程序】 clc clear clf n=1000; rs=10^(-10); %停机准则 m=10; disp('Lanczos 算法') %定义对称正定阵与 b
1 1000, 2 59.8858, 999 10.0961, 1000 0.01,
经过 k=100,基本收敛达到精度要求。
【结论】 后者的收敛速度要大于前者。说明当 A 的最大特征值远大于第二个最大特征 值, 最小特征值远小于第二个最小特征值时,收敛速度只与 2. 对于同样的例子, 比较 CG 和 Lanczos 的计算结果. 【程序】
高等数值分析实验作业一
机械系 光辉 2014310205
1. 构造例子说明 CG 的数值性态 . 当步数 = 阶数时 CG 的解如何 ? 当 A 的最 大特征值远大于第二个最大特征值, 最小特征值远小于第二个最小特征值时 方 法的收敛性如何? 问题 1 【程序】 clc clear n=1000; %定义对称正定阵与 b lans=sort(rand(n,1),'descend'); D=diag(lans); Q=orth(rand(1000,1000)); A=Q*D*Q'; b=rand(n,1); %初始情况 x0=eye(n,1); r0=b-A*x0; p(:,1)=r0; %执行第一步 af(1)=dot(r0,r0)/dot(p(:,1),A*p(:,1)); x(:,1)=x0+af(1)*p(:,1); r(:,1)=b-A*x(:,1); bat(2)=dot(r(:,1),r(:,1))/dot(r0,r0); p(:,2)=r(:,1)+bat(2)*p(:,1); %执行 k 步 K=n; for k=2:1:K k af(k)=dot(r(:,k-1),r(:,k-1))/dot(A*p(:,k),p(:,k)); x(:,k)=x(:,k-1)+af(k)*p(:,k); r(:,k)=b-A*x(:,k);
数值分析实验报告-清华大学--线性代数方程组的数值解法

数值分析实验报告-清华大学--线性代数方程组的数值解法(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--线性代数方程组的数值解法实验1. 主元的选取与算法的稳定性问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。
但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。
主元的选择从数学理论上看起来平凡,它却是数值分析中十分典型的问题。
实验内容:考虑线性方程组 n n n R b R A b Ax ∈∈=⨯,,编制一个能自动选取主元,又能手动选取主元的求解线性方程组的Gauss 消去过程。
实验要求:(1)取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157,6816816816 b A ,则方程有解T x )1,,1,1(* =。
取n=10计算矩阵的条件数。
让程序自动选取主元,结果如何?(2)现选择程序中手动选取主元的功能。
每步消去过程总选取按模最小或按模尽可能小的元素作为主元,观察并记录计算结果。
若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。
(3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用。
(4)选取其他你感兴趣的问题或者随机生成矩阵,计算其条件数。
重复上述实验,观察记录并分析实验结果。
程序清单n=input('矩阵A 的阶数:n=');A=6*diag(ones(1,n))+diag(ones(1,n-1),1)+8*diag(ones(1,n-1),-1); b=A*ones(n,1);p=input('计算条件数使用p-范数,p='); cond_A=cond(A,p) [m,n]=size(A);Ab=[A b];r=input('选主元方式(0:自动;1:手动),r=');Abfor i=1:n-1switch rcase(0)[aii,ip]=max(abs(Ab(i:n,i)));ip=ip+i-1;case (1)ip=input(['第',num2str(i),'步消元,请输入第',num2str(i),'列所选元素所处的行数:']);end;Ab([i ip],:)=Ab([ip i],:);aii=Ab(i,i);for k=i+1:nAb(k,i:n+1)=Ab(k,i:n+1)-(Ab(k,i)/aii)*Ab(i,i:n+1);end;if r==1Abendend;x=zeros(n,1);x(n)=Ab(n,n+1)/Ab(n,n);for i=n-1:-1:1x(i)=(Ab(i,n+1)-Ab(i,i+1:n)*x(i+1:n))/Ab(i,i);endx运行结果(1)n=10,矩阵的条件数及自动选主元Cond(A,1) =×103Cond(A,2) = ×103Cond(A,inf) =×103程序自动选择主元(列主元)a.输入数据矩阵A的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=0b.计算结果x=[1,1,1,1,1,1,1,1,1,1]T(2)n=10,手动选主元a. 每步消去过程总选取按模最小或按模尽可能小的元素作为主元矩阵A 的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:1(2)(2) 6.0000 1.00007.00004.6667 1.0000 5.66678.0000 6.000015.0000[]8.00001.000015.00006.0000 1.00008.0000 6.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:2…(实际选择时,第k 步选择主元处于第k 行) 最终计算得x=[, , , , , , , , , ]Tb. 每步消去过程总选取按模最大的元素作为主元 矩阵A 的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:2(2)(2)8.0000 6.0000 1.000015.0000-3.50000.7500-4.250008.0000 6.0000 1.000015.0000[]8.0000 6.000015.00008.0000 1.00006.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:3…(实际选择时,第k 步选择主元处于第k+1行) 最终计算得x=[1,1,1,1,1,1,1,1,1,1]T(3)n=20,手动选主元a. 每步消去过程总选取按模最小或按模尽可能小的元素作为主元 矩阵A 的阶数:n=20计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:1(2)(2) 6.0000 1.00007.00004.6667 1.0000 5.66678.0000 6.000015.0000[]8.00001.000015.00006.0000 1.00008.0000 6.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:2…(实际选择时,第k 步选择主元处于第k 行) 最终计算得x=[,,,,,,,,,,,,,,,,,,,]T b. 每步消去过程总选取按模最大的元素作为主元 矩阵A 的阶数:n=20计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:2(2)(2)8.0000 6.0000 1.000015.0000-3.50000.7500-4.250008.0000 6.0000 1.000015.0000[]8.0000 6.000015.00008.0000 1.00006.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:3…(实际选择时,第k步选择主元处于第k+1行)最终计算得x=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]T(4)A分别为幻方矩阵,Hilbert矩阵,pascal矩阵和随机矩阵简要分析计算(1)表明:对于同一矩阵,不同范数定义的条件数是不同的;Gauss消去法在消去过程中选择模最大的主元能够得到比较精确的解。
清华大学高等数值分析实验设计及答案
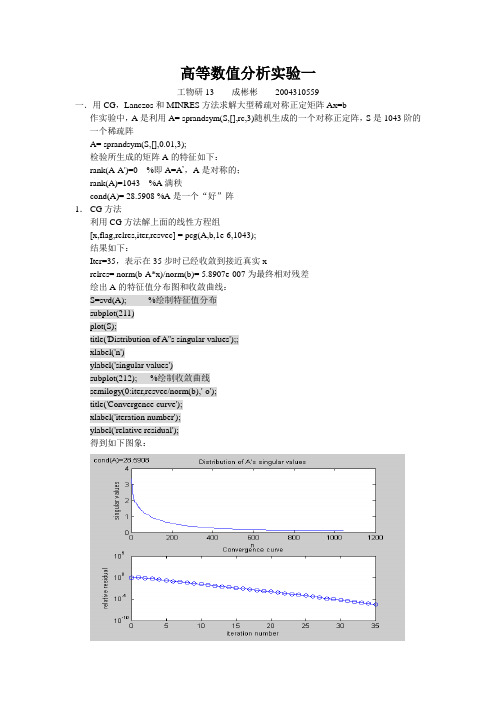
高等数值分析实验一工物研13 成彬彬2004310559一.用CG,Lanczos和MINRES方法求解大型稀疏对称正定矩阵Ax=b作实验中,A是利用A= sprandsym(S,[],rc,3)随机生成的一个对称正定阵,S是1043阶的一个稀疏阵A= sprandsym(S,[],0.01,3);检验所生成的矩阵A的特征如下:rank(A-A')=0 %即A=A’,A是对称的;rank(A)=1043 %A满秩cond(A)= 28.5908 %A是一个“好”阵1.CG方法利用CG方法解上面的线性方程组[x,flag,relres,iter,resvec] = pcg(A,b,1e-6,1043);结果如下:Iter=35,表示在35步时已经收敛到接近真实xrelres= norm(b-A*x)/norm(b)= 5.8907e-007为最终相对残差绘出A的特征值分布图和收敛曲线:S=svd(A); %绘制特征值分布subplot(211)plot(S);title('Distribution of A''s singular values');;xlabel('n')ylabel('singular values')subplot(212); %绘制收敛曲线semilogy(0:iter,resvec/norm(b),'-o');title('Convergence curve');xlabel('iteration number');ylabel('relative residual');得到如下图象:为了观察CG方法的收敛速度和A的特征值分布的关系,需要改变A的特征值:(1).研究A的最大最小特征值的变化对收敛速度的影响在A的构造过程中,通过改变A= sprandsym(S,[],rc,3)中的参数rc(1/rc为A的条件数),可以达到改变A的特征值分布的目的:通过改变rc=0.1,0.0001得到如下两幅图以上三种情况下,由收敛定理2.2.2计算得到的至多叠代次数分别为:48,14和486,由于上实验结果可以看出实际叠代次数都比上限值要小较多。
清华大学数值分析实验报告

数值分析实验报告一、 实验3。
1 题目:考虑线性方程组b Ax =,n n R A ⨯∈,n R b ∈,编制一个能自动选取主元,又能手动选取主元的求解线性代数方程组的Gauss 消去过程。
(1)取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=6816816816 A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157 b ,则方程有解()T x 1,,1,1*⋯=。
取10=n 计算矩阵的条件数。
分别用顺序Gauss 消元、列主元Gauss 消元和完全选主元Gauss 消元方法求解,结果如何?(2)现选择程序中手动选取主元的功能,每步消去过程都选取模最小或按模尽可能小的元素作为主元进行消元,观察并记录计算结果,若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。
(3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用.(4)选取其他你感兴趣的问题或者随机生成的矩阵,计算其条件数,重复上述实验,观察记录并分析实验的结果。
1. 算法介绍首先,分析各种算法消去过程的计算公式, 顺序高斯消去法:第k 步消去中,设增广矩阵B 中的元素()0k kk a ≠(若等于零则可以判定系数矩阵为奇异矩阵,停止计算),则对k 行以下各行计算()(),1,2,,k ikik k kka l i k k n a ==++,分别用ik l -乘以增广矩阵B 的第k 行并加到第1,2,,k k n ++行,则可将增广矩阵B 中第k 列中()k kka 以下的元素消为零;重复此方法,从第1步进行到第n-1步,则可以得到最终的增广矩阵,即()()(),n n n B Ab ⎡⎤=⎣⎦; 列主元高斯消去法:第k 步消去中,在增广矩阵B 中的子方阵()()()()k kkkknk k nknn a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦中,选取()k k i k a 使得()(k)max k k i k ik k i na a ≤≤=,当k i k ≠时,对B 中第k 行与第k i 行交换,然后按照和顺序消去法相同的步骤进行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数值分析第二次实验作业T1.构造例子特征值全部在右半平面时, 观察基本的Arnoldi 方法和GMRES 方法的数值性态, 和相应重新启动算法的收敛性. Answer:(1) 构造特征值均在右半平面的矩阵A :根据实Schur 分解,构造对角矩阵D 由n 个块形成,每个对角块具有如下形式,对应一对特征值i i i αβ±ii i i i S αββα-⎛⎫= ⎪⎝⎭这样D=diag(S 1,S 2,S 3……S n )矩阵的特征值均分布在右半平面。
生成矩阵A=U TAU ,其中U 为正交阵,则A 矩阵的特征值也均在右半平面。
不妨构造A 如下所示:2211112222/2/2/2/2N NA n n n n ⨯-⎛⎫⎪ ⎪ ⎪- ⎪= ⎪ ⎪ ⎪- ⎪ ⎪⎝⎭ 由于选择初值与右端项:x0=zeros(2*N,1);b=ones(2*N,1);则生成矩阵A 的过程代码如下所示:N=500 %生成A 为2N 阶 A=zeros(2*N); for a=1:NA(2*a-1,2*a-1)=a; A(2*a-1,2*a)=-a; A(2*a,2*a-1)=a; A(2*a,2*a)=a; endU = orth(rand(2*N,2*N)); A1 = U'*A*U;(2) 观察基本的Arnoldi 和GMRES 方法编写基本的Arnoldi 函数与基本GMRES 函数,具体代码见附录。
function [x,rm,flag]=Arnoldi(A,b,x0,tol,m) function [x,rm,flag]=GMRES(A,b,x0,tol,m)输入:A 为方程组系数矩阵,b 为右端项,x0为初值,tol 为停机准则,m 为人为限制的最大步数。
输出:x 为方程的解,rm 为残差向量,flag 为解是否收敛的标志。
外程序如下所示: e=1e-6; m=700;tic[xA,rmA,flagA]=Arnoldi(A1,b,x0,e,m);toctic[xG,rmG,flagG]=GMRES(A1,b,x0,e,m);tocsubplot(1,2,1);semilogy(rmA)title('ArnoldiÊÕÁ²ÇúÏß')xlabel('µü´ú²½Êýk')ylabel('log(||rk||)')subplot(1,2,2);semilogy(rmG)title('GMRESÊÕÁ²ÇúÏß')xlabel('µü´ú²½Êýk')ylabel('log(||rk||)')得到:得到两种方法的收敛曲线如上所示,将计算结果整理在下表中:结果讨论:1.从图中可以看出,基本的Arnoldi方法经过546步收敛,基本的GMRES方法经过526步收敛,基本的GMRES收敛速度会略快于基本的Arnoldi方法。
2.从图中可以看出,GMRES方法的的性态较Arnoldi方法更好。
Arnoldi方法会有平台和不光滑段,但是由于GMRES具有的残差最优性,GMRES方法平稳地收敛,收敛曲线也更光滑。
(3)观察重新启动的Arnoldi和GMRES方法在上述两个函数的基础上,编写了重新启动的Arnoldi函数(详情见附录):function [x,rm,flag,Maxi]=ArnoldiM(A,b,x0,tol,m,Maxm)输入:m为给定步数,Maxm为人为限制的最大重启次数。
输出:x为方程的解,rm为残差向量,flag为解是否收敛的标志,Maxi为重启次数。
首先编写程序,计算重启次数Maxi与给定步数m的关系,为选取给定步数m给出依据:num_restartA=[];num_restartG=[];for m=10:10:150tic[xG,rmG,flagG,MaxiG]=GMRESM(A,b,x0,tol,m,Maxm);[xA,rmA,flagA,MaxiA]=ArnoldiM(A,b,x0,tol,m,Maxm);num_restartA=[num_restartA MaxiA];num_restartG=[num_restartG MaxiG];tocendm1=10:10:150;plot(m1,num_restartA,'o-',m1,num_restartG,'*-')从上述结果中看到在m=50之后,重启次数随着给定步长的增加减少很慢,进入饱和。
故可以取m=50,最大步数可知在50步以,运算程序如下所示:m=50;Maxm=50;tic[xA,rmA,flagA,MaxiA]=ArnoldiM(A,b,x0,tol,m,Maxm);toctic[xG,rmG,flagG,MaxiG]=GMRESM(A,b,x0,tol,m,Maxm);tocm1=1:MaxiA;m2=1:MaxiG;plot(m1,log10(rmA),'o-',m2,log10(rmG),'*-')title('Á½ÖÖÖØÆôËã·¨µÄÊÕÁ²ÇúÏß')xlabel('ÖØÆô´ÎÊýk')ylabel('log(||rk||)')得到的收敛曲线结果如下图所示:得到两种方法的收敛曲线如上所示,将计算结果整理在下表中:结果讨论:1.重启次数随着m的增大而减小,当m增大到一定程度如50之后,减小很缓慢,当m非常大的时候,就过度到了基本算法。
重启的算法如何选择合适的m的因问题而不同。
2.重启算法的总迭代次数(重启次数×m)要多于基本的算法。
这是由于在重启动时,从另一个我们认为更好的初值点(其实不一定好)x0重新开始计算,可能会丢掉一些之前算过的信息。
3.重启算法与基本算法相比,虽然总迭代次数增加了,但是运算速度却能大大提高,运行时间远远小于基本算法(尤其是重启GMRES算法)。
4.一般情况,对于同一个题目,重启的GMRES方法收敛速度要比Arnoldi方法快;5.总的来说,对题中的矩阵A,四种方法均能稳定地收敛。
T2. 对于1 中的矩阵, 将特征值进行平移, 使得实部有正有负, 和1 的结果进行比较,方法的收敛速度会如何? 基本的Arnoldi 算法有无峰点? 若有, 基本的GMRES 算法相应地会怎样?Answer:对A 的特征值进行平移,如对S 矩阵的实部统一减去一个数s ,则小单元矩阵S 对应的一对特征值变为()i i s i αβ-±,当矩阵A 构造同上题,那么控制s 的大小,即控制了实部为负的特征值的个数。
i i i i i s S s αββα--⎛⎫= ⎪-⎝⎭这里将上面的矩阵生成做如下改造:clear all ; N=500 tol=1e-6; m=50; Maxm=50; A=zeros(2*N); s=1.5for a=1:NA(2*a-1,2*a-1)=a-s; A(2*a-1,2*a)=-a; A(2*a,2*a-1)=a; A(2*a,2*a)=a-s; endU = orth(rand(2*N,2*N)); A1 = U'*A*U;改变s 的值,进而改变实部为负的特征值个数,计算结果整理如下表所示:结果讨论:1. 当开始有负半平面的特征值时,个数比较少时(如小于100时),随着个数的增加,基本的Arnoldi 和基本的GMRES 迭代次数明显变多,收敛速度明显变慢;当负半平面特征值个数继续增加(如大于100时),两者的迭代次数减少,收敛速度明显变快,并且将比第一题的收敛速度快很多,迭代次数少很多。
2. 当开始有负半平面的特征值时,个数比较少时(如小于100时),随着个数的增加,Arnoldi出现峰点,峰点个数与其特征值的分布有关系,但整体仍收敛。
这是由于负特征值的存在,使得海森贝格矩阵H 发生近似奇异而发生近似中断而引起的。
然而,GMRES的残100200300400500600700800迭代次数 k-5-4-3-2-1123log (| |r k | |)差始终平稳下降,当Aronldi 出现尖峰时,GMRES 的残差不变具有最优性。
T3. 对1 中的例子固定特征值的实部, 变化虚部, 比较收敛性。
Answer:首先对T1的代码进行简单修改,实部不变,虚部进行一定的放大(引入系数k )。
每个对角块具有如下形式,对应一对特征向量'i i i αβ+''ii ii S αββα⎛⎫-= ⎪⎝⎭上式中的'i i k ββ=相应代码如下所示(以Arnoldi 为例),取k=0.2,0.5,1,2,5这五种情况。
N=500A1=zeros(2*N); k1=0.2; for a=1:NA1(2*a-1,2*a-1)=a; A1(2*a-1,2*a)=-k1*a; A1(2*a,2*a-1)=k1*a; A1(2*a,2*a)=a; endU = orth(rand(2*N,2*N)); A1 = U'*A1*U;%篇幅所限,此处省去了A2~A5,同理可得。
k5=5; for a=1:NA5(2*a-1,2*a-1)=a; A5(2*a-1,2*a)=-k5*a; A5(2*a,2*a-1)=k5*a; A5(2*a,2*a)=a; endU = orth(rand(2*N,2*N)); A5 = U'*A5*U;x0=zeros(2*N,1); b=ones(2*N,1); e=1e-6; m=1000;[xA1,rmA1,flagA1]=Arnoldi(A1,b,x0,e,m); [xA2,rmA2,flagA2]=Arnoldi(A2,b,x0,e,m); [xA3,rmA3,flagA3]=Arnoldi(A3,b,x0,e,m); [xA4,rmA4,flagA4]=Arnoldi(A4,b,x0,e,m);[xA5,rmA5,flagA5]=Arnoldi(A5,b,x0,e,m);m1=1:size(rmA1,2);m2=1:size(rmA2,2);m3=1:size(rmA3,2);m4=1:size(rmA4,2);m5=1:size(rmA5,2);plot(m1,log10(rmA1),m2,log10(rmA2),m3,log10(rmA3),m4,log10(rmA4),m5,l og10(rmA5))title('»ù±¾Arnoldi·½·¨ÊÕÁ²ÇúÏß')xlabel('µü´ú´ÎÊýk')ylabel('log(||rk||)')hg1 = legend('k=0.2', 'k=0.5','k=1','k=2','k=5');计算结果如下所示:结果讨论:1.随着比例因子k的增大,虚部被放大,Arnoldi方法和GMRES方法的收敛速度均减慢,迭代次数增加;2.同时,随着比例因子k的增大,Arnoldi过程跳动越来越严重,峰点个数增加,发生近似中断的次数增加;而GMRES方法的残差始终保持单调平稳下降。
