圆心角圆周角练习题.doc
圆心角圆周角练习题
圆心角圆周角练习题圆心角和圆周角是圆内角的一种特殊形式，它们在几何学中具有重要的地位。
本文将介绍关于圆心角和圆周角的一些练习题，帮助读者加深对这一概念的理解。
一、选择题1. 在同一个圆中，圆心角和对应的圆周角的关系是：A. 圆心角大于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角小于对应的圆周角2. 已知在同一个圆中，圆心角的度数为56°，则对应的圆周角的度数为：A. 56°B. 112°C. 224°3. 在圆O中，∠ACB是圆心角，则它所对应的圆周角的度数为：A. 30°B. 60°C. 120°4. 若∠ACD是圆O中的圆心角，且其度数为72°，则弧AB所对应的圆周角的度数为：A. 72°B. 144°C. 288°5. 在同一个圆中，圆心角和对应的弧所对应的圆周角之间的关系是：A. 圆心角小于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角大于对应的圆周角二、填空题1. 在同一圆中，一条弧的度数等于其所对应的圆周角的度数，则这条弧所对应的圆心角的度数为________。
2. 在圆O中，已知∠ACB是圆心角，则它所对应的圆周角的度数为________。
3. 在同一个圆中，圆心角的度数等于所对应的弧所对应的圆周角的度数，则该弧所对应的圆周角的度数为________。
三、解答题1. 在同一个圆中，圆心角和对应的圆周角的关系是什么？为什么？2. 已知在同一个圆中，圆心角的度数为60°，则对应的圆周角的度数是多少？并通过计算或推理进行解答。
3. 在圆O中，∠ACB是圆心角，则它所对应的圆周角的度数是多少？并通过计算或推理进行解答。
4. 若∠ACD是圆O中的圆心角，且其度数为90°，则弧AB所对应的圆周角的度数是多少？并通过计算或推理进行解答。
总结：本文通过选择题、填空题和解答题的形式，对圆心角和圆周角的概念进行了练习和探讨。
垂径定理、弦、弧、圆心角、圆周角练习
CEOAD B600BB九年垂径定理、弦、弧、圆心角、弦心距练习1. 已知：AB 交圆O 于C 、D ，且AC ＝BD. 求证：OA ＝OB2. 如图所示，是一个直径为650mm 的圆柱形输油管的横截面，若油面宽 AB=600mm ，求油面的最大深度。
3.. 如图所示，在⊙O 中，AB 、AC 为互相垂直且相等的两条弦，OD ⊥AB ，OE ⊥AC ，垂足分别为D 、E ，求证：四边形OEAD 为正方形。
4．如图所示，已知AB 为圆O 的直径，AC 为弦，OD ∥BC 交AC 于D ，OD=cm 2，求BC 的长；5．本市新建的滴水湖是圆形人工湖．为测量该湖的半径，小杰和小丽沿湖边选取A ，B ，C 三根木柱，使得A ，B 之间的距离与A ，C 之间的距离相等，并测得BC 长为240米，A 到的距离为米，如图所示．请你帮他们求出滴水湖的半径．6．如图，用一块直径为a 的圆桌布平铺在对角线长为a 的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x 为（ Ａ．)1aＢ．12a Ｃ．24a Ｄ．(2a - 7．如图，⊙O 的半径为5，弦AB 的长为8，点M 在线段AB （包括端点AB ，）上移动，则OM 的取值范围是（ ） Ａ．35OM ≤≤ Ｂ．35OM <≤ 45OM <≤8．如图，已知⊙O 的半径为5mm ，弦8mm AB =，则圆心O 到AB 的距离是（ ）A ．1mmB ．2mmC ．3mmD ．4mm9．如图，底面半径为5dm 的圆柱形油桶横放在水平地面上，向桶内加油后，量得长方形油面的宽度为8dm ，则油的深度（指油的最深处即油面到水平地面的距离）为（ ）Ａ．2dmＢ．3dmＣ．2dm 或3dmＤ．2dm 或8dm10．如图，已知在⊙O 中，直径10MN=，正方形ABCD 的四个顶点分别在半径OM ，OP 以及O 上，并且45POM =∠，则AB 的长为 ．11．如图，在半径为2的⊙O 中，弦AB 的长为_______AOB =∠12．在⊙O 中，弦CD 与直径AB 相交于点P ，夹角为30，且分直径为1:5两部分，6AB =厘米，则弦CD 的长为（Ａ．Ｂ．Ｃ．Ｄ．13．如图，在⊙O 中，AB 是弦，OC AB ⊥，垂足为C ，若AB ，6OC =，则O 的半径OA 等于（ ）Ａ．16Ｂ．12Ｃ．10Ｄ．814. 如图所示，破残的圆形轮片上，弦AB 的垂直平分线交弧AB 于点C ， 交弦AB 于点D 。
圆的定义圆心角圆周角训练题(含答案)
圆的定义圆心角圆周角训练题一、单选题（共17题；共34分）1.（2020九上·江苏月考）下列说法错误的是（）A. 长度相等的两条弧是等弧B. 直径是圆中最长的弦C. 面积相等的两个圆是等圆D. 半径相等的两个半圆是等弧2.（2019九上·台安期中）下列说法中，不正确的个数是（）①优弧一定比劣弧长；②面积相等的两个圆是等圆；③长度相等的弧是等弧；④经过圆心的一个定点可以作无数条弦；⑤经过圆内一定点可以作无数条直径.A. 1个B. 2个C. 3个D. 4个3.（2019九上·沭阳月考）下列命题：①直径相等的两个圆是等圆；②等弧是长度相等的弧；③圆中最长的弦是通过圆心的弦；④一条弦把圆分为两条弧，这两条弧不可能是等弧.其中真命题是( )A. ①③B. ①③④C. ①②③D. ②④4.（2019九上·贾汪月考）下列说法中，错误的是（）A. 半圆是弧B. 半径相等的圆是等圆C. 过圆心的线段是直径D. 直径是弦5.（2018九上·下城期末）下列命题中是真命题的为（）A. 弦是直径B. 直径相等的两个圆是等圆C. 平面内的任意一点不在圆上就在圆内D. 一个圆有且只有一条直径6.（2020九上·浙江期中）如图，是的直径，，，则的度数是（）.A. 52°B. 57°C. 66°D. 78°7.（2019九上·柳江月考）如图，AB是⊙O的直径，，∠COD=34°，则∠AOE的度数是( )A. 51°B. 56°C. 68°D. 78°8.（2019九上·邯郸月考）如图,AB是O的直径, ,∠BOC=40°，则∠AOE的度数为（）A. 30°B. 40°C. 50°D. 60°9.（2019九上·余杭期中）如图，在△ABC中，∠C＝90°，的度数为α，以点C为圆心，BC长为半径的圆交AB于点D，交AC于点E，则∠A的度数为（）A. 45º－αB. αC. 45º＋αD. 25º＋α10.（2020九下·南召月考）如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（）A. AB=ADB. BC=CDC.D. ∠BCA=∠DCA11.（2020九上·无锡月考）在半径为的圆中，长度等于的弦所对的弧的度数为（）A. B. C. 或 D. 或12.（2020·西湖模拟）如图，已知点A，B，C，D，E是⊙O的五等分点，则∠BAD的度数是（）A. 36°B. 48°C. 72°D. 96°13.（2020·衢州模拟）如图，在⊙O中，＝，∠A＝40°，则∠B的度数是（）A. 60°B. 40°C. 50°D. 70°14.（2020·乾县模拟）如图，△ABC内接于⊙O，连接AO并延长交BC于点D，若∠B=70°，∠C=50°，则∠ADB 的度数是（）A. 70°B. 80°C. 82°D. 85°15.（2019九上·龙湖期末）如图，在⊙O中，若点C是的中点，∠A=50°，则∠BOC=( )A. 40°B. 45°C. 50°D. 60°16.（2019九上·道外期末）如图，，是的直径，，若，则的度数是（）A. 32°B. 60°C. 68°D. 64°17.（2019九上·光明期中）如图，已知AB是⊙O的直径，∠CBA=25°，则∠D的度数为（）A. B. C. D.参考答案一、单选题1.【答案】A【解析】【解答】解：A、等弧就是指能完全重合的两段弧，所以长度相等的弧的度数不一定是等弧，故错误；B、直径是圆中最长的弦，正确；C、面积相等的两个圆是等圆，正确；D、半径相等的两个半圆是等弧，正确.故答案为：A.2.【答案】C【解析】【解答】在同圆或等圆中，优弧一定比劣弧长，所以①错误；面积相等的两个圆半径相等，则它们是等圆，所以②正确；能完全重合的弧是等弧，所以③错误；经过圆内一个定点可以作无数条弦，所以④正确；经过圆内一定点可以作无数条直径或一条直径，所以⑤错误.故答案为：C.3.【答案】A【解析】【解答】解：①直径相等的两个圆能重合，所以是等圆，①是真命题；②长度相等的弧不一定能重合，所以不一定是等弧，②是假命题；③圆中最长的弦是直径，通过圆心的弦是直径，③是真命题；④一条弦把圆分成两条弧，这两条弧可以是半圆，所以可能是等弧，④是假命题.故答案为：A.4.【答案】C【解析】【解答】解：A、半圆是弧，所以A选项的说法正确；B、半径相等的圆是等圆，所以B选项的说法正确；C、过圆心的弦为直径，所以C选项的说法错误；D、直径是弦，所以D选项的说法正确.故答案为：C.5.【答案】B【解析】【解答】解：弦不一定是直径，A是假命题；直径相等的两个圆是等圆，B是真命题；平面内的任意一点在圆上、圆内或圆外，C是假命题；一个圆有无数条直径，D是假命题；故选：B．6.【答案】C【解析】【解答】解：∵AB是⊙O的直径，，∠COD=38°，∴∠BOC=∠COD=∠DOE=38°.∴∠BOE=114°，∴∠AOE=180°-114°=66°.故答案为：C.7.【答案】D【解析】【解答】解：∵，∠COD=34°，∴∠BOC=∠COD=∠DOE=34°，∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-34°-34°-34°= 78° .故答案为：D.8.【答案】D【解析】【解答】解：∵，∠BOC=40°∴∠BOC=∠COD=∠EOD=40°∴∠BOE=120°∴∠AOE=180°-∠BOE=60°．9.【答案】A【解析】【解答】解：如图，连接CD，∵的度数为，∴∠DCE= ，∵BC=CD，∴∠CBD=∠BDC= ，∵∠C＝90°，∴∠CBD+∠A=90°，∴，∴；故选择：A.10.【答案】B【解析】【解答】解：A.∵∠ACB与∠ACD的大小关系不确定，∴AB与AD不一定相等，故本选项错误；B.∵AC平分∠BAD，∴∠BAC=∠DAC，∴BC=CD，故本选项正确；C.∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等，故本选项错误；D.∠BCA与∠DCA的大小关系不确定，故本选项错误。
中考圆专题基础练习题
圆专题一、圆心角、圆周角1.如图，设⊙O的半径的为R,且AB=AC=R,则∠BAC=_______.2.如图，AB为⊙O的弦，∠OAB=75O ,则此弦所对的优弧是圆周的______。
4.如图，在△ABC 中，∠C 是直角，∠A=32O 18’ ，以点C 为圆心、BC 为半径作圆，交AB 于点D,交AC 于点E,则⋂BD 的度数是______。
5.如图，点O 是△ABC 的外心，已知∠ACB=100O ,则劣弧⋂AB 所对的∠AOB=______度。
6.如图，AB 是⊙O 的直径，CD 与AB 相交于点E, ∠ACD=60O , ∠ADC=50O ,则∠AEC=______度。
7.如图，以等腰△ABC 的边AB 为直径的半圆，分别交AC 、BC 于点D 、E,若AB=10, ∠OAE=30O,则DE=______。
8.在锐角△ABC 中，∠A=50O ,若点O 为外心，则∠BOC=_____;若点I 为内心，则∠BIC=______；若点H 为垂心，则∠BHC=________.9.若△ABC 内接于⊙O ，∠A=n O,则∠BOC=_______.10.如图，已知AB 和CD 是⊙O 相交的两条直径，连AD 、CB ，那么α和β的关系是（ ） A.α=β B.β>21α C.β<21α D.β=2α 11.如图，在⊙O 中，弦AC 、BD 交于点E ，且⋂⋂⋂==CDBC AB ，若∠BEC=130O ,则∠ACD 的度数为（ ）A.15OB.30OC.80OD.105O12.如图，AB 为半圆的直径，AD ⊥AB,点C 为半圆上一点，CD ⊥AD,若CD=2,AD=3,求AB 的长。
13.如图，AO ⊥BO,AO 交⊙O 于点D ，AB 交⊙O 于点C, ∠A=27O,试用多种方法求⋂DC 、⋂BC 的度数。
14.求证：如果AB 和CD 为⊙O 内互相垂直的两条弦，那么∠AOC 和∠BOD 互补。
浙教版九年级数学上册《圆心角、圆周角》练习题
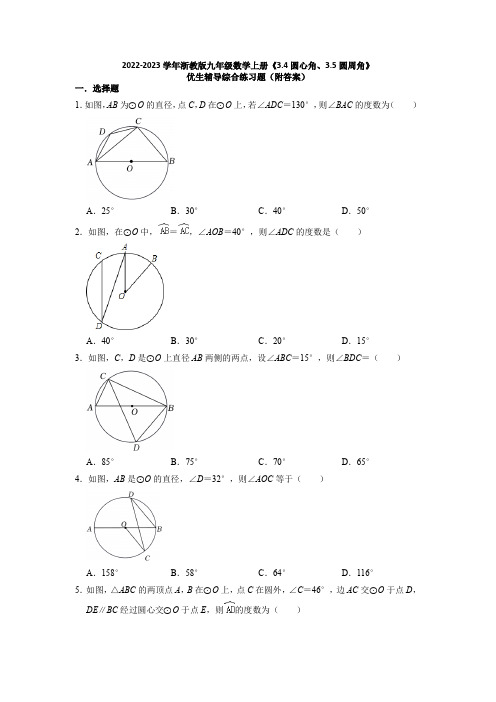
2022-2023学年浙教版九年级数学上册《3.4圆心角、3.5圆周角》优生辅导综合练习题（附答案）一．选择题1．如图，AB为⊙O的直径，点C，D在⊙O上，若∠ADC＝130°，则∠BAC的度数为（）A．25°B．30°C．40°D．50°2．如图，在⊙O中，＝，∠AOB＝40°，则∠ADC的度数是（）A．40°B．30°C．20°D．15°3．如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝15°，则∠BDC＝（）A．85°B．75°C．70°D．65°4．如图，AB是⊙O的直径，∠D＝32°，则∠AOC等于（）A．158°B．58°C．64°D．116°5．如图，△ABC的两顶点A，B在⊙O上，点C在圆外，∠C＝46°，边AC交⊙O于点D，DE∥BC经过圆心交⊙O于点E，则的度数为（）A．44°B．80°C．88°D．92°6．一副学生三角板放在一个圈里恰好如图所示，顶点D在圆圈外，其他几个顶点都在圆圈上，圆圈和AD交于点E，已知AC＝8cm，则这个圆圈上的弦CE长是（）A．6cm B．6cm C．4cm D．cm 二．填空题7．如图，AB为⊙O的直径，点C、D在⊙O上．若∠ACD＝50°，则∠BAD的大小为°．8．如图所示，在△ABC中，AB＝AC，以AB为直径作半圆O，交BC于点D，交AC于点E．若∠BAC＝44°，BD＝2，则弧AE的度数是，DC的长为．9．如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，以点B为圆心，BC长为半径画弧，交边AB于点D，则CD的长为．10．在半径为r的圆中，长度为r的弦所对的圆周角的度数是．11．如图，在⊙O中，∠BAC＝15°，∠ADC＝20°，则∠ABO的度数为．12．如图，A，B，C，D都是⊙O上的点，OA⊥BC，垂足为E，若∠OBC＝20°，则∠ADC 等于度．13．如图，矩形ABCD中，AB＝6，以点D为圆心，CD长为半径的圆弧与以BC为直径的半圆O相交于点E，若的度数为60°，则直径BC长为．14．如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在该圆内．将正方形ABCD绕点A逆时针旋转，当点D第一次落在圆上时，点C旋转到C′，则∠C′AB＝°．15．如图，OA、OB是⊙O的半径且OA＝OB＝1，AB＝，在⊙O上一点C，使BC＝，则∠BAC的度数为．三．解答题16．如图，在下列4×4（边长为1）的网格中，已知△ABC的三个顶点A，B，C在格点上，请分别按不同要求在网格中描出一个格点D，并写出点D的坐标．（1）将△ABC绕点C顺时针旋转90°，画出旋转后所得的三角形，点A旋转后落点为D；（2）经过A，B，C三点有一条抛物线，请找到点D，使点D也落在这条抛物线上；（3）经过A，B，C三点有一个圆，请找到一个横坐标为2的点D，使点D也落在这个圆上，①点D的坐标为；②点D的坐标为；③点D的坐标为．17．如图，在⊙O中，B，C是的三等分点，弦AC，BD相交于点E．（1）求证：AC＝BD；（2）连接CD，若∠BDC＝25°，求∠BEC的度数．18．如图，AB是⊙O的直径，弦CD⊥AB于点M，连接CO，CB．（1）若AM＝2，BM＝8，求CD的长度；（2）若CO平分∠DCB，求证：CD＝CB．19．如图所示，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E，连接AC、OC、BC．（1）求证：∠ACO＝∠BCD；（2）若EB＝8，CD＝24，求⊙O的直径．20．如图，AB是⊙O的直径，点C，E都在⊙O上，OC⊥AB，＝2，DE∥AB交OC 于点D，延长OC至点F，使FC＝OC，连接EF．（1）求证：CD＝OD．（2）若⊙O的直径是4，求EF的长．21．如图，AD为⊙O的直径，∠BAD＝∠CAD，连接BC．点E在⊙O上，AB＝BE，求证：（1）BC平分∠ACE；（2）AB∥CE．22．如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．（1）求证：CF＝BF；（2）若AD＝6，⊙O的半径为5，求BC的长．23．如图，AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，且OC平分∠ACD，延长AC与DB交于点E，过点C作CF⊥OC交DE于点F．（1）求证：∠A＝∠E．（2）若BF＝5，，求⊙O的半径．24．如图，Rt△ABC中，AC＝CB，点E，F分别是AC，BC上的点，△CEF的外接圆交AB 于点Q，D．（1）如图1，若点D为AB的中点，求证：∠DEF＝∠B；（2）在（1）问的条件下：①如图2，连接CD，交EF于H，AC＝4，若△EHD为等腰三角形，求CF的长度．②如图2，△AED与△ECF的面积之比是3：4，且ED＝3，求△CED与△ECF的面积之比（直接写出答案）．（3）如图3，连接CQ，CD，若AE+BF＝EF，求证：∠QCD＝45°．参考答案一．选择题1．解：∵四边形ABCD是圆内接四边形，∴∠ADC+∠B＝180°，∵∠ADC＝130°，∴∠B＝180°﹣130°＝50°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠BAC＝90°﹣∠B＝40°．故选：C．2．解：连接CO，如图：∵在⊙O中，＝，∴∠AOC＝∠AOB，∵∠AOB＝40°，∴∠AOC＝40°，∴∠ADC＝∠AOC＝20°，故选：C．3．解：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠ABC＝15°，∴∠CAB＝75°，∴∠BDC＝∠CAB＝75°，故选：B．4．解：∵∠D＝32°，∴∠BOC＝2∠D＝64°，∴∠AOC＝180°﹣64°＝116°．故选：D．5．解：∵DE||BC，∴∠C＝∠ADE＝46°，∴的度数是92°，∴的度数为180°﹣92°＝88°．故选：C．6．解：作AH⊥CE于H，如图，∠ACB＝90°，∠ABC＝∠BAC＝45°，∠BAD＝30°，∴∠BCE＝∠BAD＝30°，∴∠ACE＝60°，在Rt△ACH中，CH＝AC＝×8＝4cm，∴AH＝CH＝4cm，∵∠AEC＝∠ABC＝45°，∴AH＝HE＝4cm，∴CE＝CH+HE＝（4+4）cm．故选：C．二．填空题7．解：连接BD，∵BD是直径，∴∠ADB＝90°，∵∠ABD和∠ACD所对的弧都是，∴∠ABD＝∠ACD＝50°，∴∠BAD＝90°﹣∠ABD＝90°﹣50°＝40°，故答案为：40．8．解：连接OE，AD，∵OA＝OE，∠BAC＝44°，∴∠BAC＝∠OEA＝44°，∴∠AOE＝92°，∴弧AE的度数是92°，∵AB为半圆O的直径，∴∠ADB＝90°，∵AB＝AC，∴AD是△ABC的中线，∴BD＝CD，∵BD＝2，∴CD＝2．故答案为：92°，2．9．解：连接CD，∵∠ACB＝90°，∠A＝30°，AB＝4，∴∠B＝60°，BC＝AB＝2，∵以点B为圆心，BC长为半径画弧，交边AB于点D，∴△BCD是等边三角形，∴CD＝BC＝2，故答案为：2．10．解：如图，作OD⊥AB，垂足为D，则由垂径定理知，点D是AB的中点，∴AD＝AB＝r，∴∠AOD＝45°，∴∠AOB＝2∠AOD＝90°，∴∠ACB＝∠AOB＝45°，∵A、C、B、E四点共圆，∴∠ACB+∠AEB＝180°，∴∠AEB＝135°，故答案为：45°或135°．11．解：连接AO，CO，则∠AOC＝2∠ADC，∠BOC＝2∠BAC，∴∠AOB＝∠BOC+∠AOC＝2∠BAC+2∠ADC＝2×15°+2×20°＝70°，∵OA＝OB，∴∠ABO＝（180°﹣∠AOB）＝55°，故答案为：55°．12．解：∵OA⊥BC，∴∠OEB＝90°，∵∠OBC＝20°，∴∠AOB＝90°﹣∠OBC＝70°，∴的度数是70°，∵OA⊥BC，OA过圆心O，∴＝，∴的度数是70°，∴圆周角∠ADC＝＝35°，故答案为：35．13．解：如图，连接BE，EC．∵BC是直径，∴∠BEC＝90°，∵的度数＝60°，∴∠BCE＝×60°＝30°，∵四边形ABCD是矩形，∴AB＝CD＝6，∠DCB＝90°，∴∠DCE＝90°﹣30°＝60°，∵DE＝DC，∴△DEC是等边三角形，∴EC＝CD＝6，∴BC＝4．故答案为：．14．解：如图，分别连接OA、OB、OD′、OC、OC′；∵OA＝OB＝AB，∴△OAB是等边三角形，∴∠OAB＝60°；同理可得△OAD′为等边三角形，∴∠OAD′＝60°，∴∠D′AB＝60°+60°＝120°；∵AC′为正方形AB′C′D′的对角线，∴∠D′AC′＝45°，∴∠C′AB＝∠D′AB﹣∠D′AC′＝120°﹣45°＝75°．故答案为75．15．解：如图，作OH⊥BC于H．连接AC．∵OH⊥BC，∴BH＝CH＝，∴∠OBH＝30°，∵OA＝OB＝1，AB＝，∴AB2＝OA2+OB2，∴∠AOB＝90°，∴∠ACB＝∠AOB＝45°，∵∠ABC＝∠ABO+∠OBC＝45°+30°＝75°，∴∠BAC＝180°﹣75°﹣45°＝60°，作点C关于直线OB的对称点C′，连接AC′，BC′，CC′，∵∠OBC＝∠OBC′＝30°，∴∠CBC′＝60°，∵BC＝BC′，∴△BCC′是等边三角形，∴∠BCC′＝60°，∴∠BAC′＝180°﹣60°＝120°，故答案为60°或120°．三．解答题16．解：（1）如图，点B的对应点为B′，点A的对应点为点D（4，2）；故①答案为：（4，2）；（2）抛物线的对称轴在BC的中垂线上，则点D、A关于函数对称轴对称，故点D（3，2），故②的答案为：（3，2）；（3）AB中垂线的表达式为：y＝x，BC的中垂线为：x＝，则圆心O为：（，），设点D（2，m），则OD＝OB，（）2+（）2＝（2﹣）2+（m﹣）2，解得：m＝0或3（舍去0），故点D（2，3）；故③的答案为（2，3）．17．（1）证明：∵B，C是的三等分点，∴＝＝，∴+＝+，∴＝，∴AC＝BD；（2）解：如图，连接CD，AD，∵∠BDC＝25°，＝＝，∴∠CAD＝∠BDA＝∠BDC＝25°，∵∠AED+∠CAD+∠BDA＝180°，∴∠AED＝180°﹣∠CAD﹣∠BDA＝130°，∴∠BEC＝∠AED＝130°．18．解：（1）∵AB是⊙O的直径，弦CD⊥AB，∴CM＝DM，∵AM＝2，BM＝8，∴AB＝10，∴OA＝OC＝5，在Rt△OCM中，OM2+CM2＝OC2，∴CM＝＝4，∴CD＝8；（2）过点O作ON⊥BC，垂足为N，∵CO平分∠DCB，∴OM＝ON，∴CB＝CD．19．（1）证明：∵AB⊥CD，∴，∴∠A＝∠BCD，∵OA＝OC，∴∠A＝∠ACO，∴∠ACO＝∠BCD；（2）解：设⊙O的半径为r，则OC＝r，OE＝OA﹣BE＝r﹣8，∵AB⊥CD，∴CE＝DE＝CD＝×24＝12，在Rt△OCE中，122+（r﹣8）2＝r2，解得r＝13，∴⊙O的直径＝2r＝26．20．（1）证明：连接OE、CE，如图，∵OC⊥AB，∴∠AOC＝90°，∵＝2，∴∠COE＝2∠AOE，∴∠COE＝60°，而OE＝OC，∴△OCE为等边三角形，∵DE∥AB，OC⊥AB，∴DE⊥OC，∴CD＝OD；（2）解：∵⊙O的直径是4，∴OE＝OC＝CF＝2，CD＝OD＝1，在Rt△ODE中，DE＝＝，在Rt△EFD中，EF＝＝＝2．21．证明：（1）∵AB＝BE，∴，∴∠ACB＝∠BCE，∴BC平分∠ACE；（2）连接OC、OB，∵OA、OB、OC是⊙O半径，∴OA＝OB＝OC，∴∠OAB＝∠OBA，∠OAC＝∠OCA，∵∠BAD＝∠CAD，∴∠ABO＝∠ACO，∵OB＝OC，∴∠OBC＝∠OCB，∴∠OBA+∠OBC＝∠OCA+∠OCB，∴∠ABC＝∠ACB，∴AB＝AC，∵AB＝BE，∴AC＝BE，∴，∴∠ABC＝∠ECB，∴AB∥CE．22．（1）证明：连接AC，如图1所示：∵C是弧BD的中点，∴∠DBC＝∠BAC，在ABC中，∠ACB＝90°，CE⊥AB，∴∠BCE+∠ECA＝∠BAC+∠ECA＝90°，∴∠BCE＝∠BAC，又C是弧BD的中点，∴∠DBC＝∠CDB，∴∠BCE＝∠DBC，∴CF＝BF．（2）解：连接OC交BD于G，如图2所示：∵AB是O的直径，AB＝2OC＝10，∴∠ADB＝90°，∴BD＝＝＝8，∵C是弧BD的中点，∴OC⊥BD，DG＝BG＝BD＝4，∵OA＝OB，∴OG是△ABD的中位线，∴OG＝AD＝3，∴CG＝OC﹣OG＝5﹣3＝2，在Rt△BCG中，由勾股定理得：BC＝＝＝2．23．（1）证明：由题意∠ACO＝∠A＝∠D．∵OC平分∠ACD，∴∠ACO＝∠OCD，∴∠OCD＝∠D．∴OC∥DE，∴∠E＝∠ACO，∴∠E＝∠A．（2）解：∵，∴设BD＝3x，OB＝4x，由（1）得∠E＝∠A＝∠CDE，OC∥DE．∵CF⊥OC，∴CF⊥DE，∴EF＝DF＝3x+5．∴BE＝3x+10，∵∠E＝∠A，∴AB＝BE，即3x+10＝8x，解得x＝2∴半径OB＝4x＝8．24．（1）证明：连接CD．在Rt△ABC中，∵AC＝CB，∴∠A＝∠B＝45°，∵CD＝DB，∴∠DCB＝∠B＝45°，∵∠DEF＝∠DCB，∴∠DEF＝∠B．（2）解：①如图2﹣1中，当EH＝HD，可证四边形CFDE是正方形CF＝2．如图2﹣2中，当EH＝ED时，∠EDH＝∠EHD＝67.5°，∵∠EDF＝∠CDB＝90°，∴∠EDH＝∠BDF＝67.5°，∴∠BFD＝180°﹣45°﹣67.5°＝67.5°，∴∠BDF＝∠BFD，∴BD＝BF，∵AC＝BC＝4，∠ACB＝90°，∴AB＝＝4，∴BD＝BF＝2，∴CF＝4﹣2．如图2﹣3中，当DA＝FH时，点E于A重合，点H与C重合，CF＝0．综上所述，满足条件的CF的值为0或2或4﹣2．②如图2﹣4中，作DM⊥AC于M，DN⊥BC于N，连接DF．∵CA＝CB，AD＝DB，∠ACB＝90°，∴CD⊥AB，∠ACD＝∠BCD＝45°，CD＝DA＝DB∴DE＝DF，∵∠ADC＝∠EDF＝90°，∴∠ADE＝∠CDF，∴△ADE≌△CDF（SAS），∴AE＝CF，S△ADE＝S△CDF，∵DC平分∠ACB，DM⊥AC，DN⊥BC，∴DM＝DN，可得四边形DMCN是正方形，∴DM＝CM＝CN＝DN，∵＝＝＝＝，∴可以假设DN＝3k，EC＝4k，则AC＝BC＝6k，AE＝CF＝2k，∴＝＝．（3）证明：连接OD，OQ，作ER⊥AB，OH⊥AB，FK⊥AB．∵ER∥OH∥FK，EO＝OF，∴RH＝HK∴OH＝（ER+FK），∵ER＝AE，FK＝FB，∴OH＝（AE+BF）＝EF＝OE＝OQ，∴∠OQD＝∠ODQ＝45°，∴∠QOD＝90°，∴∠QCD＝45°．。
圆周角圆心角垂径定理练习
江苏通海中学周飞初三数学周末练习班级：姓名：学号：一．选择题（共8小题）1．（2013•丽水）一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是（）5C2．（2012•茂名）如图，AB是⊙O的直径，AB⊥CD于点E，若CD=6，则DE=（）则OP的长为（）4．（2013•黄石）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为（）．．6．（2007•仙桃）如图，已知：AB是⊙O的直径，C、D是上的三等分点，∠AOE=60°，则∠COE是（）二．填空题（共8小题）9．（2009•郴州）如图，在⊙O中，，∠A=40°，则∠B=_________度．10．如图，在⊙O中，=，如果∠AOC=65°，则∠BOD=_________．11．（2011•阜新）如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=18°，则∠AOC的度数为_________度．12．（2010•湘西州）如图，在⊙O中，半径为5，∠AOB=60°，则弦长AB=_________．13．（2013•漳州）如图，一个宽为2厘米的刻度尺（刻度单位：厘米），放在圆形玻璃杯的杯口上，刻度尺的一边与杯口外沿相切，另一边与杯口外沿两个交点处的读数恰好是3和9，那么玻璃杯的杯口外沿半径为_________厘米．14．（2013•西宁）如图，AB为⊙O的直径，弦CD⊥AB于点E，若CD=6，且AE：BE=1：3，则AB=_________．15．（2013•上海）在⊙O中，已知半径长为3，弦AB长为4，那么圆心O到AB的距离为____．16．（2012•遵义）如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为_________．三．解答题（共8小题）17．（2011•佛山）如图，已知AB是⊙O的弦，半径OA=20cm，∠AOB=120°，求△AOB的面积．18．（2010•长春）如图，将一个两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D，E，量出半径OC=5cm，弦DE=8cm，求直尺的宽．19．（2006•青岛）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面；（2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．20．如图所示，在⊙O中，AB与CD是相交的两弦，且AB=CD，求证：．21．如图在⊙O中，AC=BC，OD=OE，求证：∠ACD=∠BCE．22．已知：如图，A、B、C、D是⊙O上的点，∠1=∠2，AC=3cm．（1）求证：=；（2）求BD的长．23．如图，点A、B、C、D在⊙O上，AB与OC、OD分别相交于E、F，AE=BF，说明AC=BD的理由．24．（2012•长春一模）如图，四边形ABCD是矩形，以AD为直径的⊙O交BC边于点E、F，AB=4，AD=12．求线段EF的长．2013年10月hylzf的初中数学组卷参考答案与试题解析一．选择题（共8小题）1．（2013•丽水）一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是（）AB=×OC==62．（2012•茂名）如图，AB是⊙O的直径，AB⊥CD于点E，若CD=6，则DE=（）AB=×3．（2012•陕西）如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（）OM=ON=4．（2013•黄石）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为（）．．==5=AB，）AM=，．6．（2007•仙桃）如图，已知：AB是⊙O的直径，C、D是上的三等分点，∠AOE=60°，则∠COE 是（）是二．填空题（共8小题）9．（2009•郴州）如图，在⊙O中，，∠A=40°，则∠B=70度．10．如图，在⊙O中，=，如果∠AOC=65°，则∠BOD=65°．=，可得，继而求得∠中，=++，=11．（2011•阜新）如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=18°，则∠AOC的度数为54度．12．（2010•湘西州）如图，在⊙O中，半径为5，∠AOB=60°，则弦长AB=5．13．（2013•漳州）如图，一个宽为2厘米的刻度尺（刻度单位：厘米），放在圆形玻璃杯的杯口上，刻度尺的一边与杯口外沿相切，另一边与杯口外沿两个交点处的读数恰好是3和9，那么玻璃杯的杯口外沿半径为厘米．AB=×cm故答案为：14．（2013•西宁）如图，AB为⊙O的直径，弦CD⊥AB于点E，若CD=6，且AE：BE=1：3，则AB=4．x=AB=4x=415．（2013•上海）在⊙O中，已知半径长为3，弦AB长为4，那么圆心O到AB的距离为．AB=×==故答案为：16．（2012•遵义）如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为4．ABAB=×三．解答题（共8小题）17．（2011•佛山）如图，已知AB是⊙O的弦，半径OA=20cm，∠AOB=120°，求△AOB的面积．∠AC=BC=AOC=∠ABOA=10cm=10cm=××cm18．（2010•长春）如图，将一个两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D，E，量出半径OC=5cm，弦DE=8cm，求直尺的宽．DM=OM==319．（2006•青岛）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面；（2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．BD=AB=AB=×20．如图所示，在⊙O中，AB与CD是相交的两弦，且AB=CD，求证：．就是已知，要证明，可以转化为证明=21．如图在⊙O中，AC=BC，OD=OE，求证：∠ACD=∠BCE．22．已知：如图，A、B、C、D是⊙O上的点，∠1=∠2，AC=3cm．（1）求证：=；（2）求BD的长．，根据在同圆或等圆中，相等的圆心角所对的弧相等得到=）由，根据在同圆或等圆中，等弧所对的弦相等得到=++，==23．如图，点A、B、C、D在⊙O上，AB与OC、OD分别相交于E、F，AE=BF，说明AC=BD的理由．，24．（2012•长春一模）如图，四边形ABCD是矩形，以AD为直径的⊙O交BC边于点E、F，AB=4，AD=12．求线段EF的长．的长度为。
圆、圆心角、圆周角 综合
图2OBAC图3OBAC《圆、圆心角、圆周角》 姓名知识点：1、 顶点在圆心，两边与圆相交的角，叫圆心角。
顶点在圆上，两边与圆相交的角，叫圆周角。
2、 圆心角定理：在同圆或等圆中，相等圆心角所对的弦相等、弧相等、所对弦的弦心距也相等。
弧的度数等于弧所对圆心角的度数。
3、 同圆或等圆中（所对）：① 圆心角相等， ② 弦相等 ③ 弧相等 ④ 弦心距相等；任选一个作为条件，其它三个结论成立。
4、 圆周角定理：圆周角的度数等于同弧所对的圆心角度数的一半（等于所对弧度数的一半）。
5、 由圆周角定理可得：半圆（或直径）所对的圆周角是直角。
90O 的圆周角所对的弦是直径，弧是半圆。
6、 等弧的概念：只有在同圆或等圆中才有相等的圆心角所对的是等弧。
夹在两平行弦间的两弧相等。
7、 在半径为R 的圆中，垂直于半径中点的弦长等于 。
例证：证明圆周角的度数等于同弧所对的圆心角度数的一半（分类讨论）圆心在角边上时 圆心在角内时 圆心在角外时 证： 证： 证：一、选择题（24分）1、下列说法不正确的是 （ ）A 圆周角的度数等于所对弧的度数的一半。
B 圆是中心对称图形，也是轴对称图形C 垂直于直径的弦必被直径平分D 劣弧是大于半圆的弧2、在⊙O 中，AB 、AC 是互相垂直的两条弦，AB=8，AC=6，则⊙O 的半径为 （ ）A 4B 5C 8D 103、同圆中两条弦长为10和12，它们的弦心距为m 和n ，则 （ ）A m ＞nB m ＜nC m ＝nD m 、n 的大小无法确定 4、平面上有4个点，它们不在同一直线上，过其中3个点作圆，可以作出不重复的圆n 个，则n 的值不可能为 （ ） A 4 B 3 C 2 D 16、如图，⊙O 的直径CD=10，AB 是⊙O 的弦，AB ⊥CD 于M ，且DM ∶MC=4∶1，则AB 的长是 （ ）A 2B 8C 16 D91图1OBACCBOADDCBEA OACBEDO A CBD CBAOM 46OP第5题 第6题 第7题6、如图，AB 、CD 为⊙O 直径，则下列判断正确的是 （ ）A AD 、BC 一定平行且相等B AD 、BC 一定平行但不一定相等 C AD 、BC 一定相等但不一定平行 D AD 、BC 不一定平行也不一定相等7、点P 为⊙O 内一点，且OP ＝4，若⊙O 的半径为6，则过点P 的弦长不可能为 （ ）A 302B 12C 8D 10.58．如图所示，已知△ACD 和△ABE 都内接于同一个圆，则∠ADC+∠AEB+∠BAC=（ ） A.90° B.180° C.270° D.360°9．如图,AB 是⊙的直径,弦AB CD ⊥于E,如果16,20==CD AB ,那么线段OE 的长为 ( ) A ．10 B.8 C.6 D.4二、填空题（30分）1、．如图，CD 是⊙O 的直径，弦AB ⊥CD ，垂足为OC 的中点M ，AB=20，分别以DM 、CM 为直径作两个大小不同和⊙O 1和⊙O 2，则图中所示阴影部分的面积为 .（结果保留π）2、已知AB 是⊙O 的弦，且AB=OA ，则∠AOB ＝ 度。
完整版)圆心角圆周角练习题
完整版)圆心角圆周角练习题知识点三：弧、弦、圆心角与圆周角1.定义圆心角为顶点在圆心的角。
2.在同圆或等圆中，弧、弦、圆心角之间的关系：两个圆心角相等，圆心角所对的弧相等（无论是优弧还是劣弧），圆心角所对的弦相等。
3.一个角是圆周角必须满足两个条件：（1）角的顶点在圆上；（2）角的两边都与圆有除顶点外的交点。
4.同一条弧所对的圆周角有两个。
5.圆周角定理：圆周角等于圆心角的一半。
6.圆周角定理的推论：（1）同弦或等弦所对的圆周角相等；（2）半圆或直径所对的圆周角相等；（3）90°的圆周角所对的弦是直径。
需要注意的是，“同弦或等弦”改为“同弧或等弧”结论就不一定成立了，因为一条弦所对的圆周角有两类，它们是相等或互补关系。
7.圆内接四边形定义为所有顶点都在圆上的多边形，圆心即为这个圆内接四边形的交点。
圆内接四边形的对角线相互垂直，且交点为对角线的中点。
夯实基础1.如果两个圆心角相等，则它们所对的弧相等，选项B正确。
2.不正确的语句为③，因为圆不一定是轴对称图形，只有圆上的任何一条直径所在直线才是它的对称轴。
3.错误的说法是D，相等圆心角所对的弦不一定相等。
4.根据圆心角的性质，∠A=2∠B，所以∠A=140°。
5.∠BAC与∠BCD互补，∠BCD与∠CBD相等，所以与∠BAC相等的角有2个，即∠CBD和∠ABD。
6.因为∠CAB为30°，所以∠ABC为60°，由正弦定理可得BC=5√3.7.根据圆周角定理，∠ACB=40°。
8.设∠A=3x，∠B=4x，∠C=6x，则∠D=360°-3x-4x-6x=120°。
9.∠DCE=∠A。
1、如图，AB是⊙O的直径，C，D是BE上的三等分点，∠AOE=60°，求证∠COE=80°。
证明：由三等分点的性质可知，BC=CD=DE，又∠AOE=60°，所以∠AOC=120°。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4
、
如图，在。
中, AB = AC,
ZB=70°,
则匕A 等
于
5
、
如图，在。
中,
若C是BD的中点，则图中与ABAC相等的角有（）
A.1
个
B.2
个
C.3
个
D.4
个
夯实基础
1.如果两个圆心角相等，那么（）
A.这两个圆心角所对的弦相等；
B.这两个圆心角所对的孤相等
C.这两个圆心角所对的弦的弦心距相等；
D.以上说法都不对
2.下列语句中不正确的有（）
①相等的圆心角所对的孤相等②平分弦的直径垂直于弦③圆是轴对称图形，任何一条直
径所在直线都是它的对称轴④长度相等的两条孤是等孤
A.3个
B.2个
C.1个
D.以上都不对
3.在同圆或等圆中，下列说法错误的是（）
A.相等弦所对的弧相等
B.相等弦所对的圆心角相等
C.相等圆心角所对的弧相等
D.相等圆心角所对的弦相等
6、如图，若AB 是。
0 的直径，AB=10cm, ZCAB=30°,贝ij BC=cm.
题型一：利用圆心角圆周角定理求角度
1、如图，AB是。
的直径，BC=CD=DE, ZCOD=34°,则匕AEO的度数是（）
A.51°
B. 56°C- 68° D. 78°A
2、圆中有两条等弦AB=AE,夹角ZA=88°,延长AE到C,使EC=BE,连接BC,如图.则
ZABC的度数是（）
A. 90°
B. 80°
C. 69°
D. 65°
3、如图所示。
O中，己矢nZBAC=ZCDA=20°,则匕ABO的度数为.
4、
在。
中，弦AB所对的劣孤为圆周的上，圆的半径等于12,则圆心角ZAOB=__________ ；
4
弦AB的长为.
5、如图，在△ ABC中，AB为。
O的直径，ZB=60°, ZBOD=100°,则NC的度数为（）A. 50° B. 60° C. 70° D. 80°
6、如图，点A、B、C在。
O上，ZAOC=60°,则NABC的度数是.
7、如图，点A、B、C、D 在。
O 上，OB_LAC,若ZBOC=56°,则ZADB=度.
8、如图，的弦CD与直径AB相交，若ZBAD=50°,则ZACD=.
9、如图，AB是OO的直径，点C是圆上一点，ZBAC=70°,则ZOCB=.
10、如图，在RtAABC中，ZC=90°, ZA=26°,以点C为圆心，BC为半径的圆分别交AB、
AC于点D、点E,则弧BD所对的圆心角的度数为（）
A. 26°
B. 64°
C. 52°
D. 128°
题型二：利用圆心角圆周角的性质定理求线段
1、如图，。
0是Z\ABC的外接圆，ZB=60°, OP±AC于点P, OP=2>/3 ,则。
O的半径
为（）
A. 4^3
B. 6^3
C. 8
D. 12
B. AB > 2CD
C. AB < 2CD
D.人8与。
的大小关系不定。
题型三：利用孤、弦、度相等心角、圆周角之间的关系证明弧相等，线段相等，角
3、如图，△ ABC 内接于OO, ZBAC=120% AB=AC, BD 为。
O 的直径，AD=6,则DC=
4、在。
中，AB = 2CD,那么()
A. AB = 2CD
1.如图，在OO 中，C、D 是直径AB ±两点，且AC=BD, MC1AB, ND1AB, M、N
在OO±.
(1)求证：AM = BN；
(2)若C、D分别为OA、OB中点，则AM=MN = NB成立吗?
2、如图，以。
O的直径BC为一边作等边△ABC,AB、AC交③。
于D、E,求证：BD=DE=EC
4、如图，QO的直径扇为10cm,弦AC为6cm, ZACB的平分线交。
O于D,求BC,
AD, BD的长.
5、如图，AB是。
的直径，C是BD的中点，CELAB于E, BD交CE于点、F.
(1)求证：CF= BF；
(2)若CD = 6, AC = 8,则。
的半径为，CE的长是 .
c
D
O E
B
6.如图，A, P, B, C是半径为8的。
O上的四点，旦满足ZBAC=ZAPC=60°,
(1)求证：Z\ABC是等边三角形；
(2)求圆心。
到BC的距离OD.
7、
如图，。
是Z\ABC的外接圆，AB是。
O的直径，D为。
O上一点，ODJ_AC,垂足为E,连接BD
(1)求证：BD平分
ZABC；
(2)当ZODB=30°时，求证：BC=OD.
8、如图所示，以■ABCD的顶点A为圆心，AB为半径作圆，作AD, BC于E, F,延长BA
交。
0于G,求证：GE = EF .。