三垂线定理及其逆定理
三垂线定理的逆定理

三垂线定理的逆定理

【练习】:
△BCD所在平面外的一点A在平面BCD内的 射影O为△BCD的垂心 求证:点B在△ACD内的射影P是△ACD的垂心。
例2.已知:四面体S-ABC中,SA⊥平面ABC, △ABC是锐角三角形,H是点A在面SBC上的 射影。 求证:H不可能是△SBC的垂心.
S
H
A
C
B
例3.已知:如图,在正方体ABCD-A1B1C1D1 中,E是CC1的中点,F是AC、BD的交点。 求证:A1F⊥平面BED.
D1
C1
A1
B1
D A
C B
二:例题分析
例1.点A为△BCD所在平面外的一点,点O为点A 在平面BCD内的射影,若AC⊥BD,AD⊥BC, 求证:AB⊥CD. A
B
D
O
C
炸鸡一样的身躯和墨绿色细小玉葱似的皮毛,头上是淡蓝色邮筒造型的鬃毛,长着淡白色熊猫一样的火龙金鳞额头,前半身是淡绿色匕首一样的怪鳞,后半身是神奇的羽毛。 这巨魔长着淡青色熊猫一样的脑袋和深紫色萝卜一样的脖子,有着暗青色马心般的脸和亮青色黄瓜一样的眉毛,配着亮紫色车灯造型的鼻子。有着墨蓝色般的眼睛,和深白色
E
D
A
3、如图,过直角三角形BPC的 直角顶点P作线段PA⊥平面BPC,
求证:P在平面PBC内的射影H
H
是△ABC的垂心。
P
C
B
D1
C1
B1 A1
E
D
F A
C G B
五.课堂小结:
三垂线定理及其逆定理的应用。
六.作业:
1.已知P是△ABC所在平面外一点,PA、PB、
PC
B
两两垂直,H是△ABC的垂心,
F
求证:PH⊥平面ABC.
三垂线定理及逆定理的应用

练习1:
如图:已知点O、B以及
A直线a在平面ຫໍສະໝຸດ 内,点A在平面外, 给出如下三个结论: ①AB⊥α ;②OA⊥a ;③OB⊥a 。 把其中两个作为条件,另一个作 为结论,共可组成多少个命题, 其中是真命题的是:
α
O
a
B
例1、点 A为 DBCD 所在平面外的 一点,点 O为点 A 在平面 BCD内的 射影,若 AC ^ BD , AD ^ BC ,
例2、在正方体ABCD-A1B1C1D1中,
E是CC1的中点,F是AC,BD的交点。
求证:A1F ^ 平面BED。 D1
A1 D B1
C1 E C F B
A
课堂练习: 1、在正方体ABCD-A1B1C1D1中,
求证:BD1 ^A1C1, BD1 ^B1C。
2、设P 是DABC所在平面外一点,当P 分别满足下列条件时,判断点P 在平 面内的射影的位置: (1)到三角形各边的距离相等; (2)到三角形各顶点的距离相等; (3)PA、PB、PC 两两垂直。
1、三垂线定理包括5个要素:一面(垂面);
四线(斜线、垂线、射影和平面内的直线。
顺口溜:一定平面,二定垂线,三找斜线,射 影可见,直线随便。
2、“三垂线”的含义: (1)垂线与平面垂直
(2)射影与平面内的直线垂直
(3)斜线与平面内的直线垂直
求证: O 为 DBCD的垂心。
A
B C
O
D
A
变形1:求证 AB ^ CD。
D
B C
O
变形2:若三棱锥的两组 对棱相互垂直,求证: 第三组对棱也垂直。
变形3:点A为DBCD所在平面外的一点, 点O为DBCD的垂心,若AO^平面BCD,求 证:AC ^ BD 。 变形4: DBCD所在平面外的一点A在平面 BCD内的射影O为DBCD的垂心,求证:点 B在DACD内的射影P是DACD的垂心。
三垂线定理及三垂线逆定理
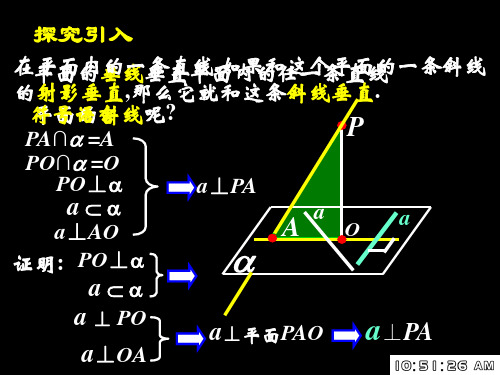
BC ⊥ PC
A O BPB=PC, M是BC的中点, 求证:BC⊥AM P
C A M
证明: PB=PC
B M= M C
BC ⊥ PM
B BC⊥AM
PA⊥平面PBC
我们要学会从纷繁的已知条件和各式各样的位置 图形中找出或者创造出符合三垂线定理的条件
P
解 题 回 顾
证明: 连结AC, CC1⊥平面ABCD BD⊥AC AC1⊥BD 同理AC1⊥A1B
D
D1 C A A1
B1
B
AC1⊥平面BA1D.
本节课到此结束,请同学们课后再 做好复习与作业。谢谢!
作业:见题单
再见!
例 在空间四边形ABCD中,已知 CD ⊥ AB , BD ⊥ AC. 求证:BC ⊥ AD . 证明:
A
作AO⊥平面BCD于点O CD ⊥ AB
CD ⊥ BO
同理 BD ⊥ CO O是△BCD的垂心 BC ⊥ DO AO⊥平面BCD BC ⊥ AD.
B O D
C
例 在正方体ABCD—A1B1C1D1中, C1 求证:AC1⊥平面BA1D.
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么它也和这条斜线的射影垂直.
三垂线定理的逆定理
在平面内的一条直线,如果和这个平面的一条斜线 的射影垂直,那么它就和这条斜线垂直.
线射垂直
定 理
逆 定 理
P
a
线斜垂直
A
O
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么它也和这条斜线的射影垂直.
α
A
O
a
P
α
P
A O
a
A
C
高中数学选修2-1三垂线定理及逆定理(一)
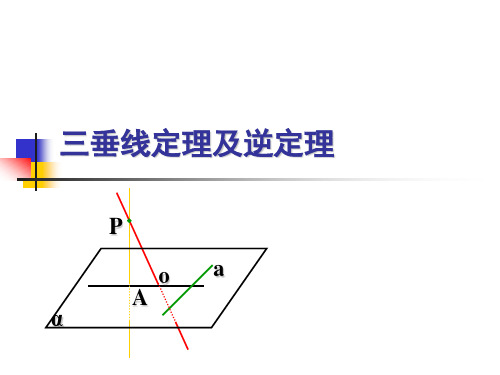
[思考2]:
在四面体A-BCD中
A
若AB CD, BC AD, 求证:AC BD.
D
B
O
C
[思考3]:
D1 A1
P
C1 B1
O M N
若O为 B1 BCC1中心, P为 D1 D 上一点, 求证:PO⊥AM
C
D A
B
[思考4]:
D1 A1 G D A B1 F B C1 E C
设正方体 ABCD A1B1C1D1 的 棱长为2, 若E为 C1C 的中点,
A
o
a
理解和深化
⒈为什么称为“三垂线”定理?
P α A o
a
三种垂直关系: ①线面垂直②线射垂直③线斜垂直 ⒉这个定理的作用是什么? 三垂线定理实质是平面内的直线和平面的斜线垂直 的判定定理.
3.如果将定理中“在平面内”的条件去掉,结 论成立吗?
P
α A
o
a
直线a必须要在平面内,如果a 不在平面内,定理就不一定成 立.
三垂线定理及逆定理
P
α
A
o
a
[思考]
如图, l 是平面α的一条斜线,如何在α内画一 l垂直? 条直线与
l
α
a
涉及到三对垂直关系
l P
A a
: PO , OA a , PA a
其中 : PO PA a OA a A - - - - - - - -三垂线定理 . PO OA a PA a - - - - - - - -三垂线逆定理 .
D1 A1 B1 D A B
C1 练习: (1)求证: D1 B B1C (2)求证: D1 B 平面AB1C C
三垂线定理及其逆定理

三垂线定理及其逆定理【学习内容分析】“三垂线定理”是安排在“直线与平面的垂直的判定与性质”后进行学习的。
它是线面垂直性质的延伸。
利用三垂线定理及其逆定理,可将空间两直线垂直与平面两直线垂直进行互相转化,具体应用表现例如辅助我们做二面角平面角等。
所以在立体几何中有核心定理的作用。
【课程目标】一.知识与技能目标理解和掌握三垂线定理及其逆定理的内容、证明和应用。
二.过程与方法目标1通过对定理的学习,培养学生观察、猜想和论证数学问题的能力。
三.情感、态度和价值观目标3、培养学生逻辑推理证明的能力和相互转化的思想。
【教学重点和难点】一.教学重点定理的理解和运用二.教学难点如何在具体图形中找出适合三垂线定理(或逆定理)的直线和平面。
【教学方法】以教师为主导,以学生为主体,以能力发展为目标,从学生的认识规律出发进行启发式教学,运用小组学习合作探究。
【教学过程】一复习引入:1.复习提问1、回顾直线与平面垂直的相关性质以及射影、斜线等概念;设计意图(因为平面的垂线、平面的斜线及射影是三垂线定理的基础,直线与平面垂直的判定与性质又是证明三垂线定理的基本方法,因此我用提问的形式让学生温故知新,作好新课的铺垫。
)2.有意设疑,引入新课。
平面的垂线垂直于平面内的每一条直线;平面的斜线不能垂直于平面的每一条直线,但也不是与每一条直线都不垂直。
那么平面的斜线与平面内的直线在什么情况下是垂直的呢?学生思考后,我再引导学生利用三角板和直尺在桌面上搭建模型(如图),使直尺与三角板的斜边垂直,引导学生猜想发现规律。
经过实验,发现直尺与三角板在平面内的直角边垂直时便与斜边垂直。
启发学生把猜想、实验后得到的结论总结出来,表达成数学命题:平面内的一条直线如果和平面的斜线的射影垂直,那么就和平面的这条斜线垂直(板书)设计意图(为了唤起学生学习的兴趣,把学生的注意力集中起来,调动学生的思维积极性,我通过提出问题,创设情景,引导学生观察、猜想,发现新的知识,培养学生的探索能力)二、新课讲授:由以上的分析,我们可以抽象出如下的一个图。
三垂线定理

三垂线定理定义:在平面内的一条直线,如果和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面的射影垂直。
具体如下:1,三垂线定理描述的是PO(斜线),AO(射影),a(直线)之间的垂直关系.2,a与PO 可以相交,也可以异面.3,三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理.关于三垂线定的应用,关键是找出平面(基准面)的垂线.至于射影则是由垂足,斜足来确定的,因而是第二位的.从三垂线定理的证明得到证明a⊥b的一个程序:一垂,二射,三证.即第一,找平面(基准面)及平面垂线第二,找射影线,这时a,b便成平面上的一条直线与一条斜线.第三,证明射影线与直线a垂直,从而得出a与b垂直。
扩展资料:三垂线定理与逆定理的核心就是两两垂直。
其中射影就是斜线的一端到另一端到平面的垂线段的连线。
三垂线定理:影垂不怕线斜(形影不离),即垂直射影垂斜线。
三垂线定理逆定理:斜垂影随其身(影随其身),即:垂直斜线垂射影。
三垂线定理

即一垂二射三证
P a α A o
一、证明线线垂直 P是侧棱 1上的一点,CP=m. 则 在线段 1C1上是否存 是侧棱CC 上的一点, 在线段A 是侧棱 在一个定点Q,使得对任意的m, 在平面APD1上的 在一个定点 ,使得对任意的 ,D1Q在平面 在平面 z 射影垂直于AP.并证明你的结论. 射影垂直于 .并证明你的结论. 推测: 应当是A 中点O 推测:点Q应当是 1C1的中点 1 , 应当是 ∵ D1O1⊥A1C1, A1 D1O1⊥A1A 平面ACC1A1 ∴D1O1⊥平面 平面ACC1A1 又AP 平面 ∴ D1O1⊥AP 根据三垂线定理知, 三垂线定理知 根据三垂线定理知,D1O1在 A 平面APD1的射影与 垂直 . x 的射影与AP垂直 平面
C
B
α A
E
由CA=30,CB=40,所以 =50. , = ,所以AB= . 由面积公式得 AB•CE=AC•CB, = , 易求得CE=24,再由勾股定理可得 易求得 ,再由勾股定理可得DE=26. .
三、证明线面垂直
例4 如图,已知正方体ABCD-A1B1C1D1中,连结BD1, ABCD连结BD 如图,已知正方体ABCD AC, AC,CB1,B1A,求证:BD1⊥平面AB1C 求证: 平面AB
D1 O1 B1 C1
的正方体AC 例2 (06湖北 )如图,在棱长为 的正方体 1中, 湖北 如图,在棱长为1的正方体
P
D B C
y
பைடு நூலகம்法二
若存在这样的点 Q , 设此点的横坐标为 x, 则 Q ( x , 1 − x , 1 ), DQ = ( x,1− x,0) , 1 对任意的m要使在平面上的射影垂直于 对任意的 要使在平面上的射影垂直于 AP ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三垂线定理及其逆定理
知识点:
1、三垂线定理;;
2、三垂线定理得逆定理;
3、综合应用; 教学过程:
1.三垂线定理:平面内一条直线,如果与这个平面得一条斜线在平面内得射影垂直,那么这条直线就与这条斜线垂直;
已知:,PA PO 分别就是平面α得垂线与斜线,AO 就是PO 在平面α得射影,,a α⊂a AO ⊥。
求证:a PO ⊥; 证明: 说明:
(1)线射垂直(平面问题)⇒线斜垂直(空间问题); (2)证明线线垂直得方法:定义法;线线垂直判定定理;三垂线定
理;
(3)三垂线定理描述得就是PO(斜线)、AO(射影)、a(直线)之间得垂直关系。
(4)直线a 与PO 可以相交,也可以异面。
(5)三垂线定理得实质就是平面得一条斜线与平面内得一条直线垂直得判定定理。
例1、已知P 就是平面ABC 外一点,,PA ABC AC BC ⊥⊥。
求证:PC BC ⊥。
例2、已知PA ⊥正方形ABCD 所在平面,O 为对角线BD 得
求证:,PO BD PC BD ⊥⊥。
例4、在正方体1AC 中,求证:1111
1,AC B D AC BC ⊥⊥; 2.写出三垂线定理得逆命题,并证明它得正确性;
命题: 已知:
求证: 证明: 说明:
例2.在空间四边形ABCD 中,设,AB CD AC BD ⊥⊥。
求证:(1)AD BC ⊥;
(2)点A 在底面BCD 上得射影就是BCD ∆得垂心; 例3、求证:如果一个角所在平面外一点到角得两边得距离相等这点在平面内得射影在这个角得平分线上 已知: 求证:
说明:可以作为定理来用。
P
C
例5.已知:Rt ABC ∆中,,3,42
A A
B A
C π
∠=
==,PA 就是面ABC 得斜线,3
PAB PAc π
∠=∠=。
(1)求PA 与面ABC 所成得角得大小;
(2)当PA 得长度等于多少得时候,点P 在平面ABC 内得射影恰好落在边BC 上;
作业:
1、正方体1111D C B A ABCD -,,E F 分别就是1,A A AB 上得点,1EC EF ⊥、 求证: 1EF EB ⊥。
2、已知:PA ⊥平面PBC ,,PB PC M =就是BC 得中点。
求证:BC AM ⊥;
3、填空并证明: (1)在四面体ABCD 中,对棱互相垂直,则A 在底面BCD
BCD 得 心。
(2)在四面体ABCD 中,AB 、AC、AD互相垂直,则A 在底面BCD 上得射影就是底面BCD 得 心
(3)在四面体ABCD 中,AB=AC=AD ,则A 在底面BCD 上得射影就是底面BCD 得 心。
(4)在四面体ABCD 中,顶点A 到BC 、CD 、DB 得距离相等,则A 在底面BCD 上得射影就是底面BCD 得 心。
4、正方体1111D C B A ABCD -中棱长a ,点P 在AC 上,Q 在BC 1上,AP =BQ =a, (1)求直线PQ 与平面ABCD 所成角得正切值; (2)求证:PQ⊥AD .
5、在正方体1111D C B A ABCD -中,设E 就是棱1AA 上得点,且1:1:2A E EA =,F 就是棱AB 上得点,12
C EF π
∠=。
求AF:FB 。
6、点P 就是ABC ∆所在平面外一点,且PA ⊥平面ABC 。
若O 与Q 分别就是ΔABC 与ΔPBC 得垂心,试证:OQ ⊥平面PBC 。
7、已知EAF ∠在平面α内,,,AT P PAE PAF αα⊂∉∠=∠,,,EAT FAT PD D αα∠=∠⊥∈。
求
证:D AT ∈;
B。
