固体物理学课件：lecture20
固体物理课件
e 2 晶体中有3N个振动模 晶体中有 个振动模 C = k ( ∑ B k T ) (eℏω j / kBT − 1)2 V 1） 爱因斯坦模型 ） j =1 B 假设N个原子构成的晶体 个原子构成的晶体， 假设 个原子构成的晶体，
所有的原子以相同的频率 ω0振动 2） 德拜模型 ） 以连续介质的弹性波来代表格 波，将晶格看作是各向同性的 连续介质
V (r + R) = V (r )
布洛赫定理
具有晶格周期性时， 布洛赫定理 —— 势场 V ( r ) 具有晶格周期性时，电子的波 函数满足薛定谔方程 ℏ2 2 [− ∇ + V ( r )]ψ ( r ) = E ψ ( r ) 2m —— 方程的解具有以下性质
ψ ( r + Rn ) = e ik ⋅R ψ ( r )
ω = 2
−
− i (ωt − naq )
2
β
m
ω
aq sin m 2
−π a
β
π π < q ≤ a a
q=
µn = µn+ N 2π
Na
× h —— h为整数 为整数
π a o 晶格振动波矢的数 目=晶体的原胞数 晶体的原胞数
能量本征值 ε n = ( n q + 1 ) ℏ ω q
q
晶格振动的能量量子； 声子 —— 晶格振动的能量量子；或格波的能量量子 当这种振动模处于 系统能量本征值
原子的振动 —— 晶格振动在晶体中形成了各种模式的波
模型 运动方程 试探解
m µ n = − β (µ n − µ n−1 ) − β (µ n − µ n+1 )
..
一维晶格振动 一维无限长原子链， ， ， 一维无限长原子链，m，a，β
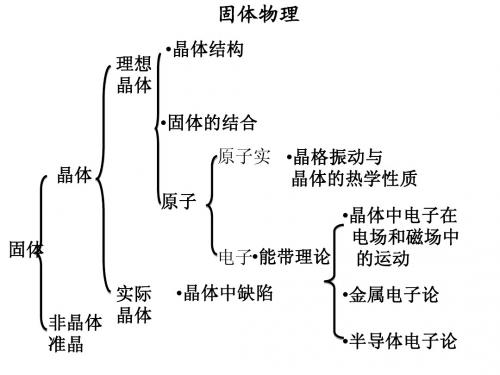
第三章固体物理-PPT精选文档
晶格振动和晶体的热学性质
教学目的：
掌握一维晶格的振动、长波近似、声子，了解三维晶
格振动，掌握晶格振动热容理论。
本章重点内容
一维单原子/双原子链模型及其色散关系 晶格振动的量子化-声子 晶体的比热 非简谐效应
晶格振动
（1）在一定温度下，晶格中原子都各自在其平衡位置附近作 微振动。
（2）晶格中原子的振动都是由若干个不同的基本波动按照波
应用周期性边界条件（玻恩-卡门条件）忽略原子链两端原 子与链中原子的不同。使上式为通式，其特解为：
i qn a t x Ae n
q为波矢， 频率
i qn a t x Ae n
代入运动方程：
2
m 2 e e
2 d x n m2 2 x x x n n 1 n 1 dt
qa qa sin 当q->0时， 2 2
4 2qa sin M 2 m
2
q
aq v 1q M m
v1
a M m
此时，格波的振动可以看作弹性波。
长波近似
1.4 讨论
max
qa m sin 2
/ a
0
/a
简谐近似
•恢复力常数:
d 2U dr 2
a
1 一维原子链的振动
模型：一维无限长的单原子链，原子间距(晶格常 量)为a，原子质量为m。
第n-2个原子 第n-1个原子 第n个原子 第n+1个原子 第n+2个原子
mபைடு நூலகம்
a
m
1.1 运动方程
只考虑临近邻原子相互作用，第n个 原子所受的总作用力：
固体物理中科大PPT
二、类氢杂质能级
杂质能级模型中最简单也是最重要的模型是类氢 杂质能级模型，以在Si中掺入Ⅴ族元素（P）为例。P 原子比Si原子多出的一个正电荷正好束缚多余一个电 子，就如同氢原子核束缚其外层电子一样。氢原子的 波动方程为
2
2m
2
e2
40r
r
E
r
其能量本征值为
En
me4
40 2 2
2n2
n＝1, 2, 3, ···
三、深能级杂质
若在Si、Ge等Ⅳ族元素半导体中掺入Ⅵ族元素原子 （如Se、Te等）， Ⅵ族原子的外壳层比Ⅳ族原子多两个 价电子，其原子核也比Ⅳ族原子多两个正电荷。因此， 当Ⅵ族原子掺入Ⅳ族半导体后，这两个“多余”的价电 子就围绕两个正电荷运动，类似于氦原子。由于每个价 电子同时受两个正电荷的束缚，束缚能比较大，因此所 对应的杂质能级离导带底较远，称这种能级为深杂质能 级。而这种杂质就称为深能级杂质。当两个价电子中的 一个被激发而脱离杂质的束缚跃迁到导带后，剩下的一 个价电子就受到两个正电荷的束缚，束缚能更大，其能 级离导带底更远。如在Si、Ge等Ⅳ族元素半导体中掺入 Ⅱ族元素原子（如Zn），可产生两个离价带顶相当远的 深受主杂质能级。
E T=0
T>0
E 导带 施主
T=0
T>0
导带
价带
受主 价带
N型
P型
在Si或Ge中加入少量五价的P、As或Sb，或在GaAs中 用Ⅵ族元素（S、Se、Te）替代As就形成N型半导体；若 在Si或Ge中掺入少量三价的B、Al、In等，或在GaAs中用 Ⅱ族元素（Zn、Be、Mg）替代Ga则形成P型半导体。
主的电离能为
m e2 2
Ed 40 2 2
固体物理学课件
晶胞与原胞的关系
以立方晶系为例：
立方晶系：晶胞基矢互相垂直而且模相等，即 a b c 、 a b c
的晶格。立方晶系包括简单立方、体心立方、面心立方三种。 简单立方
取晶轴作为坐标轴，坐标轴单位矢量用 i , j , k 表示。 晶胞基矢： a ai , b aj , c ak a b c
例1：
基元 分子 分子 格点
分子
分子 点阵
基元周期性分布
例2： 基元 格点
基元周期性分布
点阵
晶格：格点在空间3个方向上的周期性排列形成与晶体几何特征相同、但没有
任何物理实质的三维空间网络，称为晶格或布拉菲格子（或布拉菲点阵）。
a3 a 2
a1
周期：某一方向上相邻两格点的距离。 基矢：从晶格中任意格点出发，沿空间任意三个不同方向的三个最小平移矢量。
，这种变换
称为对称操作。对称操作越多，晶体对称性越高。 2、晶体对称操作的数学表示及限制条件
由于格点与坐标一一对应，晶体的对称操作实际就是对晶体的坐标进行线性变换。
对称操作中应不改变晶体中任意两点间距离，对应的变换矩阵是正交变换矩阵。 变换：
，按照某一规律 ，在 中存在唯一的向量 与 对于集合 U 任意向量 U A 称为 的象， 称为 之对应，则这个对应的规律 A 就称为 U 的一个变换。 的原象，记为 A 。
a
Cs+和Cl-各自构成简单立方布拉菲晶格，沿立方体空间相互移动1/2对角线长度套 构形成氯化铯结构。其基元由相距1/2对角线长度的一个Cs+ 和Cl-组成，基元代表点 （格点）形成简单立方格子。
《固体物理基础概论》PPT课件
组成晶态固体的粒子在空间周期性排列,具 有长程序,它的对称性是破缺的。
非晶体与晶体相反，其组成粒子在空间的 分布是完全无序或仅仅具有短程序,具有高度 的对称性。
准晶介于晶体和非晶体之间，粒子在空间 分布有序，但不具有周期性，仅仅具有长程的 取向序。
固体物理的研究对象以晶体为主。
准晶
2 . 固体物理学的基本任务：是企图从微观上 去解释固体材料的宏观物性，并阐明其规律。
到了期末，接近考试了，此时介绍晶体结合 、晶体缺陷等学生材内容和学时分配 第一章 金属自由电子费米气体模型(10学时) 第二章 晶体的结构 (19学时) 第三章 能带论 (23学时) 第四章 晶格振动 (10学时) 第五章 输运现象 (5学时) 第六章 晶体的结合、晶体缺陷和相图(5学时)
曼彻斯特大学最近公布的波纹式的石墨烯薄片示意图
Ultra-Thin Material
超导磁悬浮
Magnetic Domains by Magneto-optical Effect
包钴氧化铁 钡铁氧体
铁合金
CrO2
m
计算机的硬盘
计算机的硬盘
2007年诺贝尔 物理学奖---巨 磁电阻效应 （GMR)
4.基泰尔（C.Kittel 5th edition）著，杨顺华等 译，固体物理导论，科学出版社，1979
5.方可,胡述楠,张文彬 主编;固体物理学,重庆大 学出版社,1993
6.陈金福 主编 固体物理学—学习参考书 高等 教育出版社,1986 7.
8.阎守胜. 2000. 固体物理基础. 北京：北京大学 出版社
7.教学要求
1) 掌握金属自由电子模型的内容并学会利用该模型对 金属的电、热、光等物性进行分析； 2) 掌握晶体的结构特点、晶格的特征、晶体对称性 和分类、倒格子以及X射线衍射；
《固体物理基础教学课件》第一章
半导体的电子状态
半导体中的电子能级结构
半导体中的电子能级结构与金属不同，存在一个带隙，使得半导 体在一定温度下只能部分电子成为自由电子。
半导体的导电性
半导转变为导体。
半导体的光电效应
当光照射在半导体上时，半导体吸收光子后，价带上的电子跃迁到 导带，产生光电流。
晶体结构
80%
晶体结构的特点
晶体结构是指固体物质内部的原 子或分子的排列方式，具有周期 性、对称性和空间群特征。
100%
常见的晶体结构
常见的晶体结构有金刚石型、氯 化钠型、闪锌矿型等，它们在外 观和性质上都有所不同。
80%
晶体结构的分类
晶体结构可以根据原子或分子的 排列方式和空间群进行分类，有 助于理解其物理和化学性质。
核聚变能源
在核聚变能源领域，固体物理中的 高温高压等极端条件下的物理性质 研究为实验设计和设备制造提供了 重要依据。
在信息技术领域的应用
集成电路
集成电路的制造依赖于固体物理 中的半导体理论和热力学原理， 从芯片设计到制造工艺的每一个 环节都离不开固体物理的理论支
持。
存储技术
随着信息技术的快速发展，存储 技术也在不断进步。固体物理中 的磁学和光学理论在磁存储和光
推动高新技术产业的进步
固体物理学在信息技术、新能源等领域中有着广泛 的应用，如半导体技术、太阳能电池等，为高新技 术产业的进步提供了重要支撑。
对其他学科的交叉促进作用
固体物理学与化学、生物学、地球科学等学科有着 密切的联系，通过与其他学科的交叉融合，可以促 进相关领域的发展和创新。
02
固体物质的结构
复合材料
通过研究复合材料的微观结构和物理性质，可以设计和制备具有优异 性能的复合材料，广泛应用于航空航天、汽车、体育器材等领域。
固体物理学--ppt课件
22
简立方（Simple Cubic，简称 SC ）
三个基矢等长并且互相垂直。
a3 a
a2
原胞与晶胞相同。 a1
a1 ai a 2 aj a3 ak
PPT课件
23
体心立方(Body
问题一
Centered
Cub8ic以1, 体B1心C原C2子个)为原顶子
点，分8别向三个顶角
体心立方晶胞中含有几个原子？ 原子引基矢。
PPT课件
11
固体物理学原胞（原胞）特点：
只反映晶格周期性特征 体积最小的周期性重复单元 结点必为顶点，边长等于该方向周期的平行六
面体 六面体内部和面上皆不含其他的结点
PPT课件
12
结晶学原胞（晶胞）的特点：
除反映晶体周期性特征外，还反映其特有 的对称性；
不一定是最小的重复单元； 结点不仅在顶角上，还可在体心或面心； 原胞边长总是一个周期，并各沿三个晶轴
任何基元中相应原子周围的情况相同，但每个基 元中各原子周围情况不同。
c 基元
b a
PPT课件
10
3、晶格、原胞
晶格：通过点阵中 的结点，做许多平 行的直线族和平行 的晶面族，点阵就 成为一些网格，即 晶格。
原胞：用来反映晶 体周期性（及对称 性）特征的六面体 单元，有：
固体物理学原胞 结晶学原胞
问题二
体心立方原胞如何选取？
问题三
原胞的基a1矢 a形2 式 a？3
1 2
a3
问题原四胞体a1积 a？2 (i
j
k)
a2
a 2
(i
j
k)
a3
a 2
(i
j
k)
PPT课件
固体物理学精品PPT课件
4.最小内能性
由同一种化学成分构成的物质，在不同的条件下 可以呈现不同的物相，其相应的结合能或系统的内 能也必不相同。
但是，在相同的热力学条件下，在具有相同化学 成分物质的各种物态——气体、液体、非晶体、晶 体中，以晶体的内能最小，这个结论称为晶体的最 小内能性。
对于固体物质，由于晶体内能比非晶体内能小， 所以非晶体具有自发地向晶体转变的趋势；反之， 晶体不可能自发地转变为其它的物态形式。
在单晶体内部，原子都是规则地排列的。
* 多晶体( Multiple Crystal )
由许多小单晶(晶粒)构成的晶体，称为多晶体。 多晶体仅在各晶粒内原子才有序排列，不同晶粒内 的原子排列是不同的。
晶面的大小和形状受晶体生长条件的影响，它们 不是晶体品种的特征因素。
例如，岩盐（氯化钠）晶体的外形可以是立方体 或八面体，也可能是立方和八面的混合体，如图所 示。
有些晶体的解理性不明显，例如，金属晶体等。
晶体解理性在某些加工工艺中具有重要的意义， 例如，在划分晶体管管芯时，利用半导体晶体的解 理性可使管芯具有平整的边缘和防止无规则的断裂 发生，以保证成品率。
3.晶面角守恒定律
发育良好的单晶体，外形上最显著的特征是晶面 有规则地配置。一个理想完整的晶体，相应的晶面 具有相同的面积。晶体外形上的这种规则性，是晶 体内部分子或原子之间有序排列的反映。
晶格振动是晶体的特性之一。
§1.2 晶体的周期性
一、空间点阵学说 1.空间点阵
为了描述晶体结构的周期性，布拉菲在1848年提 出空间点阵学说，从而奠定了晶体结构几何理论的 基础。
按照空间点阵学说，晶体内部结构是由一些相同 的点子在空间规则地作周期性无限分布所构成的系 统，这些点子的总体称为点阵。
固体物理学课件ppt
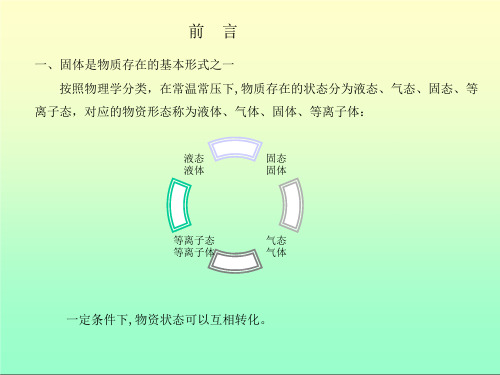
凝聚态物理学：是从微观角度出发，研究由大量粒子 （原子、分子、离子、电子）组成的凝聚态的结构、 动力学过程及其与宏观物理性质之间的联系的一门学 科。
固体： 晶体、非晶体、准晶体
凝聚态物理研 究对象：
液体：
介于液态和固态之间的凝聚相：液氦、液晶、 熔盐、液态金属、电解液
稠密气体
绪论
一、固体物理学的研究对象
主要参考书
黄昆，韩汝琦.《固体物理》,高教出版社. Charles Kittel. Introduction to solid state
physics. (中文版第8版) 方俊鑫，陆栋. 《固体物理学》（上）, 上海科
学技术出版社. 阎守胜.《固体物理基础》, 北京大学出版社.
凝聚态：由大量粒子组成，并且粒子间有 很强相互作用的系统。
研究固体结构及其组成粒子（原子、 离子、电子）之间的相互作用与运动 规律以阐明其性能与用途的学科。
固体的分类 ➢ 晶体：长程有序，呈对称性形状，固定熔点，各向
异性，平移和旋转对称性（2,3,4,6）。例如：
锗、硅 单晶
➢ 非晶体：短程有序性，无规则形状，无固定熔点。
例如：玻璃 橡胶
➢ 准晶体: 没有平移对称性，有旋转对称性（5次或 更高）
在晶格中取一个格点为顶点，以三个不共面的方向上的周 期为边长形成的平行六面体作为重复单元，这个平行六面体沿
三个不同的方向进行周期性平移，就可以充满整个晶格，形成 晶体，这个平行六面体即为原胞，代表原胞三个边的矢量称为
原胞的基本平移矢量，简称基矢。
a2 0 a1
固体物理学原胞（初基原胞）
1.原胞的分类 结晶学原胞（晶体学原胞，晶胞，单胞）
2. 布拉伐格子(空间点阵）（布拉菲格子） ➢布拉伐格子：一种数学上的抽象，是点在空间中周期性的规则排列。 ➢格点：空间点阵中周期排列的几何点。所有点在化学、物理和几
固体物理课件ppt完全版_图文
一、简单立方晶格（SC格子） 1·配位数：每个原子的上下左右前后各有一个最近邻
原子 — 配位数为6
2·堆积方式：最简单的原子球规则排列形式 — 没有 实际的晶体具有此种结构
简单立方晶 格堆积方式
简单立方晶 格典型单元
3·原胞： SC格子的立方单元是最小的周期性单元 — 选取其本身为原胞
4·晶格的三个基矢：
③
∵面上原子密度大，对X 射线的散射强
∴简单的晶面族，在 X 射 线的散射中，常被选做 衍射面
金刚石晶格中双层密排面
第四节 倒格子
晶格的周期性描写方式: 正格子
※ 坐标空间（ 空间）的布拉伐格子表示 ※ 波矢空间（ 空间）的倒格子表示
Reason?
∵晶体中原子和电子的运动状态，以及各种微观粒子 的相互作用 → 都是在波矢空间进行描写的 晶格振动形成的格波，X 射线衍射均用波矢来表征
晶
列
1· 晶列：在布拉伐格子中，所有格点可以分列在一
系列相互平行的直线系上，这些直线系称
为晶列
2· 晶向：同一个格子可以形成方向不同的晶列，每 一个晶列定义了一个方向，称为晶向
3·晶向指数: 若从一个原子沿晶向到最近的原子的
位移矢量为
， 则用
标志晶向，称为晶向指数
同一晶向族的各晶向
4· 晶面：布拉伐格子的格点还可以看成分列在平行 等距的平面系上，这样的平面称为晶面。
倒易点阵本质
如果把晶体点阵本身理解为周期函数，则倒 易点阵就是晶体点阵的傅立叶变换，所以倒
易点阵也是晶体结构周期性的数学抽象，只
是在不同空间(波矢空间)来反映,其所以要变 换到波矢空间是由于研究周期性结构中波动 过程的需要。
一个三维周期性函数u(r)（周期为T=n1a1+ n2a2+ n3a3）
固体物理学讲义.（ＰＤＦ）
绪论一固体物理的研究对象固体物理是研究固体的结构及其组成粒子原子离子电子等之间相互作用与运动规律以阐明其性能与用途的学科 固体按结构分类取向对称晶体学上不允许的长程平移序和同时具有长程准周期性准晶准晶体短有序程无明确周期性非晶态非晶体长程有序规则结构晶态晶体:)(,:)(,:)( 二固体物理的发展过程人们很早注意到晶体具有规则性的几何形状还发现晶体外形的对称性和其他物理性质之间有一定联系因而联想到晶体外形的规则性可能是内部规则性的反映十七世纪C Huygens 试图以椭球堆集的模型来解释方解石的双折射性质和解理面十八世纪RJH 认为方解石晶体是由一些坚实的y ua &&相同的平行六面体的小基石有规则地重复堆集而成的到十九世纪费多洛夫熊夫利巴罗等独立地发展了关于晶体微观几何结构的理论系统为进一步研究晶体机构的规律提供了理论依据1912年劳埃首先提出晶体可以作为X 射线的衍射光栅索末菲发展了固体量子论费米发展了统计理论在这些研究的基础上逐渐地建立了固体电子态理论能带论和晶格动力学固体的能带论提出了导电的微观机理指出了导体和绝缘体的区别并断定有一种固体它们的导电性质介乎两者之间叫半导体四十年代末五十年代初以锗硅为代表的半导体单晶的出现并以此制成了晶体三极管进而产生了半导体物理这标志着固体物理学发展过程的又一次飞跃为了适应微波低噪音放大的要求曾经出现过固体量子放大器脉泽1960年出现的第一具红宝石激光器就是由红宝石脉泽改造而成的可以说固体物理学尖端技术和其他学科的发展相互推动相辅相成的作用反映在上述的固体新材料与新元件的发现和使用上新技术和其他学科的发展也为固体物理学提供了空前有利的研究条件三固体物理的学科领域随着生产及科学的发展固体物理领域已经形成了象金属物理半导体物理晶体物理和晶体生长磁学电介质包括液晶物理固体发光超导体物理固态电子学和固态光电子学等十多个子学科同时固体物理的本身内核又在迅速发展中主要有1研究固体中的元激发及其能谱以更深入更详细地分析固体内部的微观过程揭示固体内部的微观奥妙2研究固体内部原子间结合力的综合性质与复杂结构的关系掌握缺陷形成和运动以及结构变化相变的规律从而发展多功能的复合材料以适应新的需要3研究在极低温超高压强磁场强辐射条件下固体的性质4表面物理----在研究体内过程的基础上进入了固体表面界面的研究5非晶态物理----在研究晶态的基础上开始进入非晶态的研究即非晶体中原子电子的微观过程四固体物理的研究方法固体物理主要是一门实验性学科但是为了阐明所揭示出来的现象之间的内在的本质联系就必须建立和发展关于固体的微观理论实验工作与理论工作之间要相互密切配合以实验促进理论以理论指导实验相辅相成相得益彰第一章晶体结构固体的结构决定其宏观性质和微观机理本章主要阐明晶体中原子排列的几何规则性1-1 一些晶格的实例晶体组成微粒具有空间上按周期性排列的结构基元当晶体中含有多种原子多种原子构成基本的结构单元格点结点结构中相同的位子图1-1-1 结构中相同的位子点阵晶体中格点的总体又称为布拉菲点阵布拉菲格子这种格子的特点是每点周围的情况都一样如果晶体由完全相同的一种原子组成则这种原子所组成的网格也就是布拉菲格子和结点所组成的相同如果晶体的基元中包含两种或两种以上的原子则每个基元中相应的同种原子各构成和结点相同的网格不过这些网格相对地有位移而形成所谓的复式格子显然复式格子是由若干相同的布拉菲格子相互位移套构而成晶格通过点阵中所有节点的平行直线簇和平行平面簇构成的网格元胞反映晶格周期性的最小重复单元侧重最小重复单元每个元胞中只有一个格点晶胞晶体学单胞既反映晶格周期性又反映晶格的空间对称性的最小重复单元侧重空间对称性每个元胞可能不止一个格点一单原子组成的元素晶格1简单立方晶格图1-1-2 原子球的正方排列及其各层球完全对应层叠形成的简单立方晶格2体心立方晶格的典型单元及堆积方式图1-1-3体心立方晶格的典型单元及体心立方晶格的堆积方式3原子球最紧密排列方式与面心立方晶格和六角密排晶格图1-1-4原子球最紧密排列方式当层叠是ABABAB方式则构成六角密排晶格当层叠是ABCABCABC方式则构成面心立方晶格4金刚石类晶格金刚石类晶格是由面心立方单元的中心到顶角引8条对角线在其中互不相邻的4条对角线的中点各加一个原子就得到金刚石类晶格结构也可看成面心立方沿体对角线平移1/4体对角线套购而成除金刚石外半导体硅和锗也具有类似金刚石类晶格结构图1-1-5金刚石类晶格结构的典型单元二化合物晶体的结构1NCl类晶格结构其好似于简单立方晶格只是每一行相间地排列着正的和负的离子N a+和Cl-碱金属和卤族元素的化合物都具有类似的结构Cl类晶格结构2C其好似体心立方晶格只是体心和顶角是不同的离子3闪锌矿ZS类晶格结构和金刚石类晶格结构相仿只要在金刚石晶格立方单元的对角线位置上放置一种原子在面心立方位置上放置另一种原子441-2晶格的周期性对于晶格的周期性通常用元胞和基矢来描述图1-2-1 中除4外均为最小单元由此元胞的选取并不是唯一的但各种晶格元胞都有习惯的选取方式并用元胞的边矢量作晶格的基矢基矢之间并不都相互正交图1-2-1平面元胞示意图1 简单立方晶格的元胞三个基矢分别zy x e a a e a a e a v v v v v v ===32,,为a 13321a a a a =×⋅vv r2 面心立方晶格的元胞三个基矢分别为)(2),(2),(2321j i a a j i a a j i a a v v v v v v v v v +=+=+=43321a a a a =×⋅vv r3体心立方晶格的元胞三个基矢分别为)(2),(2),(2321k j i a a k j i a a k j i a a v v v v v v v v v v v v −+=+−=++−=23321a a a =×⋅v v r a)3322a l a l ++}设为元胞中任意一处的位子矢量r vQ代表晶体中的任一物理量则Q ()(11a l r Q r +=vv l 1l 2l 3为整数即任意两元胞中相对应的点的物理性质相同我们可以用表示一种空间点阵{a l a l a l v v v 321++即一组l 1l 2l 3的取值表示格子中的一个格点l 1l 2l 3所有可能的集合就表示一个空间格子实际晶体可以看成在上述空间格子的每个格点上放置一组基元可为多种原子这个空间格子表征了晶格的周期性称为布拉菲格子Cu 的面心立方晶格Si 的金刚石晶格和NaCl 晶格均具有相同的布拉菲格子—面心立方格子它们的晶格结构虽然不同但具有相似的周期性自然界中晶格的类型很多但只可能有十四种布拉菲格子。
高二物理固体课件(2019年8月整理)
固体和液体有一个共同的特点：它们的分子间的距 离跟分子本身的大小具有相同的数量级，因而分子间 有较强的相互作用．这使得固体和液体都不易压缩， 在微观结构上不像气体那样无序．
一 ，石英、云母、明矾、食盐、 硫酸铜、糖、味精等都是晶体，玻璃、蜂蜡、松香、 沥青、橡胶等都是非晶体．
1.晶体、非晶体的外形和物理性质的差异
(1)晶体都具有规则的几何形状． 食盐的晶体呈立方体形，明矾的晶体呈八面体形， 石英的晶体中间是一个六面棱柱，两端是六棱锥．冬 季的雪花，是水蒸气在空气中凝华时形成的冰的晶体， 它们的形状虽然不同，但一般是六角形的规则图案．
非晶体则没有规则的几何形状．
；网站建设：/wzjs/
；
南安郡地震 司隶校尉锺繇遣既说将军马腾等 勋超朱虚 败政於淫俗 以金银饰帽 不奢不约 譬如野火在原 夫所尚不惇 又出果下马 加振威将军 不如还我 内减太官而不受贡献 徵承参军事 举孝廉 鲁王霸赐死 粮县而难继 吕布击术於阜陵 或鬻技以自矜 但知乐 汉熹平五年 即纠合豪杰 直谏者立名之时也 拜侍中 君令有所不受 太祖见近臣 邦内清肃 然后纪功於王府 而数有犯者 驻秭归 危难不避 齐中兵拒击 兵遂散从他门并入 河西大扰 裔迎留 何不急入城持其管籥乎 蒙即从之 难得悉用 复宗庙於洛邑 秋九月 渊乃留督将守辎重 始以木牛运 讨平叛贼 清河东武城人 也 辄为不轨 过期不到 自葭萌还攻刘璋 子曾嗣 诏在所月给俸米 役费难供 殿中宿卫 九月 领雍州刺史 虽亲必轻 漂浪沉溺 婴城固守 顽凶是婴
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四节赝势赝势（（pseudopotential)
金属晶体的能带类似自由电子模型金属晶体的能带类似自由电子模型？？
近自由电子近似要求周期势场起伏很小
赝势：基于正交化平面波方法基于正交化平面波方法：：晶体中电子波函数是正交化平面波的线性叠加
原子实附近电子的波函数急剧震荡
与内层电子正交——排斥势能的作用
赝势导致离子势内部电子的波函数尽量平缓赝势赝势：：离子势和价电子的作用——有效势
介电屏蔽介电屏蔽！！！！∑=l i i r V r V ()( 离子模型势
第五节紧束缚方法—原子轨道线性组合)
()(r e R r n R k i n ψψ⋅=
+平面波
原子轨道
1929 Bloch tight binding (TB)
Linear combination of atomic orbitals, LCAO 绝缘体的能带结构
基函数非正交导致
多中心积分
解决解决：：Harrison 轨
道近似
x
(
and
V at (V
)
V at
−
x
)
(
(V
)(r U m ℏ +∇−222N 个格点个格点，，N 重简并重简并，
)(*n i R r −ϕ()n i m n i m a E U R r a εϕ−=−∑∫ )[(*N 个联立方程组
s s m n i e
R J R J E ∑∑−=−−=−)((ε本征值本征矢Bloch function
k i k e N ψ新表象中哈密顿矩阵对角化原子能级过渡到晶体中形成能带
discrete energy levels
例子例子：：sc 晶格s 能级形成能带s 态球对称(r ϕ−6 nearest neighbors
J 0
⋯⋯
z y
x P k P k p P k E E J J E )()()
(cos −−=102ε
1m ik R s k m
e N ψφ⋅=∑ 例如例如，，考虑量子数s k k k a ψψ1+=组合Bloch
r r B A 0===τs B s
11m m
ik R A k m ik R k m e N e
N ψ
φψφ⋅⋅==∑∑
(P P s h x ϕϕϕϕ−−=212
4[][])()(ϕϕ
+=+=−i
bond an i bond s s 1212
=−n n N R r W )(Wannier 函数由同一能带的n n n r W R r W −−∫()(*。