立体几何(同步)-潍坊市某中学高中数学二轮复习
2023高中数学立体几何复习 题集附答案

2023高中数学立体几何复习题集附答案一、立体几何基础知识立体几何是数学中的一个重要分支,主要研究空间内的图形、体积和表面积等相关性质。
掌握立体几何的基础知识对于高中数学学习尤为重要。
下面是一些常见的立体几何概念及其性质:1. 空间中的点、线、面是立体几何中最基本的概念。
点是没有长度、宽度和高度的,线是由无数个点组成的,面是由无数条线组成的。
2. 立体是由许多平面相互连接而成的。
这些平面称为面,每个面都有其特定的几何形状,如三角形面、矩形面等。
3. 空间中的距离有两种:直线距离和曲线距离。
直线距离是两点之间最短的距离,而曲线距离则是沿着曲线的长度。
4. 空间中的体积是指一个物体占据的空间大小。
常见的几何体体积计算公式有:长方体的体积为底面积乘以高,球体的体积为4/3乘以π半径的立方,圆柱体的体积为底面积乘以高等。
5. 表面积是指立体图形外表面的总面积。
计算几何体表面积的公式与计算体积的公式类似,只是不同几何体的取值不同。
二、复习题1. 长方体A的长、宽、高分别为3cm、4cm和5cm,计算长方体A的表面积和体积。
解答:长方体的表面积公式为S = 2(ab + ac + bc),其中a、b和c分别是长方体的三个边长。
代入数据后,可得长方体A的表面积为:S = 2(3*4 + 3*5 + 4*5) = 94cm²长方体的体积公式为V = lwh,其中l、w和h分别是长方体的三个边长。
代入数据后,可得长方体A的体积为:V = 3*4*5 = 60cm³因此,长方体A的表面积为94cm²,体积为60cm³。
2. 一个四棱锥的底面是一个边长为6cm的正方形,其高度为8cm。
计算该四棱锥的体积和表面积。
解答:四棱锥的体积公式为V = 1/3 * 底面积 * 高度。
底面为正方形,因此底面积为6²=36cm²。
代入数据后,可得四棱锥的体积为:V = 1/3 * 36 * 8 = 96cm³四棱锥的表面积公式为S = 底面积 + 侧面积。
高中数学二轮复习 立体几何

高中数学二轮复习——立体几何一、空间几何体及三视图:正俯视图长对正、正侧视图高平齐、俯侧视图宽相等.例1.用一些棱长为1cm 的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图则这个几何体的体积最大是 cm 3.图1(俯视图) 图2(主视图)例2.一个多面体的直观图及三视图如图所示,则多面体A CDEF 的体积为 .例3.如图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体共有 个. 例4.如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是 2cm 。
例 5.矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B -AC -D ,则四面体ABCD 的外接球的体 积为例6.一个几何体的三视图中,正视图和侧视图都是矩形,俯视图是等腰直角三角形(如图),根据图中标注的长 度,可以计算出该几何体的表面积是 .主视图俯视图左视图2 俯视图主视图 左视图21 238π61252420+例7、一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )A .球B .三棱锥C .正方体D .圆柱例8、已知三棱锥错误!未找到引用源。
的所有顶点都在球错误!未找到引用源。
的求面上,错误!未找到引用源。
是边长为错误!未找到引用源。
的正三角形,错误!未找到引用源。
为球错误!未找到引用源。
的直径,且错误!未找到引用源。
;则此棱锥的体积为( )错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
例1、7 例2、 例3、5 例4、 例5、例6、12+42 例7、D 例8、A 二、定理类命题的判断例1.下列命题中错误的是( )(A )如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面β (B )如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β (C )如果平面αγ⊥平面,平面βγ⊥平面,=l αβ⋂,那么l γ⊥平面 (D )如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β例2、已知1α,2α,3α是三个相互平行的平面.平面1α,2α之间的距离为1d ,平面2α,3α之间的距离为2d .直线l 与1α,2α,3α分别相交于1P ,2P ,3P ,那么“12PP =23P P ”是“12d d =”的( ) A.充分不必要条件 B.必要不充分条件 C .充分必要条件 D .既不充分也不必要条件例3、1l ,2l ,3l 是空间三条不同的直线,则下列命题正确的是( ) (A)12l l ⊥,23l l ⊥13l l ⇒ (B )12l l ⊥,23l l ⇒13l l ⊥(C)233l l l ⇒ 1l ,2l ,3l 共面 (D )1l ,2l ,3l 共点⇒1l ,2l ,3l 共面 例4、给定下列四个命题:其中,为真命题的是 ( )①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. A .①和② B .②和③ C .③和④ D .②和④例5、已知直线 l 、m ,平面α、β,且l α⊥,m β⊂,则//αβ是l m ⊥的( )654565俯视图侧视图正视图A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件例6.已知a 、b 为直线,α、β为平面.在下列四个命题中,正确命题的个数是( ) ① 若a ⊥α,b ⊥α,则a ∥b ; ②若 a ∥α,b ∥α,则a ∥b ;③ 若a ⊥α,a ⊥β,则α∥β;④ 若α∥b ,β∥b ,则α∥β. A . 1B . 3C . 2D . 0例7、.设l 、m 、n 为不同的直线,βα、为不同的平面,有如下四个命题:( ) ①若βαβα//,l ,l 则⊥⊥ ②若βαβα⊥⊂⊥l ,l 则, ③若n l n m m l //,,则⊥⊥ ④若n m n m ⊥⊥则且βαβα////, A.0B.1C.2D.3例8、已知空间两条不同的直线n m ,和两个不同的平面,αβ,则下列命题中正确的是( )A .若//,,//m n m n αα⊂则B .若,,m m n n αβα=⊥⊥ 则C .若//,//,//m n m n αα则D .若//,,,//m m n m n αβαβ⊂= 则例9、设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β; (2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直; (4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直。
高中数学二轮复习立体几何(2)教案含答案(全国通用)

专题五 立体几何必考点一 空间几何体的三视图、表面积与体积[高考预测]——运筹帷幄1.以三视图为背景的几何体的识别问题.2.空间几何体与三视图相结合,计算几何体的表面积和体积. 3.球及有关组合体的表面积与体积. [速解必备]——决胜千里 1.一个物体的三视图的排列规则俯视图放在正视图的下面,长度与正视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样,即“长对正、高平齐、宽相等”.2.(1)设长方体的相邻的三条棱长为a 、b 、c 则体对角线长为a 2+b 2+c 2(2)棱长为a 的正方体的体对角线长等于外接球的直径,即3a =2R .(3)若球面上四点P 、A 、B 、C 构成的线段P A 、PB 、PC 两两垂直,且P A =a ,PB =b ,PC =c ,则4R 2=a 2+b 2+c 2,把有关元素“补形”成为一个球内接长方体(或其他图)[速解方略]——不拘一格类型一 有关几何体的三视图的计算[例1] (1)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15解析:基本法:由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥.设正方体的棱长为1,则三棱锥的体积为V 1=13×12×1×1×1=16, 剩余部分的体积V 2=13-16=56. 所以V 1V 2=1656=15,故选D.速解法:如图所示,VA -A 1B 1D 1=13VABD -A 1B 1D 1=16V 正方体 VA -A 1B 1D 1=15VABCD -B 1C 1D 1 答案:D方略点评:基本法是具体计算几何体的体积,速解法是根据几何体间的体积关系求得答案.(2)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =( )A.1 B.2C.4 D.8解析:基本法:由已知可知,该几何体的直观图如图所示,其表面积为2πr2+πr2+4r2+2πr2=5πr2+4r2.由5πr2+4r2=16+20π,得r=2.故选B.速解法:由几何体特征可知,球的表面积,圆的面积,圆柱侧面积都含有“π”,只有圆柱的轴截面面积不含“π”,∴即2r·2r=16,∴r=2,故选B.答案:B方略点评:(1)基本法是具体计算出几何体的表面积的表达式.速解法是根据几何体特征想出表面积表达式特征由部分几何体求r.(2)此类题关键是将三视图恢复为直观图,并找清几何体的标量,代入公式计算.1.如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.1727B.59C.1027D.13解析:基本法:该零件是两个圆柱体构成的组合体,其体积为π×22×4+π×32×2=34π cm 3,圆柱体毛坯的体积为π×32×6=54π cm 3, 所以切削掉部分的体积为54π-34π=20π cm 3,所以切削掉部分的体积与原来毛坯体积的比值为20π54π=1027,故选C. 答案:C2.(2016·高考全国丙卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A .18+36 5B .54+18 5C .90D .81解析:先根据三视图确定几何体的形状,再求其表面积.由三视图可知该几何体是底面为正方形的斜四棱柱,其中有两个侧面为矩形,另两个侧面为平行四边形,则表面积为(3×3+3×6+3×35)×2=54+18 5.故选B. 答案:B类型二 球及其组合体[例2] (1)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( ) A .36π B .64π C .144π D .256π解析:基本法:画出球的直观图,利用锥体的体积公式求解. 如图,设球的半径为R ,∵∠AOB =90°,∴S △AOB =12R 2.∵V O -ABC =V C -AOB ,而△AOB 面积为定值,∴当点C 到平面AOB 的距离最大时,V O -ABC 最大,∴当C 为与球的大圆面AOB 垂直的直径的端点时,体积V O -ABC 最大为13×12R 2×R =36,∴R =6,∴球O 的表面积为4πR 2=4π×62=144π.故选C.速解法:设球的半径为r, 则V O -ABC =13×12×r 2h ≤16r 3=36,故r =6.故S 球=4πr 2=144π. 答案:C方略点评:基本法是根据直观图,找到C 点位置.,速解法是利用V O -ABC 的表达式的代数关系(≤16r 3)直接求得r .(2)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4 B .16π C .9π D.27π4解析:基本法:如图所示,R 2=(4-R )2+2,。
2021新高考数学(山东专用)二轮复习专题限时集训11 立体几何 Word版含解析

姓名,年级:时间:专题限时集训(十一) 立体几何1。
(2019·全国卷Ⅰ)如图,直四棱柱ABCD.A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A.MA1N的正弦值.解:(1)连接B1C,ME。
因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=错误!B1C.又因为N为A1D的中点,所以ND=错误!A1D.由题设知A1B1 错误!DC,可得B1C错误!A1D,故ME错误!ND,因此四边形MNDE为平行四边形,所以MN∥E D.又MN⊄平面EDC1,所以MN∥平面C1DE。
(2)由已知可得DE⊥D A.以D为坐标原点,错误!的方向为x轴正方向,建立如图所示的空间直角坐标系D。
xyz,则A(2,0,0),A1(2,0,4),M(1,错误!,2),N(1,0,2),错误!=(0,0,-4),错误!=(-1,错误!,-2),错误!=(-1,0,-2),错误!=(0,-错误!,0).设m=(x,y,z)为平面A1MA的法向量,则错误!所以错误!可取m=(错误!,1,0).设n=(p,q,r)为平面A1MN的法向量,则错误!所以错误!可取n=(2,0,-1).于是cos<m,n>=错误!=错误!=错误!,所以二面角A。
MA1.N的正弦值为错误!.2.(2019·全国卷Ⅲ)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.图1 图2(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B。
CG。
A的大小.[解](1)证明:由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,BE∩BC=B,故AB⊥平面BCGE。
高三数学二轮专题复习教案――立体几何
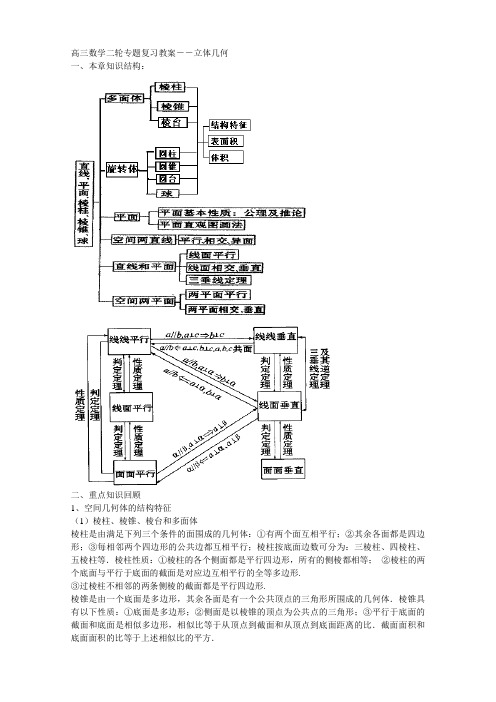
高三数学二轮专题复习教案――立体几何一、本章知识结构:二、重点知识回顾1、空间几何体的结构特征(1)棱柱、棱锥、棱台和多面体棱柱是由满足下列三个条件的面围成的几何体:①有两个面互相平行;②其余各面都是四边形;③每相邻两个四边形的公共边都互相平行;棱柱按底面边数可分为:三棱柱、四棱柱、五棱柱等.棱柱性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.棱锥是由一个底面是多边形,其余各面是有一个公共顶点的三角形所围成的几何体.棱锥具有以下性质:①底面是多边形;②侧面是以棱锥的顶点为公共点的三角形;③平行于底面的截面和底面是相似多边形,相似比等于从顶点到截面和从顶点到底面距离的比.截面面积和底面面积的比等于上述相似比的平方.棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.由棱台定义可知,所有侧棱的延长线交于一点,继而将棱台还原成棱锥.多面体是由若干个多边形围成的几何体.多面体有几个面就称为几面体,如三棱锥是四面体.(2)圆柱、圆锥、圆台、球分别以矩形的一边,直角三角形的一直角边,直角梯形垂直于底边的腰所在的直线,半圆以它的直径所在直线为旋转轴,旋转一周而形成的几何体叫做圆柱、圆锥、圆台、球圆柱、圆锥和圆台的性质主要有:①平行于底面的截面都是圆;②过轴的截面(轴截面)分别是全等的矩形、等腰三角形、等腰梯形;③圆台的上底变大到与下底相同时,可以得到圆柱;圆台的上底变小为一点时,可以得到圆锥.2、空间几何体的侧面积、表面积(1)棱柱侧面展开图的面积就是棱柱的侧面积,棱柱的表面积就是它的侧面积与两底面面积的和.因为直棱柱的各个侧面都是等高的矩形,所以它的展开图是以棱柱的底面周长与高分别为长和宽的矩形.如果设直棱柱底面周长为c,高为h,则侧面积S ch=侧.若长方体的长、宽、高分别是a、b、c,则其表面积2() S ab bc ca=++表.(2)圆柱的侧面展开图是一个矩形.矩形的宽是圆柱母线的长,矩形的长为圆柱底面周长.如果设圆柱母线的长为l,底面半径为r,那么圆柱的侧面积2πS rl=侧,此时圆柱底面面积2πS r=底.所以圆柱的表面积222π2π2π()S S S rl r r r l=+=+=+侧底.(3)圆锥的侧面展开图是以其母线为半径的扇形.如果设圆锥底面半径为r,母线长为l,则侧面积πS rl=侧,那么圆锥的表面积是由其侧面积与底面面积的和构成,即为2πππ()S S S rl r r r l=+=+=+侧底.(4)正棱锥的侧面展开图是n个全等的等腰三角形.如果正棱锥的周长为c,斜高为h',则它的侧面积12S ch'=侧.(5)正棱台的侧面积就是它各个侧面积的和.如果设正棱台的上、下底面的周长是c c',,斜高是h',那么它的侧面积是12S ch'=侧.(6)圆台侧面展开图是以截得该圆台的圆锥母线为大圆半径,圆锥与圆台的母线之差为小圆半径的一个扇环.如果设圆台的上、下底面半径分别为r r',,母线长为l,那么它的侧面积是π()S r r l'=+侧.圆台的表面积等于它的侧面积与上、下底面积的和,即2222π()πππ() S S S S r r l r r r r r l rl''''=++=+++=+++侧上底下底.(7)球的表面积24πS R =,即球的表面积等于其大圆面积的四倍.3、空间几何体的体积(1)柱体(棱柱、圆柱)的体积等于它的底面积S 和高h 的积,即V Sh=柱体.其中底面半径是r ,高是h 的圆柱的体积是2πV r h=圆柱.(2)如果一个锥体(棱锥、圆锥)的底面积是S ,高是h ,那么它的体积是13V Sh=锥体.其中底面半径是r ,高是h 的圆锥的体积是21π3V r h=圆锥,就是说,锥体的体积是与其同底等高柱体体积的13.(3)如果台体(棱台、圆台)的上、下底面积分别是S S ',,高是h,那么它的体积是1()3V S S h=+台体.其中上、下底半径分别是r R ,,高是h 的圆台的体积是221π()3V r Rr R h=++圆台.(4)球的体积公式:334R V π=.4、中心投影和平行投影(1)中心投影:投射线均通过投影中心的投影。
山东省潍坊市昌乐县第二中学2020届高三二轮立体几何过关检测

一、单项选择题(每小题5分)
1.一个水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为()
A. + B.2+ C. + D. +
2.如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则BB1与平面AB1C1所成的角的大小为()
A. B. C. D.
二、多项选择题(每小题5分)
5.设a、b、c是空间的三条直线,α、β是空间的两个平面,则下列命题中成立的是()
A.当c⊥a时,若c⊥β,则a∥β
B.当b⊂α时,若b⊥β,则α⊥β
C.当b⊂α,且c是a在α内的射影时,若b⊥c,则a⊥b
D.当b⊂α,且c⊄α时,若c∥b,则c∥α
4.边长为6的两个等边 , 所在的平面互相垂直,则四面体 的外接球的体积为( ).
A. B. C. D.
【答案】B
【解析】如图所示: 为三角形 过中心 且垂直平面 的直线,
为三角形 过中心 且垂直平面 的直线, 与 相交于 点.
由球的性质知:四面体 的外接球球心为 点.
因为 , 为 的中心,所以 .
4、填空题(每题5分)
7.正四ห้องสมุดไป่ตู้体ABCD的棱长为4,E为棱BC的中点,过E作其外接球的截面,则截面面积的最小值为__________.
【答案】:4π
【解析】将四面体ABCD补为正方体,如图所示,则正方体的外接球就是正四面体的外接球.设球心为O,面积最小的截面是与OE垂直的截面.由图可知,这个截面是底面正方形的外接圆,因为BC=4,所以半径为2,其面积为π×22=4π.
2023-2024学年山东省潍坊市高中数学人教A版 必修二第八章 立体几何章节测试-14-含解析

①③①③①②③1. 正方体 的棱长为 ,点 为棱 的中点.下列结论:①线段 上存在点 ,使得 平面;②线段上存在点,使得平面;③平面 把正方体分成两部分,较小部分的体积为 ,其中所有正确的序号是( )A. B. C. D. 已知平面 , , 满足,, 则已知直线a 、l ,平面 , 满足 , , , 则如果空间中两个角的两条边分别对应平行,则这两个角相等用一个平面去截一个正方体,截面图形有可能是等边三角形,不可能是直角三角形2. 以下说法的是( )错误A. B. C. D. 若,则若,则若,则若,则3. 设 , 是两个不同的平面, , 是两条不同的直线,且 , ( )A. B. C. D. 4. 某几何体的三视图如图所示,则该几何体的体积为( )1A. B. C. D.16π21π5. 如图某空间几何体的正视图和俯视图分别为边长为2的正方形和正三角形,则该空间几何体的外接球的表面积为()A. B. C. D. 1236. 已知圆柱和圆锥的底面重合,且母线长相等,设圆柱、圆锥的表面积分别为S 1 , S 2 , 则的值为()A. B. C. D. 必定可以并且只可以作一个至少可以作一个至多可以作一个一定不能作7. 过平面外一条直线作平面的平行平面( )A. B. C. D. 直线AB 上直线BC 上直线CA 上△ABC 内部8. 如图所示,在斜三棱柱ABC ﹣A 1B 1C 1中,∠BAC=90°,BC 1⊥AC ,则C 1在面ABC 上的射影H 必在( )A. B. C. D. 9. 三棱锥P-ABC 的三条侧棱PA ,PB ,PC 两两垂直,PA=1,PB=2,PC=3,且这个三棱锥的顶点都在同一个球面上,则这个球面的表面积为 ( )A.B.C.D.10. 某几何体由若干大小相同的正方体组合而成,其三视图均为如图所示的图形,设该几何体的表面积为,其外接球的表面积为 ,则的值为()A. B. C. D.11. 以下命题(其中 , 表示直线,表示平面)中,正确的命题是( )若 , , 则若 , , 则若 , , 则若 , , 则A. B. C. D. ① ④① ③② ④② ③12. 已知两条直线m ,n ,两个平面α,β,给出下面四个命题:① ②③;; ④其中正确命题的序号是( )A. B. C. D. 13. 若一个圆锥的轴截面是边长为2的等边三角形,则这个圆锥的侧面积为 .14. 现给出以下四个命题:①已知 中,角A ,B ,C 的对边为a ,b ,c ,当 , , 时,满足条件的三角形共有1个;②已知 中,角A ,B ,C 的对边为a ,b ,c ,若三角形,这个三角形的最大角是 ;③设 是两条不同的直线,, 是两个不同的平面,若 , ,则 ;④设 是两条不同的直线, , 是两个不同的平面,若, ,则 其中正确的序号是 (写出所有正确说法的序号).15. 已知圆柱的底面圆的半径与球 的半径相同,若圆柱与球 的体积相等,则它们的表面积之比.(用数值作答)16. 对于一个底边在x 轴上的正三角形ABC ,边长AB=2,采用斜二测画法做出其直观图,则其直观图的面积是 .17. 如图所示,平面 , 点在以为直径的上, , , 点为线段的中点,点在半圆上(弧长小于弧长),且三棱锥的体积.(1) 求证:平面;(2) 平面平面;(3) 设二面角的大小为 , 求的值.18.在直三棱柱ABC﹣A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E,F分别是A1C1, BC的中点.(1)证明:C1F∥平面ABE;(2)设P是BE的中点,求三棱锥P﹣B1C1F的体积.19. 已知三棱锥中,△与△均为等腰直角三角形,且∠,,为上一点,且平面.(1) ;(2) 过作三棱锥的截面分别交于,若四边形为平行四边形,求此四边形的面积.20. 如图,在四棱锥中,底面ABCD为直角梯形,,,平面底面ABCD,Q为AD的中点,M是棱PC上的点,,,(1) 求证:平面平面PAD;(2) 若,求二面角的大小.21. 如图,在四棱锥中,底面是边长为1的菱形,,,为的中点,为的中点,点在线段上,且 .(1) 求证:平面;(2) 若平面底面,且,求平面与平面所成锐二面角的余弦值.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)(3)18.19.(1)(2)20.(1)(2)(1)(2)。
2023-2024学年山东省潍坊市高中数学人教A版 必修二第八章 立体几何专项提升-2-含解析

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年山东省潍坊市高中数学人教A版 必修二第八章 立体几何专项提升(2)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)若 , ,则 若 , ,则若 , , ,则 若 , , ,则 1. 已知 ,是两条不同的直线, , 是两个不重合的平面,则下列命题中正确的是( )A. B. C. D. ①②③④2. 将正方形ABCD 沿对角线BD 折成直二面角A-BD-C ,有如下四个结论:①AC ⊥BD ;②△ACD 是等边三角形;③AB 与平面BCD 所成的角为60°;④AB 与CD 所成的角为60°.其中错误的结论是( )A. B. C. D. 8π3. 四面体ABCD 的四个顶点都在球O 的球面上,AB=2,BC=CD=1,∠BCD=60°,AB ⊥平面BCD ,则球O 的表面积为( )A. B. C. D.若l ⊥m ,l ⊥n ,m ⊂α,n ⊂α,则l ⊥α若l∥m ,l ⊄α,m ⊂α,则l ∥α若α⊥β,α∩β=l ,m ⊂α,m ⊥l ,则m ⊥β若α⊥β,m ⊥α,n ⊥β,则m ⊥n 4. 已知α,β是两个不同的平面,l ,m ,n 是不同的直线,下列命题不正确的是( )AA. B. C. D. 若 ,, 则若 , , 则若 , , 则若 , , 则5. 已知 ,是两条不重合的直线, , 是两个不重合的平面,下列结论正确的是()A. B. C. D.6. 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为矩形的棱台称为刍童.如图所示的某刍童中,,为上、下底面的中心,平面,,,侧棱所在直线与直线所成的角为45°,则该刍童的体积为()A. B. C. D.①②①②④③④①④7. 如图,在正方体,点P 在线段上运动,则下列判断正确的是()①平面平面②平面③异面直线与所成角的取值范围是④三棱锥的体积不变A. B. C. D. 一定存在与平行的平面,也一定存在与α平行的平面一定存在与平行的平面,也一定存在与α垂直的平面一定存在与垂直的平面,也一定存在与α平行的平面一定存在与垂直的平面,也一定存在与α垂直的平面8. 已知直线与直线m 是异面直线,直线在平面α内,在过直线m 所作的所有平面中,下列结论正确的是 ( )A. B. C. D. 129. 如图,正方体的棱长为1,点在棱的延长线上,且,点是侧面内的一动点,若平面,则点的轨迹的长度是()A. B. C. D. 垂直于同一直线的两条直线平行若一条直线垂直于两条平行线中的一条,则它垂直于另一条10. 下列命题中正确的是( )A. B.若一条直线与两条平行线中的一条相交,则它与另一条相交一条直线至多与两条异面直线中的一条相交C. D. 若 , , 则若 , , 则若 , , , 则若 , , , 则11. 已知 , 是两条不重合直线, , 是两个不重合平面,则下列说法正确的是( )A. B. C. D. 12. 矩形ABCD 中,AB= 4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B -AC -D ,则四面体ABCD 的外接球的体积为( )A. B. C. D.13. 直平行六面体的底面是菱形,两个对角面面积分别为Q 1 , Q 2 , 直平行六面体的侧面积为 .14. 已知定直线 , 定点 , 则直线与点A 确定的平面有 个(请填写个数).15. 一个几何体的三视图如图所示,则该几何体的体积为 .16. 如图,在一个倒置的高为2的圆锥形容器中,装有深度为h 的水,再放入一个半径为1的不锈钢制的实心半球后,半球的大圆面、水面均与容器口相平,则h 的值为 .17. 已知菱形边长为 , ,以 为折痕把 和 折起,使点 到达点 的位置,点 到达点的位置, , 不重合.(1) 求证:;(2) 若,求点到平面的距离.18. 如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,E,F分别为PA,BD的中点,PA=PD=AD=2.(1) 证明:EF∥平面PBC;(2) 若,求二面角E﹣DF﹣A的正弦值.19. 如图,在四棱锥中,平面ABCD,,E为棱PC上不与点C重合的点.(1) 求证:平面平而PAC;(2) 若,且二面角的平面角为45°,求三棱锥的体积.20. 如图,平面,在中,,,交于点D,,,,.(1) 证明:;(2) 求直线与平面所成角的正弦值.21. 已知空间四边形ABCD的两条对角线的长AC=6,BD=8,AC与BD所成的角为30o, E,F,G,H分别是AB,BC,CD,D A的中点,求四边形EFGH的面积.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)(1)(2)(1)(2)20.(1)(2)21.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.立体几何1.掌握球、棱柱、棱锥、棱台的表面积和体积的计算公式,能用公式解决简单的实际问题. 2.能用斜二测画法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合)的直观图.3.能借助长方体,认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系.4.能从定义和基本事实出发,借助长方体,通过直观感知,了解空间中直线与直线、直线与平面、平面与平面的平行和垂直的关系.5.能用已获得的结论证明空间基本图形位置关系的简单命题.1.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40︒,则晷针与点A 处的水平面所成角为( )A .20︒B .40︒C .50︒D .90︒【答案】B【解析】画出截面图如下图所示,其中CD 是赤道所在平面的截线;l 是点A 处的水平面的截线,依题意可知OA l ⊥;AB 是晷针所在直线,m 是晷面的截线, 依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥. 由于40AOC ∠=︒,//m CD ,所以40OAG AOC ∠=∠=︒,由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒,所以40BAE OAG ∠=∠=︒, 也即晷针与点A 处的水平面所成角为40BAE ∠=︒.【点睛】本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质.2.已知空间中不过同一点的三条直线l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】依题意,,m n l 是空间不过同一点的三条直线,当,,m n l 在同一平面时,可能////m n l ,故不能得出,,m n l 两两相交; 当,,m n l 两两相交时,设mn A =,m l B =,n l C =,根据公理2可知,,m n 确定一个平面α, 而B m α∈⊂,C n α∈⊂,根据公理1可知,直线BC 即l α⊂,所以,,m n l 在同一平面,综上所述,“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件. 【点睛】本小题主要考查充分、必要条件的判断,考查公理1和公理2的运用.一、选择题.1.设m ,n 是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题: ①若m α⊥,n α∥,则m n ⊥ ②若αβ∥,βγ∥,m α⊥,则m γ⊥ ③若m α∥,n α∥,则//m n④若αγ⊥,βγ⊥,则αβ∥ 其中正确命题的序号是( ) A .①和② B .②和③C .③和④D .①和④【答案】A【解析】对于①,因为n α∥,所以经过n 作平面β,使l βα=,可得n l ∥,又因为m α⊥,l α⊂,所以m l ⊥,结合n l ∥得m n ⊥.由此可得①是真命题; 对于②,因为αβ∥且βγ∥,所以αγ∥,结合m α⊥,可得m γ⊥,故②是真命题; 对于③,设直线m 、n 是位于正方体上底面所在平面内的相交直线, 而平面α是正方体下底面所在的平面,则有m α∥且n α∥成立,但不能推出//m n ,故③不正确; 对于④,设平面α、β、γ是位于正方体经过同一个顶点的三个面, 则有αγ⊥且βγ⊥,但是αβ⊥,推不出αβ∥,故④不正确, 综上所述,其中正确命题的序号是①和②.2.在正方体1111ABCD A B C D -中,如图,M 、N 分别是正方形ABCD 、11BCC B 的中心.则过点1C 、M 、N 的截面是( )A .正三角形B .正方形C .梯形D .直角三角形【答案】A【解析】如下图所示,连接BN 、BD 、1BC ,由于M 、N 分别为正方形ABCD 、11BB C C 的中心,则M 、N 分别为BD 、1BC 的中点,所以,过点1C 、M 、N 三点的截面为1BC D △,易知1BC D △为正三角形. 因此,过点1C 、M 、N 三点的截面为正三角形.3.某三棱锥的三视图如图所示,如果网格纸上小正方形的边长为1,则该三棱锥的体积为( )A .4B .8C .12D .24【答案】A【解析】由三视图还原几体何体如图,三棱锥D ABC -是从长为4,宽为4,高为3的长方体中截得, 所以11423432D ABC V -=⨯⨯⨯⨯=.4.如图,正三角形ABC 为圆锥的轴截面,D 为AB 的中点,E 为弧BC 的中点,则直线DE 与AC 所成角的余弦值为( )A .13B .12C .2D .34【答案】C【解析】如图所示,取BC 中点O ,BO 中点F ,连接,,,OD OE FE DF ,则OD AC ∥, 所以ODE ∠就是直线DE 与AC 所成角, 设4AB =,则2OD =,1OF =,2OE =,可得DF =,EF = 则DE ==因为E 为弧BC 的中点,可得OE BC ⊥,进而可得OE ⊥平面ABC , 因为OD ⊂平面ABC ,所以OE OD ⊥,在直角ODE △中,可得cos 2OD ODE DE ∠==,即直线DE 与AC 所成角的余弦值为2.5.已知,m n 是两条不重合的直线,,αβ是两个不重合的平面,则下列命题中,错误的是( )A .若,m n m α⊥⊥,则n α∥B .若,,m n m n αα⊄∥∥,则n α∥C .若,,m n m n αβ⊥⊥⊥,则αβ⊥D .若,m ααβ∥∥,则m β∥或m β⊂【答案】A【解析】对于A :若,m n m α⊥⊥,则n α∥或n ⊂α,故A 错误,BCD 正确. 6.如图所示,正方体1111ABCD A B C D -中,,E F 分别为棱AB ,1CC 的中点,则在平面11ADD A 内与平面1D EF 平行的直线( )A .不存在B .有1条C .有2条D .有无数条【答案】D【解析】平面11ADD A 与平面1D EF 有公共点1D , 由公理3知平面11ADD A 与平面1D EF 必有过1D 的交线l ,在平面11ADD A 内与l 平行的直线有无数条,且它们都不在平面1D EF 内, 由线面平行的判定定理可知它们都与平面1D EF 平行.7.如图,在四面体ABCD 中,截面PQMN 是正方形,则在下列命题中,错误的为( )A .AC BD ⊥B .AC ∥截面PQMNC .AC BD =D .异面直线PM 与BD 所成的角为45︒【答案】C【解析】因为截面PQMN 是正方形,所以PQ MN ∥、QM PN ∥, 则PQ ∥平面ACD 、QM ∥平面BDA , 所以PQ AC ∥,QM BD ∥,由PQ QM ⊥可得AC BD ⊥,故A 正确; 由PQ AC ∥可得AC ∥截面PQMN ,故B 正确;异面直线PM 与BD 所成的角等于PM 与QM 所成的角,故D 正确.8.已知三棱锥P ABC -的四个顶点都在球O 的球面上,PA ⊥平面ABC ,ABC △是边长为2的等边三角形,若球O 的体积为π3,则直线PC 与平面PAB 所成角的正切值为( )A .11B .11C D 【答案】A【解析】设ABC △的中心为E ,M 为AB 的中点,过O 作OD PA ⊥,则D 为PA 的中点,∴CPM ∠是直线PC 与平面PAB 所成角.∵ABC △是边长为2的等边三角形,∴233OD AE CM ===,∵34π33OP ⋅=,∴OP =∴2PA PD ===,∴PM ==,∴tan CM CPM PM ∠==9.如图,正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,M 为棱1BB 的中点,则下列结论中错误的是( )A .1D O ∥平面11A BCB .MO ⊥平面11A BCC .二面角M AC B --等于90︒D .异面直线1BC 与AC 所成的角等于60︒【答案】C【解析】对于A ,连接11B D ,交11A C 于E ,则四边形1D OBE 为平行四边形, 故1D O BE ∥,∵1D O ⊄平面11A BC ,BE ⊂平面11A BC ,∴1D O ∥平面11A BC ,故正确; 对于B ,连接1B D ,因为O 为底面ABCD 的中心,M 为棱1BB 的中点, ∴1MO B D ∥,易证1B D ⊥平面11A BC ,则MO ⊥平面11A BC ,故正确;对于C ,因为BO AC ⊥,MO AC ⊥,则MOB ∠为二面角M AC B --的平面角,显然不等于90︒, 故错误;对于D ,∵11AC A C ∥,∴11AC B ∠为异面直线1BC 与AC 所成的角,11A C B △为等边三角形,1160AC B ∴∠=︒,故正确.10.在平面五边形ABCDE 中,60A ∠=︒,AB AE ==BC CD ⊥,DE CD ⊥,且6BC DE ==.将五边形ABCDE 沿对角线BE 折起,使平面ABE 与平面BCDE 所成的二面角为120︒,则沿对角线BE 折起后所得几何体的外接球的表面积为( )A .B .84πC .252πD .126π【答案】C【解析】设ABE △的中心为1O ,矩形BCDE 的中心为2O , 过1O 作垂直于平面ABE 的直线1l ,过2O 作垂直于平面BCDE 的直线2l , 则由球的性质可知,直线1l 与2l 的交点O , 即几何体ABCDE 外接球的球心.取BE 的中点F ,连接1O F ,2O F ,由条件得123O F O F ==,12120O FO ∠=︒.连接OF ,因为12OFO OFO ≅△△,从而1OO =. 连接OA ,则OA 为所得几何体外接球的半径.又16O A =,则22211273663OA OO O A =+=+=,故所得几何体外接球的表面积等于252π.11.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,60DAB ∠=︒,侧面PAD 为正三角形,且平面PAD ⊥平面ABCD ,则下列说法错误的是( )A .在棱AD 上存在点M 使AD ⊥平面PMB B .异面直线AD 与PB 所成的角为90︒C .二面角P BC A --的大小为45︒D .BD ⊥平面PAC 【答案】D【解析】解:如图,对于A ,取AD 的中点M ,连接,PM BM ,∵侧面PAD 为正三角形,∴PM AD ⊥,又底面ABCD 是菱形,60DAB ∠=︒,∴ABD △是等边三角形, ∴AD BM ⊥, 又PMBM M =,PM ,BM ⊂平面PMB ,∴AD ⊥平面PBM ,故A 正确;对于B ,∵AD ⊥平面PBM ,∴AD PB ⊥,即异面直线AD 与PB 所成的角为90︒,故B 正确;对于C ,∵平面PBC平面ABCD BC =,//BC AD ,BC ∴⊥平面PBM ,∴BC PB ⊥,BC BM ⊥,∴PBM ∠是二面角P BC A --的平面角,设1AB =,则BM =,PM =在PBM Rt △中,tan 1PMPBM BM∠==,即45PBM ∠=︒,故二面角P BC A --的大小为45︒, 故C 正确;对于D ,假设BD ⊥平面PAC ,则BD PA ⊥, 又依题意平面PAD ⊥平面ABCD ,AD BM ⊥,则BM⊥平面PAD ,故BM PA ⊥,而BD ,BM 相交,且在平面ABCD 内,故PA ⊥平面ABCD ,与PM ⊥平面ABCD 矛盾,因此BD 与平面PAC 不垂直,故D 错误.12.在棱长为2的正方体1111ABCD A B C D -中,P 是1BDC △内(不含边界)的一个动点,若11A P BC ⊥,则线段1A P 的长的取值范围为( )A .B .C .D .【答案】C【解析】由正方体的性质可知,11A BDC -是正四面体,且正四面体的棱长为∵P 在1BDC △内,∴1A P的最大值为1111AC A B A D ===, 1A P 的最小值是1A 到平面1BDC 的距离,设1A 在平面1BDC 的射影为H ,则H 为正三角形1BDC的中心,3BH =,1A H === ∴1A P, 又因为P 不在三角形1BDC 的边上,所以1A P的范围是.二、填空题.13.已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.【答案】1【解析】设圆锥底面半径为r ,母线长为l ,则π2π12π2π2r l r l ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩, 解得1r =,2l =.14.一个长方体被一平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为 .【答案】48【解析】根据几何体的三视图得该几何体的体积为长宽高分别为6,4,4的长方体体积的一半, 即体积为1446482⨯⨯⨯=.15.如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,点E ,F 分别为PA ,PD的中点,则平面BCFE 将四棱锥P ABCD -所分成的上下两部分的体积的比值为 .【答案】35【解析】设四棱锥P ABCD -的体积为V ,连接FA ,FB ,则下面部分几何体的体积为F ABCD B AEF V V --+, 其中12F ABCD V V -=,11112448B AEF B APF B ADP P ABD V V V V V ----====, 所以58F ABCD B AEF V V V --+=, 则上面部分几何体的体积为5388V V V -=,故平面BCFE 将四棱锥P ABCD -所分成的上下两部分的体积的比值为35.16.已知三棱锥P ABC -中,满足1PA BC ==,PC AB ==2AC =,则当三棱锥体积最大时,直线AC 与PB 夹角的余弦值是 .【答案】5【解析】如图所示,因为ABC △的面积为定值,所以当平面PAC ⊥平面ABC 时,三棱锥PAC 体积最大,过P 作//PE AC ,过A 作AE PE ⊥,所以BPE ∠为AC 与PB 所成角或补角. 过点P 作PD AC ⊥交AC 于D ,则PD ⊥平面ABC ,所以AE ⊥平面ABC ,即AE AB ⊥,因为1PA =,PC =,2AC =,所以PAC △为直角三角形,所以PD AE ==12AD PE ==, 因为1BC =,AB =2AC =,所以ABC △为直角三角形,π6BAC ∠=,所以211732424BD =+-⋅=,则2375442BP =+=,2315344BE =+=,所以1515cos 5BPE +-∠==-, 因此直线AC 与PB夹角的余弦值是5.。
