中位线直角三角形中线长定理的运用
华东师大初中数学九年级上册三角形中位线定理 知识讲解[精品]
![华东师大初中数学九年级上册三角形中位线定理 知识讲解[精品]](https://img.taocdn.com/s3/m/784d64c9daef5ef7bb0d3c1d.png)
三角形中位线定理【学习目标】1. 理解三角形的中位线的概念,掌握三角形的中位线定理.2. 掌握中点四边形的形成规律.【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系. (2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点二、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点诠释:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.【典型例题】类型一、三角形的中位线1、(2016•北京)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.【思路点拨】(1)根据三角形中位线定理得MN=AD,根据直角三角形斜边中线定理得BM=AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.【答案与解析】(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,MN=AD,在RT△ABC中,∵M是AC中点,∴BM=AC,∵AC=AD,∴MN=BM.(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)可知,BM=AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴BN2=BM2+MN2,由(1)可知MN=BM=AC=1,∴BN=【总结升华】本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.举一反三:【变式】如图,矩形OABC的顶点A、C分别在x轴、y轴正半轴上,B点坐标为(3,2),OB与AC交于点P,D、E、F、G分别是线段OP、AP、BP、CP的中点,则四边形DEFG的周长为_____.【答案】5;解:∵四边形OABC是矩形,∴OA=BC,AB=OC;BA⊥OA,BC⊥OC.∵B点坐标为(3,2),∴OA=3,AB=2.∵D、E、F、G分别是线段OP、AP、BP、CP的中点,∴DE=GF=1.5; EF=DG=1.∴四边形DEFG的周长为(1.5+1)×2=5.2、如图,在△ABC中,已知点D、E、F分别是AB、BC、CA的中点,AH是高.(1)若BC=10,AH=8,则四边形ADEF的面积为.(2)求证:∠DHF=∠DEF.B【思路点拨】(1)由三角形面积公式可知:△BDE、△EFC的面积都等于△ABC面积的四分之一,进而可求出四边形ADEF的面积.(2)首先证明四边形ADEF是平行四边形,进而可得∠DEF=∠DAF,再利用直角三角形的中线性质得线段相等,从而得角等,最终可得到∠DAF=∠DEF,即可证出∠DHF=∠DEF.【答案解析】(1)解:∵BC=10,AH=8,∴S△ABC=×8×10=40,∵点D、E、F分别是AB、BC、CA的中点,∴△BDE、△EFC的面积都等于△ABC面积的,∴四边形ADEF的面积=40﹣20=20,故答案为:20;(2)证明:∵D、E、F分别是△ABC各边中点,∴DE∥AC,EF∥AB,∴四边形ADEF是平行四边形,∴∠DEF=∠DAF,∵AH是△ABC的高∴△ABH、△ACH是直角三角形,∵点D、点F是斜边AB、AC中点,∴DH=DA,HF=AF,∴∠DAH=∠DHA,∠FAH=∠FHA,∴∠DAH+∠FAH=∠FHA+∠DHA,即∠DAF=∠DHF , ∴∠DEF=∠DHF .【总结升华】此题主要考查了平行四边形的性质与判定,三角形的中位线定理,直角三角形的性质,解决题目的关键是证明∠DHF=∠DAF 与∠DAF=∠DEF .3、如图所示,在△ABC 中,M 为BC 的中点,AD 为∠BAC 的平分线,BD ⊥AD 于D ,AB =12,AC =18,求MD 的长.【思路点拨】本题中所求线段MD 与已知线段AB 、AC 之间没有什么联系,但由M 为BC 的中点联想到中位线,另有AD 为角平分线和垂线,根据等腰三角形“三线合一”构造等腰三角形ABN ,D 为BN 的中点,DM 即为中位线,不难求出MD 的长度. 【答案与解析】解:延长BD 交AC 于点N .∵ AD 为∠BAC 的角平分线,且AD ⊥BN , ∴ ∠BAD =∠NAD ,∠ADB =∠ADN =90°,在△ABD 和△AND 中,BAD NAD AD =ADADB ADN ∠∠⎧⎪⎨⎪∠∠⎩== ∴ △ABD ≌△AND(ASA) ∴ AN =AB =12,BD =DN .∵ AC =18,∴ NC =AC -AN =18-12=6, ∵ D 、M 分别为BN 、BC 的中点, ∴ DM =12CN =162⨯=3.【总结升华】当条件中含有中点的时候,可以将它与等腰三角形的“三线合一”、三角形的中线、中位线等联系起来,进行联想,必要时添加辅助线,构造中位线等图形. 举一反三:【变式】如图所示,四边形ABCD 中,Q 是CD 上的一定点,P 是BC 上的一动点,E 、F 分别是PA 、PQ 两边的中点;当点P 在BC 边上移动的过程中,线段EF 的长度将( ).A .先变大,后变小B .保持不变C .先变小,后变大D .无法确定 【答案】B ;解: 连接AQ .∵ E 、F 分别是PA 、PQ 两边的中点,∴ EF 是△PAQ 的中位线,即AQ =2EF .∵ Q 是CD 上的一定点,则AQ 的长度保持不变, ∴ 线段EF 的长度将保持不变.4、我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题:(1)如图1,在△ABC 中,AB=AC ,点D 在BC 上,且CD=CA ,点E 、F 分别为BC 、AD 的中点,连接EF 并延长交AB 于点G .求证:四边形AGEC 是等邻角四边形;(2)如图2,若点D 在△ABC 的内部,(2)中的其他条件不变,EF 与CD 交于点H ,图中是否存在等邻角四边形,若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.【思路点拨】(1)运用中位线的性质,找出对应相等的角;(2)根据题意易知满足条件的四边形即为第一题的四边形. 【答案与解析】解:(1)取AC 的中点H ,连接HE 、HF∵点E 为BC 中点∴EH 为△ABC 的中位线∴EH∥AB,且EH=12AB 同理FH∥DC,且FH=12DC∵AB=AC,DC=AC ∴AB=DC ,EH=FH ∴∠1=∠2∵EH∥AB,FH∥DC ∴∠2=∠4,∠1=∠3 ∴∠4=∠3∵∠AGE+∠4=180°,∠GEC+∠3=180° ∴∠AGE=∠GEC∴四边形AGEC是邻角四边形(2)存在等邻角四边形,为四边形AGHC.【总结升华】本题考查了三角形的中位线以及等腰三角形的性质的综合运用.本题较灵活,要求学生能够把题中的条件转化成角,从而找出相等的角来解题.举一反三:【变式】如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是()A.4 B.3 C.2 D.1【答案】D;解:连接DE并延长交AB于H,∵CD∥AB,∴∠C=∠A,∠CDE=∠AHE,∵E是AC中点,∴AE=CE,∴△DCE≌△HAE,∴DE=HE,DC=AH,∵F是BD中点,∴EF是△DHB的中位线,∴EF=12 BH,∴BH=AB-AH=AB-DC=2,∴EF=1.类型二、中点四边形5、如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)求证:四边形EFGH是正方形;(2)若AD=2,BC=4,求四边形EFGH的面积.【思路点拨】(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.(2)连接EG ,利用梯形的中位线定理求出EG 的长,然后结合(1)的结论求出2EH =92,也即得出了正方形EHGF 的面积. 【答案与解析】证明:(1)在△ABC 中,E 、F 分别是AB 、BC 的中点,故可得:EF =12AC ,同理FG =12BD ,GH =12AC ,HE =12BD , 在梯形ABCD 中,AB =DC ,故AC =BD ,∴EF =FG =GH =HE , ∴四边形EFGH 是菱形. 设AC 与EH 交于点M ,在△ABD 中,E 、H 分别是AB 、AD 的中点, 则EH∥BD, 同理GH∥AC, 又∵AC⊥BD,∴EH⊥HG,∴四边形EFGH 是正方形. (2)连接EG . 在梯形ABCD 中,∵E、G 分别是AB 、DC 的中点, ∴EG=12(AD +BC )=3. 在Rt△EHG 中,∵222EH GH EG +=,EH =GH , ∴2EH =92,即四边形EFGH 的面积为92. 【总结升华】此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的中位线定理得出EH =HG =GF =FE ,这是本题的突破口. 举一反三:【变式】如图,E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点. (1)判断四边形EFGH 的形状,并说明你的理由;(2)连接BD 和AC ,当BD 、AC 满足何条件时,四边形EFGH 是正方形.【答案】解:(1)四边形EFGH 是平行四边形.理由:连接AC ,∵E、F 分别是AB 、BC 的中点,∴EF∥AC,且EF =12AC , 同理,HG∥AC,且HG =12AC ,∴EF∥HG,且EF =HG ,∴四边形EFGH 是平行四边形;(2)当BD =AC ,且B D⊥AC 时,EFGH 是正方形. 理由:连接AC ,BD ,∵E、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点, ∴EF=GH =12AC ,EH =FG =12BD ,EH∥BD,GH∥AC, ∵BD=AC ,BD⊥AC,∴EH=EF =FG =GH ,EH⊥GH,∴四边形ABCD 是菱形,∠EHG=90°, ∴四边形EFGH 是正方形.。
中位线及其应用

中位线及其应用知识定位中位线在初中几何或者竞赛中占据非常大的地位,它的有关知识是今后我们学习综合题目或者三角形综合的重要基础。
中位线的证明性质以及应用,必须熟练掌握。
本节我们通过一些实例的求解,旨在介绍数学竞赛中中位线相关问题的常见题型及其求解方法本讲将通过例题来说明这些方法的运用。
知识梳理1、三角形中位线定义(1)三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线与三角形的中线区分:三角形中线是连接一顶点和它的对边中点的线段,而三角形中位线是连接三角形两边中点的线段。
(2)三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半。
如图,在ABC ∆中,点D 、E 分别为边AB 、AC 的中点,则DE 为ABC ∆的中位线。
几何语言描述:因为D 、E 分别为边AB 、AC 的中点,所以DE//BC,且DE=12BC提示 a :“平行且等于第三边的一半”,具体应用时要根据题目的要求灵活进行选择,并 不一定要把两个结论都写出来。
b :一个三角形有三条中位线。
c :经过三角形一边的中点且与另一边平行的直线,必平分第三边,这是一种重要 的作辅助线的方法。
2、三角形中位线的性质(1)三角形中位线平行于第三边,并且等于第三边的一半。
梯形中位线平行于两底,并且等于两底和的一半。
(2)中位线性质定理的结论,兼有位置和大小关系,可以用它判定平行,计算线段的长度,确定线段的和、差、倍关系。
(3)运用中位线性质的关键是从出现的线段中点,找到三角形或梯形,包括作出辅助线。
(4)中位线性质定理,常与它的逆定理结合起来用。
它的逆定理就是平行线截比例线段定理及推论,①一组平行线在一直线上截得相等线段,在其他直线上截得的线段也相等②经过三角形一边中点而平行于另一边的直线,必平分第三边③经过梯形一腰中点而平行于两底的直线,必平分另一腰补充:有关线段中点的其他定理还有:①直角三角形斜边中线等于斜边的一半②等腰三角形底边中线和底上的高,顶角平分线互相重合③对角线互相平分的四边形是平行四边形④线段中垂线上的点到线段两端的距离相等因此如何发挥中点作用必须全面考虑。
初中数学-三角形中的中线的用法教师版
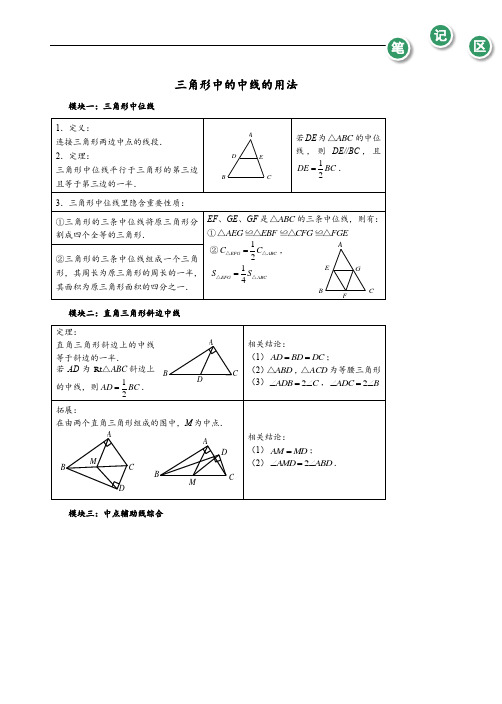
三角形中的中线的用法模块一:三角形中位线 1.定义:连接三角形两边中点的线段. 2.定理:三角形中位线平行于三角形的第三边且等于第三边的一半.若DE 为ABC △的中位线,则DE//BC ,且12DE BC =.3.三角形中位线里隐含重要性质: ①三角形的三条中位线将原三角形分割成四个全等的三角形.EF 、GE 、GF 是ABC △的三条中位线,则有:①AEG EBF CFG FGE △△△△≌≌≌②12EFG ABC C C =△△,14EFG ABC S S =△△②三角形的三条中位线组成一个三角形,其周长为原三角形的周长的一半,其面积为原三角形面积的四分之一. 模块二:直角三角形斜边中线 定理:直角三角形斜边上的中线等于斜边的一半.若AD 为Rt ABC △斜边上的中线,则12AD BC =.相关结论:(1)AD BD DC ==; (2)ABD △,ACD △为等腰三角形 (3)2ADB C ∠=∠,2ADC B ∠=∠拓展:在由两个直角三角形组成的图中,M 为中点.相关结论:(1)AM MD =;(2)2AMD ABD ∠=∠. 模块三:中点辅助线综合E DCB AMMABCDA BCDDCBAFA B CE G(1)如图1-1,在ABC△中,D,E,F分别是AB,BC,AC的中点,若ABC△的周长为20cm,则DEF△的周长为__________.(2)如图1-2,在Rt ABC△中,30A∠=︒,1BC=,点D,E分别是直角边BC,AC的中点,则DE的长为__________.图1-1 图1-2(3)如图1-3,ABC△中,6AB AC==,8BC=,AE平分BAC∠交BC于点E,点D为AB的中点,连接DE,则BDE△的周长是__________.(4)如图1-4,在四边形ABCD中,E、F分别为AB、CD的中点.求证:1()2EF AC BD<+.图1-3 图1-4【解析】(1)10cm.(2)1.(3)10.(4)证明:取AD的中点M,连结EM和FM.∵E、F是AB、CD中点,∴12EM BD=,12FM AC=.又∵EF EM FM<+,∴1()2EF AC BD<+.【教师备课提示】考察中位线产生的线段长度关系.第(4)题利用中位线构造出长为12AC,12BD的线段并将线段集中;也可以求证1()2EF AD BC<+,方法是取AC 或BD的中点.FEDCBA模块一三角形中位线例题1MAB CDEF(1)如图2-1,在四边形ABCD 中,P 是对角线BD 的中点,E ,F 分别是AB ,CD 的中点,AD BC =,18PEF ∠=︒,则PFE ∠的度数是__________度.(2)如图2-2,已知四边形ABCD 的对角线AC BD =,E 、F 分别是AD 、BC 的中点,连结EF 分别交AC 、BD 于M 、N ,求证:AMN BNM =∠∠.(3)已知,如图2-3四边形ABCD 中,AD BC =,E 、F 分别是AB 和CD 的中点,AD 、EF 、BC 的延长线分别交于M 、N 两点.求证:AME BNE ∠=∠.图2-1 图2-2 图2-3【解析】(1)18.(2)设AB 的中点为G ,连结GE 、GF ,容易证得:GE //BD ,12EG BD =,GF //AC ,12EF AC =,从而GF GE =,GEF GFE ∠=∠, ∴AMN BNM =∠∠.(构造中位线来利用对角线相等的条件,也可以取AC 或BD 的中点.) (3)连接AC ,取AC 中点H ,连接FH 、EH .∵DF CF =,AH CH =,∴FH//AD ,12FH AD =,同理,12EH BC =,EH//BC , ∵AD BC =,∴EH FH =,∴HFE HEF ∠=∠, ∵FH//AM ,EH//BC , ∴AM E HFE ∠=∠,HEF BNE ∠=∠, ∴AME BNE ∠=∠.【教师备课提示】考察中位线的性质,学会通过构造中位线去利用已知的条件.CM FEND B AA CDM FE NB例题2CM FE G NDB AA H C D MF E NB如图,在ABC △中,D 、G 分别为AB 、AC 上的点,且BD CG =,M 、N 分别是BG 、CD 的中点,过MN 的直线交AB 于点P ,交AC 于点Q ,求证:AP AQ =.【解析】连DG ,找DG 的中点E ,连ME 、NE ,∵M 、N 分别是BG 与CD 的中点.∴ME//AB ,12ME BD =,NE//AC ,12NE GC =.∴APQ EMN ∠=∠,AQP ENM ∠=∠.∵BD GC =,∴EM EN =, ∴EMN ENM ∠=∠,∴APQ AQP ∠=∠,∴AP AQ =. 【教师备课提示】还可以取BC 中点.总结:已知四边形对角线中点,则取一边中点,可出两条中位线,学会构造出中位线去利用题目中给出的等量关系.已知:在ABC △中,90ABC ∠=︒,点E 在直线AB 上,ED 与直线AC 垂直,垂足为D ,且点M 为EC 中点,连接BM 、DM .(1)如图4-1,若点E 在线段AB 上,探究线段BM 与DM 及BM D ∠与BCD ∠所满足的数量关系,并直接写出你得到的结论;(2)如图4-2,若点E 在BA 延长线上,你(1)中的结论是否发生变化?写出你的猜想并证明.图4-1 图4-2【解析】(1)BM DM =,2BMD BCD ∠=∠;(2)结论不变,由题意知MB MC MD ==,∴2BME BCM ∠=∠,2DME DCM ∠=∠,两式相减,得2BMD BCD ∠=∠.NM PQG D C BAEA BC DG Q PM N 图2图1BEM CDAMEDCBA例题3模块二直角三角形斜边中线例题4如图,90MON∠=︒,ABC△中,90BAC∠=︒,2AB=,1AC=,AB在MON∠上滑动,求OC的最大值.【解析】取AB的中点D,连结OD、DC,则1OD=,2DC=,可得12OC≤+,即OC的最大值为12+(O、D、C三点共线时).在Rt ABC△中,90BAC∠=︒,AD BC⊥,E、F、G分别是AB、AC、BC的中点,M 是DG的中点,求证:ME MF=.【解析】连结DF、EG,可证DF GE=,MDF MGE∠=∠,MD MG=,则MDF MGE△≌△,得证.例题5模块三中点辅助线综合例题6如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点.求证:BF EF =.【解析】方法一:如图1,取AC 中点M ,取AD 中点N ,连BM ,MF ,NF ,EN . ∵90ABC AED ∠=∠=︒,1122BM AC FN EN AD MF ====,,∴BMF FNE △≌△,∴BF EF =,方法二:如图2,延长CB 到M ,使得MB BC =, 延长DE 到N ,使得NE DE =, 连接AM ,AN ,MD ,CN . 由90ABC AED ∠=∠=°,AMC △,ADN △是等腰三角形,F 是CD 中点,则BF //MD ,12BF MD =,EF//CN ,12EF CN =,MAD CAN △≌△,MD CN =,∴BF EF =,此题的两种解法中综合了中点的三个基本用法:等腰三角形三线合一;直角三角形斜边中线;中位线,即以下三个模型:图2图1MNN MACBDEF F EDB CA例题7FEDB C A(1)如图1-1,在ABC△中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE 交AC于F.若AB=10厘米,AC=16厘米,则DE的长度为__________.(2)如图1-2,已知,在四边形ABCD中,AD BC=,P是对角线BD的中点,N是DC 的中点,M是AB的中点,30DBC∠=︒,70ADB∠=︒.求MNP∠度数.图1-1 图1-2【解析】(1)3厘米;(2)∵在四边形ABCD中,P是对角线BD的中点,M、N分别是AB、CD的中点,∴NP,PM分别是CDB△与DAB△的中位线,∴12PN BC=,12PM AD=,PN//BC,PM//AD,∴30NPD DBC∠=∠=︒,70MPB ADB∠=∠=︒,∴110DPM∠=︒;∴140NPM∠=︒,∵AD BC=;∴PN PM=,故NMP△是等腰三角形.∵140NPM∠=︒,∴20PMN PNM∠=∠=︒.复习巩固模块一三角形中位线演练1(1)如图2-1,ABC △中,过点A 分别作ABC ∠、ACB ∠的外角平分线.....的垂线..AD 、AE ,垂足为D 、E .求证:①//ED BC ;②1()2ED AB AC BC =++.(2)(四川省中考题)如图2-2,已知:AD 是ABC △的中线,AE 是ABD △的中线,且AB BD =,求证:2AC AE =.图2-1 图2-2【解析】(1)①分别延长AD 、AE 与直线BC 交于点F 、G ,∵BD ⊥AD ,且BD 为ABF ∠的角平分线∴AD FD =,且AB BF =(等腰三角形的三线合一) 同理可得AE GE =,AC GC =, ∴DE 为AFG △的中位线,∴ED //BC ,且12DE FG =.②由(1)知12DE FG =,且AB BF =,AC GC =,∴111()()222ED FG=FB BC CG AB BC AC =++=++.(2)取AC 的中点F ,连结DF ,易得DF//AB ,12DF AB =,ADF BAD ∠=∠,而1122DE BD AB ==,故DF DE =.再证ADE ADF △≌△,∴AE AF =,∴2AC AE =.C ED BA演练2CF E D B A(1)如图3-1,四边形ABCD 中,90ADC ∠=︒,取AC 中点O ,BC 中点E ,连接OD 、OE 、DE ,20CAD CAB ∠=∠=︒,则DOE ∠=__________.(2)如图3-2所示,ABC △中,AH BC ⊥于H ,点E 、D 、F 分别是AB 、BC 、AC 的中点,10cm HF =,则ED 的长度是__________.图3-1 图3-2【解析】(1)60︒.(2)10cm .(1)如图4-1,在ABC △中,2B C ∠=∠,M 是BC 中点,AD BC ⊥于D .求证:12DM AB =.(2)如图4-2,已知:ABD △和ACE △都是直角三角形,且90ABD ACE ∠=∠=︒,BAD CAE ∠=∠.连接DE ,设M 为DE 的中点.求证:MB MC =.【解析】(1)法一:取AB 中点G ,连结GD 、GM ,则12GD AB =,GM AC ∥.则GMD C ∠=∠. 而GD GB B GDB GMD DGM =⇒∠=∠=∠+∠ C DGM =∠+∠,由于2B C ∠=∠,所以DGM C GMD ∠=∠=∠.∴12MD GD AB ==. OEDC B AMEDCBA模块二直角三角形斜边中线演练3模块三中点辅助线综合演练4CAB GNDMC AB D M法二:同理可以取AC的中点N,连接DN,MN.(2)如图,分别取AD、AE的中点P、Q,连接PB、PM、QC、QM,由P、M、Q分别是AD、DE、AE的中点,∴PM//AE,12PM AE=,QM//AD,12QM AD=,∵ABD△、ACE△是直角三角形,∴12PB AD=,12CQ AE=,∴PB QM=,PM QC=,∵BAD CAE∠=∠,∴ADB AEC∠=∠,∴DPB CQE∠=∠,由AD//QM,AE//PM,∴APM AQM∠=∠,∴BPM MQC∠=∠,∴BPM MQC△≌△,∴MB MC=.QPAB CDE M图3。
专题22 三角形中位线定理应用问题(解析版)

专题22 三角形中位线定理应用问题1.三角形中位线的定义:连接三角形两边中点的线段叫做三角形的中位线。
2.三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
3.对三角形中位线的深刻理解(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的. (3)三角形的中位线不同于三角形的中线.【例题1】(2020•福建)如图,面积为1的等边三角形ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,则△DEF 的面积是( )A .1B .12C .13D .14 【答案】D【解析】根据三角形的中位线定理和相似三角形的判定和性质定理即可得到结论.∵D ,E ,F 分别是AB ,BC ,CA 的中点,1214∴DE =12AC ,DF =12BC ,EF =12AB ,∴DF BC =EF AB =DE AC =12,∴△DEF ∽△ABC ,∴S △DEFS △ABC =(DE AC )2=(12)2=14, ∵等边三角形ABC 的面积为1,∴△DEF 的面积是14.【对点练习】(2019内蒙古赤峰)如图,菱形ABCD 周长为20,对角线AC 、BD 相交于点O ,E 是CD 的中点,则OE 的长是( )A .2.5B .3C .4D .5【答案】A .【解析】∵四边形ABCD 为菱形,∴CD =BC ==5,且O 为BD 的中点, ∵E 为CD 的中点,∴OE 为△BCD 的中位线,∴OE =CB =2.5。
【点拨】掌握菱形特点,根据三角形中位线定理解决问题。
【例题2】(2020•临沂)如图,在△ABC 中,D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,H 为AF 与DG 的交点.若AC =6,则DH = .【解析】1.【分析】由三等分点的定义与平行线的性质得出BE =DE =AD ,BF =GF =CG ,AH =HF ,DH 是△AEF 的中位线,易证△BEF ∽△BAC ,得EF AC =BE AB ,解得EF =2,则DH =12EF =1. 【解析】∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC ,∴△BEF ∽△BAC ,∴EF AC =BE AB ,即EF 6=BE 3BE ,解得:EF =2,∴DH =12EF =12×2=1,【对点练习】(2019广西梧州)如图,已知在△ABC 中,D 、E 分别是AB 、AC 的中点,F 、G 分别是AD 、AE 的中点,且FG =2cm ,则BC 的长度是 cm .【答案】8.【解析】利用三角形中位线定理求得FG=DE,DE=BC.如图,∵△ADE中,F、G分别是AD、AE的中点,∴DE=2FG=4cm,∵D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=8cm【点拨】连续两次应用三角形中位线定理处理本题,是关键。
八年级全等三角形中的中点、中线问题

全等三角形中的中点、中线问题三角形中线的定义:三角形顶点和对边中点的连线三角形中线的相关定理: 直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合) 三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线. 三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边.中线中位线相关问题(涉及中点的问题)见到中线(中点),我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式),尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见.【例1】 如图,AC DE ∥,BC EF ∥,AC DE =.求证:AF BD =.FEDCBA【巩固】如图所示:AB CD ∥,AB CD =.求证:AD BC ∥.DCBA【例2】 如图,已知AB DC =,AD BC =,O 是BD 中点,过O 点的直线分别交DA 、BC 的延长线于E F ,.求证:E F ∠=∠21OFEDCBA【例3】 如图,AB CD ,相交于点O ,OA OB =,E 、F 为CD 上两点,AE BF ∥,CE DF =.求证:AC BD ∥. OF E DBA【巩固】如图,在梯形ABCD 中,AD BC ∥,E 为CD 中点,连结AE 并延长AE 交BC 的延长线于点F .求证:FC AD =.FEDCBA【例4】 已知:如图,梯形ABCD 中,AD BC ∥,点E 是CD 的中点,BE 的延长线与AD 的延长线相交于点F .求证:BCE FDE ∆∆≌.DFECBA【例5】 如图,在ABC ∆中,D 是BC 边的中点,F ,E 分别是AD 及其延长线上的点,CF BE ∥.求证:BDE CDF ∆∆≌.FEDCBA【例6】 已知ACB ∆,B ACB ∠=∠,D ,E 分别是AB 及AC 延长线上的一点,且BD CE =,连接DE 交底BC于G ,求证GD GE =.GED C BA【例7】 如左下图,在矩形ABCD 中,E 为CB 延长线上一点且AC CE =,F 为AE 的中点.求证:BF FD ⊥.F EDCBA【例8】 如右下图,在ABC ∆中,BE 、CF 分别为边AC 、AB 的高,D 为BC 的中点,DM EF ⊥于M .求证:FM EM =.MFED CB A【例9】 已知:ABC ∆中,AM 是中线.求证:1()2AM AB AC <+.MCBA【例10】 在△ABC 中,59AB AC ==,,则BC 边上的中线AD 的长的取值范围是什么?【例11】 如图,ABC ∆中,<AB AC ,AD 是中线.求证:<DAC DAB ∠∠.DCBA【例12】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.FEDC BA【例13】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,AF 与EF 相等吗?为什么?FED CBA【例14】 如图所示,已知ABC ∆中,AD 平分BAC ∠,E 、F 分别在BD 、AD 上.DE CD =,EF AC =.求证:EF ∥ABFACD E B【例15】 ABC ∆中,AB AC >,AD 、AE 分别是BC 边上的中线和A ∠的平分线,则AD 和AE 的大小关系是AD ______AE .(填“>”、 “<”或“=”)E AB CD 【例16】 已知AM 为ABC ∆的中线,AMB ∠,AMC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>.FE AB D C【巩固】在Rt ABC ∆中,90A ∠=︒,点D 为BC 的中点,点E 、F 分别为AB 、AC 上的点,且ED FD ⊥.以线段BE 、EF 、FC 为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形或钝角三角形?FEDCBA【例17】 如图所示,在ABC ∆中,D 是BC 的中点,DM 垂直于DN ,如果2222BM CN DM DN +=+,求证()22214AD AB AC =+.NMDCBA【巩固】在Rt ABC ∆中,F 是斜边AB 的中点,D 、E 分别在边CA 、CB 上,满足90DFE ∠=︒.若3AD =,4BE =,则线段DE 的长度为_________.FEDCBA【例18】 如图所示,在ABC ∆中,AB AC =,延长AB 到D ,使B D A B =,E 为AB 的中点,连接CE 、CD ,求证2CD EC =.ECB A【例19】 已知ABC ∆中,AB AC =,BD 为AB 的延长线,且BD AB =,CE 为ABC ∆的AB 边上的中线.求证2CD CE =EDCB A1. 如图,AC 、BD 相交于O 点,且AC BD =,AB CD =,求证:OA OD =.ABCDO2. 如图所示:AF CD =,BC EF =,AB DE =,A D ∠=∠.求证:BC EF ∥.A BCD EF3. 如图所示,在ABC ∆和A B C '''∆中,AD 、A D ''分别是BC 、B C ''上的中线,且AB A B ''=,AC A C ''=,AD A D ''=,求证ABC A B C '''∆∆≌.DCB AD'C'B'A'4. 如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交AB 于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.F GE DCBA5. 如图所示,90BAC DAE ∠=∠=︒,M 是BE 的中点,AB AC =,AD AE =,求证AM CD ⊥.MECBA。
三角形中线长定理 直角三角形射影定理

《三角形中线长定理与直角三角形射影定理》一、引言在几何学中,三角形是最基本的几何图形之一,而三角形中线长定理和直角三角形射影定理则是三角形内部各条线段关系的重要定理。
本文将以这两个定理为主题,深入探讨它们的意义、应用和证明方法,以帮助读者全面地理解这一部分几何知识。
二、三角形中线长定理1. 定理表述三角形中线长定理是指三角形中线的性质,其中线是连接一个三角形的两个顶点与中点的线段。
具体而言,三角形中线长定理表述为:在一个三角形中,两个中线的长度相等,且等于第三个中线的一半。
2. 意义与应用三角形中线长定理的意义在于它揭示了三角形内部各线段之间的等长关系,为解决相关问题提供了依据。
在实际应用中,这个定理常常用于计算三角形的各边长度、面积等问题,尤其在建筑、工程等领域有着广泛的应用价值。
3. 证明方法对于三角形中线长定理的证明,我们可以采用几何推理和数学运算相结合的方法进行证明。
具体而言,可以利用向量、中位线定理、勾股定理等几何知识来进行推导,最终得出结论。
这一证明过程不仅可以帮助我们深入理解定理的本质,也有助于培养我们的逻辑思维能力。
三、直角三角形射影定理1. 定理表述直角三角形射影定理是指在直角三角形中,三条射影的性质。
其中,射影是垂直于斜边的边线。
具体而言,直角三角形射影定理表述为:在一个直角三角形中,斜边上的高等于两条直角边上的高的乘积。
2. 意义与应用直角三角形射影定理的意义在于它揭示了直角三角形内部各射影之间的数学关系,为求解与直角三角形有关的问题提供了重要工具。
在实际应用中,这个定理常常用于测量、工程设计、地理测量等领域,为解决实际问题提供了依据。
3. 证明方法对于直角三角形射影定理的证明,我们可以采用几何相似性和数学运算相结合的方法进行证明。
具体而言,可以利用三角形相似性、直角三角形的性质等进行推导,最终得出结论。
这一证明过程可以帮助我们更深入地理解定理的内涵,提高我们的几何推理能力。
中位线直角三角形中线长定理的运用

a
10
变1:如图,△ABC和△CDE都是 等腰直角三角形,F是AE中点,试 判断△BDF的形状。
a
11
a
4
4.如图,△ABC中,AB=6,AC=10, AE平分
5.如图,四边形ABCD中,O为AC,BD 的交点,AC=BD,E,F分别是AB,CD 的中点,E,F交AC,BD于M,N点,判断 △MON的形状。
a
6
Rt△斜边上中线的等于斜边的 一半
三角形的中位线定理
a
1
1,如图,△ABC中,DE是中位线, F是BC中点,证明:DE、AF互相 平分。
a
2
2.如图,四边形ABCD中,E,F,G,H分 别是各边中点,证明:EFGH是平行 四边形。
a
3
3.如图,△ABC中,BD,CE分别是 中线,交于G点,F,H分别是 BG,CG的中点,证明:GB=2GD
a
7
6.如图,△ABC中,BF,CE分别是 高,M是EF的中点,D是BC的中 点,证明:DM⊥EF
M
a
8
7.如图,Rt△ABC中,∠B=90°, ∠C=30°,E是AC中点,F满足 BF=AB,求∠AFE的度数。
a
9
8.如图,△ABC和△CDE都是等腰 直角三角形,且B是DC中点,F是 AE中点,试判断△BDF的形状。
苏教版八年级下册数学[三角形中位线定理 知识点整理及重点题型梳理]
![苏教版八年级下册数学[三角形中位线定理 知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/9c586fc4aef8941ea76e059e.png)
苏教版八年级下册数学重难点突破知识点梳理及重点题型巩固练习三角形中位线定理【学习目标】1. 理解三角形的中位线的概念,掌握三角形的中位线定理.2. 掌握中点四边形的形成规律.【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点二、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点诠释:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.【典型例题】类型一、三角形的中位线1、(2016•北京)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.【思路点拨】(1)根据三角形中位线定理得MN=AD,根据直角三角形斜边中线定理得BM=AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.【答案与解析】(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,MN=AD,在RT△ABC中,∵M是AC中点,∴BM=AC,∵AC=AD,∴MN=BM.(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)可知,BM=AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴BN2=BM2+MN2,由(1)可知MN=BM=AC=1,∴BN=【总结升华】本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.举一反三:【变式】如图,矩形OABC的顶点A、C分别在x轴、y轴正半轴上,B点坐标为(3,2),OB与AC交于点P,D、E、F、G分别是线段OP、AP、BP、CP的中点,则四边形DEFG的周长为_____.【答案】5;解:∵四边形OABC是矩形,∴OA=BC,AB=OC;BA⊥OA,BC⊥OC.∵B点坐标为(3,2),∴OA=3,AB=2.∵D、E、F、G分别是线段OP、AP、BP、CP的中点,∴DE=GF=1.5; EF=DG=1.∴四边形DEFG的周长为(1.5+1)×2=5.2、如图,在△ABC中,已知点D、E、F分别是AB、BC、CA的中点,AH是高.(1)若BC=10,AH=8,则四边形ADEF的面积为.(2)求证:∠DHF=∠DEF.HF EDCBA【思路点拨】(1)由三角形面积公式可知:△BDE、△EFC的面积都等于△ABC面积的四分之一,进而可求出四边形ADEF的面积.(2)首先证明四边形ADEF是平行四边形,进而可得∠DEF=∠DAF,再利用直角三角形的中线性质得线段相等,从而得角等,最终可得到∠DAF=∠DEF,即可证出∠DHF=∠DEF.【答案解析】(1)解:∵BC=10,AH=8,∴S△ABC=×8×10=40,∵点D、E、F分别是AB、BC、CA的中点,∴△BDE、△EFC的面积都等于△ABC面积的,∴四边形ADEF的面积=40﹣20=20,故答案为:20;(2)证明:∵D 、E 、F 分别是△ABC 各边中点,∴DE ∥AC ,EF ∥AB ,∴四边形ADEF 是平行四边形,∴∠DEF=∠DAF ,∵AH 是△ABC 的高∴△ABH 、△ACH 是直角三角形,∵点D 、点F 是斜边AB 、AC 中点,∴DH=DA ,HF=AF ,∴∠DAH=∠DHA ,∠FAH=∠FHA ,∴∠DAH+∠FAH=∠FHA+∠DHA ,即∠DAF=∠DHF ,∴∠DEF=∠DHF .【总结升华】此题主要考查了平行四边形的性质与判定,三角形的中位线定理,直角三角形的性质,解决题目的关键是证明∠DHF=∠DAF 与∠DAF=∠DEF .3、如图所示,在△ABC 中,M 为BC 的中点,AD 为∠BAC 的平分线,BD ⊥AD 于D ,AB =12,AC =18,求MD 的长.【思路点拨】本题中所求线段MD 与已知线段AB 、AC 之间没有什么联系,但由M 为BC 的中点联想到中位线,另有AD 为角平分线和垂线,根据等腰三角形“三线合一”构造等腰三角形ABN ,D 为BN 的中点,DM 即为中位线,不难求出MD 的长度.【答案与解析】解:延长BD 交AC 于点N .∵ AD 为∠BAC 的角平分线,且AD ⊥BN ,∴ ∠BAD =∠NAD ,∠ADB =∠ADN =90°,在△ABD 和△AND 中,BAD NAD AD =ADADB ADN ∠∠⎧⎪⎨⎪∠∠⎩== ∴ △ABD ≌△AND(ASA)∴ AN =AB =12,BD =DN .∵ AC =18,∴ NC =AC -AN =18-12=6,∵ D 、M 分别为BN 、BC 的中点,∴ DM =12CN =162⨯=3. 【总结升华】当条件中含有中点的时候,可以将它与等腰三角形的“三线合一”、三角形的中线、中位线等联系起来,进行联想,必要时添加辅助线,构造中位线等图形.举一反三:【变式】如图所示,四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,E、F分别是PA、PQ两边的中点;当点P在BC边上移动的过程中,线段EF的长度将( ).A.先变大,后变小 B.保持不变 C.先变小,后变大 D.无法确定【答案】B;解:连接AQ.∵ E、F分别是PA、PQ两边的中点,∴ EF是△PAQ的中位线,即AQ=2EF.∵ Q是CD上的一定点,则AQ的长度保持不变,∴线段EF的长度将保持不变.4、我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题:(1)如图1,在△ABC中,AB=AC,点D在BC上,且CD=CA,点E、F分别为BC、AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;(2)如图2,若点D在△ABC的内部,(2)中的其他条件不变,EF与CD交于点H,图中是否存在等邻角四边形,若存在,指出是哪个四边形,不必证明;若不存在,请说明理由.【思路点拨】(1)运用中位线的性质,找出对应相等的角;(2)根据题意易知满足条件的四边形即为第一题的四边形.【答案与解析】解:(1)取AC的中点H,连接HE、HF∵点E为BC中点∴EH为△ABC的中位线∴EH∥AB,且EH=12AB同理FH∥DC,且FH=12DC∵AB=AC,DC=AC∴AB=DC,EH=FH∴∠1=∠2∵EH∥AB,FH∥DC∴∠2=∠4,∠1=∠3∴∠4=∠3∵∠AGE+∠4=180°,∠GEC+∠3=180°∴∠AGE=∠GEC∴四边形AGEC是邻角四边形(2)存在等邻角四边形,为四边形AGHC.【总结升华】本题考查了三角形的中位线以及等腰三角形的性质的综合运用.本题较灵活,要求学生能够把题中的条件转化成角,从而找出相等的角来解题.举一反三:【变式】如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是()A.4 B.3 C.2 D.1【答案】D;解:连接DE并延长交AB于H,∵CD∥AB,∴∠C=∠A,∠CDE=∠AHE,∵E是AC中点,∴AE=CE,∴△DCE≌△HAE,∴DE=HE,DC=AH,∵F是BD中点,∴EF是△DHB的中位线,∴EF=12 BH,∴BH=AB-AH=AB-DC=2,∴EF=1.类型二、中点四边形5、如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)求证:四边形EFGH 是正方形;(2)若AD =2,BC =4,求四边形EFGH 的面积.【思路点拨】(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD 入手,进行正方形的判断.(2)连接EG ,利用梯形的中位线定理求出EG 的长,然后结合(1)的结论求出2EH =92,也即得出了正方形EHGF 的面积. 【答案与解析】证明:(1)在△ABC 中,E 、F 分别是AB 、BC 的中点,故可得:EF =12AC ,同理FG =12BD ,GH =12AC ,HE =12BD , 在梯形ABCD 中,AB =DC ,故AC =BD ,∴EF=FG =GH =HE ,∴四边形EFGH 是菱形.设AC 与EH 交于点M ,在△ABD 中,E 、H 分别是AB 、AD 的中点,则EH∥BD,同理GH∥AC,又∵AC⊥BD,∴EH⊥HG,∴四边形EFGH 是正方形.(2)连接EG .在梯形ABCD 中,∵E、G 分别是AB 、DC 的中点,∴EG=12(AD +BC )=3. 在Rt△EHG 中, ∵222EH GH EG +=,EH =GH ,∴2EH =92,即四边形EFGH 的面积为92. 【总结升华】此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的中位线定理得出EH =HG =GF =FE ,这是本题的突破口.举一反三:【变式】如图,E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点.(1)判断四边形EFGH 的形状,并说明你的理由;(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形.【答案】解:(1)四边形EFGH是平行四边形.理由:连接AC,∵E、F分别是AB、BC的中点,∴EF∥AC,且EF=12 AC,同理,HG∥AC,且HG=12 AC,∴EF∥HG,且EF=HG,∴四边形EFGH是平行四边形;(2)当BD=AC,且BD⊥AC时,EFGH是正方形.理由:连接AC,BD,∵E、F、G、H分别是边AB、BC、CD、DA的中点,∴EF=GH=12AC,EH=FG=12BD,EH∥BD,GH∥AC,∵BD=AC,BD⊥AC,∴EH=EF=FG=GH,EH⊥GH,∴四边形ABCD是菱形,∠EHG=90°,∴四边形EFGH是正方形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
7.如图,Rt△ABC中,∠B=90°, ∠C=30°,E是AC中点,F满足 BF=AB,求∠AFE的度数。
8.如图,△ABC和△CDE都是等腰 直角三角形,且B是DC中点,F是 C和△CDE都是 等腰直角三角形,F是AE中点,试 判断△BDF的形状。
三角形的中位线定理
1,如图,△ABC中,DE是中位线, F是BC中点,证明:DE、AF互相 平分。
2.如图,四边形ABCD中,E,F,G,H分 别是各边中点,证明:EFGH是平行 四边形。
3.如图,△ABC中,BD,CE分别是 中线,交于G点,F,H分别是 BG,CG的中点,证明:GB=2GD
4.如图,△ABC中,AB=6,AC=10, AE平分∠BAC,BE垂直AE,D是 BC中点,求DE的长度。
5.如图,四边形ABCD中,O为AC,BD 的交点,AC=BD,E,F分别是AB,CD 的中点,E,F交AC,BD于M,N点,判断 △MON的形状。
Rt△斜边上中线的等于斜边的 一半
6.如图,△ABC中,BF,CE分别是 高,M是EF的中点,D是BC的中 点,证明:DM⊥EF
