勤学早九年级数学下第章相似单元检测题
勤学早九年级数学下第章相似单元检测题

勤学早九年级数学下第章相似单元检测题本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March29.勤学早九年级数学(下)第27章《相似》单元检测题(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)一、选择题(每小题3分,共30分)1.(教材变式·9下P25习题1改)将等边三角形的三边各扩大2倍后得到的三角形是( A ) A .等边三角形 B .锐角三角形 C .直角三角形 D .钝角三角形2.在△ABC 和△A ′B ′C ′中,∠A =68°,∠B =40°,∠A ′=68°,∠C ′=72°,那么这两个三角形( B ) A .不相似B .相似C .全等D .无法确定3.(2015蚌埠)如图,△ABC 中,DE ∥BC ,AD =5,BD =10,AE =3,则CE 的长为( B ) A .9 B .6 C .3 D .4B EDA4.图中的两个三角形是位似图形,则它们的位似中心是( A ) A .点PB .点QC .点RD .点S5.(2015潍纺改)如图,点D 在△ABC 的边AC 上,要使△ADB 与△ABC 相似,添加一个条件,错误..的是( C ) A .∠ABD =∠CB .∠ADB =∠ABCC .AB CBBD CD=D .AD ABAB AC=C ABD6.(2015枣庄)如图,□ABCD 中,点N 是AB 上一点,且BN =2AN ,AC 、DN 相交于点M ,则AM :MC的值是( B ) A .3:11B .1:3C .1:9D .3:10ADCBMN7.△ABC 中,∠ACB =90°,将△ABC 按如图的位置放在直角坐标系中,若点A 的坐标为(0,2),点C 的坐标为(1,0),点B 的横坐标为4,则点B 的纵坐标为( C ) A .1 B . C .D .8.如图,△ABC 中,∠C =90°,以AB 上一点O 为圆心作⊙O ,分别切AC 、BC 于E 、D ,AC =8,BC =6,则⊙O 的半径长为( B )A .5B .247C . D.127AB9.直线1l ∥2l ∥3l ,且1l 与2l 的距离为1, 2l 与3l 的距离为3,把一块含有45°角的直角三角形如图放置,顶点A 、B 、C 恰好分别落在三条直线上,AC 与直线2l 交于点D ,则线段BD 的长度为( A )A .254 B .253 C .203 D .154l 1l 2l 3ABD10.(2016武汉原创题)如图,等边△ABC 的边长为3,P 为BC 上一点,且BP =1,D 为AC 上一点,DE⊥AP 交AP 于E ,若∠APD =60°,则DEAE=________ (2)二、填空题(每小题3分,共18分)11.如图,请你补充一个条件,使△ABC ∽△ACD ,这个条件是 . (∠ACD =∠B)ABCD12.△ABC 与△DEF 的相似比为3:4,则△ABC 与△DEF 的面积比为 . (9:16)13.在□ABCD 中,E 在DC 上,若DE :EC =1:2,则△CEF 与△ABF 的周长比为 . (2:3)14.(教材变式·9下P42习题5改)如图,△ABC 中,DE ∥FG ∥BC ,AD :DF :FB =1:2:3,若EG =3,则AC = . (9)E FGD A15.如图,在平面直角坐标系中,△OBA ∽△DOC ,边OA 、OC 都在x 轴的正半轴上,已知B (6,8),∠BAO =∠OCD =90°,OD =5,双曲线y=kx(x >0)经过点D ,则k 的值是 . (12)16.如图,在平面直角坐标系中,等边△ABC 的顶点B 、C 的坐标分别为(1,0),(3,0),过坐标原点O的一条直线分别与AB 、AC 交于点M 、N ,若OM =MN ,则点M 的坐标为)三、解答题(共8小题,共72分)17.(本题8分)如图,点D 、E 在BC 上,且FD ∥AB ,FE ∥AC ,求证:△ABC ∽△FDE .ADFEC解:∵FD ∥AB ,∴∠B =∠FDE ,又∵FE ∥AC ,∴∠C =∠FED , ∴△ABC ∽△FDE18.(本题8分))如图,A 、B 两点被池塘隔开,在AB 外取一点C ,连接AC ,BC ,在AC 上取点M ,使AM =3MC ,作MN ∥AB 交BC 于N ,量得MN =38m ,求AB 的长.解:AB =152m19.(本题8分)如图,△ABC 中,D 、E 分别是边BC 、AB 的中点,AD ,CE 相交于G .求证:12GE GD GC GA == ABDEG解:连ED ,则ED ∥AC ,且ED =12AC ,证△DEG ∽△ACG20.(本题8分)如图,每个小方格都是边长为1个单位的小正方形,A 、B 、C 三点都是格点(每个小方格的顶点叫格点),其中A (1,8),B (3,8),C (4,7).(1)若D (2,3),请在网格图中画出一个格点△DEF ,使△DEF ∽△ABC ,且相似比为2:1; (2)填空:DF 的长是_________.x解:(1)略; (2)DF =21.(本题8分)如图,等边△ABC 的边长是6,点E 、F 分别在AC 、BC 边上,AE =CF ,连接AF 、BE 相交于点P .(1)求∠APB 的度数;(2)若AE =2,求BP ·BE 的值.A B CEPF解:(1)易证△ABE ≌△CAF ,易求∠APB =120° (2)证△BPF ∽△BCE ,∴BP ·BE =BF ·BC =4×6=2422.(本题10分)(2015黄冈改)如图,△ABC 中,AB =AC ,以AC 为直径的⊙O 交AB 于点M ,交BC于点N ,连接AN ,过点C 的切线交AB 的延长线于点P .(1)求证:∠BCP =12∠BAC ; (2)若34BP BC ,求ANPC的值. A解:(1)∵AC 为⊙O 直径,∴∠ANC =90°,∵AB =AC ,∴∠BAN =∠CAN ,∵∠BCP +∠ACB =∠CAN+∠ACB =90°. ∴∠BCP =∠CAN =12∠BAC (2)连MN ,则∠BMN =∠ACB =∠ABC ,∴∠AMN =∠PBC ,又∠BCP =∠BAN ,∴△AMN ∽△CBP,∴AN PC =MN BP ,易证MN =BN =CN ,∴AN PC =12BCBP=12·43=2323.(本题10分)如图,矩形ABCD 中,AB =6,AD =8,动点P 从点D 出发,以每秒5个单位的速度向点B 匀速运动,同时动点Q 从点A 出发,以每秒4个单位的速度向点D 匀速运动,运动的时间为t 秒(0<t <2).(1)如图1,连接CQ ,当t 为何值时CQ =BC ; (2)如图2,连接AP 、BQ ,若BQ ⊥AP ,求t 的值.B C DA QBCDAQP图1 图2解:(1)∵AQ=4t ,AD=8,∴DQ=8-4t ,又∵AB=6,∴由勾股定理得CQCQ =BC 8,解得t =2 (2)过点P 作PE ⊥AD ,垂足哦日E ,∴AB ∥PE ,∴DE DA =PE AB =DP DB ,∴8DE =6PE =510t, ∴DE =4t ,EP =3t ,∴EP =3t ,∴AE =8-4t ,∵∠ABQ +∠BAP =90°,∠EAP +∠BAP =90°, ∴∠ABQ =∠EAP ,∵∠BAQ =∠AEP ,∴△BAQ ∽△AEP ,∴BA AE =AQ PE ,即684t -=43tt, 解得t =7824.(本题12分)(2016武汉改编题)已知点P (m ,n )是抛物线y=14-2x -2上的一个动点,点A 的坐标为(0,-3).【特别探究】(1)如图1,直线l 过点Q (0,-1)且平行于x 轴,过P 点作PB ⊥l ,垂足为B ,连接PA ; ①当m =0时,PA =_________,PB =_________; ②当m =2时,PA =_________,PB =_________;【猜想验证】(2)对于m 取任意一实数,猜想PA 与PB 的大小关系,并证明你的猜想; 【拓展应用】(3)请利用(2)的结论解决下列问题:若过动点P 和点Q (0,-1)的直线交抛物线于另一点D ,且PA =4AD ,求直线PQ 的解析式(图2为备用图).yxyxPQOlABQOA解:(1)①1,1 ②2,2(2)PA与PB相等,理由如下:设P(m,14-2m-2),则B(m,-1),∵PA2221234m m⎛⎫+--+⎪⎝⎭22114m⎛⎫+⎪⎝⎭142m+1,PB=-1-(14-2m-2)=142m+1,∴PA=PB;(3)过点Q(0,-1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(2)得PB=PA,DE=DA,∵PA=4AD,∴PB=4DE,∵DE∥PB,∴△QDE∽△QPB,QEQB=DEPB=14, 设P(m,14-2m-2),则B(m,-1),PB=142m+1,∴E点坐标为(14m,-1),D点坐标为[14m,-14(14m)2-2],∴ED=-1+14(14m)2+2=1642m+1,∴142m+1=4(1642m+1),解得m1=4,m2=-4,∴P点坐标为(4,-6)或(-4,-6);当P点坐标为(4,-6)时,直线PQ的解析式为y=-54x-1;当点P坐标为(-4,-6)时,直线PQ的解析式为y=54x-1,即PO的解析式为y=-54x-1或y =54x-1。
九年级数学下册《第二十七章相似》单元测试卷-带答案(人教版)

九年级数学下册《第二十七章相似》单元测试卷-带答案(人教版)一、选择题1.下列两个图形一定是相似图形的是()A.菱形B.矩形C.等腰三角形D.等边三角形2.下列各组数中,成比例的是().A.1,-2,-3,-6B.1,4,2,-8C.5,6,2,3D.3.若ABC DEF~且相似比为1:4,则ABC与DEF的面积比为()A.1:4B.4:1C.1:16D.16:14.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为()A.1.5m B.1.6m C.1.86m D.2.16m5.如图,△ABC与ΔA′B′C′位似,位似中心为点O且23A CAC='',△ABC的面积为9,则ΔA′B′C′面积为()A.92B.6C.4D.946.已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD相似的是() A.B.C.D.7.如图,AB CD EF.若ACCE=12,BD=4,则DF的长为()A .2B .4C .6D .88.如图,已知ABC ,点D 是BC 边中点,且ADC BAC.∠∠=若BC 6=,则AC =( )A .3B .4C .42D .329.图,电灯P 在横杆AB 的正上方,AB 在灯光下的影子为CD ,AB||CD ,3AB =米,5CD =米,点P 到AB 的距离是2.4米,则P 到CD 的距离为( )A .3.6米B .4米C .5米D .5.4米10.如图,在平面直角坐标系中,△ABC 与△A 1B 1C 1是位似图形.其中BC△B 1C 1=1△2,则△ABC 与△A 1B 1C 1的周长之比是( )A .1△4B .2△1C .1△2D .1△3二、填空题11.两个相似多边形的周长比是2:3,其中较小多边形的面积为12 2cm ,则较大多边形的面积为2cm .12.如图,点D 、E 、F 、G 分别在锐角ΔABC 的边上,四边形DEGF 为矩形,DE=2DF Δ6ADE S =BF+CG=83,则ΔABC S = .13.如图,ABC 与111A B C 位似,位似中心是点O ,若112OA OA =::,则ABC 与111A B C 的周长比是 .14.如图,平面直角坐标系中,O 为原点,点A ,B 分别在y 轴、x 轴的正半轴上,Rt AOB 的两条外角平分线交于点P ,且点P 在反比例函数(0)ky k x=>的图象上,PA ,PB 的延长线分别交x 轴、y 轴于点C ,D ,连结CD .OCD 的面积为9,则k 的值是 ;当点A 的坐标为(02),时,则点B 的坐标是 .三、解答题15.如图,菱形ABCD 和菱形ECGF 的边长分别为2和3,△A =120°,则图中阴影部分的面积是多少?16.如图,弦BC经过圆心D,AD△BC,AC交△D于E,AD交△D于M,BE交AD于N.求证:△BND△△ABD.17.已知如图,Rt△ABC中,△C=90°,CD是斜边上的高,求证:CD2=AD•BD.18.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连结AC并延长到点D,使CD= 12AC,连结BC并延长到点E,使CE=12BC,连结DE.量得DE的长为15米,求池塘两端A,B的距离.19.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)①将△ABC 绕点A 顺时针旋转90°后得到△AB 1C 1,在图①中画出△AB 1C 1,并求出在旋转过程中△ABC 扫过的面积;②在图②中以点O 为位似中心,将△ABC 缩小为原来的12,并写出点C 的对应点的坐标. 四、综合题20.在4×4的正方形方格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上.(1)填空:△ABC= °,△ABC 的面积为 . (2)判断△ABC 与△DEF 是否相似,并说明理由.(3)请在图中再画一个和△ABC 相似但相似比不为1的格点三角形.21.如图,ABC 为O 的内接三角形AD BC ⊥,垂足为D ,直径AE 平分BAD ∠,交BC 于点F ,连结BE .(1)求证:AEB AFD ∠=∠;(2)若105AB BF ==,,求DF 的长;22.如图,已知点()36B -,,()30C -,以坐标原点O 为位似中心,在第四象限将OBC 缩小为原来的三分之一(即新图形与原图形的相似比为13:).(1)画出缩小后的图形; (2)写出B 点的对应点坐标;(3)如果OBC 内部一点M 的坐标为()x y ,,写出点M 经位似变换后的对应点坐标.23.如图,△ABC 是边长为m 的正三角形,D ,E ,F 分别在边AB ,BC ,CA 上,AE ,BF 交于点P ,BF ,CD 交于点Q ,CD ,AE 交于点R ,若AD AB = BE BC = CF CA =k (0<k < 12).(1)求△PQR 的度数; (2)求证:△ARD△△ABE ;(3)求△PQR 与△ABC 的面积之比(用含k 的代数式表示)参考与答案解析1.【答案】D【解析】【解答】解:A、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;C、两等腰三角形不一定相似,故此选项不符合题意;D、两个等边三角形的对应边的比相等,对应角一定相等,故两个等边三角形一定相似,故此选项符合题意.故答案为:D.【分析】利用相似多边形的判定:所有的对应边成比例,且所有的对应角分别相等的两个多边形相似,可对A,B作出判断;利用相似三角形的判定定理及等腰三角形的性质,可对C,D作出判断. 2.【答案】D【解析】【解答】解:A、1326-≠--不符合题意;B、1248≠-不符合题意;C、5263≠不符合题意;D 263=符合题意.故答案为:D.【分析】如果前两个数据的比值等于后两个数据的比值,那么这四个数据就成比例,据此一一判断得出答案.3.【答案】C【解析】【解答】解:∵△ABC△△DEF,且相似比为1:4∴△ABC与△DEF的面积比为1:16故答案为:C.【分析】相似三角形的面积比等于相似比的平方,据此解答即可.4.【答案】A【解析】【解答】∵BE△AD∴△BCE△△ACD∴CB CEAC CD=,即CB CEAB BC DE EC=++∵BC=1,DE=1.8,EC=1.2 ∴1 1.21 1.8 1.2AB =++∴1.2AB=1.8 ∴AB=1.5m . 故答案为:A .【分析】先证明△BCE△△ACD ,再利用相似三角形的性质可得CB CEAC CD=,即 CB CE AB BC DE EC =++再将数据代入计算可得 1 1.21 1.8 1.2AB =++,最后求出AB 的长即可。
人教版九年级数学下册第二十七章《相似》单元练习题(含答案)

人版教九年级数学下册第二十七章《相似》单元练习题(含答案)一、单选题1.如图,若DE ∥FG ∥BC ,AD =DF =FB ,则S △ADE ∶S 四边形DFGE ∶S 四边形FBCG =( )A .2∶6∶9B .1∶3∶5C .1∶3∶6D .2∶5∶82.如图,点D ,E ,F 分别在△ABC 的各边上,且DE ∥BC ,DF ∥AC ,若AE :EC =1:2,BF =6,则DE 的长为( )A .1B .2C .3D .43.如图,在▱ABCD 中,AB=12,AD=8,∠ABC 的平分线交CD 于点F ,交AD 的延长线于点E ,CG⊥BE,垂足为G ,若EF=2,则线段CG 的长为( )A .152B .43C .15D 554.如果两个相似正五边形的边长比为1:10,则它们的面积比为( )A .1:2B .1:5C .1:100D .1:105.在△ABC 中,点D 、E 分别在AB 、AC 的延长线上,下列不能判定DE //BC 的条件是A .::EA AC DA AB =;B .::DE BC DA AB =; C .::EA EC DA DB =;D .::AC EC AB DB =.6.下列说法中正确的是( )A .两个平行四边形一定相似B .两个菱形一定相似C .两个矩形一定相似D .两个等腰直角三角形一定相似7.如图,四边形ABCD 中,//AB DC ,点E 在CB 延长线上,ABD CEA ∠=∠,若32AE BD =,1BE =,那么DC 的长为( )A .32B .1C .52D .28.(2019•内江)如图,将△ABC 沿着过BC 的中点D 的直线折叠,使点B 落在AC 边上的B 1处,称为第一次操作,折痕DE 到AC 的距离为h 1;还原纸片后,再将△BDE 沿着过BD 的中点D 1的直线折叠,使点B 落在DE 边上的B 2处,称为第二次操作,折痕D 1E 1到AC 的距离记为h 2;按上述方法不断操作下去……经过第n 次操作后得到折痕D n ﹣1E n ﹣1,到AC 的距离记为h n .若h 1=1,则h n 的值为( )A .1112n -+B .112n +C .2112n --D .212n - 9.下列图形是相似图形的是( )A .所有矩形B .所有菱形C .所有直角三角形D .所有正六边形10.如图,为了测量一池塘的宽DE ,在岸边找一点C ,测得CD=30m ,在DC 的延长线上找一点A ,测得AC=5m ,过点A 作AB∥DE,交EC 的延长线于B ,测得AB=6m ,则池塘的宽DE 为( )A .25mB .30mC .36mD .40m11.如图,在ABC 中,点D ,E ,F 分别在边,,AB AC BC 上,若DE BC ∥,EF AB ∥,则下面所列比例式中正确的是( )A .AD DE BD BC =B .BF EF BC AD = C .AE BF EC CF = D .EF DE AB BC= 12.如图,在△ABC 中,∠ADE=∠B,DE :BC=2:3,则下列结论正确的是( )A .AD :AB=2:3B .AE :AC=2:5C .AD :DB=2:3 D .CE :AE=3:2二、填空题 13.如果两个相似三角形的面积比为4:9,那么这两个三角形的相似比为_________.14.在平面直角坐标系中,已知点A (-4,2),B (-2,-2),以原点为位似中心,位似比为12,把△AOB 缩小,则点A 的对应点A ′的坐标是___________. 15.如图,在平面直角坐标系中,O 为坐标原点,点A 、B 的坐标分别为(0,4)、(-3,0),点E 、F 分别为AB 、BO 的中点,分别连接AF 、EO ,交点为P ,点P 坐标为( )A 、(-,)B 、(-,2)C 、(-1,)D 、(-1,2)16.已知ABC 与DEF 的相似比为3:5,则它们的周长比为________.17.如图,在△ABC 中,∠ABC=90°,且BC=6,AB=3,AD 是∠BAC 的平分线,与BC 相交于点E ,点G 是BC 上一点,E 为线段BG 的中点,DG⊥BC 于点G ,交AC 于点F ,则FG 的长为_____.18.在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2).延长CB 交x 轴于点A 1,作第1个正方形A 1B 1C 1C;延长C 1B 1交x 轴于点A 2,作第2个正方形A 2B 2C 2C 1,…,按这样的规律进行下去,第2019个正方形的面积是_________.19.如图,在正方形ABCD 中,点P 是AB 上一动点(不与A ,B 重合),对角线AC 、BD 相交于点O ,过点P 分别作AC 、BD 的垂线,分别交AC 、BD 于点E 、F ,交AD 、BC 于点M 、N .下列结论:①APE AME ∆≅∆;②PM PN AC +=;③222PE PF PO +=;④POF BNF ∆∆;⑤当PMN AMP ∆∆时,点P 是AB 的中点.其中正确的结论有_____.20.将一副三角尺如图所示叠放在一起,则 .三、解答题21.如图,已知ABC ∆中,AB =8,AC =6,点D 是线段AC 的中点,点E 在线段AB 上,若ADE ∆与ABC ∆相似,求AE 的长.22.如图,△ABC 与△A 1B 1C 1是位似图形.在网格上建立平面直角坐标系,使得点A 的坐标为(1,﹣6).(1)在图上标出点,△ABC 与△A 1B 1C 1的位似中心P .并写出点P 的坐标为 ;(2)以点A 为位似中心,在网格图中作△AB 2C 2,使△AB 2C 2和△ABC 位似,且位似比为1:2,并写出点C 2的坐标为 .23.已知如图,是△的边上一点,∥,交边于点,延长至点,使,联结,交边于点,联结(1)求证:;(2)如果,求证:24.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.(1) 求证:△AEF与△ABE相似;(2)试说明:BD2=AD·DF.25.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF 来测量操场旗杆AB 的高度,他们通过调整测量位置,使斜边DF 与地面保持平行,并使边DE 与旗杆顶点A 在同一直线上,已知DE =0.5米,EF =0.25米,目测点D 到地面的距离DG =1.5米,到旗杆的水平距离DC =20米,求旗杆的高度.26.已知ABC 中90,ABC =∠点D E 、分别在边BC 、边AC 上,连接,,DE DF DE ⊥点F 、点C 在直线DE 同侧,连接,FC 且AB DE k BC DF==. (1)点D 与点B 重合时,①如图1,1k =时,AE 和FC 的数量关系是 ;位置关系是 ;②如图2,2k =时,猜想AE 和FC 的关系,并说明理由;(2)2BD CD =时,③如图3,1k =时,若26,CDF AE S ==,求FC 的长度;④如图4,2k =时,点M N 、分别为EF 和AC 的中点,若10AB =,直接写出MN 的最小值.27.已知AB 为⊙O 的直径,C 在⊙O 上,过点C 的直线与AB 的延长线交于点P ,若AC =PC ,∠PCB =∠P ,(1)求证:PC 为⊙O 的切线;(2)若点M 为弧AB 的中点,CM 交AB 于点N .且AB =4,求CN 的长.28.如图,AF 是ABC △的高,点D 、E 分别在AB 、AC 上,且DE BC ∥,DE 交AF 于点G .设10AD =,30AB =,24AC =,12GF =.(1)求AE 的长;(2)求点A 到DE 的距离.29.如图,在ABC 中,E 、F 分别是AB 和AC 上的点,且//EF BC ,如果9AB =,4AE =,3AF =,那么FC 的长是多少?参考答案1.B2.C3.C4.C5.B6.D7.A8.C9.D10.C11.C12.A13.2:314.(-2,1)或(2,-1)15.C .16.3:517.9352- 18.403835()2⨯19.①②③⑤20..21.AE=4或94. 22.(1)如图,连接对应点A 1和A ,连接对应点C 1和C ,交点即P 点,由图可知P 点坐标为(-1,-2).(2)∵△AB 2C 2和△ABC 位似,且位似比为1:2,∴AC 2:AC=1:2,AB 2:AB=1:2.∴点C 2的坐标为(1,-3).23.(1)∵DE∥BC,∴△ADE∽△ABC,△EFG∽△CBG,∴又∵DE=EF,∴,∴;(2)∵CF 2=FG•FB,∴,又∵∠CFG=∠CFB,∴△CFG∽△BFC,∴∠FCE=∠CBF,又∵DF∥BC,∴∠EFG=∠CBF,∴∠FCE=∠EFG,又∵∠FEG=∠CEF,∴△EFG∽△ECF,∴,∴,即CG•CE=BC•DE.24.⑴∵△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE,又∵BD=CE,∴△ABD≌△BCE,∴∠BAD=∠CBE,又∠ABC=∠BAC,∴∠ABE=∠EAF,又∵∠AEF=∠BEA,∴△AEF∽△BEA.⑵由(1)得:∠BAD=∠FBD,又∵∠BDF=∠ADB,∴△BDF∽△ADB,∴BDAD=DFBD,即BD2=AD·DF.25.旗杆的高度为11.5m26.(1)①AE=FC;AE⊥FC;②AE=2FC;AE⊥FC;(2)③FC =6;④MN的最小值为53.27.(1)证明:连接OC,∵OA=OC,∴∠A=∠ACO,∵AC=PC,∴∠A=∠P,∵∠PCB=∠P,∴∠ACO=∠PCB,又∵AB是⊙O的直径,∴∠ACB=90°,即∠ACO+∠OCB=90°,∴∠PCB+∠OCB=90°,即∠PCO=90°,∴OC⊥PC∵OC是⊙O的半径,∴PC是⊙O的切线.(2)连接OM、OC.过点C作CD⊥OB于点D.∵直径AB=4∴OB=OM=2由(1)得,∠ACO=∠PCB,∠A=∠P∵∠ACO=∠PCB,AC=PC,∠A=∠P∴△AOC≌PBC(ASA)∴OC=BC∵OB=OC∴△OCB是等边三角形∴∠CBD=60°,∵CD⊥OB∴OD=BD=1,CD CDN=90°∵点M为AB的中点,OM为⊙O的半径∴OM⊥AB∴∠MON=90°∴∠MON=∠CDN=90°∵∠ONM=∠DN∴△ONM~△DNC∴OM ON CD DN=1DNDN-=∴DN=﹣3由勾股定理得,CD2+DN2=CN22+(3)2=CN2∴CN=28.(1)8 (2)629.15 4。
新人教版初中数学九年级数学下册第二单元《相似》测试(包含答案解析)(2)

一、选择题1.如图,D 是△ABC 的边BC 上一点,AC =4,AD =2,∠DAB =∠C .如果△ACD 的面积为15,那么△ABD 的面积为( )A .15B .10C .152D .52.在ABC 中,D ,E 分别为,BC AC 上的点,且2AC EC =,连结,AD BE ,交于点F ,设:,:x CD BD y AF FD ==,则( )A .1y x =+B .1x y x+=C .413y x =+ D .21xy x-=- 3.下列判断正确的是( ) A .对角线相等的四边形是矩形B .将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似C .如果两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比可能是4:3D .若点C 是AB 的黄金分割点,且AB =6cm ,则BC 的长约为3.7cm 4.如图,在ABC 中,中线BE ,CD 相交于点O ,连接DE ,下列结论:①12DE BC =;②12S S =△DOE △COB ;③AD OE AB OB=;④16ODE ADC S S =△△.其中结论正确的是( ).A .①②B .①③C .①②③D .①③④5.如图,点D 、E 分别在CA 、BA 中的延长线上,若DE ∥BC ,AD =5,AC =10,DE =6,则BC的值为( )A .10B .11C .12D .136.如图,在平面直角坐标系中,ABC 的顶点坐标分别是()1,2A ,()1,1B ,()3,1C ,以原点为位似中心,在原点的同侧画DEF ,使DEF 与ABC 成位似图形,且相似比为2:1,则线段DF 的长度为( )A .25B .2C .4D .57.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm ,光源到屏幕的距离为90cm ,且幻灯片中的图形的高度为7cm ,则屏幕上图形的高度为( )A .21cmB .14cmC .6cmD .24cm8.如图,已知在ABC 中,D 为BC 上一点,//EG BC ,分别交AB ,AD ,AC 于点E ,F ,G ,则下列比例式正确的是( )A .AE EFBE BD = B .EF AFDC AD = C .AC FGCG DC= D .AE FGAB DC= 9.如图,在平行四边形ABCD 中,点E 在边DC 上,DE :EC=5:2,连接AE 交BD 于点F ,则△DEF 的面积与△BAF 的面积之比为( )A .5:7B .10:4C .25:4D .25:4910.已知四个数2,3,m ,3成比例的线段,那么m 的值是( ) A .3B .233C .2D .2311.如图,已知点E 是正方形ABCD 的边AB 边上的黄金分割点,且,AE EB >若1S 表示AE 为边长的正方形面积,2S 表示以BC 为长,BE 为宽的矩形面积,3S 表示正方形ABCD 除去1S 和2S 剩余的面积,则32:S S 的值为( )A .51- B .51+ C .352D .35+ 12.如图,四边形ABCD 是正方形,E 是BC 的中点,连接AE 与对角线BD 相交于点G ,连接CG 并延长,交AB 于点F ,连接DE 交CF 于点H .以下结论:①CDE BAE ∠=∠;②CF DE ⊥;③AF BF =;④22CE CH CF =⋅.其中正确结论的个数有( )A .1B .2C .3D .4二、填空题13.如图,△ABC 中,∠C =90°,BC =8cm ,AC =6cm ,点P 沿BC 边以2cm/s 的速度从点B 向点C 移动,同时点Q 沿CA 边以1cm/s 的速度从点C 向点A 移动.若以点C 、P 、Q 构成的三角形与△ABC 相似,则运动时间为____________秒.14.如图,D E 、分别是ABC 的边AB BC 、上的点,且//,DE AC AE CD 、相交于点O ,若:1:25DOE COA S S =△△,则BECE的值是________.15.如图,点D 是ABC 的边AB 上的一点,//DE BC 交AC 于点E ,作//DF AC 交BC 于点F ,分别记ADE ,BDF ,平行四边形DFCE ,ABC 的面积为1S ,2S ,3S ,S 有以下结论:①若12S S ,则DE 为ABC 的中位线;②若13S S =,则23BC DE =; ③212S S S =;④3122S S S =.其中正确的是______.(把所有正确结论的序号都填上)16.贺哲同学的身高1.86米,影子长3米,同一时刻金老师的影子长2.7米,则金老师的身高为________米(结果保留两位小数)。
九年级数学下册初三数学相似单元测试题及答案

相似单元测评(时间:90分钟,满分:100分)一、选择题(每题3分,共36分)1.下列两个图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形. 其中一定相似的有( )A.2组B.3组C.4组D.5组2.如图,在正方形网格上有6个斜三角形:①△ABC,②△BCD,③△BDE,④△BFG,•⑤△FGH,⑥△EFK,其中②~⑥中与三角形①相似的是( )A.②③④B.③④⑤C.④⑤⑥D.②③⑥3.应中共中央总书记胡锦涛同志的邀请,中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的“大唐芙蓉园”,该园占地面积约为800000m2,若按比例尺1:2000缩小后,其面积大约相当于( )A.一个篮球场的面积B.一张乒乓球台台面的面积C.《陕西日报》的一个版面的面积D.《数学》课本封面的面积4.如图,小明设计两个直角,来测量河宽BC,他量得AB=2米,BD=3米,CE=9米,•则河宽BC为( )A.5米B.4米C.6米D.8米5.如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,则的值等于( )A. B. C.1 D.6.如果整张报纸与半张报纸相似,则此报纸的长与宽的比是( )A.2:1B.C.4:1D.7.△ABC的面积被平行于BC的两条线段三等分,如果BC=12cm,•那么这两条线段中较短的一条的长是( )A.8cmB.6cmC.D.8.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE•平分∠ABC,则下列关系式中成立的有( )①;②;③;④CE2=CD×BC;⑤BE2=AE ×BC.A.2个B.3个C.4个D.5个9.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )A.1个B.2个C.3个D.4个10.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )A.△ABM∽△ACBB.△ANC∽△AMBC.△ANC∽△ACMD.△CMN∽△BCA11.在直角坐标系中,已知点A(-2,0),B(0,4),C(0,3),过C作直线交x轴于D,使以D、O、C为顶点的三角形与△AOB相似.这样的直线最多可以作( )A.2条B.3条C.4条D.6条12.(淄博)如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A 处,沿OA所在的直线行走14米到点B时,人影的长度( )A.增大1.5米B.减小1.5米C.增大3.5米D.减小3.5米二、填空题(每题3分,共24分)13.在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在地面上的影长为40米,则古塔高为________.14.(江苏常州)如图,在△ABC中,D、E分别是AB和AC中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=_______,△ADE•与△ABC•的周长之比为_______,•△CFG与△BFD的面积之比为________.15.已知D、E两点分别在△ABC的边AB、AC上,DE∥BC,且△ADE的周长与△ABC•的周长之比为3:7,则AD:DB=________.16.△ABC三边的长分别是2cm、3cm、4cm,与其相似的△DEF的最短边是8cm,那么它的最长边的边长是________.17.(湖南岳阳)如图,要使△ACD∽△ABC,只需添加条件_______(•只要写出一种合适的条件即可).18.如图是幻灯机的工作情况,幻灯片与屏幕平行,光源距幻灯片30cm,•幻灯片距屏幕1.5m,幻灯片中的小树高8cm,则屏幕上的小树高是______.19.如图,在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,那么CD=______.20.如图,梯形ABCD中,AD∥BC,AC、BD交于O点,S△AOD:S△COB=1:9,则S△DOC:S=_______.△BOC三、解答题(第21题~24题每题6分,第25、26题每题8分,共40分)21.(湖北荆州)如图,梯形ABCD中,∠A=∠B=90°,且AD=AB,∠C=45°,将它分割成4个大小一样,都与原梯形相似的梯形(在图形中直接画分割线,不需要说明)22.(苏州)如图,梯形ABCD中,AB∥CD,且AB=2CD,E、F分别是AB、BC的中点,EF与BD相交于点M.(1)求证:△EDM∽△FBM;(2)若DB=9,求BM.23.如图,在离树AB的3米远处竖一长2米的杆子CD,站在离杆子1米远EF处的人刚好越过杆顶C看到树顶A,这个人高EF=1.5米,求树高.24.在《九章算术》“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木.问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,再向西行1775步到B处,正好看到A处的树木(即点D在直线AB上),求小城的边长.25.一块直角三角形木板,一直角边是1.5米,另一直角边长是2米,要把它加工成面积最大的正方形桌面,甲、乙二人的加式方法分别如左图和右图所示,请运用所学知识说明谁的加工方法符合要求.26.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B 以2cm/s的速度移动,点Q沿DA边从点D开始向A以1cm/s的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6)那么:(1)当t为何值时,△QAP为等腰直角三角形?(2)对四边形QAPC的面积,提出一个与计算结果有关的结论;(3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?答案与解析一、选择题1.A 提示:③⑥;2.B3.C 提示:面积比相似比的平方;4.B 提示:由题意知△ABD∽△ACE,;5.B 提示:AD=BD=BC,△ABC∽△BCD;6.B 提示:根据题意设报纸的长为x,宽为y,有;7.C 提示:面积比相似比的平方;8.B 提示:②③④成立;9.B 提示:①③正确;10.B 提示:由CM=CN,∴∠CMN=∠CNM,∴∠AMB=∠ANC,又,∴△ANC∽△AMB;11.C 提示:如图:12.D 提示:设AM=x,BN=y,.二、填空题13.30米提示:设古塔高为h,;14.2,1:2,1:615.3:416.16cm17.∠1=∠ABC或∠2=∠ACB或AC2=AD·AB(答案不唯一)18.48cm19.420.1:3 提示:∵S△AOD:S△COB=1:9,,∵△AOD与△DOC等高,∴S△AOD:S△=1:3,DOC∴S△DOC:S△BOC=1:3.三、解答题21.如图22.(1)证:∵E是AB的中点,∴AB=2EB,∵AB=2CD,∴CD=EB.又AB∥CD,•∴四边形CBED是平行四边形.∴CB∥DE,∴∴△EDM∽△FBM.(2)解:∵△EDM∽△FBM,∴.∵F是BC的中点,∴DE=2BF.∴DM=2BM.∴BM=DB=3.23.3.5米提示:延长AE、BF交于点P,由由.24.解:设小城的边长为x步,根据题意,Rt△AHD∽Rt△ACB,因为有,即,去分母并整理,得x2+34x-71000=0,解得x1=250,x2=-284(不合题意,舍去),所以小城的边长为250步.25.乙加工的方法合理.提示:设甲加工桌面长xm,过点C作CM⊥AB,垂足是M,与GF相交于点N,由GF∥DE,可得三角形相似,而后由相似三角形性质可以得到CN:CM=•GF:AB,即(CM-x):CM=x:AB.由勾股定理可得AB=2.5,由面积相等可求得CM=1.2,•故此可求得x=;设乙加工桌面长ym,由FD∥BC,得到Rt△AFD∽Rt△ACB,所以AF:AC=FD:BC,即(2-y):2=y:1.5,解得y=,很明显x<y,故x2<y2,所以乙加工的方法符合要求.26.(1)对于任何时刻t,AP=2t,DQ=t,QA=6-t,当QA=AP时,△QAP•是等腰直角三角形,即6-t=2t,t=2秒.(2)S△QPC=S△QAC+S△APC =(36-6t)+6t=36cm2,在P、Q两点移动的过程中,四边形QAPC的面积始终保持不变(或P、Q两点到对角线AC的距离之和保持不变)(3)分两种情况:①当时△QAP∽△ABC,则从而t=1.2,②当时△PAQ∽△ABC,则从而t=3.。
新人教版初中数学九年级数学下册第二单元《相似》测试题(含答案解析)
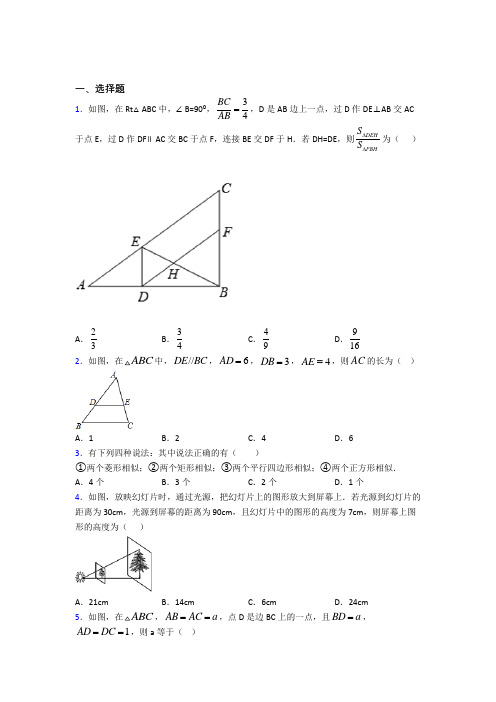
一、选择题1.如图,在Rt△ABC中,∠B=90⁰,34 BCAB=,D是AB边上一点,过D作DE⊥AB交AC于点E,过D作DF∥AC交BC于点F,连接BE交DF于H.若DH=DE,则DEHFBHSS∆∆为()A.23B.34C.49D.9162.如图,在ABC中,//DE BC,6AD=,3DB=,4AE=,则AC的长为()A.1 B.2 C.4 D.63.有下列四种说法:其中说法正确的有()①两个菱形相似;②两个矩形相似;③两个平行四边形相似;④两个正方形相似.A.4个B.3个C.2个D.1个4.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为()A.21cm B.14cm C.6cm D.24cm5.如图,在ABC,AB AC a==,点D是边BC上的一点,且BD a=,1AD DC==,则a等于()A .512+B .51-C .1D .2 6.如图,△ABC 、△FGH 中,D 、E 两点分别在AB 、AC 上,F 点在DE 上,G 、H 两点在BC 上,且DE ∥BC ,FG ∥AB ,FH ∥AC ,若BG :GH :HC=4:6:5,则△ADE 与△FGH 的面积比为何?( )A .2:1B .3:2C .5:2D .9:4第II 卷(非选择题) 请点击修改第II 卷的文字说明参考答案7.如图,已知在ABC ∆中,点D 、E 分别是AB 和AC 的中点,BE 、CD 相交于点O ,若2DOE S ∆=,则BOC S ∆=( )A .4B .6C .8D .108.已知P 是线段AB 的黄金分割点,且51AB =,则AP 的长为( ). A .2 B 51 C .251D .359.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,延长至点G ,连接BG ,过点A 作AF ⊥BG ,垂足为F ,AF 交CD 于点E ,则下列错误的是( )A .AD AC AC AB = B .AD CD CD BD =C .DE CD CD DG = D .EG BD EF BG = 10.已知两个三角形相似,其中一个三角形的两个内角分别为72,63︒︒,则另一个三角形的最小内角为( )A .72︒B .63︒C .45︒D .不能确定 11.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,E 为BC 的中点,连接AE 交BD 于点F ,若1OF =,则BD 的长为( )A .5B .6C .7D .812.如图,在△ABC 中,DE ∥BC ,12AD BD =,则AE EC=( )A .13B .12C .23D .32二、填空题13.如图,点D 是ABC 的边AB 上的一点,//DE BC 交AC 于点E ,作//DF AC 交BC 于点F ,分别记ADE ,BDF ,平行四边形DFCE ,ABC 的面积为1S ,2S ,3S ,S 有以下结论:①若12S S ,则DE 为ABC 的中位线;②若13S S =,则23BC DE =;③()212S S S =+; ④3122S S S =.其中正确的是______.(把所有正确结论的序号都填上)14.如图,已知点M 是△ABC 的重心,AB =123,MN ∥AB ,则MN =__________15.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A ,在近岸取点D ,B ,使得A ,D ,B 在一条直线上,且与河的边沿垂直,测得10m BD =,然后又在垂直AB 的直线上取点C ,并量得30m BC =.如果20m DE =,则河宽AD 为_________m .16.如图,在正方形纸片ABCD 中,对角线AC 、BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰好与BD 上的点F 重合,展开后,折痕DE 分别交AB 、AC 于点E ,G ,连接GF ,下列结论中正确的是__________. (填序号)①67.5AGE ∠=︒;②四边形AEFG 是菱形;③2BE OF =;④:21DOG OGEF S S =四边形:△.17.如图,已知△ABC 中,∠B =90°,BC =3,AB =4,D 是边AB 上一点,DE ∥BC 交AC 于点E ,将△ADE 沿DE 翻折得到△A ′DE ,若△A ′EC 是直角三角形,则AD 长为_____.18.如图,在Rt ABC ∆中,90ACB ∠=︒,//CD AB ,ABC ∠的平分线BD 交AC 于点E ,若10AB =,6BC =,则AE =_______.19.如图,在四边形ABCD 中,点E 在AD 上,EC//AB ,EB//DC ,若△ABE 面积为5 , △ECD 的面积为1,则△BCE 的面积是________.20.若25x y =,则x y y+=____________. 三、解答题21.如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C ,D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连接BG ,DE .我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG .线段DE 的长度关系及所在直线的位置关系; ②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;(2)将原题中正方形改为矩形(如图4-6)且AB a ,BC b =,CE ka =,(),0CG kb a b k =≠>,第(1)题①中得到C 的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由;(3)在第(2)题图5中,连接DG 、BE ,且3a =,2b =,12k =,求22BE DG +的值.22.如果一条线段可以将一个三角形分成两个三角形,其中一个是等腰三角形,另一个三角形与原三角形相似,我们把这样的三角形叫做完美三角形,这条线段叫做这个完美三角形的完美分割线.(1)根据完美三角形的定义,老陆、栋栋、勇士分别提出如下命题:①等腰直角三角形是完美三角形; ②含30°的直角三角形是完美三角形;③等边三角形不是完美三角形.在上述三个命题中,是真命题的为______.(填序号)(2)如图1,在ABC 中,CD 为角平分线,40A ∠=︒,60B ∠=︒.求证:CD 为ABC 的完美分割线.(3)如图2,在ABC 中,5AB =,6BC =,4AC =.求证:ABC 是完美三角形.23.如图,在ABC 中,BA BC =,以AB 为直径的O 分别交AC 、BC 于点D 、E ,BC 的延长线与O 的切线AF 交于点F .(1)求证:2ABC CAF ∠=∠;(2)若210AC =,:1:4CE EB =,求AF 的长.24.如图1,点()8,1A 、(),8B n 都在反比例函数()0m y x x=>的图象上,过点A 作AC x ⊥轴于C ,过点B 作BD y ⊥轴于D .(1)求m 的值和直线AB 的函数关系式;(2)动点P 从O 点出发,以每秒2个单位长度的速度沿线段OD 向点D 运动,同时动点Q 从O 点出发,以每秒1个单位长度的速度沿线段OC 向C 点运动,当动点P 运动到点D 时,点Q 也停止运动,设运动的时间为t 秒.如图2,当点P 运动时,如果作OPQ △关于直线PQ 的对称图形'O PQ △,是否存在某时刻t ,使得点'O 恰好落在反比例函数的图象上?若存在,求'O 的坐标和t 的值﹔若不存在,请说明理由.25.如图,在等边ABC ∆中,点D 是边AC 上一动点(不与点,A C 重合),连接BD ,作AH BD ⊥于点H ,将线段AH 绕点A 逆时针旋转60︒至线段AE ,连接CE (1)①补全图形;②判断线段BH 与线段CE 的数量关系,并证明;(2)已知4AB =,点M 在边AB 上,且1BM=,作直线HE . ①是否存在一个定点P ,使得对于任意的点D ,点P 总在直线HE 上,若存在,请指出点P 的位置,若不存在,请说明理由;②直接写出点M 到直线HE 的距离的最大值.26.()1如图1,四边形ABCD 和BEFG 都是正方形,将正方形BEFG 绕点B 按顺时针方向旋转,记旋转角为,a 则图中AG 与CE 的数量关系是__ ,AG 与CE 的位置关系是_ _ ;()2如图2,四边形ABCD和BEFG都是矩形,且2,2BC AB BE BG==,将矩形BEFG 绕点B按顺时针方向旋转,记旋转角为,a图中AG与CE的数量和位置关系分别是什么?请仅就图2的情况给出证明;参考答案【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】易证DE∥BC,可得34BC DEAB AD==,因为DH=DE,得35DE DHAE AE==,又因为DF∥AC,所以35BH DHBE AE==,所以32BHHE=,根据相似三角形的面积比等于相似比的平方即可求得.【详解】∵DE⊥AB,∴∠ADE=90°,∵∠B=90°,∴∠ADE=∠B,∴DE ∥BC ∴34BC DE AB AD ==,△DEH ∽△FBH ∴35DE AE = 又∵DH=DE ∴35DE DH AE AE == ∵DF ∥AC ∴35BH DH BE AE == ∴32BH HE = ∴4=9DEH FBH S S ∆∆ 故选C【点睛】本题考查相似三角形的性质与判定,掌握相似三角形的面积比等于相似比的平方是解题关键.2.D解析:D【分析】根据平行线分线段成比例求出EC ,即可解答.【详解】解:∵DE ∥BC , ∴AD AE DB EC =,即643EC=, 解得:EC=2,∴AC=AE+EC=4+2=6;故选:D .【点睛】 本题考查了平行线分线段成比例定理,解决本题的关键是熟记平行线分线段成比例定理. 3.D解析:D【分析】直接利用相似图形的判定方法分别判断得出答案.【详解】解:①两个菱形不一定相似,因为对应角不一定相等;②两个矩形不一定相似,因为对应边不一定成比例;③两个平行四边形不一定相似,因为形状不一定相同;④两个正方形相似,正确.故选:D .【点睛】本题考查了相似多边形的判定,正确掌握判定方法是解题的关键.4.A解析:A【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答即可.【详解】解:如图所示,∵DE ∥BC ,∴△AED ∽△ABC , ∴AE DE AC BC=, 设屏幕上的图形高是x cm ,则30790x=, 解得:x=21. 答:屏幕上图形的高度为21cm ,故选:A .【点睛】本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.5.A解析:A【分析】证明△ABC ∽△DAC 得AB BC DA AC =,然后列方程求解即可. 【详解】解:∵AB AC a ==,∴∠B=∠C又∵1AD DC ==,∴∠C=∠DAC∴△ABC ∽△DAC∴AB BC DA AC= ∴11a a a +=解得,12a +=或152a (舍去) 故选:A【点睛】本题考查了相似三角形的判定与性质,解题的关键是理解题意,灵活运用所学知识解决问题. 6.D解析:D【解析】 分析:只要证明△ADE ∽△FGH ,可得2⎛⎫= ⎪⎝⎭△△FGH ADE S DE S GH ,由此即可解决问题. 详解:∵BG :GH :HC=4:6:5,可以假设BG=4k ,GH=6k ,HC=5k ,∵DE ∥BC ,FG ∥AB ,FH ∥AC ,∴四边形BGFD 是平行四边形,四边形EFHC 是平行四边形,∴DF=BG=4k ,EF=HC=5k ,DE=DF+EF=9k ,∠FGH=∠B=∠ADE ,∠FHG=∠C=∠AED , ∴△ADE ∽△FGH ,∴2299=64ADE FGH S DE k S GH k ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭. 故选D .点睛:本题考查相似三角形的判定和性质,平行四边形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.7.C解析:C【分析】根据三角形中位线定理得到DE=12BC ,DE ∥BC ,得到△DOE ∽△COB ,根据相似三角形的面积比等于相似比的平方计算,得到答案.【详解】 ∵D 、E 分别是AB 和AC 的中点, ∴12DE BC =,//DE BC , ∴DOE COB ∆∆∽,∴2DOE COB S DE S BC ∆∆⎛⎫= ⎪⎝⎭,即BOC214S ∆=,解得,8BOC S ∆=,故选:C .【点睛】本题考查了相似三角形的判定和性质、三角形中位线定理,掌握相似三角形的判定定理和性质定理是解题的关键.8.C解析:C【分析】若点P 是靠近点B 的黄金分割点,则12AP AB =,然后代入数据计算即可;若点P 是靠近点A 的黄金分割点,先求出BP ,再利用线段的和差即可求出AP .【详解】解:若P 是靠近点B 的黄金分割点,则)111222AP AB ==⨯=;若P 是靠近点A 的黄金分割点,则)12BP AB ===,∴121AP AB BP =-=-=;故选:C .【点睛】是解题的关键. 9.D解析:D【分析】通过证明△ACD ∽△ABC ,可得AD AC AC AB =,通过证明△ACD ∽△CBD ,可得AD CD CD BD =,通过△ADE ∽△GDB ,△ACD ∽△CBD ,可得DE CD CD DG=,通过证明△GEF ∽△GBD ,可得=EG BG EF BD,即可求解. 【详解】解:∵CD ⊥AB ,∴∠ADC =∠CDB =90°,∴∠BCD +∠ABC =90°,∵∠ACB =90°,∴∠ACD +∠BCD =90°,∴∠ACD =∠ABC ,又∵∠ACB =∠ADC =90°,∴△ACD ∽△ABC , ∴AD AC AC AB=, 故A 选项不合题意;∵∠ACD =∠ABC ,∠ADC =∠BDC ,∴△ACD ∽△CBD , ∴AD CD CD BD= 故B 选项不合题意;∵AF ⊥BG ,∴∠AFB =90°,∴∠FAB +∠GBA =90°,∵∠GDB =90°,∴∠G +∠GBA =90°,∴∠G =∠FAB ,又∵∠ADE =∠GDB =90°,∴△ADE ∽△GDB , ∴=AD DE GD BD, ∴AD •BD =DE •DG ,∵△ACD ∽△CBD , ∴=AD CD CD BD, ∴CD 2=AD •BD ,∴CD 2=DE •DG , ∴DE CD CD DG=, 故C 选项不合题意;∵∠G =∠G ,∠EFG =∠GDB =90°,∴△GEF ∽△GBD , ∴=EG BG EF BD故D 选项符合题意,故选:D .【点睛】本题主要考查相似三角形的判定及其性质,解题的关键是熟练掌握相似三角形的判定方法及其性质.10.C解析:C根据相似三角形的性质、三角形的内角和定理可得出另一个三角形的三个内角度数,由此即可得.【详解】由相似三角形的性质得:另一个三角形的两个内角分别为72,63︒︒,则另一个三角形的第三个内角为180726345︒-︒-︒=︒,因此,另一个三角形的最小内角为45︒,故选:C .【点睛】本题考查了相似三角形的性质、三角形的内角和定理,熟练掌握相似三角形的性质是解题关键.11.B解析:B【分析】根据平行四边形的性质知AD=2BE ,BC ∥AD ,BO=OD ,设BF=a ,得DF=a+2,由BC ∥AD 知△BEF ∽△DAF ,据此得=BF DF 12=BE DA ,得出BF 的长,从而得出BD 的长. 【详解】解:∵点E 是BC 中点,∴BC=2BE ,∵四边形ABCD 是平行四边形,∴BC=AD ,BC ∥AD ,BO=OD ,∴AD=2BE ,设BF=a ,∵OF=1,∴BO=DO=a+1,则DF=a+2,∵BC ∥AD∴△BEF ∽△DAF , 12∴==BF BE DF DA ∴1,22=+a a 解得a=2,经检验a=2是原方程的解∴BF=2,∴BO=DO=3,∴BD=6故选:B .本题主要考查相似三角形的判定与性质,解题的关键是掌握平行四边形的性质和相似三角形的判定与性质.12.B解析:B【分析】直接利用平行线分线段成比例定理得出答案即可.【详解】解:∵DE ∥BC , ∴AE EC =12AD BD =. 故选:B .【点睛】 本题考查了平行线分线段成比例定理,了解定理的内容是解答此题的关键.二、填空题13.①②③④【分析】①根据相似三角形的面积比等于相似比的平方得出AD=BD 求出AE=CE 即可得出答案;②根据相似三角形的面积比等于相似比的平方得出AM=2MN 即可得出答案;③由平行线可得对应线段成比例再 解析:①②③④【分析】①根据相似三角形的面积比等于相似比的平方得出AD=BD ,求出AE=CE ,即可得出答案; ②根据相似三角形的面积比等于相似比的平方得出AM=2MN ,即可得出答案; ③由平行线可得对应线段成比例,再由相似三角形的面积比等于对应边的平方比,进而代入求解即可;④先判断出△BFD ∽△DEA ,然后根据面积比等于相似比的平方得出△ABC 的面积,进而根据S 3=S ABC -S ADE -S DBF 可得出答案【详解】解:①、∵DE ∥BC ,DF ∥AC ,∴△ADE ∽△ABC ,△BDF ∽△BAC ,∵S 1=S 2,22()()∴=AD BD AB AB∴AD=BD ,∵DE ∥BC ,∴AE=EC ,∴DE 是△ABC 的中位线,∴①正确;②、过A 作AN ⊥BC 于N ,交DE 于M ,∵DE ∥BC ,∴AN ⊥DE ,∵DE ∥BC ,DF ∥AC ,∴四边形DECF 是平行四边形,∴DE=CF ,∵S 1=S 3,12∴⨯⨯=⨯DE AM CF MN ∴AM=2MN ,∵DE ∥BC ,∴△ADE ∥△ABC ,2223∴===+DE AM MN BC AN MN MN ∴2BC=3DE ,∴②正确;③、∵DE ∥BC ,DF ∥AC∴四边形DECF 是平行四边形,∴DE=CF ,DF=CE ,∵相似三角形的面积比等于对应边的平方比,12==S S AD BD AB AB S S 121+=+=S S AD BD AB ABS S 12S S S =∴212S S S =;∴③正确; ④∵由题意得:△BFD ∽△DEA ,∴可得:21=S BD ADS 21211∴=+s s BD AB S S=x ∵ABC S =S ,22()∴=S BD S AB∴可得122=++S S S S 又∵△ADE 、△DBF 的面积分别为S 1和S 2,32S =--==ABC ADE DBF S S S S ,∴④正确; 故答案为:①②③④.【点睛】本题考查了面积及等积变换、相似三角形的性质和判定等,难度适中,对于此类题目要先根据相似得出比例式,然后根据比例的性质得出要求图形的面积表达式,进而得出答案. 14.【分析】根据三角形重心的性质可得AD=BD=CM :CD=2:3由MN ∥AB 可得△CMN ∽△CDB 再根据相似三角形的性质求解即可【详解】解:∵点M 是△ABC 的重心∴AD=BD=CM :CD=2:3∵MN解析:【分析】根据三角形重心的性质可得AD=BD=12AB =CM :CD=2:3,由MN ∥AB 可得△CMN ∽△CDB ,再根据相似三角形的性质求解即可.【详解】解:∵点M 是△ABC 的重心,∴AD=BD=12AB =CM :CD=2:3, ∵MN ∥AB ,∴△CMN ∽△CDB , ∴23MN CM DB CD ==,23=,解得MN =.故答案为:【点睛】本题考查了三角形的重心和相似三角形的性质,熟练掌握上述知识是解题的关键. 15.20【分析】证出ADE 和ABC 相似然后根据相似三角形对应边成比例列式求解即可【详解】解:∵AB⊥DEBC⊥AB∴DE∥BC∴ADE∽ABC∴即解得:AD=20m故答案为:20【点睛】本题考查了相似三解析:20【分析】证出ADE和ABC相似,然后根据相似三角形对应边成比例列式求解即可.【详解】解:∵AB⊥DE,BC⊥AB,∴DE∥BC,∴ADE∽ABC,∴AD DEAB BC=,即201030 ADAD=+,解得:AD=20m.故答案为:20.【点睛】本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键.16.①②③【分析】根据正方形的性质菱形的判定等腰直角三角形的性质相似三角形的性质勾股定理一一判断即可【详解】解:如图∵四边形ABCD为正方形∴∠AOB=90°∠BAO=∠OAD=∠ODA=45°∵折叠正解析:①②③【分析】根据正方形的性质、菱形的判定、等腰直角三角形的性质,相似三角形的性质,勾股定理一一判断即可.【详解】解:如图∵四边形ABCD为正方形,∴∠AOB=90°,∠BAO=∠OAD=∠ODA=45°,∵折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的F重合,∴∠1=∠2=12∠ODA=22.5°,EA=EF,∠4=∠5,∠EFD=∠EAD=90°,∴∠3=∠GAD+∠1=45°+22.5°=67.5°,即∠AGE=67.5°;故①正确,∵∠4=90°-∠1=67.5°,∴∠3=∠4=∠5,∴AE=AG=EF,AG∥EF,∴四边形AEFG为菱形;故②正确,∴GF∥AB,EF=GF,∴∠6=∠7=45°,∴△BEF和△OGF都是等腰直角三角形,∴,OF,∴;故③正确,设OF=a,则a,a,∴OB=+1)a,∴OD=+1)a,DF=DO+OF=()a,∵∠DOG=∠DFE=90°,∴△DOG∽△DFE,221(),2DOGDFES DOS DF∆∆∴===∴S△DOG:S四边形OGEF=1:1.故④错误.故答案为①②③【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形和等腰直角三角形的性质.17.或【分析】先根据勾股定理得到AC=5再根据平行线分线段成比例得到AD:AE=AB:AC=4:5设AD=x则AE=A′E=xEC=5﹣xA′B=2x﹣4在Rt△A′BC中根据勾股定理得到A′C再根据△解析:78或258【分析】先根据勾股定理得到AC=5,再根据平行线分线段成比例得到AD:AE=AB:AC=4:5,设AD=x,则AE=A′E=54x,EC=5﹣54x,A′B=2x﹣4,在Rt△A′BC中,根据勾股定理得到A′C,再根据△A′EC是直角三角形,根据勾股定理得到关于x的方程,解方程即可求解.【详解】解:在△ABC中,∠B=90°,BC=3,AB=4,∴AC=5,∵DE∥BC,∴AD :AB =AE :AC ,即AD :AE =AB :AC =4:5,设AD =x ,则AE =A ′E =54x ,EC =5﹣54x ,A ′B =24x ﹣, 在Rt △A ′BC 中,A ′C =22(24)3x -+,∵△A ′EC 是直角三角形,∴①当A '落在边AB 上时,∠EA ′C =90°,∠BA ′C =∠ACB ,A ′B =3×cot ∠ACB =39344⨯=, ∴AD =1974248⎛⎫-= ⎪⎝⎭;②点A 在线段AB 的延长线上(22(24)3x -+)2+(5﹣54x )2=(54x )2, 解得x 1=4(不合题意舍去),x 2=258.故AD 长为78或258. 故答案为:78或258. 【点晴】本题考查了勾股定理和平行线等分线段成比例定理,掌握相关知识是解决问题的关键.18.5【分析】首先由勾股定理求出AC 再证明得到进而列方程求解即可【详解】解析:5【分析】首先由勾股定理求出AC ,再证明~ABE CDE ∆∆,得到AB AE CD CE=,进而列方程求解即可.【详解】 90ACB ∠=︒,10AB =,6BC =,8AC ∴==,∴设AE x =,则8CE x =-, BD 平分ABC ∠,ABD DBC ∴∠=∠,又//AB CD ,ABD BDC ∴∠=∠,DBC BDC ∴∠=∠,6BC CD ∴==,//AB CD ,∴~ABE CDE ∆∆,AB AE CD CE∴= 1068x x∴=- 解得5x =,5AE ∴=故答案为:5.【点睛】此题主要考查了相似三角形和判定与性质,熟练掌握并能灵活运用相似三角形和判定与性质定理是解答此题的关键.19.【分析】由EC ∥ABEB ∥DC 可得∠A=∠CED ∠AEB=∠D 证得△ABE 与△ECD 相似由△ABE 的面积为5△CDE 的面积为1可得AB :CE=:1又由EC ∥AB 可得△ABE 与△BCE 等高然后由等高三【分析】由EC ∥AB ,EB ∥DC ,可得∠A=∠CED ,∠AEB=∠D ,证得△ABE 与△ECD 相似,由△ABE的面积为5,△CDE 的面积为1,可得AB :1又由EC ∥AB ,可得△ABE 与△BCE 等高,然后由等高三角形的面积比等于对应底的比,求得△BCE 的面积.【详解】∵EC ∥AB ,∴∠A=∠CED ,∵EB ∥DC∴∠AEB=∠D ,∴△ABE ∽△ECD , ∴22ABE ECD 551S BE AB CD CES ⎛⎫⎛⎫==== ⎪⎪⎝⎭⎝⎭, ∴AB CE =AB =, ∵△ABE 以AB 为底边的高与△BCE 以CE 为底的高相等,∴ABEBCE SAB S CE ==BCE S ∴==【点睛】本题考查了相似三角形的判定与性质.注意相似三角形的面积比等于相似比的平方、等高三角形面积的比等于其对应底的比.20.【分析】由根据比例的性质即可求得的值【详解】解:∵∴=故答案为:【点睛】此题考查了比例的性质此题比较简单注意熟记比例变形 解析:75【分析】 由25x y =,根据比例的性质,即可求得x y y+的值. 【详解】 解:∵25x y = ∴x y y +=2+57=55. 故答案为:75. 【点睛】此题考查了比例的性质,此题比较简单,注意熟记比例变形.三、解答题21.(1)①BG DE =,BG DE ⊥.②BG DE =,BG DE ⊥仍然成立.详见解析;(2)BG DE ⊥成立,BG DE =不成立,详见解析;(3)654. 【分析】 (1)①利用正方形的性质,证明BCG DCE ≌△△,利用全等三角形的性质可得:BG=DE ,∠CBG=∠CDE ,再证明:∠EDC+∠DGO=90°,从而可得结论;②同①,先证明:BCG DCE ≌△△,利用全等三角形的性质可得:BG DE =,CBG CDE ∠=∠,再证明:90CDE DHO ∠+∠=︒,从而可得结论;(2)利用矩形的性质,证明BCG DCE △∽△,可得:CBG CDE ∠=∠,再证明90CDE DHO ∠+∠=︒,从而可得结论;(3)连接,,BD GE 利用BG DE ⊥,结合勾股定理证明:2222BE DG BD GE +=+,再把3a =,2b =,12k =代入,即可得到答案. 【详解】解:(1)①BG DE =,BG DE ⊥.理由如下:如图1,延长BG 交DE 于O ,∵四边形ABCD 、CGFE 是正方形,∴BC=CD=AB ,CG=CE ,∠BCD=∠ECD=90°,∵在BCG 和DCE 中BC CD BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩,∴BCG DCE ≌△△,∴BG=DE ,∠CBG=∠CDE ,∵∠CBG+∠BGC=90°,又∵∠DGO=∠BGC ,∴∠EDC+∠DGO=90°,∴∠DOG=1809090︒-︒=︒,∴BG ⊥DE ,即BG=DE ,BG ⊥DE ;②BG DE =,BG DE ⊥仍然成立.如图2,∵四边形ABCD 、四边形CEFG 都是正方形,∴BC CD =,CG CE =,90BCD ECG ∠=∠=︒,∴BCG DCE ∠=∠,∵在BCG 与DCE 中,,BC CD BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩∴BCG DCE ≌△△,∴BG DE =,CBG CDE ∠=∠,又∵BHC DHO ∠=∠,90CBG BHC ∠+∠=︒,∴90CDE DHO ∠+∠=︒,∴90DOH ∠=︒,∴BG DE ⊥.(2)BG DE ⊥成立,BG DE =不成立.如图5,∵四边形ABCD 、四边形CEFG 都是矩形,且AB CD a ==,BC b =,CG kb =,(),0CE ka a b k =≠>, ∴BC CG b DC CE a==,90BCD ECG ∠=∠=︒, ∴BCG DCE ∠=∠, ∴BCG DCE △∽△,∴CBG CDE ∠=∠,又∵BHC DHO ∠=∠,90CBG BHC ∠+∠=︒,∴90CDE DHO ∠+∠=︒,∴90DOH ∠=︒,∴BG DE ⊥.显然:.BG DE ≠(3)如图5,连接,,BD GE∵BG DE ⊥,∴222OB OD BD +=,222OE OG GE +=,222OB OE BE +=,222OG OD DG += ∴22222222BE DG OB OE OG OD BD GE +=+++=+,又∵3a =,2b =,12k =,CE ka =,CG kb =, 2222222211323321222BD GE ⎛⎫⎛⎫⎛⎫∴=+=⨯+⨯=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,, ∴22222236523124BD GE ⎛⎫+=+++= ⎪⎝⎭, ∴22654BE DG +=. 【点睛】本题考查的是勾股定理的应用,正方形,矩形的性质,三角形全等的判定与性质,三角形相似的判定与性质,掌握以上知识是解题的关键.22.(1)①②③(2)证明见解析.(3)证明见解析.【分析】(1)根据等腰直角三角形的性质和完美三角形判定即可求证①;根据含30°的直角三角形的性质、角平分线的性质、完美三角形判定即可求证②;根据等边三角形的性质和完美三角形判定即可求证③;(2)由40A ∠=︒,60B ∠=︒.可得∠ACB =80°,继而判定△ABC 不是等腰三角形,△ACD 是等腰三角形,再由△BCD ∽△BAC 即可证明结论;(3)作CAD B ∠=∠,易知△CAD ∽△CBA ,继而根据相似三角形的性质可得CD 、AD 的长,继而判定△ABD 是等腰三角形,继而求证△ABC 是完美三角形.【详解】解:(1)①等腰直角三角形底边的中线将原三角形,分成两个等腰直角三角形,CD ∴为等腰直角ACB △的完美分割线,等腰直角ACB △是完美三角形,故①正确;②在Rt ACB △中,90ACB ∠=︒,30B ∠=︒,60CAB ∠=︒,当AD 平分CAB ∠时,30CAD DAB B ∠=∠=∠=︒,ACD BCA ∴∽,ADB △是等腰三角形,AD ∴是直角ACB △的完美分割线,∴含30°角的直角三角形是完美三角形,故②正确;③一条线段不可能将等边三角形分成一个等边三角形和一个等腰三角形,故等边三角形不可能是完美三角形,故③正确,∴真命题有①②③.(2)40A ∠=︒,60B ∠=︒,80ACB ∴∠=︒∴△ABC 不是等腰三角形,∵CD 平分∠ACB , 1402ACD BCD ACB ∴∠=∠=∠=︒, 40ACD A ∴∠=∠=︒,∴△ACD 为等腰三角形,40DCB A ∠=∠=︒,CBD ABC ∠=∠,∴△BCD ∽△BAC ,CD ∴是△ABC 的完美分割线.(3)作CAD B ∠=∠,CAD B ∠=∠,C C ∠=∠,CAD CBA ∴∽△△,CA CD AD CB CA AB∴==, 4CA =,6CB =,5AB = 4645CD AD ==,83CD ∴=,103AD =, 810633BD BC CD =-=-=, BD AD ∴=,ABD ∴是等腰三角形,AD ∴是ABC 的完美分割线,ABC ∴是完美三角形.【点睛】本题考查新定义的理解,各类三角形的判断及性质,相似三角形的判定及其性质的应用,解题的关键是熟练运用所学知识点.23.(1)见解析;(2)152【分析】(1)根据切线性质可知90CAB CAF ∠+∠=︒,所得等式两边同乘2可得22180CAB CAF ∠+∠=︒,在等腰三角形ABC 中,2180CAB ABC ∠+∠=︒,联立两个等式即可证明.(2)连接AE ,设CE x =,根据等腰三角形性质及勾股定理可得3AE x =,在Rt AEC 中运用勾股定理得出CE 、AE 的值,再根据AEF BEA ∽△△计算得出AF 的值.【详解】(1)证明:∵AB 为O 的直径,AF 是O 的切线,∴AF AB ⊥,90CAB CAF ∠+∠=︒,等式两边同乘2可得:22180CAB CAF ∠+∠=︒①;∵BA=BC ,∴CAB ACB ∠=∠,∴在ABC 中,2180CAB ABC ∠+∠=︒②,联立①和②可得:222CAB CAF CAB ABC ∠+∠=∠+∠,∴2ABC CAF ∠=∠.(2)解:连接AE ,如图:∵:1:4CE EB =,BA=BC ,设CE x =,90AEB =︒∠(直径所对圆周角是直角), ∴在Rt AEB 中,45AB CE EB x x x =+=+=,4BE x =,22=(5)(4)3AE x x x -=,∵在Rt AEC 中,222AE CE AC +=,即()(222321040x x +==,∴解得:2x =,AE=6,AB=10,∵AE ⊥BF ,FAE ABE ∠=∠(弦切角度数等于它所夹弧度所对圆周角度数),∴FAE ABE ∽, ∴FA AB AE BE =,即1068FA =, 解得:152FA =. 【点睛】本题考查切线性质的综合运用,用勾股定理解三角形,灵活运用切线性质和勾股定理是解题关键.24.(1)直线AB 的解析式为9y x =-+;(2)存在,()'4,2O ,52t =,见解析; 【分析】 (1)由于点A (8,1)、B (n ,8)都在反比例函数m y x=的图象上,根据反比例函数的意义求出m ,n ,再由待定系数法求出直线AB 的解析式;(2)①由题意知:OP=2t ,OQ=t ,由三角形的面积公式可求出解析式;②通过三角形相似,用t 的代数式表示出O′的坐标,根据反比例函数的意义可求出t 值.【详解】 解:(1)∵点()8,1A 、(),8B n 都在反比例函数m y x =的图象上, ∴818=⨯=m , ∴8y x =, ∴88n=,即1n =.设AB 的解析式为y kx b =+,把()8,1、()1,8B 代入上式得:818k b k b +=⎧⎨+=⎩,解得:19k b =-⎧⎨=⎩. ∴直线AB 的解析式为9y x =-+.(2)存在.当'O 在反比例函数的图象上时,作PE y ⊥轴,'O F x ⊥轴于F ,交PE 于E ,则90E ∠=︒,'2PO PO t ==,'QO QO t ==.由题意知:'PO Q POQ ∠=∠,'90'QO F PO E ∠=︒-∠,'90'EPO PO E ∠=︒-∠,∴''PEO O FQ △△, ∴''''PE EO PO O F QF QO ==, 设QF b =,'O F a =,则PE OF t b ==+,'2O E t a =-, ∴22t b t a a b+-==, 解得:45a t =,35b t =, ∴84',55O t t ⎛⎫ ⎪⎝⎭, 当'O 在反比例函数的图象上时,84855t t ⋅=, 解得:52t =±, ∵反比例函数的图形在第一象限,∴0t >,∴52t =, ∴()'4,2O ,当52t =秒时,'O 恰好落在反比例函数的图象上. 【点睛】 本题主要考查了反比例函数的意义,利用图象和待定系数法求函数解析式,相似三角形的判定和性质,熟练掌握反比例函数的意义和能数形结合是解决问题的关键.25.(1)①见解析;②BH CE =,证明见解析;(2)①存在,点P 是边BC 的中点;②3【分析】(1)①按要求画出图形即可;②根据全等三角形对应边相等来回答;(2)①点P 为直线HE 与BC 的交点;②通过△BPM ∽△BAP 问题可解;【详解】(1)①如图; ②BH CE =证明ABH ACE ∆≅∆即可(2)①存在点P 是边BC 的中点,理由:设直线HE 与边BC 交于点P可由60ACB AEP ︒∠=∠=得点,,,A E C P 共圆,因为90AEC ︒∠=,所以90APC ︒∠=,即P 是BC 的中点.②如图, 当MP ⊥HE 时,MP 最大,理由:4,2,1AB BP BM ===,BM BP BP AB ∴=,B B ∠∠=,∴△BPM ∽△BAP ,∴∠BMP=∠BPA=90︒ , 2222213BP BP BP ∴=-=-=【点睛】本题考查等腰三角形的性质,全等三角形的判定和性质,点到直线的距离,旋转,相似三角形的判定和性质,勾股定理和圆的有关知识知识,综合性较强.26.(1)AG=CE ,AG ⊥CE ;(2)CE=2AG ,理由见详解.【分析】(1)根据题意易得AB=CB ,BG=BE ,∠ABC=∠GBE=90°,则有∠ABG=∠CBE ,进而可证△ABG ≌△CBE ,然后问题可证,延长AG 交BC 、CE 与点H 、M ,然后根据三角形全等的性质及直角三角形的性质可求解;(2)由题意易得∠ABG=∠CBE ,则可证△ABG ∽△CBE ,进而问题可得证.【详解】解:(1)∵四边形ABCD 和BEFG 都是正方形,∴AB=CB ,BG=BE ,∠ABC=∠GBE=90°,∴∠ABG+∠GBC=90°,∠CBE+∠GBC=90°,∴∠ABG=∠CBE ,∴△ABG ≌△CBE (SAS ),∴AG=CE ,延长AG 交BC 、CE 与点H 、M ,如图所示:∴∠GAB=∠ECB ,∵∠GAB+∠AHB=90°,∠AHB=∠CHM ,∴∠ECB+∠CHM=90°,∴AM ⊥CE ,即AG ⊥CE ,故答案为AG=CE ,AG ⊥CE ;(2)CE=2AG ,理由如下:∵四边形ABCD 和BEFG 都是矩形,∴∠ABC=∠GBE=90°,∴∠ABG+∠GBC=90°,∠GBC+∠CBE=90°,∴∠ABG=∠CBE ,∵2,2BC AB BE BG ==,∴△ABG ∽△CBE , ∴2BC CE AB AG==, ∴CE=2AG .【点睛】 本题主要考查矩形与正方形的性质及相似三角形的性质与判定,熟练掌握矩形与正方形的性质及相似三角形的性质与判定是解题的关键.。
(常考题)人教版初中数学九年级数学下册第二单元《相似》测试卷(包含答案解析)(2)

一、选择题1.下列各组线段能成比例的是( )A .1.5cm ,2.5cm , 3.5cm ,4.5cmB .1cm ,2cm ,3cm ,4cmC .3cm , 6cm , 4cm , 8cmD .2cm ,10cm ,5cm ,15cm 2.如图,ABC 和CDE △都是等边三角形,点G 在CA 的延长线上,GB GE =,若10BE CG +=,32AG BE =,则AF 的长为( )A .1B .43C .95D .2 3.如图,在菱形ABCD 中,660AB DAB =∠=︒,,A ,E 分别交BC 、BD 于点E 、F ,2CE =,连接CF ,以下结论:①ABF CBF ≌;②点E 到AB 的距离是23;③ADF 与EBF △的面积比为3∶2:④ABF 的面积为为183,其中正确的是( )A .①④B .①③④C .①②④D .①②③④ 4.如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图一定相似的有( )A .1个B .2个C .3D .4个5.如图,在边长为2的正方形ABCD 中,对角线AC 与BD 相交于点O ,点P 是BD 上的一个动点,过点P 作EF ∥AC ,分别交正方形的两条边于点E ,F ,连接OE ,OF ,设BP =x ,△OEF 的面积为y ,则能大致反映y 与x 之间的函数关系的图像为( )A .B .C .D . 6.如果两个相似三角形的对应高之比是1:2,那么它们的周长比是( )A .1:2B .1:4C .1:2D .2:17.如图,D 、E 分别是△ABC 的边AB 、BC 上的点,且DE ∥AC ,AE 、CD 相交于点O ,若S △DOE :S △COA =1:9,则S △BDE :S △CDE 的值是( ).A .1:2B .1:3C .1:4D .2:5 8.如图,直线12//l l ,:2:3AF FB =,:2:1BC CD =,则:AE EC 是( )A .1:2B .1:4C .2:1D .3:29.如图,在ABCD 中,7AB =,3BC =,ABC ∠的平分线交CD 于点F ,交的延长线于点E ,若2BF =,则线段EF 的长为( )A .4B .3C .83D .74 10.如图,在△ABC 中,AB =AC=5,BC =25,若点O 为△ABC 三条高的交点,则OA 的长度为( )A .352B .253C .5D .35411.如图,已知点E 是正方形ABCD 的边AB 边上的黄金分割点,且,AE EB >若1S 表示AE 为边长的正方形面积,2S 表示以BC 为长,BE 为宽的矩形面积,3S 表示正方形ABCD 除去1S 和2S 剩余的面积,则32:S S 的值为( )A .512-B .512+C .352 D .352+ 12.如图,在△ABC 中,DE ∥BC ,12AD BD =,则AE EC=( )A .13B .12C .23D .32二、填空题13.如图,△ABC 中,∠C =90°,BC =8cm ,AC =6cm ,点P 沿BC 边以2cm/s 的速度从点B 向点C 移动,同时点Q 沿CA 边以1cm/s 的速度从点C 向点A 移动.若以点C 、P 、Q 构成的三角形与△ABC 相似,则运动时间为____________秒.14.如图,D E 、分别是ABC 的边AB BC 、上的点,且//,DE AC AE CD 、相交于点O ,若:1:25DOE COA S S =△△,则BE CE的值是________.15.贺哲同学的身高1.86米,影子长3米,同一时刻金老师的影子长2.7米,则金老师的身高为________米(结果保留两位小数)。
2023年人教版九年级数学下册第27章《相似》复习检测卷(一)附答案解析

2023年九年级数学下册第27章《相似》复习检测卷(一)考试范围:§27.1图形的相似~27.2相似三角形的判定满分:120分一、选择题(每小题3分,共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ,其中点A 、B 、C 的对应点分别是D 、E 、F ,则∠D 与∠A 的关系为()A .∠D =∠AB .∠D =3∠AC .∠D =6∠AD .∠D =9∠A2.如图,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()3.如图,已知直线a ∥b ∥c ,直线m 、n 与a 、b 、c 分别交于点A 、C 、E ,B 、D 、F ,AC =8,CE =12,BD =6,则DF 的长为()A .4B .5C .9D .74.如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,F 为BC 边上一点,连接AF交DE 于点G ,则下列结论中一定正确的是()A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=5.如图,在正方形网格上有两个三角形,且△ABC 和△DEF 相似,则∠BAC 的度数为()A .135°B .125°C .115°D .105°6.如图,△ACP ∽△ABC ,若∠A =100°,∠ACP =20°,则∠ACB 的度数是()A .80°B .60°C .50°D .30°7.如图,在□ABCD 中,EF ∥AB ,DE ∶EA =2∶3,EF =4,则CD 的长为()A .6B .8C .9D .108.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm 、6cm 和9cm ,另一个三角形的最短边长为2.5cm ,则它的最长边为()A .3cmB .4cmC .4.5cmD .5cm9.如图,在矩形ABCD 中,AB =a ,AD =3,按照图中的方式将它分成完全相同的三个矩形,如果每一个小矩形都与矩形ABCD 相似,则a 的值为()第5题第3题第4题第6题第7题第9题第10题A .22B .23C .33D .3210.如图,正方形ABCD 的边长为4,E 是BC 边上一点,过点E 作EF ⊥AE 交CD 边于点F ,则CF 的最大值是()A .0.5B .1C .1.5D .2二、填空题(每小题3分,共18分)11.如图,添加一个条件__________________,使△ADE ∽△ACB .12.如图,在□ABCD 中,E 是AD 的中点,EC 交对角线BD 于点F ,则BF ∶FD 的值为_________.13.如图,在△ABC 中,DE ∥BC ,若AD =1,BD =3,BC =8,则DE 的长为________.14.已知654a b c==,且a +b -2c =6,则a 的值为_______.15.如图,在Rt △OAC 中,O 为坐标原点,直角顶点C 在x 轴的正半轴上,反比例函数ky x=(k >0)在第一象限的图象经过OA 的中点B ,交AC 于点D ,连接OD ,若△OCD ∽△ACO ,则直线OA 的解析式为_______.16.如图,直线l 1∥l 2∥l 3,直线l 1与l 2之间的距离为2,直线l 2与l 3之间的距离为1,等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上,则等边三角形的边长是______.三、解答题(共8题,共72分)17.(8分)如图,四边形ABCD ∽四边形A 'B 'C 'D ',∠BCD =125°,分别求x 、y 、α的值.18.(8分)如图,在矩形ABCD 中,点E 、F 分别在BC 、CD 上,AE ⊥BF 于点M ,若BC =2AB ,探究AE 与BF 的数量关系,并证明你的结论.第10题第11题第16题第12题第13题第15题19.(8分)如图,在四边形ABCD中,AC平分∠BAD,∠ADC=∠ACB=90°.(1)求证:AC2=AB·AD;(2)若BC=3,AB=5,求CD的长.20.(8分)如图,在矩形ABCD中,E是AD上一点,连接BE.(1)请用尺规在BE上求作一点P,使得△PCB∽△ABE(不写作法,保留作图痕迹);(2)若AE=3,AB=4,BC=6,求EP的长.21.(8分)如图,在△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;(2)作DE∥AB交AC于点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.22.(10分)在△ABC中,AB=6,AC=8,点D、E分别在AB、AC上,连接DE,设BD=x(0<x<6),CE=y(0<y<8).(1)当x=2,y=5时,求证:△AED∽△ABC;(2)若△ADE和△ABC相似,求y与x的函数表达式.23.(10分)如图,在△ABC中,∠ABC=90°,D是斜边AC的中点,连接DB.过点A作AE⊥BD于点F,交BC于点E.(1)求证:EB2=EF・EA;(2)若AB=4,CE=3BE,求AE的长.24.(12分)(1)【问题背景】如图1,D是等边△ABC中AB边上的点,以CD为边在CD的上方作等边△CDE,连接AE,求证:BD=AE;(2)【尝试应用】如图2,D是Rt△ABC中AB边上的一点,∠B=90°,∠BAC=30°,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,∠CED=30°,连接AE,请探究BD与AE的数量关系,并说明理由;(3)【拓展创新】如图3,在Rt△ABC中,∠ABC=90°,点D在AB边上,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,43DE ABCD BC==,DE交AC于F,若AD=3BD,求AFDF的值.《相似》阶段检测卷(一)考试范围:§27.1图形的相似~27.2相似三角形的判定满分:120分一、选择题(每小题3分,共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ,其中点A 、B 、C 的对应点分别是D 、E 、F ,则∠D 与∠A 的关系为()A .∠D =∠AB .∠D =3∠AC .∠D =6∠A D .∠D =9∠A【答案】A .详解:依题意,△ABC 与△DEF 的三边成比例,∴△ABC ∽△DEF ,∴∠A =∠D ,故选A .2.如图,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()【答案】C .详解:由两个角分别相等的两个三角形相似,知选项A 和B 中的阴影三角形与原三角形相似,选项D 中,阴影三角形的∠A 的两边分别为4-1=3,6-4=2,∵4623=,∠A =∠A ,∴选项D 中的阴影三角形与原三角形相似.而选项C 中,不能保证∠B 的两边成比例,故选C .3.如图,已知直线a ∥b ∥c ,直线m 、n 与a 、b 、c 分别交于点A 、C 、E ,B 、D 、F ,AC =8,CE =12,BD =6,则DF 的长为()A .4B .5C .9D .7【答案】C .详解:∵a ∥b ∥c ,∴AC BD CE DF =,即8612DF=,解得DF =9,故选C . 4.如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,F 为BC 边上一点,连接AF 交DE 于点G ,则下列结论中一定正确的是()A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=【答案】C .详解:∵DE ∥BC ,∴BD CE AD AE =,故C 对;AD AEAB AC=,故A 错;AG AE ADAF AC AB==,故D 错;选项B 中的4条线段不成比例,故D 错.故选C .5.如图,在正方形网格上有两个三角形,且△ABC 和△DEF 相似,则∠BAC 的度数为()A .135°B .125°C .115°D .105°【答案】A .详解:∵△ABC 和△DEF 相似,观察角的大小,∠BAC =∠DEF =90°+45°=135°,故选A . 6.如图,△ACP ∽△ABC ,若∠A =100°,∠ACP =20°,则∠ACB 的度数是()A .80°B .60°C .50°D .30°【答案】B .详解:在△ACP 中,∵∠A =100°,∠ACP =20°,∴∠APC =60°.∵△ACP ∽△ABC ,∴∠ACB =∠APC =60°,故选B .7.如图,在□ABCD 中,EF ∥AB ,DE ∶EA =2∶3,EF =4,则CD 的长为()A .6B .8C .9D .10【答案】D .详解:∵EF ∥AB ,∴EF DEAB DA=,∵DE ∶EA =2∶3,EF =4,∴4223AB =+,∴AB =10,则CD =AB =10,故选D .8.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm 、6cm 和9cm ,另一个三角形的最短边长为2.5cm ,则它的最长边为()A .3cmB .4cmC .4.5cmD .5cm【答案】C .详解:设所求的最长边为xcm ,则592.5x=,解得x =4.5,故选C .9.如图,在矩形ABCD 中,AB =a ,AD =3,按照图中的方式将它分成完全相同的三个矩形,如果每一个小矩形都与矩形ABCD 相似,则a 的值为()A .B .C .D .【答案】C .详解:小矩形的边边分别为13a 和3,∵小矩形与矩形ABCD 相似,∴13a ∶3=3∶a ,解得a =±(舍去负值),∴a =C .10.如图,正方形ABCD 的边长为4,E 是BC 边上一点,过点E 作EF ⊥AE交CD 边于点F ,则CF 的最大值是()A .0.5B .1C .1.5D .2【答案】B .详解:∵∠B =∠C =90°,AE ⊥EF ,可证△ABE ∽△ECF ,∴AB BECE CF=,设BE =x ,则CE =4-x ,∴44x x CF =-,∴CF =14x (4-x )=-14(x -2)2+1,当x =2时,CF 取得最大值1,故选B .二、填空题(每小题3分,共18分)11.如图,添加一个条件__________________,使△ADE ∽△ACB .【答案】答案不唯一,可以填下列中的一个:∠ADE =∠C ,∠AED =∠B ,AD AEAC AB=.12.如图,在□ABCD 中,E 是AD 的中点,EC 交对角线BD 于点F ,则BF ∶FD的值为_________.【答案】2.详解:∵四边形ABCD 为平行四边形,∴BC =AD ,BC ∥AD .∵E 为AD 的中点,∴BC =AD =2DE ,由AD ∥BC ,得△BCF ∽DEF ,∴BF ∶FD =BC ∶DE =2.13.如图,在△ABC 中,DE ∥BC ,若AD =1,BD =3,BC =8,则DE 的长为________.【答案】2.详解:∵DE ∥BC ,∴AD DE AB BC =,即1138DE=+,∴DE =2.14.已知654a b c==,且a +b -2c =6,则a 的值为_______.【答案】12.详解:∵654a b c==,故可设a =6x ,b =5x ,c =4x ,代入a +b -2c =6,得:6x +5x -2(4x )=6,解得x =2,∴a =6x =12.15.如图,在Rt △OAC 中,O 为坐标原点,直角顶点C 在x 轴的正半轴上,反比例函数ky x=(k >0)在第一象限的图象经过OA 的中点B ,交AC 于点D ,连接OD ,若△OCD ∽△ACO ,则直线OA 的解析式为_______.【答案】y =2x .详解:设B (t ,k t ),则直线OA 的解析式为y =2ktx .∵B 为OA 的中点,∴A (2t ,2k t ),∴D (2t ,2k t ),OC =2t ,CD =2k t ,CA =2kt.∵△OCD ∽△ACO ,∴OC CD AC OC =,∴OC 2=AC ·CD ,∴4t 2=2k t ·2k t,∴k 2=4t 4,∵k >0,∴k =2t 2,∴直线OA 的解析式为y =2x .16.如图,直线l 1∥l 2∥l 3,直线l 1与l 2之间的距离为2,直线l 2与l 3之间的距离为1,等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上,则等边三角形的边长是______.【答案】2213.F详解:过C 作CE ⊥AC 交AB 的延长线于D ,过C 作CF ⊥l 1于F ,交l 3于H ,过E 作ED ⊥FC 交延长线于D ,∵∠AFC =∠ACE=∠CDE =90°,∴△ACF ∽△CED ,∴DE CD CECF AF AC==,∵△ABC 为等边△,∴CE ,AB =BC =BE ,则CD AF .依题意,FH =FC +CH =2+1=3,由AB =BE ,l 1∥l 3∥ED ,得DH =FH =3,CD =4,∴AF CD AC .三、解答题(共8题,共72分)17.(8分)如图,四边形ABCD ∽四边形A 'B 'C 'D ',∠BCD =125°,分别求x 、y 、α的值.【答案】∵四边形ABCD ∽四边形A 'B 'C 'D ',∴∠C ′=∠C =125°,∴∠α=360°-80°-75°-125°=80°,且AD AB BC A D A B B C =='''''',即45316x y==,解得x =20,y =12.答:x =20,y =12,α=80°.18.(8分)如图,在矩形ABCD 中,点E 、F 分别在BC 、CD 上,AE ⊥BF 于点M ,若BC ,探究AE 与BF 的数量关系,并证明你的结论.【答案】BF AE ,理由如下:∵四边形ABCD 是矩形,∴∠ABC =∠C ,∵AE ⊥BF ,∴∠AMB =∠BAM +∠ABM =90°,又∵∠ABM +∠CBF =90°,∴∠BAM =∠CBF ,∴△ABE ∽△BCF ,∴AE AB BF BC ==,∴BF AE .19.(8分)如图,在四边形ABCD 中,AC 平分∠BAD ,∠ADC =∠ACB =90°.(1)求证:AC 2=AB ·AD ;(2)若BC =3,AB =5,求CD 的长.【答案】(1)∵AC 平分∠BAD ,∴∠DAC =∠CAB .∵∠ADC =∠ACB =90°,∴△ADC ∽△ACB ,∴AD ACAC AB=,∴AC 2=AB ·AD .(2)在Rt △ABC 中,∵BC =3,AB =5,由勾股定理,得AC =4.∵AC 2=AB ·AD ,∴42=5AD ,∴AD =165.在Rt △ADC 中,CD 125.20.(8分)如图,在矩形ABCD 中,E 是AD 上一点,连接BE .(1)请用尺规在BE 上求作一点P ,使得△PCB ∽△ABE(不写作法,保留作图痕迹);(2)若AE =3,AB =4,BC =6,求EP 的长.【答案】(1)如图所示;(2)由勾股定理,得BE 5,由△PCB ∽△ABE ,得BP BC AE BE =,即635BP =,∴BP =185,∴EP =BE -BP =5-185=75.21.(8分)如图,在△ABC 中,AB =2,BC =4,D 为BC 边上一点,BD =1.(1)求证:△ABD ∽△CBA ;(2)作DE ∥AB 交AC 于点E ,请直接写出另一个与△ABD 相似的三角形,并求出DE 的长.【答案】(1)∵AB =2,BC =4,BD =1,∴AB BDBC AB=,又∠ABD =∠CBA ,∴△ABD ∽△CBA .(2)如图,∵DE ∥AB ,∴△CDE ∽△CBA ,∵△ABD ∽△CBA ,∴△CDE ∽△ABD ,∴DE CD BD AB =,即4112DE -=,∴DE =1.5.22.(10分)在△ABC 中,AB =6,AC =8,点D 、E 分别在AB 、AC 上,连接DE ,设BD =x (0<x <6),CE =y (0<y <8).(1)当x =2,y =5时,求证:△AED ∽△ABC ;(2)若△ADE 和△ABC 相似,求y 与x 的函数表达式.【答案】(1)∵AB =6,BD =x =2,∴AD =4.∵AC =8,CE =y =5,∴AE =3.∴AD AEAC AB=.又∵∠EAD =∠BAC ,∴△AED ∽△ABC .(2)分两种情况,1°当△ADE ∽△ABC 时,AD AE AB AC =,则6868x y --=,∴y =43x (0<x <6).2°当△ADE ∽△ACB 时,AD AE AC AB =,则6886x y --=,∴y =34x +72(0<x <6).23.(10分)如图,在△ABC 中,∠ABC =90°,D 是斜边AC 的中点,连接DB .过点A 作AE ⊥BD 于点F ,交BC 于点E .(1)求证:EB 2=EF ・EA ;(2)若AB =4,CE =3BE ,求AE 的长.【答案】(1)∵AE ⊥BD ,∴∠BFE =90°=∠ABC .又∵∠BEF =∠AEB ,∴△EBF ∽△EAB ,∴BE EFAE BE=,∴EB 2=EF ・EA .(2)在Rt △ABC 中,∵D 为斜边AC 的中点,∴BD =CD ,∴∠DBC =∠C .由(1),得△EBF∽△EAB,∴∠EBF=∠EAB,∴∠C=∠EAB.又∠ABE=∠CBA,∴△BAE∽△BCA,∴AB BEBC AB=,∴AB2=BE·BC.∵AB=4,CE=3BE,∴BC=4BE,42=BE(4BE),∴BE=2.∴AE=.24.(12分)(1)【问题背景】如图1,D是等边△ABC中AB边上的点,以CD为边在CD的上方作等边△CDE,连接AE,求证:BD=AE;(2)【尝试应用】如图2,D是Rt△ABC中AB边上的一点,∠B=90°,∠BAC=30°,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,∠CED=30°,连接AE,请探究BD与AE的数量关系,并说明理由;(3)【拓展创新】如图3,在Rt△ABC中,∠ABC=90°,点D在AB边上,以CD为边在CD的上方作Rt△CDE,使∠CDE=90°,43DE ABCD BC==,DE交AC于F,若AD=3BD,求AFDF的值.【答案】(1)∵△ABC与△CDE均为等边三角形,∴BC=AC,CD=CE,∠ACB=∠DCE=60°,∴∠BCD=∠ACE,∴△BCD≌△ACE,∴BD=AE.(2)AE=2BD,理由如下:∵∠BAC=∠DEC=30°,∠B=∠EDC=90°,∴△ABC∽△EDC,∴BC AC CD CE=.由条件得∠ACB=∠DCE,AC=2BC,∴∠BCD=∠ACE,∴△BCD∽△ACE,∴12BD BCAE AC==,∴AE=2BD.(3)由(2)得,△BCD∽△ACE,∴AE ACBD BC=,∵43DE ABCD BC==,∴53ACBC=,∴53AE ACBD BC==设BD=a,则AD=3BD=3a,AB=4a,BC=3a,CDa,AE=53BD=53a.∵△AFE∽△DFC ,∴53aAF AEDF CD=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29.勤学早九年级数学(下)第27章《相似》单元检测题(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)一、选择题(每小题3分,共30分)1.(教材变式·9下P25习题1改)将等边三角形的三边各扩大2倍后得到的三角形是( A ) A .等边三角形 B .锐角三角形C .直角三角形D .钝角三角形2.在△ABC 和△A ′B ′C ′中,∠A =68°,∠B =40°,∠A ′=68°,∠C ′=72°,那么这两个三角形( B ) A .不相似 B .相似 C .全等 D .无法确定3.(2015蚌埠)如图,△ABC 中,DE ∥BC ,AD =5,BD =10,AE =3,则CE 的长为( B ) A .9 B .6 C .3D .4B EDA4.图中的两个三角形是位似图形,则它们的位似中心是( A ) A .点PB .点QC .点RD .点S5.(2015潍纺改)如图,点D 在△ABC 的边AC 上,要使△ADB 与△ABC 相似,添加一个条件,错误..的是( C ) A .∠ABD =∠C B .∠ADB =∠ABCC .AB CB BD CD = D .AD ABAB AC=C ABD6.(2015枣庄)如图,□ABCD 中,点N 是AB 上一点,且BN =2AN ,AC 、DN 相交于点M ,则AM :MC 的值是( B )A .3:11B .1:3C .1:9D .3:10ADCBMN7.△ABC 中,∠ACB =90°,将△ABC 按如图的位置放在直角坐标系中,若点A 的坐标为(0,2),点C 的坐标为(1,0),点B 的横坐标为4,则点B 的纵坐标为( C ) A .1B .C .D .8.如图,△ABC 中,∠C =90°,以AB 上一点O 为圆心作⊙O ,分别切AC 、BC 于E 、D ,AC =8,BC =6,则⊙O 的半径长为( B )A .5B .247C . D.127AB9.直线1l ∥2l ∥3l ,且1l 与2l 的距离为1, 2l 与3l 的距离为3,把一块含有45°角的直角三角形如图放置,顶点A 、B 、C 恰好分别落在三条直线上,AC 与直线2l 交于点D ,则线段BD 的长度为( A )A .254 B .253C .203D .154l 1l 2l 3A CBD10.(2016武汉原创题)如图,等边△ABC 的边长为3,P 为BC 上一点,且BP =1,D 为AC 上一点,DE ⊥AP交AP 于E ,若∠APD =60°,则DEAE=________ (2)二、填空题(每小题3分,共18分)11.如图,请你补充一个条件,使△ABC ∽△ACD ,这个条件是 . (∠ACD =∠B)ABCD12.△ABC 与△DEF 的相似比为3:4,则△ABC 与△DEF 的面积比为 . (9:16)13.在□ABCD 中,E 在DC 上,若DE :EC =1:2,则△CEF 与△ABF 的周长比为 . (2:3)14.(教材变式·9下P42习题5改)如图,△ABC 中,DE ∥FG ∥BC ,AD :DF :FB =1:2:3,若EG =3,则AC = . (9)E FGD A B15.如图,在平面直角坐标系中,△OBA ∽△DOC ,边OA 、OC 都在x 轴的正半轴上,已知B (6,8),∠BAO =∠OCD =90°,OD =5,双曲线y=kx(x >0)经过点D ,则k 的值是 . (12)16.如图,在平面直角坐标系中,等边△ABC 的顶点B 、C 的坐标分别为(1,0),(3,0),过坐标原点O 的一条直线分别与AB 、AC交于点M 、N ,若OM =MN ,则点M 的坐标为________ (4,4)三、解答题(共8小题,共72分)17.(本题8分)如图,点D 、E 在BC 上,且FD ∥AB ,FE ∥AC ,求证:△ABC ∽△FDE .ADFEC解:∵FD ∥AB ,∴∠B =∠FDE ,又∵FE ∥AC ,∴∠C =∠FED , ∴△ABC ∽△FDE18.(本题8分))如图,A 、B 两点被池塘隔开,在AB 外取一点C ,连接AC ,BC ,在AC 上取点M ,使AM =3MC ,作MN ∥AB 交BC 于N ,量得MN =38m ,求AB 的长.解:AB =152m19.(本题8分)如图,△ABC 中,D 、E 分别是边BC 、AB 的中点,AD ,CE 相交于G .求证:12GE GD GC GA == ABEG解:连ED ,则ED ∥AC ,且ED =12AC ,证△DEG ∽△ACG20.(本题8分)如图,每个小方格都是边长为1个单位的小正方形,A 、B 、C 三点都是格点(每个小方格的顶点叫格点),其中A (1,8),B (3,8),C (4,7).(1)若D (2,3),请在网格图中画出一个格点△DEF ,使△DEF ∽△ABC ,且相似比为2:1;(2)填空:DF 的长是_________.x解:(1)略; (2)DF =21.(本题8分)如图,等边△ABC 的边长是6,点E 、F 分别在AC 、BC 边上,AE =CF ,连接AF 、BE 相交于点P .(1)求∠APB 的度数;(2)若AE =2,求BP ·BE 的值.A B CEPF 解:(1)易证△ABE ≌△CAF ,易求∠APB =120°(2)证△BPF ∽△BCE ,∴BP ·BE =BF ·BC =4×6=2422.(本题10分)(2015黄冈改)如图,△ABC 中,AB =AC ,以AC 为直径的⊙O 交AB 于点M ,交BC 于点N ,连接AN ,过点C 的切线交AB 的延长线于点P .(1)求证:∠BCP =12∠BAC ; (2)若34BP BC ,求ANPC的值. AC解:(1)∵AC 为⊙O 直径,∴∠ANC =90°,∵AB =AC ,∴∠BAN =∠CAN ,∵∠BCP +∠ACB =∠CAN +∠ACB =90°. ∴∠BCP =∠CAN =12∠BAC (2)连MN ,则∠BMN =∠ACB =∠ABC ,∴∠AMN =∠PBC ,又∠BCP =∠BAN ,∴△AMN ∽△CBP,∴AN PC =MN BP ,易证MN =BN =CN ,∴AN PC =12BCBP=12·43=2323.(本题10分)如图,矩形ABCD 中,AB =6,AD =8,动点P 从点D 出发,以每秒5个单位的速度向点B匀速运动,同时动点Q 从点A 出发,以每秒4个单位的速度向点D 匀速运动,运动的时间为t 秒(0<t <2).(1)如图1,连接CQ ,当t 为何值时CQ =BC ; (2)如图2,连接AP 、BQ ,若BQ ⊥AP ,求t 的值.B C DAQBCDAQP图1 图2解:(1)∵AQ=4t ,AD=8,∴DQ=8-4t ,又∵AB=6,∴由勾股定理得CQCQ =BC 8,解得t =2; (2)过点P 作PE ⊥AD ,垂足哦日E ,∴AB ∥PE ,∴DE DA =PE AB =DP DB ,∴8DE =6PE =510t, ∴DE =4t ,EP =3t ,∴EP =3t ,∴AE =8-4t ,∵∠ABQ +∠BAP =90°,∠EAP +∠BAP =90°, ∴∠ABQ =∠EAP ,∵∠BAQ =∠AEP ,∴△BAQ ∽△AEP ,∴BA AE =AQ PE ,即684t -=43tt, 解得t =7824.(本题12分)(2016武汉改编题)已知点P (m ,n )是抛物线y=14-2x -2上的一个动点,点A 的坐标为(0,-3).【特别探究】(1)如图1,直线l 过点Q (0,-1)且平行于x 轴,过P 点作PB ⊥l ,垂足为B ,连接PA ; ①当m =0时,PA =_________,PB =_________; ②当m =2时,PA =_________,PB =_________;【猜想验证】(2)对于m 取任意一实数,猜想PA 与PB 的大小关系,并证明你的猜想; 【拓展应用】(3)请利用(2)的结论解决下列问题:若过动点P 和点Q (0,-1)的直线交抛物线于另一点D ,且PA =4AD ,求直线PQ 的解析式(图2为备用图).解:(1)①1,1 ②2,2(2)PA 与PB 相等,理由如下:设P (m ,14-2m -2),则B (m ,-1), ∵PA 142m +1,PB=-1-(14-2m -2)=142m+1,∴PA=PB;(3)过点Q(0,-1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(2)得PB=PA,DE=DA,∵PA=4AD,∴PB=4DE,∵DE∥PB,∴△QDE∽△QPB,QEQB=DEPB=14, 设P(m,142m-2),则B(m,-1),PB=142m+1,∴E点坐标为(14m,-1),D点坐标为[14m,-14(14m)2-2],∴ED=-1+14(14m)2+2=1642m+1,∴142m+1=4(1642m+1),解得m1=4,m2=-4,∴P点坐标为(4,-6)或(-4,-6);当P点坐标为(4,-6)时,直线PQ的解析式为y=-54x-1;当点P坐标为(-4,-6)时,直线PQ的解析式为y=54x-1,即PO的解析式为y=-54x-1或y=54x-1。
